Abstract
A theoretical study of resonant vibrational excitation, dissociative recombination and dissociative excitation processes of the beryllium monohydride cation, BeH+, induced by electron impact, is reported. Full sets of ro-vibrationally-resolved cross sections and of the corresponding Maxwellian rate coefficients are presented for the three processes. Particular emphasis is given to the high-energy behaviour. Potential curves of  ,
,  and
and  symmetries and the corresponding resonance widths, obtained from R-matrix calculations, provide the input for calculations which use a local complex-potential model for resonant collisions in each of the three symmetries. Rotational motion of nuclei and isotopic effects are also discussed. The relevant results are compared with those obtained using a multichannel quantum defect theory method. Full results are available from the Phys4Entry database.
symmetries and the corresponding resonance widths, obtained from R-matrix calculations, provide the input for calculations which use a local complex-potential model for resonant collisions in each of the three symmetries. Rotational motion of nuclei and isotopic effects are also discussed. The relevant results are compared with those obtained using a multichannel quantum defect theory method. Full results are available from the Phys4Entry database.
Export citation and abstract BibTeX RIS
1. Introduction
Because of its low core-plasma radiation losses, high oxygen gathering capability and reduced erosion and migration (relative to other plasma facing materials), beryllium has been chosen as a first wall material in the main chamber of the International Thermonuclear Fusion Reactor (ITER) [1, 2]. The interaction of a hydrogen fusion plasma with the Be reactor walls will result in release of both atomic Be and Be hydrides (BeH, BeH2) into the bulk. The experiments with deuterium plasma–Be–wall interaction, performed in the linear divertor plasma simulator PISCES-B [3–5], have indeed demonstrated copious production of BeD molecules reaching 80% of the total Be release at plasma ion impact energies of ∼10 eV and 40% at 70–90 eV ion energies [5]. In a recent experiment on JET (with Be first wall and tungsten divertor) the BeD fraction was found to be about 33% of the total Be release at the ion impact energy of 75 eV [6]. The molecular-dynamics simulations [5, 7] confirm these experimental findings and predict even a higher fraction of BeD molecules in the total beryllium erosion. This indicates that the chemistry in low-temperature edge regions ( eV) of a hydrogen plasma interacting with a beryllium wall, will be dominated by the processes of beryllium hydride BeH (and its ionization and dissociation products) with the basic plasma constituents.
eV) of a hydrogen plasma interacting with a beryllium wall, will be dominated by the processes of beryllium hydride BeH (and its ionization and dissociation products) with the basic plasma constituents.
Collision processes with BeH and BeH+ with electrons, as well as their reactions with H and H+, are therefore of great importance for transport modelling studies of beryllium in edge plasmas and for the molecular diagnostics of these plasmas based on the BeH and BeH+ radiation. Unfortunately, due to the high toxicity of beryllium, no measurements on electron scattering process with BeH+ are available in literature and the required cross section information for these processes are very scarce. Thus, calculations seem to be the only way to obtain these data. For the BeH+ ion the collision processes studied so far are the electron-impact electronic excitation [8] and the dissociative recombination [9–14]. In particular, we note that only a few studies considered vibrationally-excited BeH+ ions [8, 12–14].
In the present paper, we study the state-resolved electron-impact vibrational excitation (VE), dissociative recombination (DR) and dissociative excitation (DE) processes of vibrationally excited BeH+ ion in its ground electronic state proceeding through the resonant states of excited BeH molecule:
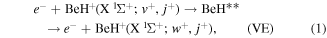
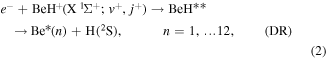
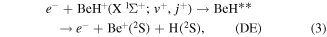
where  and
and  refer to the ro-vibrational levels of BeH+. Processes (1)–(3) are described by the local complex potential model of resonant scattering theory [10, 15]. The resonant states BeH** have been characterised using the molecular R-matrix method [16]. The cross sections of the above processes, for a number of initial ro-vibrational states
refer to the ro-vibrational levels of BeH+. Processes (1)–(3) are described by the local complex potential model of resonant scattering theory [10, 15]. The resonant states BeH** have been characterised using the molecular R-matrix method [16]. The cross sections of the above processes, for a number of initial ro-vibrational states  (and final
(and final  states in VE) are calculated in the energy range from threshold to 10 eV. The local complex potential results are compared with the results of multichannel quantum defect theory (MQDT) [10, 12–14, 17–21].
states in VE) are calculated in the energy range from threshold to 10 eV. The local complex potential results are compared with the results of multichannel quantum defect theory (MQDT) [10, 12–14, 17–21].
The article is organized as follows: in section 2 we describe our molecular structure calculations for the BeH+ ion and resonant states of BeH. In section 3 we briefly outline the local complex potential model of resonant scattering theory and we present the results of our cross sections and reaction rate coefficients for  . In sections 4 and 5 the influence of rotational motion of nuclei and the isotopic effects on the cross sections, are respectively discussed. Finally, in section 6 we give our conclusions.
. In sections 4 and 5 the influence of rotational motion of nuclei and the isotopic effects on the cross sections, are respectively discussed. Finally, in section 6 we give our conclusions.
2. Potential energy curves (PECs)
PECs for the ground electronic state  and the first excited electronic state
and the first excited electronic state  of BeH+ were calculated by using the ab-initio quantum chemistry code MOLPRO [22]. In this section and in the next one we will refer to rotationaless results for
of BeH+ were calculated by using the ab-initio quantum chemistry code MOLPRO [22]. In this section and in the next one we will refer to rotationaless results for  . We leave the discussion of the rotational effects in the section 4. The calculation used internally-contracted multi-reference configuration interaction (CI) level of theory with a cc-pVTZ basis set and were performed in C2v symmetry. These calculations kept the
. We leave the discussion of the rotational effects in the section 4. The calculation used internally-contracted multi-reference configuration interaction (CI) level of theory with a cc-pVTZ basis set and were performed in C2v symmetry. These calculations kept the  orbital frozen and used 9 active orbitals,
orbital frozen and used 9 active orbitals,  , and 34 external orbitals
, and 34 external orbitals  , for a total of 44 contractions. The calculations covered 30 internuclear distances between
, for a total of 44 contractions. The calculations covered 30 internuclear distances between  and
and  .
.
The ab-initio R-matrix method [16, 23] was used to determine the positions and widths of BeH resonant states in the electron-BeH+ scattering, as a function of the internuclear distance. An initial CI calculation was first performed at the BeH+ equilibrium bond length  using the Slater-type orbital (STO) basis set of Bagus et al [24]. The basis set contained 5 s-type, 4 p-type, 2 d-type and 1 f-type STOs centred on the Be atom and 3 s-type, 1 p-type and 1 d-type STOs centred on the H atom respectively. A set of molecular orbitals containing 17 σ, 9 π, 4 δ and 1 ϕ were then built using the STOs. Subsequently, a self-consistent field calculation was performed for the lowest BeH+ states using these molecular orbitals. Finally, 17 σ, 9 π and 4 δ were used in a CI calculation using a
using the Slater-type orbital (STO) basis set of Bagus et al [24]. The basis set contained 5 s-type, 4 p-type, 2 d-type and 1 f-type STOs centred on the Be atom and 3 s-type, 1 p-type and 1 d-type STOs centred on the H atom respectively. A set of molecular orbitals containing 17 σ, 9 π, 4 δ and 1 ϕ were then built using the STOs. Subsequently, a self-consistent field calculation was performed for the lowest BeH+ states using these molecular orbitals. Finally, 17 σ, 9 π and 4 δ were used in a CI calculation using a  complete active space (CAS) target model as it gave good agreement of the vertical excitation energies for the target at the equilibrium bond length. Calculations were then repeated for 55 internuclear distances, from
complete active space (CAS) target model as it gave good agreement of the vertical excitation energies for the target at the equilibrium bond length. Calculations were then repeated for 55 internuclear distances, from  to
to  , to yield the BeH+ target PECs. To get the bound states, an inner region calculation was first made with the CAS target model mentioned above, supplemented by continuum orbitals obtained from a truncated partial wave expansion about the molecular centre of mass. The inner region solutions were then used to construct an R-matrix at the boundary. The R-matrix was propagated to
, to yield the BeH+ target PECs. To get the bound states, an inner region calculation was first made with the CAS target model mentioned above, supplemented by continuum orbitals obtained from a truncated partial wave expansion about the molecular centre of mass. The inner region solutions were then used to construct an R-matrix at the boundary. The R-matrix was propagated to  in the outer region where, in addition to the Coulomb potential, the diagonal and off diagonal dipole and quadrupole moments of the BeH+ target states were included. Bound states were then found using the searching algorithm of Sarpal et al [25]. For the resonant states, the R-matrix was propagated to
in the outer region where, in addition to the Coulomb potential, the diagonal and off diagonal dipole and quadrupole moments of the BeH+ target states were included. Bound states were then found using the searching algorithm of Sarpal et al [25]. For the resonant states, the R-matrix was propagated to  and was matched to asymptotic Coulomb functions obtained using a Gailitis expansion [26]. Resonances were detected and fitted to a Breit–Wigner profile to obtain their positions and widths. Calculations were repeated for 55 internuclear distances in the range
and was matched to asymptotic Coulomb functions obtained using a Gailitis expansion [26]. Resonances were detected and fitted to a Breit–Wigner profile to obtain their positions and widths. Calculations were repeated for 55 internuclear distances in the range  –
– to obtain the BeH bound state PECs, resonance curves and resonance widths as a function of the internuclear distance. The full details can be found in [9, 27].
to obtain the BeH bound state PECs, resonance curves and resonance widths as a function of the internuclear distance. The full details can be found in [9, 27].
A total of 12 resonant states in  (5 states),
(5 states),  (5 states) and
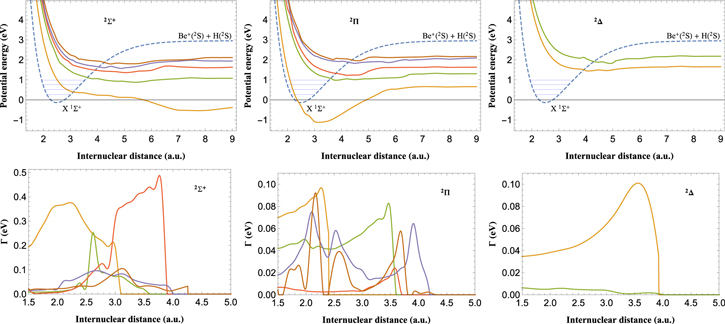
(5 states) and  (2 states) symmetries were considered. The final PECs and widths are summarized in figure 1 for BeH+ and BeH
(2 states) symmetries were considered. The final PECs and widths are summarized in figure 1 for BeH+ and BeH resonant states where a splining procedure was applied to the calculated points. Table 1 contains the list of vibrational levels of BeH+ with dissociation energies.
resonant states where a splining procedure was applied to the calculated points. Table 1 contains the list of vibrational levels of BeH+ with dissociation energies.
Figure 1. Potential energy curves (top line) and widths (bottom line) for BeH resonant states in
resonant states in  ,
,  and
and  scattering channels for
scattering channels for  . Dashed line refers to potential energy curve for BeH+ ground electronic state where the first vibrational levels are marked.
. Dashed line refers to potential energy curve for BeH+ ground electronic state where the first vibrational levels are marked.
Download figure:
Standard image High-resolution imageTable 1.
Energies of ground electronic state of BeH+ vibrational levels for  . Dissociation energies are De = 3.085 eV and
. Dissociation energies are De = 3.085 eV and  .
.
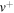
|
 (eV) (eV) |
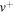
|
 (eV) (eV) |
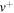
|
 (eV) (eV) |
|---|---|---|---|---|---|
| 0 | 0.000 | 7 | 1.613 | 14 | 2.670 |
| 1 | 0.261 | 8 | 1.801 | 15 | 2.765 |
| 2 | 0.513 | 9 | 1.977 | 16 | 2.844 |
| 3 | 0.755 | 10 | 2.142 | 17 | 2.906 |
| 4 | 0.985 | 11 | 2.294 | 18 | 2.942 |
| 5 | 1.204 | 12 | 2.433 | ||
| 6 | 1.414 | 13 | 2.560 |
Calculations for the BeH molecular symmetries were performed in [10], by using the Kohn method to get potential curves and autoionization widths for resonant states. Comparison of the two methods is widely discussed in [27]. We only mention here that an evident difference in BeH resonant states is represented by the appearance in R-matrix calculations of an extra  curve attributable to a larger CAS and target basis. However, discrepancy between the two methods arise also for the potentials of Σ and Π symmetries which, as discussed later in section 3.2, can generate different behaviour in the cross sections for dissociative recombination.
curve attributable to a larger CAS and target basis. However, discrepancy between the two methods arise also for the potentials of Σ and Π symmetries which, as discussed later in section 3.2, can generate different behaviour in the cross sections for dissociative recombination.
3. Cross sections
Bardsley's local potential complex approach [15] was adopted to describe the resonant electron–BeH collisions. In this section, we limit ourself just to the basic equations of model, while the complete treatment is given elsewhere [28–30]. For the processes in (1)–(3), occurring through the rth resonant state of BeH
collisions. In this section, we limit ourself just to the basic equations of model, while the complete treatment is given elsewhere [28–30]. For the processes in (1)–(3), occurring through the rth resonant state of BeH and with electron energy
and with electron energy  , the resonant nuclear wave function, represented by
, the resonant nuclear wave function, represented by  , is calculated from the following equation:
, is calculated from the following equation:
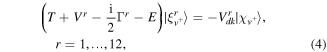
where T is the nuclear kinetic operator,  is the rth resonant complex potential and
is the rth resonant complex potential and  is the total energy of the process.
is the total energy of the process.  is the continuum-discrete coupling and
is the continuum-discrete coupling and  is the initial wave function of the BeH+ corresponding to the vibrational level
is the initial wave function of the BeH+ corresponding to the vibrational level  . Once the resonant nuclear wave function is known, the corresponding cross sections for a specific process can be calculated according to the formulae reported in the next subsections. As the resonant states have different symmetries, in the following the couplings between resonances are neglected and the total cross section is given by the coherent sum over the 12 resonant contributions. For the DR where each contribution will be given for
. Once the resonant nuclear wave function is known, the corresponding cross sections for a specific process can be calculated according to the formulae reported in the next subsections. As the resonant states have different symmetries, in the following the couplings between resonances are neglected and the total cross section is given by the coherent sum over the 12 resonant contributions. For the DR where each contribution will be given for  .
.
Maxwellian rate coefficients for the three resonant processes in (1)–(3) have been calculated according to the following formula,
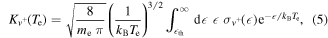
where  is the threshold energy,
is the threshold energy,  is the global cross section summed over all the resonant states for the considered scattering process starting from the initial vibrational levels,
is the global cross section summed over all the resonant states for the considered scattering process starting from the initial vibrational levels,  , of the BeH+. Te is the electron temperature. me is the electron mass and kB the Boltzmann constant.
, of the BeH+. Te is the electron temperature. me is the electron mass and kB the Boltzmann constant.
The cross section data have been calculated with an accuracy up to the third digit.
3.1. Vibrational excitation
VE partial cross sections for process (1) occurring through the rth resonant state and as a function of the electron energy  is given by [31]:
is given by [31]:

where k is the incoming electron momentum and  is the vibrational wave function of the BeH+ molecular ion in the final vibrational level
is the vibrational wave function of the BeH+ molecular ion in the final vibrational level  . The total cross section is given by the sum over the partial cross sections. The spin-statistic factors are
. The total cross section is given by the sum over the partial cross sections. The spin-statistic factors are  , for
, for  ,
,  and
and  symmetries respectively.
symmetries respectively.
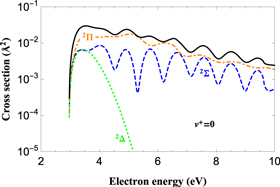
Figure 2 shows the results for the  transition and for total and single contributions coming from the
transition and for total and single contributions coming from the  ,
,  and
and  scattering channels. Strong oscillations are found in the
scattering channels. Strong oscillations are found in the  cross sections close to the threshold energy. These can be attributed to the quasi-bound vibrational levels of the lowest resonant electronic state of
cross sections close to the threshold energy. These can be attributed to the quasi-bound vibrational levels of the lowest resonant electronic state of  symmetry. According to figure 1 (central panel), in fact, this state is characterized by a potential well whose minimum is placed below that of the
symmetry. According to figure 1 (central panel), in fact, this state is characterized by a potential well whose minimum is placed below that of the  ground state of BeH+ ion. This implies that the incident electron can be captured also at very low energy so that the system can transit, near the threshold, to the resonant vibrational levels of the
ground state of BeH+ ion. This implies that the incident electron can be captured also at very low energy so that the system can transit, near the threshold, to the resonant vibrational levels of the  state of the BeH** molecule. These threshold oscillations have also been observed for other systems such as electron scattering from O2 molecule [29]. Small features also appear just above 1 eV, probably due to vibrational levels belonging to the next two resonant electronic states and falling in the Franck–Condon (FC) region of the
state of the BeH** molecule. These threshold oscillations have also been observed for other systems such as electron scattering from O2 molecule [29]. Small features also appear just above 1 eV, probably due to vibrational levels belonging to the next two resonant electronic states and falling in the Franck–Condon (FC) region of the  ground state. At the larger energies, regular and wide oscillations characterize the cross sections, attributable to the FC overlap among the target vibrational wave functions with the vibrational continuum of all the resonant potential curves for the
ground state. At the larger energies, regular and wide oscillations characterize the cross sections, attributable to the FC overlap among the target vibrational wave functions with the vibrational continuum of all the resonant potential curves for the  symmetry [28]. The same interpretation applies to the regular oscillations also seen in the cross section for the
symmetry [28]. The same interpretation applies to the regular oscillations also seen in the cross section for the  symmetry at all energies. The resonant potential curves for this case, shown in figure 1 (left panel), do not support any bound vibrational levels inside the FC region. The resonant potential curves of figure 1 (right panel) also explain the behaviour of the
symmetry at all energies. The resonant potential curves for this case, shown in figure 1 (left panel), do not support any bound vibrational levels inside the FC region. The resonant potential curves of figure 1 (right panel) also explain the behaviour of the  cross sections. The two resonant Δ states, also of repulsive nature, enter the FC region at an energy about 2 eV, where we may expect the largest overlap in the FC densities. This explains the maximum in the corresponding cross sections shown in figure 2 which are found at the same incident energy. Finally, the total cross sections in the same figure (black curve) follow closely the largest contribution represented by the
cross sections. The two resonant Δ states, also of repulsive nature, enter the FC region at an energy about 2 eV, where we may expect the largest overlap in the FC densities. This explains the maximum in the corresponding cross sections shown in figure 2 which are found at the same incident energy. Finally, the total cross sections in the same figure (black curve) follow closely the largest contribution represented by the  cross section, except in the region around 1–3 eV where that of the
cross section, except in the region around 1–3 eV where that of the  symmetry prevails.
symmetry prevails.
Figure 2. Cross sections for the  resonant vibrational excitation as a function of the incident electron energy. The panel shows the contributions coming from the
resonant vibrational excitation as a function of the incident electron energy. The panel shows the contributions coming from the  ,
,  and
and  scattering channels (broken curves) as well as the total cross sections (full-black line).
scattering channels (broken curves) as well as the total cross sections (full-black line).
Download figure:
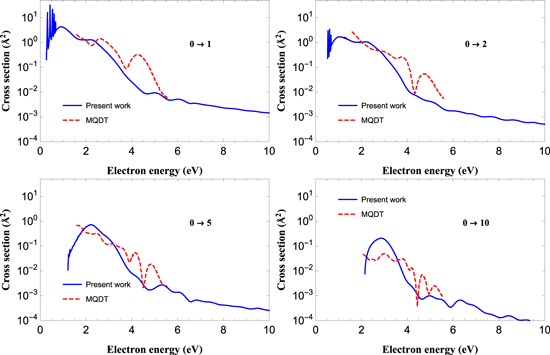
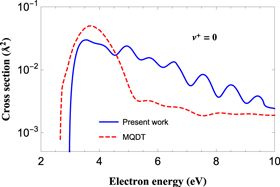
Standard image High-resolution imageFigure 3 shows a comparison between the present total cross sections and the low- and medium-energy results of MQDT method [12]. The data computed with this last method, are obtained using PECs calculated at the MRCI level and the complex-Kohn variational method for potential curves and widths of the same resonant states considered in the present work [10]. The comparison given by figure 3 is quite satisfactory. However, we note that the PECs calculated in [10] give significantly different scattering parameters to the ones used here. The main differences are observed for the  and
and  symmetries. In the first case (see figure 1 in [12]) two potential curves of BeH** molecule, running quite below the BeH+ ground state, are observed, unlike figure 1 of the present work (second panel) where only one bound state is present. For the Δ symmetry, [10, 12] report one curve only, of bound nature and which crosses the ground state close to the energy of
symmetries. In the first case (see figure 1 in [12]) two potential curves of BeH** molecule, running quite below the BeH+ ground state, are observed, unlike figure 1 of the present work (second panel) where only one bound state is present. For the Δ symmetry, [10, 12] report one curve only, of bound nature and which crosses the ground state close to the energy of  level, instead of two repulsive curves, shown in figure 1 (right panel), whose stabilization points are placed at higher energies. We can expect that these different features in the two sets of input data, will lead inevitably to differences in the calculated cross sections. However, these differences are completely negligible from the point of view of the kinetic modelling.
level, instead of two repulsive curves, shown in figure 1 (right panel), whose stabilization points are placed at higher energies. We can expect that these different features in the two sets of input data, will lead inevitably to differences in the calculated cross sections. However, these differences are completely negligible from the point of view of the kinetic modelling.
Figure 3. Vibrational excitation cross sections summed over all the symmetries: present results (full line) compared with MQDT/Kohn calculations [12] (dashed line).
Download figure:
Standard image High-resolution image3.2. Dissociative recombination
For dissociative recombination process in (2) the corresponding partial cross section, through the rth resonant state, is given by [31]:

where K is the asymptotic momentum ( ) of the dissociating fragments Be and H with reduced mass μ and k is the incoming electron momentum.
) of the dissociating fragments Be and H with reduced mass μ and k is the incoming electron momentum.
Partial and total cross sections are shown in figure 4 for  . The threshold of the processes for each symmetry can be guessed by looking at the figure 1. The first panel, in fact, shows that the cross section for
. The threshold of the processes for each symmetry can be guessed by looking at the figure 1. The first panel, in fact, shows that the cross section for  symmetry starts at zero energy, as a matter of the fact the level
symmetry starts at zero energy, as a matter of the fact the level  is above the asymptote of the lowest resonant curve shown in the figure. The cross section for
is above the asymptote of the lowest resonant curve shown in the figure. The cross section for  symmetry start, instead, at the dissociation energy, right above 0.5 eV, of the bound BeH state shown in the second panel of figure 1. For
symmetry start, instead, at the dissociation energy, right above 0.5 eV, of the bound BeH state shown in the second panel of figure 1. For  symmetry, finally, the opening of the first channel occurs at the energy of about 1.5 eV (third panel). This last cross section falls off dramatically for larger energies, with respect to the other two cases where the cross sections curves decrease less rapidly and with an oscillating behaviour. This can be explained if we note that the potential curves of
symmetry, finally, the opening of the first channel occurs at the energy of about 1.5 eV (third panel). This last cross section falls off dramatically for larger energies, with respect to the other two cases where the cross sections curves decrease less rapidly and with an oscillating behaviour. This can be explained if we note that the potential curves of  symmetry enter the FC region at an energy of about 2–3 eV, where the cross section reaches its maximum, then, for higher energies, the potential curves get out of the FC region, so that the cross sections symmetrically decrease. Figure 5 shows comparison between the present results and MQDT calculations for the direct DR process [12] starting from
symmetry enter the FC region at an energy of about 2–3 eV, where the cross section reaches its maximum, then, for higher energies, the potential curves get out of the FC region, so that the cross sections symmetrically decrease. Figure 5 shows comparison between the present results and MQDT calculations for the direct DR process [12] starting from  and
and  vibrational levels. The two sets of data show evident differences in their behaviour at very low energy. Near to threshold the MQDT cross sections show very high cross section values (
vibrational levels. The two sets of data show evident differences in their behaviour at very low energy. Near to threshold the MQDT cross sections show very high cross section values ( ) while the present calculations predict a vanishing trend. This can be explained in terms of the
) while the present calculations predict a vanishing trend. This can be explained in terms of the  contribution to the total cross section which, we may suppose, becomes prevalent at low energies. One of the two potential curves of this symmetry, calculated in [10] (see also figure 1 in [12]) shows, in fact, a repulsive behaviour which can lead to dissociation after the incident electron is captured by the cation. Moreover, because this resonant curve lies below the
contribution to the total cross section which, we may suppose, becomes prevalent at low energies. One of the two potential curves of this symmetry, calculated in [10] (see also figure 1 in [12]) shows, in fact, a repulsive behaviour which can lead to dissociation after the incident electron is captured by the cation. Moreover, because this resonant curve lies below the  target ground state for internuclear distances
target ground state for internuclear distances  , it constitutes an open channel with zero-energy threshold. This is not the case in the present calculations, where all the resonant curves, inclusive those of
, it constitutes an open channel with zero-energy threshold. This is not the case in the present calculations, where all the resonant curves, inclusive those of  symmetry, lie above the lowest vibrational level of BeH+.
symmetry, lie above the lowest vibrational level of BeH+.
Figure 4. Dissociative recombination total cross sections (full black line) and partial contributions in  ,
,  and
and  scattering channels (broken lines) for
scattering channels (broken lines) for  , as a function of the electron energy.
, as a function of the electron energy.
Download figure:
Standard image High-resolution imageFigure 5. Dissociative recombination cross sections: comparison between the present calculations (full line) and MQDT/Kohn results [12] (dashed line).
Download figure:
Standard image High-resolution imageHowever, this is not the only aspect that gives a different threshold behaviour of the two methods. Indeed we have performed calculations (not shown) using both, the R-matrix PECs and the PECs of [10, 12] and again a diverging trend is observed at the threshold, in agreement with the previous discussion. However, the divergence is not as steep as in the case of MQDT results of figure 5, which is expected as discussed above for a zero-threshold process. This suggests that the MQDT model gives a better description of the cross section behaviour at very low energies, compared to the results obtained with R-matrix curves within the local complex-potential model.
For higher energies above ∼2 eV, the present calculations can be compared with the results for  of the [10] (figure 6) and [32] (figure 2), which report the cross sections for DR process obtained by using the wave packet method (WPM) for the description of the nuclear dynamics, and the Kohn method for potential and width calculations. These data, in good agreement with the present MQDT calculations at the threshold (see also figure 7 of [12]), show very rapid decay for energies above 2 eV becoming, at 10 eV, about two orders of magnitude smaller than the present results obtained with the R-matrix curves. We do not have an explanation for such a large discrepancy, which, however, cannot be attributed to the different potential curves used in WPM calculations. In fact, our calculations performed using the Kohn potentials, as explained above, give practically the same results of figure 5 at large energies.
of the [10] (figure 6) and [32] (figure 2), which report the cross sections for DR process obtained by using the wave packet method (WPM) for the description of the nuclear dynamics, and the Kohn method for potential and width calculations. These data, in good agreement with the present MQDT calculations at the threshold (see also figure 7 of [12]), show very rapid decay for energies above 2 eV becoming, at 10 eV, about two orders of magnitude smaller than the present results obtained with the R-matrix curves. We do not have an explanation for such a large discrepancy, which, however, cannot be attributed to the different potential curves used in WPM calculations. In fact, our calculations performed using the Kohn potentials, as explained above, give practically the same results of figure 5 at large energies.
Figure 6. Dissociative excitation total cross section (full black curve) and partial contributions in  ,
,  and
and  scattering channels (broken curves) for
scattering channels (broken curves) for  , as a function of the electron energy.
, as a function of the electron energy.
Download figure:
Standard image High-resolution imageThe above analysis suggests that the MQDT method gives a better description of the scattering process below ∼ 0.1 eV, so that the corresponding cross sections can be recommended in modelling applications, while for energies higher than 4 eV, the present calculation with R-matrix data should be used. In the intermediate energy region of 0.1–4 eV, the two methods substantially agree.
3.3. Dissociative excitation
Analogously to the VE processes, dissociative excitation partial cross section is given by:
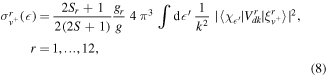
where  is the continuum wave function of BeH+ with energy
is the continuum wave function of BeH+ with energy  representing the free Be+, H and electron. The integration was extended from the threshold, represented by the BeH+ dissociation limit, up to 10 eV.
representing the free Be+, H and electron. The integration was extended from the threshold, represented by the BeH+ dissociation limit, up to 10 eV.
The results for  are shown in figure 6. In this figure, the cross sections start at the common threshold of 2.951 eV, which is the dissociation energy, D0, of the
are shown in figure 6. In this figure, the cross sections start at the common threshold of 2.951 eV, which is the dissociation energy, D0, of the  ground electronic state of the BeH+ (see table 1). The largest contribution, in all the range of the explored energies, comes from
ground electronic state of the BeH+ (see table 1). The largest contribution, in all the range of the explored energies, comes from  symmetry. These cross sections do not suffer pronounced oscillations, as can be instead seen for the
symmetry. These cross sections do not suffer pronounced oscillations, as can be instead seen for the  cross sections, and this is probably due to the fact that the repulsive branch of the lowest resonant state runs parallel and near to that of the
cross sections, and this is probably due to the fact that the repulsive branch of the lowest resonant state runs parallel and near to that of the  cation, so that we may expect that the continuum wave functions of the two states overlap more or less constructively. Finally, a rapid decay is again found for the
cation, so that we may expect that the continuum wave functions of the two states overlap more or less constructively. Finally, a rapid decay is again found for the  symmetry cross sections at higher energies, as in figure 4; this decrease is probably due to the behaviour of the FC densities, as discussed for the DR case.
symmetry cross sections at higher energies, as in figure 4; this decrease is probably due to the behaviour of the FC densities, as discussed for the DR case.
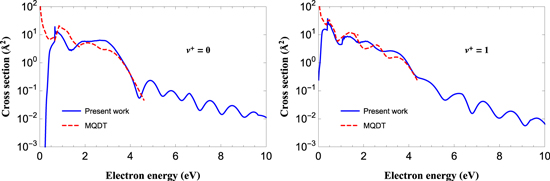
Figure 7 compares the present total dissociative excitation cross sections with the MQDT results [12]. Differences can again be observed, like different thresholds and oscillating structures, still attributable to the different sets of input parameters employed in the two calculations. In the present calculations contribution of direct dissociation is neglected. As shown for the case of electron collision with  [33] non-resonant contribution should be important for dissociation. We will take this effect into account in future investigations.
[33] non-resonant contribution should be important for dissociation. We will take this effect into account in future investigations.
Figure 7. Comparison of total dissociative excitation cross sections (full blue curve) and MQDT/Kohn calculations (broken red curves) for  as a function of the electron energy.
as a function of the electron energy.
Download figure:
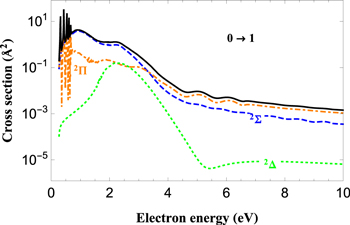
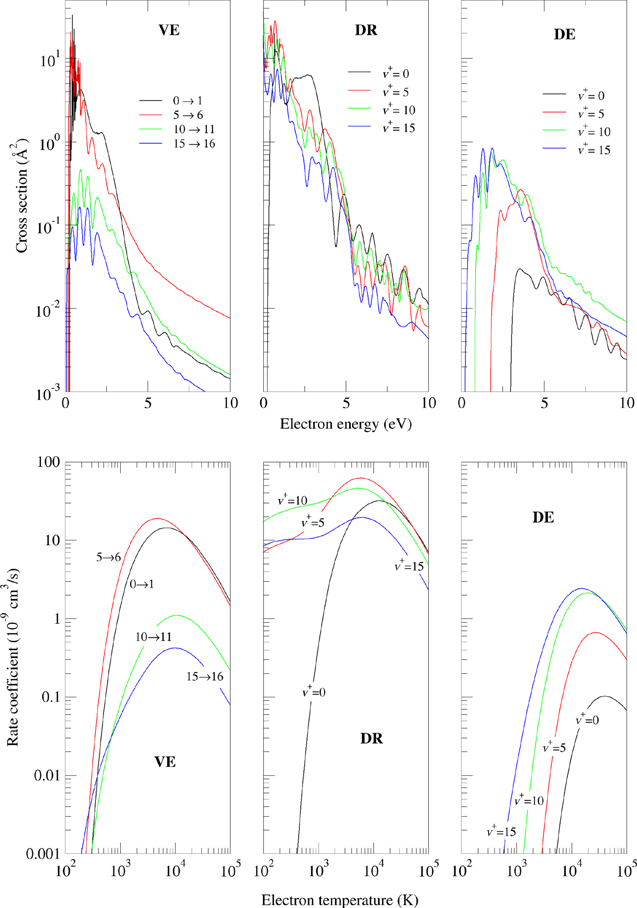
Standard image High-resolution imageTo conclude this section, figure 8 summarizes the recommended results for the global cross sections and the corresponding Maxwellian rate coefficients for  for all three processes discussed in the paper. In particular, in the left panels show the cross sections for one-quantum transitions in the VE process, which play an important role in plasma kinetics due to their quasi-elastic character, while the other two panels show the cross section data for DR and DE processes starting from some selected vibrational level of the target. The largest difference between the present rate calculations and the low-energy MQDT results shown in figure 10 of [12] is observed for the DR process for
for all three processes discussed in the paper. In particular, in the left panels show the cross sections for one-quantum transitions in the VE process, which play an important role in plasma kinetics due to their quasi-elastic character, while the other two panels show the cross section data for DR and DE processes starting from some selected vibrational level of the target. The largest difference between the present rate calculations and the low-energy MQDT results shown in figure 10 of [12] is observed for the DR process for  . In fact, in the range
. In fact, in the range  K the MQDT result displays an increasing trend in the rate constant, caused by the divergent behaviour of the corresponding cross section (see figure 5), in contrast to the rapid drop off of the present results.
K the MQDT result displays an increasing trend in the rate constant, caused by the divergent behaviour of the corresponding cross section (see figure 5), in contrast to the rapid drop off of the present results.
Figure 8. Summary on the global cross sections (top row) and the corresponding rate coefficients (lower row) for  and summed over the resonant states for the three precesses considered in the text. The cross sections are plotted for some selected vibrational excitation (left panel), for dissociative recombination and dissociative excitation (central and right panels) starting from the vibrational levels shown in the figure.
and summed over the resonant states for the three precesses considered in the text. The cross sections are plotted for some selected vibrational excitation (left panel), for dissociative recombination and dissociative excitation (central and right panels) starting from the vibrational levels shown in the figure.
Download figure:
Standard image High-resolution image4. Effect of nuclei rotational motion
In this section, the effects of rotation of the BeH+ target ion on the cross sections is considered. Rotational effects are taken into account in the model by adding the centrifugal term,  , to the PECs of ion and resonant states, where
, to the PECs of ion and resonant states, where  is the BeH+ rotational quantum number. A total of 52 rotational states,
is the BeH+ rotational quantum number. A total of 52 rotational states,  , are found before the BeH+ potential become completely dissociative. Table 2 reports the number of rotational states compatible with each of the vibrational levels listed in table 1.
, are found before the BeH+ potential become completely dissociative. Table 2 reports the number of rotational states compatible with each of the vibrational levels listed in table 1.
Table 2. Number of rotational states supported by each vibrational level of BeH+.
|
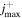
|
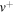
|
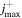
|
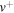
|
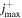
|
|---|---|---|---|---|---|
| 0 | 51 | 7 | 39 | 14 | 21 |
| 1 | 50 | 8 | 37 | 15 | 18 |
| 2 | 49 | 9 | 35 | 16 | 14 |
| 3 | 47 | 10 | 32 | 17 | 10 |
| 4 | 45 | 11 | 30 | 18 | 3 |
| 5 | 43 | 12 | 27 | ||
| 6 | 41 | 13 | 24 |
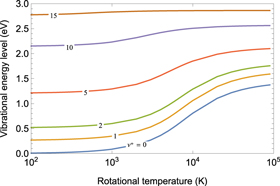
By assuming a Boltzmann distribution for the rotational levels at temperature Tr, the j-averaged energy of vibrational level  can be computed as:
can be computed as:
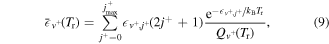
where  is the energy of ro-vibrational level
is the energy of ro-vibrational level  and
and  is the partition function of the system. The behaviour of the rotationally-averaged energy for some vibrational levels as a functions of rotational temperature Tr is shown in figure 9. Analogously, the j-averaged cross section as a function of the rotational temperature is given by:
is the partition function of the system. The behaviour of the rotationally-averaged energy for some vibrational levels as a functions of rotational temperature Tr is shown in figure 9. Analogously, the j-averaged cross section as a function of the rotational temperature is given by:
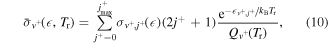
where  represents a generic ro-vibrational specific cross section for the processes in (1)–(3).
represents a generic ro-vibrational specific cross section for the processes in (1)–(3).
Figure 9. Effect of rotational temperature on j-averaged vibrational levels of BeH+.
Download figure:
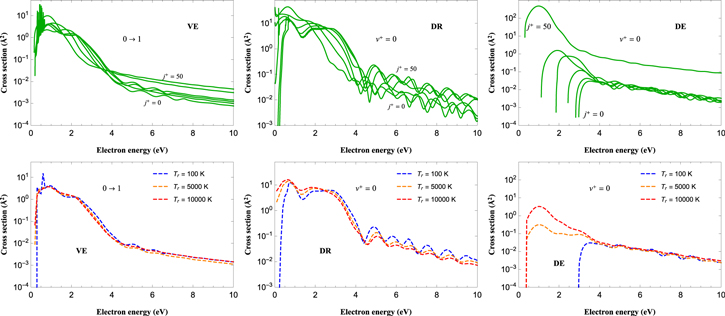
Standard image High-resolution imageFigure 10 summarizes the effects of rotation on the cross sections for the three processes VE, DR and DE. The left-hand side of the figure shows the ro-vibrational specific cross sections and the right-hand side shows the cross sections thermal-averaged over rotational motion. Due to the huge number of resonant states, the cross sections do not show strong dependence on rotational quantum number. Large differences are observed, for rotation-dependent cross sections, at energies above 2 eV for VE and DR processes and a threshold effect for DE process. There are no marked effect on the results for thermally-averaged cross sections (right panels) far from the thresholds.
Figure 10. Summary on rotational effects on the cross section of the three processes considered in the text for BeH+. On the top row: the cross sections for rotational quantum numbers  (solid lines); on the bottom row: the j-averaged cross sections (dashed lines), for different rotational temperatures as shown in the panels.
(solid lines); on the bottom row: the j-averaged cross sections (dashed lines), for different rotational temperatures as shown in the panels.
Download figure:
Standard image High-resolution image5. Isotopic effects
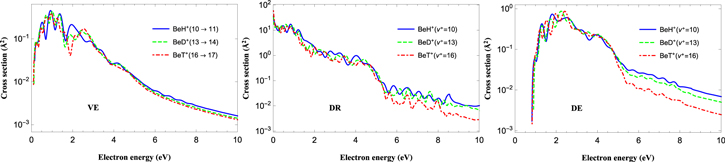
Before closing this paper, an other question regarding the BeH+ isotopic species must be addressed. As in the actual reactor machines, in fact, deuterium is currently the working gas and in the future ITER tokamak both deuterium and tritium are expected to be routinely employed. Therefore, electron-molecule collision studies should include the isotopic variants of the BeH+ molecular species. This deserves careful extensive further calculations. Here we display preliminary results only, coming from the extension of our calculations to some cases involving BeD+ and BeT+ and figure 11 shows a comparison of VE, DR and DE cross sections for the three molecular isotopes. It should be noted that the curves are calculated for different initial vibrational levels corresponding, however, to about the same energy eigenvalue (see table 3). The three curves exhibit similar behaviour as well as close values for all the three cases. This is an expected result, already found in literature in other situations [34]. In fact, due to the different energy spacing of the vibrational manifold in the three molecular ions, levels with about the same energy are identified by different quantum numbers, but the FC vertical energies, involved in a given resonant process, are then almost the same for all the three isotopes.
Figure 11. Cross section comparison for the VE, DR and DE resonant processes involving the three molecular isotopes initially in a  vibrational level as shown in the panels and for j = 0.
vibrational level as shown in the panels and for j = 0.
Download figure:
Standard image High-resolution imageTable 3. Energy (eV) of vibrational levels for three isotopes with respect to the bottom of BeH+ potential energy curve for j = 0. The present results are in good agreement with the experimental data of [35].
|
BeH+ | BeD+ | BeT+ |
|---|---|---|---|
| 0 | 0.134 | 0.100 | 0.085 |
| 1 | 0.396 | 0.296 | 0.253 |
| 2 | 0.648 | 0.486 | 0.417 |
| 3 | 0.890 | 0.672 | 0.577 |
| 4 | 1.121 | 0.852 | 0.734 |
| 5 | 1.340 | 1.026 | 0.886 |
| 6 | 1.549 | 1.193 | 1.034 |
| 7 | 1.748 | 1.354 | 1.176 |
| 8 | 1.937 | 1.510 | 1.315 |
| 9 | 2.113 | 1.660 | 1.449 |
| 10 | 2.278 | 1.805 | 1.580 |
| 11 | 2.430 | 1.943 | 1.706 |
| 12 | 2.569 | 2.075 | 1.828 |
| 13 | 2.695 | 2.200 | 1.946 |
| 14 | 2.807 | 2.319 | 2.059 |
| 15 | 2.903 | 2.431 | 2.167 |
| 16 | 2.981 | 2.535 | 2.270 |
| 17 | 3.041 | 2.633 | 2.368 |
| 18 | 3.077 | 2.722 | 2.462 |
| 19 | 2.804 | 2.549 | |
| 20 | 2.877 | 2.632 | |
| 21 | 2.941 | 2.709 | |
| 22 | 2.995 | 2.780 | |
| 23 | 3.038 | 2.846 | |
| 24 | 3.068 | 2.904 | |
| 25 | 2.956 | ||
| 26 | 3.000 | ||
| 27 | 3.037 | ||
| 28 | 3.064 |
6. Conclusions
In conclusion, in the present paper we discussed the theoretical cross sections and corresponding Maxwellian rate coefficients for resonant electron collision processes involving ro-vibrationally excited BeH+ ion and its isotopes. In particular, we considered VE, dissociative recombination and dissociative excitation processes at energies of interest for kinetics modelling in thermo-nuclear fusion simulations. The potential curves, required for the cross section calculation, were computed using the chemistry code MOLPRO for the  electronic state of BeH+ molecular ion, which was found to support 19 vibrational levels in the ground rotational state. The UK molecular R-matrix code was employed to determine the resonant states of BeH** neutral molecule along with the corresponding widths. Twelve resonant states of
electronic state of BeH+ molecular ion, which was found to support 19 vibrational levels in the ground rotational state. The UK molecular R-matrix code was employed to determine the resonant states of BeH** neutral molecule along with the corresponding widths. Twelve resonant states of  ,
,  and
and  symmetry are considered in the calculations.
symmetry are considered in the calculations.
The resonant collision cross section were evaluated by using the local optical potential model to describe the nuclear dynamics. The results were compared with those obtained by using the MQDT method employing the resonant potential curves and widths obtained, in previous calculations, by the Kohn variational method. The comparison with the present results shows some disagreement, which can partly be attributed to different sets of input data used in the two calculations. Finally, the effect of the rotational motion of nuclei and the isotopic effect were discussed. For the three processes studied, we found the computed cross sections depend weakly on the rotational state of BeH+.
The full set of cross sections data and rate coefficients obtained in this work are available at the Phys4Entry database [36].
Acknowledgments
This work received funding from the project 'Apulia Space', PON 03PE-00067.6 from DTA Brindisi (Italy). We acknowledge the French LabEx EMC3, via the projects PicoLIBS (No. ANR-12-BS05-0011-01) and EMoPlaF-Attractivité, the BIOENGINE project (sponsored by the European fund FEDER and the French CPER), the Fédération de Recherche Fusion par Confinement Magnétique - ITER, the ANR-project HYDRIDES, the CNRS/INSU-program PCMI and the European COST Program CM1401 (Our Astrochemical History). VL would like to thank the Politecnico di Bari-DICATECh (Italy) for the kind hospitality during the preparation of the present article.