Monte Carlo calculation of monoenergetic and polyenergetic DgN coefficients for mean glandular dose estimates in mammography using a homogeneous breast model

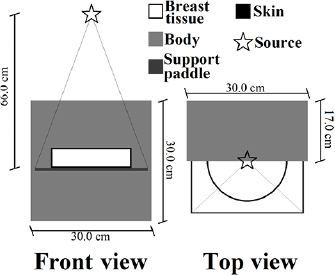
The breast was modelled as a cylinder with a semi-circular cross section with a radius of 10 cm (Sarno et al 2016b). It was made of a homogeneous mixture of adipose and glandular tissue surrounded by a layer simulating the skin. Breast tissue and skin composition were those proposed by Hammerstein et al (1979) as reported in Boone (1999). The skin thickness was 1.45 mm, as shown in the most recent literature (Huang et al 2008, Shi et al 2013). Figure 1 shows the irradiation geometry adopted in this work.

Zoom In Zoom Out Reset image size

The breast compressed thickness (skin included) ranged between 3 cm and 8 cm with 1 cm steps, and the modelled breasts presented a glandular fraction by mass of 0.1%, 14.3%, 25.0%, 50.0%, 75.0% and 100.0%. The patient body was modelled as a box of water of size 30  ×  30  ×  17 cm³. In order to take into account the backscatter radiation from the breast support, this was modelled as a 0.2 cm thick PMMA plate (26  ×  14 cm²) as used in Sechopoulos et al (2015). The compression paddle was not included (Sarno et al 2016b). The x-ray source was simulated as a monoenergetic and isotropic point source placed at 66 cm from the breast support at the chest-wall side, centered with respect to the breast support. In order to show the influence of the focal spot dimension on the estimated DgN, we run simulations for finite size focal spot of 0.3  ×  0.3 mm² square focal spot. The beam was collimated in order to irradiate a 26  ×  14 cm² surface at the breast bottom surface. The heel effect was not simulated.

The Monte Carlo code used in this work was based on GEANT4 toolkit version 10.00 and employed the physic list Option4. It was validated versus data provided by AAPM TG195 cases 1–3 (Sechopoulos et al 2015). In particular for the validation case 3, where the MGD to the breast for monoenergetic and polyenergetic x-ray beams in mammography is simulated, our code showed a difference of less than 0.5% (Sarno et al 2016b). In Sarno et al 2016a, we reproduced the DgN coefficients reported in Boone et al (2002) with a difference of only 0.2%, on average. A further validation versus literature data was also provided in Sarno et al (2018c), where conversion factors for MGD calculation in digital breast tomosynthesis reported in Dance et al (2011) were reproduced with a difference lower than 0.4%. In addition, the MC code adopted in this work was also validated versus measurement data acquired with a laboratory scanner (Sarno et al 2018c).

The x-ray photoelectric, coherent and incoherent scatter interactions were simulated. Electrons with energy down to 990 eV were tracked. The MGD was calculated as follows:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {\rm MGD}=\frac{\sum\nolimits_{i}{{{G}_{i}}\left(E \right)\cdot E_{i}^{{\rm dep}}}}{{{f}_{{\rm g}}}\cdot {{W}_{{\rm b}}}},\nonumber \end{align} \tag{ 1 }$$

where $E_{i}^{{\rm dep}}$ is the energy released at the interaction event i, f _g is the breast glandular fraction by mass, and W_b is the breast mass (skin excluded). The factor G (Boone et al 1999), dependent on the photon energy E, was evaluated as:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle G\left(E \right)=~\frac{{{f}_{{\rm g}}}\cdot {{\left(\frac{{{\mu}_{{\rm en}}}}{\rho} \right)}_{{\rm g}}}}{{{f}_{{\rm g}}}\cdot {{\left(\frac{{{\mu}_{{\rm en}}}}{\rho} \right)}_{{\rm g}}}+\left(1-{{f}_{{\rm g}}} \right)\cdot {{\left(\frac{{{\mu}_{{\rm en}}}}{\rho} \right)}_{{\rm a}}}}.\nonumber \end{align} \tag{ 2 }$$

Here, µ_en/ρ is the energy-dependent mass energy absorption coefficient of glandular (subscript g) and adipose (subscript a) tissues, evaluated by considering the functional interpolation given by Fedon et al (2015). The G-factor was evaluated interaction-by-interaction, at the current energy of the interacting photon (Wilkinson and Heggie 2001). Finally, the DgN values were computed as:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {\rm DgN}~=\frac{{\rm MGD}}{K},\nonumber \end{align} \tag{ 3 }$$

where the incident air kerma, K, was calculated as follows (Sarno et al 2017c):

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle K=\underset{i}{\mathop \sum}\,\frac{{{E}_{i}}~\cdot {{\left(\frac{{{\mu}_{{\rm en}}}}{\rho} \right)}_{{\rm air}}}}{S\cdot \cos {{\theta}_{i}}},\nonumber \end{align} \tag{ 4 }$$

where E_i is the energy of the ith photon which passes through a scoring surface S, (µ_en/ρ)_air is the mass energy absorption coefficient of the (dry) air obtained from the NIST database, and θ_i is the angle between the photon direction and the normal to S. No backscatter is taken into account in the K evaluation. The scoring region was a square of 3  ×  3 cm² and placed at 2 cm above the breast support and with its center at 4 cm from the patient-chest. The breast was not in place during the K calculation. The air kerma was rescaled to its value at the breast upper surface using the inverse square law. All simulations were performed with a monoenergetic x-ray beam ranging between 4.25 keV and 49.25 keV (0.5 keV step) and the computed values presented a statistical uncertainty lower than 0.1%, reached with 10⁸–10⁹ generated photons. Data in this work are shown in compliance with the recommendations of the AAPM Task group 268 (Sechopoulos et al 2018).

In order to reduce the amount of the produced data, the DgN coefficient curves (as a function of the energy) were fitted with 8th order polynomial curves. The polynomial coefficients were computed via MATLAB R2017a (MathWork Inc.) and a least absolute residual method. The zero-order coefficients were forced to 0.

Following Boone et al (2002), polyenergetic DgN coefficients (DgN_p) were computed from the monoenergetic DgN values, via a spectral weighting procedure:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {\rm Dg}{{{\rm N}}_{{\rm p}}}=\frac{\sum\nolimits_{{{E}_{\min}}}^{{{E}_{\max}}}\Phi \left(E \right)\cdot \vartheta \left(E \right)\cdot DgN\left(E \right)\cdot \Delta E}{\sum\nolimits_{{{E}_{\min}}}^{{{E}_{\max}}}\Phi \left(E \right)\cdot ~\vartheta \left(E \right)\cdot \Delta E},\nonumber \end{align} \tag{ 5 }$$

where ϕ(E) is the un-normalized spectrum at the entrance skin surface (photons/mm²) and ϑ(E) is the photon fluence to air kerma conversion factor (mGy · mm²/photons). For completeness, the x-ray spectra were computed first as in Boone et al (1997) (producing the Model #1 below), and then as in Hernandez et al (2017) (producing the Model #2), for comparison. The final DgN_p provided in this work have been produced by means of the x-ray spectral models in Hernandez et al (2017), who provided the most recent spectral models. Table 1 shows the various spectra used in this work.

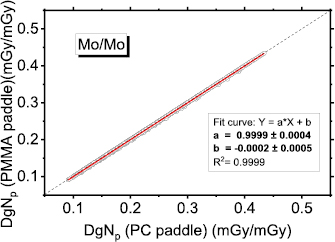
In order to take into account the presence of the compression paddle (which was not simulated) we added a 2 mm thick polycarbonate (PC) layer (European Commission 2006) in the calculation of the x-ray source spectrum. The HVL values indicated in the table 1 are those calculated after the introduction of the compression paddle in the spectra computation. For the case of mammographic units with a PMMA compression paddle, we calculated the influence in the spectra shaping of a 2 mm thick PMMA added filter. There is no practical difference between the cases of PC or PMMA in the beam path (figure A1 in the appendix).

The HVL was calculated without taking into account the contribution of the x-ray scatter, so being consistent with the EU QA protocols (European Commission 2006, Gennaro et al 2018). For each anode/filter and tube voltage combination, two spectra were used with two different HVLs. They were tuned by changing the added filtration thickness. Since DgN_p coefficients present a linear relation with the HVL beam (Wu et al 1991), this procedure will permit to estimate MGD in different mammography units which can present different HVL values. In addition, to ease the user handling of this coefficient datasets, we developed in MATLAB (MathWork Inc.) an executable program with a graphical user interface for the computation of DgN_p coefficients for any given mammographic spectrum.

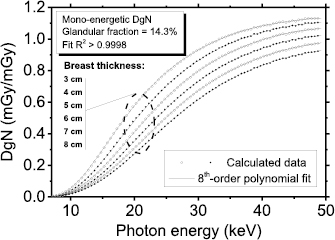
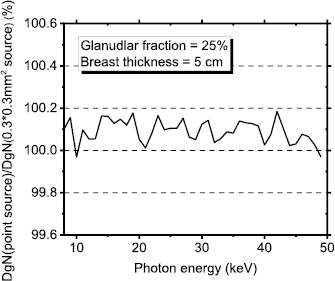
Figure 2 shows the computed monoenergetic DgN coefficients as a function of the photon energy, for a 14.3% glandular breast, with breast thickness from 3 cm to 8 cm. The supplementary material (stacks.iop.org/PMB/64/125012/mmedia) reports the fitting coefficients for monoenergetic DgN for breasts with thickness ranging between 3 cm and 8 cm and for glandular fraction by mass (skin excluded) of 0.1%, 14.3%, 25.0%, 50.0%, 75.0% and 100.0%. Due to boundary condition, the fitting curves are usable only in the photon energy range 8–49 keV. Percent ratio between DgN calculated for an isotropic point source and those for a 0.3  ×  0.3 mm² square source for monoenergetic beam ranging between 8 keV and 49 keV is reported in appendix (figure A2). The simulated breast presented 25.0% glandular fraction by mass and a compressed breast thickness of 5 cm. The differences are negligible and it resulted smaller than the MC statistical uncertainty for the investigated energy range.

Zoom In Zoom Out Reset image size

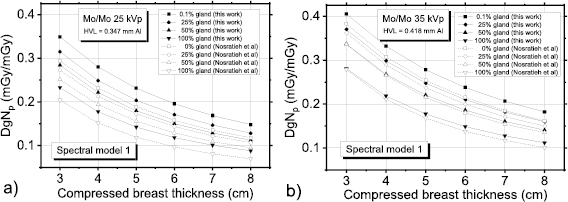
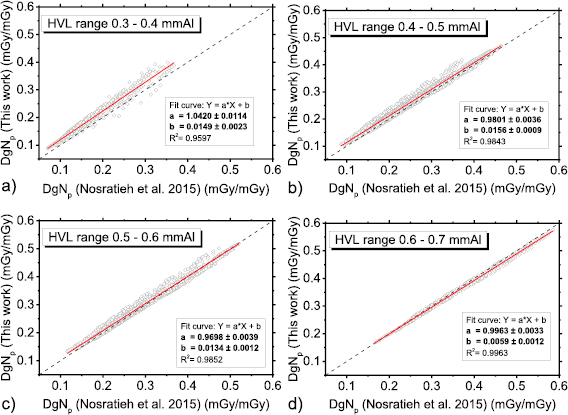
Figure 3 shows polyenergetic DgN coefficients for Mo/Mo spectra at 25 kVp (figure 3(a)) and at 35 kVp (figure 3(b)) computed in this work by means of the spectral model indicated in Boone et al (1997). For comparison, coefficients provided in Nosratieh et al (2015) are also shown. In all the cases shown in figure 3, the coefficients calculated in this work had the highest values, and the differences reduce for higher tube voltages (figure 3(b)). Figure 4 shows DgN_p coefficients evaluated within this work versus those in Nosratieh et al (2015), for several HVL ranges. Although the breast models are different, small differences in the DgN values were present between this work and Nosratieh et al (2015). As expected, the linear fits indicate that the discrepancies are smaller for higher HVLs, since the impact of the breast model reduces for more penetrating x-ray beams (Sarno et al 2016b). The DgN_p coefficients computed in this work by adopting the spectral model in Boone et al (1997), are 5% higher than those in Nosratieh et al (2015), on average (figure 5). The differences extend up to 27% (data in Nosratieh et al (2015) taken as reference), and in about 25% of the cases, the values of this work are lower than those in Nosratieh et al (2015) (figure 5).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figure 6 shows the DgN_p coefficients as a function of the beam HVL, calculated for 28 kVp tube voltage and for given breast and anode/filter combinations—Mo/Mo (figure 7(a)) and W/Al (figure 7(b)). The HVL was varied by varying the thickness of the added filter. Linear fits to the data points (R²  >  0.999) confirmed that the DgN_p coefficients have a linear dependence on the beam HVL, when all the other parameters are fixed.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

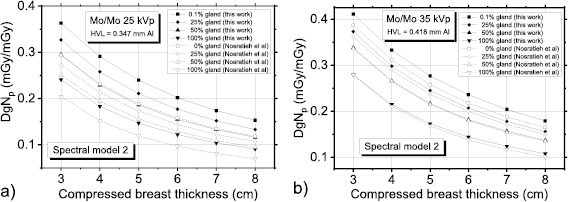
The figure 7 compares polyenergetic DgN coefficients provided in Nosratieh et al (2015) to those computed in this work for Mo/Mo spectra at 25 kVp (figure 7(a)) and 35 kVp (figure 7(b)). These coefficients have been computed by adopting the spectral model proposed in Hernandez et al (2017). In this comparison, we observed that DgN_p coefficients calculated in this work were systematically higher, the differences reducing for increasing tube voltages (figure 7(b)).

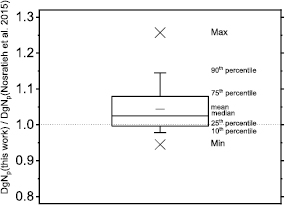
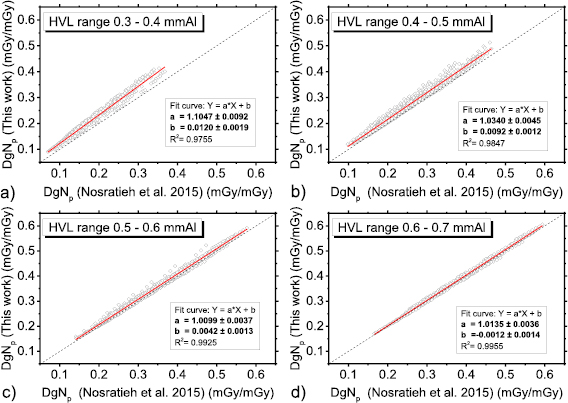
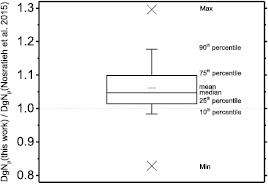
Figure 8 shows DgN_p coefficients evaluated in this work by means of the spectral model proposed in Hernandez et al (2017), versus those in Nosratieh et al (2015), for several HVL ranges. The differences decrease as the beam HVL increases. Indeed, the DgN_p coefficients computed in this work are about 10% higher (linear fit curve slope of about 1.10 in figure 8(a)) than those in Nosratieh et al (2015) in the HVL range 0.3–0.4 mmAl; these differences reduce to about 1% for HVL ranges on 0.5–0.6 mmAl and 0.6–0.7 mmAl. On average, our coefficients are 6% higher than those in Nosratieh et al (2015); this difference ranges between  −18% and 30%, for the compared cases (figure 9). About 50% of DgN_p coefficients computed in this work differed from those in Nosratieh et al (2015) by less than 10%, while 10% of the computed coefficients are at least 20% higher than the latter (figure 9).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In order to compare the spectral models, figure 10 shows the ratio between the DgN_p coefficients calculated in this work, by adopting the spectral model in Hernandez et al (2017) divided by those evaluated by adopting the spectra in Boone et al (1997). More than 80% of the compared data differ by less than 5% in absolute terms.

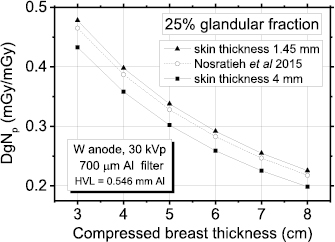
Zoom In Zoom Out Reset image size

Figure 11 shows DgN_p coefficients for a W/Al spectrum (HVL  =  0.546 mmAl) and 25% breast glandularity. Here, the coefficients determined by Nosratieh et al (2015) are plotted together with those computed in this work with the spectra modelled following Hernandez et al (2017). For comparison, in order to reproduce the breast model of Nosratieh et al (2015), we have also modelled the breast with a skin thickness of 4 mm (made of skin tissue). As for the spectral model of the previous paragraph, the DgN_p coefficients calculated by simulating the skin with a thickness of 1.45 mm do not differ significantly from those in Nosratieh et al (2015). On the other hand, when the skin is modelled with a thickness of 4 mm, as done in this last case, the discrepancies are larger. However, it is worth noting that in Nosratieh et al (2015) the 4 mm thick skin layer composition of the breast model is the same as the inner breast portion and its thickness was tuned in order to present the same attenuation as in the case of 4 mm skin with a real breast composition.

Zoom In Zoom Out Reset image size

The DgN_p coefficients for all the spectra contained in table 1 are available by request to the corresponding author. They have been computed for compressed breast thickness ranging between 3 cm and 8 cm and breast glandular fraction by mass of 0.1%, 14.3%, 25.0%, 50.0%, 75.0% and 100.0%, and by adopting the spectral model presented in Hernandez et al (2017).

We developed a Windows-based application for deriving spectrally weighted DgN_p coefficients calculated for arbitrary x-ray spectra. User input via a specific graphical user interface are the breast glandular fraction by mass, the compressed breast thickness and an arbitrary x-ray spectrum whose tabular entries (photon energy, intensity) are uploaded from the user storage. The DgN_p coefficients are calculated using the monoenergetic DgN curve fits produced in this work (supplementary material), based on a breast model which includes a skin thickness of 1.45 mm. Spectra produced with a tube voltage up to 49 kV can be entered.