Abstract
Over the last two decades, iron oxide based nanoparticles ferrofluids have attracted significant attention for a wide range of applications. For the successful use of these materials in biotechnology and energy, surface coating and specific functionalization is critical to achieve high dispersibility and colloidal stability of the nanoparticles in the ferrofluids. In view of this, the magnetic behavior of clusters of ultra-small MnFe2O4 nanoparticles covered by bovine serum albumin, which is known as a highly biocompatible and environmentally friendly surfactant, is investigated by magnetization measurements, and numerical simulations at an atomic and mesoscopic scale. The coating process with albumin produces a change in the structure, actual size and shape distribution of clusters of exchange coupled particles, giving rise to a distribution of blocking temperatures. The coated system exhibits a superspin glass (SSG) behavior with the SSG freezing temperatures similar to the uncoated ones, providing evidence that the strength of the dipolar interactions is not affected by the presence of the albumin. The DFT calculations show that the albumin coating reduces the surface anisotropy and the saturation magnetization in the nanoparticles leading to lower values of the coercive field in agreement with the experimental findings. Our results clearly demonstrate that the albumin coated clusters of MnFe2O4 particles are ideal systems for energy and biomedical applications since colloidal and thermal stability as well as biosafety is obtained through the albumin coating.
Export citation and abstract BibTeX RIS
1. Introduction
During the last few decades magnetic nanoparticles (MNPs) have been extensively studied for their remarkable chemical and physical properties, particularly the magnetic ones, which are different from their bulk counterparts [1]. MNPs with suitable surface modification and functionalization are considered to be good candidates in a plethora of applications [2, 3]. Magnetic iron oxide NPs have become one of the most used magnetic materials in an extensive range of applications because they are low cost, and have low toxicity and unique magnetic properties. Among them, recently spinel-type metal-doped iron oxide nanoparticles became object of growing interest [4–8]. The study of ultra-small MnFe2O4 nanoparticles has demonstrated interesting magnetic properties, as high saturation magnetization, collective superspin glass and exchange bias behavior due to strong interparticle interactions and surface/interface effects [9–12]. These magnetic characteristics make them suitable for water purification, photocatalysis, biomedical and energy applications [13–16].
The nanometer-sized metal oxide-based NPs are easily oxidized and cannot maintain their stability in liquids because of the agglomeration. Moreover, some of them are toxic and not environmentally friendly. Therefore, a suitable coating is essential to overcome such limitations increasing their biosafety [17–19] and environmental sustainability. Different surface modifications have been reported that can enhance or deteriorate the magnetic properties of mixed metal ferrite nanoparticles [10, 20–23]. A lot of attention has been drawn into albumin coated nanoparticles [24–27]. Albumin is one of the most studied proteins that have a strong affinity for a variety of inorganic molecules binding to different sites [28]. It is a soluble protein in the plasma of the circulatory system and acts in the transport and deposition of endogenous and exogenous substances. Albumin can readily undergo conformational changes and is classed as a soft protein due to its relatively flexible structure. The charge, coulombic and van der Waals forces, hydrophobic interactions, sorbate conformational stability and surface area that the particle provides, are important factors for the interaction between a protein and a material [29]. Moreover, this protein can adsorb metals and therefore it is expected to show strong affinity towards transition metal ions because of the existence of aminoacid residues, like histidine and cysteine [30]. It has also been reported that at high bovine serum albumin (BSA) concentrations, BSA induces maghemite particle aggregation [31]. Therefore, albumin coated nanoparticles are expected to have different magnetic properties compared to the uncoated nanoparticles.
In the frame of a wide study several samples of MnFe2O4 nanoparticles have been prepared and coated by albumin. In particular, MnFe2O4 nanoparticles with mean diameter ∼6 nm have been covered by BS-albumin, functionalized with a model drug and then the biological activity was evaluated [32]. It has been clearly demonstrated that the covering process induces some particles aggregation, leading to a modification of their magnetic properties. The effect of aggregation on magnetic properties represents a key point for the application of MNPs-based systems in biomedicine, catalysis, energy (e.g. ferrofluids for thermoelectricity). In view of this we prepare ultra-small MnFe2O4 nanoparticles of diameter ∼2 nm and cover them with albumin in order to evaluate and understand the effect of aggregation.
Our magnetic measurements elaborated by DFT and Monte Carlo calculations demonstrate that the albumin coating affects both the internal magnetic characteristics of the nanoparticles, i.e. magnetocrystalline anisotropy and the saturation magnetization, and the assembly morphology of the studied system, i.e. creation of isolated clusters of nanoparticles.
2. Experimental and numerical methods
2.1. Synthesis of MnFe2O4 nanoparticles and their albumin coating
Manganese ferrite nanoparticles were synthesized by co-precipitation of Fe3+ and Mn2+ in water/toluene/sodium dodecylbenzenesulfonate reverse micelle system. The detailed synthesis procedure was described in [33] and a short description is summarized in the supporting information (SI), available online at stacks.iop.org/NANO/31/025707/mmedia. This sample will be labeled as MFO. Manganese ferrite nanoparticles having mean crystalline size of about 2 nm were entrapped in bovine serum albumin (BSA; Sigma) by using a water-in-oil single microemulsion system as described in [32]. Details are summarized in the SI. The albumin coated samples will be labeled as MFO_BSA.
2.2. Magnetic characterization techniques
DC magnetization measurements were performed using a Quantum Design SQUID magnetometer (Hmax = ±5 T). Temperature dependence of Magnetization was investigated using zero-field-cooled (ZFC) and field-cooled (FC) protocols. First the sample was cooled down from room temperature to 5 K in zero magnetic field; then, a static magnetic field of 2.5 mT was applied. MZFC was measured during the warm up from 5 to 300 K, whereas MFC was recorded during the subsequent cooling. The field dependence of the remanent magnetization was measured using the isothermal remanent magnetization (IRM) and direct current demagnetization (DCD) protocols. The DCD curve was obtained by saturating the sample and then measuring the remanence MDCD(H) after applying the reverse fields Hrev up to the maximum field Hmax (5 T). The IRM curve was obtained starting from a totally demagnetized state by applying a positive magnetic field and measuring the remanence MIRM(H) when the field was removed; the process was repeated by increasing the field gradually up to Hmax.
2.3. The model
We perform multiscale modeling to study the magnetic behavior of the Mn ferrite nanoparticles coated with albumin. Our modeling starts with DFT calculations to investigate how the albumin molecules are bonding on the Mn ferrite surface and consequently how they influence the magnetic properties of the particle. Then an atomic scale model of a single Mn ferrite particle is developed that takes into account its spinel structure and its 2 nm size. Finally a mesoscopic scale approach has been developed, to model the nanoparticles assembly taking input from the DFT parameters, by rescaling them properly using the atomic scale modeling. Therefore, in our mesoscopic model, the effect of the albumin coating on the magnetic properties is introduced via the rescaled mesoscopic parameters of the magnetization and anisotropy. Monte Carlo simulations in this mesoscopic scale system were performed to calculate the magnetic properties of the assembly.
2.3.1. Electronic structure calculations
First-principles calculations based on spin-polarized density functional theory were performed for an ultra-small MnFe2O4 particle bonded to albumin protein using the Vienna Ab Initio Simulation Package (VASP) [34, 35]. The electronic charge density and the local potential were expressed in plane wave basis sets. Electronic relaxation was performed with accuracy of 10−4 eV, while the Ionic relaxation with 10−3 eV/atom. The Perdew–Burke–Ernzerhof approximation was used to calculate the exchange correlation functional.The interactions between the electrons and ions were described using the projector-augmented-wave method.
The overall three-dimensional structure of bovine serum albumin (BSA), shown by x-ray crystallography, has a heart shape [36]. Structurally, albumin consists of three homologous domains I, II, and III. Each domain contains two sub-domains (A and B), which contains 4 and 6 α-helices, respectively. In our model, the particle is covered partially by sections of the albumin protein (section IIB) at the top and bottom face.
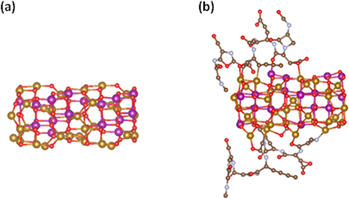
The modeled particle consists of 4 atomic layers of Mn ferrite (inverse spinel), covered by sections of the BSA protein. The relaxed structures are shown in figure 1 [37]. After the ionic relaxation, the size of the Mn ferrite particle is 1.6 nm × 0.7 nm × 0.6 nm. A Mn ion is found to create bond only with O atoms, whereas Fe ions create bonds with O, C and N atoms. A Mn atom shows an increased magnetic moment by ∼0.6 μB. Fe atom bonded with C shows a decreased moment by ∼0.05 μB. Fe atom bonded with Ν shows a decreased magnetic moment by ∼0.27 μB. No systematic behavior has been found for the Fe atoms bonded with O, as some of them show an increased and some of them a decreased magnetic moment with respect to the uncoated case. This can be attributed to the different environment constructed around the magnetic ion.
Figure 1. Calculated relaxed structures for the (a) uncoated, (b) coated with albumin Mn ferrite particle (Mn: purple balls, Fe: yellow balls, O: red balls, C: brown balls, N: cyan balls) [37].
Download figure:
Standard image High-resolution imageAs we can see in figure 1(b) the albumin is partially coating the Mn ferrite nanoparticle giving room for the touching between the nanoparticles in the formed clusters as described in section 2.1. The mean value of the magnetic moment of the bonded atoms is increased by 1.8% with respect to the uncoated case. Due to the general expansion and distortion of the cell, neighboring magnetic atoms are found at larger distances and displaced positions with respect to the uncoated case. In this case, the mean magnetic moment of the distorted layer of atoms is decreased by 2.8% and that of the inner atoms is decreased by 1.75%. Overall the mean value the surface spins has an increased magnetic moment of 0.07 μΒ with respect to the uncoated case. The general distortion affects also the environment of inner atoms leading to a reduction of the mean moment close to 0.17 μΒ with respect to the uncoated case. In order to estimate the variation of the magnetic anisotropy energy (MAE), the energy of the system is calculated by rotating all spins coherently along different spin axis including LS orbit coupling.
In table 1 the results of the electronic structure calculations of the mean magnetic moment per atom type, the total magnetic moment and MAE energy for the uncoated and the coated with albumin particle are reported.
Table 1. Mean magnetic moment per atom type and the total magnetic moment for the coated and uncoated Mn Ferrite particle.
| Mn ferrite sample | Mean moment per Fe (μB) | Mean moment per Mn (μB) | Saturated magnetic moment (μB) | MAE energy (meV) |
|---|---|---|---|---|
| Uncoated | 4.03 | 4.27 | 197.555 | 2.1 |
| Coated | 3.99 | 4.02 | 192.475 | 1.94 |
From table 1 we can see that (a) the coated particle has smaller magnetic moment per atom for each type of atoms resulting to smaller total magnetic moment by 3%. This reduction is further enhanced with increasing number of bonded atoms at the nanoparticle surface according to our calculations and (b) the coated particle has lower MAΕ compared to the uncoated one. The relative difference is approximately 7.5%.
In the uncoated nanoparticles the coordination symmetry is greatly reduced for the metal cations at the surface due to missing of some coordination oxygen atoms. In the coated with albumin nanoparticles, the adsorbed ligands can be considered that they take the positions of the missing oxygen atoms. Even though the surface is spatially distorted in terms of number of neighbors, the surrounding environment tends to recover the bulk phase which makes the crystal field of the surface metal ion more closely resembling that of the bulk material. Importantly, these changes account for the reduction in the anisotropy of the coated sample.
2.3.2. Monte Carlo simulations of the assembly of coated MnFe2O4 nanoparticles
The macroscopic magnetic behavior of the coated assembly of MnFe2O4 nanoparticles has been studied and compared with that of the uncoated assembly of MnFe2O4. In both cases we take input from the electronic structure calculations for the nanoparticles anisotropy and magnetization.
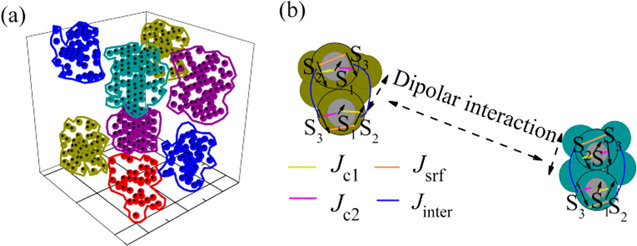
We model the assembly of MnFe2O4 nanoparticles coated with albumin as a group of well separated small clusters of nanoparticles as shown in figure 2.
Figure 2. (a) Modeling of the albumin coated clusters of ultra-small MnFe2O4 nanoparticles with a core/surface morphology, (b) enlarged schematic representation of two selected dipolarly interacting pairs of nanoparticles core (S1)/surface (S2, S3) that belong to two neighboring clusters in each pair the exchange intraparticle (Jc1, Jc2, Jsrf) and the exchange interparticle interactions (Jinter) between macrospins are depicted.
Download figure:
Standard image High-resolution imageThe clusters are surrounded by the long albumin molecules so they are not touching each other while the nanoparticles in the clusters can be in physical contact. This model is considered based on the experimental evidence (i.e. high temperature irreversibility of the ZFC-FC magnetization curve) of the formation of clusters when the uncoated MnFe2O4 nanoparticles were dispersed in the albumin solution. We consider N ultra-small spherical ferrimagnetic nanoparticles with core/surface morphology that takes into account also surface effects, located randomly on the nodes of a cubic lattice inside a box of 10α × 10α × 10α where α is the smallest inter-particle distance. The clusters of nanoparticles are created by dividing the box into eight regions with size 5α × 5α × 5α each and variable particle concentration (p1 = 30%, p2 = 40%, p3 = 50%, p4 = 60%, p5 = 70%, p6 = 60%, p7 = 40%, p8 = 50%) (figure 2) for each cluster, but under the constraint that the total concentration is p = 50% the same as in the case of the simulated uncoated assembly as described in [9].
In our simulations each nanoparticle is described by a set of three classical spin vectors one for the core  1i and two for the surface
1i and two for the surface  2i and
2i and  3i with magnetic moment mn = MnVn/MsV, i = 1, ..., N (total number of particles), n = 1 stands for the core and n = 2, 3 for the 'up' and 'down' surface sublattices of the nanoparticle, respectively. V is the particle volume and MS its saturation magnetization. Vn and Mn are the volume and the saturation magnetization of the core, the 'up' and the 'down' surface sublattices spins.
3i with magnetic moment mn = MnVn/MsV, i = 1, ..., N (total number of particles), n = 1 stands for the core and n = 2, 3 for the 'up' and 'down' surface sublattices of the nanoparticle, respectively. V is the particle volume and MS its saturation magnetization. Vn and Mn are the volume and the saturation magnetization of the core, the 'up' and the 'down' surface sublattices spins.
The total energy of the system [9] for the N nanoparticles is:

The first, second and third energy term in equation (1) in the square brackets describe the nearest-neighbor Heisenberg exchange interaction between the core spin and the two surface spins, and the exchange interaction between the surface spins, respectively. The fourth and the fifth terms give the anisotropy energy for the core and the surface spins (in the square brackets) assumed uniaxial with ê1i, ê2i, ê3i being the anisotropy random easy-axes direction. The sixth term gives the dipolar interactions among all spins in the nanoparticles where the magnetic moments of the three macrospins of each particle are defined as m1 = M1V1/MsV, m2 = M2V2/MsV, and m3 = M3V3/MsV and Dij is the dipolar interaction tensor. The next term describes the inter-particle exchange interactions between the nanoparticles in contact inside each cluster, where 〈i, j〉 denotes summation over nearest neighbors. The last term is the Zeeman energy (êh being the direction of the magnetic field).
The energy parameters of the equation (1), as they are entered in the simulations, have been normalized by the factor 20 × KC V1, where V1 is the core volume of the nanoparticle, so they are dimensionless.
The parameters of the intra-particle exchange coupling constants between the core spin and the surface spins are jc1 = 0.5, jc2 = 0.45, and the exchange coupling constant between the surface spins jsrf = −1.0, as were calculated in [9] for uncoated nanoparticles system. Here we set jsrf = −0.8 for the albumin coated clusters of nanoparticles, because our DFT calculations have shown that the bonding with the albumin causes expansion of the neighboring magnetic atoms at the surface of the Mn ferrite nanoparticles and consequently reduction of the effective exchange coupling strength.
The effective anisotropy constants for the core is taken kC = 0.05 and for the surface is ksrf = 1.0 which is larger than in the core taking into account the reduced surface symmetry [9] for the simulated uncoated sample. For the albumin coated sample, our DFT calculations indicate that the surface anisotropy is reduced due to the existence of the albumin (see section 2.3.1), consequently the effective surface anisotropy constant is taken here ksrf = 0.8, that is 20% reduction from the surface anisotropy of the uncoated nanoparticles. We consider larger reduction of the surface anisotropy comparing with the DFT calculations to include different percentage of the surface coating and higher surface volume since the modeled particle here is of 2 nm size.
There is not exact microscopic model for the calculation of the exchange coupling constants between the nanoparticles. So we treat them as free parameters. Thus we consider the inter-particle exchange coupling constant between the nanoparticles in contact in the cluster jinter = −0.80 larger than that of the uncoated case (jinter = −0.50), since the presence of albumin brings closer the trapped nanoparticles in the clusters and enhances the fraction of the shell that comes into contact with the neighboring shells of these nanoparticles. The reduced dipolar strength is taken [9] g = μ0(MsV)2/(4πd320KcV1) ~ 3 (where d is the smallest distance between two nanoparticles equal to the particle's diameter d = 2 nm) for both systems.
The saturation magnetization ratios have been extracted from atomic scale calculations for the spinel structure of a 2 nm diameter MnFe2O4 nanoparticle, assuming 0.5 nm surface thickness, and they are m1 = 0.1, m2 = 0.5, m3 = 0.4 in case of the uncoated nanoparticles assembly [9]. According to previous experimental results of [27] and our DFT calculations (see section 2.3.1) the surface magnetic moments are reduced due to the existence of albumin so we consider m2 = 0.45 and m3 = 0.4 that is 10% reduction from the initial value, since we considered average larger coverage than the one at the DFT calculations. We also expect that the clustering inside the albumin can reduce the total magnetization. The external magnetic field is H. The thermal energy is kBT (where T is the temperature).
The magnetic configuration was obtained by the Monte Carlo simulation technique, with the implementation of the Metropolis algorithm [38]. The Monte Carlo simulations results for a given temperature and applied field were averaged over 60 samples with various spin configurations, realizations of the easy-axes distribution and different spatial configurations for the nanoparticles. The calculation of the (ZFC)/(FC) magnetization curves is a three steps process: (1) the system is cooled at a constant temperature rate dΤ = 0.05 from temperature T = 5 to T = 0.01 at zero applied field H = 0 (2) the sample is heated from temperature T = 0.01 to T = 5 at the same constant temperature rate under the application of a magnetic field Happ and the ZFC magnetization curve is monitored and (3) by cooling down the system in the presence of the applied field up to T = 0.01 we calculate the FC magnetization curve.
The demagnetization curve DCD and isothermal remanence IRM curve are calculated using the same procedure as the experimental DCD and IRM measurements described in section 2.2. The ΔM(H) plots were calculated using the expression ΔM(H) = MDCD(H)—(1–2MIRM (H)) [39].
3. Results and discussion
As has been already discussed in [33], MnFe2O4 uncoated nanoparticles show mean crystallite size (obtained by XRD analysis) ∼2 nm, whereas the value obtained by the powder specific area (278 m2 g−1) is about 4 nm, providing evidence that clusters of particles consisting of some aggregated crystallites are formed.
These particles have been covered by albumin using the procedure described in [32] (summarized in SI) for ∼6 nm Mn ferrite nanoparticle. In [32] it has been clearly demonstrated (by TEM, SEM and BET) that the covering procedure of albumin induces some further particle aggregation. Since the covering protocol we use is exactly the same as in [30], we expect that in our system of ∼2 nm MnFe2O4 nanoparticles, the albumin coating induces the same type of particle aggregation.
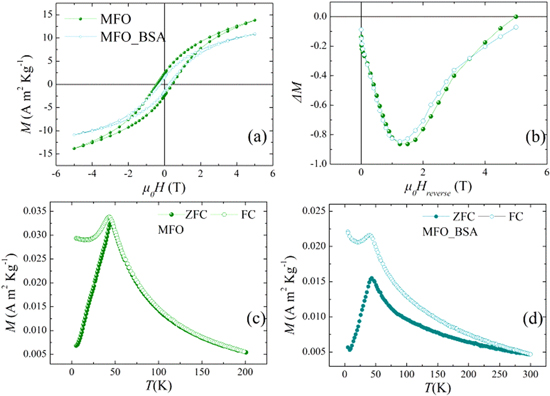
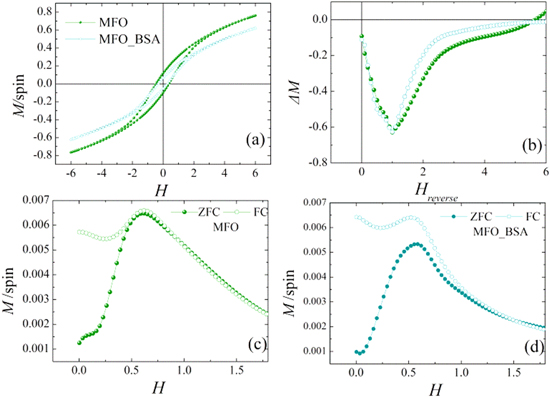
Figure 3 shows the experimental results of the hysteresis loops (a), the ΔM plot (see in SI) (b), the ZFC/FC magnetization curves of the MnFe2O4 uncoated particles [9] (c) and of the coated with albumin clusters of MnFe2O4 nanoparticles (d).
Figure 3. Experimental results at T = 5 K for the hysteresis loops (a), ΔM plots of uncoated MnFe2O4 nanoparticles (MFO sample) and the albumin-coated particles (MFO_BSA sample) (b). (c) ZFC/FC magnetization curves for the uncoated nanoparticles (MFO sample). (d) ZFC/FC magnetization for the albumin-coated particles (MFO_BSA sample) curves at Happ = 2.5 mT.
Download figure:
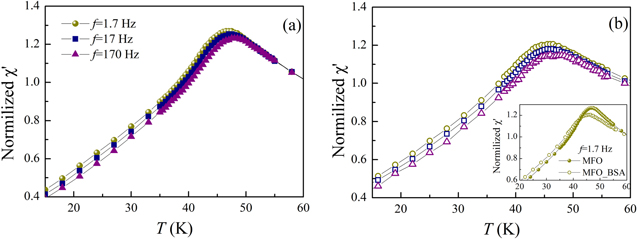
Standard image High-resolution imageThe hysteresis loop of the uncoated system has coercive field HC and high-field magnetization values higher than those of the albumin coated system. ΔM plots indicate the predominance of dipolar interparticle interactions [39] and the presence of surface effects [40]. The sharp maximum of the ZFC and FC curves at the same temperature indicates a SSG state below ∼45 K for both systems (figures 3(c) and (d)). Therefore, the albumin coating has a minor effect with respect to the dipolar interactions which are responsible for the SSG behavior. This is further confirmed by the similarity of their ac magnetic susceptibility curves shown in figure 4 for three different frequencies, suggesting similar dynamical properties. The ac-susceptibility data show some dispersion above Tmax for that system, in agreement with the magnetic irreversibility observed in the magnetization curves of MFO_BSA.
Figure 4. Temperature dependence of the in-phase component of the ac susceptibility (χ') at different frequencies (1.7, 17, 170 Hz) normalized to χ' (f = 1.7 Hz, T = 60 K) recorded with ZFC protocol for uncoated (MFO sample) (a) and coated with albumin (MFO_BSA sample) (b) MnFe2O4 nanoparticles. Inset: comparison between the χ' curves for the uncoated (MFO sample) and the albumin-coated (MFO_BSA sample) nanoparticles for f = 1.7 Hz.
Download figure:
Standard image High-resolution imageMoreover, ZFC/FC magnetization curves of the coated with albumin nanoparticles (figure 3(d)) show irreversibility at Tirr ≈ 300 K higher (∼6 times) than Tirr of the uncoated sample. This temperature difference indicates the existence of a large cluster size distribution, unlike in the uncoated system, providing also a qualitative measure of the width of the cluster size distribution. Therefore, we expect that some very large clusters of nanoparticles exist in the coated system whose moments become unblocked at the very high Tirr.
Figure 5 shows the corresponding Monte Carlo simulation results of the hysteresis loops (a), ΔM plot (b) and ZFC/FC magnetization curves of the MFO sample (c) of [9] together with those of the MFO_BSA sample (d).
Figure 5. Monte Carlo simulation results of the hysteresis loops at temperature T = 0.01 (a), ΔM plots at T = 0.01 (b), the ZFC/FC magnetization curves at Happ = 0.03 of uncoated MnFe2O4 nanoparticles [9] (MFO sample) (c) and their albumin-coated clusters (MFO_BSA sample) (d).
Download figure:
Standard image High-resolution imageOur calculations show that the existence of exchange coupled nanoparticles in the albumin coated clusters and the reduction of the surface anisotropy in the nanoparticles, due to the presence of albumin, produces 31% reduction of the coercive field HC compared to the uncoated sample. Both samples show (figure 5(b)) the same minimum ΔM value at almost the same field value Hrev indicating that the dipolar strength does not change with the addition of the albumin coating in the nanoparticles. The simulated hysteresis curves and ΔM plots reproduce very well the experimental results presented in figures 3(a) and (b).
In addition, the Monte Carlo calculated ZFC magnetization curves of the albumin coated and uncoated particles (figures 5(c) and (d) respectively) show maxima at almost the same temperature value Tmax ∼0.6 in agreement with the experimental results signaling the collective freezing of particles below Tmax. On the other hand, the coated clusters system shows irreversible temperature Tirr (∼2 times) higher than that of the uncoated sample. This temperature difference is smaller than the corresponding measured and it is attributed to the narrower cluster size distribution in the simulations.
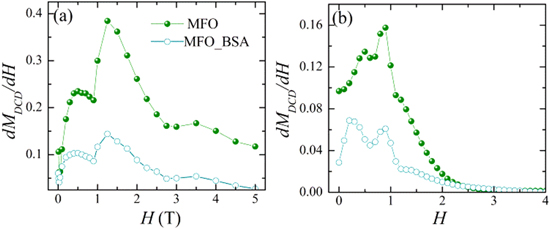
The irreversible susceptibility χirr = dMDCD/dH derived by the DCD curve is considered to be a measure of the energy barrier distribution. In nanoparticles assembly, the energy barrier distribution is associated with a distribution of particles' coercivities and is generally called the switching field distribution [41]. In figure 6, the dMDCD/dH derived from the experimental MDCD (a) and from the Monte Carlo simulated MDCD (b) are shown.
Figure 6. (a) Distribution of switching field (dMDCD/dH) at 5 K and (b) Monte Carlo simulation results of the dMDCD/dH at temperature T = 0.01 for uncoated MnFe2O4 nanoparticles (MFO sample) and clusters of MnFe2O4 nanoparticles coated with albumin (MFO_BSA sample).
Download figure:
Standard image High-resolution imageInterestingly, the irreversible susceptibility shows two maxima at two different field values for both nanoparticles systems though in other studies on ferrites nanoparticles only one maximum is observed [42]. The higher field value H = 1.25 T is the one around which the ΔM amplitude takes its minimum value (in module) in figure 3(b) for both systems. Thus, it corresponds to the maximum of the energy barrier distribution determined by the dipolar interaction energies. The lower field value H ∼ 0.5 T corresponds to the switching field value at which the anisotropy energy barrier of the single particle is overcome. This particle anisotropy energy barrier is mainly due to the highly anisotropic surface layer. The Monte Carlo simulation results of the dMDCD/dH are in very good agreement with the experimental findings verifying the existence of strong effective anisotropy of the MnFe2O4 nanoparticles and of strong dipolar interactions. Note that the Monte Carlo simulations clearly show (clearer than the experimental dMDCD/dH) that the first maximum corresponds to slightly smaller Hrev in the case of coated nanoparticles as expected since the surface anisotropy is reduced. Differences between experimental and Monte Carlo simulation results of dMDCD/dH curve are attributed to the larger cluster distribution in the experimental system.
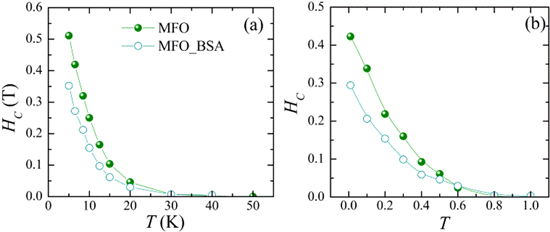
The temperature dependence of the coercive field HC of albumin coated and uncoated MnFe2O4 nanoparticles is presented in figure 7 for the experimental systems (figure 7(a)) and the corresponding simulations (figure 7(b)). HC follows an exponential decay with temperature. There is good agreement between the simulations and the experimental findings. The lower surface anisotropy reduces the values of the HC with respect to the uncoated system for all temperatures.
Figure 7. (a) Experimental results after field cooling 1 T and (b) Monte Carlo simulation results, after field cooling Hcool = 2.5, of the temperature dependence of the coercive field (HC) for MnFe2O4 nanoparticles coated with albumin (MFO sample) and the uncoated ones [9] (MFO_BSA sample).
Download figure:
Standard image High-resolution image4. Conclusions
Chemically synthesized albumin coated MnFe2O4 nanoparticles are studied and compared with uncoated assembly of MnFe2O4 nanoparticles. DFT calculations and Monte Carlo simulation results demonstrate that albumin causes the decrease in the magnetization and surface anisotropy comparing to the uncoated nanoparticles, resulting in a large decrease in the coercive field. Moreover, the formation of albumin coated clusters of exchange coupled nanoparticles during the coating process leads to high irreversibility temperatures. Remarkably the introduction of albumin coating does not affect the strength of the dipolar interactions as indicated by the similarity of the ac measurements and the freezing temperatures (ZFC maxima), while it has an effect on the intrinsic magnetic properties of the nanoparticles. These results make the albumin coated MnFe2O4 nanoparticles good candidates for energy (e.g. magnetic fluid for thermo-electricity) and biomedical applications where colloidal and thermal stability and biocompatibility in magnetically driven nano-architectures are needed.
Acknowledgments
This work was supported by the European Union's Horizon 2020 Research and Innovation Programme: under grant agreement No. 731976 (MAGENTA). KNT, MV and NN acknowledge the computational time granted from the Greek Research & Technology Network (GRNET) in the Greek National HPC facility ARIS (http://hpc.grnet.gr) under project MNBIE (pr005030).