Abstract
We present an exact solution of the continuum Bogolyubov-de-Gennes Hamiltonian for Majorana bound states (MBSs) generated in a superconductor–semiconductor hybrid topological nanowire. The full energy spectra that include the band states and in-gap states could be obtained. We show that for relatively short wire length, the zero energy mode could be induced even in the topological trivial regime, which also indicates oscillatory dependence on the chemical potential. With the increase of the Zeeman field, the MBSs are almost fully spin-polarized and do not localize at the wire ends gradually. We also extend our discussion to the property of Majorana modes in an inhomogeneous nanowire, in which a local gate voltage is applied to one end of the nanowire. It is found that the local potential barrier or well could modulate the Majorana energy splitting periodically. The leakage of MBSs to the potential region is exponentially suppressed for the barrier case. A potential well could induce near-zero-energy bound states and these states merge with MBSs, leading to the delocalization of MBSs. In the potential well region, both the spin-up and spin-down components of the trivial states account for a significant proportion, which can be detected experimentally.
Export citation and abstract BibTeX RIS
1. Introduction
The search of Majorana fermions [1] have attracted increased attention in recent years in condensed matter physics [2–6], due to their fundamental interest and potential application in topological quantum computing [7–13]. In solid states, the evidence of Majorana bound states (MBSs) has popped up at the ends of semiconductor–superconductor hybrid nanowires [14–16], chains of single atoms [17], iron-based superconductors [18–20], topological insulators [21, 22], and the quantum anomalous Hall insulator [23]. Of all the Majorana platforms, the one that has attracted the most excitement is the system based on semiconductor nanowire with Rashba spin–orbit interaction and in proximity to an s-wave superconductor [2, 15, 24]. Among several smoking gun signals for MBSs, the standout is the so-called zero-bias conductance peak, which has been observed in the charge transport measurements of both nanowires [25, 26] and spin chains [27]. However, the zero-bias signature could also arise from other non-Majorana mechanisms [24, 28]. So far, the existence of Majorana quasiparticles has been one of the most important issues in the study of topological superconductors.
One possibility to check the existence of MBSs is to look for signs that the MBSs are hybridizing with each other. For a finite nanowire, the wave functions of MBSs decay exponentially along the wire and their hybridization produces a finite Majorana energy splitting  M ∼ exp(−L/ξ) [29], where L is the length of the nanowire and ξ is the coherence length of the superconductor. The strength of Majorana energy splitting could be tuned periodically by the Zeeman field or the chemical potential of the nanowire. The exponential suppression of energy splitting with increasing wire length is observed in the InAs nanowire segments with epitaxial aluminium, which forms a proximity-induced superconducting Coulomb island [30]. The oscillation of the Majorana energy splitting as a function of the magnetic field is also demonstrated in the experiment [30]. However, the energy splitting indicates a damping oscillation with increase in magnetic field, which contradicts to the theoretical prediction [29, 31]. Recently, a possible explanation for this observation is proposed by considering a position-dependent spin–orbit coupling [32]. This implies that the inhomogeneity in the nanowire could induce many significant physical consequences [33].
M ∼ exp(−L/ξ) [29], where L is the length of the nanowire and ξ is the coherence length of the superconductor. The strength of Majorana energy splitting could be tuned periodically by the Zeeman field or the chemical potential of the nanowire. The exponential suppression of energy splitting with increasing wire length is observed in the InAs nanowire segments with epitaxial aluminium, which forms a proximity-induced superconducting Coulomb island [30]. The oscillation of the Majorana energy splitting as a function of the magnetic field is also demonstrated in the experiment [30]. However, the energy splitting indicates a damping oscillation with increase in magnetic field, which contradicts to the theoretical prediction [29, 31]. Recently, a possible explanation for this observation is proposed by considering a position-dependent spin–orbit coupling [32]. This implies that the inhomogeneity in the nanowire could induce many significant physical consequences [33].
Theoretically, since MBSs were proposed to be realized in a semiconductor nanowire-superconductor hybrid system, numerous studies have analyzed the model Hamiltonian by using the tight-binding model and direct numerical diagonalization [34–37]. Up to now, the solution of the continuum Bogolyubov-de-Gennes (BdG) equation about non-zero energy Majorana mode, is based on the variational calculation or small expansion [31]. In the long wire length limit, the approximation is appropriate. However, it is difficult to judge its accuracy in other complex regimes. The exact solution of the continuum Hamiltonian for MBSs in the finite-size case is expected to provide additional insights into the nature of MBSs. An exact solution for the continuum BdG equation of the superconductor–semiconductor hybrid nanowire system is still missing.
Motivated by this, here we present an exact solution of the continuum BdG equation for MBSs with a finite splitting energy in a topological superconductive nanowire by means of the trial wave function method [38]. The open boundary condition at wire ends is taken in the calculation. This method could give the full energy spectra of the BdG Hamiltonian and the corresponding wave functions. The paper is organized as follows. In section 2 we introduce the BdG model for the MBSs and provide the calculation procedure within an exact treatment. In section 3 we discuss the dependence of the splitting energy on the system parameters in a homogeneous nanowire. We extend the discussion to the inhomogeneous case in section 4. The spatial distribution of MBS wave functions is investigated after applying a local gate voltage. Finally, a summary is presented in section 5.
2. Bogolyubov-de-Gennes equations and exact solutions
We focus on one of the most promising system for generating MBSs, which is by inducing superconductivity on a semiconductor nanowire with Rashba spin–orbit coupling. Under a proper application of external Zeeman field, the nanowire resembles a one-dimensional topological superconductor hosting MBSs at its two ends. Following the earlier work, the one-dimensional BdG Hamiltonian for the present system can be written as [14]
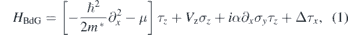
where Vz is the effective Zeeman field, σi and τi (i = x, y, z) are Pauli matrices acting on the spin and particle–hole spaces, μ is the system chemical potential strength, α represents the spin–orbit coupling, and Δ is the proximity-induced superconductor gap in the wire. Here we concentrate on the exact one-dimensional case and study the finite-size effects.
We study the non-zero-energy solution of MBSs by employing the trial wave function method. Due to the finite size of the system, the non-zero-energy solution of MBSs could be obtained, and their spinor wave functions do not possess a standard form as the zero-energy mode with Ψ = (ψ, iσyψ*) any more. In order to get the non-zero-energy solution of MBSs, we need to solve the BdG equation HBdGΨ(x) = EΨ(x) with vanishing boundary conditions, where E is the eigenenergy and Ψ(x) is the corresponding wave function. We solve the BdG equation by using the trial wave function of the following form
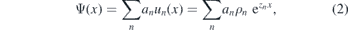
where un(x) are the eigenstate of the equation HBdGun(x) = Eun(x) and are assumed to have the form 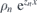 , an are the corresponding coefficients. The zn of a non-trivial solution must satisfy the quartic equation that can be obtained from the secular equation about zn
, an are the corresponding coefficients. The zn of a non-trivial solution must satisfy the quartic equation that can be obtained from the secular equation about zn

This is a strict relationship between an eigenenergy and its wave function. For a semi-infinite nanowire case, the Majorana mode is exact zero energy and its wave function has been investigated in detail [31]. The condition that Majorana zero modes appear in the nanowire is 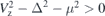 [15].
[15].
After solving the equation (3), we can obtain all values of zn for a given E. For each zn, the corresponding un(x) without renormalization is given by
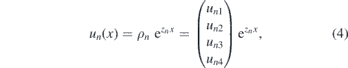
and the four components are
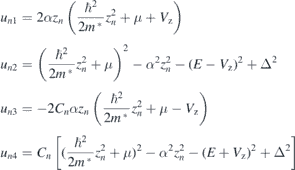
with
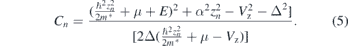
One can prove that Cn = 1 for the exact zero-energy mode E = 0.
To determine the energy of in-gap bound states, the boundary conditions of a wave function for a wire with finite length are needed. At the boundary x = ±L/2 (L is the wire length), we impose boundary conditions such that the wave function vanishes at the ends, Ψ(±L/2) = 0. Combining equations (2) with (4), we can get eight equations about an (n = 1, 2..., 8) from boundary conditions  . It is required that the coefficient matrix about an has a vanishing determinant and the secular equation about E becomes
. It is required that the coefficient matrix about an has a vanishing determinant and the secular equation about E becomes
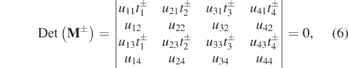
where  ,
,  and zm are four roots with non-negative real part. Details are given in the appendix
and zm are four roots with non-negative real part. Details are given in the appendix
Because of the complexity of the Hamiltonian, it is difficult to obtain the analytical expression of Majorana energy splitting. The energy spectrum and the wave functions are solved numerically from equation (6). However, for strong enough Zeeman splitting, the explicit formula about Majorana energy splitting is presented by trial function method [as shown in equation (13)]. It is noted that the numerical methods in general refer to the tight-binding calculation. Here the trial wave function method is used to solve the BdG equation with a set of proper boundary conditions, which usually refers to the analytical treatment.
In the following, we present and discuss the numerical results on the energy spectra and the corresponding wave functions of the semiconductor–superconductor hybrid system in the homogeneous and the inhomogeneous case respectively. We derive an analytic formula of the splitting energy of Majorana modes for a finite effective p-wave superconducting nanowire.
3. Homogeneous case
In figure 1, we present the splitting energy of Majorana modes as a function of Zeeman field Vz for different wire lengths with the chemical potential μ = 0.2 meV. In addition to the energy levels of MBSs, the full low-energy spectra are also illustrated in figure 1. Two lowest-energy spectra obtained by using tight binding method are plotted for comparison. When performing the tight-binding method (TB), we usually need to firstly discretize the continuum model into a lattice model, where only the hopping between the nearest neighbor sites is considered. Therefore, the energy spectrum and eigenstates obtained from the tight-binding method are the approximated results. Differently, no approximation is considered when performing the trial-wave functions method. In this sense, the trial wave function method is better than TB. When Vz exceeds a critical value  (
(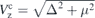 ), the energy band experiences a closing and reopening process, corresponding to the topological phase transition. For
), the energy band experiences a closing and reopening process, corresponding to the topological phase transition. For  , a set of Majorana energy mode appears near the zero energy. It is shown that the energy splitting of Majorana modes is oscillatory and the splitting strength becomes stronger with the increase of Zeeman field. For a longer nanowire, the finite-size effect becomes weaker and the splitting energy is suppressed, while the oscillation period becomes smaller. Importantly, the oscillation of zero mode splitting is always accompanied by the oscillation of other in-gap states. Different from the MBSs, they are prohibited by the topology. These in-gap states and their oscillatory behaviors are a manifestation of the finite-size effect. Our numerical results indicate that the oscillation magnitude of band gap is comparable to that of zero mode splitting for relatively large Zeeman field.
, a set of Majorana energy mode appears near the zero energy. It is shown that the energy splitting of Majorana modes is oscillatory and the splitting strength becomes stronger with the increase of Zeeman field. For a longer nanowire, the finite-size effect becomes weaker and the splitting energy is suppressed, while the oscillation period becomes smaller. Importantly, the oscillation of zero mode splitting is always accompanied by the oscillation of other in-gap states. Different from the MBSs, they are prohibited by the topology. These in-gap states and their oscillatory behaviors are a manifestation of the finite-size effect. Our numerical results indicate that the oscillation magnitude of band gap is comparable to that of zero mode splitting for relatively large Zeeman field.
Figure 1. Low-energy spectra obtained by using the trial wave function method (TWF) as a function of Vz for different wire lengths with μ = 0.2 meV (a) L = 1 μm and (b) L = 2 μm. Two lowest-energy spectra obtained by using the tight binding method (TB) are plotted (the red dash dot line) for comparison [the number of sites used in calculation are N1 = 100 and N2 = 200 for (a) and (b)]. The parameters used in the calculation are Δ = 0.25 meV, α2m*/2ℏ2 = 0.05 meV, and m* = 0.015me, where me is the electron mass.
Download figure:
Standard image High-resolution imageIn figure 2, we demonstrate the splitting energy of Majorana modes as a function of the chemical potential for different wire lengths with applied external Zeeman field Vz = 1.0 meV. Two lowest-energy spectra obtained by using tight binding method are also plotted. The energy gap closes at two critical points ±μc (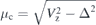 ), and the MBSs appear in the topological regime (−μc, μc). Similar to the case of varying Zeeman field, the splitting energy of Majorana mode also shows an oscillation behavior and the oscillatory magnitude increases with the increase of the chemical potential. For μ < −μc, no discrete energy levels are found in the energy gap. However, in another topological trivial phase with μ > μc, there are several discrete energy levels appear in the gap, as shown in figure 2. For a relatively short wire, even the zero-energy mode appears and it also oscillates as a function of chemical potential. The zero-energy modes in the trivial phase are induced by the finite-size effect. When we increase the chemical potential, these modes have a different behavior to that of MBSs in the topological phase. They are not topologically protected and easier to be destroyed by disorder. For the case of longer wire, the oscillation of zero energy mode in the topological phase becomes weaker and its period is smaller. In the topological trivial phase, the zero energy mode disappears gradually, and the discrete energy modes are away from zero energy further with the increase of the chemical potential of the nanowire.
), and the MBSs appear in the topological regime (−μc, μc). Similar to the case of varying Zeeman field, the splitting energy of Majorana mode also shows an oscillation behavior and the oscillatory magnitude increases with the increase of the chemical potential. For μ < −μc, no discrete energy levels are found in the energy gap. However, in another topological trivial phase with μ > μc, there are several discrete energy levels appear in the gap, as shown in figure 2. For a relatively short wire, even the zero-energy mode appears and it also oscillates as a function of chemical potential. The zero-energy modes in the trivial phase are induced by the finite-size effect. When we increase the chemical potential, these modes have a different behavior to that of MBSs in the topological phase. They are not topologically protected and easier to be destroyed by disorder. For the case of longer wire, the oscillation of zero energy mode in the topological phase becomes weaker and its period is smaller. In the topological trivial phase, the zero energy mode disappears gradually, and the discrete energy modes are away from zero energy further with the increase of the chemical potential of the nanowire.
Figure 2. Low-energy spectra obtained by using the trial wave function method (TWF) as a function of μ for different wire lengths with Vz = 1.0 meV (a) L = 1 μm and (b) L = 2 μm. Two lowest-energy spectra obtained by using tight binding method (TB) are plotted (the red dash dot line) for comparison [the number of sites used in calculation are N1 = 100 and N2 = 200 for (a) and (b)]. Other parameters are taken as that of figure 1.
Download figure:
Standard image High-resolution imageIn the strong Zeeman field regime that Vz ≫ m*α2/ℏ2, Δ, the spins nearly polarize and one can project the original Hamiltonian into a simpler one-band problem. To leading order, one obtains an effective p-wave like Hamiltonian [9, 38–40]
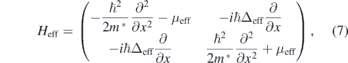
where μeff = μ + Vz/2 and the effective p-wave pairing field is Δeff = αΔ/Vz. Assuming the trial wave function
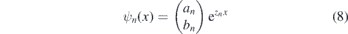
and substituting it into the eigenequation, the secular equation about zn is given by
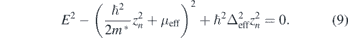
The wave function Ψ(x) of the eigenstates can be considered as a linear combination of ψn(x),
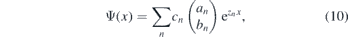
where

By using the vanishing boundary condition ψ(x = ±L/2) = 0, we finally arrive at the transcendental equation for the bound state energies
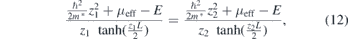
where z1 and z2 are the roots with positive real part. After some algebra, we obtain an analytical expression of the Majorana energy splitting
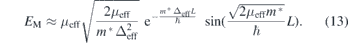
The appearance of the sine function with a function of L, Vz and μ as its arguments can account for the oscillation behaviors of the Majorana energy splitting. The factor in front of the sine function, which is an increasing function of μ or Vz, gives rise to an increasing oscillation amplitude. One can also notice an exponential damping of the oscillation amplitude as a function of L.
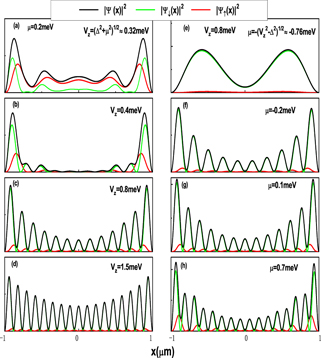
Once an eigenenergy of the system is found, its corresponding wave function and probability density distribution in real space could be obtained. Since Hamiltonian equation (1) is written down in terms of the Nambu spinor 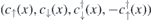 , the wave function of an eigenstate takes the form Ψ(x) = (ψ↑(x), ψ↓(x), ϕ↓(x), ϕ↑(x)). In figure 3, we present the probability density |Ψσ(x)|2 = |ψσ(x)|2 + |ϕσ(x)|2 (σ = ↑, ↓) and |Ψ(x)|2 = |Ψ↓(x)|2 + |Ψ↑(x)|2 of the wave function along the wire for different Zeeman fields with a fixed chemical potential μ = 0.2 meV and different chemical potentials with a fixed Zeeman field Vz = 0.8 meV. The nanowire we considered has a length L = 2 μm. From the above discussions, the finite-size effect is supposed to be more weaker. Near the transition point
, the wave function of an eigenstate takes the form Ψ(x) = (ψ↑(x), ψ↓(x), ϕ↓(x), ϕ↑(x)). In figure 3, we present the probability density |Ψσ(x)|2 = |ψσ(x)|2 + |ϕσ(x)|2 (σ = ↑, ↓) and |Ψ(x)|2 = |Ψ↓(x)|2 + |Ψ↑(x)|2 of the wave function along the wire for different Zeeman fields with a fixed chemical potential μ = 0.2 meV and different chemical potentials with a fixed Zeeman field Vz = 0.8 meV. The nanowire we considered has a length L = 2 μm. From the above discussions, the finite-size effect is supposed to be more weaker. Near the transition point  , the wave function for MBSs is mainly localized at both ends of the wire, and there is no oscillatory overlap between two well-separated wave packets. In the case where Vz is small, two spin parts |Ψ↓(x)|2 and |Ψ↑(x)|2 contribute comparably to the |Ψ(x)|2, as shown in figure 3(a). With the increase of Vz, the main wave packets move along the wire gradually and the distribution indicates an oscillatory behavior. For a strong enough Vz, the distribution of the MBSs is not restricted to the wire ends any more and |Ψ(x)|2 mainly comes from |Ψ↓(x)|2 [see figures 3(c) and (d)]. Majorana modes could nearly polarize in a specified direction [9], here, the z direction. Other Majorana spin related properties have been investigated [41]. Although a Majorana mode is stable in the topological region, the wave function of a Majorana mode is almost equally distributed in the wire for large Vz, as indicated in figure 3(d). In this case, the topologically protected Majorana mode is not bound states any more. In the figures 3(e)–(h), we vary the chemical potential of the nanowire. The applied Zeeman field Vz = 0.8 meV is large enough to show that the spin component of wave density |Ψ↑(x)|2 is suppressed. At the lower critical point μ = −μc, the wave function of MBSs is localized at the ends of a nanowire and no oscillatory overlap is formed. As we tune the chemical potential away from this critical point and into the topological regime, the overlap of wave functions of two end MBSs becomes oscillatory. Near two critical points μ = ±μc, the Majorana zero mode shows quite different behavior. For μ ∼ μc, there are two imaginary roots and the Majoarana wave function displays the envelope oscillation. While for μ ∼ −μc, all the roots are real and the wave function exponentially decays along the wire.
, the wave function for MBSs is mainly localized at both ends of the wire, and there is no oscillatory overlap between two well-separated wave packets. In the case where Vz is small, two spin parts |Ψ↓(x)|2 and |Ψ↑(x)|2 contribute comparably to the |Ψ(x)|2, as shown in figure 3(a). With the increase of Vz, the main wave packets move along the wire gradually and the distribution indicates an oscillatory behavior. For a strong enough Vz, the distribution of the MBSs is not restricted to the wire ends any more and |Ψ(x)|2 mainly comes from |Ψ↓(x)|2 [see figures 3(c) and (d)]. Majorana modes could nearly polarize in a specified direction [9], here, the z direction. Other Majorana spin related properties have been investigated [41]. Although a Majorana mode is stable in the topological region, the wave function of a Majorana mode is almost equally distributed in the wire for large Vz, as indicated in figure 3(d). In this case, the topologically protected Majorana mode is not bound states any more. In the figures 3(e)–(h), we vary the chemical potential of the nanowire. The applied Zeeman field Vz = 0.8 meV is large enough to show that the spin component of wave density |Ψ↑(x)|2 is suppressed. At the lower critical point μ = −μc, the wave function of MBSs is localized at the ends of a nanowire and no oscillatory overlap is formed. As we tune the chemical potential away from this critical point and into the topological regime, the overlap of wave functions of two end MBSs becomes oscillatory. Near two critical points μ = ±μc, the Majorana zero mode shows quite different behavior. For μ ∼ μc, there are two imaginary roots and the Majoarana wave function displays the envelope oscillation. While for μ ∼ −μc, all the roots are real and the wave function exponentially decays along the wire.
Figure 3. The probability density |Ψ(x)|2, |Ψ↓(x)|2 and |Ψ↑(x)|2 of MBSs in a topological nanowire for L = 2 μm. Other parameters are taken as that of figure 1.
Download figure:
Standard image High-resolution image4. Inhomogeneous case
The present trial wave function method also allows us to extend the discussion to the inhomogeneous nanowire case, which is expected to provide new evidence for the Majorana existence. In this section we consider an inhomogeneous case where a nanowire has two segments with different chemical potentials. The proposed scheme is shown in figure 4(a). The lengths of two segments are L1 = 1.5 μm, L2 = 0.5 μm respectively, and are assumed to be much larger than any decay length. This assumption means the Majorana energy splitting is much smaller than the induced superconducting gap. To solve the BdG equation of the entire nanowire, we invoke continuity of the wave functions and their first derivative, i.e. Ψ(x = 0+) = Ψ(x = 0−), ∂xΨ(x = 0+) = ∂xΨ(x = 0−), and impose vanishing boundary conditions at two ends, Ψ(x = −L1) = Ψ(x = L2) = 0. The eigenenergies and their wave functions of the inhomogeneous nanowire can be found in various regimes by matching the boundary conditions.
Figure 4. (a) Scheme of the device. A semiconductor nanowire is in contact with a s-wave superconductor which leads to proximity-induced superconductivity in the nanowire. The nanowire is divided into two parts, and a local gate voltage VG2 is applied. (b) Two different physical regimes of the inhomogeneous nanowire. The left panel corresponds the chemical potential μ2 in the pink region which is lower than the critical value 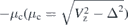 , while the right panel represents the case μ2 > μc.
, while the right panel represents the case μ2 > μc.
Download figure:
Standard image High-resolution imageIn figure 5, the low-energy spectra of full system are plotted as a function of the chemical potential μ2 controlled by a local gate voltage applied on the shorter segment. The longer segment is in topological superconducting phase. In the topological nontrivial regime of the shorter segment, it is shown in figure 5 that the MBS energy is periodically modulated by the local gate voltage. The barrier region is formed in the shorter segment of the nanowire for −μ2 > −μ1, while a well region is formed in the shorter segment in the case of for −μ2 < −μ1. For the potential well case with the chemical potential exceeding the upper topological transition point 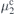 (
( ), there still exist some oscillatory near-zero-energy modes, while such near-zero-energy states are absent in the barrier case where the chemical potential of the shorter segment is smaller than the lower topological transition value
), there still exist some oscillatory near-zero-energy modes, while such near-zero-energy states are absent in the barrier case where the chemical potential of the shorter segment is smaller than the lower topological transition value 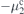 . Figure 5 suggests that the Majorana energy oscillation can be tuned by locally modulating the chemical potential in one part of the nanowire.
. Figure 5 suggests that the Majorana energy oscillation can be tuned by locally modulating the chemical potential in one part of the nanowire.
Figure 5. Numerical results of low-energy spectra as a function of the chemical potential μ2 of the short part with Δ = 0.25 meV, Vz = 1.0 meV and μ1 = 0.2 meV. The longer segment is a topological superconductor in the present parameter setting.
Download figure:
Standard image High-resolution imageWe present the spatial probability density distribution of the Majorana wave function by tuning the local gate voltage in figure 6. It is illustrated that the Majorana wave function is almost spatially localized in the topological superconductor region for the barrier case [see figures 6(a) and (b)]. With the increase of the local gate voltage, the entire nanowire is tuned into the topological regime and the MBSs are localized at two wire ends asymmetrically due to the chemical potential difference of two segments [see figure 6(c)]. As the local gate voltage increases further and the shorter segment is driven out of the topological regime, the Majorana state could also penetrate into the well region, as shown in figures 6(d)–(f). There exists a near-zero-energy state in the well region and it could merge with the Majorana state. The wave functions of the lowest-energy bound states in these two regimes indicate different behaviors, but they could coexist in the nanowire. As shown in right panels of figure 6, it is interesting that both spin components of the trivial Andreev bound states in the potential well region account for a significant proportion, while MBSs in the topological region are almost fully spin-polarized.
Figure 6. The probability density |Ψ(x)|2, |Ψ↓(x)|2, and |Ψ↑(x)|2 of MBSs as a function of x. Other parameters are taken as that of figure 5.
Download figure:
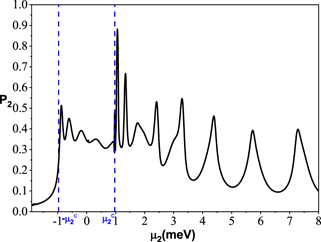
Standard image High-resolution imageWe now proceed to investigate the dependence of the leakage of MBSs on the local gate voltage μ2 in the gated region. In figure 7, we plot total probability P2 of the lowest eigenstate in the gated region of the nanowire as a function of the gate voltage μ2. We see that the leakage of the MBSs depends significantly on the gate voltage. For a low enough gate voltage case that  , the wave functions of the MBSs are almost localized in the topological region. In this case, the probability densities |Ψ|2 in the gated region are exponentially suppressed with the decrease of μ2. For the case that the gated region is in the topological regime, i.e.,
, the wave functions of the MBSs are almost localized in the topological region. In this case, the probability densities |Ψ|2 in the gated region are exponentially suppressed with the decrease of μ2. For the case that the gated region is in the topological regime, i.e.,  , the MBSs are well located in the two wire ends and P2 equals to 1/2 approximately. As μ2 increases further and the gated region is in the trivial phase again, the probability leakage magnitude indicates strong oscillation and does not decay even for the strong enough well, as shown in figure 7. Indeed, for
, the MBSs are well located in the two wire ends and P2 equals to 1/2 approximately. As μ2 increases further and the gated region is in the trivial phase again, the probability leakage magnitude indicates strong oscillation and does not decay even for the strong enough well, as shown in figure 7. Indeed, for  the near-zero-energy Andreev bound states in the trivial region are expected to live, as proved in figure 2 and hybridize with MBSs in the topological region. When an inhomogeneous topological nanowire with part of it being topological trivial, strictly speaking, we can not tell whether a lowest-energy state is topological or not. Physically, we can treat it as the coalescence of a topological state and an Andreev bound state. However, the appearance of these Andreev bound states in topological trivial region could strongly influence the local measurement of Majorana properties [24]. In the experiments, the tunnel probe is attached to the gated part of the nanowire and is thus predominantly coupled to the Andreev states. Therefore, the measured electrical signature such as the conductance, may not be the manifestation of MBSs. It is important to distinguish the signature of MBSs from the weak coupling between the tunnel probe at the end of the wire and trivial Andreev states in the gated region of the wire.
the near-zero-energy Andreev bound states in the trivial region are expected to live, as proved in figure 2 and hybridize with MBSs in the topological region. When an inhomogeneous topological nanowire with part of it being topological trivial, strictly speaking, we can not tell whether a lowest-energy state is topological or not. Physically, we can treat it as the coalescence of a topological state and an Andreev bound state. However, the appearance of these Andreev bound states in topological trivial region could strongly influence the local measurement of Majorana properties [24]. In the experiments, the tunnel probe is attached to the gated part of the nanowire and is thus predominantly coupled to the Andreev states. Therefore, the measured electrical signature such as the conductance, may not be the manifestation of MBSs. It is important to distinguish the signature of MBSs from the weak coupling between the tunnel probe at the end of the wire and trivial Andreev states in the gated region of the wire.
Figure 7. Total probability of Ψ(x) in the short part as a function of μ2. Other parameters are taken as that of figure 5.
Download figure:
Standard image High-resolution imageA recent experimental paper by Albrecht et al [30] reports the apparent observation of exponential topological protection in Majorana nanowires. The observation can be explained by the overlap of the two MBSs localized at the two ends of the nanowire is exponentially small as the increase of the wire length. However, the magnetic field dependence of the MBS energy splitting indicates a damping oscillation, which contradicts with the theoretical predictions. To explain this disagreement, some possible scenarios are proposed [42–45]. One of them suggested that for an inhomogeneous nanowire [43–45], the appearance of the trivial Andreev bound states plays an essential role. Our results indicate that in a simple scenario, the trivial Andreev states are hard to survive in the case of a high potential barrier imposed at one end of the nanowire, which is previously expected to prevent the leakage of MBSs. The wave function of MBSs is exponentially suppressed in the barrier region and is hard to leak out of the topological region. However, there always exists a near-zero-energy Andreev bound states in the gated well region. The measured conductance signature about MBSs are unavoidable to coalesce with the feature of Andreev bound states. It is interesting that in a deep gated well region, both the spin-up and spin-down components of the trivial Andreev bound states make considerable contribution in the wave function distribution. In contrast, the MBSs are almost fully spin-polarized. Such a feature could be detected experimentally [26, 46].
5. Conclusion
In summary, we present an exact solution of the continuum BdG equation for MBSs generated in a superconductor–semiconductor hybird topological nanowire using the trial wave function method. In the simple homogeneous case, it is found that the zero-energy mode could also be produced in the topological trivial regime for a shorter nanowire, which also have oscillatory dependence on the chemical potential. The behaviors of Majorana energy splitting could be well explained by an analytic formula we derived using the trial wave function method.
In the inhomogeneous case, we investigate the low-energy spectra as a function of the chemical potential of the gated region and probability density distribution along the nanowire. Our numerical results show that a chemical potential barrier can prevent the leakage of MBSs and suppress the appearance of extra near-zero-energy Andreev bound states. In contrast, for a chemical potential well case, the trivial Andreev bound states are always generated and coalesced with MBSs at the interface of two parts. Different from MBSs which are almost fully spin-polarized, both spin components of Andreev bound states are significant in the well region. Such a feature could be served as a probe to discriminate the MBSs and Andreev bound states.
Acknowledgments
We acknowledge the helpful discussion with Prof Shun-Qing Shen and Prof Hai-Zhou Lu. This work was supported by the Natural Science Foundation of China under Grant No. 61474018 and No. 11574173, the Fundamental Research Funds for the Central Universities (No. ZYGX2019J100) and the Open Project of State Key Laboratory of Low-Dimensional Quantum Physics (Grant No. KF202008).
Appendix A.: The derivation of equation (6)
In this appendix, we present a detailed derivation of equation (6). For any zn, there exists another root −zn and its wave function is given by
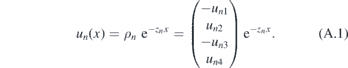
Therefore, the total wave function can be expressed as
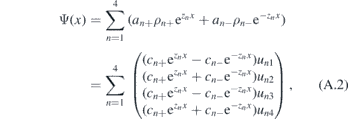
where zn (n = 1, 2, 3, 4) are the roots with Re[zn] ⩾ 0. Defining the functions
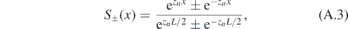
one can get
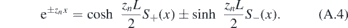
At the boundary x = ±L/2, the wave function equals to zero Ψ(±L/2) = 0. Because S±(L/2) = 1 and S±(−L/2) = ±1, we get the boundary condition
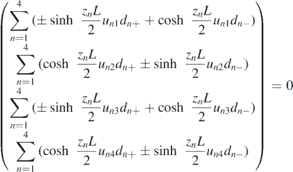
with dn± = (an+ ± an−).
From above boundary condition, we have
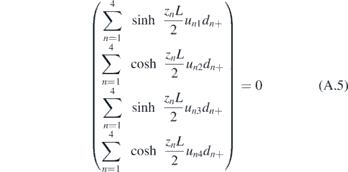
and
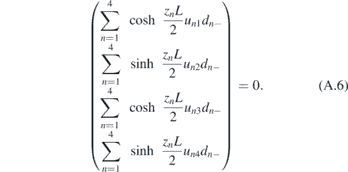
To obtain the nonzero solution of dn±, the secular equations about E becomes
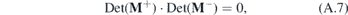
where
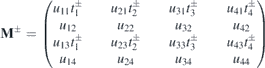
with  and
and  .
.