Abstract
The water confined within a surfactant bilayer is studied using different water models via molecular dynamics simulations. We considered four representative rigid models of water: the SPC/E and the TIP4P/2005, which are commonly used in numerical calculations and the more recent TIP4Q and SPC/ε models, developed to reproduce the dielectric behaviour of pure water. The static dielectric constant of the confined water was analyzed as a function of the temperature for the four models. In all cases it decreases as the temperature increases. Additionally, the static dielectric constant of the bilayer-water system was estimated through its expression in terms of the fluctuations in the total dipole moment, usually applied for isotropic systems. The estimated dielectric was compared with the available experimental data. We found that the TIP4Q and the SPC/ε produce closer values to the experimental data than the other models, particularly at room temperature. It was found that the probability of finding the sodium ion close to the head of the surfactant decreases as the temperature increases, thus the head of the surfactant is more exposed to the interaction with water when the temperature is higher.
Export citation and abstract BibTeX RIS
This article was amended on 26 Apr 2018 to correct the corresponding author information.
1. Introduction
Significant progress has been made to understand the structural and thermodynamic aspects of the surfactant-solution interactions. Sodium dodecyl sulfate (SDS) surfactant exhibits a broad interest in numerous applications. Bilayers formed by SDS are essential for many purposes, for instance in biological systems [1], in industrial applications such as enhanced oil-recovery [2, 3], mineral beneficiation [4], coatings, medicine [5], food and cosmetics. Actually, the colloidal science has a growing interest in applications where biological bilayers are present. These applications often involve the adsorption and deposition of complexes and/or the control of the surface layer composition. The SDS molecule has two regions, a polar head and a non-polar tail. The interaction of SDS with water combined with other factors such as the thermodynamic conditions, the concentration of surfactant, the presence of salt, etc produces a broad class of structures, for example spherical micelles, rodlike shapes, hexagonal and lamellar phases, bilayers and foams, which modify the properties of the mixture.
Several simulation studies have been performed to understand thermodynamic, structural and electrical properties of SDS surfactant in aqueous medium. The agreement of the calculated properties with the experimental data depends on the quality of the force field used in the simulations. Recently, Tang et al [6] performed molecular dynamics simulations of SDS in water with the aim of studying both, the effect of the force field (for surfactant, water and ions) and the simulation conditions, on the formation of spherical micelles and other shapes. Nevertheless, as far as we know there are not studies showing the effect of using different water models on the dielectric properties of these systems. Actually, this would have been a difficult task, particularly because until a few years ago, the experimental dielectric constant of pure water was very difficult to reproduce using the existing rigid models.
Regarding water models for molecular simulations, there has been an extensive effort in trying to accurately predict the properties of water. Although water is a molecule with a few atoms, its behaviour is quite complex. In fact, water shows a number of abnormalities in its thermodynamic and transport properties, it also exhibits a quite complex phase diagram. There are now several molecular models useful to predict these properties. In 2002 Guillot [7] conducted a review of 46 different water models indicating the lack of success in reproducing water properties. Since then, there has been a great progress in predicting several of them. Vega et al [8] carry out an overview for various rigid and non-polarizable water models. They tested 17 properties for solid and liquid–vapor systems evaluating the performance of each of them and providing a critical view of the successes and failures in simulating this ubiquitous component.
The dielectric constant describes the extent to which a liquid concentrates electric flux. This quantity is relevant to quantify the solubility and permeability of polar or charged species in multicomponent systems for example, in electrolyte solutions, mixtures of ionic liquids and polar solvents, protein-drug complexes in solution, etc.
A successful rigid water model such as the TIP4P/2005 fails to reproduce the dielectric constant at room temperature and normal pressure, it gives about 58 [9], although predicts a better dielectric constant than its predecessor TIP4P for which the value is 50 [8], it is still far from the experimental value of 78.5 [8]. In fact, the SPC/E produces a better value of the dielectric constant equal to 70.8 [10]. With the recent advances new models have emerged. Alejandre et al developed the TIP4Q force field [11]. This model is rigid, consists of four sites with the same geometry as that of the TIP4P, its parameters were adjusted to reproduce the experimental dielectric constant at 298 K, the maximum density of liquid water and the equation of state at low pressures. Izadi et al [12] proposed the optimal 3-charge, 4-point rigid water model, which produces a dielectric constant of 78.4 at standard conditions. Fuentes et al [13] developed the SPC/ε rigid model, it has the original SPC/E geometry, but a new set of charges. The SPC/ε model gave similar thermodynamics and dynamic properties as those of the SPC and SPC/E, but its dielectric constant 80.2, is in better agreement with the experimental value. So, new parametrizations of rigid water models have emerged to reproduce the dielectric constant of pure water via molecular simulations.
On the other hand, there are very few experiments where the dielectric constant of SDS surfactant in aqueous medium has been measured [14]. Systems involving lipid or surfactant layers are very interesting and useful by themselves. They serve as models of foams, microemulsions, biological membranes and liquid films, which play a crucial role in different processes. There has been an important and valuable effort in quantifying the dielectric properties of bilayers or interfaces [15, 16]. For instance, Nymeyer et al [17] proposed a method to determine the position-dependent dielectric profile and obtain the dielectric constant in the different regions of mixed nonhomogeneous systems. They focused on determining how the dielectric constant changes as a function of the distance to the core of a membrane. Ballenegger and Hansen [18] have directed their efforts to validate the concept of a local dielectric permittivity starting from the statistical mechanical description, a linear response theory and extensive molecular dynamics simulations. Expressions for a local permittivity tensor were derived for planar and spherical geometries. However, when analyzing the information in the literature there is not consensus on how this calculation should be done when molecular simulation methods are applied. Firstly because these systems lack isotropy. So, some works focus on exploring the anisotropy [19, 20] and others in attributing an effective character to the dielectric constant [21]. Experimentally, there are recent studies where electrostatic force microscopy is used and the dielectric constant of a lipid bilayer is measured, to which a scalar character is attributed [22]. As a scalar, the dielectric constant of a lipid bilayer is generally low. For example, for a DPPC bilayer (1,2-dipalmitoyl-sn-glycero-3-phosphocholine), the dielectric constant value varies between 2 and 3 [22]. There are also experimental measurements of effective dielectric constant of mixtures of surfactants in water at  C [14]. However, we did not find studies where the dielectric constant of a liquid water film supported by layers of surfactant, was measured.
C [14]. However, we did not find studies where the dielectric constant of a liquid water film supported by layers of surfactant, was measured.
In this work we present a study of the water confined between two layers of surfactant emulating a liquid film. Two of the most employed models of water are considered, the SPC/E [23] and the TIP4P/2005 [9]; as well as two innovative models, the SPC/ [13] and the TIP4Q [11]. The aim of this work is to analyze the performance of these four water models in terms of the dielectric constant of the water confined between two surfactant layers of sodium dodecyl sulfonate (C12H25SO3Na), for which the acronym SDS will be preserved. We would like to emphasize that the calculation of the static dielectric constant of anisotropic systems using molecular simulation is not a routine calculation or a computation that it is easily achievable, so the results will be discussed in terms of the formula without anisotropy, applied to the confined water and to the entire system. The isotropic formula is applicable to homogeneous systems and is certainly not the most adequate to evaluate the dielectric behavior of a system with the geometry of a bilayer. However, it is the most direct to quantify roughly the effects of confinement using some of the most commonly used models.
[13] and the TIP4Q [11]. The aim of this work is to analyze the performance of these four water models in terms of the dielectric constant of the water confined between two surfactant layers of sodium dodecyl sulfonate (C12H25SO3Na), for which the acronym SDS will be preserved. We would like to emphasize that the calculation of the static dielectric constant of anisotropic systems using molecular simulation is not a routine calculation or a computation that it is easily achievable, so the results will be discussed in terms of the formula without anisotropy, applied to the confined water and to the entire system. The isotropic formula is applicable to homogeneous systems and is certainly not the most adequate to evaluate the dielectric behavior of a system with the geometry of a bilayer. However, it is the most direct to quantify roughly the effects of confinement using some of the most commonly used models.
The rest of the work is presented as follows: in section 2 the models and methods are given, section 3 contains the simulation details, the results are discussed in section 4 and conclusions are given in section 5.
2. Models and method
We consider an all-atom description of the bilayer-water system, meaning that we include every atom explicitly. The interactions were calculated using the OPLS-AA force field energy function [24]. Since Canongia-Lopes et al [25] developed a parametrization of ionic liquids, in which the sulfate and sulfonate anions parameters are compatible with the OPLS-AA force field, we used them. The potential energy function is
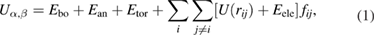
where,  is the interaction energy between molecules α and β, Ebo is the bond energy
is the interaction energy between molecules α and β, Ebo is the bond energy  , kb,ij is the spring constant between two bonded atoms i and j, rij is the distance between them and r0,ij is the equilibrium distance. The angular energy Ean, is
, kb,ij is the spring constant between two bonded atoms i and j, rij is the distance between them and r0,ij is the equilibrium distance. The angular energy Ean, is  , where
, where  is the angular constant relating the atoms i, j and k,
is the angular constant relating the atoms i, j and k,  is the bond angle and
is the bond angle and  is the equilibrium angle that relates three bonded atoms. A third contribution to the potential energy is the torsion energy, Etor. It is given as
is the equilibrium angle that relates three bonded atoms. A third contribution to the potential energy is the torsion energy, Etor. It is given as

where  is the Fourier coefficient that relates four bonded atoms,
is the Fourier coefficient that relates four bonded atoms,  is the dihedral angle for the i − j − k − l atoms and m takes values from
is the dihedral angle for the i − j − k − l atoms and m takes values from  , where N is the number of terms to consider in the series. The last contribution to the potential energy is the interaction between non-bonded atoms. This contribution represents the pair-wise sum of the energies of all possible interacting non-bonded atoms i and j. The non-bonded energy accounts for short-ranged repulsion, van der Waals attraction, and electrostatic interaction. The energy term that describes the attraction and repulsion is modeled using the Lennard-Jones (LJ) potential, U(rij), given by
, where N is the number of terms to consider in the series. The last contribution to the potential energy is the interaction between non-bonded atoms. This contribution represents the pair-wise sum of the energies of all possible interacting non-bonded atoms i and j. The non-bonded energy accounts for short-ranged repulsion, van der Waals attraction, and electrostatic interaction. The energy term that describes the attraction and repulsion is modeled using the Lennard-Jones (LJ) potential, U(rij), given by

where rij is the distance between i and j,  is the length at which the potential between is zero and
is the length at which the potential between is zero and  is the well depth. Finally, the electrostatic interaction is modeled using a Coulombic potential, it is a function of the charges on the non-bonded atoms, qi and qj and on the distance rij, calculated by
is the well depth. Finally, the electrostatic interaction is modeled using a Coulombic potential, it is a function of the charges on the non-bonded atoms, qi and qj and on the distance rij, calculated by  . The scaling factor fij in equation (1) is 1 for LJ and Coulombic interactions, except for intramolecular interactions separated by three bonds, where a value of 0.5 is used.
. The scaling factor fij in equation (1) is 1 for LJ and Coulombic interactions, except for intramolecular interactions separated by three bonds, where a value of 0.5 is used.
As explained in the introduction, there are many water models reported in the literature. In the present study two popular and two novel water models are used: SPC/E [23], TIP4P/2005 [9], SPC/ε [13] and TIP4Q [11]. The geometry and parameters of these water models are listed in table 1. For the later two, the parameters were included in the force field files.
Table 1. Parameters of the rigid water models with three and four sites, kB is the Boltzmann constant. The dipole moment produced by each model is ![$\mu=q_{\rm H}[2r_{\rm OH}{\cos(\theta/2)}-r_{\rm OM}]$](https://content.cld.iop.org/journals/0953-8984/30/19/195001/revision2/cmaab9eeieqn015.gif) .
.
| rOH (Å) | θ (degrees) |  |
 |
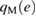 |
rOM (Å) |  (Å) (Å) |
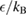 (K) (K) |
|
|---|---|---|---|---|---|---|---|---|
| SPC/E | 1 | 109.47 | 0.4238 | −0.8476 | 0.0 | 0.0 | 3.166 | 78.2 |
| SPC/ε | 1 | 109.47 | 0.4450 | −0.89 | 0.0 | 0.0 | 3.166 | 78.2 |
| TIP4P/2005 | 0.9572 | 104.52 | 0.5564 | 0.0 | −1.1128 | 0.1546 | 3.1589 | 93.2 |
| TIP4Q | 0.9572 | 104.52 | 0.525 | 0.5 | −1.550 | 0.069 | 3.1666 | 93.2 |
For the bilayer-water systems, a set of parameters capable of describing the conformational space of molecules and ions is used and they were written to satisfy the equations related to the force field. The parameters of the SDS molecule such as bond lengths, charges, bond and dihedral angles, and LJ parameters are taken from Canongia-Lopes et al [25]. The nomenclature used for the atoms in the SDS surfactant is presented in figure 1 and the modified parameters of this molecule are given in table 2. The rest of the parameters were taken from the OPLS-AA force field file and remained unchanged. This SDS model was used in all the simulations for the different water models.
Figure 1. Nomenclature adopted in the allocation of parameters for the sodium dodecyl sulfonate ( ). The surfactant carries a net negative charge of −1e, while their counterions carry charge +1e (not shown).
). The surfactant carries a net negative charge of −1e, while their counterions carry charge +1e (not shown).
Download figure:
Standard image High-resolution imageTable 2. Parameters of sodium dodecyl sulfonate employed in the simulations, taken from [25].
| Atom | q (e) |  (kJmol−1) (kJmol−1) |
σ (Å) | Angles | 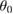 (degrees) (degrees) |
 (kJ mol−1 rad−2) (kJ mol−1 rad−2) |
|---|---|---|---|---|---|---|
| S1 | 1.18 | 1.046 | 3.55 | O1-S1-O2 | 114.0 | 484.5 |
| O1 | –0.68 | 0.837 | 3.15 | O3-S1-C1 | 104.5 | 435.0 |
| C1 | –0.14 | 0.276 | 3.50 | S1-C1-H1 | 107.3 | 195.15 |
| C2 | –0.12 | 0.276 | 3.50 | S1-C1-C2 | 113.3 | 291.5 |
| H1 | 0.00 | 0.126 | 2.50 | — | — | — |
| Bond | r0 (nm) | kr (kJ mol−1 nm−2) | Dihedral | V1 (kJ mol−1) | V2 (kJ mol−1) | V3 (kJ mol−1) |
| C1-S1 | 0.1792 | 985000 | O1-S1-C1-H1 | 0 | 0 | 1.625 |
| O1-S1 | 0.1455 | 266655 | O2-S1-C1-C2 | 0 | 0 | 1.3938 |
| — | — | — | S1-C1-C2-H4 | 0 | 0 | 1.3797 |
| — | — | — | S1-C1-C2-C3 | –16.1 | −2.0046 | 0.7674 |
3. Simulation details
All molecular dynamics simulations are carried out using the GROMACS (version 4.6.4) simulation package [26]. As a first step we carried out simulations of pure water to calculate the dielectric constant, radial distribution functions, density profiles and surface tension of the SPC/E, TIP4P/2005, SPC/ε and TIP4Q water models. At this stage we performed NPT and liquid–vapor NVT simulations, the later were used to calculated the surface tension at 298 K, while the NPT runs were prepared at 298 K and 105 Pa (1 bar). We obtained a dielectric constant of 72.7, 58.0, 80.6 and 80.1, respectively, whereas the corresponding surface tension values were 62.3, 68.0, 72.2 and 69.0. In this way we ensured that these properties are in agreement with those reported in the literature for the models under consideration [11, 13, 23, 27]. The simulated conditions were the same as those used in the references just given.
As already mentioned an OPLS-AA force field is used and molecular dynamics simulation are carried out to obtain structural and electrical properties of the water confined between two surfactant layers. Firstly, to build the bilayer-water systems a water block with 4878 water molecules is placed in the middle of a parallelepiped simulation cell with box lengths,  nm, and Lz = 20 nm surrounded by two layers of SDS surfactant, one at each side and orientated perpendicular to the z-axis. Regarding the surfactant molecules, the topology OPLS-AA file was built by TopolGen.pl version 1.1_dev written by Lemkul [28]. This file was generated automatically from the pdb file of SDS, which was built using PyMOL package version 1.7.0.0 [29]. Each bilayer consisted of 78 surfactant molecules and each molecule carried a charge −1e. With these number of surfactants, water molecules and box area we have a surface density close to the experimental value [30]. In addition, 156 sodium ions carrying charge +1e were randomly added to the water block to leave the system electrically neutral. After the construction of the whole simulation cell, the energy was minimized using the steepest descent method with 1000 steps to remove high-energy contacts that might have formed during the construction process. Once the energy is minimized, an NPT-semiisotropic pressure coupling is used [31]. Being Lz the variable length and
nm, and Lz = 20 nm surrounded by two layers of SDS surfactant, one at each side and orientated perpendicular to the z-axis. Regarding the surfactant molecules, the topology OPLS-AA file was built by TopolGen.pl version 1.1_dev written by Lemkul [28]. This file was generated automatically from the pdb file of SDS, which was built using PyMOL package version 1.7.0.0 [29]. Each bilayer consisted of 78 surfactant molecules and each molecule carried a charge −1e. With these number of surfactants, water molecules and box area we have a surface density close to the experimental value [30]. In addition, 156 sodium ions carrying charge +1e were randomly added to the water block to leave the system electrically neutral. After the construction of the whole simulation cell, the energy was minimized using the steepest descent method with 1000 steps to remove high-energy contacts that might have formed during the construction process. Once the energy is minimized, an NPT-semiisotropic pressure coupling is used [31]. Being Lz the variable length and  the box area, Lz is allowed to fluctuate according to the component of the pressure Pzz, in this way we obtained the Lz side of the box that leads the system to the imposed pressure of 105 Pa. Newton's equations of motion are solved using the leap-frog algorithm [32] with a time step of 2 fs, the total number of steps was
the box area, Lz is allowed to fluctuate according to the component of the pressure Pzz, in this way we obtained the Lz side of the box that leads the system to the imposed pressure of 105 Pa. Newton's equations of motion are solved using the leap-frog algorithm [32] with a time step of 2 fs, the total number of steps was  , equivalent to 200 ns as time of simulation. In all the simulation the temperature is kept constant by using a Berendsen thermostat with a parameter of 0.5 ps. Periodic boundary conditions are applied in the three directions of the simulation cell. The PME method [26] is used to calculate the reciprocal interactions with a mesh of grid spacing of 0.12 nm in every direction and a spline of order 4. The short range potential is truncated at 1.2 nm. The bond distances are kept constant using the LINCS procedure [33].
, equivalent to 200 ns as time of simulation. In all the simulation the temperature is kept constant by using a Berendsen thermostat with a parameter of 0.5 ps. Periodic boundary conditions are applied in the three directions of the simulation cell. The PME method [26] is used to calculate the reciprocal interactions with a mesh of grid spacing of 0.12 nm in every direction and a spline of order 4. The short range potential is truncated at 1.2 nm. The bond distances are kept constant using the LINCS procedure [33].
4. Results and discussion
Figure 2 shows a snapshot of the system at 298 K and 105 Pa for the TIP4Q model. The water molecules are in the middle region. At the interfaces are the SDS surfactants forming layers. The sodium ions are observed close to the head of the surfactant.
Figure 2. Bilayer and water in equilibrium at 298 K and 105 Pa using the TIP4Q water model (water: pink-oxygen, white-hydrogen; SDS: cyan-carbon, white-hydrogen, yellow-sulfur, red-oxygen; ions: blue-sodium).
Download figure:
Standard image High-resolution imageAn important feature in these systems is the spatial distribution of the molecules, which can be quantified via the density profiles of the components. Therefore, we start by presenting them.
4.1. Density profiles
Figure 3 shows the average density profiles of water, SDS and ions, obtained for the different water models along the z-axis at 298 K and 105 Pa.
Figure 3. Partial density profile of each species in the system in z-direction for each water model at 298 K and 105 Pa.
Download figure:
Standard image High-resolution imageThe water profiles show a high density in the central region that decays at the interfaces. It is observed that the SPC/ε model produces the highest water density whereas the other models give essentially the same value. The SDS profiles display peaks at the interfaces, corresponding to the polar heads while the extremes of these curves show the local density of the tails, localized further from the water. Averaging the two interfaces, the SPC/E model gives the lowest density of the polar heads while the tails density is practically the same for the four models. Finally, the profiles of sodium ions exhibit a high density in the interfacial regions, which is related to the strong electrostatic attraction between the head of the surfactant and the sodium. From time to time, some ions are found into the bulk water, but on average they remain close to the head, therefore the ion density is very low in the water slab.
4.2. Radial distribution functions
In order to have an idea of the spatial distribution of the molecules in the systems, we calculated the radial distribution functions,  , of atom pairs. The
, of atom pairs. The  of the sulfur–ion and sulfur–water oxygen pairs, calculated at 298 K and 105 Pa are shown in figure 4 for the four water models. The sulfur–ion
of the sulfur–ion and sulfur–water oxygen pairs, calculated at 298 K and 105 Pa are shown in figure 4 for the four water models. The sulfur–ion  functions displayed in figure 4(a), show a high probability of finding these pairs of atoms close in the system. It is observed that the first maxima of the
functions displayed in figure 4(a), show a high probability of finding these pairs of atoms close in the system. It is observed that the first maxima of the  for the SPC/E and TIP4Q have slightly lower values than those of the SPC/ε and TIP4P/2005 models. Conversely, the sulfur–water oxygen distribution functions
for the SPC/E and TIP4Q have slightly lower values than those of the SPC/ε and TIP4P/2005 models. Conversely, the sulfur–water oxygen distribution functions  of the SPC/E and TIP4Q gave higher values than those obtained with the SPC/ε and TIP4P/2005 models, shown in figure 4(b). The radial distribution functions of the other pairs were very similar for the different models (not shown).
of the SPC/E and TIP4Q gave higher values than those obtained with the SPC/ε and TIP4P/2005 models, shown in figure 4(b). The radial distribution functions of the other pairs were very similar for the different models (not shown).
Figure 4. Radial distribution functions of (a) the sulfur and sodium ion pair and (b) the sulfur and water–oxygen (OW) of the different water models, calculated at 298 K and 105 Pa.
Download figure:
Standard image High-resolution imageFigure 5(a) shows the radial distribution function of the sulfur and sodium pair at different temperatures and 105 Pa for the TIP4P/2005 water model. The function exhibits a high correlation at r = 0.37 nm indicating that at this distance the probability of finding this pair is the highest, which is understood in terms of electrostatic interactions, since the head of the surfactant is negatively charged and in counterpart the sodium has positive charge. This maximum in probability occurs at the interface between the surfactant and water. Additionally, the results suggest that when the temperature increases, the probability of finding the sulfur–sodium pair decreases. Such behavior is related to a growth of the mobility of the atoms due that there is an increase in their kinetic energy. Beyond this peak at 0.37 nm, the probability decreases drastically and a rapid leveling of the  beyond the main binding peak is observed. These results are in agreement with those published by Sammalkorpi et al [34], who studied SDS molecules in simple point charge (SPC) water and calculated the sodium–sulfur radial distribution function.
beyond the main binding peak is observed. These results are in agreement with those published by Sammalkorpi et al [34], who studied SDS molecules in simple point charge (SPC) water and calculated the sodium–sulfur radial distribution function.
Figure 5. Radial distribution functions of (a) the sulfur and sodium ion pair and (b) the sulfur and water–oxygen (OW) using the TIP4P/2005 water model at different temperatures and 105 Pa.
Download figure:
Standard image High-resolution imageFigure 5(b) shows the  at different temperatures and 105 Pa. The oxygen atom corresponds to those of the TIP4P/2005 model. The results show a high peak at r = 0.37 nm for all the temperatures considered. These peaks are lower than the main peaks in the sulfur–sodium function, i.e. the sulfur whose charge is negative, interacts strongly with sodium ions regardless the temperature. Beyond this distance the radial distribution function oscillates until approximately 0.7 nm. It shows a peculiar behavior from 0.5 nm to 0.8 nm suggesting the existence of structured water at these distances. Moreover, the probability of finding the sulfur–oxygen pair increases as the temperature rises, which can be explained by considering that at high temperatures the kinetic energy of the atoms increases and the sodium ions are more easily removed from the head of the surfactants, allowing the sulfur and water oxygen to interact more strongly between them. Nevertheless, the peaks at distances greater than 0.37 nm diminish with the increase of the temperature and the surrounding water becomes less structured.
at different temperatures and 105 Pa. The oxygen atom corresponds to those of the TIP4P/2005 model. The results show a high peak at r = 0.37 nm for all the temperatures considered. These peaks are lower than the main peaks in the sulfur–sodium function, i.e. the sulfur whose charge is negative, interacts strongly with sodium ions regardless the temperature. Beyond this distance the radial distribution function oscillates until approximately 0.7 nm. It shows a peculiar behavior from 0.5 nm to 0.8 nm suggesting the existence of structured water at these distances. Moreover, the probability of finding the sulfur–oxygen pair increases as the temperature rises, which can be explained by considering that at high temperatures the kinetic energy of the atoms increases and the sodium ions are more easily removed from the head of the surfactants, allowing the sulfur and water oxygen to interact more strongly between them. Nevertheless, the peaks at distances greater than 0.37 nm diminish with the increase of the temperature and the surrounding water becomes less structured.
Figure 6 shows the radial distribution function of (a) the water oxygen–oxygen and (b) the oxygen–ion pairs for the TIP4P/2005 model at different temperatures and 105 Pa. In figure 6(a) the main feature is the peak at r = 0.28 nm, after this distance the function oscillates between maxima and minima with the increase of the separation until 0.7 nm, for longer distances it attenuates to a constant value. For the lowest temperature 273 K the highest correlation is observed, while at the highest temperature of 373 K the lowest peak is obtained and the function does not oscillate. At 298 K the water in the bilayer exhibits a higher peak in the OW–OW distribution function than that observed in bulk water, which can be attributed to the confinement. For the correlation between water and sodium ions, it is observed in figure 6(b) that the first maximum, located at  nm decreases considerably as the temperature increases, the remaining maxima also decrease their intensity and the position of some minima increase and shift to slightly longer distances.
nm decreases considerably as the temperature increases, the remaining maxima also decrease their intensity and the position of some minima increase and shift to slightly longer distances.
Figure 6. Radial distribution function of (a) the oxygen–oxygen and (b) oxygen–ion pairs in the bilayer-water system using the TIP4P/2005 model at different temperatures and 105 Pa.
Download figure:
Standard image High-resolution image4.3. Static dielectric constant: confined water and bilayer-water system
In simulations of an isotropic phase, the static dielectric constant is often calculated from the fluctuations in the total dipole moment  of the system through the relationship [35]
of the system through the relationship [35]

where  is the volume and T is the temperature. The dielectric constant of pure water has been calculated from molecular simulations using water models that differ in geometry, polarity, number of sites, among others. It proved to be a difficult task to reproduce the experimental value using rigid models. In an extensive evaluation of different properties of water, it was found that the SPC/E performs better than many other models, however the error with respect to the experimental dielectric constant is about
is the volume and T is the temperature. The dielectric constant of pure water has been calculated from molecular simulations using water models that differ in geometry, polarity, number of sites, among others. It proved to be a difficult task to reproduce the experimental value using rigid models. In an extensive evaluation of different properties of water, it was found that the SPC/E performs better than many other models, however the error with respect to the experimental dielectric constant is about  .
.
In this work, we focus on analyzing the performance of four rigid water models in the bilayer-water system, two of which are the most commonly employed in simulations: the SPC/E and the TIP4P/2005, and two that were recently proposed: the SPC/ε and the TIP4Q models. The later two come from a reparametrization of the existent SPC/E and TIP4P/2005 force fields, but reproduce the experimental dielectric constant in a wide range of temperature at normal pressure. In the literature there are important efforts to calculate and measure the dielectric constant of lipid bilayers and films [15, 16, 19, 20, 22, 36, 37]. However none of them offer a direct route that could be easily applied in this sort of calculations and obtain a scalar estimate. Here we used the GROMACS utility  to compute this quantity [26].
to compute this quantity [26].
4.3.1. Confined water.
First, we analyzed the confined water between the two SDS layers by applying equation (4) to the solvent group, which allows to evaluate the effect of confinement with respect to the water in bulk using the models already mentioned. The results are shown in figure 7. The dielectric constant of confined water decreases as the temperature increases. The TIP4P/2005 model produces the lowest values, immediately above, are those of SPC/E potential. The TIP4Q and SPC/ε models produce practically the same values, except for temperatures 288 and 298 K. This behavior is very similar to that found in bulk water for these models, whose dielectric constant values, taken from the [11] and [13], are shown in figure 7 with open symbols.
Figure 7. Static dielectric constant of the confined water as a function of the temperature using the models displayed on the figure (full symbols). The dielectric constant of bulk water calculated using the same models are also shown (open symbols). They were taken from [11] (TIP4P/2005, TIP4Q) and [13] (SPC/E, SPC/ε).
Download figure:
Standard image High-resolution imageIn terms of the different rigid water models, we observed the same trend as that found for bulk water. However, the fact of having the water confined between the two layers of surfactant clearly influences the dielectric constant, decreasing its value with respect to that of bulk water. This estimate indirectly measures the influence of the SDS layers. We observed that the dielectric constant converges reasonably well for temperatures greater than 298 K with 200 ns of simulation time. However, for T < 298 K we observed larger fluctuations in the total dipole moment, and the dielectric constant decay is not linear, similarly to the behavior observed in bulk water.
4.3.2. Bilayer-water system.
Regarding the bilayer-water system, there is little experimental information on the dielectric constant at standard conditions of pressure and temperature. Drummond et al [14] reported the experimental dielectric constant of an SDS-water mixture among other surfactant-water mixtures at 298.15 K and 105 Pa equal to 57.7. Despite its great importance, as far as we know there is still not information regarding scalar estimates of the dielectric constant of the film here considered, although there are studies on Newton black films where the dielectric response of water is analyzed in terms of the mean electric field, the electrostatic potential and the dielectric displacement across the water-surfactant interfaces [37], finding an anomalous behavior: very different of that expected as if the water were considered as an uniform dielectric medium.
So, we decided to apply equation (4) to all the groups in order to estimate the dielectric constant of the surfactant bilayer-water system. The results are shown in figure 8 for (a) the SPC/E, (b) the SPC/ε, (c) the TIP4P/2005 and (d) the TIP4Q water models. Full black symbols are results from this work.
Figure 8. Dielectric constant as a function of the temperature for the bilayer-water system using different water models (full black symbols). The green point is the experimental dielectric constant of an aqueous solution of SDS at 298.15 K and 105 Pa [14]. The red points are the experimental dielectric constant values of pure water [38].
Download figure:
Standard image High-resolution imageThe green point is the experimental value measured by Drummond et al [14] for an SDS-water mixture, the red circles are the experimental data of pure water at 105 Pa. In general, we found that the bilayer-water system has a lower dielectric constant than the experimental data of pure water. It is also a decreasing function of temperature. An outstanding feature is that the dielectric constant drops abruptly with temperature. This behavior is very different from that observed for bulk and confined water. When the SDS contribution is calculated, we observed a decreasing function of temperature (not shown) that could partially explain the abrupt drop, however the water and SDS contributions to the dielectric constant are clearly non-additive.
The maximum value of the dielectric constant is reached at the lowest simulated temperature of 273 K for all water models, whereas the minimum value was found at 373 K. Except for the SPC/E water, the rest of the models exhibit a plateau in the dielectric constant for temperatures higher than 315 K. The bilayer remained stable at all temperatures. In figure 8(a), where the dielectric constant of the bilayer-SPC/E water is shown, it is observed that ε is overestimated as compared to the experimental value of the mixture at 298 K. The results for the bilayer-SPC/ε system are shown in panel (b). We found that the ε obtained at 298 K slightly overestimates the experimental value of Drummond et al in about 8.4%, however it is closer than that obtained with the SPC/E model. This trend is in agreement with that of pure water since the experimental value is 78.5 and that reported for the SPC/ε is 80.2 [13]. In panel (c) the dielectric constant of the bilayer interacting with TIP4P/2005 water is presented, it shows an abrupt decay going from 273 to 288 K, whereas for higher temperatures it varies slowly. Comparing with panels (a), (b), and (d) at 298 K, we observe that ε is underestimated. This underestimation had already been observed when pure water is simulated with the TIP4P/2005 model, the dielectric constant  [9] is below the experimental data. Finally, panel (d) shows the bilayer interacting with the TIP4Q model. We obtained
[9] is below the experimental data. Finally, panel (d) shows the bilayer interacting with the TIP4Q model. We obtained  at 298 K, it is very close to the experimental value of 57.7. In fact it is in excellent agreement: it overestimates the experimental data by only 1.89%. Since for pure water, the TIP4Q and the SPC/ε closely approximate to the experimental dielectric constant, we believe they inherit their dielectric behavior to the bilayer-water system, in particular, at standard conditions. This observation is also related to the transferability property of molecular models.
at 298 K, it is very close to the experimental value of 57.7. In fact it is in excellent agreement: it overestimates the experimental data by only 1.89%. Since for pure water, the TIP4Q and the SPC/ε closely approximate to the experimental dielectric constant, we believe they inherit their dielectric behavior to the bilayer-water system, in particular, at standard conditions. This observation is also related to the transferability property of molecular models.
5. Conclusions
Based on the molecular dynamics of a system constituted by a block of water surrounded by two SDS surfactant layers, a study of the dielectric constant at different temperatures and at pressure 105 Pa was conducted. Four rigid models, the SPC/E, the SPC/ε, the TIP4P/2005 and the TIP4Q were used for modeling the water. The results of density profiles show that sodium ions remain mostly in the region of the interface between water and surfactant. In addition, the radial distribution functions indicate that sodium ions remain near the surfactant head with a high probability. As the temperature increases a greater mobility of the molecules is expected (greater kinetic energy), allowing the water molecules to displace the sodium ions from the surfactant, decreasing the probability of being together and increasing the chance of the surfactant head-water pair occurs.
The dielectric constant of the confined water was calculated. In general it is lower that that of pure water for all the temperatures. It was found that the TIP4P/2005 produces the lowest values whereas the SPC/ε and the TIP4Q gave the highest dielectric constant. With regard to the estimate of the dielectric constant of the bilayer-water system, the overall behavior is that ε decreases with increasing temperature, indicating a decrease of the electric flow. As compared with the available experimental data of the effective dielectric constant of an SDS-water mixture, measured by Drummond et al, the SPC/ε and the TIP4Q models are the best in predicting the dielectric constant of the bilayer-water system. This fact may be connected with the performance of the models in reproducing the dielectric constant of pure water. The bilayers modeled with SPC/E and TIP4P/2005 waters presented the greater differences with respect to the available experimental data. Certainly the bilayer-water systems are anisotropic, and it should be taken into account when analyzing their dielectric behavior, however it is also relevant to evaluate the dielectric constant that the isotropic formula produces in order to improve the calculation of this important property and take advantage of improved water models. To derive a formula for anisotropic dielectric constants, one could consider the statistical mechanics reasoning leading to equation (4). This involves the position-dependent dielectric constant o dielectric profile [17]. There are some attempts, however, additional work is required for the establishment and test of these formulas [18].
Acknowledgments
This work was supported by Programa para el Desarrollo Profesional Docente (SEP-México). Support from the CA Física Computacional de la Materia Condensada and VIEP-BUAP is acknowledged. The authors thankfully acknowledge the computer resources, technical expertise and support provided by the Laboratorio Nacional de Supercómputo del Sureste de México, CONACYT network of national laboratories.









