Abstract
A giant magnetocaloric effect across the ferromagnetic (FM) to paramagnetic (PM) phase transition was observed in chemically synthesized Co2FeAl Heusler alloy nanoparticles with a mean diameter of 16 nm. In our previous report, we observed a significant enhancement in its saturation magnetization (Ms) and Curie temperature (Tc) as compared with the bulk counterpart. Motivated by those results, we aim here to explore the magnetocaloric properties near the Tc. The magnetic entropy change ( ) shows a positive anomaly at 1252 K.
) shows a positive anomaly at 1252 K.  increases linearly with the magnetic field, and a large value of ∼15 J kg−1 K−1 is detected under a moderate field of 14 kOe. It leads to a net relative cooling power of 89 J kg−1 for the magnetic field change of 14 kOe. To confirm the nature of magnetic phase transition, a detailed study of its magnetization is performed. The Arrott plot and nature of universal curve conclude that the FM to PM phase transition in the present system is of second-order.
increases linearly with the magnetic field, and a large value of ∼15 J kg−1 K−1 is detected under a moderate field of 14 kOe. It leads to a net relative cooling power of 89 J kg−1 for the magnetic field change of 14 kOe. To confirm the nature of magnetic phase transition, a detailed study of its magnetization is performed. The Arrott plot and nature of universal curve conclude that the FM to PM phase transition in the present system is of second-order.
Export citation and abstract BibTeX RIS
1. Introduction
Heusler alloys (HAs) are materials of enormous interest due to their multifunctional properties including magnetoresistance (MR) [1], half-metallicity (i.e. 100 spin polarization at the Fermi edge) [2–7], spin filtering [8], spin injection [9], shape memory [10, 11] and thermoelectric effect [12]. These half-metallic ferromagnets exhibit a unique band structure at the Fermi energy (EF), where one spin channel shows metallic nature and another spin channel displays a non-conducting or semiconducting gap. An interesting character of HAs is that the structural, magnetic and magnetocaloric properties can easily be tuned by controlling their elemental compositions or partial substitution by other elements [13–16]. In 1983, de Groot et al, firstly reported such behavior in NiMnSb HA [17]. The X2
YZ (X/Y: transition metals; Z: main group element) Heusler compounds, generally known as full-HAs, may be crystalized in the cubic L21 (i.e. fully-ordered) structures under the space group  [18]. However, the ideal L21 phase is difficult to achieve, especially in the nanoscale regime; therefore, they are generally crystalized in either partial-disordered (i.e. B2 type) [19] or fully disordered (i.e. A2 type) [20] phases. The half-metallic nature, large magnetic moment and high Tc of Heusler compounds (specially, in Co2-based), make them potential candidates for spintronic applications [20–22]. Additionally, the magnetocaloric (MC) effect has also been explored in HAs [23–25]. The materials that can potentially be used as magnetic refrigerants near to or above room temperature are of great interest [13, 26, 27]. In this regard, materials exhibiting a giant magnetocaloric effect (GMCE) would be promising [16, 24, 28–30]. GMCE was initially observed in Gd5(Si2Ge2) [29, 31]. Nevertheless, the high cost of Gadolinium makes it unsuitable for commercial magnetic refrigerators. Moreover, there are many other key challenges from the materials perspective to improve performance and implementation in devices [32]. The peak of the entropy change (
[18]. However, the ideal L21 phase is difficult to achieve, especially in the nanoscale regime; therefore, they are generally crystalized in either partial-disordered (i.e. B2 type) [19] or fully disordered (i.e. A2 type) [20] phases. The half-metallic nature, large magnetic moment and high Tc of Heusler compounds (specially, in Co2-based), make them potential candidates for spintronic applications [20–22]. Additionally, the magnetocaloric (MC) effect has also been explored in HAs [23–25]. The materials that can potentially be used as magnetic refrigerants near to or above room temperature are of great interest [13, 26, 27]. In this regard, materials exhibiting a giant magnetocaloric effect (GMCE) would be promising [16, 24, 28–30]. GMCE was initially observed in Gd5(Si2Ge2) [29, 31]. Nevertheless, the high cost of Gadolinium makes it unsuitable for commercial magnetic refrigerators. Moreover, there are many other key challenges from the materials perspective to improve performance and implementation in devices [32]. The peak of the entropy change ( ) was found to be significantly higher in HAs [24, 33, 34] with first-order magnetic phase transition, which is necessary for efficient cooling. However, thermal and magnetic hysteresis present in such systems limits their practical usefulness. This further motivates researchers to search for other Heusler based materials. Lately, a few works on the MC properties of Co-based HAs have been reported [13, 35, 36]. They exhibit second-order phase transition and are found to be usable as magnetic refrigerants due to their broad working temperature range and absence of thermal and magnetic hysteresis. The spin orbit coupling is stronger in Co-based HAs [37]; therefore, the magnetocrystalline anisotropic exchange interaction might be responsible in their magnetic ordering. Practically, there is no system available which strictly follows the Stoner's itinerant model or Heisenberg theory for the localized spin. No particular theory can completely explain the magnetism of such 3d intermetallic compounds. Therefore, it is necessary to explore their magnetism near the phase transition.
) was found to be significantly higher in HAs [24, 33, 34] with first-order magnetic phase transition, which is necessary for efficient cooling. However, thermal and magnetic hysteresis present in such systems limits their practical usefulness. This further motivates researchers to search for other Heusler based materials. Lately, a few works on the MC properties of Co-based HAs have been reported [13, 35, 36]. They exhibit second-order phase transition and are found to be usable as magnetic refrigerants due to their broad working temperature range and absence of thermal and magnetic hysteresis. The spin orbit coupling is stronger in Co-based HAs [37]; therefore, the magnetocrystalline anisotropic exchange interaction might be responsible in their magnetic ordering. Practically, there is no system available which strictly follows the Stoner's itinerant model or Heisenberg theory for the localized spin. No particular theory can completely explain the magnetism of such 3d intermetallic compounds. Therefore, it is necessary to explore their magnetism near the phase transition.
As a young research field, earlier studies on Heusler nanoalloys have been focused on their synthesis, structure, and magnetic characterizations (see refs. [20, 38], and the references therein). Consequently, further investigations are required to verify their technical importance in magnetic refrigeration and microactuators. Previously, we have reported the size modulated structural and magnetic properties of Co2FeAl (CFA) nanoparticles (NPs). CFA-NPs crystallized in cubic A2-disorder phase. Their microstructural analysis reveals that NPs are spherical and crystalline in nature with an average particle size of 16 nm. Moreover, they exhibit pronounced enhancement in Ms and Tc as compared with bulk counterpart. A record magnetic moment and Tc of 6.5 µB/f.u. (25% higher than the bulk) and 1261 K (15% higher than the bulk), respectively, have been observed [20]. As a rule of thumb, to get a huge MC response, the material should have a higher magnetic moment [27]; therefore, a large magnetic entropy change ( ) is expected in CFA-NPs. Here, we report the MC effect of CFA-NPs, near the FM-PM phase transition.
) is expected in CFA-NPs. Here, we report the MC effect of CFA-NPs, near the FM-PM phase transition.
2. Experimental details
CFA-NPs were synthesized using the co-precipitation and thermal deoxidization method. The precursor salts were CoCl2 · 6H2O (99%), Fe(NO3)3 · 9H2O (99%) and Al2(NO3) · 18H2O (98%). The detailed description of the sample preparation was described in our previous report [20]. NPs were analyzed by x-ray diffraction (XRD), high-resolution transmission electron microscopy (HRTEM) and selected area electron diffraction (SAED) techniques. MC properties were studied using high-temperature vibrating sample magnetometer of Lake Shore Cryotronics. In magnetization measurements, the powder sample was placed into a disposable boron nitride cup as provided by Lake Shore Cryotronics.
3. Results and discussion
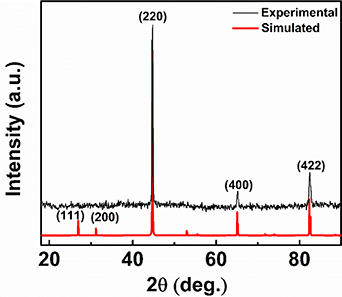
The simulated and experimental XRD data of CFA-NPs are shown in figure 1. The prominent Bragg peaks of (220), (400) and (422) establish that the present system is crystallized in A2 disordered phase, but not in L21 phase [20]. Note that (111) and (200) superlattice reflections, which are absent in our case, are required to conclude the L21 structure [7]. The lattice constant, as calculated from the noticeable (220) Bragg peak is 5.72 Å. This closely matches with the bulk value [39].
Figure 1. Experimental and simulated XRD patterns of Co2FeAl NPs.
Download figure:
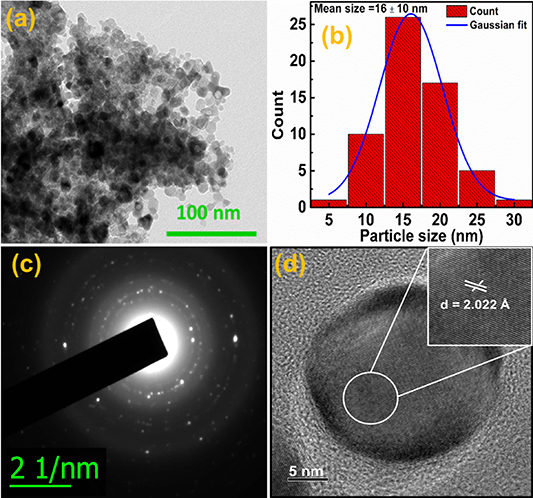
Standard image High-resolution imageThe NPs are analyzed using HRTEM imaging (figure 2). As evident from figure 2(a), particles are nearly spherical in shape. The image is further examined for particle size distribution using the ImageJ software. The size-distribution histogram, along with the fitted Gaussian profile, is shown in figure 2(b). According to the histogram, the NPs are of sizes 16 ± 10 nm. The SAED pattern (see figure 2(c)) features concentric rings accompanied by dots. This indicates that particles are crystalline in nature. The image of a single NP with an even higher resolution is shown in figure 2(d). The presence of observable lattice fringes confirm the high crystallinity of the particles. An enlarged portion of the image has been presented in the inset of figure 2(d). The interplanar spacing of 2.022 Å is equivalent to the (220) plane of the cubic phase of CFA-NPs, and is consistent with the XRD results.
Figure 2. (a) Transmission electron microscopy image of CFA-NPs. (b) A histogram for the size distribution of NPs. (c) SAED pattern and (d) high-resolution images displaying the lattice planes and crystallinity; inset represents enlarged portion of the image.
Download figure:
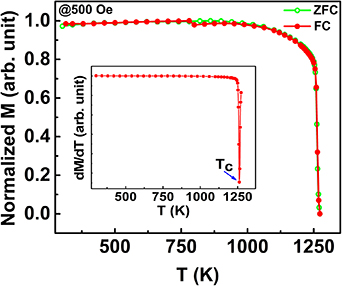
Standard image High-resolution imageThermomagnetic zero-field-cooled (ZFC) and field-cooled (FC) curves of CFA-NPs, measured in a 500 Oe field, in the temperature range of 300 K–1273 K, are shown in figure 3. Both the ZFC and FC curves of CFA are smooth and exhibit a clear FM to PM phase transition around the Tc. The M(T) curves resemble a continuous or second order FM-PM phase transition [40]; this argument is further supported by the absence of the thermal hysteresis in the present system. This motivated us to further investigate its phase transition and MC properties.
Figure 3. Thermo-magnetization curves of the Co2FeAl NPs in the temperature interval of 300 K–1273 K measured at 500 Oe. Inset represents the derivative of M(T) curve of Co2FeAl for the precise determination of phase transition temperature (Tc).
Download figure:
Standard image High-resolution imageThe Tc is calculated from the peak value of dM/dT vs temperature (T) curve, and is found to be 1261 K (see the inset of figure 3). To analyze the MC effect of CFA-NPs, isothermal magnetization M(H) is investigated at various temperatures with a temperature interval of 2 K around the Tc, as shown in figure 4(a). The magnetization (M) increases gradually with the field up to 4 kOe and thereafter approaches a constant value. Then, the M value decreases with increasing T, suggesting the magnetic transition from a low-T ferromagnetic to a high-T paramagnetic phase. The large change in M at 1251 K–1253 K isotherms indicates the possibility of large MC effect of CFA-NPs around this temperature range. In order to see the hysteresis losses and their effects in MC properties, we have measured M(H) isotherms in a decreasing field (14 kOe–0 Oe) mode (not shown here), and have not found any difference as compared with the M(H) isotherms in the increasing field (0 Oe–14 kOe) mode. The magnetization curves taken during heating and cooling processes near the Tc coincide with each other, exhibiting a negligible hysteresis for all the temperature ranges. Such reversibility of the magnetic transition is essential from the application point of view in magnetic refrigeration.
Figure 4. (a) Isothermal magnetization M(H) curves of CFA-NPs measured around Tc. (b) Arrott plot of the isotherms measured near the phase transition.
Download figure:
Standard image High-resolution imageIn order to see whether the Landau mean-field theory of the phase transition is valid for CFA-NPs system, a conventional Arrott plot (M2 vs H/M) [41] is constructed as shown in figure 4(b). The Arrott plot should generate a set of parallel straight lines for the mean field values of the critical exponents  and
and  . The line passing through the origin should resemble the isotherm exactly at the critical temperature (Tc). As seen from figure 4(b), the Arrott plot does not generate parallel straight lines. Moreover, a substantial non-linearity with downward curvature can be seen even at the high field region. Thus, the mean field theory cannot explicate the phase transition of the present system. From Banerjee's criterion [42], the Arrott curves exhibiting a positive slope specify that the FM-PM phase transition is of second order. The magnetic entropy change,
. The line passing through the origin should resemble the isotherm exactly at the critical temperature (Tc). As seen from figure 4(b), the Arrott plot does not generate parallel straight lines. Moreover, a substantial non-linearity with downward curvature can be seen even at the high field region. Thus, the mean field theory cannot explicate the phase transition of the present system. From Banerjee's criterion [42], the Arrott curves exhibiting a positive slope specify that the FM-PM phase transition is of second order. The magnetic entropy change,  is calculated by using Maxwell relation [24]:
is calculated by using Maxwell relation [24]:
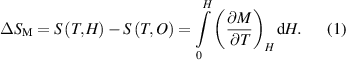
As the experimental values of magnetization data are only available at discrete values of temperature, the integral in this equation may be replaced by the summation. It can be understood from equation (1) that the magnetic entropy change will be maximum only when ∂M/∂T is maximum. The sign of  is determined by the sign of ∂M/∂T. When it is positive, it will be called a conventional MC effect [43]. The change in magnetic entropy (
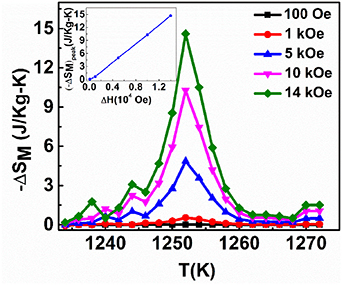
is determined by the sign of ∂M/∂T. When it is positive, it will be called a conventional MC effect [43]. The change in magnetic entropy ( ) with respect to T is shown in figure 5. The magnetic entropy change show a positive anomaly at 1252 K. A large value of
) with respect to T is shown in figure 5. The magnetic entropy change show a positive anomaly at 1252 K. A large value of  ∼15 J kg−1 K−1 is detected for change of the magnetic field of 14 kOe.
∼15 J kg−1 K−1 is detected for change of the magnetic field of 14 kOe.
Figure 5. Magnetic entropy change ( ) with temperature for CFA-NPs; inset figure depicts the change of peak value of
) with temperature for CFA-NPs; inset figure depicts the change of peak value of  with respect to the change in field.
with respect to the change in field.
Download figure:
Standard image High-resolution imageThe obtained value of  is comparable in magnitude with the peak value of another GMCE material Gd5Si2Ge2 [29], which is very well known in the field of refrigeration technology. It is much larger, i.e. at least three times the peak value of expensive Gd [29]. Our results show higher or at least comparable MC values as compared to other Heusler materials such as Fe2CoAl [44], Mn1−x
Crx
CoGe [45], MnCo1−x
Zrx
Ge [46] and Mn1-xAlxCoGe [47]. We also compare our results to the Heusler based thin films (see table 1). As a matter of fact, the small mass of thin films makes it challenging to evaluate MC properties quantitatively, particularly the adiabatic temperature change (D
Tad). Because of this, a limited number of publications are available on the MC properties of thin films of metals and compounds. Most of them are concerned with the study of MC effect in Ni–Mn–X (X = Ga, In, Sn) thin films. Recarte et al [48] deposited NiMnGa film with thickness of 0.4 µm onto alumina substrate. The film exhibited a magnetostructural phase transition at 346 K, and the magnetic entropy change (
is comparable in magnitude with the peak value of another GMCE material Gd5Si2Ge2 [29], which is very well known in the field of refrigeration technology. It is much larger, i.e. at least three times the peak value of expensive Gd [29]. Our results show higher or at least comparable MC values as compared to other Heusler materials such as Fe2CoAl [44], Mn1−x
Crx
CoGe [45], MnCo1−x
Zrx
Ge [46] and Mn1-xAlxCoGe [47]. We also compare our results to the Heusler based thin films (see table 1). As a matter of fact, the small mass of thin films makes it challenging to evaluate MC properties quantitatively, particularly the adiabatic temperature change (D
Tad). Because of this, a limited number of publications are available on the MC properties of thin films of metals and compounds. Most of them are concerned with the study of MC effect in Ni–Mn–X (X = Ga, In, Sn) thin films. Recarte et al [48] deposited NiMnGa film with thickness of 0.4 µm onto alumina substrate. The film exhibited a magnetostructural phase transition at 346 K, and the magnetic entropy change ( ) was found to be 8.5 J kg−1 K−1, at the 60 kOe field. Niemann et al [49] observed inverse MC effect in epitaxially grown metamagnetic Ni–Co–Mn–In film (0.2 µm) on MgO (001) substrate. The resulting
) was found to be 8.5 J kg−1 K−1, at the 60 kOe field. Niemann et al [49] observed inverse MC effect in epitaxially grown metamagnetic Ni–Co–Mn–In film (0.2 µm) on MgO (001) substrate. The resulting  , was −8.8 J kg−1 K−1 at 353 K for the magnetic field change of 90 kOe. Lately, Yüzüak et al [50] detected inverse MCE in epitaxial Ni–Mn–Sn/MgO thin films of 200 nm thickness. The
, was −8.8 J kg−1 K−1 at 353 K for the magnetic field change of 90 kOe. Lately, Yüzüak et al [50] detected inverse MCE in epitaxial Ni–Mn–Sn/MgO thin films of 200 nm thickness. The  and relative cooling power (RCP) were −1.5 J kg−1 K−1 and 33.9 J Kg−1 at 10 kOe field, respectively. A comparison of all the values, as discussed above, are tabulated in table 1.
and relative cooling power (RCP) were −1.5 J kg−1 K−1 and 33.9 J Kg−1 at 10 kOe field, respectively. A comparison of all the values, as discussed above, are tabulated in table 1.
Table 1. A comparison of the magnetic entropy change ( ), RCP, Δ
H, Tc, and nature of the phase transition in present system and other magnetocaloric materials.
), RCP, Δ
H, Tc, and nature of the phase transition in present system and other magnetocaloric materials.
| Materials |
 (J kg−1 K−1) (J kg−1 K−1) | RCP (J kg−1) | Field range (ΔH) in kOe | Tc (K) | Nature of the phase transition | Refs. | |
|---|---|---|---|---|---|---|---|
| Heusler alloy NPs | Co2FeAl | ∼15 | 89 | 14 | 1261 | Second order | Present work |
| Fe2CoAl | 2.65 | 44 | 20 | 830 | Second order | [44] | |
| Bulk Heusler alloys | Mn1−x Crx CoGe | ∼28.5 | 50 | 322 | First order | [45] | |
| MnCo1−x Zrx Ge | 7.2 | 266 | 50 | 274 | First order | [46] | |
| Co2Cr0.25Mn0.75Al | 3.5 | ∼285 | 90 | 720 | Second order | [13] | |
| Mn1−x Alx CoGe | 12 | 303 | 50 | 286 | First order | [47] | |
| Giant MC Materials | Gd5Si2Ge2 | 18 | 20 | 276 | First order | [29] | |
| (MnNiSi)1−x (FeCoGa)x | 25 | 191.8 | 50 | 323 | First order | [16] | |
| Fe-Rh | 20 | — | 20 | First order | [30] | ||
| MCE in Heusler thin films | NiMnGa | 8.5 | [48] | ||||
| Ni–Co–Mn–In | −8.8 | — | 90 | 353 | — | [49] | |
| Ni–Mn–Sn | −1.5 | 33.9 | 10 | ∼270 | — | [50] | |
| Others | Fe68.5Mo5Si13.5B9Cu1Nb3 | ∼1.1 | 63 | 15 | ∼475 | [27] | |
| Fe50Rh50 particles | 9.7 | 230 | 30 | — | First order | [55] | |
As seen from the inset of figure 5, the  peak height is very sensitive to the field change (ΔH) from H = 5 kOe onwards. It increases linearly relative to ΔH and the width of the peak decreases. RCP is an important parameter to evaluate the usefulness of the material for magnetic refrigeration. This parameter is also used for a comparison with other MC materials. It is a measure of the amount of heat transferred between the hot and cold reservoirs in an ideal refrigeration cycle and defined as: RCP =
peak height is very sensitive to the field change (ΔH) from H = 5 kOe onwards. It increases linearly relative to ΔH and the width of the peak decreases. RCP is an important parameter to evaluate the usefulness of the material for magnetic refrigeration. This parameter is also used for a comparison with other MC materials. It is a measure of the amount of heat transferred between the hot and cold reservoirs in an ideal refrigeration cycle and defined as: RCP =  , where
, where  represents full width at half maximum of the
represents full width at half maximum of the  vs T curve [51]. The large value of RCP of 89 J Kg−1 (see figure 6) was observed at the change of magnetic field of 14 kOe, which signifies a large heat conversion capacity in a refrigeration cycle.
vs T curve [51]. The large value of RCP of 89 J Kg−1 (see figure 6) was observed at the change of magnetic field of 14 kOe, which signifies a large heat conversion capacity in a refrigeration cycle.  also represents the span of working-temperature, which is found to be around ∼6 K in the present system. Zverev et al [52] and Engelbrecht et al [53] previously suggested that a material having a broad peak of
also represents the span of working-temperature, which is found to be around ∼6 K in the present system. Zverev et al [52] and Engelbrecht et al [53] previously suggested that a material having a broad peak of  is much better than that of materials with a sharp peak of magnetic entropy change for cooling applications. Therefore, in order to fine-tune the Tc and the temperature span of the CFA-NPs, studies of composition optimization are in progress. The refrigeration capacity (RC) and entropy change (
is much better than that of materials with a sharp peak of magnetic entropy change for cooling applications. Therefore, in order to fine-tune the Tc and the temperature span of the CFA-NPs, studies of composition optimization are in progress. The refrigeration capacity (RC) and entropy change ( ) have shown a linear behavior (see figures 5 and 6) with respect to magnetic field. The increasing nature of the peak value of the entropy change with ΔH can be suitable for Ericsson-cycle refrigeration applications [54]. And therefore, the study of magnetic and MC properties on Co2-based HAs might be useful for the application of multistage magnetic refrigeration [13]. From a simple linear extrapolation of our data to 50 kOe, will give an approximate value of RCP = 305 J Kg−1, and
) have shown a linear behavior (see figures 5 and 6) with respect to magnetic field. The increasing nature of the peak value of the entropy change with ΔH can be suitable for Ericsson-cycle refrigeration applications [54]. And therefore, the study of magnetic and MC properties on Co2-based HAs might be useful for the application of multistage magnetic refrigeration [13]. From a simple linear extrapolation of our data to 50 kOe, will give an approximate value of RCP = 305 J Kg−1, and  = 50 J kg−1 K−1. In comparison to the recently reported high-T MC material Co2Cr1−x
Mnx
Al HA [13], having Tc of 720 K on the same field scale (i.e. 50 kOe), our value of entropy change (
= 50 J kg−1 K−1. In comparison to the recently reported high-T MC material Co2Cr1−x
Mnx
Al HA [13], having Tc of 720 K on the same field scale (i.e. 50 kOe), our value of entropy change ( ) is 20 times larger and the RC value is slightly larger or at least comparable with that material.
) is 20 times larger and the RC value is slightly larger or at least comparable with that material.
Figure 6. Dependence of RCP with magnetic field near the phase transition (Tc).
Download figure:
Standard image High-resolution imageFranco et al [56] proposed a master curve that is used to see the nature of the magnetic phase transition. This curve can be plotted as the normalized entropy change ( ) where
) where  , with respect to the rescaled temperature (θ) defined by
, with respect to the rescaled temperature (θ) defined by
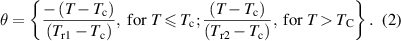
In equation (2), Tc represents the temperature at which  is attained. The reference temperatures
is attained. The reference temperatures  and
and  below and above the Tc, are taken as the temperatures corresponding to
below and above the Tc, are taken as the temperatures corresponding to  In figure 7, all the curves (
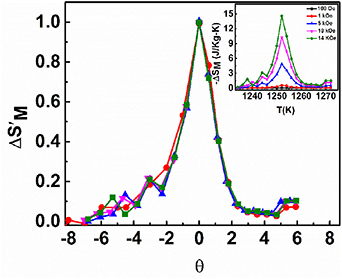
In figure 7, all the curves ( vs θ) of CFA-NPs, taken at different magnetic fields, are merged into a single universal curve (see the inset of figure 7 for a comparison), which confirms a second-order magnetic phase transition. Such types of phenomenological curves were previously reported for materials exhibiting second-order phase transition [56–58]. The present study suggests a possibility of using this material in high temperature cooling applications such as multi-stage magnetic refrigeration, where cooling from high temperature is desired in more than one stage [59]. Such multistage refrigerators are highly suitable in industry, where the low temperature of one stage acts as the upper temperature for the next stage [59, 60].
vs θ) of CFA-NPs, taken at different magnetic fields, are merged into a single universal curve (see the inset of figure 7 for a comparison), which confirms a second-order magnetic phase transition. Such types of phenomenological curves were previously reported for materials exhibiting second-order phase transition [56–58]. The present study suggests a possibility of using this material in high temperature cooling applications such as multi-stage magnetic refrigeration, where cooling from high temperature is desired in more than one stage [59]. Such multistage refrigerators are highly suitable in industry, where the low temperature of one stage acts as the upper temperature for the next stage [59, 60].
Figure 7. The normalized entropy change ( ) as a function of rescaled temperature (θ) near the phase transition for CFA-NPs; inset shows
) as a function of rescaled temperature (θ) near the phase transition for CFA-NPs; inset shows vs T at different fields.
vs T at different fields.
Download figure:
Standard image High-resolution image4. Conclusions
We have performed a detailed investigation on the structure, magnetic phase transition and magnetocaloric effect in Co2FeAl NPs. The positive slope of the Arrot curve suggests second order FM to PM phase transition near the Tc. The normalized entropy change ( ) with respect to the rescaled temperature (θ) at different fields collapsed into a single universal curve, further confirms the phase transition to be of second-order. Owing to the abrupt change in magnetization and a large peak value (∼15 J kg−1 K−1) of the magnetic entropy change, CFA-NPs system exhibits GMCE across the phase transition (Tc). The observed peak value is superior or at least comparable to those of the other MC materials on a comparison of the peak heights. The present study provides a window for future research on tuning the Tc and MC effect of Co2-based Heusler nanoalloys by controlling the elemental composition and/or partial substitution of the other elements.
) with respect to the rescaled temperature (θ) at different fields collapsed into a single universal curve, further confirms the phase transition to be of second-order. Owing to the abrupt change in magnetization and a large peak value (∼15 J kg−1 K−1) of the magnetic entropy change, CFA-NPs system exhibits GMCE across the phase transition (Tc). The observed peak value is superior or at least comparable to those of the other MC materials on a comparison of the peak heights. The present study provides a window for future research on tuning the Tc and MC effect of Co2-based Heusler nanoalloys by controlling the elemental composition and/or partial substitution of the other elements.
Acknowledgments
A Ahmad acknowledges the University Grants Commission, New Delhi and Ministry of Education (MoE), India for providing the research fellowship. Amal Kumar Das acknowledges the financial support from the Department of Science and Technology (DST), India (Project No. EMR/2014/001026). The fruitful discussion with Dr Ramchandra Sahoo is highly acknowledged.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the corresponding authors.