Laser-induced nonsequential double ionization of helium: classical model calculations

The double ionization (DI) of the atoms and molecules induced by short, intense laser pulses has been widely investigated (for a review see, e.g., reference [1]) since the experimental observation of unexpected large DI yields [2–5]. The measured DI rates were found several orders of magnitude higher than those calculated assuming independent ionization of the two electrons. Obviously, this discrepancy indicates that DI proceeds by a mechanism in which the electron–electron correlation plays important role. The enhanced contribution of the correlated DI (called 'nonsequential double ionization', NSDI) at lower laser intensities and the dominance of the non-correlated DI ('sequential double ionization', SDI) at higher intensities result in the characteristic 'knee' shape of the DI yield as a function of the laser intensity.

Now there is a widely shared consensus that NSDI can be explained by a recollision mechanism [6, 7] in which an electron liberated by the laser field in the next half cycle returns to the ion core and inelastically scatters with a second electron. The letter scattering may lead to DI in different scenarios. In the recollision-impact-ionization (RII) mechanism the first electron directly knocks out the second electron. In the recollision-induced-excitation-with-subsequent ionization (RESI) mechanism the second electron is first promoted to an excited state, and then it is ionized by the laser field. RESI may proceed also in that way that the first electron is recaptured into an excited state of the ion core with simultaneous excitation of the second electron. In this case the field-induced decay of the transient doubly excited state leads to DI [8].

Kinematically complete experiments applying the cold target recoil ion momentum spectroscopy (COLTRIMS) (for a review see, e.g., reference [9]) supported the picture of the recollision mechanism [10–13]. By means of this technique, called also as 'reaction microscope', the momentum of all the reaction products can be determined. Particularly, the correlated two-electron momentum distribution (CMD) and the momentum distribution of the doubly ionized target atom obtained by the COLTRIMS experiments provided important information about the two-electron dynamics in NSDI [14–38].

A large amount of theoretical works, applying classical, semiclassical and quantum mechanical models have been devoted to explore the laser-induced NSDI (for a review see, e.g., references [39, 40]). The fully classical models [41–71] are based on the solution of the Newton's equations of motion. In the semiclassical approaches [72–85] typically the first step of the recollision mechanism, the tunneling ionization is treated quantum mechanically. A considerable number of quantum mechanical models are based on the solution of the time-dependent Schrödinger equation [81, 86–93]. Several works applied the strong-field approximation [94] and the intense-field many-body S-matrix [39] theory [95–103]. The so-called quantitative rescattering (QRS) theory [104] proved to be an efficient description of NSDI [105–107]. Assuming the recollision mechanism, the theoretical models in general provided results in accordance with the experimental observations.

The present theoretical work was motivated by the recent kinematically complete experiment by Henrichs et al [33] carried out for DI of helium induced by 45 fs, 394 nm linearly polarized laser pulses. The measurements were made at laser intensities of 3.5, 4.6, and 5.7 ×  10¹⁴ W cm⁻². The theoretical interpretation of the results of this experiment is challenging, because both the RII and RESI process can be excluded energetically. In the recollision process the maximum kinetic energy of the recolliding electron gained from the laser field is 3.17 U_p (see, e.g., reference [42]), where U_p is the ponderomotive energy. Even at the highest laser intensity 3.17 U_p = 26 eV, i.e., the maximum recolliding energy is much below the second ionization potential of helium (54 eV), and, moreover, it does not reach the first excitation threshold of the He⁺ ion (40.8 eV). However, contrary to this fact, the measured data indicated the dominance of NSDI: from the momentum correlations of the electron pairs in the direction perpendicular to the field the authors concluded that the electrons are set free simultaneously. As an explanation of their observations, they assumed the absorption of many additional photons in the recollision process.

It was an interesting question whether the classical description is still applicable for DI under the above experimental conditions. According to the authors of reference [33], their study is between the cases of the two-photon double ionization in the perturbative regime [108] and the long-wavelength tunneling regime [1]. The latter strong-field regime is characterized by γ ≪ 1, where $\gamma ={\left[{I}_{\mathrm{p}}/\left(2 {U}_{\mathrm{p}}\right)\right]}^{1/2}$ is the Keldysh parameter (I_p : ionization potential of the atom). Even for the largest laser intensity applied in the experiment γ = 1.2, that means that the considered laser-atom interaction is at the limit of the applicability of the classical description. The limit is manifested also in some quantum features of the experimental data: the authors of reference [33] observed a multipeak structure in the correlated two-electron energy distribution at laser intensity of 3 × 10¹⁴ W cm⁻², which could be interpreted by quantum-mechanical selection rules [109]. However, there have been previous studies [50, 71] which showed that classical models could be used with success for the treatment of DI of helium induced by laser pulse of similar parameters as that in reference [33].

For the investigation of this problem we carried out calculations in the widely used classical ensemble model. The solution of Newton's equations for the two electrons moving in the classical laser field failed to reproduce the experimental findings. As the most important result of the present work, we proposed a new path way for NSDI. It consists of two steps. In the first step a transient double excited state is formed, which decays via 'over the barrier ionization' in the second step, releasing the two electrons simultaneously. In the paper we show that by the inclusion of the new pathway the classical ensemble model reproduced the main features of the experimental data of Henrichs et al [33].

In construction of the CEA model we applied the classical trajectory Monte Carlo (CTMC) method proposed originally by Abrines and Percival [110] for the description of ion-atom collisions. The method is based on the solution of the classical mechanical equations of motion of the particles. We applied the three-dimensional, non-relativistic, three-body version of the theory.

In the classical treatment of the helium atom one is faced with the difficulty due to its instability. Classically the energy exchange between the electrons is not limited, after a time autoionization occurs. To prevent this, several methods have been proposed (for a review see, e.g., reference [111]). In our model we stabilized the helium atom by replacing the Coulomb potential for the electron–nucleus (e–n) and the electron–electron (e–e) interaction with a soft potential [112] defined as

$$\begin{equation}{V}_{ij}=\frac{{Z}_{i}{Z}_{j}}{\sqrt{{r}_{ij}^{2}+{c}_{\alpha \beta }^{2}}},\end{equation} \tag{ 1 }$$

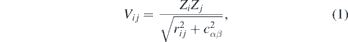
here Z_i and Z_j are the charges of the ith and jth particle, and r_ij is the distance between them. The c_αβ parameter is different for the e–n and e–e interaction. We achieved long-time stability with c_en = 0.872 a.u. and c_ee = 0.05 a.u. We note that the soft-core Coulomb potential has been applied in the overwhelming majority of the theoretical works dealing with the laser-induced DI [44–54, 56–72, 77, 83, 86, 87, 90].

The potential (1) yields forces between the particles:

$$\begin{equation}{\mathbf{F}}_{ij}\left(r\right)=\frac{{Z}_{i}{Z}_{j}}{{{r}_{ij}^{\prime }}^{3}}{\mathbf{r}}_{ij}\quad \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} {r}_{ij}^{\prime }=\sqrt{{r}_{ij}^{2}+{c}_{\alpha \beta }^{2}}.\end{equation} \tag{ 2 }$$

Thus the Newton's equations of motion for particles of masses m_i (i = 1, 2, 3) take the following form:

$$\begin{equation}{m}_{i}\frac{{\mathrm{d}}^{2}{\mathbf{r}}_{i}}{\mathrm{d} {t}^{2}}=\sum _{j\left(\ne i\right)=1}^{3}\frac{{Z}_{i}{Z}_{j}}{{{r}_{ij}^{\prime }}^{3}}{\mathbf{r}}_{ij}+{Z}_{i}\mathbf{E}\left(t\right).\end{equation} \tag{ 3 }$$

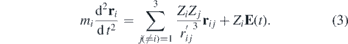
The laser pulse (intensity) was assumed to be of Gaussian shape with full width of half maximum (FWHM) of 45 fs. Accordingly, the electric field E(t) in the above equation was taken as

$$\begin{equation}\mathbf{E}\left(t\right)={E}_{0}{\left\{\mathrm{exp}\left[-{\left(t/\tau \right)}^{2}\right]\right\}}^{1/2}\mathrm{cos}\left(\omega t\right) \hat{\mathbf{k}},\end{equation} \tag{ 4 }$$

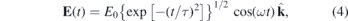
here ω is the frequency of the laser light, τ is obtained from the relationship 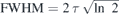$\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}=2 \tau \sqrt{\mathrm{ln} 2}$, and E₀ is the amplitude of the electric field. E₀ in atomic units is related to the laser intensity I expressed in W cm⁻² by 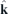$0.533{\times}1{0}^{-8}\sqrt{I}$. $\hat{\mathbf{k}}$ is a unit vector along the z-axis defining the direction of the polarization.

The equations of motion were solved using a fifth-order Runge–Kutta method. The trajectories of the particles were followed through 140 optical cycles that covered almost the full time of the pulse: at the beginning and end of the pulse the electric field decreased to 0.3% of its maximum value.

For the choice of the initial position and momentum coordinates of the electrons we applied a similar trial and error method as that proposed by Cohen [111]. In the first step of our procedure we consider the two electrons independently. We choose the magnitude of their position and momentum randomly in a given interval with uniform distribution. To minimize the calculation time we optimized the length of the intervals. For the ground state of helium we used the interval [0, 1.6 a.u.] for the position, and [0, 1.7 a.u.] for the momentum. We determine the angular coordinates of the electrons also randomly following the prescription the one-electron CTMC (see, e.g., reference [113]). Then we determine the total energy of the two electrons including their interaction. The sampling was accepted if the difference between the calculated energy and the binding energy of the helium atom (−2.904 a.u.) was within 1%.

The integration of the equations of motion was started well before the pulse to ensure the equilibration of the distribution of the phase space coordinates of the two electrons. The equilibrium was reached allowing the electrons to circulate around the nucleus twenty times. It took about 110 a.u., in good agreement with the equilibration time chosen in other works using the soft-core Coulomb potential (see, e.g., references [50, 71]). Figure 1 compares the initial and the equilibrium distributions of the one-electron position, momentum and energy. For a DI event at the end of the pulse the integration was continued until the energies of the electrons reached their asymptotical values. Typically 5 × 10⁵ two-electron trajectories were traced.

Zoom In Zoom Out Reset image size

We made the calculations for the same laser parameters as those used in the experiment. At the largest laser intensity used in the experiment (5.7 ×  10¹⁴ W cm⁻²) we obtained that DI proceeded sequentially (SDI), i.e., the role of the electron correlation was small. This finding is in contrast to the experiment: according to the measured correlated two-electron longitudinal momentum distribution, at this laser intensity the two electrons are dominantly emitted side by side into the same hemisphere, i.e., DI is highly correlated. With decreasing laser intensity the experiment showed increasing contribution of back-to-back (anti-correlated) emission events. Such a trend was also observable in our calculations, but in a smaller extent.

The lack of the correlated two-electron emission in our model can be understood by considering the single ionization. In figure 2 we plotted the one-electron energies and the total electron energy in the helium atom as a function of the time for a single-ionization event. The one-electron energy of the ith electron is defined as a sum of its kinetic energy and its potential energy in the field of the nucleus. The total electron energy is the sum of the one-electron energies and the interaction energy between the electrons. Notice the increasing fluctuation of electron energies with increasing field strength: the initially small difference between the electron energies increases, and the field induces oscillations of increasing amplitude between the low- and high-energy electron (for a later reference we call this state as 'highly polarized'). As a result of this process, after a time the high-energy electron is easily released by the field. At the same time, the remaining electron is deeply bound in the ionized atom, therefore its chance for the field-induced ionization is small. This means that the second electron will hardly be released in the same or the subsequent optical cycle, but it may be ionized at a much later time during the pulse. In the latter case, however, the interaction between the two electrons is small, the DI event is non-correlated.

Zoom In Zoom Out Reset image size

We attempted to improve our model by the inclusion of the tunneling effect. We applied two approaches: (i) the static approximation in which the tunneling probability is expressed by the WKB formula [114], and (ii) the widely used quasi-static ADK theory [115]. In the latter approach we followed the prescriptions of Yudin and Ivanov [75] for the determination of the initial position and momentum coordinates of the electrons after the tunneling. The results obtained by our modified model were still not satisfactory.

The differentiation of the one-electron energies has a further consequence, namely that the atom may gain energy from the field. One sees in figure 2 that the total electron energy increases well before the ionization occurs. However, it means that the atom becomes unstable: the c_αβ soft-Coulomb potential parameters optimized for the ground state do not stabilize the excited atom, i.e., it may decay via spontaneous autoionization. The electron emission in the latter case is isotropic in contrast to the experimentally observed momentum distribution that is concentrated along the polarization direction.

The excited atom, without changing its total energy, can be stabilized with new, suitably chosen c_αβ parameters in the same way as described in section 2. In a separate calculation we allow the new electron configuration to evolve into equilibrium. As a result of the stabilization, the low-(high) one-electron energy increases (decreases), the energies get again close to each other, i.e., the stabilized configuration is a doubly excited state. The lowest doubly excited ${\left(2{\text{s}}^{2}\right)}^{1}$S state of the helium lies above the ground state by 57.83 eV (see, e.g., reference [116]), i.e., the total energy of the atom in this state is −21.17 eV (−0.78 a.u.). Therefore, it is natural to stabilize the atom when the total electron energy reaches this level.

For the doubly excited state of −0.78 a.u. binding energy a long-time stability was achieved with c_en = 3.188 a.u. The stabilization was not sensitive to the c_ee parameter, therefore we did not change it. The interval for the random choice of the initial position coordinates for the double excited state was [0, 5.6 a.u.], and that for the momentum coordinates was [0, 0.9 a.u.]. Equilibrium was reached again allowing the electrons to circulate around the nucleus twenty times. Figure 3 compares the initial and the equilibrium distributions of the one-electron position, momentum and energy.

Zoom In Zoom Out Reset image size

At the time moment when the total electron energy reaches −0.78 a.u., the position and momentum coordinates of the two electrons are replaced by those obtained by the restabilization of the atom. We note that we made a series of calculations in which we restabilized the atom at different values (thresholds) of the total electron energy. We varied the threshold between −1.5 a.u and −0.5 a.u. in a step of 0.1 a.u. We found best agreement with the experiment at −0.8 a.u. This result strongly supports the proposed mechanism of NSDI involving the first doubly excited state of helium.

We can justify the above restabilization procedure by considering the quantum mechanical description of the laser-induced DI. We may approach the wave function by a superposition of singly- and doubly excited two-electron states (including excitations also into the continuum). The time evolution of the wave function is governed by the time-dependent Schrödinger equation. When the total electron energy reaches and exceeds the level of the first doubly excited state, the weight of the initially dominating singly excited states decreases and the contribution of the doubly excited states increases. At the double excitation thresholds this is expected to proceed resonantly. In our model we mimic the rapid change of the wave function by a sudden transition from the highly polarized singly excited state to the restabilized, doubly excited state. The probability of the transition is unity, because we always stabilize the atom when the energy condition is fulfilled. In the quantum mechanical treatment the occupation probability of the doubly excited states is certainly smaller, which means that our model probably overestimates the DI channel proceeding through the formation of doubly excited states.

We note that there have been studies [50, 68, 71] dealing with the laser-induced NSDI of the helium atom in which the c_en soft-core potential parameter (called also as nuclear screening parameter) was changed. In those works c_en was reduced to 0.4 in references [50, 71], and to 0.6, 0.4, and 0.1 in reference [68] in order to provide a more realistic description of the electron–ion interaction in the recollision process. It was changed when the distance r between the firstly ionized electron and the ion core reached a certain value (r = 5 and 10 a.u. in references [50, 71] and reference [68], respectively). Obviously, the reason of the adjustment of c_en in our procedure is different from that of the above works, we need it to restabilize the doubly excited atom. At the same time, there is a common feature of the two procedures: because of the requirement of the energy conservation the sudden change of c_en causes a discontinuity in the time dependence of the electron trajectories.

To distinguish the modified model from the original CEA model, we use the abbreviation CEA-DE (classical ensemble approximation with inclusion of doubly excited states).

Figure 4 shows the one-electron energies and the total electron energy in the helium atom as a function of the time for two DI events calculated in the CEA-DE model at laser intensity of 10¹⁵ W cm⁻². The arrows show the time moment when the excited atom is stabilized. One sees that in a short time (within half optical period) after the stabilization both electrons are simultaneously released by the laser field. The question may arise whether before the field-induced DI the resonant 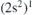${\left(2{\text{s}}^{2}\right)}^{1}$ S state may decay via autoionization, decreasing in this way the probability of DI. The width of this resonance is 0.138 eV (0.0051 a.u.) [116] corresponding to a lifetime of 197 a.u. This is much longer than the optical period (54.4 a.u.), therefore the probability of the autoionization is negligible.

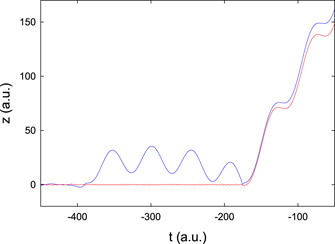
Zoom In Zoom Out Reset image size

The panels (a) and (b) of figure 4 present the examples of two types of DI events occurring with about 50%–50% probabilities. The first one (figure 4(a)) is fast process (called prompt DI) initiated by the large fluctuations of the one-electron energies as discussed above. The second type (figure 4(b)) is a slow process (called delayed DI) in which one of the electrons is first excited to a near-zero energy level. The motion of this electron is quasi-free, its energy is mostly positive, but sometimes it is negative. The negative energy periods indicate that the attractive Coulomb force keeps the electron in the vicinity of the atomic core for longer time (see figure 5). Since the electron mostly stays at larger distances from the core, its interaction with the other electron is small. However, after a time the two electrons approach each other and exchange energy. The atom in this way gains enough energy from the field to fulfill the condition of the double excitation.

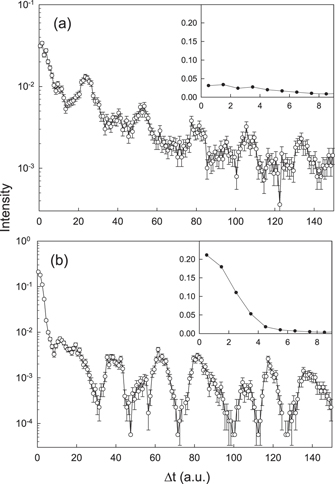
Zoom In Zoom Out Reset image size

Figure 6 shows the distribution of the time difference Δt = |t₁ − t₂| for the DI events at laser intensity of 10¹⁵ W cm⁻². t_i is the time moment when the ith electron is liberated from the atom. In panel (a) and (b) the calculations were made using the CEA and CEA-DE model, respectively. CEA-DE resulted in much stronger time correlation than CEA, as it is seen from the comparison of the insets of the two figures. The inclusion of the doubly excited states had a dramatic effect: the probability of DI increased by several factors at small Δt values; the two electrons are dominantly emitted within 1/4 optical period.

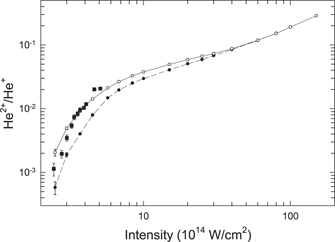
Zoom In Zoom Out Reset image size

In figure 7 we present the results obtained for the double-to-single ionization (DI/SI) ratio in the laser intensity range (2.5–150) × 10¹⁴ W cm⁻². The ratios calculated in the CEA and CEA-DE model are compared with the measured data of Henrichs et al [33]. The latter data were normalized to the CEA-DE curve at 3.7 × 10¹⁴ W cm⁻². The normalization factor is 16, i.e., the theory largely overestimates the experiment. This discrepancy is partly due to our procedure in which the probability of the formation of the intermediate excited states is unity (see above). According to the figure, the inclusion of the excited states has a small effect on the DI/SI ratio at high laser intensities. With decreasing intensity the difference between the two curves increases, at the lowest intensity CEA-DE exceeds CEA by a factor more than three. Both curves show the 'knee structure'; it is somewhat more pronounced for CEA-DE. At higher intensities the measured data follow well the tendency of the theoretical curves, however, at low intensities they decrease more rapidly than the theoretical values.

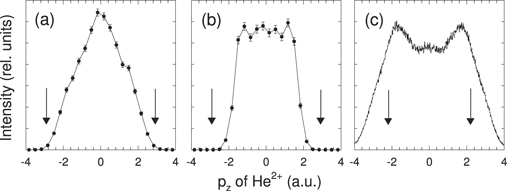
Zoom In Zoom Out Reset image size

In figure 8 we compare the calculated and measured distributions of the longitudinal momentum of the He²⁺ recoil ion (i.e., the momentum component of He²⁺ parallel to the light polarization) at laser intensity of 5.7 × 10¹⁴ W cm⁻². According to the figure, the CEA model completely fails to reproduce the measured momentum distribution. The prediction of the CEA-DE model is closer to the experiment. It shows, however, only a flat plateau around p_z = 0 at this laser intensity, in contrast to the minimum observed in the experiment. The arrows in the figure indicate the maximum longitudinal momentum that the He²⁺ ion can gain from the laser field, ${\pm}4\sqrt{{U}_{\mathrm{p}}}$. The momentum values obtained in our calculations are within these limits. The measured broad distribution, however, extends to a larger range.

Zoom In Zoom Out Reset image size

In figure 9 we plotted the distribution of the calculated and measured momentum of the He²⁺ recoil ion in two dimensions: along the direction parallel with the light polarization and along a direction perpendicular to the polarization (the p_z and p_x momentum component of He²⁺, respectively). Here, again a better agreement with the experiment was achieved with the CEA-DE model: it correctly reproduces the double humped structure of the observed distribution. The striking difference between the calculated and measured distribution is that the latter one is much broader in both directions.

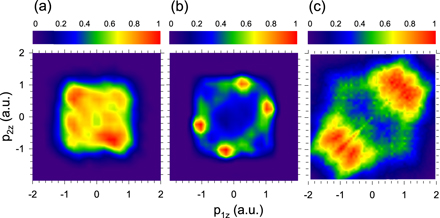
Zoom In Zoom Out Reset image size

The contour maps in figure 10 show the calculated and measured correlated longitudinal momentum distributions of the electron pairs released by the laser light. In panels (a) and (b) we plotted the results obtained by the CEA and the CEA-DE model, respectively. The distribution obtained by CEA is almost homogenous, i.e., the correlation between the momenta of the electrons is small. This is in contrast to the measured distribution shown in panel (c) which indicates that the two electrons are dominantly emitted side by side into the same hemisphere. This feature is qualitatively reproduced by the CEA-DE calculations. Furthermore, the correlation pattern obtained by CEA-DE has a similar overall rhomboid shape as that observed in the experiment. The rhomboid shape is due to the contribution of the back-to-back emissions. There are, however, significant differences between the measured and calculated distributions. The regions of the maximum intensities in the calculated distribution are more pronounced and better separated than in the measured one. Furthermore, in our calculations we did not find DI events that appear in the measured distribution as a narrow line along the diagonal. It is hard to explain the origin of these events physically, since for the correlated DI the strong Coulomb repulsion between the electrons leads to a deep minimum at momenta p_1z ≈ p_2z . However, it may be a quantum mechanical effect, and further experiments were needed to confirm the existence of this interesting phenomenon. We note that our CEA-DE results are strongly supported by the recent measurements of Shaaran et al [37]. The correlated momentum distribution obtained by the authors for DI of argon by 25 fs, 800 nm laser pulses of intensity of 1.5 ×  10¹⁴ W cm⁻² (see figure 1(a) of reference [37]) is very similar to the distribution calculated in the CEA-DE model.

Zoom In Zoom Out Reset image size

Figure 11 shows the results of CEA-DE calculations obtained for the one- and two-dimensional distribution of the longitudinal momentum of the He²⁺ recoil ion and for the correlated longitudinal momentum distribution of the electron pairs as a function of the intensity of the laser pulse. Comparing these results with the experimental data measured at laser intensity of 5.7 ×  10¹⁴ W cm⁻² (see figures 8(c), 9(c), and 10(c)) one may conclude that the CEA-DE model provides better agreement with the data at somewhat higher laser intensity, at 6.8 ×  10¹⁴ W cm⁻². Particularly, the calculated recoil ion momentum distribution shown in figure 11(b) has a similar shape as that of the measured one. We note that the intensity 6.8 ×  10¹⁴ W cm⁻² is at the border of the 20% experimental error range of the intensity 5.7 ×  10¹⁴ W cm⁻².

Zoom In Zoom Out Reset image size

In the following, we consider the question of the origin of the peak doubling appearing in the first and third quadrant in the plane of the correlated momentum distribution. The two peaks are located symmetrically with respect to the diagonal, and they are particularly well separated in the distribution obtained by the CEA-DE model. To check whether the peak doubling is caused by the Coulomb repulsion between the liberated electrons, we repeated the calculations in that way that we turned off the e–e Coulomb interaction at the time moment of DI (defined by the time when the second electron is also released). Indeed, according to figure 12, the two peaks merged into one. This proves that the peak doubling is a direct manifestation of the electron correlation in DI. We note that this feature of the correlated electron momentum distribution has been analyzed in several studies of NSDI [21, 69, 70, 89]. However, in these works only qualitative explanations were given. It is an interesting question that in what extent the separation of the two peaks depends on the atomic species, the properties of the laser pulse, and the mechanism by which the electrons are set free. Since the maximum momentum transferred to the electrons depends only on U_p, the separation of the peaks can likely be expressed by a simple scaling function that depends only on the parameters of the laser pulse.

Zoom In Zoom Out Reset image size

Our CEA-DE calculations resulted in much narrower momentum distributions of the recoil ion and electrons than those observed in the experiment. A possible reason for this discrepancy is that we did not take into account the momentum resolution applied in the experiment. To check the effect of the finite resolution, we convolved our calculated distributions with a Gaussian. Henrichs et al [33] did not publish the momentum resolutions of their experiment. Assuming a momentum uncertainty as large as 0.2 a.u. (FWHM), the convolution resulted in only a slight improvement in the description of the experimental data. A small correction of the calculated results is expected also from the inclusion of the laser focus volume effect (see, e.g., reference [117]), because according to the authors of reference [33] the gas target applied in the experiment was much narrower than the Rayleigh length. This means that the broadening may have also physical origin, it may be caused by the contributions of other mechanisms of DI that are not considered in the present work.

At the beginning of this section we showed the importance of the long-time evolution of the motion of the electrons in a process leading to DI. This finding indicates that in case of a restricted time evolution one may obtain a different result. To check this, we reduced the original 45 fs pulse time (140 optical cycles) to 4.5, 9 and 18 fs (14, 28, 56 optical cycles, respectively). The calculations were made in the CEA model, i.e., without considering intermediate doubly excited states. The obtained correlated longitudinal momentum distributions are shown in figure 13. The surprising conclusion of these results is the strongly correlated side-by-side electron emission obtained by considering small number optical cycles. With increasing number of cycles the correlation becomes weaker. Similar behavior of the correlated electron momentum distribution was reported Chen et al [61] on the basis of their CEA calculations made for NSDI of argon induced by 790 nm laser pulses. Their results obtained for pulses of 4 and 16 optical cycles showed also decreasing electron correlation with increasing pulse time.

Zoom In Zoom Out Reset image size

The stronger electron correlation for small pulse duration has two reasons. First, the short pulse time does not allow the two electrons to separate far away at the time of the emission, therefore the Coulomb repulsion between them is strong. Second, during the short pulse time the system cannot evolve into the highly polarized two-electron state, whose formation strongly reduces the probability of NSDI.

We applied the classical mechanical approach for the description of DI induced by relatively long (45 fs), short-wavelength (394 nm) laser pulses from helium. At the laser intensities of the experiment by Henrichs et al [33] the results of our classical ensemble model applying the soft-core Coulomb potential resulted in DI events that did not show the strong electron–electron correlation observed in the measured data.The lack of the correlated DI events can be understood considering that at the given laser intensities the RII and RESI processes are below threshold. The basic features of the experiment were reproduced by assuming an energetically more favorable two-step process: the formation of a transient double excited state in the first step, and the simultaneous release of the two electrons by the electric field of the laser light in the second step.

Of course, more realistic description of DI is expected from the quantum mechanical (QM) treatment of the process, particularly from the solution of the time-dependent Schrödinger equation (TDSE). Such a theoretical work may consider the experiences obtained by the present classical analysis. So far the solution of TDSE has been restricted for a few optical cycles due to the extreme computational requirements of such calculations [88]. Obviously, for long laser pulses reliable results are expected by increasing the number of the cycles. Furthermore, our results call the attention for the inclusion of the double excited states in the expansion of the total wave function. The appearance of the quasi-free state observed in the classical simulation is a further interesting question of the future QM studies of DI.

We thank Dr R Dörner for providing the numerical data of the experiment presented in reference [33]. This work was supported by the Hungarian Scientific Research Fund (Grant No. K128621), the National Research, Development and Innovation Office (Grant No. 2018-1.2.1-NKP-2018-00010), and the National Information Infrastructure Development Program.