Abstract
In the recent manuscript (Ikehata 2022 Inverse Problems38 075009), the author made some comments on our previous work (Sini and Yoshida 2012 Inverse Problems28 055013) saying that few arguments in the proof of lemma 3.5 might be incomplete for 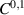 -regular domains. In this note, we reply to his comments by showing that, for C1-regular domains, those arguments are correct.
-regular domains. In this note, we reply to his comments by showing that, for C1-regular domains, those arguments are correct.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Let 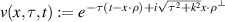 , where ρ is a unit vector, with
, where ρ is a unit vector, with 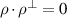 , and τ and t are two positive parameters. The enclosure method is a reconstruction scheme proposed, two decades ago, by Ikehata to reconstruct (geometrical features of) interfaces from remote measurements using v as a test function (and eventually other test functions). In the case where the mathematical model has a lower order term (i.e. of Helmholtz type), some extra conditions were needed to justify this method. In [1], an approach was proposed to remove these extra conditions. It is based on appropriate a priori estimates that control the lower order terms to deal with the lack of positivity. In a recent manuscript, see [2], section 4, the author made some comments saying that the justification of the estimates in lemma 3.5 of [1], see the estimates (1) and (2) below, might not be complete. The object of this note is to clarify this issue. To go straight to the point, we consider only the critical value of the parameter t:
, and τ and t are two positive parameters. The enclosure method is a reconstruction scheme proposed, two decades ago, by Ikehata to reconstruct (geometrical features of) interfaces from remote measurements using v as a test function (and eventually other test functions). In the case where the mathematical model has a lower order term (i.e. of Helmholtz type), some extra conditions were needed to justify this method. In [1], an approach was proposed to remove these extra conditions. It is based on appropriate a priori estimates that control the lower order terms to deal with the lack of positivity. In a recent manuscript, see [2], section 4, the author made some comments saying that the justification of the estimates in lemma 3.5 of [1], see the estimates (1) and (2) below, might not be complete. The object of this note is to clarify this issue. To go straight to the point, we consider only the critical value of the parameter t: 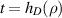 where
where 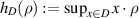 and use the notation
and use the notation 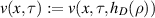 (as in lemma 3.5 of [1]).
(as in lemma 3.5 of [1]).
Let D be a bounded and Lipschitz regular domain in 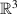 . Following the notations in [1], section 3.2, we introduce the sets
. Following the notations in [1], section 3.2, we introduce the sets 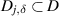 ,
, 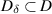 as follows. For any
as follows. For any 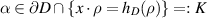 , define
, define 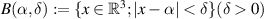 . Then,
. Then, 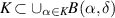 . Since K is compact, there exists
. Since K is compact, there exists 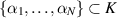 such that
such that 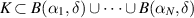 . Then, we define
. Then, we define  and
and 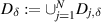 . We have
. We have 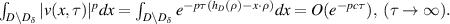
Assume now that D is of class C1, therefore 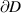 has a well defined (exterior) unit normal vector field
has a well defined (exterior) unit normal vector field 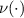 . The plane
. The plane 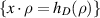 intersects
intersects 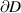 , at the points αj
's, with ρ as a normal vector to it. Then
, at the points αj
's, with ρ as a normal vector to it. Then 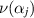 and ρ are parallel, see below, namely
and ρ are parallel, see below, namely 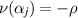 taking into account the orientation of the normal with respect to D. After the translation, of αj
to the origin, and the rotation, taking
taking into account the orientation of the normal with respect to D. After the translation, of αj
to the origin, and the rotation, taking 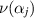 to
to 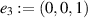 ,
,  takes the form, with δ smaller if needed,
takes the form, with δ smaller if needed, 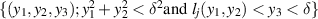 with lj
as a local representation of
with lj
as a local representation of 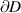 near αj
. Using these transformations and the property
near αj
. Using these transformations and the property 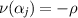 , we obtain
, we obtain
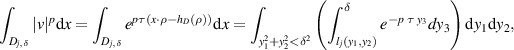
and then, with appropriate positive constants 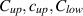 and clow
, we have
and clow
, we have
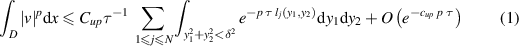
and
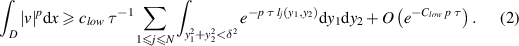
The estimates (1) and (2) are the ones in lemma 3.5 in [1]. The corresponding estimates for 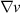 are deduced from the relation
are deduced from the relation 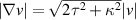 .
.
Let us now show why 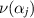 and ρ are parallel. Recall that, after translation and rotation,
and ρ are parallel. Recall that, after translation and rotation, 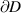 is represented, near αj
, as
is represented, near αj
, as  with lj
of class C1 and
with lj
of class C1 and 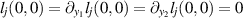 . Accordingly, the plane
. Accordingly, the plane 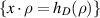 becomes, after translation and rotation,
becomes, after translation and rotation, 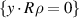 where R is the rotating matrix. We set
where R is the rotating matrix. We set 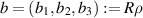 and
and 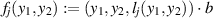 . This is a C1-regular function and it reaches its maximum, 0, at
. This is a C1-regular function and it reaches its maximum, 0, at 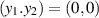 (as
(as 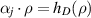 ). Therefore
). Therefore 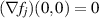 . This implies that
. This implies that 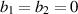 as
as 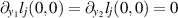 , hence
, hence 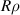 is parallel to
is parallel to 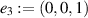 , i.e. ρ is parallel to
, i.e. ρ is parallel to 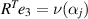 .
.
As we can see, the arguments in [1] to prove (1) and (2) are enough for a C1-regular domain D. The analysis above is shown for a complex geometrical optics solution with a linear phase v. It applies the same way to the other complex geometrical optics (CGOs) as well (with logarithmic phase for instance) as the one used in [1]. In addition, the CGOs with linear phase used in electromagnetism and elasticity have a similar form as the one considered here. Therefore, the results in [1] and also the ones derived later for other models including the electromagnetism and elasticity are correct for a C1-regular domain D.
Finally, we mention that in [2] the 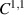 -regularity of the domain is required to justify this method.
-regularity of the domain is required to justify this method.
Data availability statement
The data cannot be made publicly available upon publication because no suitable repository exists for hosting data in this field of study. The data that support the findings of this study are available upon reasonable request from the authors.
