Abstract
Conditionally convergent series are infinite series whose result depends on the order of the sum. One of the most famous examples of conditionally convergent series of interest in Physics is the calculation of Madelung's constant α in ionic crystals. The appearance of this type of series is quite disturbing to students and often causes misunderstandings. In this work we analyze the physical meaning of the conditional convergence from a pedagogical point of view. The problem is posed using a toy model of ionic crystal in which the lattice sums can be calculated explicitly for various forms of expansion of the crystal about a central core. It is seen directly how the Coulomb series does not converge to α when there are charge accumulations on the surfaces. Therefore, it becomes clear what the appropriate strategy should be when choosing the order of summation to arrive at the correct value of α.
Export citation and abstract BibTeX RIS
1. Introduction
The calculation of the Madelung constant is one of the topics commonly studied in introductory courses of Solid State Physics mainly because of its interest in the computation of the cohesive energy of ionic crystals [1, 2]. Apart from elementary applications such as the prediction of crystal structures of alkali halides [1], the Madelung constant has also importance in other fields of material science such as the determination of optical phonon modes in ionic uniaxial crystals [3], exciton energies in alkali halides [4], evaluation of ionization energies of rare-earth ions doped into ionic crystals [5] or even study of properties of copper oxides of high critical temperature [6].
To compute the cohesive energy of an AB-type ionic crystal it becomes necessary to calculate the electrostatic energy of a particular reference ion. The energy is obtained as a sum of potential energy terms due to the interaction of the reference ion with all other ions in the crystal. For example, in a NaCl crystal each ion is surrounded by 6 ions of apposite sign at a distance r, 12 ions of the same sign at a distance √2r, 8 ions of opposite sign at √3r, 6 of the same sign at 2r, etc, and the potential energy of the reference ion is given by
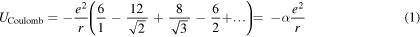
where e is the elementary charge, and α the Madelung constant, which for the NaCl structure is given by α = 1.74756. Similar sums can be performed for other ionic lattices and tables of Madelung constants can be easily found in the literature.
Although the sum (1) contains infinite terms, the Madelung constant can also be calculated for a finite number of ions. In these cases, there is a range of Madelung constants corresponding to ions in different environments [7]. In particular, the constants for ions near the surface are of interest in surface physics [8] and studies of nanocrystals [9]. Here however we will refer to the Madelung constant of the bulk.
If we take the reference ion at the origin of coordinates the Madelung constant in an AB-type ionic crystal is written as a lattice sum in the form

where ri
is the distance to the origin of the ith ion divided by the distance between first neighbours, and Zi
= +1 or −1 if the sign of that ion is different or the same as that of the reference ion. Sum (2) is extended to all ions except the reference ion. Except for the constant 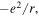 α is equal to the electrostatic interaction energy of an arbitrary ion with the rest of the crystal.
α is equal to the electrostatic interaction energy of an arbitrary ion with the rest of the crystal.
One of the most puzzling aspects of the series (2) is that it is conditionally convergent, i.e. its value depends on the order of the sum. This feature is quite disturbing to students, since it rarely occurs in physics. Often the student wonders how the order can affect the sum if the sum is a commutative operation and how one can speak of a unique Madelung constant for a given crystal structure if the series does not have a well-defined value. The situation is even worse if the students are familiar with a mathematical theorem due to Riemann that states that the terms of a conditionally convergent series can rearranged so that the sum can be made to converge to any given number or even to diverge. Although the solution to these questions is well known and has been correctly stated in various texts of Solid State Physics [1], the implications of these questions are often not well understood. The purpose of this paper is to develop this point from a pedagogical point of view keeping the mathematics at a minimum level. Our discussion will be carried out using a toy model of an ionic crystal where the series sum (2) can be calculated in several ways with relative ease. This will be the aim of the main section of the paper, section 2. We will find the Madelung constant of the crystal and analyze how the electric charge distributions on the crystal surfaces are when the series sum (2) is not equal to the constant α. We will conclude that although strictly speaking there is no single answer for the value of the Madelung constant in an infinite crystal, there is a well-defined value from the physical point of view. This is obviously the value used in practice. Finally, in section 3 we will briefly present some ideas on how to take advantage of the content of this paper to address the topic of Madelung's constant in undergraduate courses or possible extensions of it in graduate courses.
2. Results and discussion
Our model for ionic crystal is a one-dimensional crystal as depicted in figure 1(a) [2]. In this crystal the calculation of α is rather straightforward. If we place an ion at the origin, the result is

Taking into account that the Taylor expansion around x = 0 for the function ln(1+x) is
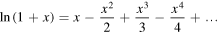
we easily have that the Madelung constant of our crystal is

Figure 1. (a) Model of the one-dimensional ionic crystal considered. (b) Scheme of the first three stages of crystal construction that gives rise to a correct value for the Madelung constant in the limit. Except for the factor 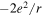 the electrostatic energy of the central ion takes the following values in each of them: 1,
the electrostatic energy of the central ion takes the following values in each of them: 1, 
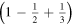 .
.
Download figure:
Standard image High-resolution imageSo far so good. Where is the problem then? The problem is that in this calculation we have tacitly assumed a specific form of ordering for the summands of the series: The series has been added precisely in the order in which equation (3) is written. This ordering corresponds in turn to a particular way of constructing the infinite crystal. The first stages of the construction of this particular form are schematized in figure 1(b). Although this way of assembling the infinite crystal may seem 'natural', it is far from being unique.
In general, an infinite crystal can be constructed as a limit form of finite crystals of increasing size, and the construction admits an infinite number of possibilities. Consider for example a construction strategy in which starting from the reference ion we add each time m ions of opposite sign and n ions of the same sign on each side of the origin. This means that at each stage we add 2 m+2n new ions. An example with m = 2, n = 1 is shown in figure 2. As can be seen, in the limit process with infinite steps we obtain the desired crystal, although at the ends of the various intermediate finite crystals there is a very abnormal charge distribution.
Figure 2. Scheme of the first three stages of the crystal construction with m = 2 y n = 1. Close to the edges there are empty cells. Except for the factor 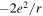 the electrostatic energy of the central ion takes the following values in each of them:
the electrostatic energy of the central ion takes the following values in each of them: 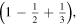

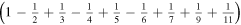 .
.
Download figure:
Standard image High-resolution imageLet us now calculate electrostatic energy 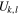 of the central ion at a stage in which there are added k ions of opposite sign and l ions of the same sign on each side of the central ion after N steps as described above. We will have k = Nm, l = Nn, and the energy of the central ion will be
of the central ion at a stage in which there are added k ions of opposite sign and l ions of the same sign on each side of the central ion after N steps as described above. We will have k = Nm, l = Nn, and the energy of the central ion will be

with
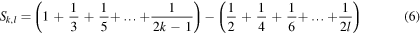
Now, the sum (6) can be written as follows
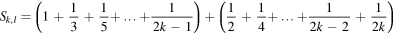
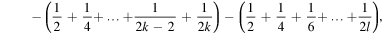
i.e.

where 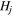 is the jth harmonic number
is the jth harmonic number 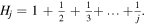
To calculate the sum (7) we will use the identity [10]

where γ ≈ 0.577 is the constant of Euler–Mascheroni and wj is a term that decreases rapidly when increasing j. More explicitly, it can be shown that wj can be expressed in terms of the so-called Bernoulli numbers Bp
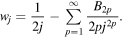
Figure 3 shows a comparative plot between the first harmonic numbers and the function  As can be seen, wj
becomes negligible for relatively low j values. For example for j = 50, we have wj
= 0.0022 Hj
As can be seen, wj
becomes negligible for relatively low j values. For example for j = 50, we have wj
= 0.0022 Hj
Figure 3. Graphic representation of the first 50 harmonic numbers (red dots) together with its asymptotic limit 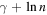 (blue dots). The quantities represented on both axes are dimensionless.
(blue dots). The quantities represented on both axes are dimensionless.
Download figure:
Standard image High-resolution imageCombining (7) y (8) we arrive at
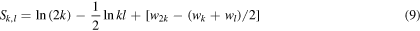
In the limit N →∞ all wj
terms are null, and 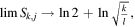 or
or

Using (6), the Coulomb energy of the reference ion in the infinite crystal constructed in that way is thus
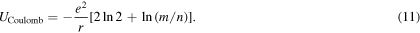
As can be seen, the term between square brackets is not equal to the Madelung constant unless m = n. In the construction process schematized in figure 1(b) one has m = n = 1, and then the constant α does indeed result. However, if the assembly strategy schematized in figure 2 is followed, m/n = 2, and the bracketed term (equal to 3ln2) is 50% larger than α. Given a central reference ion, if more ions of opposite sign are placed in each crystal construction step than ions of the same sign (m > n), the resulting constant is greater than α. In the opposite situation the opposite occurs. By varying the ratio m/n the energy of the central ion can have any arbitrary value.
It is understood then that, in practice, the situation of interest is that of figure 1(b), since the crystal must be constructed in such a way that in all stages of construction there is no appreciable contribution of the electric charges at the ends. In other words, in practice no charge accumulations can be maintained at the ends (as in figure 2) and it is therefore impossible to have a crystal different from the one shown in figure 1(b). Note that in the rearrangement of figure 2, terms arising from distant ions are included while terms arising from closer ones are omitted. For the case of a finite crystal this way of construction gives a totally unrealistic model because it would mean the inclusion of ions that do not exist and the omission of ions that do exist. Only in the arrangement of figure 1(b) the infinite series can approximate the value of the finite sum.
In three-dimensional crystals the long range of the Coulomb interaction can cause the lattice sums to give values that deviate from α not only if there are charges on the surfaces but also when there are dipole moments. In these cases, the corresponding series must be added so that in the construction of the crystal there is no appreciable contribution from charges or dipole moments on the surfaces. In crystals with the structure of NaCl, the celebrated Evjen method [11, 12] with expanding cubes provides a way to achieve a sufficiently symmetric arrangement of ions so that net charges, dipolar, quadrupolar, and octupolar terms cancel out [1]. In this way the series quickly converges to the correct value of α. Over time different strategies (like variants of the Evjen method or Ewald summations) have been devised to further accelerate convergence and obtain accurate α values [12–15]. But in any case it is interesting to comment that special care must always be taken with apparently 'reasonable' construction processes. For example, if in the NaCl case the sum is made over expanding spheres, as tacitly stated in equation (1), instead of over expanding cubes it fails to converge! [16].
3. Conclusions
In summary, the one-dimensional example discussed in this work illustrates in a simple way the physical reasons why the lattice sum (2) is conditionally convergent, and clarifies how to choose the order of summation to obtain a right value for α. This example can be used as an introduction to the topic before presenting the different existing methods to calculate α in three-dimensional crystals. The example can be fully developed in less than one lecture during an undergraduate course, or it can be presented as a guided assignment for students to complete. Anyway, the benefits to the student in terms of clarity are obvious since it justifies with simplicity the order in which the terms of the series should be added: Only with the 'correct' ordering does the sum of the infinite series approximate the corresponding sum of a real finite crystal.
The example can even serve as a starting point for more advanced studies in 2 or 3 dimensions involving the calculation of α for different shapes of the constructed crystal (e.g. spherical, cubic, parallelepipedic). Since the sum generated for each shape implies a rearrangement of its terms, a dependence of α on the crystal shape is to be expected. This is of interest in the physics of nanocrystals.
Acknowledgments
This work was supported by the Basque Country Government (Project No. IT1458-22).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).





