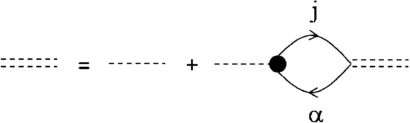Abstract
We theoretically investigate the photoabsorption cross-section of a cluster of alkali atoms embedded in a single-mode quantum microcavity. We show that if the energy of the giant plasmonic resonance lies close to the energy of the cavity mode, the strong coupling between the plasmon and cavity photon can occur which is characterized by mode anticrossing and observation of the doublet structure in the photoabsorption spectrum. The characteristic values of the Rabi splitting are expected to be several orders of magnitude larger than those observed in single quantum dot–cavity systems.
Export citation and abstract BibTeX RIS
1. Introduction
Strong coupling between light and matter excitations attracts growing interest of the physical community. The problem is important not only because of the fundamental aspects brought forward by the interaction of material systems with photons [1], but also due to the possibility of using the strong coupling phenomena for the creation of optoelectronic devices of the new generation, such as polariton lasers [2], optical logic gates [3], all-optical integrated circuits [4], terahertz light sources [5] and others.
Coupling of a zero-dimensional (0D) quantum system to a single photon mode, which forms the subject of cavity quantum electrodynamics (cQED), is of particular importance from this point of view due to the potential application of cQED to quantum information processing [6–8]. In the domain of the condensed matter, the system which recently attracted particular attention consists of a quantum dot (QD) coupled to a single microcavity mode [9–13]. The material excitations in the QD are exciton-bound electron–hole pairs. Owing to their spatial confinement and energy-level discretization, they can be brought in strong coupling with the mode of a microcavity: if a resonant absorber of light is embedded in a microcavity, it results in a new regime of mixed light modes. The condition of the strong coupling of the absorber and the cavity is that the light–matter interaction induced splitting, known as the Rabi splitting, is greater than the spectral linewidths (inverse lifetimes) of both the photon and exciton modes. Photonic confinement can be realized in a variety of structures, such as a pillar (etched planar cavity) [10], the defect of a photonic crystal [11] or the whispering gallery mode of a microdisc [12, 13], among others. In [10–12], such structures have demonstrated the Rabi doublet in their optical spectra which characterizes the mode anticrossing that marks the overcome of dissipation by the coherent exciton–photon interaction. The characteristic values of the Rabi splitting for QDs are typically of the order of 10–100 μeV which is 3–4 orders of magnitude smaller than that for the planar microcavities with quantum wells as an active element. A small value of the Rabi splitting makes achievement of the regime of strong coupling in 0D systems a technically complicated task and limits the possibilities of its practical implementations.
A natural question arises: can a strong-coupling regime be observed for material excitations other than excitons? One of the main candidates is the collective plasmonic excitation in metals. For planar metallic structures, the dispersion of the surface plasmon lies outside the light cone that makes its direct optical excitation impossible [14] and rules out the possibility of the observation of any strong coupling effects. This is not true, however, for more complicated structures containing metallic nanowire arrays [15] and metallic nanorods [16] for which the effects of strong coupling were shown to be extremely pronounced and experimentally observed Rabi splitting can be as big as 250 meV [15]. This number exceeds, by an order of magnitude, the values of Rabi splitting for exciton–photon coupling in planar inorganic microcavities [17] and is comparable to Rabi splittings observed in organic structures [18].
In this paper, we consider another type of hybrid metal-dielectric structure consisting of the single metallic cluster embedded inside a single-mode photonic cavity. The collective motion of electrons in the cluster against the positively charged ionic background leads to the formation of a surface plasmonic mode responsible for the appearance of a giant resonance in the photoabsorption spectra [19–24]. If the energy of the plasmon is close to that of the photonic mode of the cavity, the processes of multiple resonant emissions and absorptions of photons by the cluster take place and hybrid plasmon–photon modes are being formed. The goal of this paper is to analyse their influence on the photoabsorption spectrum of the system and to estimate the corresponding values of the Rabi splitting.
2. Model
To illustrate the onset of the strong-coupling regime in the cluster–cavity system, we will focus on the metallic clusters formed by alkali atoms (Li, Na, K), as they are the most exhaustively studied from both theoretical and experimental points of view. The geometry of the system we consider is shown in figure 1.
Figure 1. System geometry: metallic cluster formed by alkali atoms Na-8 embedded in a single-mode microcavity. The cavity photons of the frequency ω0 undergo multiple re-emissions and re-absorptions by the collective excitation of the cluster forming light–matter hybrid polariton eigenmodes of the system.
Download figure:
Standard imageThe theoretical basis of studying the collective phenomena in clusters is provided by the jellium model in which N electrons (one per each alkali atom) are moving in the spherically symmetric electrostatic potential Vb(r) formed by the uniform background of the positive ions calculated as the convolution of the Coulomb electrostatic potential with smooth charge distribution
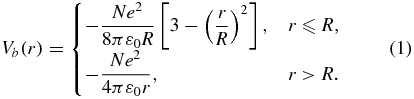
This assumption is generally believed to be well justified for the alkaline clusters with closed shells [20], i.e. for N = 8, 18, 20, 34, 40, 58, 92, .... However, we want to underline that our results are of general character and should be qualitatively the same for clusters with partially filled shells and for clusters consisting of the non-alkali atoms, but the computation procedure becomes more tricky in these latter cases4.
Let us consider an alkali-metal cluster with transition frequencies ωαj = ωj − ωα = ℏ−1(Ej − Eα) where the indices α and j correspond to the occupied and unoccupied single-electron states, respectively. In the case when electron–electron interactions are neglected or treated within the Hartree–Fock approximation, each single electron transition is coupled to the external photons independently. As the oscillator strengths of these individual transitions are small, their coupling with the cavity mode results in small values of the Rabi splitting (of the order of magnitude of those observed in QD–cavity systems).
However, the account of many-body corrections can change the picture dramatically. The Coulomb interaction leads to the formation of the collective excitation of the cluster known as the Giant plasmonic resonance which has a huge oscillator strength (several orders of magnitude larger than oscillator strengths of individual transitions) [19–22, 24]. Consequently, one can expect high values of the Rabi splitting in the coupled cluster–cavity system.
3. Formalism
The interaction of the electromagnetic field with material objects is described by dipole matrix elements of the transitions dαj. The account of many electron processes results in renormalization of the dipole matrix elements which become frequency dependent. They are denoted as D(0)αj(ω) in our further discussion. An account of processes of multiple re-emissions and re-absorbtions of photons in a microcavity leads to further renormalization Dαj(ω).
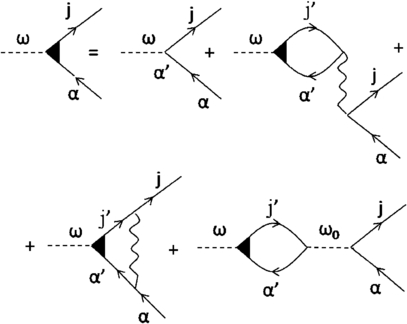
Figure 2 illustrates the diagrammatic representation of the equation for Dαj(ω) in the system we consider, and graphical representations of renormalized and bare dipole matrix elements of photoabsorption Dαj(ω) and dαj are presented in figure 3. On the right-hand side of figure 2, the first diagram corresponds to the direct photoabsorption, the second two diagrams account for the influence of dynamical polarizability in the random phase approximation with exchange (RPAE) and give rise to a giant plasmon resonance and the last one accounts for the multiple re-emissions and re-absorptions of the cavity photon. In the figures, the straight lines with arrows correspond to the electrons in the cluster at vacant and filled orbitals j, α, the wave lines correspond to the Coulomb interaction, while the dotted lines correspond to the cavity photons of frequency ω0. Using the Goldstone technique of evaluation of the Feynmann diagrams, one can find the renormalized dipole matrix elements from the following set of algebraic equations
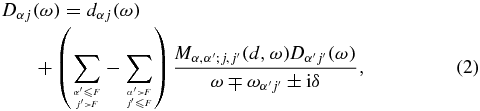
where the first and second sums correspond to the 'time forward' and 'time backward' diagrams, respectively, and

In the above formula, 〈|VC|〉 are the matrix elements of the exact Coulomb interaction with both the direct and exchange parts. The linewidths δ and γ correspond to the finite lifetime of the one-electron excitations and cavity photons, and gαj are the matrix elements of the interaction between the transitions α → j and cavity mode, which are proportional to the dipole matrix elements of the transitions and can be estimated as [25]
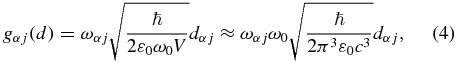
where V ≈ (λ0/2)3 denotes the cavity volume.
Figure 2. Diagrammatic representation of the equation for the renormalized dipole matrix element of the transition. The straight lines with arrows correspond to the electrons in the cluster at vacant and filled orbitals j, α, the wave lines to the Coulomb interaction and the dotted lines to the cavity photons of frequency ω0.
Download figure:
Standard imageFigure 3. Diagrammatic representation of renormalized and bare dipole matrix elements of the transition.
Download figure:
Standard imageNote that solving the system of equations (2) is equivalent to accounting the Coulomb RPAE diagrams and coupling between transitions in the cluster and the cavity mode up to the infinite order. Together, they describe the formation of the hybrid plasmon–photon excitations in the cluster–cavity system.
The response of the system can be described in terms of the photoabsorption cross-section and is proportional to the imaginary part of the dipole dynamical polarizability
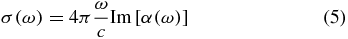
which can be found using the standard formula
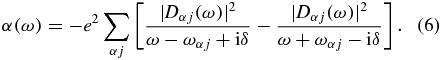
The energies of the eigenstates of the system can be found from the poles of the dressed Green's function for the cavity photon represented diagrammatically in figure 4. The double dashed line corresponds to the renormalized Green's function of the photon, while the single dotted line corresponds to Green's function of the bare photon G0 = 2ω0/(ω2 − ω20 + 2iω0γ). The symbol dot in the diagram corresponds to the renormalized matrix element of the cluster–cavity coupling gαj[D(0)(ω)], accounting for many-body interactions in the cluster but neglecting multiple re-emissions and re-absorptions of the cavity photon as latter processes are already accounted for in the diagram of the Dyson equation for the dressed photon (figure 4) and should not be counted twice. Mathematically, the values of D(0)αj(ω) can be found from the system of the equations analogical to those represented in the diagrammatic form in figure 2 but with the last diagram on the right-hand side being absent. Green's function of the dressed photon reads
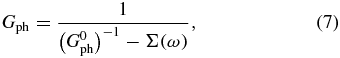
where
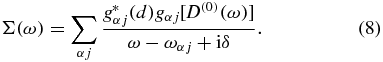
The eigenfrequencies of the hybrid eigenmodes can be found from the poles of expression (7) giving the following transcendent equation:
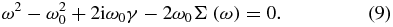
Figure 4. The diagrammatic representation of the Dyson equation for Green's function of the cavity photon. The double dashed line corresponds to the renormalized Green's function of the photon, the single dotted line—to Green's photon of the bare photon. The dot on the diagram corresponds to the renormalized matrix element of the cluster–cavity coupling accounting for many-body interactions in the cluster but neglecting multiple re-emissions and re-absorptions.
Download figure:
Standard imageBefore we proceed with presenting the results of the numerical modelling, let us analyse the limiting cases.
If the cavity is absent, electron–electron interactions renormalize dipole matrix elements of the transitions D(0)αj(ω) which become frequency dependent and form sharp peaks at the frequency ω = ωpl, corresponding to the characteristic frequency of the giant plasmon resonance [19–22, 24]. On the other hand, if one neglects the Coulomb interactions (which corresponds to the retaining of the first and last diagrams only in the diagrammatic equation presented in figure 2) and considers the coupling of the individual single transition to the cavity mode, the equations for the renormalized dipole matrix element and the dressed photonic Green's function can easily be solved
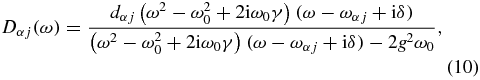
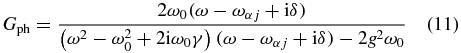
The poles of these expressions determine the energies of the new hybrid eigenstates of the system. The condition of achievement of the strong-coupling regime characterized by the mode anticrossing at a resonance (ω0 = ωαj) is given by a standard expression 4g2 > (δ − γ)2 [26].
4. Results and discussion
Let us now present the results of numerical modelling of the realistic cluster–cavity systems. We consider Na-8, 9+, 21+, 42++ clusters embedded in a photonic cavity in the position where the electric field of the cavity mode reaches its maximum (we explain our choice of clusters below). The light mode structure in a microcavity is a standing wave (sin-like oscillating) with nodes at some coordinates. The typical size of a cavity (and light wavelength also) is in micrometres, while the size of a cluster is in angstroms. Thus, we can approximately assume that the cluster is embedded in some local point in the cavity. If one puts a cluster in a node of the wave, the interaction of the matter mode with the light mode is absent but can be increased by moving the cluster towards the antinode. The stronger the coupling, the more pronounced the effect and the Rabi splitting. The energy of the cavity mode ω0 is supposed to lay close to the energy of the giant plasmon resonance ωpl. The energies of single-electron states in the cluster were calculated within the jellium model using Hartree–Fock approximation. The non-radiative linewidths of all the individual transitions in the cluster were taken to be the same and corresponding to δ = 1 meV.
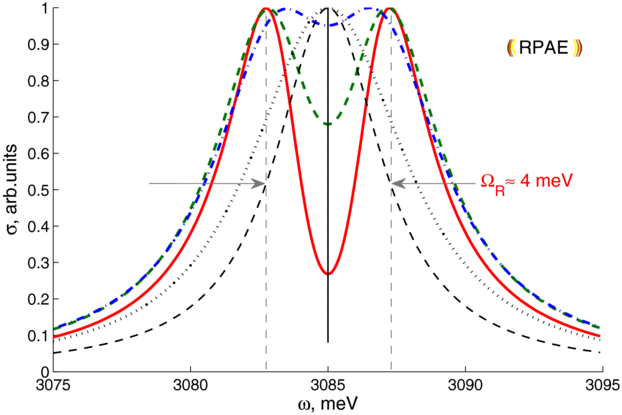
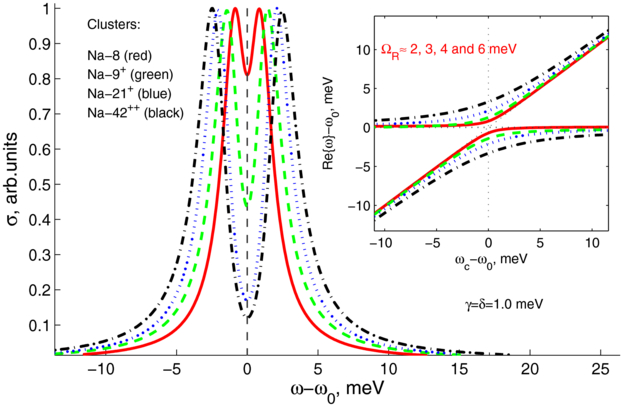
Figure 5 illustrates the photoabsorption cross-section of the cavity–cluster system as a function of frequency of the external laser excitation for the case when the energy of the giant plasmon is tuned in resonance with the energy of the photonic mode ω0 = ωpl. If the lifetime of the photons in a microcavity τ is low (γ ≈ ℏ/τ is high), we can observe one peak on the photoabsorption spectrum (see figure 5; note that all the plots are normalized to unity). However, the situation qualitatively changes if the lifetime increases. In this case, the strong-coupling regime is being established and two peaks appear in the photoabsorption spectrum. The distance between the peaks corresponds to the Rabi splitting and increases with the increase of the lifetime of the cavity mode; it can reach the values of about 1.8, 2.1, 4.2 and 6.9 meV for Na-8, Na-9+, Na-21+ and Na-42++ clusters, respectively (according to the model presented in current work). These values are several orders of magnitude larger than those observed in single QD–cavity systems [9–13].
Figure 5. Cluster Na-21+ photoabsorption cross-sectional spectrum—system response on the exciting emission of light for different broadening of a cavity mode (in meV): 1 (red/solid)—quasi-ideal microcavity, 2 (green/dashed), 4 (blue/dash-dotted) and 6 (black/dotted)—limiting case which is close to the absence of the cavity. The Rabi splitting ΩR decreases with the photon's lifetime being decreased and finally disappears at γ ≈ 7 meV. See the text for details.
Download figure:
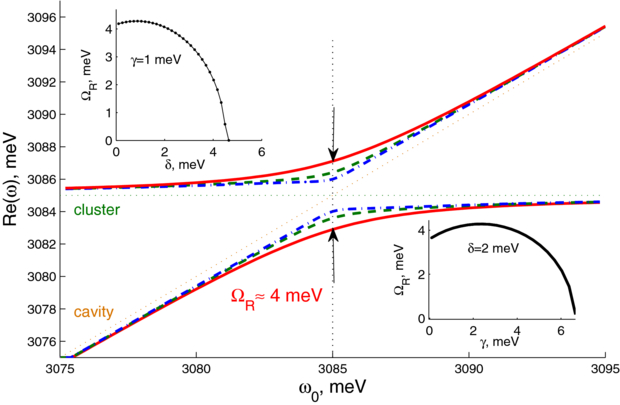
Standard imageFigure 6 shows the energies of the hybrid modes of the Na-21+ cluster coupled to a microcavity for different broadenings of the cavity mode. The Rabi splitting can be found as a distance between the two branches at the anticrossing point corresponding to ω = ω0 and ω = ωpl. It varies from ≈0 (γ = 6.5 meV) to 4.2 meV (for γ = 2.2 meV). Insets illustrate dependences of the splitting on the inverse lifetimes γ and δ. Note that the results presented in figures 5 and 6 are in good agreement with each other.
Figure 6. Energies of hybrid modes of the Na-21+ cluster for different lifetimes of the photons (in meV): 1.0 (red/solid), 4.0 (green/dashed) and 6.0 (blue/dash-dotted). Illustration of the crossover from the strong- to weak-coupling regime. When γ ≈ 7 meV, the splitting ΩR ≈ 0 and one can see two solutions corresponding to the bare photon and plasmon ω1 = ω0 and ω2 = ωpl (dotted curves named 'cavity' and 'cluster'). Insets show dependences of the Rabi splitting ΩR on the inverse lifetimes of the photon γ and plasmon δ. The maxima on the dependences correspond to optimal combinations of the parameters (see the discussion at the end of section 3).
Download figure:
Standard imageThe main problem from the point of view of experimental observability of the Rabi splitting in such systems is the large width of the plasmon resonance [19]. However, there exist two main ways to bypass it. The first solution is to use positively charged clusters: it is well known that the optical response of metal clusters has a charge dependence [23], and the higher the charge state, the narrower the spectrum. Apparently, it is important for the experimental observability of the Rabi splitting. The second way of manipulation of the width is connected with the possibility of using clusters embedded in rare gas matrices. For instance, in the case of Na+9Ar164, the plasmon peak seems to be narrower than that in the case of pure Na-9+ [27]. For these reasons in this paper, we consider not only the Na-8 neutral cluster, but also positive ions of sodium clusters with closed shells Na-9+, Na-21+ and Na-42++. The plasmonic peak can also become narrower at the lower temperatures. Note if a cluster is embedded in a dielectric matrix, the refractive index of the matrix can change the interaction between the cluster and the cavity. In fact, the dielectric constant ε enters equation (4) together with ε0; thus, g ∼ ε−1/2 and decreases with ε being increased. Therefore, the Rabi splitting also decreases.
Figure 7 illustrates the Rabi splitting dependence on the number of atoms in the cluster. For Na-8, we have small splitting of about 1 meV; notwithstanding for Na-42++ cluster, the splitting reaches the value of about 7 meV. We expect that in bigger clusters the Rabi splitting will increase further and reach the values of dozens of meV.
Figure 7. Photoabsorption cross-sectional spectrum for different sodium clusters: Na-8 (red/solid), Na-9+ (green/dashed), Na-21+ (blue/dotted) and Na-42++ (black/dash-dotted). The frequency is counted from the position of the giant plasmon resonance in the corresponding cluster. The Rabi splitting ΩR varies from ≈ 2 to 6 meV with the increase of number of atoms in the cluster. Inset illustrates anticrossing for different clusters (the numerical solutions of the Dyson equation for the photon Green's function, see equations (7)–(9)). The inverse lifetimes of the photon and plasmon modes, γ and δ, were taken equal to 1 meV.
Download figure:
Standard image5. Conclusions
In conclusion, we have analysed the spectrum of photoabsorption of individual sodium clusters embedded in a single-mode photonic microcavity. We have shown that in the region of the giant plasmonic resonance, the regime of strong coupling between plasmon and cavity photon can be achieved which manifests itself by the formation of the Rabi doublet and mode anticrossing. A cluster can be considered as a 0D object with the size comparable to those of the QDs. However, due to the many-body effects, it demonstrates Rabi splittings several orders of magnitude larger than other 0D quantum objects.
Acknowledgments
The authors thank V K Ivanov for useful discussions. This work was supported by Rannis 'Center of Excellence in Polaritonics' and FP7 IRSES project 'POLAPHEN'. RGP thanks the University of Iceland for hospitality.
Footnotes
- 4
The difficulty of the consideration of the clusters with partially filled shells comes from the necessity to account for a great number of the transitions between various thermae with different orbital momenta, which becomes a technically complicated task even for N = 8. The standard way to overcome this difficulty consists in using the so-called average therm approximation, which becomes exact for the clusters with completely filled shells. From the point of view of qualitative results, there is of course no difference between the clusters with fully and partially filled shells.