Abstract
We investigate how the driving field affects the bound states in the one-dimensional two-particle Bose–Hubbard model with an impurity. In the high-frequency regime, compared with the static lattice [Phys. Rev. Lett. 109 (2012) 116405], a new type of Floquet bound state can be obtained even for a weak particle–particle interaction by tuning the driving amplitude. Moreover, the localization degree of the Floquet bound molecular state can be adjusted by tuning the driving frequency, and even the Floquet bound molecular state can be changed into the Floquet extended state when the driving frequency is below a critical value. Our results provide an efficient way to manipulate bound states in the many-body systems.
Export citation and abstract BibTeX RIS
In recent years, there has been growing interest in bound states. It has been demonstrated that the bound states play an important role in dynamics of a quenched Bose–Einstein condensate[1] and a lattice Bose gas,[2] quantum information,[3] electron transport,[4] etc. Bound states can be divided into two categories.[5–10] The one is an ordinary bound state with an energy lying outside the continuous spectrum of scattered states, i.e., bound state outside the continuum (BOC), and the other one is the bound state in the continuum (BIC). BIC states that were originally pointed out by Neumann and Wigner[11] are difficult to observe in quantum system. The first attempt to realize a BIC experimentally was taken by Capasso et al.[12] More recently, BIC states have been demonstrated experimentally in photonic structures[13–16] using the analogy between optical systems and quantum mechanics. As shown in other studies, moving to the many-particle framework makes the physics rather different. In a few recent works, it has been shown that particle interaction enhances the formation of BIC states and makes them robust.[17,18] Two-particle BIC states have been predicted to exist in defective Hubbard lattices, either in the bulk[17] or at the surface.[18] Such previous studies have been limited to consider static (i.e., undriven) Hubbard lattices.
Periodic driving fields have been extensively used to control quantum tunneling and transport.[19–28] Along this line, periodic driving fields have also been used to control bound states. For a single particle, bound states driven by ac fields have been studied by the Floquet theory[29–31] and the concept of Floquet BIC states has been introduced, i.e., BIC states that arise in a time-periodic Hamiltonian. In particular, the appearance of Floquet BIC states for a single particle hopping on a defective lattice, induced by a strong oscillating force, has been theoretically predicted.[31] Nevertheless, the single-particle Floquet BIC states are fragile against perturbations of system parameters. A type of robust two-particle BIC state that can be called the Floquet–Hubbard BIC state is found in a wide range of parameter space, which is induced in a homogeneous Hubbard semilattice by an intense oscillating electric field, does not require fulfilment of resonance conditions, and is thresholdless.[32] However, how to control the robust two-particle Floquet bound state by the periodic driving field is still unclear.
In this Letter, we investigate how to manipulate Floquet bound states in a driven two-particle Bose–Hubbard model with an impurity. In the high-frequency limit, the time-dependent Hamiltonian can be mapped onto an effective Hamiltonian with a rescaled tunneling rate, and a type of Floquet BOC molecular state can be obtained even for a weak particle–particle interaction by tuning the driving amplitude. Moreover, the localization degree of the Floquet bound molecular state can be adjusted by tuning the driving frequency for a fixed driving amplitude.
We consider a system of two interacting bosons held in a driven one-dimensional optical lattice with an impurity at site l = 0. The corresponding Hamiltonian of the system can be written as

where the operator 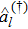 annihilates (creates) a boson at site l,
annihilates (creates) a boson at site l, 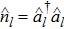 is the corresponding number operator, J denotes the nearest-neighbor tunneling rate, U is the on-site interaction energy, V is the impurity potential strength, ε is the driving amplitude, and ω is the driving frequency. A localized impurity and the periodic driving can be realized in optical lattice experiments.[33–35] For simplicity, we take
is the corresponding number operator, J denotes the nearest-neighbor tunneling rate, U is the on-site interaction energy, V is the impurity potential strength, ε is the driving amplitude, and ω is the driving frequency. A localized impurity and the periodic driving can be realized in optical lattice experiments.[33–35] For simplicity, we take  and adopt the parameter J as a unit to rescale the other parameters U, V, ε and ω, such that they become dimensionless.
and adopt the parameter J as a unit to rescale the other parameters U, V, ε and ω, such that they become dimensionless.
For a system consisting of two bosons, the state vector 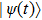 of the Hamiltonian (1) can be expanded in the Fock space as[36]
of the Hamiltonian (1) can be expanded in the Fock space as[36]

with 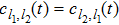 due to the indistinguishability of the two bosons. This indicates that the probability amplitude of finding the two bosons at the same site l is
due to the indistinguishability of the two bosons. This indicates that the probability amplitude of finding the two bosons at the same site l is 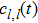 , whereas the probability amplitude of finding the two bosons at different sites l1 and l2 (
, whereas the probability amplitude of finding the two bosons at different sites l1 and l2 (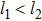 ) is
) is 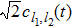 . Substituting the ansatz (2) into the Schrödinger equation
. Substituting the ansatz (2) into the Schrödinger equation  , we obtain the following coupled equations for the probability amplitudes
, we obtain the following coupled equations for the probability amplitudes
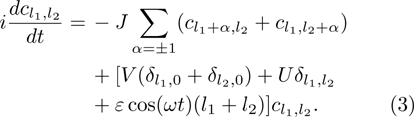
Under the condition of ![$J\ll \max [\omega, \sqrt{| \varepsilon | \omega }]$](https://content.cld.iop.org/journals/0256-307X/34/7/070304/revision1/cpl_34_7_070304_ieqn10.gif) , one can implement the high-frequency Floquet analysis. By introducing the transformation
, one can implement the high-frequency Floquet analysis. By introducing the transformation ![${c}_{{l}_{1},{l}_{2}}(t)={a}_{{l}_{1},{l}_{2}}(t)\exp [-i\tfrac{\varepsilon }{\omega }\sin (\omega t)({l}_{1}+{l}_{2})]$](https://content.cld.iop.org/journals/0256-307X/34/7/070304/revision1/cpl_34_7_070304_ieqn11.gif) , and averaging the rapidly oscillating terms, one can obtain an effectively undriven system
, and averaging the rapidly oscillating terms, one can obtain an effectively undriven system
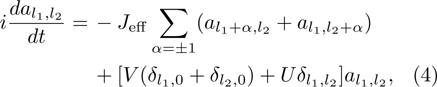
where the rescaled coupling strength 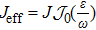 depends on the values of
depends on the values of 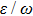 , with
, with 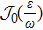 being the zero-order Bessel functions. Therefore, the modulus
being the zero-order Bessel functions. Therefore, the modulus  can change from zero to one, and equal zero at some specific values of
can change from zero to one, and equal zero at some specific values of  (such as
(such as 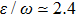 and 5.52).
and 5.52).
To show how the continuum bands of the extended states change with the driving parameters, we introduce two quantities to identify the three different quasienergy bands. The one is the mean of the sum of distance of two bosons to the defect at a given random instant of the oscillating period, 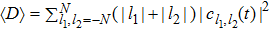 , where we consider a finite lattice with
, where we consider a finite lattice with 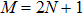 . Due to the period of function
. Due to the period of function ![$\exp [-i\tfrac{\varepsilon }{\omega }\sin (\omega t)({l}_{1}+{l}_{2})]$](https://content.cld.iop.org/journals/0256-307X/34/7/070304/revision1/cpl_34_7_070304_ieqn20.gif) is T, we can construct the Floquet state by setting
is T, we can construct the Floquet state by setting 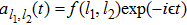 . Then the probability amplitudes
. Then the probability amplitudes 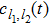 satisfy the relation
satisfy the relation 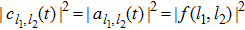 . Thus we have
. Thus we have 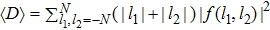 . The other is the probability of finding at least one boson outside of a ball of radius N/2 and centered at the defect,
. The other is the probability of finding at least one boson outside of a ball of radius N/2 and centered at the defect, 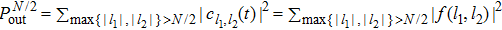 . For the special case
. For the special case 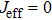 , the effective Hamiltonian of Eq. (4) has three continuum bands of the extended states, whose eigenvalues are
, the effective Hamiltonian of Eq. (4) has three continuum bands of the extended states, whose eigenvalues are 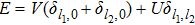 , which is similar to the time-independent case in Ref. [17]. For the general case
, which is similar to the time-independent case in Ref. [17]. For the general case 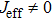 , we must employ numerical technique.
, we must employ numerical technique.
Selecting the typical high-frequency ω = 40,[37] and fixing the other parameters J = 1, V = −1.5 and U = 6, we numerically show the two quantities  and
and  as a function of the quasienergy
as a function of the quasienergy  for two different driving amplitudes ε = 1 and ε = ω in Fig. 1. We use M = 41 sites and open boundary condition. For the weak driving amplitude
for two different driving amplitudes ε = 1 and ε = ω in Fig. 1. We use M = 41 sites and open boundary condition. For the weak driving amplitude 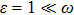 , we can see that the results of the high-frequency Floquet analysis (4) agree well with the ones from the original Hamiltonian (1), as shown in Fig. 1(a). For the strong driving amplitude ε = ω in Fig. 1(b), the results of the effective model have small deviation from the ones of the original time-dependent Hamiltonian. However, their band edges coincide with each other and the band widths of the three continuum bands are shortened. Comparing Fig. 1(a) with Fig. 1(b), we find that there exists a new type of Floquet state indicated by the arrow in the gap between the first and third continuum quasienergy bands. The new Floquet state is actually a Floquet BOC molecular state, which corresponds to the state that two bosons are captured by the impurity. The Floquet BOC molecular state can also be obtained even for a weaker interaction, when the effective particle interaction strength
, we can see that the results of the high-frequency Floquet analysis (4) agree well with the ones from the original Hamiltonian (1), as shown in Fig. 1(a). For the strong driving amplitude ε = ω in Fig. 1(b), the results of the effective model have small deviation from the ones of the original time-dependent Hamiltonian. However, their band edges coincide with each other and the band widths of the three continuum bands are shortened. Comparing Fig. 1(a) with Fig. 1(b), we find that there exists a new type of Floquet state indicated by the arrow in the gap between the first and third continuum quasienergy bands. The new Floquet state is actually a Floquet BOC molecular state, which corresponds to the state that two bosons are captured by the impurity. The Floquet BOC molecular state can also be obtained even for a weaker interaction, when the effective particle interaction strength 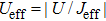 exceeds a certain critical value.
exceeds a certain critical value.
Fig. 1. (Color online) Plot of the two quantities 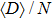 and
and 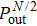 versus the quasienergy for two different driving amplitudes (a) ε = 1 and (b) ε = ω. The blue points describe the results from the original driven Hamiltonian (3), while the red circles represent the results from the effectively non-driven system (4). The Floquet bound state is indicated by the arrow. The values of other parameters are set as ω = 40, J = 1, V = −1.5 and U = 6. We use a finite lattice with M = 41 sites.
versus the quasienergy for two different driving amplitudes (a) ε = 1 and (b) ε = ω. The blue points describe the results from the original driven Hamiltonian (3), while the red circles represent the results from the effectively non-driven system (4). The Floquet bound state is indicated by the arrow. The values of other parameters are set as ω = 40, J = 1, V = −1.5 and U = 6. We use a finite lattice with M = 41 sites.
Download figure:
Standard imageThe quantity  or
or 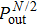 can also be used to discern the Floquet bound states from the Floquet extended states. The extended state is very sensitive to the size of the lattice, while a bound state is independent of the lattice size if the lattice size is much larger than the characteristic size of its wave function. Therefore, for the Floquet extended state, the value of
can also be used to discern the Floquet bound states from the Floquet extended states. The extended state is very sensitive to the size of the lattice, while a bound state is independent of the lattice size if the lattice size is much larger than the characteristic size of its wave function. Therefore, for the Floquet extended state, the value of 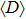 would change with the site number M. However, for the Floquet bound state, it would converge to a finite value with the increase of M. We plot
would change with the site number M. However, for the Floquet bound state, it would converge to a finite value with the increase of M. We plot 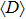 versus quasienergy for a smaller lattice M = 31 and a larger lattice M = 51 in Fig. 2(a). The state indicated by the arrow in Fig. 2(a) does not move as the lattice is enlarged, and it corresponds to the Floquet bound state. In additional, the degree of localization of the Floquet state can also be described by the participation ratio
versus quasienergy for a smaller lattice M = 31 and a larger lattice M = 51 in Fig. 2(a). The state indicated by the arrow in Fig. 2(a) does not move as the lattice is enlarged, and it corresponds to the Floquet bound state. In additional, the degree of localization of the Floquet state can also be described by the participation ratio  ,
, 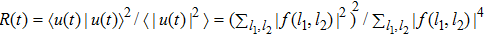 .[7,16] Here
.[7,16] Here 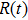 is periodic with period T, with
is periodic with period T, with 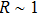 for strongly localized states, whereas
for strongly localized states, whereas 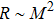 ,
, 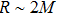 and
and 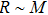 for extended states from the first, the second and the third continuum bands, respectively. In Fig. 2(b), we numerically plot the participation ratio R (in a log scale) versus the quasienergy. We find that there only exists one Floquet bound state, which is just counterpart in Fig. 2(a).
for extended states from the first, the second and the third continuum bands, respectively. In Fig. 2(b), we numerically plot the participation ratio R (in a log scale) versus the quasienergy. We find that there only exists one Floquet bound state, which is just counterpart in Fig. 2(a).
Fig. 2. (Color online) The two quantities 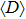 and R in a log scale versus the quasienergy in (a) and (b), respectively. The blue point marks the smaller lattice case with M = 31, while the red circle indicates the larger lattice case with M = 51. The Floquet bound state is indicated by the arrow. The other parameters are the same as those of Fig. 1(b).
and R in a log scale versus the quasienergy in (a) and (b), respectively. The blue point marks the smaller lattice case with M = 31, while the red circle indicates the larger lattice case with M = 51. The Floquet bound state is indicated by the arrow. The other parameters are the same as those of Fig. 1(b).
Download figure:
Standard imageTo show the validity of the high-frequency Floquet analysis, for a fixed driving amplitude, we consider the low-frequency regime to study the properties of Floquet bound states including both the Floquet BOC and BIC molecular states. It is worth noting that two different types of Floquet bound states appear in different specific parameter regions. Firstly, we consider the Floquet BOC molecular state. The participation ratio R in a log scale as a function of quasienergy is depicted for different driving frequencies ω = 10, 7, 5 and 4 in the first row of Fig. 3. The corresponding squared eigenstate of Floquet BOC quasienergy 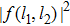 is shown in the second row of Fig. 3. For the high-frequency case ω = 10, the Floquet BOC molecular state is the state that two bosons are strongly localized in the vicinity of the impurity. However, as the driving frequency reduces from the high frequency ω = 10 to the moderate frequency ω = 4, the Floquet BOC molecular state is no longer strongly localized at the origin and becomes extended along the diagonal
is shown in the second row of Fig. 3. For the high-frequency case ω = 10, the Floquet BOC molecular state is the state that two bosons are strongly localized in the vicinity of the impurity. However, as the driving frequency reduces from the high frequency ω = 10 to the moderate frequency ω = 4, the Floquet BOC molecular state is no longer strongly localized at the origin and becomes extended along the diagonal 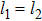 . We note that, in Fig. 3(d), there exists the other three Floquet bound states corresponding to three minimum values of the participation ratio. However, the three Floquet bound states are not the molecular states by analyzing the dynamical features of their squared quasienergy eigenstates. Therefore, the localization degree of the Floquet BOC molecular state can be manipulated by tuning the driving frequency. The Floquet BOC molecular state disappears when the driving frequency is further reduced to ω = 3. The two bosons only display single-particle behavior in the lower frequency regime.
. We note that, in Fig. 3(d), there exists the other three Floquet bound states corresponding to three minimum values of the participation ratio. However, the three Floquet bound states are not the molecular states by analyzing the dynamical features of their squared quasienergy eigenstates. Therefore, the localization degree of the Floquet BOC molecular state can be manipulated by tuning the driving frequency. The Floquet BOC molecular state disappears when the driving frequency is further reduced to ω = 3. The two bosons only display single-particle behavior in the lower frequency regime.
Fig. 3. (Color online) Both the participation ratio R in a log scale (the first row) and the corresponding squared Floquet BOC quasienergy eigenstate 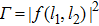 (the second row) for different driving frequencies (a) ω = 10, (b) ω = 7, (c) ω = 5 and (d) ω = 4. The driving amplitude is fixed as ε = 10, and the other parameters are the same as those of Fig. 1. The Floquet BOC molecular state is indicated by the arrow.
(the second row) for different driving frequencies (a) ω = 10, (b) ω = 7, (c) ω = 5 and (d) ω = 4. The driving amplitude is fixed as ε = 10, and the other parameters are the same as those of Fig. 1. The Floquet BOC molecular state is indicated by the arrow.
Download figure:
Standard imageIn the following we discuss the dependence of the Floquet BIC molecular state on the driving frequency. For the static lattice, there exists a type of robust two-particle BIC state in the subregion of 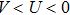 and the BIC state tends to the bound molecular state as
and the BIC state tends to the bound molecular state as 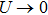 .[17] Selecting the parameters as U = −0.4 and V = −2, and the other parameters are the same as those of Fig. 3, we plot the participation ratio R for two different driving frequencies in the first row of Fig. 4. To more clearly distinguish the Floquet BIC molecular states from the extended states, the quantity
.[17] Selecting the parameters as U = −0.4 and V = −2, and the other parameters are the same as those of Fig. 3, we plot the participation ratio R for two different driving frequencies in the first row of Fig. 4. To more clearly distinguish the Floquet BIC molecular states from the extended states, the quantity 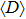 is depicted in the second row of Fig. 4. The squared eigenstate of Floquet BIC quasienergy
is depicted in the second row of Fig. 4. The squared eigenstate of Floquet BIC quasienergy 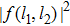 with the minimum R, is also shown in the third row of Fig. 4. The two bosons become greatly extended along the diagonal
with the minimum R, is also shown in the third row of Fig. 4. The two bosons become greatly extended along the diagonal 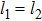 in the intermediate frequency regime ω = 6, compared with the high-frequency ω = 40. When the driving frequency is selected as the proper moderate frequency ω = 5, the Floquet BIC molecular state disappears and it is converted into the Floquet extended state. These results indicate that one can tune the localization degree of the Floquet bound molecular states by solely adjusting the driving frequency as compared with the static lattice.
in the intermediate frequency regime ω = 6, compared with the high-frequency ω = 40. When the driving frequency is selected as the proper moderate frequency ω = 5, the Floquet BIC molecular state disappears and it is converted into the Floquet extended state. These results indicate that one can tune the localization degree of the Floquet bound molecular states by solely adjusting the driving frequency as compared with the static lattice.
Fig. 4. (Color online) The participation ratio R (the first row), the quantity  (the second row), and the squared Floquet BIC quasienergy eigenstate
(the second row), and the squared Floquet BIC quasienergy eigenstate 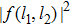 (the third row) for different driving frequencies (a) ω = 40 and (b) ω = 6. The parameters are set as U = −0.4 and V = −2, and the other parameters are the same as those of Fig. 3.
(the third row) for different driving frequencies (a) ω = 40 and (b) ω = 6. The parameters are set as U = −0.4 and V = −2, and the other parameters are the same as those of Fig. 3.
Download figure:
Standard imageIn summary, we have investigated how to manipulate Floquet bound states in a driven two-particle Bose–Hubbard model with an impurity. In the high-frequency limit, the time-dependent Hamiltonian can be mapped onto an effective Hamiltonian with a rescaled tunneling rate, and a type of Floquet BOC molecular state is found by tuning the driving amplitude. Furthermore, we explore the properties of the Floquet bound molecular states for low driving frequencies. The Floquet bound molecular states including both the Floquet BOC state and the BIC state extend along the diagonal  in the intermediate frequency regime and disappear for the sufficiently small driving frequency.
in the intermediate frequency regime and disappear for the sufficiently small driving frequency.
Therefore, on the one hand, the transition from no Floquet BOC molecular state to the appearance of Floquet BOC molecular state can be obtained by tuning the driving amplitude in the high-frequency limit. On the other hand, for a fixed driving amplitude, we can adjust the localization degree of the Floquet bound molecular state by tuning the driving frequency, and even the Floquet bound molecular state can be changed into the Floquet extended state in the sufficiently low driving frequency regime. With currently available experimental techniques for observing bound state,[38] it is possible to test our theoretical predictions. It is also possible to apply our analysis for treating the case of more complex driving fields, such as multifrequency driving fields and the driving field with a time-dependent amplitude.
Footnotes
- *
Supported by the National Natural Science Foundation of China under Grants Nos 11374375, 11574405, 11465008 and 11547125, the Hunan Provincial Natural Science Foundation under Grant Nos 2015JJ4020 and 2015JJ2114, and the Scientific Research Fund of Hunan Provincial Education Department under Grant No 14A118.




