Constrained dynamics of excitation transfer due to a structured nano system

A variety of intriguing optical near-field phenomena have been observed in nanoscale systems in recent years, and now are going to be applied to unique nanofabrication and nanophotonic devices [1]. One of the elementary processes of such phenomena is excitation transfer via an optical near field [2, 3]. Research on excitation transfer has led to some innovation in nanophotonic and nanoelectronic information technologies [4, 5]. The control of excitation transfer via the near field has recently been reported in a semiconductor nanostructure, where the excitation transfer is controlled by a shift of excitonic energy levels depending on spin states in dilute magnetic and nonmagnetic semiconductor quantum wells under an external magnetic field [6]. Energy and spin transfer has been observed by the difference in the degree of polarization between the cases with and without the external magnetic field.

In this paper, we present a full-quantum-mechanical theory to understand and formulate excitation transfer via the optical near field. In this theory, the localized near-field photons in nanoscale space are distinguished from propagating far-field photons. We clarify a mechanism of the near-field excitation transfer and estimate the effective interaction between matter and near-field photons. This paper is organized as follows. In section 2, we introduce a full-quantum-mechanical model of double semiconductor quantum wells coupled to far-field and near-field photons and formulate the near-field excitation transfer. In section 3, we calculate population dynamics, photoluminescence and degree of polarization and discuss the effect of near-field interaction on energy and spin transfer. Finally, we summarize this study and present future outlook in section 4.

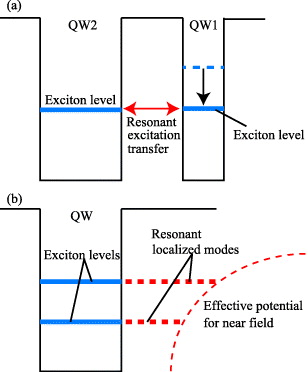
We consider a semiconductor nanostructure composed of dilute magnetic and nonmagnetic semiconductor quantum wells. The thickness of the barrier layer between quantum wells is large enough to prevent electronic tunneling transfer; namely, excitation transfer only originates from near-field interaction. Excitonic states in double quantum wells are considered to be isolated two-level systems as shown in figure 1(a). When the excitonic levels are not resonant, excitation transfer cannot occur. However, resonant dipole–dipole transfer can occur when the excitonic levels become resonant by the energy shift under an external field. Excitons in quantum wells interact with far-field and near-field photons where two kinds of photons are distinguished in this theory. The Hamiltonian of the total system is described as follows:

$$\begin{eqnarray} H &=& H_{\rm S} + H_{\rm F} + H_{\rm SF} + H_{\rm N} + H_{\rm SN}, \end{eqnarray}\noindent \tag{ 1 }$$

$$\begin{eqnarray} H_{\rm S} &=& \sum_{l=1}^2 \hbar \omega_l^{\rm ex} a_l^\dagger a_l, \end{eqnarray}\noindent \tag{ 2 }$$

$$\begin{eqnarray} H_{\rm F} &=& \int\!\mathrm{d}\textbf{k}\,\, \hbar \omega^{\rm F}_{\textbf{k}} b_{\textbf{k}}^\dagger b_{\textbf{k}}, \end{eqnarray}\noindent \tag{ 3 }$$

$$\begin{eqnarray} H_{\rm SF} &=& \sum_{l=1}^2 \int\!\mathrm{d}\textbf{k}\,\, \hbar F_l (a_l^\dagger b_{\textbf{k}} + b_{\textbf{k}}^\dagger a_l), \end{eqnarray}\noindent \tag{ 4 }$$

$$\begin{eqnarray} H_{\rm N} &=& \sum_{l=1}^2 \hbar \omega_l^{\rm ex} c_l^\dagger c_l, \end{eqnarray}\noindent \tag{ 5 }$$

$$\begin{eqnarray} H_{\rm SN} &=& \sum_{l=1}^2 \sum_{l^\prime=1}^2 \hbar G (a_l^\dagger c_{l^\prime} + c_{l^\prime}^\dagger a_l). \end{eqnarray}\noindent \tag{ 6 }$$

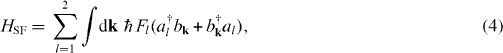
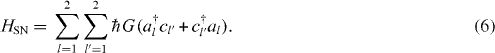
The first term H_S represents the energy of excitons in double quantum wells, where ω^ex_l is the excitonic frequency and a^†_l and a_l are the creation and annihilation operators of an exciton in the quantum well l. The second term H_F represents the energy of far-field photons, where ω^F_k is the photon frequency and b^†_k and b_k are the creation and annihilation operators of a far-field photon with a wave number k. The third term H_SF represents the interaction between excitons and far-field photons, where the interaction coefficient is given by F_l = [c³/(8π²τ₀ω^ex2_l)]^1/2 (c and τ₀ are the speed of light and the radiative lifetime of an exciton in the quantum well l, respectively). The fourth term H_N represents the energy of near-field photons, where c^†_l and c_l are the creation and annihilation operators of a near-field photon in mode l. We consider that the localized near-field photons are bound in the effective potential near the surfaces of quantum wells as shown in figure 1(b). The bound states of the near-field photons have discrete energy levels. The near-field photons are dressed with information on matter [7, 8]; therefore we assume that the frequencies of the near-field photons in modes 1 and 2 are resonant with the excitonic frequencies in quantum wells 1 and 2, respectively. Moreover, we assume that the interaction between matter and near-field photons takes the same form as the far-field interaction; the interaction between excitons and near-field photons are given by equation (6). The interaction coefficient G is a phenomenological parameter and is defined later.

Zoom In Zoom Out Reset image size

The dynamics of the system is described by one-body density-matrix elements, which are population of excitons in the quantum well l: n^ex_l(t) = 〈a^†_la_l〉(t), far-field-assisted polarization: p^F_l(k,t) = 〈b^†_ka_l〉(t), near-field-assisted polarization: p^N_l,l'(t) = 〈c^†_l'a_l〉(t), transfer via near-field photons: T_l,l' = 〈a^†_la_l'〉(t), density of far-field photons with the wave number k: n^F(k,t) = 〈b^†_kb_k〉(t), and density of near-field photons in mode l: n^N_l(t) = 〈c^†_lc_l〉(t). We derive the closed-form equations of motion for such matrix elements as follows:

$$\begin{eqnarray} \frac{\partial}{\partial t} n_l^{\rm ex}(t) &=& -2 \int\!\mathrm{d}\textbf{k}\,\, F_l \Im[p_l^{\rm F}(\textbf{k}, t)] -2 \sum_{l^\prime=1}^2 G \Im[p_{l, l^\prime}^{\rm N}(t)],\nonumber \\ \end{eqnarray}\noindent \tag{ 7 }$$

$$\begin{eqnarray} \frac{\partial}{\partial t} p_l^{\rm F}(\textbf{k}, t) &=& -\mathrm{i}(\omega_l^{\rm ex}-\omega_{\textbf{k}}^{\rm F}-\mathrm{i}\,\gamma_{\rm F})p_l^{\rm F}(\textbf{k}, t) +\mathrm{i}\,F_l n_l^{\rm ex}(t),\nonumber \\ \end{eqnarray}\noindent \tag{ 8 }$$

$$\begin{eqnarray} \frac{\partial}{\partial t} p_{l, l^\prime}^{\rm N}(t) &=& -\mathrm{i}(\omega_l^{\rm ex}-\omega_{l^\prime}^{\rm N}-\mathrm{i}\,\gamma_{\rm N})p_{l, l^\prime}^{\rm N}(t) \nonumber \\ & & +\mathrm{i}\,G n_l^{\rm ex}(t) +\mathrm{i}G T_{{\bar l}, l}(t), \end{eqnarray}\noindent \tag{ 9 }$$

$$\begin{eqnarray} \frac{\partial}{\partial t} T_{{\bar l}, l}(t) &=& \mathrm{i}(\omega_{\bar l}^{\rm ex}-\omega_l^{\rm ex}+\mathrm{i}\,\gamma_{\rm T}) T_{{\bar l}, l}(t) \nonumber \\ & & +\mathrm{i}\sum_{n=1}^2 G p_{{\bar l}, n}^{\rm N}(t)^\ast [2n_l^{\rm ex}(t)-1] \nonumber \\ & & -\mathrm{i}\sum_{n=1}^2 G p_{l, n}^{\rm N}(t) [2n_{\bar l}^{\rm ex}(t)-1]\nonumber \\ & &+i\int d{\bf k}\,\,F_l p_{\bar l}^{\rm F}({\bf k}, t)^\ast [2n_{l}^{\rm ex}(t)-1]\nonumber\\ &&-i\int d{\bf k}\,\, F_{\bar l}p_l^{\rm F}({\bf k}, t)[2n_{\bar l}^{\rm ex}(t)-1], \end{eqnarray}\noindent \tag{ 10 }$$

$$\begin{eqnarray} \frac{\partial}{\partial t} n^{\rm F}(\textbf{k}, t) &=& 2\sum_{l=1}^2 F_l \Im[p_l^{\rm F}(\textbf{k}, t)], \end{eqnarray}\noindent \tag{ 11 }$$

$$\begin{eqnarray} \frac{\partial}{\partial t} n_l^{\rm N}(t) &=& 2\sum_{l^\prime=1}^2 G \Im[p_{l^\prime, l}^{\rm N}(t)]. \end{eqnarray} \tag{ 12 }$$

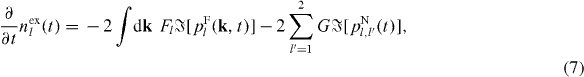
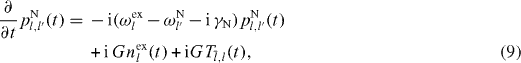
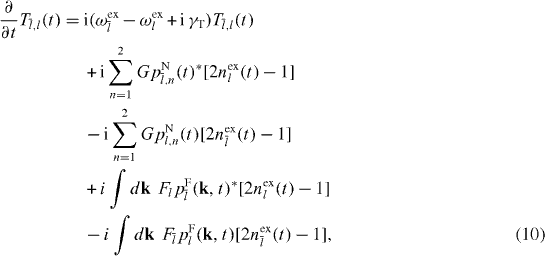
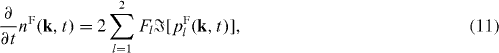
The far- and near-field-assisted polarizations originate from spontaneous emission from excitons, which effects are included through the second terms in the right-hand side of equations (8) and (9), respectively. Moreover, only the near-field-assisted polarization is affected by the excitation-transfer process represented by the third term in the right-hand side of equation (9). When ∂n^F/∂t > 0 and ∂n^N/∂t > 0 (∂n^F/∂t < 0 and ∂n^N/∂t < 0), equations (11) and (12) describe the emission (absorption) processes of far- and near-field photons, respectively. The time evolution of the photoluminescence spectrum is calculated by I(ω,t) = [∂n^F(k,t)/∂t]_|k|=ω/c [9, 10]. The interactions between excitons and near-field photons are normalized as ${\tilde G}=G/G_0$, where G₀ = [γ_N/(2τ₀)]^1/2. In the case of ${\tilde G}=1$, the time scale of near-field interaction corresponds to τ₀.

We numerically demonstrate the population dynamics in double quantum wells by the excitation transfer via the optical near field. In the initial state, the population in the quantum wells 1 (QW1) and 2 (QW2) are given by n^ex₁(t = 0) = 1 and n^ex₂(t = 0) = 0.2, respectively, and other matrix elements are zero. We calculate the dynamics in two cases when the excitonic levels in QW1 and QW2 are resonant and nonresonant. In the nonresonant case, the gap between excitonic levels in QW1 and QW2 is given by Δ = 3 meV, which corresponds to the excitonic energy shift in the dilute magnetic semiconductor quantum well under the external magnetic field B = 6 T in a recent experiment [6]. Because the dynamics of polarization is faster than the other dynamics, we use adiabatic approximation. Moreover, this study focuses on the effect of near-field transfer on the population dynamics; therefore we assume that γ_T = 0. The near-field interaction is given by ${\tilde G}=1$.

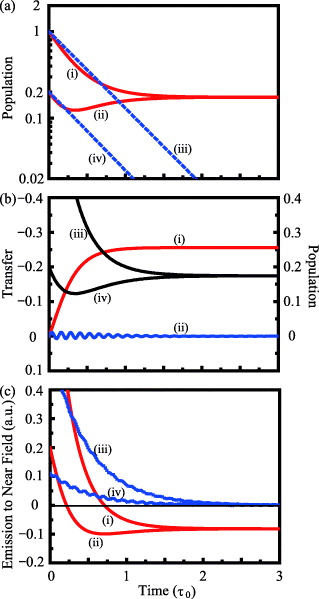
The population dynamics between QW1 and QW2 is shown in figure 2(a). In the resonant case, lines (i) and (ii) reveal that although the population in both quantum wells decrease by spontaneous emission in the early stage where time is t/τ₀ < 0.25, the population in QW2 increases after t/τ₀ > 0.25 and the population in both quantum wells coincides finally on the stationary value; namely, the excitation transfer occurs from QW1 to QW2. In the nonresonant case, the population in both quantum wells decrease exponentially by simply the spontaneous emission of the far-field photons and excitation transfer cannot occur. Figure 2(b) shows the effect of the near-field transfer on the population dynamics. By comparison between lines (i) and (iv) in the resonant case, we find that the population in QW2 is larger than the real part of −T₁₂ when t/τ₀ < 0.25, which reveals that the near-field spontaneous emission is more dominant than the near-field transfer process in equation (9) and the excitation transfer cannot occur. On the other hand, when t/τ₀ > 0.25, the real part of −T₁₂ becomes larger than the population in QW2, which reveals that the near-field transfer becomes more dominant than the near-field spontaneous emission and the excitation transfer can occur. In the nonresonant case, the real part of −T₁₂ is much smaller than the population as shown by line (ii); namely, the near-field transfer cannot contribute to the population dynamics. Figure 2 (c) shows the emission rate of near-field photons: ∂n^N_l/(∂t). If ∂n^N_l/(∂t) > 0, the near-field photons are emitted from QW l, and if ∂n^N_l/(∂t) < 0, the near-field photons are absorbed to the QW l. In the resonant case, we find that the emission rates of QW1 and QW2 are positive and negative, respectively, when 0.25 < t/τ₀ < 0.75. In this interval, the near-field photons emitted from the QW1 are absorbed to the QW2; the excitation transfer process via the near-field photons becomes most dominant for the population dynamics. In the nonresonant case, the emission rates are continuously positive and the near-field photons have no contribution to the excitation transfer.

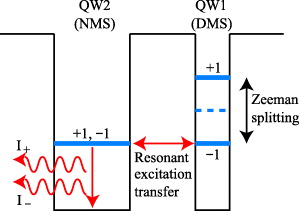
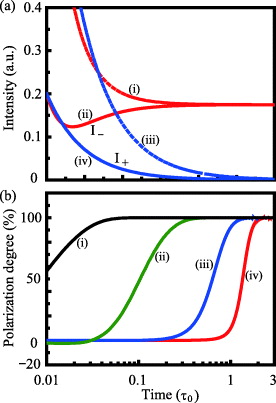
Zoom In Zoom Out Reset image size

Finally, we estimate the effective interaction between the excitonic states in quantum wells and the near-field photons. In a recent experiment, the excitation transfer has been controlled by the shift of excitonic energy levels depending on spin states in dilute magnetic and nonmagnetic semiconductor quantum wells (DMSQW and NMSQW) under the external magnetic field as shown in figure 3, and the energy and spin transfer has been observed by the difference in the degree of polarization between the cases with and without the external magnetic field [6]. Because the thickness of the barrier layer between quantum wells is large enough to prevent electronic tunneling transfer, the excitation transfer originates only from the near-field interaction. In the case without the external magnetic field, the excitonic levels in DMSQW and NMSQW are not resonant. However, under the external magnetic field, the excitonic levels with spin +1 and −1 are divided by the Zeeman effect in only DMSQW, and the excitonic level with spin −1 becomes resonant with NMSQW as shown in figure 3. Although excitation transfer can occur between resonant excitonic levels with spin −1, it cannot occur between nonresonant levels with spin +1. As a result, the difference between the excitons with spin −1 and +1 appears in the observation of photoluminescence from NMSQW. The degree of polarization is defined by P = (I₋ − I₊)/(I₋ + I₊), where I₋ and I₊ are the photoluminescence intensities from the excitons with spin −1 and +1, respectively, in the NMSQW. In our theoretical model, the cases of spin −1 and +1 correspond to the resonant and nonresonant cases, respectively. Figure 4(a) shows the time-resolved photoluminescence from the excitonic states in the double quantum wells under the same conditions as figure 2. The degree of polarization is calculated by lines (ii) and (iv) which correspond to I₋ and I₊, respectively. Figure 4(b) shows the time evolution of the degree of polarization, and lines (i), (ii), (iii) and (iv) correspond to the cases of ${\tilde G}=$ 10, 1, 0.1 and 0.01, respectively. The degree of polarization increases from 0 to 100%, which reveals that excitation transfer can occur only between excitonic states with spin −1. Furthermore, because the time scale of the excitation transfer depends on the near-field interaction ${\tilde G}$, we can estimate ${\tilde G}$ from a comparison between the theoretical and experimental results. Although the effects of realistic systems such as excitation processes and phonon systems should be investigated as our next problem, ${\tilde G}=0.1$ is obtained in this research with the use of the effective model of near-field excitation transfer.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In conclusion, we have presented here the effective model and a full-quantum-mechanical formulation of the excitation transfer via the optical near field in double semiconductor quantum wells. In this model, localized near-field photons are bound in the effective potential near the surfaces of quantum wells and can be distinguished from propagating far-field photons. We have clarified the effect of near-field photons on the excitation transfer and estimated the effective interaction between excitonic states and the optical near field.

Although we consider only the excitation transfer resulting from the near-field interaction in this study, the interaction between phonons and excitons also has a crucial role in excitation transfer. In short, even if the excitonic energy levels are not resonant, the excitation transfer can occur with the assistance of the emission and absorption of phonons [6]. Moreover, because the optical near field is closely coupled to the material degree of freedom [7, 8], the contribution of phonons becomes indispensable for the near-field excitation transfer. Thus, the investigation of the phonon effect remains a crucial problem addressed in our next study, but we hope that the results of this study stimulate the development of nanophotonic and nanoelectronic technologies with the use of near-field excitation transfer.

This study was supported by the KAKENHI (no. 23104715) and by Program to Disseminate Tenure Tracking System of the Ministry of Education, Culture, Sports, Science and Technology, Japan. KK is grateful to CASIO Science Promotion Foundation for financial support.