EXTRAGALACTIC INTERSTELLAR EXTINCTION CURVES: INDICATORS OF LOCAL PHYSICAL CONDITIONS

As we shall discuss in the following paragraphs in this section, normalized interstellar extinction curves (ISECs) are now available for many lines of sight in the Milky Way Galaxy (MWG), in the Small and Large Magellanic Clouds (SMC and LMC), in Local Group objects, and increasingly in objects at high redshift. The ISECs have a great variety of shapes. This variety is conventionally attributed to variations in the relative abundances of the different components that contribute to interstellar extinction.

In this paper, we consider whether these changes in component abundances are in fact related to changes in the local physical conditions in the regions observed. If so, then normalized ISECs actually contain information about the local physics. For nearby objects, the local physics can usually be studied in a variety of ways. However, for distant objects at high redshift this may not possible, and therefore the normalized ISECs–if they can be obtained–may be an important source of information about those objects. If this approach is valid, then normalized ISECs may help to classify the nature of high redshift objects. Our purpose in this paper, therefore, is to attempt to establish a connection between local physics and measured ISECs.

Extensive measurements of the local interstellar extinction exist along hundreds of lines of sight in the MWG (e.g., Valencic et al. 2004; Fitzpatrick & Massa 2007, 2009; Gordon et al. 2009), and along tens of lines of sight in the LMC and in the SMC (e.g., Gordon et al. 2003; Cartledge et al. 2005). The MCs provide the nearest galaxies in which we can easily measure dust extinction at different positions through a galaxy. In such environments, stars are fainter and, consequently, the number of measured ultraviolet curves in both galaxies is much smaller than in the MWG. Measured ISECs in the MWG, LMC, and SMC have many similarities: a strong rise from the near-infrared to the far-ultraviolet, together with a tendency for the dust-to-gas ratio to vary in proportion to metallicity. The MWG, LMC, and SMC show apparently similar amounts of refractory elements (Draine 2011). As in the MWG, significant regional variations are observed in the MCs, in particular in the relative strength of the 217.5 nm feature (e.g., Gordon et al. 2003). This is, indeed, a crucial point. The ultraviolet extinction bump is ubiquitous in the diffuse interstellar medium (ISM) in the MWG. However, the bump is weak or missing in interstellar dust in the LMC, SMC, and M31. Gordon et al. (1999) found evidence of a strong bump in the core of the dwarf spiral M33. However, a recent detailed analysis of the stellar population in M33 suggests that the extinction curve in this galaxy might be similar to the average LMC extinction profile (Fitzpatrick 1999), presenting a bump weaker than in the average ISEC of the MWG and a steeper far-ultraviolet rise (Tolea 2009).

Accurate measurements of ISECs are almost exclusively limited to the Galaxy, the LMC, and the SMC, because at greater distances it becomes impossible to obtain the photometry or spectroscopy of individual stars needed for extinction determinations. In the last decade observers have discovered huge quantities of interstellar dust near the most distant quasars in the very young universe, only 700 million years after primordial nucleosynthesis. Such studies (e.g., Jiang et al. 2006) indicate that high redshift quasar systems have already been enriched with dust up to a level comparable to nearby dusty galaxies. The relation between dust content and metal enrichment places important constraints on chemical galactic evolution models. Unfortunately, there is a large scatter in the gas-to-dust ratio for a given metallicity throughout the metallicity range, even in the local universe (e.g., Rémy-Ruyer et al. 2014). There is a vigorous debate and two distinct scenarios for the origin of dust at high redshifts in which supernovae and lower-mass asymptotic giant branch stars are involved (e.g., Gall et al. 2011). Exploiting the Herschel satellite at far-infrared wavelengths Matsuura et al. (2011) presents the first direct evidence that substantial amounts of dust can be created in supernovae. Matsuura et al. (2011) observations demonstrate the presence of dust in supernova SN1987A in a much larger amount than previously known and Matsuura et al. (2011) inferred that indeed most of the refractory material in the ejecta of the supernova has condensed into dust. Although substantial, the dust production rate does not appear to be sufficient to eliminate the need for grain growth in the ISM in the LMC as well as, for comparison, in our own Galaxy (McKee 2011). Whatever the case may be, dust exists at the highest redshifts probed so far (z ∼ 6).

About two decades ago, quasars with damped Lyα systems in the foreground were studied by Pei et al. (1991) and found to be on average redder than those without. These authors found that the ISECs in their sample of five quasars are not consistent with the Galactic extinction law, marginally compatible with the LMC extinction and fully compatible with SMC extinction. Such findings were questioned by Murphy & Liske (2004) who found no trace of extinction. York et al. (2006) found no evidence of the 217.5 nm bump, and ISECs similar to SMC extinction in a sample of quasars of the Sloan Digital Sky Survey. ISECs that differ from the SMC, LMC, and MWG have been obtained in the case of active galactic nuclei (AGNs), although mildly reddened quasars appear to follow an SMC-like dust-reddening law (e.g., Hopkins et al. 2004). In the case of star-forming galaxies, ISECs are difficult to infer due to the crowding of dust with emitting sources. Starburst galaxies can be characterized by a lack of the 217.5 nm absorption feature, like the SMC, and a steep far-ultraviolet rise, intermediate between those in the SMC and the MWG ISECs. However, for ultraviolet luminous galaxies, the ISECs range between those typical of the SMC and LMC, with some of them exhibiting weak bumps as in the LMC (Noll & Pierini 2005). In general, a significant 217.5 nm bump is observed in the spectra of star-forming galaxies at z ∼ 2, indicating an LMC-like extinction curve (Noll et al. 2007). Chen et al. (2006) analyzed the ISECs for 10 gamma-ray burst (GRB) host galaxies, finding relatively flat and gray profiles, together with others displaying a close resemblance to the MWG, but with no bump. Such an inventory of extragalactic ISECs could be much longer, testifying to a great variety of galactic environmental conditions.

Variations in normalized ISECs along different lines of sight in the MWG, and from one galaxy to another, are routinely interpreted as arising from changes in the relative abundances of the components that contribute to the extinction (e.g., Whittet 2002; Draine 2009). In current models, these components are silicates, carbons of various kinds, and polycyclic aromatic hydrocarbon (PAH) molecules (Draine 2003); voids in the solids may also be included (e.g., Zubko et al. 2004). Refractory materials are predominantly amorphous, with a small crystalline component of silicates (e.g., Li 2009), while some crystalline carbon might exist in the form of nano-diamonds (e.g., Pirali et al. 2007).

If the observed variations could be related to differences in the local physical conditions or to an evolutionary process in the interstellar gas, then ISECs could be a very useful tool in defining those physical conditions in external galaxies. Our purpose in this work is to explore the sensitivity of normalized ISEC shapes to the relative abundances of dust grain components induced by changes in the local physical conditions, and to relate these physical conditions to several broad categories of galaxy type. The novel aspect of this work is that in the dust model used, the various component contributions to the interstellar extinction are related and respond to the local conditions in galaxies.

We describe the model in more detail in Section 2, and we apply it to describe the extinction properties of the SMC and LMC in Section 3. In Section 4 we define the range of the parameters to be considered and we derive the expected trends in the extinction profiles. Synthetic ISECs for galaxies at high redshift are presented in Section 5, selecting parameters based on rather limited information on physical conditions in different galaxy types. In the last section we draw some conclusions about the application of this model of extragalactic extinction.

Since our ultimate aim in this work is to use measured ISECs for distant galaxies as indicators of local physical conditions in those galaxies, we must use a model of dust in which the optical properties of the dust grains respond to those local conditions. One such model was proposed by Jones et al. (1990), where those authors summarized the ideas of papers in the preceding years. That model has been extended by Iatì et al. (2008), Cecchi-Pestellini et al. (2008, 2010) to include the effects of a population of PAHs on the ISEC. We shall call this dust model the "unified" model, as several components that are commonly assumed to be present in interstellar dust are linked together in a non-arbitrary way, through interaction with the local physics and in an evolving situation.

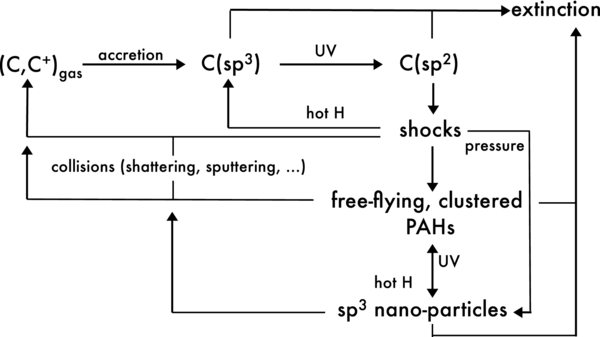
The unified model starts from an understanding that dust grains evolve in the ISM. They are formed in the envelopes of cool stars and in novae and supernovae, and are destroyed in shocks. The conventional components of silicates and carbons have different responses to shocks: silicates are much more resistant than carbons. Even if the silicates and carbons are produced as separate populations, the destruction of solid carbons to atoms and small molecules will lead to carbon deposition on silicate cores. In the hydrogen-rich ISM, the unified model assumes that the carbon is deposited as H-rich carbon, i.e., with sp³ (polymeric) bonding. Thus, this model envisages that a typical grain will consist of a silicate core (possibly containing voids) with a hydrocarbon mantle. The sp³ hydrocarbon mantle suffers photo-darkening in the interstellar radiation field; in this process, hydrogen is driven out so that the material is converted toward sp² (graphitic) bonding. Thus, the carbonaceous mantle in this model is expected to consist essentially of two layers, a more recently deposited sp³ layer on top of a longer-established and photo-darkened sp² layer.

Recently, Jones et al. (2013) and Hirashita & Voshchinnikov (2014) put forward dust models incorporating the effects of grain growth mechanisms, together with their processing in molecular clouds. In the evolutionary scenario described by Jones et al. (2013) aliphatic carbon deposition is assumed to occur in dense clouds, whereas processing occurs in diffuse clouds. If it is assumed that in diffuse interstellar regions photo-processing rates are fast enough, the outer layer of freshly deposited, still unprocessed, aliphatic material would be so thin as to be negligible. In our model of mantle accretion and processing, which we consider to occur in the diffuse ISM (and not in molecular clouds) we allow for an ample range in the values of relevant parameters, and quantitatively follow the time evolution of grain mantles, using a time-dependent gas-phase chemistry model to determine the time-dependent deposition rate. This is a significant difference from the Jones et al. (2013) model, in which mantle thickness and the fractions of processed and unprocessed carbon are not allowed to vary but stem from assumptions. Hirashita & Voshchinnikov (2014) examined the effects of two major growth mechanisms of dust grains—accretion and coagulation—on the extinction curve. To reproduce the large flavors of MWG ISECs these authors are forced to tune the coagulation rates of the silicate and carbonaceous components to different values. In its present version, however, the model is unable to reproduce MC-type extinction profiles, because both bump and far-ultraviolet rise are suppressed at late evolutionary times.

The sp³ → sp² conversion changes the optical properties of the grains on a timescale (the so-called photo-darkening timescale) that in unshielded regions of the MWG ISM is on the order of or less than a few tenths of a million years (e.g., Mennella et al. 2001). The computed ISECs determined from our model are time-dependent because of two factors: the gradual accumulation of carbon atoms on dust grains, and the photo-darkening of the resulting hydrocarbon mantle. Ultimately, the hydrocarbon layers are removed by shocks (Jones et al. 1990, 1996; Jones 2012a, 2012b, 2012c) on a timescale that is determined by the dynamical activity in the galaxy; in the MWG, this is probably a few million years. Jones et al. (1996) determined that about 80% of the mass of grains is shattered into very small grains whose sizes presumably have the dimensions of free-flying PAH molecules or clusters. The mantle yield of such fragments and their conversion to sp³ bonding carriers via hot hydrogen atom implantations (e.g., Furton & Witt 1993), or pressure-induced formation of nano-diamonds (Le Guillou et al. 2010), depends on a number of factors, such as, e.g., the shock velocity. Production of PAHs can also occur in C-rich asymptotic giant branch stars, with a timescale of ∼2 Gyr (Tielens 2005). We do not incorporate such sources of aromatic molecules in the model. The rate of loss of PAHs is also ultimately controlled by the level of activity within the galaxy, such molecules being readily destroyed by ultraviolet photolysis and cosmic rays; these interactions determine their lifetime (Micelotta et al. 2011). Thus, in this silicate/hydrocarbon unified model, the various components contributing to extinction are related. More active galaxies tend to have a smaller PAH population relative to carbon dust, together with the presence of a significant fraction of sp³ carbonaceous nano-particles, in which the π* ← π resonance is suppressed with respect to the σ* ← σ one (e.g., nano-diamonds, Rai & Rastogi 2010). The cycle then repeats, with deposition on the now bare silicate grains and growth of carbon mantles. Thus, an ISEC computed on the basis of this model will show a time-dependence that reflects the rates of deposition, photo-darkening, shocks, and sp² → sp³ conversion rate. A series of papers has shown that this unified model is capable of fitting observed ISECs from a variety of well-studied lines of sight (Zonca et al. 2011; Mulas et al. 2013).

The time-dependent equations describing carbon deposition on to the silicate cores and its subsequent photo-darkening have been reported in several papers (e.g., Cecchi-Pestellini & Williams 1998) and are not repeated here. Cecchi-Pestellini et al. (2014) reduced these equations to a more compact form by introducing a new variable, s, representing a modified time, where

$$\begin{equation} {d}s = T_{\rm k}^{1/2} n_{\rm H} {d}t. \end{equation} \tag{ 1 }$$

Here, T_k is the gas kinetic temperature and n_H is the number density of hydrogen nuclei in the gas. We define s_pd as $T_{\rm k}^{1/2} n_{\rm H} \tau _{\rm pd}/\chi$, where τ_pd and χ are the photo-darkening timescale and the intensity of the interstellar ultraviolet radiation field with respect to the standard MWG value, respectively.

Cosmic rays process the PAHs in diffuse clouds, where the destruction due to interstellar shocks is less efficient. Micelotta et al. (2011) found the lifetime of PAHs against cosmic-ray impacts to proceed at the inverse collisional rate, approximately proportional to the integrated cosmic-ray flux. The fractional abundance of PAHs in external galaxies $f_{\rm PAH}^{\rm EG}$ may be given approximately in terms of our own galaxy PAH concentration

$$\begin{equation} \frac{\displaystyle f_{\rm PAH}^{\rm EG}}{\displaystyle f_{\rm PAH}^{\rm MWG}} = \left(\frac{\displaystyle \zeta ^{\rm EG}}{\displaystyle \zeta ^{\rm MWG}} \right)^{-1}, \end{equation} \tag{ 2 }$$

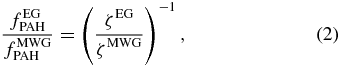
where ζ is the cosmic-ray ionization rate, considered a crude measure of galactic activity. This is plausible, since activity implies massive star formation which in turn generates higher fluxes of cosmic rays. We adopt Equation (2) in this work.

Here the dust grains and mantles, and any included cavity, are assumed to be spherically symmetrical. Thus, the grains are assumed to consist of a central spherical void plus three concentric shells: silicate + hydrocarbon sp² + hydrocarbon sp³. The computational methods for determining the optical properties of such four-component systems have been reported elsewhere (e.g., Cecchi-Pestellini et al. 2012). The grains have a conventional power-law size distribution ∝(a + w)^−q, a, and w being the grain radius and the mantle thickness, respectively. For the best-fitting MWG ISEC, the power-law exponent is determined to be q ∼ 3.5 (as in Mathis et al. 1977; the so-called Mathis, Rumpl, and Nordsieck (MRN) distribution), and the distribution includes both "small" grains (radii 5–12 nm) and "large" grains radii (60–500 nm; Mulas et al. 2013). The optical constants of the various solid materials in the model are those used by Mulas et al. (2013).

The PAH contribution to extinction is represented by two Lorentz profiles that have been parameterized to fit the ab initio photo-absorption cross sections of a sample of 54 different types of PAH in four charge states (Cecchi-Pestellini et al. 2008). The Lorentz profile at lower energies, L_π, mimicks the π^⋆ ← π resonance in PAHs, accounting for most of the bump in the extinction while the second, L_σ, producing the far-ultraviolet nonlinear extinction rise, describes the low-energy tail of the σ^⋆ ← σ plasmon resonance or the extinction cross-sections of sp³ carbon particles in the Rayleigh regime. Since the electronic photo-absorption cross-sections of PAHs fall to zero more quickly than Lorentzians at low energies, Mulas et al. (2013) introduced an exponential damping factor 1/1 + exp[(c₁ − λ⁻¹)/c₂]. However, the two Lorentz functions are independent, thereby controlling the relative ratio between sp² and sp³ bond carriers.

In the same way as for Equation (2) a relation can be established between aromatic structures and H-processed carbon nano-particles, as measured by the intensity ratio ${\cal R}= L_\sigma /L_\pi$ of the two Lorentz profiles

$$\begin{equation} \frac{\displaystyle {\cal R}^{\rm EG}}{\displaystyle {\cal R}^{\rm MWG}} = \left(\frac{\displaystyle \zeta ^{\rm EG}}{\displaystyle \zeta ^{\rm MWG}}\right)^\kappa \end{equation} \tag{ 3 }$$

in which κ is a free parameter that depends on the galactic dynamical activity. In Figure 1 we summarize the evolution of carbon in response to interstellar conditions according to the prescription of the present model.

Zoom In Zoom Out Reset image size

Before discussing ISECs in distant objects we validate our model by applying it to two representative extinction profiles characteristic of the SMC and LMC. Data are taken from Cartledge et al. (2005) and refer to the lines of sight AzV 18 (SMC) and Sk-68 129 (LMC). The SMC ISM toward AzV 18 produces extinction with no 217.5 nm bump and a steep far-ultraviolet rise, while the one in the LMC shows a hint of the bump and a firm far-ultraviolet rise, stronger than in the MWG but less sharp than in the SMC.

To fit the normalized extinction profiles we used a modified version of C MPFIT implementation of a Levemberg–Marquardt nonlinear least squares algorithm (details are found in Mulas et al. 2013). The free parameters of the solid component are a₋ the lower limit of the radius of the small grain component, a₊ the upper limit of the "small"grain component, b₋ the lower limit of the "big"grain component, b₊ the upper limit of the "big"grain component, q the exponent of the MRN power-law size distribution f_v the vacuum fraction of silicate cores, w the total carbonaceous mantle thickness, and $f_{sp_2}$ the fraction of sp² material of the carbonaceous mantle width. The free parameters of the molecular component are the peak wavenumber of the first Lorentzian σ₁, the FWHM of the first Lorentzian γ₁, the peak wavenumber of the second Lorentzian σ₂, the FWHM of the second Lorentzian γ₂, c₁ the center of the exponential cutoff, and c₂ the width of the exponential cutoff. The abundances of PAH relative to the classical grains, f_PAH, and the intensity ratio of the two Lorentz profiles, ${\cal R}$, are obtained by the fitting procedure.

The derived ISECs are shown in Figure 2(a), while the inferred dust parameters are reported in Table 1, together with the results for the average MWG ISEC. The results shown in Table 1 can be read, in the framework of the present model, as an evolutionary sequence depending on the activity of the galaxy, i.e., the MWG (κ = 0), LMC (κ ∼ 1), and SMC (κ ∼ 2). Of course, this is not strictly true since, for both the LMC and SMC, the exploited lines of sight are not representative of the whole galaxy. Nevertheless, it is suggestive that the increasing activity of a galaxy reduces the bump strength, and the far-ultraviolet rise increases. The homogenous fit of all the galactic ECs observed in the SMC and LMC and in M31 (for the average ISEC; see Bianchi et al. 1996) is in progress, and will be the subject of a future paper.

Zoom In Zoom Out Reset image size

Table 1. Inferred Dust Parameters

	a−	a+	b−	b+	w	q	fv	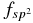$f_{sp^2}$	σ1	γ1	σ2	γ2	c1	c2	fPAH	${\cal R}$
	(nm)								(μm−1)
MWGa	5.1	11.9	63.3	491	1.3	3.47	0.45	0.98	4.48	0.46	9.73	2.61	1.5	0.46	0.570	11.5
SMC	5.0	14.0	53.3	453	∼0	3.47	0.49		4.54	0.72	9.32	3.49	2.7	0.68	0.013	1024
LMC	5.0	14.5	63.0	646	1.6	3.49	0.62	0.31	4.57	0.34	11.6	4.57	0.0	3.6	0.325	71.5

Note. ^aMulas et al. (2013).

Download table as:  ASCIITypeset image

We also show in Figure 2(b) a fit to an unusual type of ISEC that possesses a weak bump and a very steep rise in the far-ultraviolet. Zafar et al. (2012) obtained the ISEC shown for the GRB afterglow GRB 080605. The characteristics of this ISEC are shared with a few lines of sight in the MWG (Valencic et al. 2003). The fit using the unified model is indicated in Figure 2(b) and requires a cosmic ray ionization rate that is twice that of the MWG and a value of κ (defined in Equation (3)) of 3. Moreover, we use the same dust-size distribution as for the MWG.

The free parameters of the model are the photo-darkening parameter s_pd incorporating density, temperature, and ultraviolet field along the line of sight, the rate of sp³ → sp² conversion, embedded in the steepness κ, see Equation (3), the evolutionary age s_ev at which the calculation is ended, and the cosmic-ray flux. The dust content of galaxies is proportional to both metallicity and gas content because, as stellar populations evolve in time and more gas is locked into stars, the metallicity of a galaxy increases while its gas content decreases. Thus, we consider the gas-to-dust ratio, ${\cal G}_D$, as an additional free parameter. ${\cal G}_D$ is directly related to the shape of normalized ISECs through the carbon accretion rate. Finally, we do not consider gas density and temperature in the list of free parameters, such quantities being incorporated in the variable s, Equation (1), and in s_pd. In general, we refer to the relatively low density diffuse regions in which the optical and ultraviolet ISECs are observationally determined; obviously, higher density star-forming regions are also present. The boundaries of the parameter space are reported in Table 2. All the quantities reported in Table 2, with the exception of κ, are calibrated with respect to the MWG values.

Table 2. Free Parameter Range

			MWG
Cosmic-ray ionization rate	ζ	0.01–1000	5 × 10−17 s−1 a
sp3 → sp2 rate steepness	κ	0–3	0
Gas-to-dust ratio	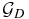${\cal G}_D$	0.01–3	6.1 × 1021 cm−2 mag−1 b
Photo-darkening time	spd/χ	0.001–100	100 cm−3 K1/2 Myr
Evolutionary age	sev	0.1–10	2000 cm−3 K1/2 Myr

Notes. ^aDalgarno (2006). ^bGudennavar et al. (2012).

Download table as:  ASCIITypeset image

Although in the following, we shall not perform fits of specific ISECs, the choice of the grain size distribution might be an issue. Modeling of the evolution of grain size distribution in galaxies at high redshift should take into account the dust production and ejection from supernovae, the destruction of newly formed dust grains by sputtering in the reverse shocks of supernova remnants, and the subsequent processing of the dust in the ISM, e.g., through grain–grain collisions driven by interstellar turbulence. Resulting size distributions are strongly model-dependent. We therefore search for possible morphological relations among MWG-, LMC-, and SMC-type ISECs, hidden by the size distribution modulation. We start from the MWG ISEC, then varying only the two parameters ζ (f_PAH) and κ ($\cal {R}$), and leaving unchanged the MWG dust size distribution (Table 1) we try to recover the ISECs along the lines of sight AzV 18 and Sk-68 129. The result is a surprisingly good agreement up to ∼6 μm⁻¹. Then, in the far-ultraviolet spectral range, synthetic ISECs depart markedly from the observed MC extinction profiles, but still maintain the correct trends. We conclude that, in the framework of the present model, ISECs with significantly different shapes may be made similar by just tuning the relative proportions of the dust constituents, as suggested by the fitting results of Table 1. We have thus used the MWG size distribution in computing ISECs for external galaxies.

We compute the normalized ISECs for particular parameter choices and follow the transformation of the extinction for a timescale over which the carbon mantles on the silicate cores are expected to survive in the diffuse ISM, i.e., s_ev. Cecchi-Pestellini et al. (2010) found that the MWG average ISEC is reached after about a few megayears' evolution. Considering typical cold neutral medium values for density, n_H = 100 cm⁻³, and kinetic temperature, T_k = 100 K, we find the value s_MWG = 2000 cm⁻³ K^1/2 Myr for the MWG. In galaxies that are more (or less) active than the MWG, this timescale will be correspondingly shorter (or longer). We use the MWG ISEC as reference model.

The most direct example of the effect of PAHs in the ISECs can be seen by comparing ISECs computed using both standard MWG parameters and modified cosmic-ray ionization rates (Figure 3(a)). The increase in ζ induces a reduction in the molecular content leading not only to the decrease of the 217.5 nm bump but also to the flattening of the curve at shorter wavelengths. Comparing models with different cosmic-ray ionization rates, it is clear that the shape of the ISEC is affected when f_PAH is decreased by just a factor of two (ζ = 0.5) in such a way that synthetic ISECs are scarcely sensitive to a further decrease in this quantity. Remarkable changes in the extinction curves are seen when the PAH content is increased (ζ < ζ_MWG). Thus, even modest fluctuations in the galactic activity may induce significant variations in the shape of normalized extinction. Incorporating the effects of the κ tuning, we can construct synthetic extinction profiles in agreement with the ISEC shape dispersion in the MWG, LMC, and SMC (Figures 3(b) and (c)).

Zoom In Zoom Out Reset image size

In Figure 3(d) we compare extinction profiles at different evolutionary ages. Since we are exploiting the MWG parameter set, the plot describes the evolution of a typical galactic diffuse interstellar cloud. The evolution of dust is well reflected in the change of the ISEC, with e.g., R_V varying from 2.9 to 3.5. However, incorporating the effects of χ variations, we note that for typical MWG physical conditions, the sp³ → sp² conversion rate is fast enough to lead to almost totally aromatic carbon mantles when s_ev ∼ 0.1 × s_MWG. Indeed, ISECs appear to be significantly insensitive to differences in the ultraviolet radiation field. Such a conclusion also is embedded in Figure 3(e) in which the increase in the gas-to-dust ratio, computed at the same evolutionary age s_ev = s_MWG, mimics effectively the evolutionary path of the extinction profile shown in Figure 3(d). This suggests that during quiescent phases the most important evolutionary process is mantle accretion. Radiation field effects increase markedly for peculiar parameter combinations such as, e.g., very small χ and large ${\cal G}_D$.

The extinction curves in Figure 3 are presented solely to show trends in the computed ISEC shapes as various key parameters are varied. They do not necessarily represent observable ISECs. The prominence of the 217.5 nm bump in some of these curves arises merely because the mean MWG ISEC (which possesses a very strong bump) was chosen as the reference model.

There is strong evidence that almost all types of high-z sources contain dust. We consider a few broad galactic classes, which we assume to be representative for a variety of galaxy types. In reality, of course, these galaxy types are not totally distinct, but may merge into one another.

Starburst galaxies are believed to have an enhanced cosmic-ray ionization rate compared to the MWG (e.g., Acciari et al. 2009; Acero et al. 2009). Their higher star formation rates (by more than a factor of three in some cases) compared to the MWG also may yield a high radiation field (e.g., Martin et al. 2009), and thus a lower s_pd, as well as a higher than solar metallicity and a slightly higher overall volume density. Partly overlapping starburst galaxies are dwarf galaxies. Observations of stellar populations suggest that the star formation in dwarf galaxies is sporadic, separated by millions to billions of years, even in isolated systems (e.g., Weisz et al. 2008). Such galaxies generally have sub-solar metallicities and, in most cases, a lower dust-to-gas ratio as well as lower than standard radiation fields. These galaxies may have an average density higher than that of the MWG. Another interesting class of objects are the early-type galaxies (ETGs), which are high metallicity galaxies where star formation is active (Bayet et al. 2012). Finally, AGNs are well known sources of X-rays and may have high cosmic-ray ionization rates (e.g., Guo & Mathews 2011) as well as stronger than standard radiation fields due to the presence of starbursts. Their metallicity can be subsolar (Weedman et al. 2005).

Early studies suggested that ${\cal G}_D^{-1}$ should be proportional to the metallicity of a galaxy (Franco & Cox 1986). While this assumption is questionable, there are strong indications that, in the local universe, the gas-to-dust ratio decreases with metallicity, although a power-law with a slope of −1 fails over the whole metallicity range, with the observed trend steepening toward low metallicities (Rémy-Ruyer et al. 2014). Recently, Fisher et al. (2014) reported observations of dust emission from I Zw 18, a nearby galaxy representative of starbursting low metallicity environments, confirming the deviation from a linear scaling of ${\cal G}_D^{-1}$ with the metallicity. Fisher et al. (2014) suggested that such behavior might be representative of starbursting galaxies with very low metallicities at very early epochs, where the metallicity may be as low as ∼1% of the solar value (Ouchi et al. 2013). In addition, Rémy-Ruyer et al. (2014) showed that a large scatter exists in the relation between the dust-to-gas ratio and metallicity, and that such scatter is intrinsic to galactic properties, reflecting regional characteristics such as the star formation history. For such reasons, as we did in the previous section, we assume ${\cal G}_D$ as a free parameter, with the prescription that low (high) metallicities imply a higher (lower) gas-to-dust ratio.

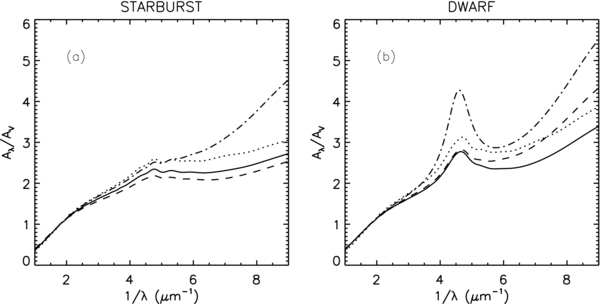
The extinction curves for our model galaxies are shown in Figure 4. Figure 4(a) shows a sample of ISECs constructed for the class of starburst galaxies. The curves have been computed using ${\cal G}_D = 1/3$, χ = 100, ζ = 10, and have been followed up to s_ev = s_MWG. Variation of parameters affect little the ISEC shapes with the exception of the activity index κ. We find that the curve evolves from the initial conditions just flattening in the far-ultraviolet, with R_V varying from 3.15 to 3.5. To include starbursting environments with low metallicities, we consider a gas-to-dust ratio ${\cal G}_D = 3$. In that case R_V = 5.5, but the ISEC shape is little affected. Significant effects are present for κ = 1. Increasing ζ the 217.5 nm feature disappears and the extinction profile approaches an SMC-type ISEC.

Zoom In Zoom Out Reset image size

In Figure 4(b) we report calculations for dwarf galaxies. We exploit ${\cal G}_D = 3$ and ζ values 0.5 and 2 to cover the observed range of activity for such galaxies which may (Cannon et al. 2002) or may not (Dolphin et al. 2003) be forming stars. ISECs evolve from R_V = 3 (s_ev = 0) to R_V = 3.5 (s_ev = s_MWG), similarly to the case of starburst galaxies, although the ISEC shapes are different. When κ = 1 the curve resembles an LMC-type profile due to the steepening of its far-ultraviolet tail. Considering the quiescent case of ζ = 0.5 we integrate the extinction profile in time up to s_ev = 10 × s_MWG to simulate a longer carbon mantle lifetime. The curve shows a strong bump and far-ultraviolet rise, being dominated by the PAH component.

Finally, ETGs produce ISECs similar to spirals with, depending on the activity, more or less pronounced bumps, although their ISECs appear to be deeper than the average MWG ISEC in the region where the two PAH resonances overlap. AGN ISECs have no distinctive features from the extinction profiles attributable to starburst galaxies.

We note that an increase in the gas-to-dust ratio in combination with a long evolutionary time leads to the construction of very thick (mainly sp² for χ > 0.001) carbon mantles. Such an increase acts simultaneously on all sizes with the result that the extinction curve radically changes its profile in particular in the bump region with the shape of the aromatic resonance that narrows and decreases relative to the grain extinction. However, such a combination of parameters is likely to be present only in a small number of peculiar objects, showing little star formation activity while still presenting large gas-to-dust ratios.

We have adopted a model of dust, here called the unified model, in which the solid and gaseous components contributing to interstellar extinction respond to their physical environment. Carbon is deposited on dust in an H-rich polymeric (sp³ bonding) form and is converted by the interstellar radiation field to H-poor graphitic (sp² bonding) form. Intermittent low velocity shocks remove the carbon mantles and populate the gas with PAHs (sp²) and with carbon clusters (sp³) that are formed by insertion of hot H atoms into the sp² lattice or pressure annealing. These species are reduced to atoms and the cycle then repeats. Extinction computed in the unified model is therefore time-dependent and depends on a number of physical parameters including the gas density and temperature, the interstellar electromagnetic and particle radiation fluxes, the gas-to-dust ratio, a parameter that determines the ratio of sp² and sp³ bond carriers, and the evolutionary period over which the process occurs.

Earlier work has shown that ISECs computed on the basis of this model are capable of fitting the variety of extinction curves measured on many sight lines in the Milky Way. In the present paper, we have shown that this model can provide excellent fits to measured extinction curves on sight lines in the LMC and SMC, and to an extinction curve deduced for the GRB afterglow GRB 080605.

A study of the sensitivity of theoretical ISECs computed using this model shows that although there are many parameters associated with the dust model and the local physics, not all of these have significant effects. The parameter of greatest importance is the cosmic-ray ionization rate (here regarded as a proxy for galactic activity). The evolutionary timescale (which in this model may be related to galactic activity) also has a significant effect on the computed ISECs.

With crude assumptions of physical conditions in distant galaxies, the unified model can be used to predict approximate ISEC shapes for different galaxy types. These show distinct behaviors, suggesting that ISECs can be used as a guide to galaxy type and therefore to local physical conditions.

Our main conclusions are as follows.

• 1.  
  The unified model is capable of accounting for the variety of ISECs seen in the MWG, the Local Group, and objects outside the Local Group.
• 2.  
  The dominant parameters in computing an ISEC based on the unified model are the solid-to-gas ratio in the components causing extinction and the sp²:sp³ ratio in the gaseous components; both of these ratios are determined by galactic activity.
• 3.  
  The evolutionary time and the gas-to-dust ratio have significant effects on computed ISECs, but the local radiation field is generally unimportant.
• 4.  
  Modest changes in dust size distributions affect the ISECs but not their characteristic shapes.
• 5.  
  The ISECs for the mean MWG, the LMC, and the SMC may represent a sequence of objects influenced by increasing galactic activity.
• 6.  
  The prediction of the unified model may be crudely summarized as: higher ζ → higher supernova rate → higher activity → weaker bump and steeper far-ultraviolet rise.
• 7.  
  Different galaxy types are expected to show different types of ISEC; ISECs may therefore be used to distinguish between types of galaxies.

The authors thank the referee, G. Clayton, for valuable comments which helped to improve an earlier version of the paper. This research has been supported by the Autonomous Region of Sardinia, Project CRP 26666 (Regional Law 7/2007, call 2010).