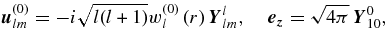ABSTRACT
The effect of magnetic fields on the frequencies of toroidal oscillations of neutron stars is derived to lowest order. We suggest that the fine structure in the quasiperiodic oscillation power spectrum of magnetars following giant flares reported by Strohmayer & Watts is magnetic splitting of degenerate toroidal modes, and we estimate a corresponding crustal magnetic field on the order of 1015 Gauss or more. We suggest that residual m, −m symmetry following such splitting, together with nonaxisymmetric or rotational splitting of the residual symmetry, might allow beating of individual frequency components that is slow enough to be observed.
Export citation and abstract BibTeX RIS
The discovery of quasiperiodic oscillations (QPOs) in the hyperflares of soft gamma-ray repeaters (Israel et al. 2005; Strohmayer & Watts 2005; Watts & Strohmayer 2006; Strohmayer & Watts 2006) has attracted much attention to the study of nonradial oscillations of neutron stars with solid crust. These oscillations were studied extensively in Hansen & Cioffi (1980) and McDermott et al. (1988) for nonmagnetic cases. Unno et al. (1989) discuss many aspects of the theory of nonradial oscillations of stars. The properties of nonradial modes of strongly magnetized neutron stars have been investigated by several authors (Duncan 1998; Piro 2005; Lee 2007, 2008; Glampedakis et al. 2006; Levin 2006, 2007; Samuelsson & Andersson 2007; Sotani et al. 2006, 2007, 2008a, 2008b; Cerda-Duran et al. 2009). Their main focus was on the study of axisymmetric modes, mediated by restoring forces from magnetic field and/or crustal strain. Duncan anticipated toroidal oscillations as a result of giant flares and noted that the magnetic field could affect their frequencies. The effects of a strong vertical magnetic field on the oscillation spectrum of a cylindrical slab model were studied in Carroll et al. (1986). The nonradial modes are generally divided into two main classes: the spheroidal and toroidal modes. Here we concentrate on the study of toroidal modes because of their possible connection with QPOs. They are defined by conditions
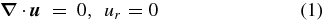
where u is a displacement vector.
Without magnetic field and rotation, toroidal modes (denoted ltn, where the index n is the number of radial nodes in the eigenfunction) have frequencies that do not depend on m. This degeneracy is lifted by the magnetic field since it breaks the spherical symmetry of the problem. In this paper we study how this happens considering the magnetic field B as a perturbation. We work in the framework of Newtonian theory. The influence of a magnetic perturbation on spheroidal modes was considered earlier (see, e.g., Unno et al. 1989). We also refer to Dahlen & Tromp (1998) for a detailed discussion of perturbation theory with applications in seismology. Assuming an oscillatory time dependence u ∝ e−iωt, where ω is the mode frequency, the equation for eigenfunctions without a magnetic field is

where the linear operator A describes the dynamics given specific parameters for the neutron star. We do not need its exact form here. All we need in perturbation theory are the results of the solution of the unperturbed model, i.e., eigenfunctions, eigenfrequencies, and the density profile. In the interest of generality, we do not specify operator A at this stage (readers interested in specific models may consult for models, e.g., Hansen & Cioffi 1980 and McDermott et al. 1988). Let us denote toroidal eigenfunctions and frequencies obtained from this equation as u(0)lm and ω(0)l. In spherical coordinates components of u(0)lm are
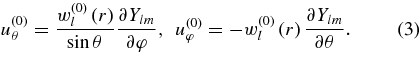
Here w(0)l(r) is a radial eigenfunction.
With a magnetic field we have

where

We now take, for simplicity, B to be the uniform field

It is helpful to use vector spherical harmonics (see, e.g., Varshalovich et al. 1988) to express the vector operators in Equations (4) and (5) in Ylm representation. Definitions of vector spherical harmonics and some useful formulae are given in the Appendix. Then, following the perturbation approach described in Unno et al. (1989), we expand the eigenvalue ω and the eigenfunction u in powers of B0. Substituting them into Equation (4) and using the orthogonality of the eigenfunctions u(0)lm, we obtain

where
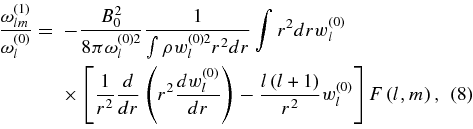
where
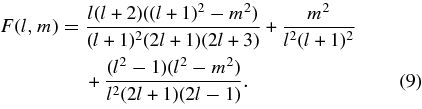
Table 1 lists values of F(l, m) for specific modes.
Table 1. Values of the Function F(l, m) for l = 5, 7, 9
| m | F(5, m) | F(7, m) | F(9, m) |
|---|---|---|---|
| 0 | 0.487 | 0.493 | 0.496 |
| 1 | 0.472 | 0.485 | 0.49 |
| 2 | 0.426 | 0.459 | 0.474 |
| 3 | 0.349 | 0.416 | 0.447 |
| 4 | 0.241 | 0.356 | 0.409 |
| 5 | 0.103 | 0.279 | 0.36 |
| 6 | ⋅⋅⋅ | 0.184 | 0.3 |
| 7 | ⋅⋅⋅ | 0.074 | 0.23 |
| 8 | ⋅⋅⋅ | ⋅⋅⋅ | 0.149 |
| 9 | ⋅⋅⋅ | ⋅⋅⋅ | 0.057 |
Download table as: ASCIITypeset image
This is the main result of our paper within the framework of a perturbative calculation. Perturbation theory is applicable when

For the case of a spherical star with uniform shear modulus μ, we may obtain a general simplification: one can use Equation (23) in McDermott et al. (1988) for radial eigenfunctions w(0)l(r) with μ = const and obtain
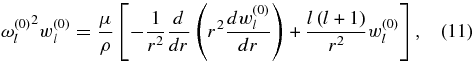
so that the integrals in numerator and denominator of the right-hand side of Equation (8) cancel. This gives
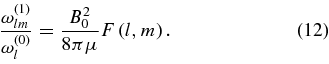
By Equation (10) perturbation theory is thus applicable when

Because of the axisymmetry of the magnetic field the (2l + 1) degeneracy in m is only partially lifted: it depends only on |m|. The mode splits into (l + 1) modes.
The "92 hertz" mode in the QPO data following the 2004 giant flare of SGR 1806−20 actually seems to be accompanied by a conglomerate of many peaks in the power spectrum, ranging from about 78 to 105 Hz (Strohmayer & Watts 2006; Watts & Strohmayer 2006), implying that at its most extreme value 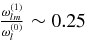 . The 92 hertz QPO is attributed to the l = 7 toroidal mode (Strohmayer & Watts 2006; Watts & Strohmayer 2006). There also seems to be a significant component at about 80 Hz (panels 1–4, and 17 of Figure 9 in Strohmayer & Watts 2006), which could be the l = 6 mode. (If the field is axisymmetric and has mirror symmetry around the equator, then the mechanism for luminosity variation proposed by Timokhin et al. (2007) works for odd l modes, where the two foot points of a given magnetic field line move in opposite directions. This introduces a twist in the magnetic field line that implies a current perturbation. In the more likely situation that the field lacks this high degree of symmetry, even l modes are also possible.) However, there are also modes in the 80–90 Hz range and also significantly above 92, up to 100 Hz or more, so it is hard to interpret the data unambiguously. While there is some evidence for systematic increase of the frequency with time, the QPO signal in any given time frame appears to be constant, and in some cases several bands appear simultaneously, separated by several Hz. We conclude that if the splitting is due to a magnetic field, it is at least 2%, and at most about 25%.
. The 92 hertz QPO is attributed to the l = 7 toroidal mode (Strohmayer & Watts 2006; Watts & Strohmayer 2006). There also seems to be a significant component at about 80 Hz (panels 1–4, and 17 of Figure 9 in Strohmayer & Watts 2006), which could be the l = 6 mode. (If the field is axisymmetric and has mirror symmetry around the equator, then the mechanism for luminosity variation proposed by Timokhin et al. (2007) works for odd l modes, where the two foot points of a given magnetic field line move in opposite directions. This introduces a twist in the magnetic field line that implies a current perturbation. In the more likely situation that the field lacks this high degree of symmetry, even l modes are also possible.) However, there are also modes in the 80–90 Hz range and also significantly above 92, up to 100 Hz or more, so it is hard to interpret the data unambiguously. While there is some evidence for systematic increase of the frequency with time, the QPO signal in any given time frame appears to be constant, and in some cases several bands appear simultaneously, separated by several Hz. We conclude that if the splitting is due to a magnetic field, it is at least 2%, and at most about 25%.
According to the calculations here, the variation is expected to be of order 0.4 to 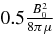 , as m ranges from 0 to 7. This implies that
, as m ranges from 0 to 7. This implies that 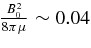 , or
, or 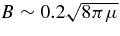 if we interpret the 2% splitting to be due to magnetic effects.
if we interpret the 2% splitting to be due to magnetic effects.
If the entire range from 78 to 105 Hz is attributed to magnetic splitting, our first order of approximation is only marginal at this strength, and a higher order calculation would give a slightly lower value for the frequency shift by a given field strength, so all we can say is that the field is of the same order as (8πμ)1/2.
The value of (4πμ)1/2 has been estimated by to be about 6 × 1015 Gauss (Thompson & Duncan 1995), so, if we assume a magnetic splitting of 2%, the value of B within the crust appears to be on the order of 1.7 × 1015 Gauss, in reasonably good agreement with that estimated for the dipole field component, 1.6 × 1015 (Woods et al. 2002; Palmer et al. 2005). Note that in the geometry used here, the field lines do not particularly lie within the crust but rather cut through it vertically at angle π/2 − θ, where θ is the latitude, so a purely toroidal field would be estimated to be somewhat weaker than the above estimate by a factor of 30% or so.
On the other hand, a toroidal field could, a priori, be larger than the poloidal field without affecting the dipole moment, and a secure observational value for the splitting could set interesting constraints on its strength. The above estimate for the toroidal field that assumes a 2% frequency shift due to magnetic fields may then set significant limits on the amount of magnetic field energy that is stored in the crust. Assuming a field of roughly 1.7 × 1015 G within the crust and a crust volume of 4π × 1017 cm3 would yield a total allowed field energy on the order of 1.5 × 1047 erg in the toroidal crustal field. This would suggest that a giant flare of energy 1046 erg or more, such as the December 27 event is thought to be, could probably not have taken place more than about 10 times during the entire history (T ≲ 104 years) of SGR 1806−20. This result can be checked to some extent because similar events would be detectable in many other nearby galaxies (Eichler 2002).
One possible observational consequence of magnetic splitting of frequency degeneracy for toroidal oscillations is the fact that it leaves m and −m modes degenerate to the extent that the field is axisymmetric about the magnetic axis. In contrast to the magnetic splitting between different |m| modes (which appears to be on the order of several hertz and implies that the beat periods would be less than the rotation period), the m and −m modes would beat more slowly, and their beating could possibly be observed on a timescale of perhaps seconds to tens of seconds. The appearance of a particular frequency band beating on and off during the QPO activity could be a signature of the m and −m modes having (or, more precisely, of their symmetric and antisymmetric combinations having) slightly different frequencies. Such beating would be a measure of a nonaxisymmetric component to the field. If, for example, the field is larger at ϕ = 0 than at ϕ = π/2, then the symmetric combination of the m = 1 and m = −1 modes, proportional to cosϕ, would have a slightly higher frequency than the anti-symmetric mode, proportional to sinϕ.
The residual m, − m degeneracy could also be removed by the inertial forces associated with the rotation of the star (as distinct from the kinematical frequency shift and rotational phase dependence produced by the rotation). For toroidal modes, the angular frequency shift due to rotation in a rotating reference frame attached to the star is mΩ/l(l + 1) (see, e.g., Pekeris et al. 1961; Strohmayer 1991), where Ω is the angular frequency of rotation. With period of rotation Prot ≃ 7.5 s one can see that the splitting is quite small and modulations of the crustal displacement amplitude (beats) are possible with period Tmod = Protl(l + 1)/2m. Since the physics of QPO variations in magnetar luminosity is somehow determined by crustal oscillations (e.g., Timokhin et al. 2007), one might also expect time modulations in the observed QPO components on timescales of order 30 s at l = m = 7.
Another effect that could be looked for is the different damping rates of the symmetric and antisymmetric combinations due to coupling with the core. In general, such damping occurs when the frequency of the mode matches the resonant Alfven frequency of some connecting field lines in the core. But the damping rate would depend on the amplitude of the crustal oscillation at the latitude and longitudes where the frequency match happens to take place, and this amplitude can differ among the various linear combinations of symmetric modes. This suggests that QPO components could resolve to narrower frequency bands as the more rapidly damped linear combination gives way to the surviving combination. Detecting such an effect, however, would require good frequency resolution.
The differences between beating, resolution to the longest lived of several modes, and continuous frequency drift should all be made clear. We are unable to see how magnetic splitting or damping by the continuum leads to continuous frequency drift, and we see little, if any, evidence for it in the data of Strohmayer & Watts (2006).
The potential wealth of data available in magnetar seismology awaits confirmation of an accepted model for it. Future observations of intermediate flares, which may be more frequent than giant flares, may provide badly needed additional data.
The authors thank Drs. A. Watts, Y. Lyubarsky, and C. Thompson for helpful discussions. We acknowledge the Israel–U.S. Binational Science Foundation, the Israel Science Foundation, and the Joan and Robert Arnow chair of Theoretical Astrophysics for generous support.
APPENDIX: VECTOR SPHERICAL HARMONICS
Vector spherical harmonics are defined as

where
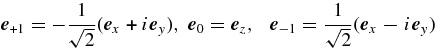
Here L can have values L = J, J ± 1 for a given J.
During the calculations the following formulae prove useful (for more information, see, e.g., Varshalovich et al. 1988):
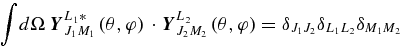
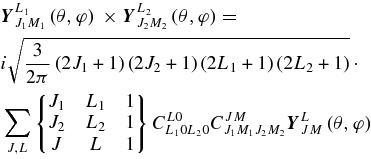
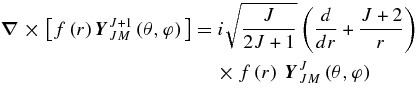
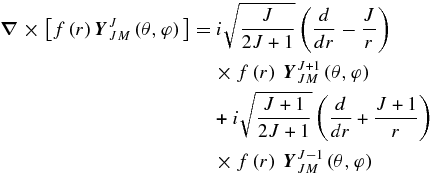
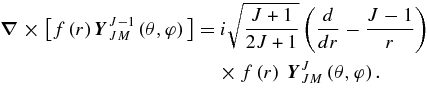
Now, taking into account that u(0)lm and ez can be represented as (e.g., Varshalovich et al. 1988)