Abstract
In this work, we probe the Gardner equation and the modified Benjamin-Bona-Mahony (mBBM) equation associated with plasma physics, acoustic-gravity waves in fluid mechanics, hydro-magnetic waves in cold plasma etc Exact wave solutions to the mentioned equations are studied analytically by the enhanced modified simple equation (EMSE) method. The solitary wave solutions are determined including free parameters. Setting definite values of the unknown parameters yield useful and stable solitary wave solutions. We have depicted some 3D and 2D graphs of the obtained solutions to comprehend the physical structure of the tangible events.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The combination of the KdV and mKdV equation is the Gardner equation. In many areas of applied mathematics and physics, videlicet, plasma physics, nonlinear physics, fluid dynamics, the Gardner equation interprets the reality. Gardner equation is the most imperative model which is in the form [1].

Many models can be extracted from this model by selecting different values of  and
and  The KdV equation attain from the Gardner equation when we set
The KdV equation attain from the Gardner equation when we set  and
and  in equation (1) which is important in the plasma physics and shallow water wave. Again, if we put
in equation (1) which is important in the plasma physics and shallow water wave. Again, if we put  and
and  model (1) turns into the mKdV equation which is significant in the study of the multi-component plasma and electric circuits [2]. Therefore, numerous physical models, which intimately connected for studying physics the Gardner equation widely used. Thus, many methods have been executed to extract exact solutions, for instance the restrictive Taylor approximation for the Gardner and KdV equation [3], an analytic N-solitary wave solution by the Hirota bilinear method [4], the sub-ODE method [5], Wazwaz [6, 7] studied this equation and attain new solitons and kink solutions through the expansion method [8], the bilinear transformation method [9] and extended homoclinic test approach [10].
model (1) turns into the mKdV equation which is significant in the study of the multi-component plasma and electric circuits [2]. Therefore, numerous physical models, which intimately connected for studying physics the Gardner equation widely used. Thus, many methods have been executed to extract exact solutions, for instance the restrictive Taylor approximation for the Gardner and KdV equation [3], an analytic N-solitary wave solution by the Hirota bilinear method [4], the sub-ODE method [5], Wazwaz [6, 7] studied this equation and attain new solitons and kink solutions through the expansion method [8], the bilinear transformation method [9] and extended homoclinic test approach [10].
The modified Benjamin-Bona-Mahony (mBBM) equation [11] is in form

This equation describes the acoustic-gravity waves in compressible fluids, the surface long waves in nonlinear dispersive media, acoustic waves in a harmonic crystals and hydro-magnetic waves in cold plasma. The mBBM model is most important in the study of shock and solitary waves. This equation is much studied in nonlinear physics. Different approaches are put in use, explicitly Manafianher is obtained the exact solutions by using the generalized (G'/G)-expansion method [11], Bekir applied the (G'/G)-expansion method [12], the Exp-function method [13], the tanh and the sine-cosine methods [14] to construct exact solutions of the mBBM equation. Therefore, to find the exclusive solutions to the mBBM equation [15] Benjamin implemented the first integral method [16] and characterizes the approximation for surface long waves in nonlinear dispersive media [17] and Layeni used the new hyperbolic auxiliary function method [18] and fully discrete Galerkin approximations [19].
In this article, we interpret the EMSE method to extract exact solution to the Gardner equation and mBBM equation. There are many complex phenomena appeared in different field of mathematical physics and engineering that can be expressed by NLEEs. To examine the NLEEs there are many methods, such as the (G'/G)-expansion method [20], the F-expansion method [21–23], the MSE method [24, 25] etc The EMSE method provides large-number of solutions to the nonlinear evolution equations than other methods, namely the tanh method, the sine-cosine method etc.
The rest of the article has been arranged as, in section 2, outline of the EMSE method has been arranged. In section 3, solutions have been determined by means of the introduced method to the Gardner and mBBM equations. In section 4, we present graphical representations of the attained solutions. Finally in section 5, we have drawn the conclusion of this article.
2. Outline of the enhanced modified simple equation method
In this part, we discuss the EMSE method in order to derive exact soliton solutions to NLEEs arise in mathematical physics and engineering problems. Let us consider a NLEE
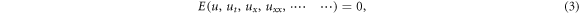
where  is an unidentified function and
is an unidentified function and  is a function of
is a function of  and its partial derivatives in which maximal order derivatives and nonlinear terms are attached. The steps of the method are as follows:
and its partial derivatives in which maximal order derivatives and nonlinear terms are attached. The steps of the method are as follows:
Step 1: We introduce the generalized wave transformation
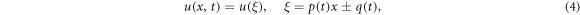
where  and
and  are differentiable functions of t. Making use of wave transformation (4), equation (3) converts into
are differentiable functions of t. Making use of wave transformation (4), equation (3) converts into
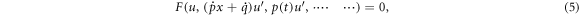
where  and
and 
Step 2:As per the EMSE method the solution structure of equation (5)is of the form
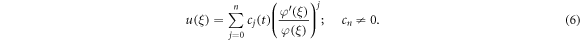
where  is arbitrary function of
is arbitrary function of  such that
such that  and
and  is an unrevealed function.
is an unrevealed function.
Step 3: In this step, we are devoted to evaluate the highest power of the series solution equation (6). To do that, we balance homogeneously among the nonlinear terms and the maximum order derivatives in equation (5).
Step 4: We compute the essential derivatives  of the considered solution
of the considered solution  and then inserting the derivatives into (5), we attained to an equation with the function
and then inserting the derivatives into (5), we attained to an equation with the function  and its derivatives as well as
and its derivatives as well as  Setting the coefficients of
Setting the coefficients of 
 equal to zero, yield a system of equations. Solving the set of equations for the polynomial of
equal to zero, yield a system of equations. Solving the set of equations for the polynomial of  and
and  we attain to the require solution of equation (2).
we attain to the require solution of equation (2).
3. Formulation of the solutions through the EMSE method
Now we will pay attention to put in use the EMSE method to extract the exact soliton solutions to the mBBM equation and the Gardner equation
3.1. The gardner equation
According to step 3, we consider the subsequent traveling wave variable
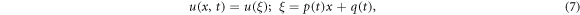
Differentiating equation (7) with respect to  yields
yields
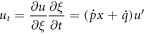
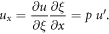
Similarly, the higher derivatives are:
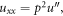
and 
Now, using the derivatives, equation (1) turns out into
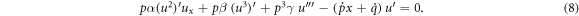
Integrating equation (8), we attain
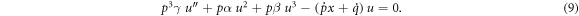
Using the balance between the principle of the highest order derivative  and the nonlinear term
and the nonlinear term  gives
gives 
Therefore, solution of equation (9) takes the shape
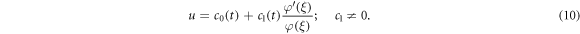
Differentiating twice equation (10) with respect to  yields
yields
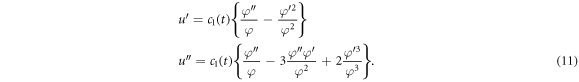
Putting (10) and (11) into equation (9), we accomplish
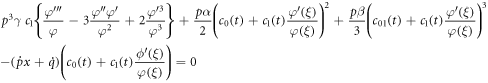
The above equation can be simplified as
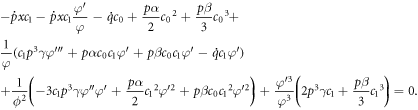
Equating the coefficient of  and
and  to zero, we attain the subsequent set of algebraic and differential equations:
to zero, we attain the subsequent set of algebraic and differential equations:

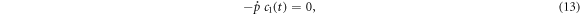
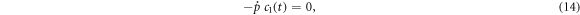
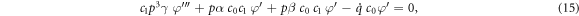
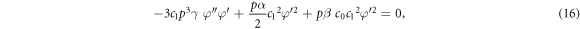

Since  and
and  then equations (13) and (14) gives the following result
then equations (13) and (14) gives the following result

From equation (12), we obtain
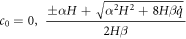
From equation (17), we attain the value of 
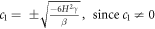
Thus equation (15) can be rewritten as
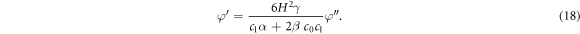
Substituting the value of  from (18) into equation (16), we achieve
from (18) into equation (16), we achieve
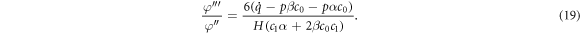
Integrating equation (19), gives
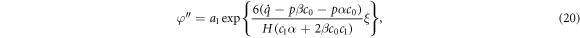
where 
Inserting the value  from equations (20) into (18), we achieve
from equations (20) into (18), we achieve
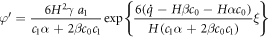
Integrating with respect to  we get
we get
where  and
and  are arbitrary functions of
are arbitrary functions of 
Putting the value of  and
and  into solution (10), we obtain the following solution
into solution (10), we obtain the following solution
Equation (22) is the exact solitary wave solution of the Burger Huxley equation.
Case 1. When  and
and  then equation (22) reduce to
then equation (22) reduce to

where 
If we set  and
and  into solution (22), we accomplish
into solution (22), we accomplish
Case 2. If  and
and  solution (22) reduce to
solution (22) reduce to
where 
On the other hand, if we set  and
and  into solution (22)
into solution (22)
Then we have ![${u}_{2,1}=\displaystyle \frac{6\dot{q}}{\alpha H}\left[1+\,\tanh \left(\tfrac{\dot{q}}{{H}^{2}\alpha }\sqrt{-\tfrac{6\beta }{\gamma }}\xi \right)\right].$](https://content.cld.iop.org/journals/2399-6528/3/12/125011/revision3/jpcoab5eacieqn57.gif)
Case 03. If  and
and  the solution o (22) becomes
the solution o (22) becomes
3.2. The modified Benjamin-Bona-Mahony equation
In this subsection, the EMSE method is used in order to establish exact soliton solutions to the mBBM equation. We consider the mBBM equation [11]:
According to step 3, we consider the following traveling wave variable

Making use of the wave variable (27), the mBBM equation converts into
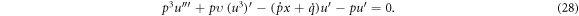
Integrating equation (28) with respect to  yields
yields
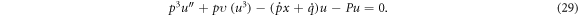
Using the homogeneous balance between the terms  and
and  we attain
we attain 
Thus, solution shape is of the form
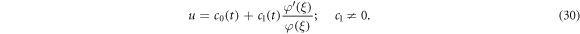
Differentiating twice solution (30) with respect to  gives
gives
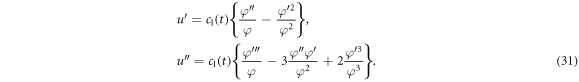
Inserting the solution (30) along with the relations presented in (31) into the equation (29), we attain
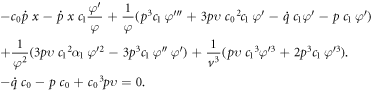
Equating the coefficient of  and
and  we derive the following equations:
we derive the following equations:
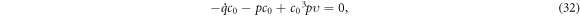
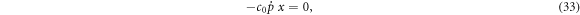
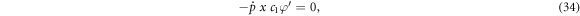
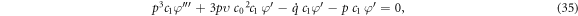
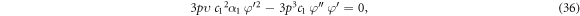
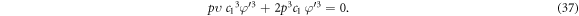
Since  and
and  then (33) and (34) give the following result
then (33) and (34) give the following result
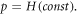
And from equation (32), we get
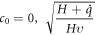
From equation (37), we attain the value of 
 since
since 
We can rewrite the equation (36) as follows:
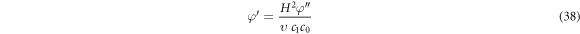
Now substituting the value of  from (38) into equation (35), provides
from (38) into equation (35), provides
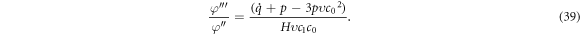
Integrating equation (39), we attain
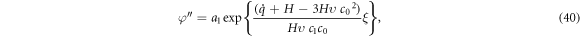
where 
Substituting the value of  into equation (39), we acquire
into equation (39), we acquire
Integrating with respect to  we get
we get
where  and
and  are arbitrary functions of
are arbitrary functions of 
Putting the value of  and
and  into the equation (30), we attain
into the equation (30), we attain
Solution (42) is the general solitary wave solution of the mBBM equation.
Case 1. If  and
and  the solution equation (42) is unbounded. So this case is rejected.
the solution equation (42) is unbounded. So this case is rejected.
Case 2. Again, if  and
and  the solution (42) reduce to
the solution (42) reduce to
where 
If we set  and
and  the solution (43) becomes
the solution (43) becomes
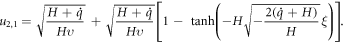
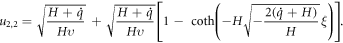
Case 3. When  and
and  solution (42) reduce to
solution (42) reduce to
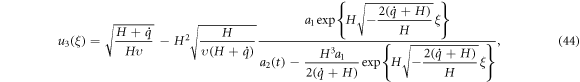
where 
If we set  and
and  into the equation (44) becomes
into the equation (44) becomes
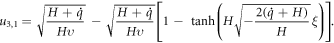
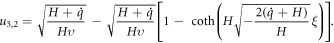
Case 4. When  and
and  then equation (42) reduce to
then equation (42) reduce to
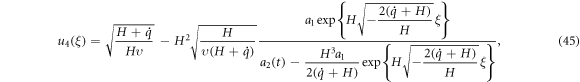
where 
If we set  and
and  into the solution (45), then it becomes
into the solution (45), then it becomes
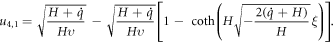
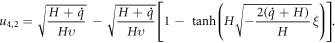
4. Graphical representations
In this section, we explain the graphical demonstration of the obtained solutions to the Gardner equation and the mBBM equation. By implementing EMSE method, we obtained further exact solution of the Gardner equation and mBBM equation through free parameters. We have depicted the 3D and 2D figure of some attained solitary wave solutions through the computer algebraic software MAPLE.
4.1. The gardner equation
In this subsection, we have discussed about the nature and attitude of the obtaining traveling wave solution to the Gardner equation by implement EMSE method. The 3D and 2D figures of the solutions (23) and (24) are provided in the underneath:
Figure 1. (a): Kink soliton of the solution (23) for 
 and
and  (b): Kink soliton of the solution (23) for
(b): Kink soliton of the solution (23) for 
 and
and  (c): Periodic soliton of the solution (23) for
(c): Periodic soliton of the solution (23) for  and
and  (d): Periodic soliton of the solution (23) for
(d): Periodic soliton of the solution (23) for 
 and
and  (e): Anti-bell shape soliton depicted from solution (24) for
(e): Anti-bell shape soliton depicted from solution (24) for  and
and  (f): Anti-bell shape soliton depicted from solution (24) for
(f): Anti-bell shape soliton depicted from solution (24) for 


 and
and  (g): Bell shape soliton of the solution (24) for
(g): Bell shape soliton of the solution (24) for  and
and  (h): Bell shape soliton of the solution (24) for
(h): Bell shape soliton of the solution (24) for 
 and
and 
Download figure:
Standard image High-resolution image4.2. The modified BBM equation
In this section, we will depict the 3D and 2D graphs of the determined solitary wave solutions to the mBBM equation. These exact solutions have different types of shape. With the help of MAPLE software, we have depicted the graphical view of some attained exact solutions.
Download figure:
Standard image High-resolution imageFigure 2. (a): Periodic soliton depicted from the solution (43) for  and
and  (b): Periodic soliton depicted from the solution (43) for
(b): Periodic soliton depicted from the solution (43) for  and
and  (c): Kink type soliton drawn from (43)) for
(c): Kink type soliton drawn from (43)) for  and
and  (d): Kink type soliton drawn from (43) for
(d): Kink type soliton drawn from (43) for  and
and  (e): Bellshape solitondrawn from solution (43) for
(e): Bellshape solitondrawn from solution (43) for  and
and  (f): Bell shape soliton drawn from solution (43) for
(f): Bell shape soliton drawn from solution (43) for  and
and  (g): Soliton drawn from solution (43)for
(g): Soliton drawn from solution (43)for  and
and  (h): Soliton drawn from solution (43) for
(h): Soliton drawn from solution (43) for  and
and  (i):Singular soliton drawn from solution (43) for
(i):Singular soliton drawn from solution (43) for  and
and  (j): Singular soliton drawn from solution (43) for
(j): Singular soliton drawn from solution (43) for 

 and
and  (k): Singular periodic soliton drawn from (43) for
(k): Singular periodic soliton drawn from (43) for  and
and  (l): Singular periodic soliton drawn from (43) for
(l): Singular periodic soliton drawn from (43) for 
 and
and 
Download figure:
Standard image High-resolution image5. Comparison of the solutions
Lin [26] examined the Gardner equation through the tanh-coth method. The tanh-coth method is also an important analytical method to examine closed form solitary wave solutions. Therefore, we have compared the attained solutions with those obtained by the tanh-coth method (Lin [26]) and shown in table 1.
Table 1. Comparison of the obtained solutions with the solutions found by Lin [26].
| Solutions found in Lin [26] | Solutions found in this article |
|---|---|
![${u}_{2}(x,t)=-\tfrac{1}{2\,{\varepsilon }^{2}}+\tfrac{1}{2\,{\varepsilon }^{2}}\,\coth \left[\tfrac{1}{2\,\varepsilon }\left(x-c\,t\right)\right].$](https://content.cld.iop.org/journals/2399-6528/3/12/125011/revision3/jpcoab5eacieqn148.gif)
|
![${u}_{1,2}\left(x,t\right)=-\tfrac{1}{2}+\tfrac{1}{2}\,\coth \left[\tfrac{1}{2}\left(x+1\right)\right].$](https://content.cld.iop.org/journals/2399-6528/3/12/125011/revision3/jpcoab5eacieqn149.gif)
|
If we put  and and  the above equation turn into the above equation turn into ![${u}_{2}(x,t)=-\displaystyle \frac{1}{2}+\displaystyle \frac{1}{2}\,\coth \left[\displaystyle \frac{1}{2}\left(x+1\right)\right].$](https://content.cld.iop.org/journals/2399-6528/3/12/125011/revision3/jpcoab5eacieqn152.gif)
|
where   
|
It is observed from the table 1 that the obtained solution  is similar to the solutions
is similar to the solutions  found by Lin [26]. It is also observable that, we have attained seven solutions. On the other hand, Lin [26] received only three solutions wherein the attained solution
found by Lin [26]. It is also observable that, we have attained seven solutions. On the other hand, Lin [26] received only three solutions wherein the attained solution  is identical to the solution
is identical to the solution  for specific values of the parameters which validates the introduced method. Besides, the attained remaining six solutions are different than the other two solutions obtained by Lin [26]. Therefore, we might assert the EMSE method is optimal than the tanh-coth method for the Gardner equation.
for specific values of the parameters which validates the introduced method. Besides, the attained remaining six solutions are different than the other two solutions obtained by Lin [26]. Therefore, we might assert the EMSE method is optimal than the tanh-coth method for the Gardner equation.
Yusufoglu [14] studied the mBBM equation through the extended tanh method. The extended tanh method is also a powerful method for searching solitary wave solutions. Therefore, we have compared the obtained solutions with those found by the extended tanh method (Yusufoglu [14]) and shown in table 2.
Table 2. Comparison of the obtained solutions with the solutions found by Yusufoglu [14].
| Solutions found in Yusufoglu [14] | Solutions found in this article |
![${u}_{2}(x,t)=\sqrt{\tfrac{-6b}{a\left(2b-1\right)}}\,\tanh \left[\left(x+\tfrac{t}{2b-1}\right)\right].$](https://content.cld.iop.org/journals/2399-6528/3/12/125011/revision3/jpcoab5eacieqn160.gif)
|

|
Setting  the above solution turns into the above solution turns into |
where     
|

|
It is noteworthy to notice from table 2 that the obtained solution  is parallel to the solutions
is parallel to the solutions  found by Yusufoglu [14]. It is also noticeable that, we have attainednine solutions; on the other hand Yusufoglu [14] found only four solutions of which the solution
found by Yusufoglu [14]. It is also noticeable that, we have attainednine solutions; on the other hand Yusufoglu [14] found only four solutions of which the solution  is similar with the attained one solution
is similar with the attained one solution  Besides, the attained remaining eight solutions have not been established by Yusufoglu [14]. Setting specific values of the parameters, we will get many new solutions from these general solutions. That is the specialty of this method.
Besides, the attained remaining eight solutions have not been established by Yusufoglu [14]. Setting specific values of the parameters, we will get many new solutions from these general solutions. That is the specialty of this method.
6. Conclusion
In this article, we have established different type of soliton solutions to the Gardner equation and the mBBM equation through the EMSE method. The solutions include the bell shaped soliton, kink, singular kink, periodic, soliton etc The method is compatible, useful and functional to substantiate new and further general closed form exact solutions to the NLEEs. We have depicted the 3D and 2D graphs to visualize the inner structure of the complicated nonlinear phenomena. This study shows that the EMSE method useful, reliable and provide adequate general solutions to NLEEs.
Acknowledgments
The authors are grateful to the anonymous referees for their important suggestions in the way of developing the manuscript.
Competing interests
There is no competing interest among the authors.
Author's contributions
The study has been conducted in collaboration among the authors. All of the authors have worked effectively to develop the study. Manuscript has been scrutinized by all of the authors.
Funding
This research has not been funded by any research grant.




