Abstract
The spin-polarization S and the spin-polarization parameters U and T of the elastically scattered electrons from Hg atoms have been computed for scattering angles 0°–180° in the energy range 1 eV 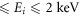 . An optical model approach is employed using a complex optical potential within the framework of the Dirac relativistic partial wave analysis. We compare our results with recent experiments and available theoretical calculations and find a reasonable agreement with experiments over a wide range of energies.
. An optical model approach is employed using a complex optical potential within the framework of the Dirac relativistic partial wave analysis. We compare our results with recent experiments and available theoretical calculations and find a reasonable agreement with experiments over a wide range of energies.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Electron scattering from atoms has a fundamental importance, in understanding the  –atom interaction and collision dynamics, as well as practical relevance. Various cross sections for this process find numerous applications in such diverse areas as Auger electron spectroscopy, electron microscopy, microbiological and materials science research, etc. Various scattering parameters, such as differential, integral, viscosity and momentum transfer cross-sections of electron–atom collisions, play a significant role in a number of practical and technological applications. Mott [1] was the first to predict the effects of polarization in the elastic electron scattering process. Since then, both the experimental and theoretical studies involving the spin-polarization in electron–atom scattering have drawn considerable attention. The spin-polarization parameters S(θ), U (θ) and T(θ)—the delicate scattering characteristics [2–5]—are used not only as battle probes for determining the accuracy of the model employed, but also play a critical role in understanding the spin-dependent interactions involved in the collision dynamics. Recently, it has been shown, in the works of Blum group [6, 7] on
–atom interaction and collision dynamics, as well as practical relevance. Various cross sections for this process find numerous applications in such diverse areas as Auger electron spectroscopy, electron microscopy, microbiological and materials science research, etc. Various scattering parameters, such as differential, integral, viscosity and momentum transfer cross-sections of electron–atom collisions, play a significant role in a number of practical and technological applications. Mott [1] was the first to predict the effects of polarization in the elastic electron scattering process. Since then, both the experimental and theoretical studies involving the spin-polarization in electron–atom scattering have drawn considerable attention. The spin-polarization parameters S(θ), U (θ) and T(θ)—the delicate scattering characteristics [2–5]—are used not only as battle probes for determining the accuracy of the model employed, but also play a critical role in understanding the spin-dependent interactions involved in the collision dynamics. Recently, it has been shown, in the works of Blum group [6, 7] on  –H and Bartschat and Santos [8] on
–H and Bartschat and Santos [8] on  –Li scattering, that spin-polarization S(θ), the Sherman function, arises also from the quantum spin-entanglement of the projectile-target system in addition to the separable total spin and Bell correlation, depending on the collision energy and scattering angle.
–Li scattering, that spin-polarization S(θ), the Sherman function, arises also from the quantum spin-entanglement of the projectile-target system in addition to the separable total spin and Bell correlation, depending on the collision energy and scattering angle.
Polarization of electrons scattered from unpolarized atoms can occur primarily due to the spin–orbit interaction between the continuum electron and the nucleus [4]. This process is often referred to as Mott scattering. Polarization of the scattered electron can also occur due to the fine-structure effect, the interplay between the spin–orbit splitting of atomic fine-structure states. The role of different spin-dependent interactions on the polarization of scattered electron has been reported in [9]. Other effects, such as electron–electron interaction, exchange processes and the outer-shell configuration, have been observed by some experimental groups [10–13]. It is well known from the above investigations that for the elastic scattering from a closed-shell configuration, like Hg, polarization of high energy electrons are produced primarily due to the spin–orbit couplings. In contrast, the fine structure effect comes into play for the open-shell system. Correlation effects, such as charge cloud polarization or electron exchange, remain important at lower collision energies.
To date, there are considerable attempts to study, both theoretically and experimentally, the elastic electron scattering by the Hg atoms using various formulas, methods and models. But, the agreement between theoretical calculations and experimental data of electron spin-polarization parameters resulting from this collision is not quite satisfactory, specially at lower incident energies [14, 15]. Many earlier investigations on the e−–Hg scattering can be traced in the review articles [3, 16]. Among the recent studies, the experimental works of Dümmler et al [17], Kaussen et al [18], Berger and Kessler [19], Möllenkamp et al [20], Hanne et al [21]; theoretical calculations due to Bostock et al [22], Kelemen and Remeta [5], Zatsarinny and Bartschat [23], Fursa et al [24], Fritsche et al [25], Haberland and Fritsche [26], McEachran and Stauffer [27] and Hasenburg et al [28]; and review work of Walker [2] are worth mentioning. In particular, Kelemen and Remeta [5], using relativistic optical potential (OP) approximation, reported the e−–Hg elastic scattering results for 0.1 eV 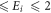 keV. Their work includes the differential cross sections (DCSs) at 10 energy-points from 9 to 300 eV and S(θ) at 9 energies from 150 to 1796 eV. They showed that S(θ), the Sherman function, reaches the maximum values, the total polarization S = ± 1 [2], in the vicinity of the critical minima of DCS for some values of the collision energy Ei and scattering angle θ.
keV. Their work includes the differential cross sections (DCSs) at 10 energy-points from 9 to 300 eV and S(θ) at 9 energies from 150 to 1796 eV. They showed that S(θ), the Sherman function, reaches the maximum values, the total polarization S = ± 1 [2], in the vicinity of the critical minima of DCS for some values of the collision energy Ei and scattering angle θ.
For e−–Hg collisions, the recent relativistic convergent close-coupling (RCCC) method of Bostock et al [22] and fully relativistic B-spline R-matrix calculations of Zatsarinny and Bartschat [23] successfully reproduced the experimental values of S(θ) of the elastic scattering in the energy range 1–14 eV. Fursa et al [24] have employed a non-relativistic CCC approach to analyze the e−–Hg scattering by considering partially the relativistic effects arising from the short-range potential due to the valence electrons. In [25, 26], spin-dependent scattering processes have been presented using another sophisticated approach, the generalized Kohn–Sham (GKS) one-particle theory, which also accounts for relativistic effects. Relativistic distorted-wave (RDW) approach has been reported in [27]. The RDW calculations utilize first-order perturbative solutions of the Dirac equation for various model potentials. In addition, the complex OP approximation has been employed in [5, 28], where relativistic effects are taken into account by including the spin–orbit interaction and the scalar part of the Dirac relativistic potential into OP as well as by the relativistic correction to the exchange potential.
Recently, the theoretical studies on the 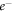 –atom scattering employing OP model (OPM) have enjoyed much success. In our previous works, we used a complex OPM within the framework of Dirac relativistic partial wave analysis (DRPWA) for the study of
–atom scattering employing OP model (OPM) have enjoyed much success. In our previous works, we used a complex OPM within the framework of Dirac relativistic partial wave analysis (DRPWA) for the study of 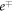 –atom (
–atom (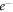 and
and 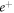 refer, respectively, to electron and positron) scattering. The imaginary part of our OPM represents the absorption potential that takes into account the loss of particle flux to all energetically possible inelastic channels [29]. The real part, on the other hand, includes the static [30], the exchange [31] and the polarization [32] potentials. In our calculations of
refer, respectively, to electron and positron) scattering. The imaginary part of our OPM represents the absorption potential that takes into account the loss of particle flux to all energetically possible inelastic channels [29]. The real part, on the other hand, includes the static [30], the exchange [31] and the polarization [32] potentials. In our calculations of 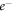 –atom scattering [33–35], we chose a global polarization potential that was a combination of the long-range Buckingham potential and short-range local-density approximation (LDA) correlation potential. In the present study, instead of Buckingham potential, a parameter free potential due to Sun et al [36] is used as the long-range part of the polarization potential, which allows us to obtain better results of spin-polarization over a wide energy range of 1 eV
–atom scattering [33–35], we chose a global polarization potential that was a combination of the long-range Buckingham potential and short-range local-density approximation (LDA) correlation potential. In the present study, instead of Buckingham potential, a parameter free potential due to Sun et al [36] is used as the long-range part of the polarization potential, which allows us to obtain better results of spin-polarization over a wide energy range of 1 eV 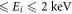 . The present DRPWA results of the spin parameters S(θ), U (θ) and T(θ) are compared with the available experimental data and other theoretical calculations.
. The present DRPWA results of the spin parameters S(θ), U (θ) and T(θ) are compared with the available experimental data and other theoretical calculations.
The rest of this paper is organized as follows. Section 2 outlines the theoretical framework. In section 3, we present and compare our results systematically with available measurements and other theoretical findings. Section 4 contains the conclusion on the present findings. Atomic units are used throughout unless otherwise stated.
2. Outline of the theory
2.1. The theoretical methodology
The Dirac equation for motion of the projectile electron with a velocity v in a central field V(r) is given in [37] as
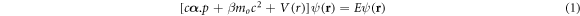
where,  is the total energy, mo is the rest mass of the projectile,
is the total energy, mo is the rest mass of the projectile, 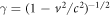 , c is the velocity of light in vacuum, Ei is the kinetic energy of the incident particle, α and β are the usual 4 × 4 Dirac matrices. The relativistic wave function
, c is the velocity of light in vacuum, Ei is the kinetic energy of the incident particle, α and β are the usual 4 × 4 Dirac matrices. The relativistic wave function 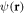 , a four-component spinor with quantum numbers κm, describing the motion of the scattered electron, is given by
, a four-component spinor with quantum numbers κm, describing the motion of the scattered electron, is given by
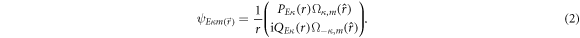
Here,  and
and  represent, respectively the radial parts of the large and small components of the scattering wave function and
represent, respectively the radial parts of the large and small components of the scattering wave function and 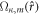 are the spherical spinors. The relativistic quantum number κ is defined as
are the spherical spinors. The relativistic quantum number κ is defined as 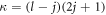 , where j and l are the total and orbital angular momentum quantum numbers that are both determined by the value of κ as
, where j and l are the total and orbital angular momentum quantum numbers that are both determined by the value of κ as 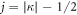 ,
, 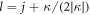 .
.
The radial functions  and
and 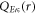 satisfy separately the following set of coupled differential equations [38]:
satisfy separately the following set of coupled differential equations [38]:

and
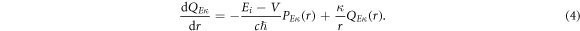
The scattering information is determined from the asymptotic form of the large component 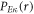 of the scattering wave function which can be expressed in terms of the complex phase-shift
of the scattering wave function which can be expressed in terms of the complex phase-shift 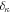 as
as
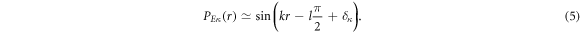
The equations (3) and (4) satisfying the asymptotic condition (5) are solved numerically using the subroutine package RADIAL [39]. In the relativistic partial wave analysis, the phase shift 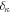 may be calculated for angular momentum value up to the maximum lmax = 25 000. The value of lmax, however, depends on the incident energy and rate of convergence. For energy above 5 MeV, where the convergence of partial wave series is slow, approximate factorization methods are used for the calculation of
may be calculated for angular momentum value up to the maximum lmax = 25 000. The value of lmax, however, depends on the incident energy and rate of convergence. For energy above 5 MeV, where the convergence of partial wave series is slow, approximate factorization methods are used for the calculation of  –atom scattering.
–atom scattering.
2.2. Spin-polarization parameters
The relativistic treatment of electron collisions enables us to calculate the polarization, which describes the measured spin-up and spin-down asymmetries in the number of scattered electrons. The expressions for the spin-polarization in terms of the scattering amplitudes is given by [3, 28]
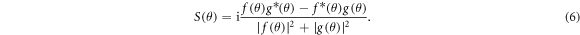
Here,  and
and 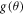 , the direct and spin-flip scattering amplitudes [40], are respectively given as
, the direct and spin-flip scattering amplitudes [40], are respectively given as
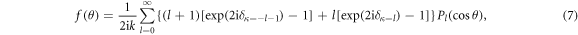
and
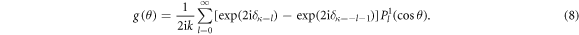
Here, 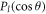 and
and 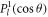 denote respectively the Legendre polynomials and associated Legendre functions, k is the relativistic wave number of the projectile that is related to the momentum p and the kinetic energy Ei by
denote respectively the Legendre polynomials and associated Legendre functions, k is the relativistic wave number of the projectile that is related to the momentum p and the kinetic energy Ei by

Equation (6) suggests that the behavior of the scattering amplitudes f (θ) and g(θ) respectively in equations (7) and (8) determines the total polarization points S = ±1 near the critical minima of DCS given by 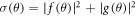 .
.
The other spin-polarization parameters 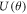 and
and 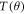 , treated in the present work, are given [3, 28] as
, treated in the present work, are given [3, 28] as
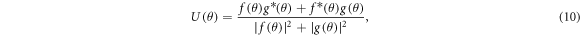
and
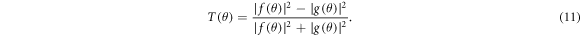
 and
and 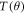 describe the relation of polarization vector during the scattering process [2]. The three spin functions obey the following conservation relation [19, 20]
describe the relation of polarization vector during the scattering process [2]. The three spin functions obey the following conservation relation [19, 20]

The values of 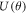 and
and 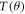 are dependent on
are dependent on 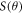 and hence are useful indicators of total polarization,
and hence are useful indicators of total polarization,  = ±1.
= ±1.
2.3. The interaction potential
The complex optical model potential Vopt(r), for the 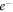 –atom effective interaction, is given by [41]
–atom effective interaction, is given by [41]
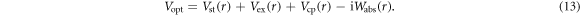
The real components Vst(r), Vex(r), Vcp(r) in (13) are the static, exchange and correlation-polarization potentials respectively. As stated earlier, the component Wabs(r) represents absorptive part which accounts for the loss of particles into various inelastic channels during the collisions. The static potential Vst(r) has been generated from the procedure adopted in Salvat et al [42], where the proton and electron densities are respectively taken as Fermi nuclear charge distribution [43] and Hartree–Fock (HF) analytical density function [44]. For e−–Hg scattering, we have used the semi-classical exchange potential of Furness and McCarthy [45] derived directly from the formal expression of the non-local exchange interaction by using a WKB like approximation for the wave functions. This is expressed as
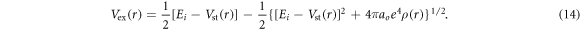
Here Ei is the incident energy of electron, ao is the Bohr radius.
The electron density function 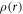 , represented by an analytical function F(r) by [44], was calculated from the numerical HF wave functions, subject to some important constraints. Thus
, represented by an analytical function F(r) by [44], was calculated from the numerical HF wave functions, subject to some important constraints. Thus

where 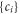 are mixing coefficients,
are mixing coefficients,

and
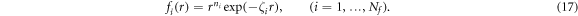
In equation (17), 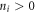 and
and 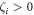 are used.
are used.
The approximation (15) for electron density consists of 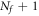 terms and includes linear
terms and includes linear 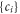 and nonlinear
and nonlinear 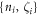 parameters taken from [44]. The electron density function
parameters taken from [44]. The electron density function 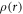 satisfies the following normalized relation
satisfies the following normalized relation
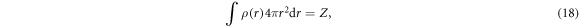
with Z being the atomic number of the target atom.
In the present work, we choose a global polarization potential Vcp [41], a combination of the parameter free long range polarization potential Vcps and LDA correlation potential Vco. Accordingly,
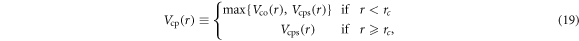
where rc is the outer radius at which short-range Vco(r) and long-range Vcps(r) intersect first.
The long range part Vcps(r) i.e. when the projectile is far from the atom, is approximated as [36]

where α = 5.1 × 10−24 cm3 is the atomic static polarizability for Hg atom and for e−-scattering the constant d can be determined by
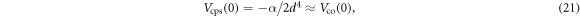
then
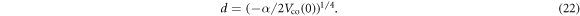
In LDA, the correlation energy of the projectile at r is the same as if it were moving within a free electron gas (FEG) of density 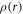 equal to the local atomic electron density. Following Padial and Norcross [32], the correlation potential is calculated as the functional derivative of the FEG correlation energy with respect to
equal to the local atomic electron density. Following Padial and Norcross [32], the correlation potential is calculated as the functional derivative of the FEG correlation energy with respect to  . It is convenient to introduce the density parameter
. It is convenient to introduce the density parameter
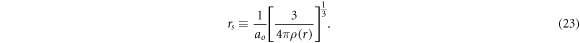
The parameterization of the correlation potential, for the electron scattering, given in Perdew and Zunger [46] is adopted as
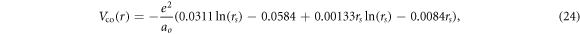
for 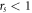 and for
and for  ,
,
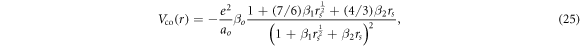
where 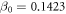 ,
, 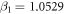 and
and  .
.
For electron scattering, Wabs(r), originally proposed by Salvat [41] by means of LDA, is given by
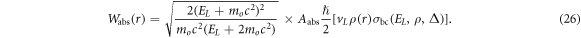
Here, vL is the velocity with which the projectile interacts as if it were moving within a homogeneous gas of density ρ and is given by  corresponding to the local kinetic energy
corresponding to the local kinetic energy  .
. 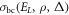 is the cross section for binary collision of electron with the degenerate FEG [45] involving energy transfers greater than a certain energy gap Δ.
is the cross section for binary collision of electron with the degenerate FEG [45] involving energy transfers greater than a certain energy gap Δ.
In the present calculation, the value of the empirical parameter Aabs is chosen to be 1/2. The value of the energy gap Δ in this calculation is adopted as the first excitation energy of Hg atom, 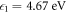 , taken from NIST Physics Reference Data [47]. The factor 1/2 in the absorption potential for electron arises due to the exchange effect in the binary collision of the incident electron with the electron gas.
, taken from NIST Physics Reference Data [47]. The factor 1/2 in the absorption potential for electron arises due to the exchange effect in the binary collision of the incident electron with the electron gas.
3. Results and discussion
3.1. Spin-polarization
The present DRPWA results of the spin-polarization 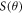 calculated within the framework of complex OPM are illustrated in figures 1–8. Here, the spin-asymmetry parameter is calculated over a wide range of energies and compared with the experiments of Dümmler et al [17] at 1.0, 1.5 and 1.9 eV; Kaussen et al [18] at 6.0, 9.0, 11.0, 12.2, 14.0, 17.0, 24.0 and 180.0 eV; Berger and Kessler [19] at 25.0, 35.0, 50.0 and 150.0 eV; Hanne et al [21] at 8.0, 10.0, 12.0, 15.0 and 18.0 eV; Duweke et al [48] at 1.4, 2.4 and 3.9 eV; Hanne et al [49] at 30.0 and 125.0 eV; Eitel et al [50] at 100.0, 150.0, 170.0, 190.0, 230.0, 400.0, 425.0, 450.0, 475.0 and 500.0 eV; Deichsel et al [51] at 3.5 eV; Jost and Kessler [52] at 180.0, 260.0, 280.0, 300.0, 320.0, 340.0, 900.0 and 1700.0 eV.
calculated within the framework of complex OPM are illustrated in figures 1–8. Here, the spin-asymmetry parameter is calculated over a wide range of energies and compared with the experiments of Dümmler et al [17] at 1.0, 1.5 and 1.9 eV; Kaussen et al [18] at 6.0, 9.0, 11.0, 12.2, 14.0, 17.0, 24.0 and 180.0 eV; Berger and Kessler [19] at 25.0, 35.0, 50.0 and 150.0 eV; Hanne et al [21] at 8.0, 10.0, 12.0, 15.0 and 18.0 eV; Duweke et al [48] at 1.4, 2.4 and 3.9 eV; Hanne et al [49] at 30.0 and 125.0 eV; Eitel et al [50] at 100.0, 150.0, 170.0, 190.0, 230.0, 400.0, 425.0, 450.0, 475.0 and 500.0 eV; Deichsel et al [51] at 3.5 eV; Jost and Kessler [52] at 180.0, 260.0, 280.0, 300.0, 320.0, 340.0, 900.0 and 1700.0 eV.
Figure 1. Angular dependence of spin-polarization  for electrons scattered from Hg at impact energies: (a) 1.0, (b) 1.4, (c) 1.5, (d) 1.9, (e) 2.4 and (f) 3.5 eV. The thick solid (red) lines are our DRPWA calculations described in the text. The solid circles are the experimental data from [17, 48, 51]. The dashed curves represent the RCCC calculations of Bostock et al [22] (1.0, 1.5, 1.9 and 2.4 eV), RHF calculations of Walker [53] (3.5 eV) and the dash–dot curves are the GKS calculations of Fritsche et al [25].
for electrons scattered from Hg at impact energies: (a) 1.0, (b) 1.4, (c) 1.5, (d) 1.9, (e) 2.4 and (f) 3.5 eV. The thick solid (red) lines are our DRPWA calculations described in the text. The solid circles are the experimental data from [17, 48, 51]. The dashed curves represent the RCCC calculations of Bostock et al [22] (1.0, 1.5, 1.9 and 2.4 eV), RHF calculations of Walker [53] (3.5 eV) and the dash–dot curves are the GKS calculations of Fritsche et al [25].
Download figure:
Standard image High-resolution imageThe DRPWA results are also compared with the theoretical calculations due to the RCCC approach of Bostock et al [22] at 1.0, 1.5, 1.9, 2.4, 3.9, 6.0, 9.0, 11.0, 12.2 and 14.0 eV; the relativistic complex OPM calculations of Kelemen and Remeta [5] (denoted by RSEPA) at 150.0, 900.0 and 1700.0 eV; the GKS theory of Fritsche et al [25] at 1.0, 1.5 and 1.9 eV and Haberland and Fritsche [26] at 6.0, 9.0, 11.0, 12.2, 14.0, 17.0, 24.0 and 180.0 eV; RDW of McEachran and Stauffer [27] at 25.0, 35.0, 50.0, 150.0 and 180.0 eV; and the relativistic Hartree–Fock (RHF) method of Walker [53] at 3.5, 8.0, 100.0, 150.0, 200.0, 260.0, 300.0, 340.0 and 500.0 eV. As far as we know, at 75.0, 700.0, 1000.0, 1500.0 and 2000.0 eV, there are neither any measured data nor any other calculated values for 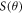 available in literature to compare with. It is anticipated that this investigation might motivate future experimental and theoretical studies shortly.
available in literature to compare with. It is anticipated that this investigation might motivate future experimental and theoretical studies shortly.
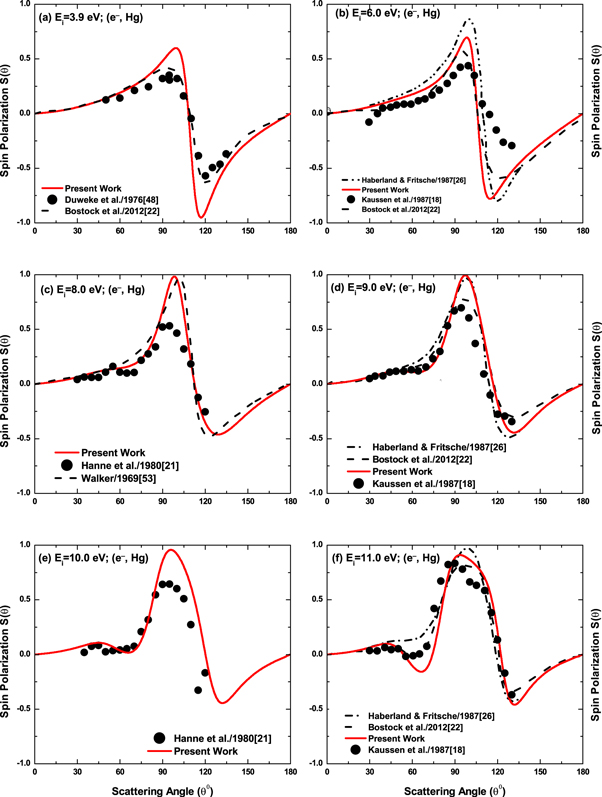
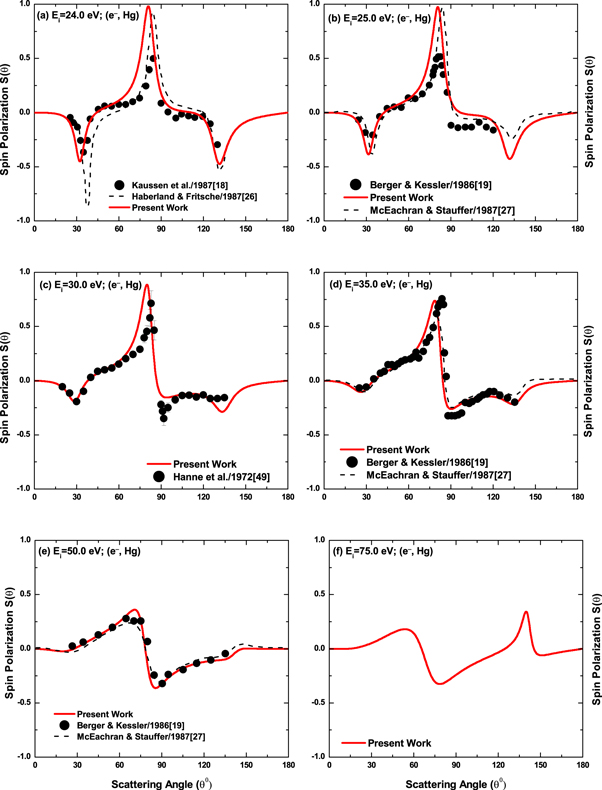
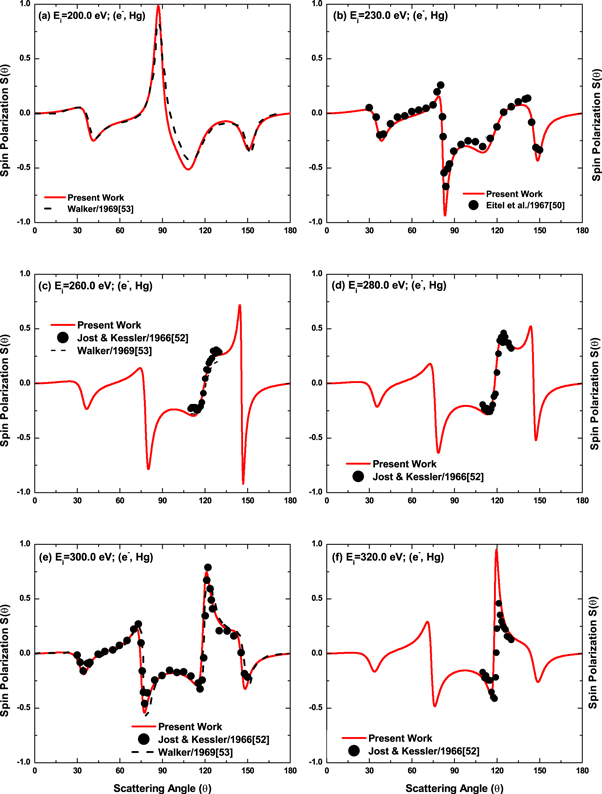
The comparison shows an excellent agreement between DRPWA results and experiments at 12.0, 12.2, 14.0 and 17.0 eV in figure 3; 30.0, 35.0, and 50.0 eV in figure 4; 100.0, 150.0, 170.0, 180.0 and 190.0 eV in figure 5; 230.0, 260.0, 280.0, 300.0 and 320.0 eV in figure 6; 340.0, 400.0, 425.0, 475.0 and 500.0 eV in figure 7; and 900.0 and 1700.0 eV in figure 8. These results also present an overall good agreement between the DRPWA results and experimental data for the energies of 8.0, 10.0, 11.0, 15.0, 18.0, 24.0, 25.0 and 125.0 eV at all angles except the regions of the absolute maxima in the positive and negative excursions. At these energies, the DRPWA results along with other theoretical calculations and experiments exhibit oscillations at about the same scattering angles with differences in magnitude. These differences may be due to the different choice of the interaction potential and different procedures among the theoretical studies. It is worth-mentioning that the DRPWA results at 9.0 eV are in well agreement with experiment despite the fact that 5d9 core excited states are listed in the NIST tables in this region at 8.79 and 9.54 eV [47]. At 200.0 eV, both the DRPWA and RHF [53] results are in excellent agreement with each other (figure 6(a)).
At lower energy region (≤6.0 eV) the DRPWA results produce less satisfactory agreement with the experiment as seen in figures 1 and 2. Before the onset of the inelastic threshold, there will be a substantial contribution of the resonance elastic scattering corresponding to the isolated levels of the composite system, Hg− 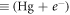 . This invasion of the indirect process cannot be modeled accurately in the OPM approach. Moreover, at the onset of the inelastic threshold, there may be an interplay between the real and imaginary parts of OP due to the dispersion effect leading to a deviation from the smooth variation in the OP parameters with energy. This trait is not also considered in the present study. Nonetheless, the present DRPWA calculations show reasonably good agreement with the data at lower scattering angles up to
. This invasion of the indirect process cannot be modeled accurately in the OPM approach. Moreover, at the onset of the inelastic threshold, there may be an interplay between the real and imaginary parts of OP due to the dispersion effect leading to a deviation from the smooth variation in the OP parameters with energy. This trait is not also considered in the present study. Nonetheless, the present DRPWA calculations show reasonably good agreement with the data at lower scattering angles up to 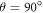 for this energy region and describe correctly the oscillatory features of the spin-polarization at Ei = 1.0 eV (figure 1(a)), Ei = 1.4 eV (figure 1(b)), Ei = 1.5 eV (figure 1(c)) and Ei = 1.9 eV (figure 1(d)). Figure 1(a) depicts the overestimations of the RCCC results due to Bostock et al [22] in describing the oscillation of the experimental data. However, the present S(θ) results also show good agreement with those due to RHF [53] at Ei = 3.5 eV (figure 1(f)) and 8.0 eV (figure 2(c)). Our DRPWA findings agree reasonably with those due to GKS of [26] at Ei = 6.0 and 9.0 eV presented respectively in figures 2(b) and (d).
for this energy region and describe correctly the oscillatory features of the spin-polarization at Ei = 1.0 eV (figure 1(a)), Ei = 1.4 eV (figure 1(b)), Ei = 1.5 eV (figure 1(c)) and Ei = 1.9 eV (figure 1(d)). Figure 1(a) depicts the overestimations of the RCCC results due to Bostock et al [22] in describing the oscillation of the experimental data. However, the present S(θ) results also show good agreement with those due to RHF [53] at Ei = 3.5 eV (figure 1(f)) and 8.0 eV (figure 2(c)). Our DRPWA findings agree reasonably with those due to GKS of [26] at Ei = 6.0 and 9.0 eV presented respectively in figures 2(b) and (d).
Figure 2. Same as figure 1, but for the impact energies: (a) 3.9, (b) 6.0, (c) 8.0, (d) 9.0, (e) 10.0 and (f) 11.0 eV. The experimental data are from Düweke et al [48] for 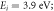 Kaussen et al [18] for 6, 9 and 11 eV and Hanne et al [21] for 8 and 10 eV. Dash–dot curves are now the calculations due to GKS of Haberland and Fritsche [26].
Kaussen et al [18] for 6, 9 and 11 eV and Hanne et al [21] for 8 and 10 eV. Dash–dot curves are now the calculations due to GKS of Haberland and Fritsche [26].
Download figure:
Standard image High-resolution imageRegarding the polarization dynamics in the scattering process our study supports the work of Kelemen and Remeta [5]. The angular positions of the critical minimum (CM) in the DCS distributions of [5] at 10 energy-points in the range 9 eV 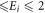 keV are linked to the corresponding total spin-polarizations
keV are linked to the corresponding total spin-polarizations  . The aforesaid connection is effectively employed to examine the conjecture [2, 5] that the total
. The aforesaid connection is effectively employed to examine the conjecture [2, 5] that the total 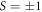 values occur in the vicinity of CM. This behavior is also evident for incident energies approaching 1 keV and beyond (see figures 8(b) and (e)). However, at lower energies, a more appropriate statement regarding the angular positions of CM and the corresponding extremum S-values may be that S(θ) swings through the S = 0 value with its maximum values in the positive and negative excursions with their angular positions determined by the derivative of the DCS values. For Ei = 9.0, 12.2, 35.0, 50.0, 100.0 and 150.0 eV with CM at
values occur in the vicinity of CM. This behavior is also evident for incident energies approaching 1 keV and beyond (see figures 8(b) and (e)). However, at lower energies, a more appropriate statement regarding the angular positions of CM and the corresponding extremum S-values may be that S(θ) swings through the S = 0 value with its maximum values in the positive and negative excursions with their angular positions determined by the derivative of the DCS values. For Ei = 9.0, 12.2, 35.0, 50.0, 100.0 and 150.0 eV with CM at  , 75°, 83°, 80°, 130° and 118° respectively in figures 2(d), 3(b), 4(d), 4(e), 5(a) and 5(c), maximum value, near to S = 1, in the positive excursion is obtained with the corresponding extremum value in the negative excursion much lesser than S = −1 excepting the case of Ei = 50.0 eV where
, 75°, 83°, 80°, 130° and 118° respectively in figures 2(d), 3(b), 4(d), 4(e), 5(a) and 5(c), maximum value, near to S = 1, in the positive excursion is obtained with the corresponding extremum value in the negative excursion much lesser than S = −1 excepting the case of Ei = 50.0 eV where 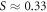 , the maximum value, even in the positive excursion. In all the above-mentioned 6 energy-points, the quantum spin-entaglement [6–8] along with other quantum effects is likely to dilute the maximum value ofS(θ) in the negative excursion.
, the maximum value, even in the positive excursion. In all the above-mentioned 6 energy-points, the quantum spin-entaglement [6–8] along with other quantum effects is likely to dilute the maximum value ofS(θ) in the negative excursion.
Figure 3. Same as figure 1, but for the impact energies (a) 12.0, (b) 12.2, (c) 14.0, (d) 15.0, (e) 17.0 and (f) 18.0 eV. Experimental data from [21] (12, 15 and 18 eV), [18] (12.2, 14 and 17 eV) and the theoretical predictions due to RCCC of [22], GKS of [26] are presented.
Download figure:
Standard image High-resolution imageFigure 4. Same as figure 1, but for the impact energies (a) 24.0, (b) 25.0, (c) 30.0, (d) 35.0, (e) 50.0 and (f) 75.0 eV. The experimental data are now from [18, 19, 49] and the theoretical calculations are due to the GKS of [26] (24 eV) and the RDW approach of McEachran and Stauffer [27] (25.0, 35.0 and 50 eV).
Download figure:
Standard image High-resolution imageFigure 5. Same as figure 1, but for the impact energies: (a) 100.0, (b) 125.0, (c) 150.0, (d) 170.0, (e) 180.0 and (f) 190.0 eV. The experimental data in solid circles are now from [18, 49, 50] and those in solid asterisks are from [19, 52]. The theoretical results are due to RSEPA of [5] for 150.0 eV; the GKS of [26] for 180 eV; the RDW of [27] for 150.0 and 180.0 eV; and the RHF of [53] for 100.0 and 150.0 eV.
Download figure:
Standard image High-resolution imageFigure 6. Same as figure 1, but for the impact energies (a) 200.0, (b) 230.0, (c) 260.0, (d) 280.0, (e) 300.0 and (f) 320.0 eV. The experimental data are from [50, 52] and the theoretical calculations are due to the RHF of [53].
Download figure:
Standard image High-resolution imageFigure 7. Same as figure 1, but for the impact energies (a) 340.0, (b) 400.0, (c) 425.0, (d) 450.0, (e) 475.0 and (f) 500.0 eV. The experimental data are from [50] (400, 425, 450, 475 and 500 eV) and [52] (340 eV) and the theoretical calculations are due to the RHF of [53] for 340.0 and 500.0 eV.
Download figure:
Standard image High-resolution image3.2. Spin-polarization parameters
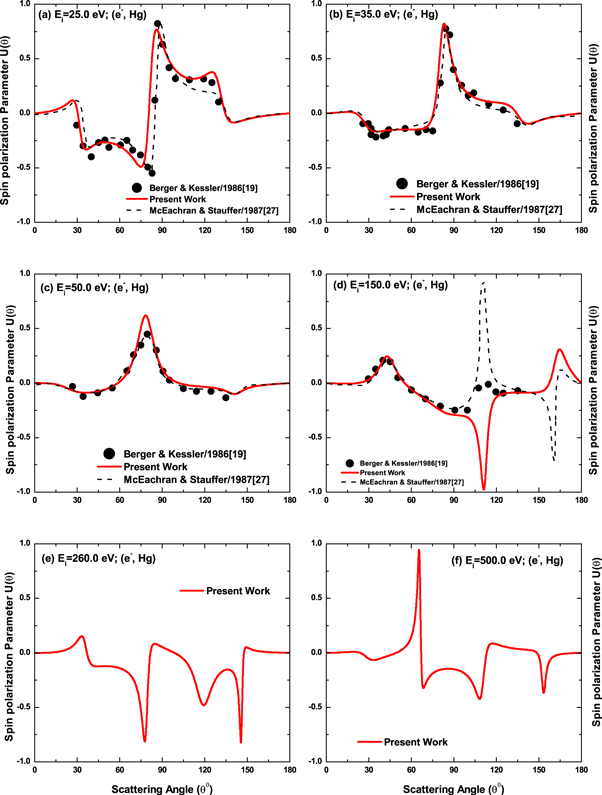
Our DRPWA results of the angular variation of parameters U (θ) and T(θ) at few selected energies (25.0, 35.0, 50.0, 150.0, 260.0 and 500.0 eV) are depicted respectively in figures 9 and 10. The angular and energy dependence of these parameters are defined by the real and imaginary parts of the direct and spin-flip scattering amplitudes. The present results at Ei = 25.0 eV (figures 9(a), 10(a)), Ei = 35.0 eV (figures 9(b), 10(b)), Ei = 50.0 eV (figures 9(c), 10(c)) and Ei = 150.0 eV (figures 9(d), 10(d)) are compared with the only available experimental data of Berger and Kessler [19] and the theoretical RDW results of McEachran and Stauffer [27]. As no experimental data and other theoretical studies of U and T parameters are available in literature at Ei = 260.0 and 500.0 eV, we have displayed only our present DRPWA results providing further impetus for experimental studies.
Figure 9 depicts the parameter of U similar to the spin-polarization S curves (figures 1–8). Our comparison shows that our DRPWA results produce excellent agreement with both the experiment and the RDW findings. But at the minimum position near 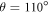 for the impact energy of 150.0 eV, the present results significantly disagree with them. Apart from slight shift in the scattering angle of the minimum position at 25.0 eV, in figure 10, the DRPWA results of T parameter agree quite well with those of both the experiment [19] and the RDW calculations of [27].
for the impact energy of 150.0 eV, the present results significantly disagree with them. Apart from slight shift in the scattering angle of the minimum position at 25.0 eV, in figure 10, the DRPWA results of T parameter agree quite well with those of both the experiment [19] and the RDW calculations of [27].
Figure 8. Same as figure 1, but for the impact energies (a) 700.0, (b) 900.0, (c) 1000.0, (d) 1500.0, (e) 1700.0 and (f) 2000.0 eV. The experimental data are from [52] and the theoretical calculations are due to the RSEPA of [5] for 900.0 and 1700.0 eV.
Download figure:
Standard image High-resolution imageFigure 9. Angular dependence of spin-polarization parameter U for electrons scattered from Hg at impact energies (a) 25.0, (b) 35.0, (c) 50.0, (d) 150.0, (e) 260.0, and (f) 500.0 eV. The thick solid (red) lines are the present DRPWA results described in the text; the solid circles are the experimental data from [19]; the dashed curves represent the RDW calculations of McEachran and Stauffer [27].
Download figure:
Standard image High-resolution imageS(θ), T(θ) and U (θ) arise from the interference effect of the direct f (θ) and spin-flip g(θ) amplitudes in equations (7) and (8) respectively and hence they are sensitive to both the spin-dependent and correlation interactions. In our DRPWA approach, S(θ), T(θ) and U (θ), although connected through equation (12), are calculated using separate expressions in (6), (10) and (11). The derived results not only agree satisfactorily with the experimental data but also the sum of their squares for a particular scattering angle at a collision energy is found to be close to unity. The sum for all the scattering angles at 500.0 eV is typically illustrated in figure 10(f), which justifies the validity of our methodology and the scattering potentials used.
Figure 10. The spin-polarization parameter 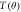 at (a) 25.0, (b) 35.0, (c) 50.0, (d) 150.0, (e) 260.0 and (f) 500.0 eV. The sources of other theoretical and experimental results are same as figure 9.
at (a) 25.0, (b) 35.0, (c) 50.0, (d) 150.0, (e) 260.0 and (f) 500.0 eV. The sources of other theoretical and experimental results are same as figure 9.
Download figure:
Standard image High-resolution image4. Conclusions
We have presented the spin-polarization parameters S, U and T for the elastic e−–Hg scattering over a wide range of scattering angles ( ) and energies (1 eV
) and energies (1 eV 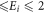 keV) using the proposed DRPWA approach. A complex
keV) using the proposed DRPWA approach. A complex 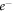 –atom OPM, with the inclusion of static, exchange, polarization and imaginary components, is used to solve the Dirac relativistic equation for obtaining the afore-mentioned observables. The present results of spin-polarization are compared with the available experimental measurements and other theoretical predictions. It is evident from the comparison with the measured values that the present relativistic model is capable of explaining the features of the spin-polarization over a wide range of energies. To the best of our knowledge, the present simple theoretical method is capable of accounting for the spin-polarization data at 42 energy-points reasonably well over a wide energy-range 1 eV
–atom OPM, with the inclusion of static, exchange, polarization and imaginary components, is used to solve the Dirac relativistic equation for obtaining the afore-mentioned observables. The present results of spin-polarization are compared with the available experimental measurements and other theoretical predictions. It is evident from the comparison with the measured values that the present relativistic model is capable of explaining the features of the spin-polarization over a wide range of energies. To the best of our knowledge, the present simple theoretical method is capable of accounting for the spin-polarization data at 42 energy-points reasonably well over a wide energy-range 1 eV 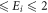 keV. The efficacy of the present collision dynamics, accuracy of the used electron density function and a judicious choice of the OP components seem to contribute to the success of the present study. The success of our present study is expected to be useful in generating accurate spin-asymmetry and other scattering parameters quite easily for other atoms needed for the applied areas.
keV. The efficacy of the present collision dynamics, accuracy of the used electron density function and a judicious choice of the OP components seem to contribute to the success of the present study. The success of our present study is expected to be useful in generating accurate spin-asymmetry and other scattering parameters quite easily for other atoms needed for the applied areas.
Acknowledgments
This work has been partially supported by the TWAS-UNISCO associateship scheme; Faculty of Science project no-32/5/52/UGC/Science-9/2015-16, Rajshahi University, Bangladesh; and Award Number(s) DE-NA0002630, National Nuclear Security Administration (NNSA). M A Uddin is thankful to Bangladesh UGC for appointing him as a UGC Professor.