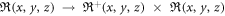T2* phase imaging and processing for brain functional magnetic susceptibility (χ) mapping

T2*-weighted magnetic resonance imaging (T2*MRI) is a widely used brain imaging approach, and produces a complex-valued volume image through the use of a gradient recalled echo (GRE) sequence [1]. For brain functional MRI (fMRI), a GRE-EPI (echo planar imaging) sequence is used to capture brain activity, producing a timeseries of complex-valued T2* images (a 4D complex T2* dataset). Recent research [2–4] shows that both T2* magnitude image and T2* phase image are related to an internal magnetic source distribution (i.e. magnetic susceptibility, denoted by χ), but neither is a faithful representation of the χ-expressed magnetic state, primarily due to the inherent MRI transformations (e.g. dipole effect) imposed on T2* image formation. The brain χ state can be reconstructed by solving an inverse problem of T2*MRI, which has been technically described by a linear model of computed inverse MRI (CIMRI) [2]. In this paper, we examine the insight the T2*MRI and CIMRI models from the perspective of spatial mapping.

The direct source of T2*MRI is an inhomogeneous fieldmap [1, 3]. For brain imaging applications, the intracranial inhomogeneous fieldmap is primarily established by a magnetization process of brain heterogeneous tissues in the main field B₀. We have described the dataflow in T2*MRI by a two-step mapping model [2, 5, 6] from a χ source to a χ-induced fieldmap and finally to a T2* image. Accordingly, we can implement CIMRI by two-step inverse spatial mappings [2]: from a T2* phase image to a fieldmap and to a χ source. In past decades, the efforts on brain χ reconstruction have been described in different terms, such as quantitative susceptibility mapping (QSM) [7–10] and χ tomography [2, 11–13]. In particular, χ tomography is a pertinent description for reproducing an internal χ source from externally observed T2* images by computationally solving an inverse T2* imaging problem [13]. CIMRI is a method (model) for implementing χ tomography.

A task-evoked blood oxygenation level dependent (BOLD) fMRI experiment produces a timeseries of complex T2* images through the use of a GRE-EPI sequence [14, 15]. Conventionally, the functional brain mapping is rendered in the 4D magnitude image dataspace. There also have been reports on functional mapping in the 4D phase image dataspace [16, 17]. Either the magnitude-based or phase-based brain functional mapping both suffer from a certain distortion due to the data transformations inherent with a MRI technology. It is understood that a T2* image (either magnitude or phase) is formed from a χ source after a cascade of MRI transformations, such as dipole-convolved magnetization, proton spin precession, intravoxel average, etc. Consequently, a T2* image bears a dependence of MRI parameters, such as B₀ and T_E. In principle, we can reconstruct the brain χ source by CIMRI, thus removing the MRI parameter dependence. As a result, a reconstructed 4D χ source dataspace enables intrinsic functional χ mapping [5, 6] or functional QSM [18].

Given a 4D image dataset from a BOLD fMRI study, we can perform brain functional analysis by independent component analysis (ICA) [19–22]. ICA is a powerful data-driven blind signal separation technique, which can decompose a spatiotemporal dataset into a number of independent spatial modes and temporal modes (IC timecourses). For a task-evoked 4D dataset, ICA can extract the task-evoked brain functional map in one spatial mode whose IC timecourse maximally correlates with the task timecourse. This is a very useful functional mapping method for an in vivo subject experiment, where the ground truth of brain internal activity is unknown. In this paper, we use ICA to extract a task-evoked functional map from a 4D fMRI dataset and its derivations.

A brain χ state can be reconstructed from a T2* phase image by a linear CIMRI model. In practice, a T2* phase image in a BOLD fMRI dataset always suffers a severe phase unwrapping phenomenon in a manifestation of image contours. Due to the conspicuous morphological alterations, a wrapped phase image is not directly useful. For functional mapping, a complex division algorithm has been proposed to extract the relative phase changes (in relation to a baseline state) for phase-based functional mapping [16, 17]. On the other hand, a phase-wrapped T2* phase image can be unwrapped by analyzing the context of 3D phase contours in a single image without interacting two phase images. There exist various 3D spatial unwrapping algorithms [23–27]. Perhaps the most efficient 3D phase unwrapping can be achieved by a Laplacian technique [28, 29], which has been used for brain phase image processing [5, 30]. In the results, we implement phase unwrapping in the time-domain by a complex division algorithm and in the space domain by a Laplacian unwrapping algorithm. We apply these two phase unwrapping approaches to T2* image processing and compare their effects on brain χ reconstruction and χ-based functional mapping.

T2*MRI serves as the underlying principle and technology of brain MRI data acquisition through the use of a GRE sequence. CIMRI is a computational model for the inverse problem of T2*MRI. Figure 1 provides a diagram of T2*MRI and CIMRI from the perspective of two-step spatial mappings. The T2* phase image processing is the first and most influential stage. In figure 2 we have diagramed two phase image processing techniques for brain χ source reconstructions and ICA-based functional mappings in different dataspaces. In the following discussion, we will address the theory and methods (as diagramed in figures 1 and 2) in more details.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

2.1. Two-step mapping model of T2*MRI

2.1.1. From source $\chi ({\bf{r}})$ to fieldmap $\;b({\bf{r}}):\Re (x,y,z)\;\to \;\Re (x,y,z)$

A complex T2* image is formed by intravoxel spin precession dephasing in an inhomogeneous fieldmap (denoted by b(r)). For brain imaging applications, the underlying source of the fieldmap is mainly the brain χ distribution of intracranial heterogeneous tissues (including static tissue parenchymal and dynamic blood tissue), ignoring electric (or dielectric) sources of brain tissues.

Let χ(r, t) denote a time series of χ-expressed brain activity. Suppose that a χ(r, t) can be decomposed into a static background distribution (denoted by χ₀(r)) and time varying changes (denoted by δχ(r, t)) in an additive way, that is

$$\begin{eqnarray}&&\chi ({\bf{r}},t)={\chi }_{0}({\bf{r}})+\delta \chi ({\bf{r}},t),\end{eqnarray} \tag{ 1 }$$

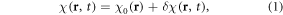
where r = (x, y, z) denotes 3D spatial coordinates, δχ represents a BOLD χ response in a brain activity, which is a small relative susceptibility change between an active state (rich in oxyhemoglobin) and an inactive state (rich in deoxyhemoglobin). Under linear magnetization of brain tissue in B₀, a full χ(r, t) state causes a dynamic fieldmap b(r, t) (the z-component of χ-induced magnetic vector fieldmap), which can be expressed by a 3D convolution at each timepoint t [31–33], that is

$$\begin{eqnarray}&&b({\bf{r}},t)={B}_{0}\chi ({\bf{r}},t){}^{*}\;{h}_{{\rm{dipole}}}({\bf{r}})\\ &&{\rm{with}}\;{h}_{{\rm{dipole}}}({\bf{r}})=\displaystyle \frac{1}{4\pi }\displaystyle \frac{3{z}^{2}-{|{\bf{r}}|}^{2}}{{|{\bf{r}}|}^{5}}\;,\end{eqnarray} \tag{ 2 }$$

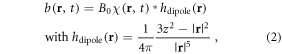
where * denotes a spatial convolution, and h_dipole(r) denotes the point magnetic dipole field, which is called a dipole kernel. It is noted in equation (2) that the χ-induced 3D fieldmap is linearly dependent upon B₀.

At each timepoint, the dipole convolution in equation (2) shows a 3D spatial mapping: from a real-valued 3D χ(r) distribution to a real-valued 3D b(r) distribution, a mapping of ℜ(x, y, z) → ℜ(x, y, z), where ℜ(x, y, z) denotes the set of real numbers defined in 3D space (x, y, z). Since the 3D convolution is a linear transformation, the fieldmap is linearly related to the χ distribution. However, the 3D mapping is a many-to-many spatial mapping due to h_dipole(x, y, z) ≠ δ(x, y, z), resulting in a morphological change of b(r) from χ(r). We refer readers to our previous publications on the dipole effect and h_dipole(r) properties (symmetry, anisotropy, and spatial derivative) [2, 3, 31, 34, 35].

2.1.2. From fieldmap $b({\bf{r}})$ to T2* complex image $C[{\bf{r}}]:$ $\Re (x,y,z)\;\to \;{\Re }^{+}(x,y,z)\;\times \;\Re (x,y,z)$

We describe T2*MRI by a spatial mapping from a continuous fieldmap distribution to a discrete T2* complex image, while suppressing the technical details of MRI frequency encoding and decoding. Fundamentally, a T2* complex image is formed by an intravoxel dephasing formula, as given by [15]

$$\begin{eqnarray}C[{\bf{r}},t;{T}_{{\rm{E}}}] & = & \displaystyle \frac{1}{| {\rm{\Omega }}| }\displaystyle \sum _{{\bf{r}}\text{'}\in {\rm{\Omega }}({\bf{r}})}\;\mathrm{exp}({\rm{i}}\gamma b({\bf{r}}{\boldsymbol{\text{'}}},t){T}_{{\rm{E}}})\\ & & ({\rm{definition}})\\ & = & A[{\bf{r}},t;{T}_{{\rm{E}}}]\mathrm{exp}({\rm{i}}P[{\bf{r}},t;{T}_{{\rm{E}}}])\\ & & ({\rm{polar}}\;{\rm{form}}),\end{eqnarray} \tag{ 3 }$$

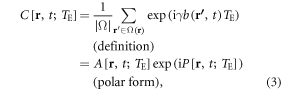
where γ denotes the proton gyromagnetic ratio, Ω(r) denote a voxel at r = (x, y, z), |Ω| the voxel size representing the number of protons inside the voxel, and 1/|Ω| serves as a normalization factor (|Ω| = Σ1). As a convention, we denote a continuous distribution with a parenthesis variable '(r)' and a discrete distribution with a square bracket variable '[r]'. Similarly, [t] denotes a number of snapshot times for a continuous time (t). The echo time T_E is explicitly included in the T2* image to remind us of the T_E dependence.

A proton spin (a spin packet in numerical simulations [3, 36, 37]) in a fieldmap b(r) contributes a trigonometric signal as represented by a complex exponent function, exp(ib(r, t)γT_E). The intravoxel average over numerous spin signals gives rise to a T2* voxel signal, which is a complex number consisting of a pair of magnitude and phase in polar form in equation (3). Therefore, at each timepoint, the intravoxel dephasing formula in equation (3) represents a multivalued spatial mapping from a continuous real-valued 3D b(r) to a pair of discrete real-valued 3D magnitude A[x, y, z] and 3D phase P[x, y, z] in terms of 3D mapping: ℜ(x, y, z) →  ℜ⁺(x, y, z) × ℜ(x, y, z), which ℜ⁺(x, y, z) denotes the set of non-negative real numbers for magnitude representation. It is pointed out that the spatial mapping ℜ(x, y, z) → ℜ⁺(x, y, z) for T2* magnitude imaging is irreversible due to the change in number range. This prevents reconstructing a brain internal fieldmap and χ source from a T2* magnitude image. From the perspective of spatial mapping, the χ reconstruction from phase image implements a 3D mapping of ℜ(x, y, z) → ℜ(x, y, z), which maintains the number range during the data transformation.

2.2. Two-step inverse mapping model of CIMRI

As addressed above, the dataflow from a continuous real χ distribution to a discrete complex T2* image involves two-step spatial mappings. As described in equation (3), a fieldmap value is related to a phase angle in the complex exponential signal; therefore, the fieldmap may be derived from the phase image by a complex logarithm function (an 'inverse' of the complex exponential function). Due to exp(ω + i2πn) = exp(ω) for any integer n, a complex exponential function is not injective, which folds large phase angles in an unbounded interval in ℜ = (−∞, ∞) into numbers in a bounded interval [−π, π). The number range bounding on phase angle values manifests itself as a phase wrapping phenomenon in a measured phase image. A complex logarithm operation cannot restore large phase angles beyond [−π, π). Instead, it only captures a principal value from a complex number as describe by [38]

$$\begin{eqnarray}&&\mathrm{Log}(C)=\;\mathrm{ln}|C|+{\rm{iArg}}(C)\\ &&{\rm{with}}\;{\rm{Arg}}(C)\in [-\pi ,\pi ),\end{eqnarray} \tag{ 4 }$$

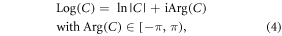
where ln(·) denotes a natural logarithm, Arg(·) a complex argument operation that extracts the principal phase values from an interval $[-\pi ,\pi ),$ and Log(·) a complex logarithm defined by principal values.

In the experiment, T2*MRI produces a pair of raw magnitude (A^raw) and raw phase (P^raw) images as expressed by

$$\begin{eqnarray}\left\{\begin{array}{ll}{A}^{{\rm{raw}}}[{\bf{r}},t;{T}_{{\rm{E}}}]=|C[{\bf{r}},t;{T}_{{\rm{E}}}]| & \in [0,\infty ),\\ {P}^{{\rm{raw}}}[{\bf{r}},t;{T}_{{\rm{E}}}]={\rm{Arg}}(C[{\bf{r}},t;{T}_{{\rm{E}}}]) & \in [-\pi ,\pi ).\end{array}\right.\end{eqnarray} \tag{ 5 }$$

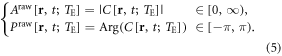
It is seen that the magnitude assumes nonnegative values in ${\Re }^{+}\;=\;[0,\infty )$ and the phase assumes bipolar values in a principal-value range of $[-\pi ,\pi )$ ⊂ ℜ. For magnitude image processing, the raw magnitude images are subject to a normalization by a scaling transformation that rescales the magnitude values such that A[r, t] ∈ [0, 1] ⊂ ℜ⁺.

In complex function theory, the phase can be valued in an arbitrary 2π-interval without a fixed reference (due to exp(i2πn) = 1). In equation (5), a T2* phase signal is conventionally valued in reference to 0, representing clockwise and counterclockwise precessions in reference to the rotating frame. During T2* dephasing for voxel signal formation, when a T2* dephasing angle (on a voxel average) goes beyond $[-\pi ,\pi ),$ it will be folded into the interval $[-\pi ,\pi )$ in the representation of a raw phase image (P^raw ∈$[-\pi ,\pi )),$ called phase wrapping. The effort on unfolding the folded phase values is called phase unwrapping, which restores the phase values in an unbounded range (P^unwrap∈ℜ = (−∞, ∞)).

Since b(r) → P[r] is a many-to-one spatial mapping (a continuous-to-discrete conversion of the spatial average over a voxel), which prevents an inverse spatial mapping (from a discrete distribution to a continuous distribution) in the context of one-to-one correspondence. However, we can reconstruct a discrete fieldmap b[r] from a discrete phase P[r] by a one-to-one mapping on a voxel basis, where b[r] denotes a discrete version of b(r).

Under linear approximation (in a small phase angle regime) [2, 3, 39] of equation (3), we obtain the 1st inverse spatial mapping, from a phase image to a fieldmap, that is

$$\begin{eqnarray}&&b[{\bf{r}}]\approx {b}^{P}[{\bf{r}}]=\displaystyle \frac{P[{\bf{r}};{T}_{{\rm{E}}}]}{\gamma {T}_{{\rm{E}}}},\\ &&{\rm{with}}\;b[{\bf{r}}]\equiv \displaystyle \frac{1}{| {\rm{\Omega }}| }\displaystyle \sum _{{\bf{r}}^{\prime} \in {\rm{\Omega }}({\bf{r}})}b({\bf{r}}{\boldsymbol{^{\prime} }}),\end{eqnarray} \tag{ 6 }$$

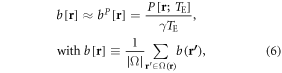
where b^P[r] denotes a phase-derived fieldmap, and b[r] the unknown truth to be inferred. The approximation in equation (6) shows that the voxel phase signal is related to the voxel-averaged field value via a one-to-one mapping with a scale factor (1/(γT_E)), which is a good approximation in small phase angle regime. It is noted that the T_E dependence is removed from the inferred fieldmap in equation (6).

In practice, the simple linear scaling relationship between fieldmap and T2* phase in equation (6) is taken for granted for QSM and χ tomography. For large phase angles (despite being unwrapped), it is a caveat to be aware that the b[r] reconstruction via equation (6) may suffer small errors due to the weak phase nonlinearity [34].

After obtaining b[r] (from an unwrapped T2* phase image in equation (6)), we proceed to implement the 2nd inverse mapping from b[r] to χ[r], which involves a 3D deconvolution problem (dipole inversion) as represented by

$$\begin{eqnarray}&&{\chi }^{{\rm{recon}}}[{\bf{r}}]=\displaystyle \frac{1}{{B}_{0}}b[{\bf{r}}]{\ast }^{-1}{h}_{{\rm{dipole}}}[{\bf{r}}],\end{eqnarray} \tag{ 7 }$$

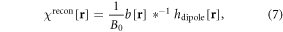
where ∗⁻¹ denotes a 3D deconvolution. It is noted that equation (7) is an inverse of equation (2) in a discrete form. Upon the discrete fieldmap available in equation (6), we can only reconstruct a discrete χ map in equation (7). If B₀ is linearly related to the χ-induced fieldmap in equation (3), here in equation (7) the B₀ dependence can be completely removed from χ^recon.

In past decades, researchers have explored different regularizations to solve the ill-posed dipole inversion problem in equation (7). Typical solutions include truncated inverse filtering (filter truncation regularization) [33, 40], iterative L1-norm or L2-norm regularizations [9, 41–44], and TV-regularized split Bregman iteration (TVB) [2, 11, 31]. Although the anisotropy (orientation dependence) of the 3D dipole kernel dictates a strong orientation effect (dipole effect), an iterative TVB algorithm can reliably (99% reproducibility) reconstruct χ source from a fieldmap acquired at a single angle [45]. The 3D deconvolution (dipole inversion in the 2nd inverse mapping) in equation (7) has been well solved.

In summary, we implement CIMRI by two-step spatial mappings, P[r] → b[r] → χ[r], in a support of discrete domain [r]. A discrete χ[r] source (unknown truth) can be computed as χ^recon[r] in equation (7). Therefore, the quality of phase image has the first and most influence on χ reconstruction. In the following section, we will address the phase image processing aspect for χ reconstruction and χ-based functional mapping.

2.3. Phase image processing of 4D T2* phase images

T2* phase image processing consists of two main aspects: phase unwrapping and background phase removal.

Phase wrapping is a common phenomenon in T2* phase imaging. It may be caused by various factors, such as high field, long echo time, χ jumps at air/tissue interfaces, etc. In principle, the phase wrapping phenomenon can be suppressed (or avoided) in a small phase angle regime $(|P|\ll \pi ).$ In practice, a brain fMRI study always acquires phase-wrapped T2* phase images in large phase angle regime for the gain of signal-to-noise ratio and contrast-to-noise ratio. Consequently, we are confronted with T2* phase wrapping problems.

There exist various 3D phase unwrapping algorithms. Perhaps the most efficient 3D unwrapping algorithm is a Laplacian technique [28, 29], which is an analytic solution that can be computationally implemented in real time. Applied to a 3D T2* phase image, the Laplacian unwrapping algorithm is expressed by [5, 30]

$$\begin{eqnarray}&&{P}^{{\rm{unwrap}}}[{\bf{r}}]={{\rm{FT}}}^{-1}\\ &&\quad \times \left\{\displaystyle \frac{{\rm{FT}}\{\mathrm{cos}\;{P}^{{\rm{raw}}}\cdot {{\rm{FT}}}^{-1}({k}^{2}\cdot {\rm{FT}}(\mathrm{sin}\;{P}^{{\rm{raw}}}))-\;\mathrm{sin}\;{P}^{raw}\cdot {{\rm{FT}}}^{-1}({k}^{{\bf{2}}}\cdot {\rm{FT}}(\mathrm{cos}\;{P}^{{\rm{raw}}}))\}}{{k}^{2}}\right\},\end{eqnarray} \tag{ 8 }$$

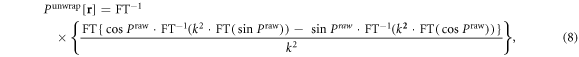
where P^raw denotes the raw T2* phase image, FT the Fourier transform, and FT⁻¹ the inverse Fourier transform, while k = |k| represents the 3D discrete coordinates in the 3D Fourier domain. As a result of phase unwrapping, we obtain an unwrapped phase image that takes on values in an unbounded range. That is, the phase unwrapping extends a distribution in a bounded range, which implements a spatial mapping from P^raw ∈$[-\pi ,\pi )$ ⊂ ℜ to P^unwrap ∈ (−∞, ∞) = ℜ.

Although there are claims that the Laplacian unwrapping algorithm is capable of removing low-pass background [28–30], we find that its background removal is incomplete. We suggest a homodyne high-pass filtering to remove the residual low-pass background, which is expressed by

$$\begin{eqnarray}&&P[{\bf{r}}]={\rm{Arg}}\left(\displaystyle \frac{\mathrm{exp}({\rm{i}}{P}^{{\rm{unwrap}}}[{\bf{r}}])}{{\rm{lowpass}}(\mathrm{exp}({\rm{i}}{P}^{{\rm{unwrap}}}[{\bf{r}}]))}\right),\end{eqnarray} \tag{ 9 }$$

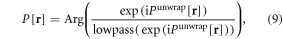
where lowpass(·) denotes a low-pass filtering, which is applied to the complex image exp(iP^unwrap[r]) as constructed from unwrapped phase image with a unit of magnitude. The homodyne high-pass filtering involves a complex division, which exhibits an adaptive phase subtraction that is superior to a conventional high-pass filtering. For a timeseries of phase-wrapped raw phase images, P^raw[r, t], we can repeat the 3D phase unwrapping in equation (8) and background removal in equation (9) for each snapshot time, thus producing a 4D phase dataset P[r, t]. In a distribution of P[r, t] at a snapshot, the uneven background is removed while the structural pattern (high-pass portion) is retained.

On the other hand, we can process a timeseries of raw phase images by a complex division, thus extracting the pure phase changes in the timeseries. The complex division algorithm is expressed by

$$\begin{eqnarray}&&\delta P[{\bf{r}},{t}_{n};{T}_{{\rm{E}}}]={\rm{Arg}}\left(\displaystyle \frac{\mathrm{exp}({\rm{i}}{P}^{{\rm{raw}}}[{\bf{r}},{t}_{n};{T}_{{\rm{E}}}])}{\mathrm{exp}({\rm{i}}{P}^{{\rm{raw}}}[{\bf{r}},{t}_{1};{T}_{{\rm{E}}}])}\right),\quad n\\ &&\quad \quad \quad \quad \quad =\;[\mathrm{1,2},\ldots ,T]\\ &&{\rm{and}}\quad \delta P[{\bf{r}},{t}_{1};{T}_{{\rm{E}}}]=\delta P[{\bf{r}},{t}_{2};{T}_{{\rm{E}}}],\end{eqnarray} \tag{ 10 }$$

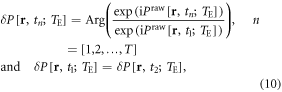
where n denotes the index of discrete time points (T snapshots), P^raw[r, t₁] is selected as a reference at an OFF state (baseline), and the reassignment of δP[r, t₁] is to avoid the zeroing of δP[r, t₁]. It is noted that the complex division in equation (10) involves phase image subtraction at two different timepoints, which may enhance noise in the presence of motion; whereas, the complex division in equation (9) is applied to a single phase image and its low-pass-filtered version, hence homodyne processing. The homodyne high-pass filtering may adaptively remove the uneven background (residual from Laplacian unwrapping processing).

In a similar way as used for deriving equation (6), we have a linear scaling mapping between a phase perturbation δP[r, t] and a fieldmap perturbation δb[r, t], which is

$$\begin{eqnarray}&&\delta b[{\bf{r}},t]\approx \delta {b}^{P}[{\bf{r}},t]=\displaystyle \frac{\delta P[{\bf{r}},t;{T}_{{\rm{E}}}]}{\gamma {T}_{{\rm{E}}}}\\ &&{\rm{with}}\;\delta b[{\bf{r}},t]\equiv \displaystyle \frac{1}{|{\rm{\Omega }}|}\displaystyle \sum _{{\bf{r}}\text{'}\in {\rm{\Omega }}({\bf{r}})}\delta b({\bf{r}}{\boldsymbol{^{\prime} }},t){\rm{.}}\end{eqnarray} \tag{ 11 }$$

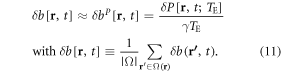
We can then reconstruct a 4D δχ[r, t] dataset from δb[r, t] by a 3D deconvolution (dipole inversion), which is

$$\begin{eqnarray}&&\delta {\chi }^{{\rm{recon}}}[{\bf{r}},t]=\displaystyle \frac{1}{{B}_{0}}\delta b[{\bf{r}},t]{\ast }^{-1}{h}_{{\rm{dipole}}}[{\bf{r}}].\end{eqnarray} \tag{ 12 }$$

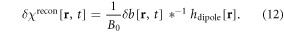
In the result, we obtain a 4D δχ[r, t] dataset that represents the pure BOLD χ responses to external stimuli, excluding the static baseline (the full χ distribution in an OFF state). Meanwhile, we also obtain a 4D χ[r, t] dataset (reconstructed in equation (7) for each timepoint) that represents the full χ distributions (including parenchymal and BOLD response) during the brain activity. It is noted that both δχ[r, t] and χ[r, t] are reconstructed by the same dipole inversion program but with different phase-derived fieldmaps. The differences between χ-based and δχ-based functional mappings are originated from P[r, t] and δP[r, t] during T2* phase processing. Usually, δP[r, t] only assumes a small value range, in a subset of the full value range for P[r, t]. Intuitively, δχ[r, t] is more suitable for brain functional analysis than χ[r, t] due to a more complete removal of the non-functional source (static baseline) in the complex division. We will justify this intuition by ICA with an experimental demonstration as seen below.

2.4. Brain functional mapping by ICA

Upon the reconstruction of 4D δχ[r, t] and χ[r, t] datasets, we can extract the task-evoked functional maps by a spatial ICA method. An ICA decomposes a spatiotemporal dataset into a number of spatial independent modes at different response timecourses. Mathematically, an ICA separates a spatiotemporal dataspace into a spatial space and a temporal space in the form of an outer product. The ICA decomposition of a 4D dataset Λ[r, t] can be expressed by

$$\begin{eqnarray}{\rm{\Lambda }}[{\bf{r}},t] & = & \displaystyle \sum _{n=1}^{N}{{\rm{\Lambda }}}_{n}^{{\rm{ICA}}}[{\bf{r}}]\otimes {{\rm{\Lambda }}}_{n}^{{\rm{ICA}}}[t]\\ {\rm{for}}\;{\rm{\Lambda }} & = & \{ \mbox{`} A\mbox{'}, \mbox{`} P\mbox{'}, \mbox{`} \delta P\mbox{'}, \mbox{`} \chi \mbox{'}, \mbox{`} \delta \chi \mbox{'}\},\end{eqnarray} \tag{ 13 }$$

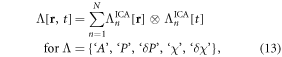
where ⨂ denotes an outer product operator and n = 1, 2, ..., N is the index of the independent component number. Usually, a PCA is performed to compress the time dimension (N < T). An independent spatial mode ${\chi }_{n}^{{\rm{ICA}}}[{\bf{r}}]$ is associated with an independent temporal mode (IC timecourse) ${\chi }_{n}^{{\rm{ICA}}}[t].$ The spatial-temporal separation in equation (13) assumes that there is no spatiotemporal interaction during brain activity.

2.5. Criterion for task-evoked ICA functional mapping

We can sort the decomposed N independent modes in a descending order according to the temporal correlation of the IC timecourse against the task timecourse, as expressed by

$$\begin{eqnarray}&&{{\rm{\Lambda }}}_{n}^{{\rm{tcorr}}}={\rm{tcorr}}({{\rm{\Lambda }}}_{n}^{{\rm{ICA}}}[t],{{\rm{task}}}^{*}[t])\quad {\rm{for}}\\ &&\quad \;\;\;{\rm{\Lambda }}=\{ \mbox{`} A\mbox{'}, \mbox{`} P\mbox{'}, \mbox{`} \delta P\mbox{'}, \mbox{`} \chi \mbox{'}, \mbox{`} \delta \chi \mbox{'}\}\\ &&{\rm{with}}\;{{\rm{task}}}^{*}[t]={\rm{conv}}({\rm{task}}[t],{\rm{hrf}}[t]),\end{eqnarray} \tag{ 14 }$$

where tcorr denotes temporal correlation, task[t] the designed task paradigm, and hrf[t] a canonical hemodynamic response function. For example, we can sort $\{{\chi }_{n}^{{\rm{ICA}}}[{\bf{r}}]\}$ in an order corresponding to ${\chi }_{1}^{{\rm{tcorr}}}\geqslant {\chi }_{2}^{{\rm{tcorr}}}\geqslant \cdot \cdot \cdot \;\geqslant {\chi }_{N}^{{\rm{tcorr}}},$ and sort $\{\delta {\chi }_{n}^{{\rm{ICA}}}[{\bf{r}}]\}$ to $\delta {\chi }_{1}^{{\rm{tcorr}}}\geqslant \delta {\chi }_{2}^{{\rm{tcorr}}}\geqslant \cdot \cdot \cdot \;\geqslant \delta {\chi }_{N}^{{\rm{tcorr}}}.$ In the sorted modes, the 1st spatial mode ${\chi }_{1}^{{\rm{ICA}}}[{\bf{r}}]$ represents the ICA-extracted task-correlated functional map in the 4D χ[r, t] dataspace, and ${\delta \chi }_{1}^{{\rm{ICA}}}[{\bf{r}}]$ represents the functional map in the 4D δχ[r, t] dataspace.

Since the ground truth of brain functional mapping in an in vivo subject experiment is unknown, we consider the 1st independent spatial mode ${{\rm{\Lambda }}}_{1}^{{\rm{ICA}}}[{\bf{r}}]$ as the task-evoked functional map in a 4D dataspace Λ[r, t] because the corresponding IC timecourse ${{\rm{\Lambda }}}_{1}^{{\rm{ICA}}}[t]$ reaches a maximum correlation ${{\rm{\Lambda }}}_{1}^{{\rm{tcorr}}}$ with the task timecourse. To a great extent, we consider ${{\rm{\Lambda }}}_{1}^{{\rm{tcorr}}}$ as a criterion on the performance of ICA functional map extraction. A large ${{\rm{\Lambda }}}_{1}^{{\rm{tcorr}}}$ indicates a better functional extraction. The spatial modes with small ${{\rm{\Lambda }}}_{1}^{{\rm{tcorr}}}$ values are basically interpreted as task-irrelevant functional activities. We are particularly interested to compare the ICA functional maps extracted in reconstructed χ and δχ dataspaces. As will be showed in the results, we observe an inequality $\delta {\chi }_{1}^{{\rm{tcorr}}}$ > ${\chi }_{1}^{{\rm{tcorr}}}$ for which we may infer that the functional map is better extracted in the δχ dataspace than in the χ dataspace.

3.1. 4D T2* data acquisition by a 7T finger tapping experiment

We conducted a human finger tapping BOLD fMRI study on a 7T system to obtain the 4D raw magnitude and phase datasets with the settings of T_R = 3 s, T_E = 29 ms, voxel size = 0.43 × 0.43 × 1.2 mm³, and task[t]: 5 cycles of '5 ON/5 OFF'. The experiment provided a 4D T2* magnitude dataset and a 4D T2* phase dataset (in the form of 234 × 234 × 32 × 50). Figure 3 shows one axial slice (at z₀ = 14.4 mm, a distance from brain top) of a raw magnitude image (in (a)) and a raw phase image (in (c)) at a snapshot. From a 3D magnitude image, we generated a 3D mask (in (b)) and used it to mask out the extracranial air space. The task paradigm is plotted in figure 3(d).

Zoom In Zoom Out Reset image size

All of the magnitude images were rescaled (normalized) to a range of [0, 1] in dimensionless units (denoted by a.u.: arbitrary unit). The raw phase images suffer severe phase wrapping phenomenon (in figure 3(c)), valued in a range of $[-\pi ,\pi )$ in units of radian (rad for short).

3.2. T2* phase processing

First, we unwrapped the wrapped phase images by performing a Laplacian unwrapping algorithm (in equation (8)) at each snapshot time. In figures 4(a) and (b) are shown two unwrapped phase images at an ON and OFF state. It is seen that the unwrapped phase images (in figures 4(a) and (b)) are valued in a range of [−6, 6] rad, which is beyond the bounded range $[-\pi ,\pi )$ for a raw phase image (in figure 3(c)). The Laplacian-unwrapped phase image still bears a spatial slowly-varying background phase, a residual uneven background that was not removed by Laplacian operation.

Zoom In Zoom Out Reset image size

By applying a homodyne high-pass filtering, we obtained a 4D phase dataset P[r, t] (as displayed in figures 4(c) and (d) with a z₀-slice) in which the static high-pass baseline structures (sulci and gyri) were retained. Meanwhile, we performed a complex division algorithm (in equation (10)) and obtained a 4D δP[r, t] dataset (as displayed in figures 4(e) and (f)). It is seen in figure 4 that we cannot perceive the BOLD phase changes between an OFF and ON state, either in P or δP dataspace. A δP image appears as a noise image, with small values (|δP| < 0.5 rad) that are far from unwrapping $(|\delta P|\ll \pi )$ . In this sense, complex division implements phase unwrapping in a time domain. Note there are drastic changes in the phase image patterns and phase image values in figure 4 (displayed with different greyscale bars).

It is seen in figures 4(e) and (f) that the complex-division-derived phase image is quite noisy (as a result of noise enhancement of image subtraction between two similar images). The weak BOLD response signals are buried in the sea of noise. We will extract the weak signals through measurement repetition with a designed task paradigm, which is essentially a time-locked signal average strategy (see below).

3.3. Brain χ reconstruction by CIMRI

Next, we reconstructed brain χ dataset from processed phase dataset by CIMRI.

Specifically, we reconstructed a 4D χ[r, t] dataset from a 4D P[r, t] dataset and a 4D δχ[r, t] dataset from a 4D δP[r, t] by repeating CIMRI for each timepoint. The results are shown in figure 5. It is seen in figures 5(a) and (b) that the reconstructed full χ distributions provide rich information on the brain tissue structure (sulci and gyri); in comparison, in figures 5(c) and (d) the reconstructed δχ distributions appear as noisy images. That is, we cannot obtain the χ-expressed brain structure information from temporally-unwrapped phase images. Again, we cannot discern the subtle differences in the baseline-retained ON/OFF χ states (in figures 5(a) and (b)) or the baseline-removed δχ states (in figures 5(c) and (d)).

Zoom In Zoom Out Reset image size

3.4. ICA on reconstructed brain χ datasets

Finally, we performed ICA on a 4D functional dataset for task-evoked functional mapping. For a number of 50 timepoints (T = 50), we compressed this temporal dimension (from 50 to 16) by PCA. ICA was applied to a 4D dataset in size of 234 × 234 × 32 × 16, producing a number of 16 components (N = 16). The 16 components were sorted in a descending order according to the response-to-task correlation (defined in equation (14)). In the result, the 1st spatial component represents the task-evoked functional map in light of the fact that its IC timecourse maximally correlates with the task timecourse. For purposes of complete comparison, the same PCA and ICA procedures were applied to five 4D datasets, A[r, t], P[[r, t], dP[r, t], χ[r, t] and δχ[r, t]. We were especially concerned with the ICA-extracted functional map and IC timecourse (the 1st pair of independent spatial and temporal modes) from datasets A[r, t], dP[r, t], and δχ[r, t]. The results of comparison are shown in figure 6. Meanwhile, we also display the ICA results from P[r, t] and χ[r, t] in figure 7. The tcorr values in figures 6 and 7 represent the temporal correlations of the ICA-extracted task-evoked response timecourses against the task stimuli timecourse. It is seen in figure 6 that ICA could extract similar response timecourses in the dataspaces {'A', 'δP', 'δχ'}, which are correlated with the task stimuli by a tcorr value of {0.93, 0.90, 0.91} respectively. In comparison, the ICA-extracted response timecourses from the dataspaces {'P', 'χ'} in figure 7 are less correlated with the task stimuli (by a tcorr value of {085, 0.87} respectively).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The behaviors of the ICA-decomposed response timecourses from different datasets are shown in figure 8, in which the maximal task correlations (at 1st timecourse) are magnified in the inset. Quantitatively, the performance of ICA-based functional mapping in a 4D dataspace is numerically characterized by a temporal correlation (tcorr) between the ICA-extracted component timecourse and the task timecourse (as defined in equation (14)). It is seen that, from n = 1 to n = 2, $\delta {\chi }_{n}^{{\rm{tcorr}}}$ exhibits a faster drop than ${\chi }_{n}^{{\rm{tcorr}}}$ does, implying $\delta {\chi }_{1}^{{\rm{tcorr}}}$ extracts a better task-evoked functional map than ${\chi }_{1}^{{\rm{tcorr}}}$ does. We may explain this observation from CIMRI-based χ tomography: CIMRI could produce more accurate δχ[r, t] reconstruction (from δP[r, t]) than χ[r, t] reconstruction (from P[r, t]) because of different degrees in linearity.

Zoom In Zoom Out Reset image size

CIMRI is a linear model of inverse T2*MRI, which was developed to reconstruct a discrete χ distribution from a T2* phase image by two-step inverse mappings. Under linear approximations [3, 34], a T2* phase image is related to a χ source by a cascade of linear data transformation, which enables CIMRI to completely remove the dependence on MRI parameters (such as B₀ and T_E). In practical applications, the χ reconstruction error may be due to various causes: (1) the nonoptimal multichannel phase combination inherent with the off-the-shelf MRI systems; (2) the nonlinearity of T2* phase imaging; (3) data alteration of T2* phase processing (including phase unwrapping and background removal); (4) singularity regularization on ill-posed dipole inversion; (5) tissue dielectric sources, etc. In this paper, we only show the effects of the T2* phase image processing aspects on brain χ reconstruction and χ-based functional mapping.

T2* phase imaging is a very complicated process. In this report, we shed light on the tissue magnetization process and T2* dephasing process for T2* complex image formation. We did not address the multichannel image combination process as widely used in commercial MRI systems. To our understanding, a complex-valued image from a commercial MRI system is optimally reconstructed (through multichannel image combination) for its magnitude but not optimally for its phase [46–51]. The non-optimal multichannel phase image combination lays a bottleneck for χ tomography. We believe that CIMRI-based χ tomography can be improved through more optimal phase imaging in the future.

Motion effect on MR phase imaging is a practical problem (as it also is for magnitude imaging). By packing the subject brain in a head coil with foams (cushions) and plastic tapes, we can minimize the brain motion effect during MRI data acquisition. Given a 4D functional dataset, we can reduce the motion effect by image registration (alignment), which is effectively and efficiently implemented by many existing software package, including SPM. It is noted the 4D phase images are aligned based on the motion parameters derived from 4D magnitude image alignment because the magnitude and phase images are homologous (generated from the same source of χ-induced fieldmap). This is a kind of phase image postprocessing that may improve the quality of dynamic raw phase images in terms of minimal misalignment.

Upon T2* phase acquisition and basic postprocessing (such as alignment), we continue T2* phase image processing in terms of phase unwrapping and background phase removal. Although there are many available phase unwrapping algorithms, the challenge of unwrapping the 3D wrapped T2* phase images accurately and efficiently in all circumstances has not been solved. The Laplacian unwrapping algorithm in equation (8) may be an effective and efficient 3D phase unwrapping algorithm when implemented in real-time. Since a Laplacian operation is capable of eliminating harmonics (in the principle of ∇²e^iϕ(r) = 0), the operation in equation (8) can suppress the harmonic background originating from sources outside the brain region of interest. Therefore, we understand that Laplacian phase unwrapping algorithm can simultaneously achieve phase unwrapping and background removal purposes [5, 30]. To date, the background phase removal has been pursued with different algorithms, such as the projection onto dipole field (PDF) algorithm [52] and the sophisticated harmonic artifact reduction for phase data (SHARP) algorithm [53]. Although these techniques can largely remove background phase, neither is a perfect solution. Specifically, the PDF algorithm is based on a mathematical orthogonal projection theorem that is not fully applicable to MRI signal decomposition (between intra- and extra-cranial regions). The SHARP algorithm is based on spherical mean values (SMV) at local spherical regions (inside the intracranial region), and it is problematic in three aspects: (1) the SMV varies as the sliding sphere changes its size; (2) a signal within a spherical region consists of contributions from both intra- and extra-sphere sources (with the extra-sphere source from extracranial and sphere-excluded intracranial regions), which are not separated in spheres; and (3) its implementation is sophisticated and inefficient. Therefore, we advocate the use of Laplacian technique for effective and efficient phase image processing.

CIMRI is implemented by two inverse spatial mappings: the 1st one is from phase to fieldmap (in equation (6)), and the 2nd one is from fieldmap to χ source (in equation (7)). In our previous publications [3, 34], we have shown the linear scaling mapping in equation (6) only holds true for a linear approximation of intravoxel dephasing signal (in small phase angle regime). In large phase angle regime, our simulations show a nonlinear phase effect on CIMRI [34]. For a 4D T2* image set acquired from a BOLD fMRI experiment, we show that a complex division algorithm can extract a phase perturbation dataset, δP[r, t] in equation (10), which represents the pure phase changes in a BOLD activity (excluding the static baseline signal). Theoretically, the availability of δP[r, t] enables the linear scaling mapping in equation (11) for the reconstruction of the fieldmap perturbation δb[r, t] and subsequently the reconstruction of susceptibility perturbation δχ[r, t]. In other words, a complex division can extract a small portion of phase perturbation from overwhelming nonlinear phase signals (though wrapped) such that we are allowed to reconstruct the corresponding portion of susceptibility perturbation through the use of linear CIMRI model. In fact, the complex division is a signal processing technique that linearizes nonlinear phase signals by extracting local, relatively small changes.

The BOLD response is very small, which only takes on a fraction of signal value (∼5%). As shown in figure 4, we cannot discern the subtle differences between an OFF state and an ON state, either in magnitude or in phase dataspaces. In figure 5, we cannot differentiate an OFF state from an ON state in reconstructed χ or δχ dataspaces either. It is also noted that the BOLD response signals in δP or δχ dataspace are buried in noise. This explains the BOLD response detection through the use of a designed task paradigm and statistic parameter mapping, which is essentially a time-locked (or time-modulated) weak signal detection technique through a paradigm of simulant repetitions.

The complex division algorithm can be considered to be a phase unwrapping algorithm in the time domain [7]. In practice, the phase changes due to a BOLD activity are always very small (typically < 0.5 rad in figure 4) such that the relative phase changes stay far from phase wrapping. Occasionally, a residual phase wrapping effect may be persisted in air/tissue interfaces where there is large jump between tissue χ properties. Furthermore, a slight misalignment among the timeseries images may also cause large phase change, in a manifestation of noise enhancement due to phase subtraction at two different snapshots. In practice, a SPM realignment program (http://fil.ion.ucl.ac.uk/spm/) is always used to register the images in a timeseries, but it cannot completely remove the motion effect (especially the intraframe non-rigid nudges). It is noted that the homodyne high-pass filtering in equation (9) also involves a complex division operation, wherein the noise is not enhanced due to the perfect self-realignment.

The notorious phase unwrapping artifacts can be removed by a 3D spatial unwrapping algorithm. In this paper, we implemented 3D phase unwrapping by a Laplacian unwrapping algorithm, which is claimed to be capable of phase unwrapping and background phase removal simultaneously [28–30]. In our experience, the Laplacian unwrapping algorithm cannot completely remove the slowly-varying background (see figures 4(a) and (b)). We suggest a homodyne high-pass filtering to remove the residual artifacts of the phase background. Due to the adaptiveness of complex division in equation (9), the homodyne filtering can remove the uneven low-pass background more effectively than the conventional high-pass filtering. We also need to mention that the combination of Laplacian unwrapping and homodyne filtering is a more powerful method for T2* phase image processing than the conventional homodyne processing. In this report, we did not examine the accuracy of the Laplacian unwrapping algorithms. Toward clinical applications, the Laplacian unwrapping algorithm should be validated and calibrated through numerical simulations and phantom tests in the future.

From a discrete phase image, we can only reconstruct a discrete χ source distribution by CIMRI. The difference between a continuous distribution and a discrete distribution decreases as the spatial resolution increases (voxel size decreases), as governed by spatial sampling theory. It has been observed (by numerical simulations) that a higher spatial resolution will cause more severe phase wrapping and turbulence [37, 54]. The phase wrapping of a T2* voxel signal is a catastrophic nonlinear behavior, which is attributed to the vector sum of trigonometric spin signals within a voxel [55]. The vector sum (or complex addition) itself is a linear operation. However, the phase calculation from a vector-summed complex number is a nonlinear operation [34]. Consequently, a T2* phase imaging is in general a nonlinear function of the fieldmap and χ source. In a special case of small phase angle regime, T2* imaging exhibits a linear mapping from a χ source. This special condition is very well satisfied when reconstructing a fieldmap perturbation from a temporal phase perturbations (δP). Therefore, we can reconstruct the pure BOLD χ response (δχ) from a complex-division-derived phase changes using the linear CIMRI model.

For an in vivo subject experiment, again, we do not know the ground truth of brain internal magnetic state. The trustworthiness of the reconstruction of brain χ distribution is critically dependent upon numerical simulations and phantom verifications of CIMRI model [2, 31, 39]. Currently, a tissue-equivalent dynamic χ phantom is not available for brain fMRI calibration (note that an electric phantom provides a dynamic electric source, but not a dynamic χ source); therefore the brain functional χ mapping is not verifiable by phantom testing. Nevertheless, we may understand the brain functions from a 4D functional dataset by a model-free ICA. It is known that ICA can only decompose a linearly mixed signal into a number of independent components without the knowledge about the signal mixing. For a task-evoked spatiotemporal dataset, ICA can decompose it into a number of independent spatial modes and temporal modes (IC timecourses). A spatial mode is interpreted as a constituent of brain activity based on its IC timecourse behavior. In particular, the spatial mode whose IC timecourse maximally correlates with the task timecourse is interpreted as the task-evoked functional map. Based on this assumption, we compare the ICA functional mappings χ and δχ dataspaces. Our results show that an ICA-extracted functional map from δχ dataspace has a stronger response than from χ dataspace, as indicated by $\delta {\chi }_{1}^{{\rm{tcorr}}}$ = 0.91 > ${\chi }_{1}^{{\rm{tcorr}}}=0.85.$ The other decomposed spatial modes are interpreted as task-irrelevant brain activities (including physiological oscillations, motion effect, and mechanical vibrations). For the inferiority of ICA decomposition in χ dataspace, one cause may be due to the nonlinearity in the P[r] → b[r] mapping in equation (6) with large phase angles [34]; another cause may be due to inaccurate background removal in T2* phase processing by the Laplacian unwrapping algorithm.

From the observation ${A}_{1}^{{\rm{tcorr}}}$ > $\delta {\chi }_{1}^{{\rm{tcorr}}}$ and ${A}_{1}^{{\rm{tcorr}}}$ > $\delta {P}_{1}^{{\rm{tcorr}}}$ in figure 8, we may conclude that ICA exhibits the best performance of task-evoked functional map extraction in magnitude dataspace. Nevertheless, from the perspective of T2* imaging, we understand that neither the T2* magnitude nor the T2* phase can faithfully represent the brain magnetic source due to the intervention of MRI technology. The inferiority of ICA functional map extraction in δχ dataspace may be attributed to the following aspects: (1) the neglect of a tissue dielectric source may cause a spatial artifact in δχ reconstruction (the dielectric source is reconstructed as a susceptibility-equivalent artificial pattern) and (2) the nonlinear transformations associated with magnitude signals may modify the statistical inter-independencies in the factor of ICA functional map extraction in magnitude dataspace. These speculations deserve further investigation in the future.

A T2* phase image is formed by intravoxel spin precession dephasing in an inhomogeneous fieldmap. This imaging process can be described by a 3D spatial mapping (ℜ(x, y, z) → (ℜ(x, y, z)). Due to a complex logarithm operation and a continuous-to-discrete conversion, the fieldmap-to-phase mapping exhibits phase wrapping and trigonometric nonlinearity in the large phase angle regime. Based on a two-step mapping model of T2*MRI (not restricted to linear mappings), we developed a linear CIMRI model to reconstruct the χ source distribution from a T2* phase image by two inverse mappings. The 1st inverse mapping is from T2* phase to fieldmap, which assumes a linear scaling one-to-one correspondence in small phase angle regime. This stage requires phase unwrapping and background removal. The 2nd inverse mapping is from fieldmap to χ source, which involves a 3D deconvolution (dipole inversion). By repeating CIMRI for χ source reconstruction at each timepoint, we obtain a 4D χ dataset from a 4D T2* phase dataset. Finally we render an ICA on a 4D dataset for functional analysis, thus implementing brain functional mapping without the knowledge of in vivo brain activity. In particular, we extract a task-evoked functional map in an independent spatial mode whose response timecourse maximally correlates with the task timecourse.

For T2* phase image processing, we report on two phase unwrapping methods. One is 3D phase unwrapping in space domain, which can be implemented efficiently by a Laplacian unwrapping technique. Upon an unwrapped phase image, we remove the residual uneven background using a homodyne high-pass image processing. Another phase unwrapping method is rendered in the time domain by a complex division, which is applicable to a 4D phase dataset. The complex division extracts relative phase changes in reference to a baseline. The small phase changes stay in phase-unwrapped distributions, which enable the linear scaling mapping between phase and fieldmap, thus facilitating the subsequent χ reconstruction by a linear CIMRI model.

In conclusion, for brain functional χ mapping, the complex division algorithm is a useful T2* phase image processing. It implements phase unwrapping (in time domain), background phase (baseline) removal, and linear phase-to-fieldmap mapping simultaneously. However, it enhances noises due to phase subtraction between two snapshots, and it fails to provide a full χ-expressed brain magnetic state. In comparison, spatially phase unwrapping processing may provide brain χ states at a certain loss of χ reconstruction accuracy due to a compromise of CIMRI linearity.

The authors thank Jennifer Robinson at The Auburn University for providing the 7T experimental data. The authors would like to acknowledge the funding support of NIHP20GM103472.

ℜ(x, y, z): a set of real numbers for values defined in 3D spatial domain (x, y, z); ℜ⁺(x, y, z): a set of nonnegative real numbers for values defined in 3D spatial domain (x, y, z); → : a mathematical mapping (or correspondence) notation to denote a data transformation; (r) = (x, y, z): continuous 3D spatial coordinate variables for a continuous 3D distribution, such as continuous χ(x, y, z) and b(x, y, z); [r] = x, y, z]: a discrete spatial coordinate index for a discrete three-dimensional array (matrix), such as χ[x, y, z] and P[x, y, z]; [r, t] = [x, y, z, t]: discrete 4D spatiotemporal variables; [r, t; T_E]: discrete 4D spatiotemporal variables with an auxiliary variable T_E.

A: magnitude (or amplitude) (normalized in [0, 1]); A^raw: raw magnitude data from MRI system ; P: phase (unwrapped); P^raw: raw phase data from MRI system (usually wrapped); P^unwrap: unwrapped phase image (generated by applying a phase unwrapping algorithm to raw (wrapped) phase image); δP: relative phase change in relative to a baseline; χ: magnetic susceptibility; δχ: relative χ change in relative to a baseline; a.u: arbitrary unit (dimensionless) for magnitude data; rad: radian for phase data; ppm: parts per million (=10 × 10⁻⁶), dimensionless unit for χ.

BOLD: blood oxygenation level dependent; fMRI: functional magnetic resonance imaging; T2*MRI: T2-weighted MRI; CIMRI: computed inverse MRI; tcorr: temporal correlation (or task correlation); ICA: independent component analysis; T_E: echo time; T_R: repetition time; Ω(r): voxel space at r; |Ω|: voxel size, it may denote either the number of proton spins (or spin packets) inside a voxel or the physical dimension of voxel space.