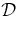ABSTRACT
This Letter presents the first theoretical study of the dynamics of a coronal mass ejection (CME) observed by STEREO-A/B. The CME was continuously tracked by SECCHI-A, providing position-time data from eruption to 1 AU. The ejecta was intersected by STEREO-B at 1 AU, where the magnetic field and plasma parameters were measured. The observed CME trajectory and the evolution of the CME magnetic field are modeled using the semianalytic erupting flux-rope model. It is shown that the best-fit theoretical solution is in good agreement—within 1% of the measured CME trajectory in the 1 AU field of view—and is consistent with the in situ magnetic field and plasma data at 1 AU.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Following their first observation by a space-borne coronagraph (Tousey 1973), coronal mass ejections (CMEs) have received extensive scientific attention (e.g., Gosling et al. 1974; Howard et al. 1985; Hundhausen 1999). It is now understood that it is the magnetic field of CME ejecta impinging on Earth's magnetosphere that drives severe disturbances in the geospace plasma environment. Two major issues in solar–terrestrial physics are (1) the nature of the forces responsible for CME acceleration and subsequent propagation through the interplanetary medium and (2) the evolution of the magnetic field of a CME. We address these questions using both a theoretical model and data from the twin Solar Terrestrial Relations Observatory (STEREO) spacecraft.
Theoretical work in conjunction with observations from Large Angle and Spectrometric Coronagraph (LASCO) has shown that CMEs can be explained, both morphologically and quantitatively, as erupting flux ropes (Chen et al. 1997, 2000) as opposed to cone-like shell structures with rotational symmetry (Hundhausen 1999). Among theoretical models, the erupting flux-rope (EFR) model of Chen (1996) has been most extensively tested and validated using LASCO data (e.g., Wood et al. 1999; Krall et al. 2001). In this ideal magnetohydrodynamic (MHD) model, the CME dynamics and the magnetic field evolution are determined by a set of coupled equations representing the toroidal hoop force with momentum coupling to the ambient solar wind (SW) via drag (Chen 1989). Beyond the LASCO field of view (FOV), the dynamics of CMEs observed by the Solar Mass Ejection Imager have been found to be consistent with the continued driving by the hoop force competing with the drag force as predicted by the EFR model (Howard et al. 2007).
It has been conjectured that a CME ejecta is manifested as a magnetic cloud (MC) at 1 AU and beyond (Burlaga et al. 1981). Theoretically, the EFR model shows that a flux rope exhibiting CME-like dynamics evolves into an MC-like structure (Chen 1996; Krall et al. 2006). Numerical simulations of flux-rope CMEs in 2.5 and 3 dimensions also show similar structures at 1 AU (e.g., Wu et al. 1999; Manchester et al. 2004). No model, however, has been directly tested against the observed evolution of CMEs and their magnetic fields due to the absence of observation. The STEREO mission provides for the first time the ability to observe, with spatial and temporal continuity, a CME from the Sun to 1 AU and measure the magnetic field and plasma properties of the ejecta.
In this Letter, we present the first quantitative comparison of theory with the observed dynamics of a CME and the in situ magnetic field of the ejecta at 1 AU. We find that (1) the best-fit solution is in good agreement—within 1% of the data—with the measured CME position throughout the 1 AU STEREO-A FOV and (2) the model CME evolves under ideal MHD into an MC-like structure that is consistent with the in situ magnetometer and plasma data measured by STEREO-B.
2. STEREO OBSERVATION AND DATA
The CME was observed on 2007 December 24 off the east limb near the equator (∼N4°) by the Sun–Earth Connection Coronal and Heliospheric Investigation (SECCHI) instruments (Howard et al. 2008) on board STEREO-A. Neither EUVI-A nor EUVI-B images revealed activities identifiable as the source on the disk. In SECCHI-A, the CME exhibited the typical flux-rope morphology with the toroidal axis inclined relative to the ecliptic (e.g., Chen et al. 2000). This is illustrated in Figure 1, with a dot ("Obs") marking STEREO-B. In the FOV of COR2-B, a faint nearly symmetric halo CME was observed. We tracked the leading edge (LE) of the CME through the SECCHI-A FOV (COR1, COR2, HI1, and HI2).
Figure 1. Geometry and coordinates of the model flux rope relative to STEREO-A. STEREO-B is indicated by "Obs," the dot just inside the LE. One leg of the flux rope is illustrated. The toroidal current Jt localized to the shaded current channel points into the figure, and V represents the velocity of the centroid of the flux rope. The flux surfaces are shifted (by the so-called Shafranov shift) because of the nonuniform force. The Radial-Tangential-Normal (RTN) coordinates are shown.
Download figure:
Standard image High-resolution imageThe HI2-A images show that the LE of the CME reached the projected position of STEREO-B on December 29 at ∼2300 UT, approximately coinciding with the detection of the CME ejecta by IMPACT (Acuña et al. 2008) and PLASTIC (Galvin et al. 2008) on STEREO-B. Combined with the halo in COR2-B, we assume that the apex of the CME propagated along the radial direction at latitude 4°N and longitude 44°E in the FOV of SECCHI-A, the angular separation between the twin spacecraft. The measured elongation is converted to the "true" heliocentric position 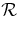 using N4° and E44°. The SECCHI-A data for the LE position are plotted in Figure 2 (diamonds and circles).
using N4° and E44°. The SECCHI-A data for the LE position are plotted in Figure 2 (diamonds and circles).
Figure 2. CME of 2007 December 24. SECCHI-A data (diamonds and circles). Solid curves are given by the best-fit theoretical solution, which has 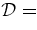 0.68. (a) Position of the LE. The error bars are uniformly set to 1%. (b) Initial dynamics in COR1 and COR2, (c) LE speed, and (d) LE acceleration. The dashed curve is dΦp(t)/dt scaled to the peak of the acceleration curve.
0.68. (a) Position of the LE. The error bars are uniformly set to 1%. (b) Initial dynamics in COR1 and COR2, (c) LE speed, and (d) LE acceleration. The dashed curve is dΦp(t)/dt scaled to the peak of the acceleration curve.
Download figure:
Standard image High-resolution imageFigure 3(a) shows the magnetometer data from IMPACT on STEREO-B in the Radial-Tangential-Normal (RTN) coordinates (Figure 1): BR (green), BT (blue), BN (magenta), and the magnitude Btot ≡ (B2R + B2T + B2N)1/2 (red), where +R points from the Sun to STEREO-B and the R–N plane contains the solar rotation axis. The original 125 ms data have been averaged over 3 minutes. The maximum value of Btot is 12.0 nT. We show in black the rotation angle in the plane of the sky, θ ≡ sin−1(BN/B) (scaled to fit the plot), where B ≡ (B2T + B2N)1/2. The two vertical lines show the extrema of θ, indicating the beginning and ending of the magnetic field rotation (Burlaga et al. 1981). The SW plasma data from PLASTIC/STEREO-B show that the proton temperature was Tp≃ (3–4) ×104 K between the extrema of θ (the ejecta) and was higher at Tp ≃ 6 × 104 K outside. The SW density was mostly 5–10 cm−3 during the period shown but was 2–5 cm−3 immediately ahead of the leading θ extremum. We conclude that the ejecta between the two vertical lines was an MC according to the criteria of Burlaga et al. (1981). The speed of the MC was approximately 340 km s−1 at maximum Btot. The fact that Btot decreases slowly behind the MC suggests that the trailing edge deviated significantly from a simple flux rope.
Figure 3. Magnetic field of the ejecta at 1 AU. (a) IMPACT/STEREO-B data (3 minute average) in RTN coordinates. BR (green), BT (blue), and BN (magenta). θ = sin−1(BN/B) is the rotation angle in the plane of the sky, scaled to fit the plot. (The actual value in radians has been multiplied by 5.) The vertical lines designate the leading and trailing edges of the MC characterized by rotation in θ(t). The observed maximum field: Btot= 12.0 nT. (b) The field of the model ejecta at 1 AU. No ambient SW field is included. Solid red curve: Btot with the flux-rope axis perpendicular to the Sun-Obs line. Solid black curve: θ(t), scaled in the same way as in panel (a). The assumed geometry is given in Figure 1 except that the observer is taken to intersect the toroidal axis. Dashed curves: Btot and θ if the observer intersects the flux-rope axis at 55°. A magnetic cloud as defined by Burlaga et al. (1981) corresponds to the current channel (Chen 1996). The flux rope includes the poloidal field beyond the extrema in θ, but the Shafranov shift (Figure 1) is neglected.
Download figure:
Standard image High-resolution image3. BEST-FIT THEORETICAL SOLUTION
In this work, the measured LE position 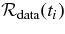 is used as the observational input to the EFR model, and the best-fit solution provides the model output. Here, ti is the measurement time.
is used as the observational input to the EFR model, and the best-fit solution provides the model output. Here, ti is the measurement time.
The average deviation of a solution  from the data relative to the error bars is given by
from the data relative to the error bars is given by 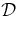 (Chen & Kunkel 2010)
(Chen & Kunkel 2010)
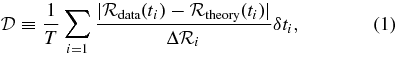
where T = ∑iδti, 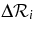 is the error bar at ti, and δti = ti+1 − ti. For this event, we use
is the error bar at ti, and δti = ti+1 − ti. For this event, we use 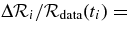 0.01 (1% error) for all i, consistent with the typical measurement uncertainties.
0.01 (1% error) for all i, consistent with the typical measurement uncertainties.
To find a solution, the initial flux-rope geometry is specified by the centroid height of the apex Z0, footpoint separation Sf, and minor radius a0 of the current channel of the flux rope. We use 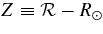 to denote the height measured from the photosphere. The model corona is given by pressure pc(Z) and density nc(Z), where pc(Z) = 2nc(Z)kTc(Z) and k is Boltzmann's constant. The overlying coronal field perpendicular to the flux rope is Bc(Z). To initialize a flux rope, we specify Sf, Z0, and Bc0 = Bc(Z0) with pc0 = pc(Z0) and nc0 = nc(Z0) given by the model corona. The requirement that the initial flux rope be in equilibrium—d2Z/dt2 = 0 and d2a/dt2 = 0—then yields the initial magnetic field, Bpa0 and
to denote the height measured from the photosphere. The model corona is given by pressure pc(Z) and density nc(Z), where pc(Z) = 2nc(Z)kTc(Z) and k is Boltzmann's constant. The overlying coronal field perpendicular to the flux rope is Bc(Z). To initialize a flux rope, we specify Sf, Z0, and Bc0 = Bc(Z0) with pc0 = pc(Z0) and nc0 = nc(Z0) given by the model corona. The requirement that the initial flux rope be in equilibrium—d2Z/dt2 = 0 and d2a/dt2 = 0—then yields the initial magnetic field, Bpa0 and  at Z0, where Bpa ≡ Bp(r = a) and
at Z0, where Bpa ≡ Bp(r = a) and 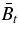 refer to the poloidal and average toroidal components of the flux-rope magnetic field. The EFR model evolves Bpa(t) and
refer to the poloidal and average toroidal components of the flux-rope magnetic field. The EFR model evolves Bpa(t) and 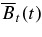 according to Bpa(t) = 2It/ca(t) and
according to Bpa(t) = 2It/ca(t) and 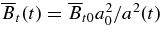 .
.
The momentum of the flux rope is coupled via drag to the model ambient medium. The drag coefficient is taken to be cd= 1, but cd in the range of 1–3 yields comparable solutions. The SW speed is smoothly increased to its asymptotic value V*sw ≡ Vc(Z → ∞) at about 25 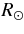 with V*sw treated as an adjustable parameter. The coronal and SW speed, density, and temperature—Vc(Z), nc(Z), and Tc(Z)—are specified according to empirical models. The above corona-SW model has not been altered from the original formulation (Chen 1996). The drag force term, however, has been improved (Chen & Kunkel 2010, Section 2.1)
with V*sw treated as an adjustable parameter. The coronal and SW speed, density, and temperature—Vc(Z), nc(Z), and Tc(Z)—are specified according to empirical models. The above corona-SW model has not been altered from the original formulation (Chen 1996). The drag force term, however, has been improved (Chen & Kunkel 2010, Section 2.1)
The initial flux rope is set into motion by increasing the poloidal flux Φp according to dΦp(t)/dt. For each set of initial values, this function is adjusted to obtain the solution that minimizes 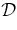 , and the initial values can be varied to obtain a range of solutions. The overall best-fit solution is given by the smallest
, and the initial values can be varied to obtain a range of solutions. The overall best-fit solution is given by the smallest 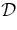 . The properties of the solution—Z(t) and a(t)—including Sf dΦp(t)/dt, and Bpa(t) and
. The properties of the solution—Z(t) and a(t)—including Sf dΦp(t)/dt, and Bpa(t) and 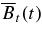 are the model predictions constrained by
are the model predictions constrained by 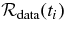 .
.
4. THEORY-DATA COMPARISON
In relating the solution to observation, we make the identification that the outermost flux surface of the flux rope at  is the CME LE position (Chen et al. 1997; Krall et al. 2001). Table 1 gives several representative minimum-
is the CME LE position (Chen et al. 1997; Krall et al. 2001). Table 1 gives several representative minimum-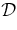 solutions and their predicted physical properties. Solution 1 provides the overall best fit and is shown in Figure 2(a) (solid curve), with the initial segment shown in Figures 2(b)–(d) (solid curves). Panels (b) and (c) show that there is a small-amplitude first-order oscillation. The acceleration of the LE and the predicted dΦp(t)/dt (dashed curve) are shown in panel (d). Two representative error bars in speed (1% in position) are shown. The acceleration after the main acceleration phase is due to the increasing ambient SW speed imparting momentum to the flux rope via drag. This solution has
solutions and their predicted physical properties. Solution 1 provides the overall best fit and is shown in Figure 2(a) (solid curve), with the initial segment shown in Figures 2(b)–(d) (solid curves). Panels (b) and (c) show that there is a small-amplitude first-order oscillation. The acceleration of the LE and the predicted dΦp(t)/dt (dashed curve) are shown in panel (d). Two representative error bars in speed (1% in position) are shown. The acceleration after the main acceleration phase is due to the increasing ambient SW speed imparting momentum to the flux rope via drag. This solution has 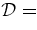 0.68, i.e., the average deviation from the data is 0.68% in the 1 AU FOV. This demonstrates that the EFR equations correctly capture the physics of the macroscopic forces acting on CMEs.
0.68, i.e., the average deviation from the data is 0.68% in the 1 AU FOV. This demonstrates that the EFR equations correctly capture the physics of the macroscopic forces acting on CMEs.
Table 1. Output Quantities of Minimum-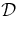 Solutionsa
Solutionsa
| No. | 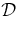 |
Sf | α0 | MTb | 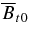 b b |
ΔTp | (dΦp/dt)max | V*sw | B1AUc | 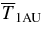 c c |
|---|---|---|---|---|---|---|---|---|---|---|
| (105 km) | (G) | (1015 g) | (G) | (minutes) | (1018 Mx s−1) | (km s−1) | (nT) | (104 K) | ||
| 1d | 0.68 | 1.8 | 1.8 | 3.3 | 2.39 | 70 | 1.0 | 441 | 11.8 | 4.30 |
| 2 | 1.10 | 1.5 | 2.0 | 1.7 | 2.41 | 66 | 0.9 | 418 | 11.9 | 4.25 |
| 3 | 1.28 | 2.5 | 2.0 | 7.3 | 2.60 | 68 | 1.4 | 486 | 12.0 | 4.38 |
| 4 | 0.80 | 1.8 | 1.6 | 4.2 | 2.32 | 70 | 1.1 | 442 | 11.8 | 4.31 |
| 5 | 0.79 | 1.8 | 2.0 | 2.7 | 2.46 | 68 | 1.0 | 441 | 11.9 | 4.28 |
| 6e | 0.78 | 1.8 | 2.0 | 3.3 | 2.63 | 64 | 1.1 | 441 | 12.3 | 4.26 |
| 7f | 0.72 | 1.8 | 1.8 | 3.3 | 3.31 | 72 | 1.1 | 440 | 13.6 | 4.16 |
| 8g | 0.71 | 1.8 | 1.8 | 3.3 | 2.39 | 70 | 1.0 | 442 | 12.6 | 6.52 |
Notes.
aFor each solution, Sf and α0 are specified initial values. V*sw and dΦp(t)/dt are varied to minimize 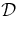 . Z0 = 8 × 104 km is estimated from the data.
. Z0 = 8 × 104 km is estimated from the data. 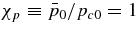 ,
, 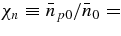 0.6, Bc0=−1 G, and cd= 1 are used for all solutions except as noted for solutions 6 and 7. The equality
0.6, Bc0=−1 G, and cd= 1 are used for all solutions except as noted for solutions 6 and 7. The equality 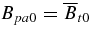 results from χp = 1. Here, subscript "0" refers to initial quantities.
bCalculated using the equilibrium force-balance conditions; see Chen (1996).
cB1AU is the field strength on the flux-rope axis.
results from χp = 1. Here, subscript "0" refers to initial quantities.
bCalculated using the equilibrium force-balance conditions; see Chen (1996).
cB1AU is the field strength on the flux-rope axis. 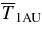 is the average temperature in the flux rope. Tsw ≃ 6.8 × 104 K in the ambient SW. T0= 1 MK at the initial height Z0.
dTotal poloidal energy injected is ΔUp = 2.0 × 1031 erg. Use ΔUp ∝ (dΦp/dt)2maxΔTp to scale to other solutions.
eχn = 1.0.
fBc0 = −1.5 G.
gThe model coronal temperature at Z0 is set to T0 = 1.5 × 106 K. The initial structure is the same as for solution 1. The calculated 1 AU flux-rope density is
is the average temperature in the flux rope. Tsw ≃ 6.8 × 104 K in the ambient SW. T0= 1 MK at the initial height Z0.
dTotal poloidal energy injected is ΔUp = 2.0 × 1031 erg. Use ΔUp ∝ (dΦp/dt)2maxΔTp to scale to other solutions.
eχn = 1.0.
fBc0 = −1.5 G.
gThe model coronal temperature at Z0 is set to T0 = 1.5 × 106 K. The initial structure is the same as for solution 1. The calculated 1 AU flux-rope density is 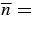 5.7 cm−3, with nsw = 5.2 cm−3.
5.7 cm−3, with nsw = 5.2 cm−3.
Download table as: ASCIITypeset image
We have varied Sf and α0 ≡ R0/a0, where R0 is the initial major radius calculated from Sf and Z0 (Chen 1996), and obtained several minimum-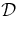 solutions (Table 1). Solutions 2 and 3 bracket Sf = 1.8 × 105 km, showing solution 1 yields a significantly better fit. Solutions 4 and 5 show influence of the aspect ratio α0. We have also varied two selected ambient coronal parameters (solutions 6 and 7) as indicated in Table 1. The value of V*sw required to minimize
solutions (Table 1). Solutions 2 and 3 bracket Sf = 1.8 × 105 km, showing solution 1 yields a significantly better fit. Solutions 4 and 5 show influence of the aspect ratio α0. We have also varied two selected ambient coronal parameters (solutions 6 and 7) as indicated in Table 1. The value of V*sw required to minimize 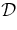 is in the range of V*sw= 440 km s−1, except for solutions 2 and 3 with significantly greater values of
is in the range of V*sw= 440 km s−1, except for solutions 2 and 3 with significantly greater values of 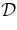 . Solutions with
. Solutions with 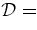 0.6–0.8 are nearly indistinguishable in appearance. For each solution, the predicted dΦp(t)/dt is characterized by its peak value and the FWHM duration ΔTp. For solution 1, the initial flux rope has Φp0 = 1.9 × 1020 Mx and Φt0 = 4.0 × 1020 Mx, with a total of ΔΦp = 4.8 × 1021 Mx injected.
0.6–0.8 are nearly indistinguishable in appearance. For each solution, the predicted dΦp(t)/dt is characterized by its peak value and the FWHM duration ΔTp. For solution 1, the initial flux rope has Φp0 = 1.9 × 1020 Mx and Φt0 = 4.0 × 1020 Mx, with a total of ΔΦp = 4.8 × 1021 Mx injected.
The centroid of the flux rope given by solution 1 reaches 1 AU with V≃ 330 km s−1 and a temperature of 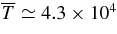 K while the model SW has Tc ≃ 6.8 × 104 K at 1 AU. The density is ∼5 cm−3 for both the flux rope and model SW. These values, obtained as the predictions of the model with no reference to any SW data, are consistent with the PLASTIC data discussed above. Here, we have taken the ambient coronal temperature at the initial apex height (Z0) to be T0 = 1 × 106 K, and an adiabatic energy equation is assumed with γ≃ 1.2. Note that the model uses a profile of the form
K while the model SW has Tc ≃ 6.8 × 104 K at 1 AU. The density is ∼5 cm−3 for both the flux rope and model SW. These values, obtained as the predictions of the model with no reference to any SW data, are consistent with the PLASTIC data discussed above. Here, we have taken the ambient coronal temperature at the initial apex height (Z0) to be T0 = 1 × 106 K, and an adiabatic energy equation is assumed with γ≃ 1.2. Note that the model uses a profile of the form 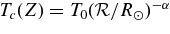 (recall
(recall 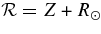 ) so that the SW temperature at 1 AU directly scales with T0. If we choose T0 = 1.5 × 106 K for the initial flux rope of solution 1, we obtain
) so that the SW temperature at 1 AU directly scales with T0. If we choose T0 = 1.5 × 106 K for the initial flux rope of solution 1, we obtain 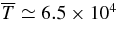 K and Tc ≃ 105 K (solution 8).
K and Tc ≃ 105 K (solution 8).
The best-fit Bpa and  for this solution (Table 1) can be used to construct a field profile—Bp(r) and Bt(r). We use the non-force-free model of Chen (1996) for this purpose. Figure 3(b) shows the magnitude Btot (red solid curve) and the rotation angle θ (black solid curve) of the model as would be measured by a stationary observer at 1 AU based on the simplified geometry in Figure 1. In constructing the synthetic field, the expansion of the minor radius a(t) during the observation is accounted for, but no distortion, major radial curvature, or ambient SW magnetic field is included. The individual components of B(t) depend on the flux-rope orientation. Because it is not possible to unambiguously reconstruct the actual CME magnetic field in three dimensions, we use physical properties of the field that can be calculated without a detailed knowledge of the flux-rope orientation: the maximum value of Btot and the extrema of the rotation angle (θ) of the field. The model field has a maximum value of Btot= 11.8 nT, which is consistent with 12.0 nT indicated by the data. This is the lower bound because STEREO-B did not necessarily pass through the center of the MC. The temporal profiles of Btot(t) and θ(t) do depend on the angle between the flux-rope axis and the observer path through the structure. The solid curves in Figure 3(b) assume that the observer intersects the flux rope perpendicularly to the axis of symmetry. If the same field is measured at an intersection angle of 55°, the profiles represented by dashed curves in Figure 3(b) result, which provide a better fit to the IMPACT magnetometer data.
for this solution (Table 1) can be used to construct a field profile—Bp(r) and Bt(r). We use the non-force-free model of Chen (1996) for this purpose. Figure 3(b) shows the magnitude Btot (red solid curve) and the rotation angle θ (black solid curve) of the model as would be measured by a stationary observer at 1 AU based on the simplified geometry in Figure 1. In constructing the synthetic field, the expansion of the minor radius a(t) during the observation is accounted for, but no distortion, major radial curvature, or ambient SW magnetic field is included. The individual components of B(t) depend on the flux-rope orientation. Because it is not possible to unambiguously reconstruct the actual CME magnetic field in three dimensions, we use physical properties of the field that can be calculated without a detailed knowledge of the flux-rope orientation: the maximum value of Btot and the extrema of the rotation angle (θ) of the field. The model field has a maximum value of Btot= 11.8 nT, which is consistent with 12.0 nT indicated by the data. This is the lower bound because STEREO-B did not necessarily pass through the center of the MC. The temporal profiles of Btot(t) and θ(t) do depend on the angle between the flux-rope axis and the observer path through the structure. The solid curves in Figure 3(b) assume that the observer intersects the flux rope perpendicularly to the axis of symmetry. If the same field is measured at an intersection angle of 55°, the profiles represented by dashed curves in Figure 3(b) result, which provide a better fit to the IMPACT magnetometer data.
The most notable discrepancy between the MC and the model ejecta is the predicted SW speed V*sw∼ 440 km s−1. The PLASTIC plasma data show Vsw∼ 350 km s−1 prior to the arrival of the MC. The actual speed of the SW with which the CME interacted along the way, however, is not known. The more detailed dependence of the predicted V*sw on other parameters will be explored in the future. Nevertheless, noting that V*sw is predicted by the CME position data only, with no reference to any SW data, we judge the prediction to be remarkably consistent with the estimated SW speed.
5. CONCLUSIONS AND DISCUSSION
We have presented the results of the application of the theoretical EFR model to the observed dynamics of a CME and the evolution of the CME magnetic field. The CME was continuously tracked by SECCHI-A and the magnetic field and the plasma parameters of the ejecta were measured by IMPACT and PLASTIC, respectively, on STEREO-B. All model output quantities are constrained by the observed CME trajectory alone. Our main findings are the following.
- 1.The minimum-
 (best-fit) initial-value solution of the ideal MHD EFR model agrees with the measured CME trajectory to within 1% in the 1 AU FOV of STEREO-A.
(best-fit) initial-value solution of the ideal MHD EFR model agrees with the measured CME trajectory to within 1% in the 1 AU FOV of STEREO-A. - 2.The predicted magnetic field B(t) at 1 AU, which is evolved from the initial field given by the initial force balance conditions and constrained only by the CME position data, is consistent with that of the MC detected by the IMPACT magnetometer aboard STEREO-B.
- 3.The temperature and the density of the model MC at 1 AU are consistent with the PLASTIC plasma data.
- 4.The best-fit value of V*sw is faster than the measured SW speed immediately preceding the observed MC.
- 5.The propagation of the model CME is determined by the superposition of the Lorentz force and drag force.
These results demonstrate that the EFR model provides a good approximation of the net driving force on the CME and represent the first theoretical model defined by a single set of initial-value equations to replicate the dynamics of a CME from the Sun to 1 AU and the measured in situ magnetic field and plasma parameters at 1 AU, an important step toward satisfying the requirement that any proposed CME model be able to produce initial-value solutions to correctly describe both the early-time and late-time dynamics.
We acknowledge beneficial discussions with R. A. Howard. We thank N. Rich and L. Simpson for their gracious assistance with the analysis of the STEREO data. The STEREO/SECCHI data are produced by an international consortium of the NRL (USA), LMSAL (USA), NASA/GSFC (USA), RAL (UK), UB-HAM (UK), MPS (Germany), CSL (Belgium), IOTA (France), and IAS (France). The work of V.K. was supported by NASA and that of J.C. by ONR.