Abstract
To understand lubrication-induced membrane permeation, the effects of permeability and membrane geometry on lubrication pressure and permeate flux are studied in a range of a wall-membrane gap width wherein the effect of lubrication cannot be resolved using the Reynolds lubrication equation. The unresolvable lubrication effect (referred to as the non-Reynolds lubrication effect) is modelled by including a higher-order effect as the wall-tangential variation of the local Couette–Poiseuille velocity. Analytical prediction of the permeate flux is then validated with the fully validated numerical simulation. The result shows that, while the traditional Reynolds lubrication model underestimates the permeate flux, the permeation with the effect of the non-Reynolds lubrication is effectively improved in a small permeability range. Furthermore, the non-Reynolds lubrication model also enables reproduction of the characteristic variation in the permeate flux along the membrane. The effective range of the permeability for the non-Reynolds permeate model is discussed through the order analysis of the pressure terms in the Reynolds and non-Reynolds lubrication regimes.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr Minami Yoda
1. Introduction
Mass transfer through a permeable membrane is a widely observed phenomenon in biological environments, for example, oxygen transport by red blood cells (RBCs), gas exchange in the alveoli, and nutrient absorption. Under healthy biological conditions, RBCs flow almost continually, and the lubrication between the RBCs may alleviate the shear stress on the membrane. Alternatively, the pressure developed due to lubrication could become significant in a narrow gap region between an RBC and the vessel wall (or between RBCs). The magnitude of the force due to lubrication was roughly estimated for a rigid spherical particle (Cooley and O'Neill 1969, O'Neill and Majumdar 1970, Jefferey and Onishi 1984, Dance and Maxey 2003); the lubrication force on the particle develops in logarithmic proportion to the surface-to-surface distance for the tangential-mode motion, and inversely proportional to the surface-to-surface distance for the normal-mode motion. Therefore, considering that the permeate flux is proportional to the pressure discontinuity across the membrane (Katchalsky and Curran 1966), lubrication may be significant in the mass transfer in biological flows.
However, the lubrication-induced mass transfer is difficult to predict or analyse by numerical simulation. One of the difficulties is solving the pressure in the inter-particle gap under a limited spatial resolution, as described in the following. Let Δ denote the grid spacing, U the relative surface speed, and µ the viscous coefficient. In addition, ε = h/Dp
is introduced, where Dp
and h are the particle diameter and gap width in the inter-particle region, respectively. The lubrication pressure in a non-spherical narrow gap is described by the Reynolds lubrication equation (Reynolds 1886) when ε is much smaller than unity and when the Reynolds number (based on Dp
and U) multiplied by ε2 is also much smaller than unity. Suppose the resolvable inter-particle gap width h ( = εDp
) is in the order of Δ (i.e. 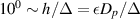 ), the lateral length scale
), the lateral length scale 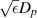 , along which the gap pressure varies largely between the orders of the reference pressure
, along which the gap pressure varies largely between the orders of the reference pressure 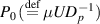 and the lubrication pressure
and the lubrication pressure 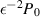 (Leal 2007), should be covered with the following number of grid points:
(Leal 2007), should be covered with the following number of grid points: 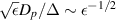 . This value is the lower bound of the necessary number of grid points, and the necessary resolution for reproducing the lubrication pressure increases upon decreasing ε, resulting in prohibitively large computations. However, for a computationally feasible mesh size, the insufficient resolution in the lubrication pressure and, therefore, the pressure discontinuity across the membrane result in poor prediction of the permeate flux.
. This value is the lower bound of the necessary number of grid points, and the necessary resolution for reproducing the lubrication pressure increases upon decreasing ε, resulting in prohibitively large computations. However, for a computationally feasible mesh size, the insufficient resolution in the lubrication pressure and, therefore, the pressure discontinuity across the membrane result in poor prediction of the permeate flux.
Another setback of lubrication-induced mass transfer is that the applicability of the Reynolds lubrication equation is strongly restricted for the non-negligible value of ε (Gu et al
2018). For example, Takeishi and Imai (2017) studied the trapping event of micro and nano particles (as a candidate of efficient drug carrier) in the RBC–RBC regions and reported that the inter-cellular distance was in the range of 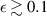 for the single-file motion of the RBCs in capillaries. Although a lubrication theory with compressibility of the porous media (i.e. the endothelial glycocalyx at 0.1–0.4 [µm] thickness) in the capillary (5–6 [µm] in diameter) was introduced for ε ∼ O[10−2] (Feng and Weinbaum 2000), this theory (as well as the ideal classical lubrication theory) may not be applicable for larger ε cases. Therefore, there may be a number of cases where the ideal condition for the Reynolds lubrication equation is violated. In this paper, we study the permeation caused by the lubrication with a non-negligible gap scale, i.e. non-Reynolds lubrication (Takeuchi and Gu 2019).
for the single-file motion of the RBCs in capillaries. Although a lubrication theory with compressibility of the porous media (i.e. the endothelial glycocalyx at 0.1–0.4 [µm] thickness) in the capillary (5–6 [µm] in diameter) was introduced for ε ∼ O[10−2] (Feng and Weinbaum 2000), this theory (as well as the ideal classical lubrication theory) may not be applicable for larger ε cases. Therefore, there may be a number of cases where the ideal condition for the Reynolds lubrication equation is violated. In this paper, we study the permeation caused by the lubrication with a non-negligible gap scale, i.e. non-Reynolds lubrication (Takeuchi and Gu 2019).
Tazaki et al (2020) indicate the possible effect of the non-Reynolds lubrication due to the non-negligible ε in a study of fluid permeation through a membrane moving tangentially in a parallel channel. Their analysis under the condition of infinitesimal permeability showed that while the Reynolds lubrication analysis indicated the order of magnitude of permeate flux as 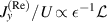 , the contribution due to the non-Reynolds regime on the permeate flux was
, the contribution due to the non-Reynolds regime on the permeate flux was 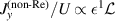 , where
, where 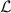 is a non-dimensionalised permeability. Therefore, considering the cases with large ε in industrial and biological applications, the permeate flux resulting from non-Reynolds lubrication due to the non-negligible
is a non-dimensionalised permeability. Therefore, considering the cases with large ε in industrial and biological applications, the permeate flux resulting from non-Reynolds lubrication due to the non-negligible  may be fundamentally important for mass transfer through a membrane.
may be fundamentally important for mass transfer through a membrane.
In this study, we focus on the contribution of non-Reynolds lubrication on the permeate flux through a corrugated membrane under the tangential motion. Permeate fluxes under both Reynolds and non-Reynolds lubrication regimes are modelled, and the nonlinear dependence of geometric parameters on the permeation flux in the non-Reynolds lubrication regime are discussed through a comparison with a fully validated numerical prediction.
2. Governing equations for numerical simulation
The fluid is an incompressible Newtonian fluid of constant density, ρ, and constant viscosity, µ. The governing equations of the fluid are the equation of continuity and the Navier–Stokes equation:


where  , t, and p are the velocity, time, and pressure, respectively.
, t, and p are the velocity, time, and pressure, respectively.
The volumetric flux of a pure fluid, i.e. a fluid without any solute, across the membrane is modelled by the following equation (Katchalsky and Curran 1966):

where  is the unit normal vector pointing from the rear-side of the membrane Ω1 to the front-side Ω2,
is the unit normal vector pointing from the rear-side of the membrane Ω1 to the front-side Ω2, 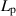 the permeable coefficient, and
the permeable coefficient, and ![$\left[\!\!\left[\,{p}\,\right]\!\!\right]$](https://content.cld.iop.org/journals/1873-7005/53/3/035501/revision3/fdrabf3b4ieqn14.gif) is the hydrostatic-pressure jump (i.e. discontinuity) across the membrane calculated using the limiting pressure values at the interface, p1 and p2, on the respective sides of the membrane as
is the hydrostatic-pressure jump (i.e. discontinuity) across the membrane calculated using the limiting pressure values at the interface, p1 and p2, on the respective sides of the membrane as ![$\left[\!\!\left[\,{p}\,\right]\!\!\right] = p_1 - p_2$](https://content.cld.iop.org/journals/1873-7005/53/3/035501/revision3/fdrabf3b4ieqn15.gif) .
.
Equations (1)–(3) are numerically solved on a rectangular mesh (i.e. non-conforming to the membrane geometry) using the same method as provided in Takeuchi et al (2019) and Tazaki et al (2020); the method guarantees the consistency between the incompressible velocity and pressure fields (Sato et al 2016, Takeuchi et al 2018). In addition, the method enables reproduction of the sharpness of the pressure discontinuity across the membrane (Takeuchi et al 2019), which was identified as an important subject for simulating fluid permeation by Miyauchi et al (2015, 2017).
3. Problem statement
We study the permeation across an infinitesimally thin, corrugated rigid membrane in a two-dimensional parallel channel moving at a constant velocity, U0, as illustrated in figure 1. The geometry and prescribed motion of the corrugated membrane are given as follows:
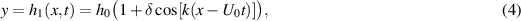
where 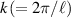 is the wavenumber, h0 the half channel width and δ is a parameter between 0 and 1. The corrugation has an infinite extension in the x direction.
is the wavenumber, h0 the half channel width and δ is a parameter between 0 and 1. The corrugation has an infinite extension in the x direction.
Figure 1. Schematic of a corrugated permeable membrane travelling at constant speed U0 in +x direction in a parallel channel.
Download figure:
Standard image High-resolution imageIn this study, for simplicity, the permeation is solved by transforming the frame attached to the moving membrane: the top- and bottom-flat walls travel at −U0 along the centre axis of the stationary corrugated membrane. The variables observed on this membrane-fixed frame are distinguished with the superscript '*'.
For the ideal geometric conditions of corrugation, the amplitude of corrugation h0
δ is sufficiently small with respect to the half channel width h0 (i.e. 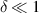 ) and h0 is much smaller than the wavelength of the corrugation (i.e.
) and h0 is much smaller than the wavelength of the corrugation (i.e.  ). The latter condition is equivalent to the aspect ratio
). The latter condition is equivalent to the aspect ratio 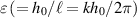 being sufficiently small, i.e.
being sufficiently small, i.e. 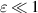 .
.
4. Modelling: asymptotic permeate flux Jy (x)
In this section, we assume that the permeability of the membrane is infinitesimal, i.e. 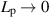 . Hereafter, the permeate flux under the infinitesimal permeability is called the asymptotic permeate flux.
. Hereafter, the permeate flux under the infinitesimal permeability is called the asymptotic permeate flux.
Assuming a negligible amplitude of corrugation, i.e. 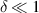 , the normal vector on the membrane surface is almost parallel to the y axis. Therefore, in the limit of zero amplitude (δ → 0), only the y component of the permeate flux
, the normal vector on the membrane surface is almost parallel to the y axis. Therefore, in the limit of zero amplitude (δ → 0), only the y component of the permeate flux 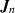 is predominant; the y component is represented as
is predominant; the y component is represented as  , where
, where 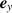 is the unit vector in the y direction (see figure 1). Solving the lubrication equation, Jy
is modelled as a function of the membrane geometry.
is the unit vector in the y direction (see figure 1). Solving the lubrication equation, Jy
is modelled as a function of the membrane geometry.
When ε and the Reynolds number 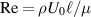 satisfy
satisfy 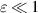 and
and 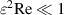 , the flow in the regions between the corrugated membrane and flat walls can be described by the Reynolds lubrication equation. Notably, the gap pressure is uniform in the wall normal direction, varying only in the x direction. Meanwhile, in the case where ε is not sufficiently small, the Reynolds lubrication equation ceases to be applicable, and the pressure in the gap also varies in the wall-normal direction; this situation is referred to as 'non-Reynolds lubrication due to the non-negligible ε'. However, if
, the flow in the regions between the corrugated membrane and flat walls can be described by the Reynolds lubrication equation. Notably, the gap pressure is uniform in the wall normal direction, varying only in the x direction. Meanwhile, in the case where ε is not sufficiently small, the Reynolds lubrication equation ceases to be applicable, and the pressure in the gap also varies in the wall-normal direction; this situation is referred to as 'non-Reynolds lubrication due to the non-negligible ε'. However, if 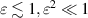 and
and 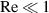 are satisfied and both the gradient and curvature of the surface profile are small, a lubrication model with a higher-order effect, i.e. the extended lubrication model (Takeuchi and Gu 2019), is applicable. For the surface profile in equation (4), the gradient and curvature of the corrugation are evaluated as h0
δk ( = 2πδε) and
are satisfied and both the gradient and curvature of the surface profile are small, a lubrication model with a higher-order effect, i.e. the extended lubrication model (Takeuchi and Gu 2019), is applicable. For the surface profile in equation (4), the gradient and curvature of the corrugation are evaluated as h0
δk ( = 2πδε) and 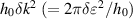 , respectively, indicating that δε should be sufficiently small.
, respectively, indicating that δε should be sufficiently small.
In this section, we highlight the effect of the non-Reynolds lubrication due to non-negligible ε on the pressure discontinuity and permeate flux, and we compare the results with those obtained by the Reynolds lubrication equation and numerical simulation.
4.1. Asymptotic flux for infinitesimal permeability by Reynolds equation
Following Tazaki et al (2020), the asymptotic permeate flux by the Reynolds equation is briefly reviewed in the following.
For a membrane of infinitesimal permeability (i.e. 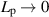 , and, therefore, Jy
→ 0), the pressures on the lower and upper sides (Ω1 and Ω2, respectively) of the corrugation,
, and, therefore, Jy
→ 0), the pressures on the lower and upper sides (Ω1 and Ω2, respectively) of the corrugation, 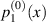 and
and 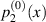 , follow independent Reynolds lubrication equations. Here, the superscript (0) denotes the 0th order approximation, i.e. the case described by the Reynolds lubrication equation. Hereafter, the value observed from the moving frame of reference on the membrane is denoted with the superscript '
, follow independent Reynolds lubrication equations. Here, the superscript (0) denotes the 0th order approximation, i.e. the case described by the Reynolds lubrication equation. Hereafter, the value observed from the moving frame of reference on the membrane is denoted with the superscript ' ', e.g.
', e.g. 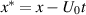 . Then, the membrane geometry and pressure are transformed as follows:
. Then, the membrane geometry and pressure are transformed as follows:
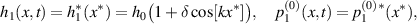
where 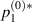 obeys the following Reynolds lubrication equation:
obeys the following Reynolds lubrication equation:
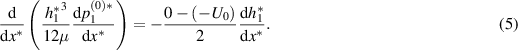
The derivation of the above equation is detailed in Tipei (1962) and Leal (2007). The pressure on the original frame of reference, which is fixed in space, is given as follows (Takeuchi et al 2019, Tazaki et al 2020):
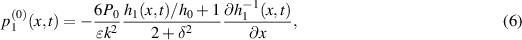
where 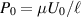 , and
, and 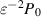 is the typical magnitude of the lubrication pressure. From both the geometric symmetry between Ω1 and Ω2 (see figure 1) and the one-dimensionality of the gap pressure
is the typical magnitude of the lubrication pressure. From both the geometric symmetry between Ω1 and Ω2 (see figure 1) and the one-dimensionality of the gap pressure 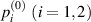 , the pressure in Ω2 is given as
, the pressure in Ω2 is given as  . Then, the asymptotic permeate flux is described as follows:
. Then, the asymptotic permeate flux is described as follows:
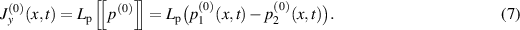
Substituting equation (6) into the above equation and using 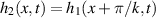
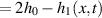 , the asymptotic permeate flux is given as:
, the asymptotic permeate flux is given as:
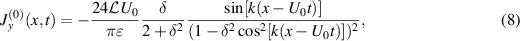
where 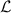 is the non-dimensional permeability defined as
is the non-dimensional permeability defined as 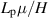 based on the full channel width H (see figure 1).
based on the full channel width H (see figure 1).
4.2. Adjusting component of the pressure through non-Reynolds lubrication
For a non-negligible value of ε, the above-mentioned theory is not applicable, and the lubrication pressure must be corrected by considering higher-order terms, i.e. the terms in O[ε2], in the governing equations.
In the extended lubrication model (Takeuchi and Gu 2019), the non-Reynolds lubrication pressure due to the non-negligible ε is decomposed into the base component and the adjusting component, 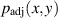 . Here, the base component, i.e.
. Here, the base component, i.e. 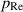 , is the solution of the Reynolds lubrication equation, equation (5); i.e.
, is the solution of the Reynolds lubrication equation, equation (5); i.e. 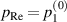 . Given
. Given 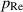 , the adjusting component is calculated as follows (Takeuchi and Gu 2019):
, the adjusting component is calculated as follows (Takeuchi and Gu 2019):

where 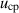 is the velocity of the locally constructed Couette–Poiseuille flow:
is the velocity of the locally constructed Couette–Poiseuille flow:
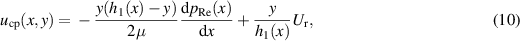
where 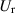 is the relative velocity of the walls in the x direction. Equation (9) implies that the adjusting component is the stress caused by the spatial variation of
is the relative velocity of the walls in the x direction. Equation (9) implies that the adjusting component is the stress caused by the spatial variation of 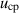 driven by the local Reynolds-lubrication pressure,
driven by the local Reynolds-lubrication pressure, 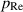 , and the wall movements. Using the base and adjusting components of the pressure, the lubrication pressure in the non-Reynolds regime is expressed as
, and the wall movements. Using the base and adjusting components of the pressure, the lubrication pressure in the non-Reynolds regime is expressed as 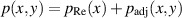 . The validity of the above model was established in Takeuchi and Gu (2019).
. The validity of the above model was established in Takeuchi and Gu (2019).
Hereafter, 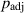 is alternatively denoted by
is alternatively denoted by 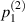 , indicating that this pressure is the higher-order (i.e. ε2 order) correction to
, indicating that this pressure is the higher-order (i.e. ε2 order) correction to 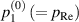 . Using equation (6), which is obtained under
. Using equation (6), which is obtained under 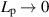 , the form of
, the form of 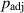 is given as follows:
is given as follows:
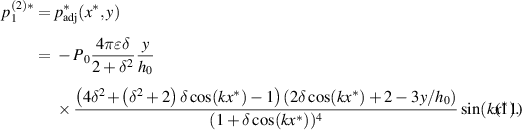
Subsequently, using equation (3), the adjusting asymptotic flux under the non-Reynolds lubrication regime is constructed as follows:
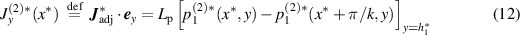
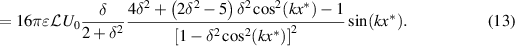
On comparing equation (8) with equation (13), 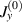 and
and 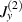 are different by two orders of magnitude in ε, which originates from the different magnitudes of
are different by two orders of magnitude in ε, which originates from the different magnitudes of 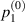 and
and 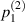 . Eventually, the full component of the flux is given as
. Eventually, the full component of the flux is given as

The dependency of the parameters on the asymptotic permeation is clearly demonstrated in the permeate flow rate calculated for the half wave length (i.e. 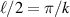 ):
):
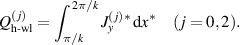
For the 0th and 2nd order solutions:
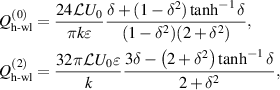
the total permeate flow rate is evaluated by the Taylor expansion with respect to δ as follows:
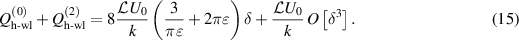
The lowest-order term in equation (15) shows that the permeate flow rate is proportional to the corrugation amplitude (δ) and the wave length (k−1). Although the dependence on the aspect ratio (ε) is more complex, the effects of the Reynolds and the non-Reynolds lubrications appear as the ε−1 and ε1 terms, respectively. This analysis is valid under the condition of 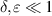 and
and 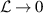 ; our preliminary analysis shows that δ in the range of
; our preliminary analysis shows that δ in the range of 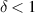 exhibits a weakly non-linear effect on the permeation, while a finite value of
exhibits a weakly non-linear effect on the permeation, while a finite value of 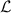 induces a strong non-linear response.
induces a strong non-linear response.
Note that, from equations (8) and (13), both 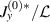 and
and 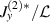 become independent of
become independent of 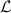 . This is also the characteristics at the infinitesimal permeability; in this limit,
. This is also the characteristics at the infinitesimal permeability; in this limit, 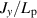 is equivalent to the
is equivalent to the 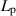 -free pressure discontinuity
-free pressure discontinuity ![$\left[\!\!\left[\,{p}\,\right]\!\!\right]$](https://content.cld.iop.org/journals/1873-7005/53/3/035501/revision3/fdrabf3b4ieqn74.gif) , as shown in equations (6) and (11). This
, as shown in equations (6) and (11). This 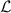 -independent nature facilitates investigation of the converging (or asymptotic) trend of the numerical simulation result at small
-independent nature facilitates investigation of the converging (or asymptotic) trend of the numerical simulation result at small 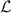 values, as will be discussed in the next section.
values, as will be discussed in the next section.
5. Results and discussion
The above analytical models are compared to the numerical simulation result. To adjust the condition to the numerical study by Tazaki et al (2020), Reynolds number is set at ρU0
H/µ = 1.0 and ε is fixed at 0.1. The spatial resolution and the time increment are set at H/Δ = 40 (i.e. h0/Δ = 20) and 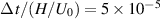 , respectively. The amplitude parameter and permeability are varied in the following ranges: δ = 0.1, 0.25, 0.45, 0.50 and
, respectively. The amplitude parameter and permeability are varied in the following ranges: δ = 0.1, 0.25, 0.45, 0.50 and 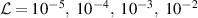 .
.
Figure 2 compares the non-dimensionalised permeate flux 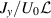 obtained by the numerical simulation (represented by symbols), the 0th order asymptotic model (equation (8); dashed line) and the full-component asymptotic model (equation (14); solid line). For all the δ cases, the numerical results show converging trends as
obtained by the numerical simulation (represented by symbols), the 0th order asymptotic model (equation (8); dashed line) and the full-component asymptotic model (equation (14); solid line). For all the δ cases, the numerical results show converging trends as 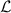 decreases. However, the distinct gaps exist between the numerical results at
decreases. However, the distinct gaps exist between the numerical results at 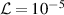 and the 0th order model, as Tazaki et al (2020) reported. Meanwhile, the full-component fluxes agree well with the asymptotic numerical results, particularly for the cases of δ = 0.10 and 0.25, indicating that the effect of the non-Reynolds lubrication can be described with equations (9) and (12) for the small δ. For the larger δ cases (i.e. δ = 0.45 and 0.50), although the prediction is slightly overestimated, the 4% discrepancy at
and the 0th order model, as Tazaki et al (2020) reported. Meanwhile, the full-component fluxes agree well with the asymptotic numerical results, particularly for the cases of δ = 0.10 and 0.25, indicating that the effect of the non-Reynolds lubrication can be described with equations (9) and (12) for the small δ. For the larger δ cases (i.e. δ = 0.45 and 0.50), although the prediction is slightly overestimated, the 4% discrepancy at 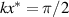 (viz.,
(viz., 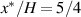 ) is still in the order of ε2.
) is still in the order of ε2.
Figure 2. The longitudinal (x*) distribution of the permeate flux divided by the normalised permeability 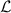
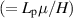 ,
, 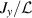 . The symbols are by the numerical result identical to those in figure 4 of Tazaki et al (2020). In the figure, 'pRe-based' means
. The symbols are by the numerical result identical to those in figure 4 of Tazaki et al (2020). In the figure, 'pRe-based' means 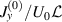 and plotted by the dashed line, whereas '(pRe+Padj)-based' plotted by the solid line includes the higher-order correction,
and plotted by the dashed line, whereas '(pRe+Padj)-based' plotted by the solid line includes the higher-order correction, 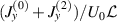 .
.
Download figure:
Standard image High-resolution imageThe profiles of δ = 0.50 are characterised by dimples, i.e. weakened permeation between a pair of local peaks along the membrane, whereas the case of δ = 0.45 is selected as a value just below the lower bound of the δ range ( ) for having a dimpled profile. More details about the condition for the emergence of the dimples is explained in appendix
) for having a dimpled profile. More details about the condition for the emergence of the dimples is explained in appendix 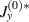 (dashed line) do not show dimples. However, the non-Reynolds component
(dashed line) do not show dimples. However, the non-Reynolds component 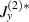 provides adjustment that distinguishes the no-dimpled (δ = 0.45) and dimpled (δ = 0.50) cases in the permeation profiles.
provides adjustment that distinguishes the no-dimpled (δ = 0.45) and dimpled (δ = 0.50) cases in the permeation profiles.
To identify the applicable range of the permeability, an order analysis is conducted for the pressure and permeation flux. In the following, we introduce the reference velocities of the fluid in the longitudinal and transverse directions as U and V, respectively. The order of magnitude of the lubrication pressure under the predominant permeation would be lower than that under an infinitesimal permeability, i.e. 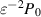 . Then, for a finite permeability, the effect of
. Then, for a finite permeability, the effect of 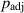 on the permeate flux is estimated. From the permeate flux
on the permeate flux is estimated. From the permeate flux  , the pressure in the Reynolds lubrication regime is evaluated as
, the pressure in the Reynolds lubrication regime is evaluated as

where as the pressure due to the non-Reynolds effect is obtained as
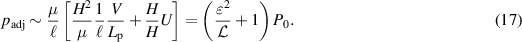
Comparing equations (16) and (17), the adjusting pressure could become relatively large for a large permeability; particularly, in the range of 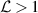 , the adjusting pressure could become even larger than
, the adjusting pressure could become even larger than 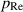 . To remain in the assumed range of the pressures,
. To remain in the assumed range of the pressures, 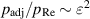 , the permeability has to be limited in the range of
, the permeability has to be limited in the range of 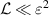 . Considering that the analytical curves at
. Considering that the analytical curves at  and 10−5 (corresponding to
and 10−5 (corresponding to 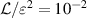 and 10−3 for the present geometry of ε = 0.1) in figure 2 reasonably reproduce the numerical result, the above order analysis effectively includes the critical terms for the lubrication-induced permeation. For an even higher permeability range (e.g.
and 10−3 for the present geometry of ε = 0.1) in figure 2 reasonably reproduce the numerical result, the above order analysis effectively includes the critical terms for the lubrication-induced permeation. For an even higher permeability range (e.g. 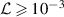 ), different higher-order models for pressure and permeation may be necessary, which is the subject of ongoing study of the present authors.
), different higher-order models for pressure and permeation may be necessary, which is the subject of ongoing study of the present authors.
6. Conclusion
Lubrication-induced permeate flux through a corrugated membrane was studied in a gap-width range wherein the Reynolds lubrication equation is not applicable (i.e. non-Reynolds lubrication regime). The effect of lubrication in the non-Reynolds regime was modelled using an extended lubrication model that considers the wall-normal variation of the pressure distribution.
While the traditional Reynolds lubrication model underestimated the permeate flux, particularly in a low-permeability range, the non-Reynolds lubrication model improved the prediction (towards the fully validated numerical result) for a small amplitude of corrugation. For a large amplitude of corrugation, the characteristic variation in permeate flux along the membrane (i.e. dimpled profile) was reproduced by including the non-Reynolds effect.
The effective range of the permeability for the non-Reynolds lubrication was discussed through the order analysis of the lubrication pressures. The results indicate the validity of the non-Reynolds lubrication model in relatively small permeabilities for problems with non-negligible gap width.
Acknowledgments
This work is partly supported by Grants-in-Aid for Scientific Research (B) Nos. 17H03174 and 19H02066, Grant-in-Aid for Early-Career Scientists No. 19K20659, and Grant-in-Aid for Challenging Research (Exploratory) No. 20K20972 of the Japan Society for the Promotion of Science (JSPS). One of the authors, S M, gratefully acknowledges the Leading Young Researcher Overseas Visit Program in Tohoku University.
Appendix A.: Condition for dimpled profile of permeate flux
The condition of δ for having a dimpled profile of asymptotic permeate flux (see figure 2(d)) is investigated. The full flux considering the pressure adjustment using the extended lubrication model is calculated as follows:
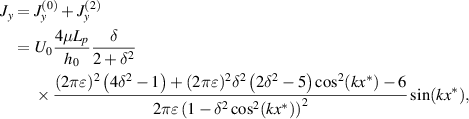
where 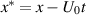 . The profile of the flux could have a pair of dimples, i.e. weakened permeation between a pair of local peaks, at
. The profile of the flux could have a pair of dimples, i.e. weakened permeation between a pair of local peaks, at 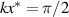 and 3π/2 as observed in figure 2(d). The condition for no-dimpled profile is as follows:
and 3π/2 as observed in figure 2(d). The condition for no-dimpled profile is as follows:
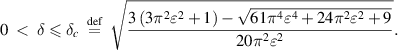
In the present case, 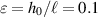 , the critical value becomes
, the critical value becomes  .
.
In addition, it is easily confirmed that the profile of 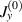 does not have dimples in
does not have dimples in  (
( ).
).




