Abstract
Recently, two kinds of integrable deformations of the string world sheet theory in the gauge/gravity correspondence have been constructed (Delduc et al 2014 Phys. Rev. Lett. 112 051601; Hollowood et al 2014 J. Phys. A: Math. Theor. 47 495402). One class of these, the k deformations associated to the more general q deformations but with 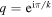 a root of unity, has been shown to be related to a particular discrete deformation of the principal chiral models and (semi-)symmetric space sigma models involving a gauged WZW model. We conjecture a form for the exact S-matrices of the bosonic integrable field theories of this type. The S-matrices imply that the theories have a hidden infinite dimensional affine quantum group symmetry. We provide some evidence, via quantum inverse scattering techniques, that the theories do indeed possess the finite-dimensional part of this quantum group symmetry.
a root of unity, has been shown to be related to a particular discrete deformation of the principal chiral models and (semi-)symmetric space sigma models involving a gauged WZW model. We conjecture a form for the exact S-matrices of the bosonic integrable field theories of this type. The S-matrices imply that the theories have a hidden infinite dimensional affine quantum group symmetry. We provide some evidence, via quantum inverse scattering techniques, that the theories do indeed possess the finite-dimensional part of this quantum group symmetry.
Export citation and abstract BibTeX RIS
1. Introduction
One of the most fascinating applications of the quantum inverse scattering method (QISM) to sigma models has been to the exact quantization of the  principal chiral model (PCM) in the 80s by Faddeev and Reshetikhin (FR) in their seminal paper [1]. The main conceptual idea was to replace the non-ultra-local Poisson bracket of the theory by a new ultra-local one that preserved the PCM equations of motion but under the time flow of a new Hamiltonian. After doing this, it was possible to construct a magnetic lattice algebra and to apply the QISM allowing for the the determination of the exact quantum spectrum and S-matrix of the
principal chiral model (PCM) in the 80s by Faddeev and Reshetikhin (FR) in their seminal paper [1]. The main conceptual idea was to replace the non-ultra-local Poisson bracket of the theory by a new ultra-local one that preserved the PCM equations of motion but under the time flow of a new Hamiltonian. After doing this, it was possible to construct a magnetic lattice algebra and to apply the QISM allowing for the the determination of the exact quantum spectrum and S-matrix of the  PCM in a thermodynamic limit. However, one drawback of this new ultra-localization trick was the lack of a systematic understanding, in the sense that the introduction of the new Poisson bracket (to be quantized) was not rigorously justified and the trick remained unused for many decades precluding the use of the QISM to other sigma models beyond the SU(2)-PCM considered by FR.
PCM in a thermodynamic limit. However, one drawback of this new ultra-localization trick was the lack of a systematic understanding, in the sense that the introduction of the new Poisson bracket (to be quantized) was not rigorously justified and the trick remained unused for many decades precluding the use of the QISM to other sigma models beyond the SU(2)-PCM considered by FR.
This situation changed only very recently when Delduc, Magro and Vicedo (DMV) in [2], using classical integrability techniques, succeeded in identifying the algebraic structure behind the FR ultra-localization mechanism. This allowed DMV to generalize the procedure to any PCM on a Lie group F and, more interestingly, to any sigma model on a symmetric space F/G, and also to the semi-symmetric spaces like  that appear in superstring theory and the AdS/CFT correspondence [3]. The generalized FR mechanism was considered by DMV only at classical level and it boils down to a very simple recipe: it is equivalent to replacing in the Poisson bracket the so-called twisting function
that appear in superstring theory and the AdS/CFT correspondence [3]. The generalized FR mechanism was considered by DMV only at classical level and it boils down to a very simple recipe: it is equivalent to replacing in the Poisson bracket the so-called twisting function  associated to the sigma model by the new FR twisting function
associated to the sigma model by the new FR twisting function  , which is a simpler—in some well defined sense—function of the spectral parameter z. The next step in the implementation of the QISM is the introduction of the lattice algebra regularization of the theory, which is the ultimate goal of the quantization procedure. The lattice Poisson algebras corresponding to the F/G sigma models and to the
, which is a simpler—in some well defined sense—function of the spectral parameter z. The next step in the implementation of the QISM is the introduction of the lattice algebra regularization of the theory, which is the ultimate goal of the quantization procedure. The lattice Poisson algebras corresponding to the F/G sigma models and to the  superstring were constructed explicitly in [2, 4] and, remarkably, they are deeply related to the Pohlmeyer reduction of the sigma models [5–7]. Unfortunately, the quantization of these lattice Poisson algebras is not known yet and it is still an open problem.
superstring were constructed explicitly in [2, 4] and, remarkably, they are deeply related to the Pohlmeyer reduction of the sigma models [5–7]. Unfortunately, the quantization of these lattice Poisson algebras is not known yet and it is still an open problem.
Despite of the fact that the FR mechanism turned out to be a very simple algebraic operation, a key ingredient was still missing, namely, the replacement of the twisting function  was not justified from a physical standpoint. After all, changing the Poisson structure is equivalent to modifying the kinetic term in the action functional and this raises the question as to whether it is possible to find an integrable deformation of the original sigma models that implements in a natural way the FR bracket in some limit of the deformation parameter.
was not justified from a physical standpoint. After all, changing the Poisson structure is equivalent to modifying the kinetic term in the action functional and this raises the question as to whether it is possible to find an integrable deformation of the original sigma models that implements in a natural way the FR bracket in some limit of the deformation parameter.
This led to the introduction of the η-deformed sigma models by DMV in [8–10], which are Yang–Baxter type deformations of the form originally introduced by Klimcik in [11] for the PCM. The η-deformed Lagrangian combines the two twisting functions 
 into a new one
into a new one  leading to a deformed interpolating Poisson bracket of the form
leading to a deformed interpolating Poisson bracket of the form  Unfortunately, the reality condition of the action and integrability properties restrict the domain of the parameter η. This translates into
Unfortunately, the reality condition of the action and integrability properties restrict the domain of the parameter η. This translates into  , which means that the FR bracket is not reachable in parameter space. In other words, it will never be the dominant bracket that has to be quantized within the FR scheme.
, which means that the FR bracket is not reachable in parameter space. In other words, it will never be the dominant bracket that has to be quantized within the FR scheme.
An entirely different kind of deformation has been emerging based originally on the observation that the S-matrix that describes the scattering of excitations on the  string world sheet theory admits a quantum group deformation [12–15]. In turn, this was motivated by the observation that the world sheet equations of motion are equivalent, via the Polhmeyer reduction, to a relativistic generalized sine-Gordon theory [5, 6] and the deformed S-matrix provides an explicit relation between both theories at the quantum level. This deformation was recently identified in [16] as a deformation of the non-abelian T-dual of the world sheet sigma model related to the (bosonic) 'λ-deformations' of the PCM introduced by Sfetsos in [17] and of the symmetric space sigma models constructed by the present authors in [18]. We call these theories the k-deformed sigma models, rather than λ-deformed, because the parameter
string world sheet theory admits a quantum group deformation [12–15]. In turn, this was motivated by the observation that the world sheet equations of motion are equivalent, via the Polhmeyer reduction, to a relativistic generalized sine-Gordon theory [5, 6] and the deformed S-matrix provides an explicit relation between both theories at the quantum level. This deformation was recently identified in [16] as a deformation of the non-abelian T-dual of the world sheet sigma model related to the (bosonic) 'λ-deformations' of the PCM introduced by Sfetsos in [17] and of the symmetric space sigma models constructed by the present authors in [18]. We call these theories the k-deformed sigma models, rather than λ-deformed, because the parameter  is fixed, a root of unity, while λ is a coupling constant. In particular, in the bosonic models λ is a running coupling in the quantum theory and, therefore, it is naturally interpreted as the running coupling of the original sigma model. It is only in the classical limit
is fixed, a root of unity, while λ is a coupling constant. In particular, in the bosonic models λ is a running coupling in the quantum theory and, therefore, it is naturally interpreted as the running coupling of the original sigma model. It is only in the classical limit  that λ is a fixed parameter.
that λ is a fixed parameter.
The k-deformed Lagrangian combines the two twisting functions and Poisson brackets exactly as discussed above but with  corresponding to
corresponding to ![$\lambda \subset [0,1]$](https://content.cld.iop.org/journals/1751-8121/49/46/465201/revision1/jpaaa42c4ieqn18.gif) , so that in the limit
, so that in the limit  the action functional indeed possesses the (generalized) FR bracket as its canonical Poisson structure. Here, we will consider the bosonic models of this type.
the action functional indeed possesses the (generalized) FR bracket as its canonical Poisson structure. Here, we will consider the bosonic models of this type.
Finding the lattice algebra regularization of the field theory is by far the most difficult and important step toward the full implementation of the QISM. It is equivalent to the regularization/quantization of the Maillet bracket [19] associated to the field theory under examination, which, for the models of present interest, is non-ultra-local. The quantization of the Maillet bracket is known to be a difficult and longstanding unsolved problem for most of the interesting integrable field theories and for this reason any successful attempt to regularize/quantize it, even in some simplifying limit, has to be considered as a useful enterprise by itself. To date, and in relation to the k-deformations, the (Maillet) lattice algebra is only known in the limit  at classical level,
at classical level,  , and for any value of the spectral parameter z. The Poisson lattice algebras coincide precisely with the ones introduced in the DMV papers mentioned above.
, and for any value of the spectral parameter z. The Poisson lattice algebras coincide precisely with the ones introduced in the DMV papers mentioned above.
In the present work, we find another limit in which we can regularize and quantize the Maillet bracket. It is defined for any value of the parameter ![$\lambda \in [0,1]$](https://content.cld.iop.org/journals/1751-8121/49/46/465201/revision1/jpaaa42c4ieqn22.gif) but only for a very specific set of values of the spectral parameter that correspond to the poles of the λ-deformed twisting function
but only for a very specific set of values of the spectral parameter that correspond to the poles of the λ-deformed twisting function  . Remarkably, the lattice algebra turns out to be nothing but the Kac–Moody lattice current algebra introduced in [20, 21]. In particular, this allows us to show in a rather simple way that the k -deformed sigma models associated to the principal chiral model on a Lie group F and to the bosonic sigma models on the symmetric spaces F/G, both possess a finite-dimensional quantum group symmetry
. Remarkably, the lattice algebra turns out to be nothing but the Kac–Moody lattice current algebra introduced in [20, 21]. In particular, this allows us to show in a rather simple way that the k -deformed sigma models associated to the principal chiral model on a Lie group F and to the bosonic sigma models on the symmetric spaces F/G, both possess a finite-dimensional quantum group symmetry  with a deformation parameter
with a deformation parameter  being a root of unity. This quantum group is the finite-dimensional piece of the infinite-dimensional affine quantum group symmetry that the S-matrix of these theories are conjectured to enjoy. Furthermore, we also show explicitly how these models naturally implement the FR ultra-localization mechanism as a continuous limiting process, i.e, as
being a root of unity. This quantum group is the finite-dimensional piece of the infinite-dimensional affine quantum group symmetry that the S-matrix of these theories are conjectured to enjoy. Furthermore, we also show explicitly how these models naturally implement the FR ultra-localization mechanism as a continuous limiting process, i.e, as  we do have that
we do have that  .
.
It is important to emphasize that in this work we are considering the (bosonic) k-deformed theories as just 1 + 1 dimensional integrable quantum field theories but not as string world sheet theories. Hence, we do not have the additional complications of a world-sheet theory, like gauge fixing and the Virasoro constraints, to contend with. In particular, in the situation studied here, the coupling λ runs with scale, whereas in the stringy context we would expect λ to be exactly marginal under the renormalization group. For applications of the k-deformation to string theory see [16, 25–30].
The paper is organized as follows. In section 2, we review the construction of the theories at the Lagrangian level. We then consider the theories at the quantum level and make a series of conjectures for the form of their exact S-matrices. This motivates the idea that the k-deformed theory has affine quantum group symmetries. In section 3, we reveal the Poisson–Lie group symmetry of the deformed sigma models, which is the classical precursor of the quantum group. We write down the Maillet  /
/ form of the Poisson brackets of the Lax operator, identify the twisting functions and find their poles. We consider the deformed theories and expand their monodromy matrix at the poles of the twisting function and find the first non-trivial non-local charges suggesting the existence of an affine quantum group. In section 4, we review the lattice Kac–Moody algebra and the quantization of the monodromy matrix evaluated at the poles of the twisting function, which generates the finite-dimensional quantum group with a root-of-unity q-deformation parameter. Finally, we draw some conclusions and directions for future work.
form of the Poisson brackets of the Lax operator, identify the twisting functions and find their poles. We consider the deformed theories and expand their monodromy matrix at the poles of the twisting function and find the first non-trivial non-local charges suggesting the existence of an affine quantum group. In section 4, we review the lattice Kac–Moody algebra and the quantization of the monodromy matrix evaluated at the poles of the twisting function, which generates the finite-dimensional quantum group with a root-of-unity q-deformation parameter. Finally, we draw some conclusions and directions for future work.
2. The deformed sigma models
We will consider two classes of bosonic k-deformed sigma models that we call the k-principal chiral models (k-PCMs) and k-symmetric space sigma models (k-SSSMs), associated to Lie groups F and symmetric spaces F/G, respectively. They are constructed in the following way. For the k-PCM case [17], one takes the PCM for an F-valued field f and then adds to it a WZW model for a second F-valued field  . The original PCM has an
. The original PCM has an  global symmetry that acts as
global symmetry that acts as  . An interaction between the PCM and WZW model is generated by gauging the common F-action
. An interaction between the PCM and WZW model is generated by gauging the common F-action

and fixing the gauge by setting f = I. The resulting theory has a global F symmetry that one can view as arising from the original FR-symmetry of the PCM4 .
For the k-SSSM case [18], one takes the F/G sigma model defined in terms of an F-valued field f and a gauge field Bμ corresponding to the G right action  with
with  . The F/G sigma model also has a global FL symmetry that acts as
. The F/G sigma model also has a global FL symmetry that acts as  with
with  . Then, as for the k-PCM case, one adds to it a WZW model for an F-valued field
. Then, as for the k-PCM case, one adds to it a WZW model for an F-valued field  and gauges the common F-action (2.1). Finally, one partially fixes the gauge by setting f = I and integrates out the gauge field Bμ. This leaves the subgroup
and gauges the common F-action (2.1). Finally, one partially fixes the gauge by setting f = I and integrates out the gauge field Bμ. This leaves the subgroup  as the remnant gauge symmetry.
as the remnant gauge symmetry.
In both cases, the final theory has the form of a gauged WZW model for a group F where the whole group F, which acts by the anomaly-free vector action  , seems to be gauged. In fact, this is incorrect because the action involves a deformation that breaks the gauge symmetry completely for the k-PCM case, and breaks it down to the subgroup
, seems to be gauged. In fact, this is incorrect because the action involves a deformation that breaks the gauge symmetry completely for the k-PCM case, and breaks it down to the subgroup  for the k-SSSM case5
:
for the k-SSSM case5
:

This action has two parameters: the level k, which is a positive integer that defines the deformation parameter ![$q=\exp [{\rm{i}}\pi /({c}_{2}(F)+k)]$](https://content.cld.iop.org/journals/1751-8121/49/46/465201/revision1/jpaaa42c4ieqn42.gif) , and the coupling constant λ which is related to the coupling constant κ of the original sigma models by means of
, and the coupling constant λ which is related to the coupling constant κ of the original sigma models by means of  .
.
The deformation appears via the term that depends on the quantity Ω which takes the form6

In the latter case, the  ,
,  , are the projectors along the
, are the projectors along the  decomposition of the Lie algebra
decomposition of the Lie algebra  , where
, where  is the Lie algebra of G. Note that the
is the Lie algebra of G. Note that the  gradation here is one of the defining elements of a symmetric space.
gradation here is one of the defining elements of a symmetric space.
In (2.2), the status of the field Aμ is rather subtle. In the k-PCM case, it is an auxiliary field that can be integrated out since it appears quadratically in the action. In the k-SSSM case, the component  is, similarly, an auxiliary field, but the component
is, similarly, an auxiliary field, but the component  is a genuine gauge field that reflects a G-gauge symmetry of the theory. It can be integrated out, but then one would have to fix the gauge on the field
is a genuine gauge field that reflects a G-gauge symmetry of the theory. It can be integrated out, but then one would have to fix the gauge on the field  . Alternatively one can fix the gauge by imposing, for example,
. Alternatively one can fix the gauge by imposing, for example,  .
.
In the limit  , with
, with  in such a way that
in such a way that

is fixed, the theories can then be shown to be the non-abelian T-duals of the PCM for the group F, or of the symmetric space sigma model for F/G, respectively, with coupling constant κ. Theories which are non-abelian T-duals of each other are related by a canonical transformation and therefore it is a reasonable hypothesis that they can be equivalent at the quantum level. The k-PCM has a global F symmetry which acts as  which is the remnant of the original FR symmetry of the PCM, while the k-SSSM has no obvious symmetries.
which is the remnant of the original FR symmetry of the PCM, while the k-SSSM has no obvious symmetries.
2.1. Integrability
The k-deformed theories are integrable at the classical level7 . To see this, we can solve for the auxiliary field Aμ in the form

The equations-of-motion can then be written in Lax form:

where, for the k-PCM

while for the k-SSSM

2.2. Quantization and S-matrices
For integrable theories, one way to quantize the theories directly is to intuit a form for the exact S-matrix by using a combination of the global symmetries, the standard S-matrix axioms along with factorization and the Yang–Baxter equation that result from integrability. Integrability at the quantum level is thought to follow if there are higher spin conserved, possibly non-local, charges whose conservation is non-anomalous in the quantum theory. The integrability of the PCM is known to be non-anomalous for any group F, while the absence of an anomaly for the F/G SSSM is not guaranteed in general. For instance, for compact symmetric spaces of definite signature it requires that the subgroup G is simple [31]8
. The quantum integrable SSSMs are then associated to either Type II symmetric spaces of the form  , which provide an equivalent way to formulate the PCM for the group G, or Type I symmetric spaces of the form
, which provide an equivalent way to formulate the PCM for the group G, or Type I symmetric spaces of the form

plus a number of possibilities involving the exceptional groups that we shall not consider here.
We make the hypothesis that the k-deformation of these theories are also integrable at the quantum level. One way to motivate this is to find a suitable ansatz for their S-matrices which can then be subject to various consistency tests. Note that there are effectively two different kinds of k-deformations of the PCM because they can also be formulated as a SSSM.
The first issue to consider is how the couplings k and λ flow in the quantum theory. The integer level k, of course, cannot have non-trivial RG flow because it multiplies the topological Wess–Zumino term in the action. However, the coupling λ does have a non-trivial RG flow. The loop counting parameter is  and to the one-loop level the beta function is9
and to the one-loop level the beta function is9

So in both cases, the coupling λ runs to zero in the UV. In this limit, by integrating out the auxiliary field Aμ, for the PCM case, and  , for the SSSM case, the theories take the form of a WZW model deformed by a current–current operator. For the PCM this is an ordinary (i.e. non-gauged) WZW model
, for the SSSM case, the theories take the form of a WZW model deformed by a current–current operator. For the PCM this is an ordinary (i.e. non-gauged) WZW model

where  are the standard Kac–Moody currents of the WZW model:
are the standard Kac–Moody currents of the WZW model:

In this case the deformation is marginally relevant, as is also clear from the form of the beta function (2.10).
For the SSSM case, the UV theory is a deformation of the gauged WZW for F/G,

where  are the Kac–Moody currents of the F/G gauged WZW model
are the Kac–Moody currents of the F/G gauged WZW model

Notice that the deformation now is relevant. In the case of a Type II symmetric space, it is worth pointing out that the WZW model involves the product group  and so there are two independent levels k1 and k2.
and so there are two independent levels k1 and k2.
The integrable deformations of WZW models, non-gauged in (2.11) and gauged in (2.13) have been studied from a CFT perspective in [35].
There is one example of the k-deformed sigma models that has been studied in some detail and will provide the inspiration for the other cases. This corresponds to the PCM case with  [36]. To start with, the PCM models associated to the classical groups have a factorized S-matrix that can be written schematically in terms of 2 particle to 2-particle matrix elements of the form [37, 38]
[36]. To start with, the PCM models associated to the classical groups have a factorized S-matrix that can be written schematically in terms of 2 particle to 2-particle matrix elements of the form [37, 38]

where  is the rapidity difference of the incoming states. The
is the rapidity difference of the incoming states. The  are scalar factors, known also as dressing phases, that are needed to satisfy the S-matrix constraints of unitarity and crossing symmetry. The states of the theory are labelled by a and b which range over
are scalar factors, known also as dressing phases, that are needed to satisfy the S-matrix constraints of unitarity and crossing symmetry. The states of the theory are labelled by a and b which range over  , the rank of F. They transform in a product of representations of F,
, the rank of F. They transform in a product of representations of F,  , where Wa is the ath fundamental, or antisymmetric representation, for unitary and symplectic groups, but are not irreducible for the orthogonal cases10
. The two factors reflect the
, where Wa is the ath fundamental, or antisymmetric representation, for unitary and symplectic groups, but are not irreducible for the orthogonal cases10
. The two factors reflect the  symmetry of the PCM which act on the group field via the left and right action:
symmetry of the PCM which act on the group field via the left and right action:  . In (2.15), the
. In (2.15), the  are intertwiners
are intertwiners

These intertwiners are the rational solutions of the Yang–Baxter equation. The significance of the  label will emerge. The S-matrix is covariant under the
label will emerge. The S-matrix is covariant under the  symmetry of the theory, but this symmetry extends to an affine Yangian symmetry. The full spectrum of the theory can then be obtained by using the bootstrap equations. The bound states are associated to the antisymmetric representations of F although for the
symmetry of the theory, but this symmetry extends to an affine Yangian symmetry. The full spectrum of the theory can then be obtained by using the bootstrap equations. The bound states are associated to the antisymmetric representations of F although for the  groups these representations are sometimes reducible.
groups these representations are sometimes reducible.
For  , in [36] it was conjectured a form for the S-matrix of the k-deformed theory of the form
, in [36] it was conjectured a form for the S-matrix of the k-deformed theory of the form

where the  factor, the one that is gauged in order to construct the deformed theory, has changed from the rational
factor, the one that is gauged in order to construct the deformed theory, has changed from the rational  factor to the quantum group generalization with a quantum group deformation parameter that is a root of unity:
factor to the quantum group generalization with a quantum group deformation parameter that is a root of unity:  . It is also important that the quantum group factor
. It is also important that the quantum group factor  is taken in the so-called interaction-round-a-face' (IRF) picture, or 'restricted-solid-on-solid' (RSOS) picture. The significance of this is that the quantum numbers in this sector are naturally interpreted as kinks. So states of the theory carry a kink charge ±1 and also a vector in the two-dimensional representation of
is taken in the so-called interaction-round-a-face' (IRF) picture, or 'restricted-solid-on-solid' (RSOS) picture. The significance of this is that the quantum numbers in this sector are naturally interpreted as kinks. So states of the theory carry a kink charge ±1 and also a vector in the two-dimensional representation of  . The detailed form of the S-matrix is written in [36]. In the present context, the fact that the particle states are kinks can be understood as arising form the non-trivial spatial boundary conditions of the WZW models11
.
. The detailed form of the S-matrix is written in [36]. In the present context, the fact that the particle states are kinks can be understood as arising form the non-trivial spatial boundary conditions of the WZW models11
.
Based on the understanding of the  k-PCM model above, it is natural to conjecture that the k-PCM for a generic group F have a S-matrix of the schematic form
k-PCM model above, it is natural to conjecture that the k-PCM for a generic group F have a S-matrix of the schematic form

with  , where
, where  is the dual Coxeter number of F. As in the
is the dual Coxeter number of F. As in the  case, the quantum group intertwiner
case, the quantum group intertwiner  is defined in the IRF or RSOS representation. These S-matrices in general were first written down in [35] and discussed in detail in [40]. Note that the scalar factors
is defined in the IRF or RSOS representation. These S-matrices in general were first written down in [35] and discussed in detail in [40]. Note that the scalar factors  here, and below, depend implicitly on the actual group F. Using TBA techniques, this conjecture has been checked for SU(2) in [36] and, more recently, for
here, and below, depend implicitly on the actual group F. Using TBA techniques, this conjecture has been checked for SU(2) in [36] and, more recently, for  in [51].
in [51].
The intertwiners  are invariant under the action of an affine quantum group
are invariant under the action of an affine quantum group  in the following sense. There is an associated co-product Δ which describes how the generators act on a tensor product:
in the following sense. There is an associated co-product Δ which describes how the generators act on a tensor product:  ,
,  . The theory is invariant under the affine quantum symmetry in the sense that
. The theory is invariant under the affine quantum symmetry in the sense that

So the S-matrix elements lie in the commutant of  acting on a tensor product representation. In the limit,
acting on a tensor product representation. In the limit,  , the quantum group reduces to the Yangian symmetry of the undeformed PCM.
, the quantum group reduces to the Yangian symmetry of the undeformed PCM.
Now we turn to the SSSM. For the Type II cases, there is an obvious form that the S-matrix should take. One simply generalizes (2.18) to

which means that the symmetry involves a tensor product of quantum groups  .
.
For the Type I theories, a bespoke construction is needed in each case based on the S-matrices that were constructed for the undeformed theories [41]. However, the form of the undeformed S-matrix leads to a natural conjecture in each case.
 : for this series the S-matrix has the form originally found by Zamolodchikov and Zamolodchikov [42]
: for this series the S-matrix has the form originally found by Zamolodchikov and Zamolodchikov [42]

with particles transforming on the N-dimensional defining representation of  , which we show explicitly. We conjecture that the k-deformed theory has an S-matrix of the form
, which we show explicitly. We conjecture that the k-deformed theory has an S-matrix of the form

with  .
.
 : for this series the S-matrix has the form
: for this series the S-matrix has the form

where  indicates the symmetric product and the particles transform in the symmetric
indicates the symmetric product and the particles transform in the symmetric  -dimensional representation of
-dimensional representation of  that acts on both factors. In this case, there are no bound states. There is an analogous set of anti-particles transforming in the conjugate representation [38]. We conjecture that the k-deformed theory has an S-matrix of the form
that acts on both factors. In this case, there are no bound states. There is an analogous set of anti-particles transforming in the conjugate representation [38]. We conjecture that the k-deformed theory has an S-matrix of the form

with  .
.
 : for this series the S-matrix has the form
: for this series the S-matrix has the form

where  indicates the antisymmetric product. For each a, the particles transforms in a product of fundamental representations
indicates the antisymmetric product. For each a, the particles transforms in a product of fundamental representations  , one for each factor. Then the
, one for each factor. Then the  indicates that these are projected onto the anti-symmetric term of the
indicates that these are projected onto the anti-symmetric term of the  which acts diagonally on both factors. We conjecture that the k-deformed theory has an S-matrix of the form
which acts diagonally on both factors. We conjecture that the k-deformed theory has an S-matrix of the form

with  .
.
3. Poisson–Lie group symmetry
In this section, we will look for the classical footprints of a quantum group which appear in the form of global Poisson–Lie group symmetries of the Lagrangian. We will show that the conserved Poisson–Lie charges are given by the monodromies of two (mutually commuting) Kac–Moody currents.
3.1. Non-local symmetries of the  -deformed actions
-deformed actions
The action (2.2) is invariant under the discrete  -transformation12
-transformation12

which, in particular, allows one to extend the range of the parameter λ from ![$[0,1]$](https://content.cld.iop.org/journals/1751-8121/49/46/465201/revision1/jpaaa42c4ieqn113.gif) to
to  . Then, after integrating out the fields
. Then, after integrating out the fields  , the resulting effective action turns out to be invariant under
, the resulting effective action turns out to be invariant under

as pointed out originally in [33], where it was shown that it severely restricts the form of the RG flow equation for λ. This last symmetry will also play an important role in the following.
We now show that the theories have global Poisson–Lie group symmetries. To do this, the natural starting point is to consider left and right infinitesimal F-transformations separately. Namely,

with  . We find
. We find

In the k-PCM case, the vector action of the group corresponds to taking  ,
,  , and then adding both variations. This leads to
, and then adding both variations. This leads to

Then, for global transformations,  provided that the fields
provided that the fields  vanish at infinity. This shows that the action is invariant off-shell under global vector transformations, as expected, and provides conserved Noether charges. As a consequence, the target space geometry of the deformed PCM is invariant under the vector action of the group F. In the k-SSSM case, we get instead
vanish at infinity. This shows that the action is invariant off-shell under global vector transformations, as expected, and provides conserved Noether charges. As a consequence, the target space geometry of the deformed PCM is invariant under the vector action of the group F. In the k-SSSM case, we get instead

which vanishes off-shell for  in the Lie algebra of G. This exhibits the invariance of the action under G gauge transformations, but also that the k-SSSM has no other obvious off-shell (Noether) symmetries. However, since these theories are classically integrable, this is not the end of the story.
in the Lie algebra of G. This exhibits the invariance of the action under G gauge transformations, but also that the k-SSSM has no other obvious off-shell (Noether) symmetries. However, since these theories are classically integrable, this is not the end of the story.
Going back to the separate transformations, (3.4), we note that both can be put in the form

for some current J and some structure constants  On shell, each current is flat and so there exists conserved quantities Γ, the non-abelian moments, such that
On shell, each current is flat and so there exists conserved quantities Γ, the non-abelian moments, such that  . It is well-known that the existence of conserved non-local charges such as these have played an important role proving the integrability of sigma models and finding their exact S-matrices; for example in [38].
. It is well-known that the existence of conserved non-local charges such as these have played an important role proving the integrability of sigma models and finding their exact S-matrices; for example in [38].
To be more explicit, let us recall that the invariance of the action under generic field transformations provides the equations-of-motion which, in our case, can always be written in the Lax form (2.6). Then, the monodromy matrix13

is conserved for generic values of z, which provides an infinite number of, generally non-local, conserved quantities. Remarkably, the left and right variations (3.4) can be written in terms of the Lax pair evaluated at specific values of the spectral parameter z:

where in the k-PCM case

and in the k-SSSM case

In both, the significance of  is that
is that

The equations (3.9) relate the conservation of  and
and  to the invariance of the action under left and right transformations, respectively, in the following sense.
to the invariance of the action under left and right transformations, respectively, in the following sense.  implies that
implies that  is flat, which provides the conserved quantities
is flat, which provides the conserved quantities  .
.
Notice that the special points z± are uniquely determined by the deformation parameter λ and, furthermore, they are mapped into each other under the discrete transformation (3.2). Below, we will see that these points are precisely the poles of the so-called twisting functions that underlies the Poisson structure of these theories.
The Hamiltonian structure of the k-PCM and the k-SSSM can be written in terms of the canonical currents [18]

which obey the classical Kac–Moody algebra14

On-shell, we can write these currents as

The key observation for the following analysis if that the Kac–Moody currents are related to the Lax connection in a very simple way; namely,

where  is the spatial component of the Lax connection. This simple observation will allow us to deduce below that the k-deformed field theories have a quantum group symmetry. Then, from (3.16) we find that the conserved quantities associated to the global
is the spatial component of the Lax connection. This simple observation will allow us to deduce below that the k-deformed field theories have a quantum group symmetry. Then, from (3.16) we find that the conserved quantities associated to the global  Poisson–Lie group action in both models take a rather universal form
Poisson–Lie group action in both models take a rather universal form

Applying (3.2) to either (3.13) or (3.15) we see that the effect of the discrete transformation is to exchange the two Kac–Moody currents

Then,  are mapped into each other under (3.2), so that one of the Poisson–Lie symmetries, say FR, can be generated by a combination of FL and Π. In section 4 below we turn to the quantum version of the algebra generated by
are mapped into each other under (3.2), so that one of the Poisson–Lie symmetries, say FR, can be generated by a combination of FL and Π. In section 4 below we turn to the quantum version of the algebra generated by  .
.
3.2. The  /
/ Maillet forms and twisting functions
Maillet forms and twisting functions
In this section, we exploit the Kac–Moody algebraic structure (3.14) of the k-deformed theories to compute the Poisson brackets of the spatial component of the Lax connection. In particular, we are interested in extracting the twisting function  induced by the
induced by the  /
/ form and study its pole structure. We begin with the k-PCM theories, and then consider the k-SSSM theories, which require a slightly different treatment.
form and study its pole structure. We begin with the k-PCM theories, and then consider the k-SSSM theories, which require a slightly different treatment.
k-PCM case:
We start by writing the spatial component of the k-PCM Lax connection for generic values of the spectral parameter in the form

with

Then, the Kac–Moody algebra (3.14) provides the Maillet  /
/ representation of the Poisson bracket
representation of the Poisson bracket

In this kind of representation, the equation is to be understood as acting on some tensor product  , where V is some faithful representation of the Lie algebra
, where V is some faithful representation of the Lie algebra  , and the index on top show which of the factors the quantity acts on, e.g.
, and the index on top show which of the factors the quantity acts on, e.g.  and
and  , etc. Quantities like
, etc. Quantities like  and
and  defined below act on both factors.
defined below act on both factors.
In (3.21), the  /
/ matrices are given by
matrices are given by

where

is the so-called twisting function and  is the tensor Casimir. Notice that
is the tensor Casimir. Notice that  has two poles located precisely at at
has two poles located precisely at at 

These poles are exactly the evaluation points displayed in (3.10) used to extract the Lie–Poisson group charges out of the monodromy matrix. The extra pole at z = 0 has no physical significance and can be removed by working with  instead. In this case, the poles are inverted
instead. In this case, the poles are inverted  and the (3.22) can be rewritten in a more suggestive way
and the (3.22) can be rewritten in a more suggestive way

where15

and

are the twisting functions of the undeformed PCM and the FR model, and  is the deformation parameter in the
is the deformation parameter in the  branch.
branch.
The  /
/ matrices satisfy a modified classical Yang–Baxter equation, mCYBE, a fact which was proven explicitly in [44]. Notice that in the FR limit
matrices satisfy a modified classical Yang–Baxter equation, mCYBE, a fact which was proven explicitly in [44]. Notice that in the FR limit  , we have
, we have

and the non-ultra-locality is completely removed. This is the celebrated ultra-localization of the PCM introduced by hand in [1]. Consequently, the k-PCM can be thought as the Lagrangian implementation of the FR ultra-localization mechanism.
The values of the s matrix at the poles are given by

Using these values in the Maillet bracket (3.21), we recover the Kac–Moody current algebra (3.14) in tensorial form

The values of  at the same poles depends on how we take the limit but are always proportional to the tensor Casimir and hence do not contribute to the Poisson bracket. However, the values at different poles vanish identically.
at the same poles depends on how we take the limit but are always proportional to the tensor Casimir and hence do not contribute to the Poisson bracket. However, the values at different poles vanish identically.
We end this section, by rewriting (3.21) in a slightly different way which will be useful when we consider the k–F/G theories. By defining

we can write the Maillet bracket as

where

k-SSSM case:
Inspired by (3.26), this time we take the following inverse twisting function

where

and c is a constant yet to be fixed by the evaluation of  at the poles of
at the poles of  .
.
The deformed twisting function is

which has four poles given by

The two poles corresponding to the positive branch of the square root are the evaluation points (3.11) used to extract the Lie–Poisson group charges out of the monodromy matrix16 . These poles are important for establishing the quantum group symmetry of the theory, as we shall see below.
The calculation we need to find  and
and  was already done in [43] for the branch
was already done in [43] for the branch  and also holds in the present case as the compatibility of the Poisson brackets is independent of the sign of
and also holds in the present case as the compatibility of the Poisson brackets is independent of the sign of  . The R-matrix corresponding to the Poisson bracket in the form (3.32) is17
. The R-matrix corresponding to the Poisson bracket in the form (3.32) is17

from which follows the  /
/ matrices in our present case
matrices in our present case

However, it is important to recall that the expressions for  written right above follows by using the following modified Lax operator
written right above follows by using the following modified Lax operator

where

It corresponds to the extension of the Lax operator out of the constraint surface by the only first class constraint present for this case

See [18] for details on the Hamiltonian approach. The Maillet bracket then follows as a simple consequence of the underlying Kac–Moody algebra structure.
Concentrating on the  matrix, after some simplification we find it can be put in the form
matrix, after some simplification we find it can be put in the form

Written in this way we can easily evaluate this function at the poles

The normalization of the central term in the Kac–Moody algebra imposes the condition

which fixes the so far unspecified constant c to be

This value for c can be verified independently by direct use of the extended Lax operator (3.40). In the limit  we have
we have

from which follows that in the coset case the non-ultra-locality can be only partially tamed [2]. As in the k-PCM case, from the Maillet bracket we recover the Kac–Moody algebra in tensor form.
3.3. Expansion of the monodromy around the poles of the twisting function
We work in the de-compatified limit, in which the monodromy matrix takes the general form18

where for the first three terms we get

The limit a and b will subsequently be taken to  , respectively. Expanding
, respectively. Expanding  around a chosen point in the complex plane and reorganizing the series in powers of the spectral parameter z, not to be confused with the integration variable z, we find the corresponding non-local charges associated to that particular point.
around a chosen point in the complex plane and reorganizing the series in powers of the spectral parameter z, not to be confused with the integration variable z, we find the corresponding non-local charges associated to that particular point.
Let us focus first on the k-PCM theory. When expanded around the poles  we find the following expression for the spatial Lax operator
we find the following expression for the spatial Lax operator

where  and
and

The expansion for the Lax operator around the poles (3.49) starts with terms of order  . These terms can be removed by judicious gauge transformations,
. These terms can be removed by judicious gauge transformations,

where the gauge transformation takes the form

around each pole, respectively. In this way, (3.48) can be written as follows

with a transformed Lax operator

defined in terms of the non-local dressed currents

Taking  and
and  , the expansion of the monodromy matrix around the poles
, the expansion of the monodromy matrix around the poles  now takes the form
now takes the form

As a result of the gauge transformation, all the charges  are non-local and the first three take the explicit form
are non-local and the first three take the explicit form

Notice that under  , which corresponds to the transformation (3.2), we do indeed have
, which corresponds to the transformation (3.2), we do indeed have  as claimed. This follows from our earlier observation that we can combine the FL group action with (3.2) to generate FR and vice versa. If we evaluate these charges at the, for us, unphysical value of the coupling constant
as claimed. This follows from our earlier observation that we can combine the FL group action with (3.2) to generate FR and vice versa. If we evaluate these charges at the, for us, unphysical value of the coupling constant  , then the two poles coalesce at
, then the two poles coalesce at  and the expansion of the monodromy produces charges that coincide with the first three Yangian charges found in [44]
and the expansion of the monodromy produces charges that coincide with the first three Yangian charges found in [44]

On the one hand, the dominant term for the expansion around z = 0 is the local Noether charge  corresponding to the global vector action of F and given by (3.5). The Poisson algebra generated by
corresponding to the global vector action of F and given by (3.5). The Poisson algebra generated by  is isomorphic to
is isomorphic to  and the higher charges
and the higher charges  ,
,  enhance this Poisson algebra to a Yangian, see [44].
enhance this Poisson algebra to a Yangian, see [44].
On the other hand, the dominant terms for the expansions around  are the non-abelian moments (3.17) associated to the global Poisson–Lie group action
are the non-abelian moments (3.17) associated to the global Poisson–Lie group action  . They will be shown to generate the finite-dimensional quantum group
. They will be shown to generate the finite-dimensional quantum group  after quantization. It is then natural to expect that higher charges enhance
after quantization. It is then natural to expect that higher charges enhance  to an affine quantum symmetry to match the symmetries of the S-matrices that we have conjectured to describe these theories in section 2. However, explicit computations of the algebra of higher charges is complicated by the non-trivial dressing factors
to an affine quantum symmetry to match the symmetries of the S-matrices that we have conjectured to describe these theories in section 2. However, explicit computations of the algebra of higher charges is complicated by the non-trivial dressing factors  , hence we expect to report about this problem in the near future. Fortunately, some evidence that this enhancement may occur in our case comes from a different kind of deformation of the
, hence we expect to report about this problem in the near future. Fortunately, some evidence that this enhancement may occur in our case comes from a different kind of deformation of the  PCM [45–47], in which a classical q-deformed Poisson algebra of symmetries induced by the squashing is studied for this particular case. What suggests this is that, technically, the situation in those references is essentially the same as ours, namely, the generators of the q-deformed symmetry group are extracted from the expansion of the monodromy matrix at the poles of the twisting function.
PCM [45–47], in which a classical q-deformed Poisson algebra of symmetries induced by the squashing is studied for this particular case. What suggests this is that, technically, the situation in those references is essentially the same as ours, namely, the generators of the q-deformed symmetry group are extracted from the expansion of the monodromy matrix at the poles of the twisting function.
For the k-SSSM theories, a similar story holds. We have exactly the same expansion as given by (3.49) but with different expressions for the current components

where  An intuitive way to seek for Yangian symmetries is to find a value of λ for which
An intuitive way to seek for Yangian symmetries is to find a value of λ for which  , see the first equation of (3.50) with
, see the first equation of (3.50) with  in the k-PCM case. Notice, however, that such a solution does not exist for the k-SSSM theories, hence we do not expect any Yangian symmetries in this case. This is in agreement with the absence of global Noether charges as noticed above around (3.6).
in the k-PCM case. Notice, however, that such a solution does not exist for the k-SSSM theories, hence we do not expect any Yangian symmetries in this case. This is in agreement with the absence of global Noether charges as noticed above around (3.6).
Then, the expansion of the monodromy matrix around the poles takes the rather universal form (3.56). The model dependence shows up in the higher charges 
 In the k-PCM they are all Lie-algebra valued while in the k–F/G they are all coset valued except for the extension associated to the first class constraint.
In the k-PCM they are all Lie-algebra valued while in the k–F/G they are all coset valued except for the extension associated to the first class constraint.
We now proceed to quantize the monodromies  and find their quantum algebra.
and find their quantum algebra.
4. Quantum lattice current algebra
In order to quantize a integrable field theory, the technical difficulties in dealing with monodromy matrix are usual addressed by introducing a lattice regulator which does not break the integrability of the theory. Unfortunately in the current setting, our theories have a non-ultra-local Poisson bracket and it is well known [19] that, even at the classical level, this precludes a direct approach to computing the Poisson bracket of the monodromy matrix for any value of the spectral parameter z.
In the quantum theory, this means that the lattice current algebra for these field theories for general values of the spectral parameter z is not even known to exist. Fortunately, we can make progress by working directly at the poles  of the twist function. Our approach in this section draws mainly on the formalism established in [20–22, 49]. Like in these references, our calculations will be restricted to
of the twist function. Our approach in this section draws mainly on the formalism established in [20–22, 49]. Like in these references, our calculations will be restricted to  19
.
19
.
4.1. The lattice current algebra at the poles
Let us recall that the equations of motion of the k-deformed theories can be re-cast in Lax form as the zero curvature condition (2.6). This form manifests an infinite-dimensional group of gauge transformations generated by the group elements 

From (3.16) we conclude that, when evaluated at the poles  , this group becomes the ordinary loop group
, this group becomes the ordinary loop group  of gauge transformations of the Kac–Moody currents
of gauge transformations of the Kac–Moody currents

which are symmetries of the Kac–Moody algebra (3.30).
Before introducing a lattice regularization of the theory we can infer, via a semi-classical analysis, that the k-deformation parameter of the quantum group generated by  is indeed a root of unity. This information can be extracted from the Maillet representation (3.21) evaluated at the poles. Introducing the parallel transport
is indeed a root of unity. This information can be extracted from the Maillet representation (3.21) evaluated at the poles. Introducing the parallel transport

which obeys

and then following Maillet [19], we find in our case

In the above, for brevity, we have not indicated the spectral parameter dependence but we should keep in mind that u depend on it. In fact, we are only interested in the result above when it is evaluated at the poles  in which
in which  , as in (3.16), picks out the Kac–Moody currents. In this case we find that
, as in (3.16), picks out the Kac–Moody currents. In this case we find that

where s is given by

and  is the sign function and in what follows we will drop the ± indices for simplicity20
.
is the sign function and in what follows we will drop the ± indices for simplicity20
.
The expression (4.6) is the classical exchange algebra we want to quantize semi-classically. We want to emphasize that at the moment we are proceeding in a rather ad hoc fashion in order to provide some inspiration for the lattice algebra defined below. By exploiting the classical commutativity of the u's and using the quantization rule21
![$-{\rm{i}}\{\ast ,\ast \}\to [\ast ,\ast ]$](https://content.cld.iop.org/journals/1751-8121/49/46/465201/revision1/jpaaa42c4ieqn219.gif) , we get
, we get

where the ellipsis denote sub-leading quantum contributions. From this we infer that, roughly speaking, we should expect something like

which is an interesting expression as it relates Maillet's s matrix, the poles and the k-deformation parameter. Notice that the effect of the tranformation (3.2) is to map 
The calculation above should not be considered as a formal one, we use it only as a source of inspiration for the type of quantum algebra we should expect. In particular, the Poisson brackets (4.6) do not obey the Jacobi identity. Indeed, we find

which never vanishes for distinct  .
.
After the naïve semi-classical approach, we are now ready to introduce the lattice algebra. The first thing is to discretize the spatial circle  in terms of N points with coordinates
in terms of N points with coordinates  ,
,  mod N in the order
mod N in the order  . Then, we define the transport matrix
. Then, we define the transport matrix

between sites. Evaluating it at the poles  defines for us the lattice variables
defines for us the lattice variables

Choosing a particular ordering, we can define two monodromy matrices on  ,
,

However, in order to keep things simpler we will concentrate on the pole  only, drop the index L and set
only, drop the index L and set 
The quantum lattice Kac–Moody algebra at the pole  is then defined by the following algebra
is then defined by the following algebra

where  (transpose) and
(transpose) and  (inverse).
(inverse).
Now, the classical continuum limit is achieved by writing

where  and
and  are solutions of the quantum/classical YBE such that
are solutions of the quantum/classical YBE such that

where  is the lattice spacing and
is the lattice spacing and  . The first step is to find the classical limit of (4.13). We find
. The first step is to find the classical limit of (4.13). We find

The next step is to take the continuum limit. We find that  and then the Kac–Moody algebra follows. The algebra (4.13) underlies the quantization of the monodromy matrix
and then the Kac–Moody algebra follows. The algebra (4.13) underlies the quantization of the monodromy matrix  .
.
Recall that classically we have

where  is the 'wave-function'
is the 'wave-function'

The gauge transformations (4.2) acting on  are now equivalent to the action of the loop group
are now equivalent to the action of the loop group  on the
on the  . On the lattice, this classical expressions become22
. On the lattice, this classical expressions become22

The wave functions also obey the following quantum exchange algebra relations

The last relation means that the classical gauge loop group is promoted to a quantum gauge group with algebra [20]

This quantum group leaves the Kac–Moody lattice algebra (4.13) invariant in the same way its classical counterpart leaves invariant the usual Kac–Moody algebra.
Writing  with
with  antisymmetric which explicitly obeys the constraint (4.15), we can find the corrected version of the Poisson bracket (4.6) for the wave-function
antisymmetric which explicitly obeys the constraint (4.15), we can find the corrected version of the Poisson bracket (4.6) for the wave-function  (in the normalization
(in the normalization  directly from the classical/continuum limit of the first two equations of the exchange algebra (4.20), namely,
directly from the classical/continuum limit of the first two equations of the exchange algebra (4.20), namely,

This Poisson bracket do obey the Jacobi identity provided the antisymmetric  -matrix is a solution of the mCYBE of the split-type [29]. See the discussion around equation (5.9) of that paper. This decomposition of
-matrix is a solution of the mCYBE of the split-type [29]. See the discussion around equation (5.9) of that paper. This decomposition of  is consistent with the requirement that it is a solution of the CYBE.
is consistent with the requirement that it is a solution of the CYBE.
The quantum monodromy matrix is given by  and satisfy the quadratic algebra
and satisfy the quadratic algebra

When we consider the following quantum factorization of the monodromy matrix

the RTT quadratic relations given by its factorized components, namely,

are compatible with (4.22). Notice that (4.24) is the analogue of equation (13) of [21] in the case of sl(2), which is another definition of the associated quantum group  . The quantum monodromy matrix
. The quantum monodromy matrix  then becomes an element of Fq. The Poisson–Lie symmetry found in the classical k-deformed theory is then promoted to a quantum group symmetry.
then becomes an element of Fq. The Poisson–Lie symmetry found in the classical k-deformed theory is then promoted to a quantum group symmetry.
The continuum limit of (4.20) is

where  is the permutation operator and
is the permutation operator and  an invertible matrix. This way of factorizing the usual R matrix comes from the theory of quasi-Hopf algebras introduced by Drinfeld23
. It was shown in [21], that this exchange algebra underlies the quantization of the Kac–Moody algebra. Indeed, the quantum version of the classical currents (4.17), namely, the quantum operators
an invertible matrix. This way of factorizing the usual R matrix comes from the theory of quasi-Hopf algebras introduced by Drinfeld23
. It was shown in [21], that this exchange algebra underlies the quantization of the Kac–Moody algebra. Indeed, the quantum version of the classical currents (4.17), namely, the quantum operators

obey the following algebra

where

and n is the size of the matrices used to represent the currents, e.g., n for the fundamental representation of  , which corresponds to the present case. Taking the ansatz for the deforming parameter
, which corresponds to the present case. Taking the ansatz for the deforming parameter

and re-scaling the quantum currents (take  in (4.17)) it was shown in [21] that the rescaled currents obey the quantum Kac–Moody algebra. Notice that in the semi-classical limit we recover our previous rough result with
in (4.17)) it was shown in [21] that the rescaled currents obey the quantum Kac–Moody algebra. Notice that in the semi-classical limit we recover our previous rough result with  . Using the duality between the Faddeev–Reshetikhin–Takhtajan
. Using the duality between the Faddeev–Reshetikhin–Takhtajan  and the Drinfeld–Jimbo
and the Drinfeld–Jimbo  realizations of quantum groups, we infer that the deformed sigma models considered so far are q-deformed with deformation parameter being a root of unity.
realizations of quantum groups, we infer that the deformed sigma models considered so far are q-deformed with deformation parameter being a root of unity.
A comment is in order. From the second equation in (3.31) and (4.15) one would naively conclude that

but the following observation shows this is not the case. The  limit is ambiguous as can be seen from
limit is ambiguous as can be seen from

and even if we ignore this and work with the non-zero answer, this identification would imply that the classical limits of (4.22) and (4.24) are trivial, which is inconsistent. Then, the poles of the twisting function are to be treated as punctures in the complex plane z with a complete separate analysis. In this respect, the quantum  -matrix and its classical counterpart
-matrix and its classical counterpart  used in (4.13) are artifacts of our quantization scheme not related to the
used in (4.13) are artifacts of our quantization scheme not related to the  operators in the Maillet bracket at all. In the classical/continuum limit, quantities should be independent of the quantization procedure but if, for instance, we consider the symmetry algebras (4.22) and (4.24) they would depend on
operators in the Maillet bracket at all. In the classical/continuum limit, quantities should be independent of the quantization procedure but if, for instance, we consider the symmetry algebras (4.22) and (4.24) they would depend on  in this limit, hence the quantized monodromy matrix should remain quantum. Notice that this does not apply to its associated KM algebra because it is independent of
in this limit, hence the quantized monodromy matrix should remain quantum. Notice that this does not apply to its associated KM algebra because it is independent of  in the classical/continuum limit, as claimed in [21].
in the classical/continuum limit, as claimed in [21].
It is noteworthy that it is the central charge k of the Kac–Moody algebra instead of parameter λ that sets the deformation of the symmetry group. This is, perhaps, surprising as one might have expected q to depend on the deformation parameter λ as in the η-deformation [8]. Presumably the reason lies in the fact that the Kac–Moody currents (3.13) obey the Kac–Moody algebra no matter what the deformation parameter λ is and hence their monodromies obey a λ-independent algebra. In this respect, the k-deformations ( ) are quite different in nature from the η-deformation (
) are quite different in nature from the η-deformation ( ). However, there is still the possibility that somehow higher spin charges appearing in the z expansion of the monodromy matrix around the poles, e.g. (3.56), introduce a λ dependence in a way yet to be understood.
). However, there is still the possibility that somehow higher spin charges appearing in the z expansion of the monodromy matrix around the poles, e.g. (3.56), introduce a λ dependence in a way yet to be understood.
5. Conclusions
In this paper, we have conjectured the form of the S-matrix theories that should describe the k-deformed principal chiral models and symmetric space sigma models. All of them exhibit affine quantum group symmetries with a deformation parameter q that is a root of unity. Then, making use of the results of [21], we have provided evidence that the quantum group symmetry appears in a direct quantization that preserves integrability in the form of a finite-dimensional quantum group symmetry, at least for the theories corresponding to  .
.
However, there are some important details that remain to be understood. For instance, the proposed S-matrices exhibit a symmetry under the affine quantum group while it seems difficult to see how to extend the symmetry of the lattice quantization in this way. A proper study of the higher spin non-local charges that appear in the expansion of the monodromy matrix at the poles of the twisting function is certainly interesting from the quantum group theory point of view. In this regard, it would be important to understand the role of these charges in relation to the conjectured affine quantum group symmetry of the S-matrices for the deformed theories.
It is also not immediately clear how to generalize the approach of [21] to the cases of theories involving the other classical Lie groups. Even more ambitious, would be the generalization to semi-symmetric space sigma models involving Grassmann fields and Lie superalgebras that are needed to apply these ideas to the superstring. In any case, leaving out the technical details, it is worth recalling that the existence of the finite-dimensional quantum group symmetry follows simply from equation (3.16). Namely, from the observation that the spatial component of the Lax operator of these theories evaluated at specific values of the spectral parameter, which are poles of the λ-deformed twisting function, is a Kac–Moody current. Remarkably, the same is true for the k-deformation of the Green–Schwarz  sigma model (see equation (3.14) of [16]) and, thus, we expect that a similar construction will reveal a finite-dimensional quantum group symmetry with a deformation parameter q that is a root of unity also in this case.
sigma model (see equation (3.14) of [16]) and, thus, we expect that a similar construction will reveal a finite-dimensional quantum group symmetry with a deformation parameter q that is a root of unity also in this case.
Acknowledgments
The authors would like to thank to Benoit Vicedo for very valuable communications at an early stage in this work. DMS is very grateful to Alessandro Torrielli for very pleasant and enlightening discussions around quantum groups and to the Surrey University for hospitality during his visits.
TJH is supported in part by the STFC grant ST/G000506/1. JLM is supported in part by MINECO (FPA2011-22594 and FPA2014-52218-P), the Spanish Consolider- Ingenio 2010 Programme CPAN (CSD2007-00042), Xunta de Galicia (GRC2013-024), and FEDER. DMS is supported by the FAPESP grant 2012/09180-9.
Footnotes
- 4
It is worth pointing out, that this simple construction does not describe the k-deformation of the full superstring world sheet theory worked out in [16].
- 5
In the Hamiltonian formulation, the first class constraints associated to F are transformed into second class constraints for the k-PCM case. For the k-SSSM this fate also befalls the first class constraints in the coset part of the Lie algebra
 to leave a G gauge symmetry.
to leave a G gauge symmetry. - 6
Notice that
 so that, in these bosonic models, Ω coincides with its transpose.
so that, in these bosonic models, Ω coincides with its transpose. - 7
- 8
Or requires the addition of supersymmetry.
- 9
- 10
If Va are the fundamental representations, then
 .
. - 11
Discussed, for example, in [39].
- 12
Since the action is also invariant under
 , this transformation is equivalent to the one written down in [28].
, this transformation is equivalent to the one written down in [28]. - 13
We assume here, that the field theories are defined on a spatial circle.
- 14
Here, we define
 and follow the conventions of [18].
and follow the conventions of [18]. - 15
In this computation we use
 , and
, and  .
. - 16
It would be interesting to find an interpretation for the negative branch poles and their relation with the monodromy matrix.
- 17
In the following, we define
 for
for  . Only
. Only  and
and  are non-vanishing and
are non-vanishing and  .
. - 18
Take
 and
and  in equation (20) of [48] and re-organize equation (22).
in equation (20) of [48] and re-organize equation (22). - 19
- 20
In what follows we fix the ambiguity on the lower limits of integration by setting
 , which is the normalization condition reproduced in the classical continuum limit of the lattice algebra regularization to be considered below. We will drop explicit dependence on x0 from the notation.
, which is the normalization condition reproduced in the classical continuum limit of the lattice algebra regularization to be considered below. We will drop explicit dependence on x0 from the notation. - 21
This kind of naïve replacement is subtle when group-like quantities have quadratic Poisson brackets but this subtlety is not relevant in the semi-classical limit.
- 22
For any value of
 the un all start with the term J1, which is the normalization condition
the un all start with the term J1, which is the normalization condition  used before in the semi-classical analysis.
used before in the semi-classical analysis. - 23
For further details we refer, for example, to section 2 of [50] in which the main properties of Drinfeld twists are reviewed.





















