Abstract
In the limit of rapid passage in a time-dependent two-level system of the Landau–Zener type, the initial state undergoes a very simple yet non-trivial rotation. This effect takes place when the Hamiltonian reaches the stationary point of the system. We explain the origin of this rotation by simple means and extend it to open non-Hermitian (NH) systems where new features appear. In addition, we find that in contrast to the Hermitian case, the point at which this simple rotation takes place is not necessarily the point of minimal energy separation. Moreover, in NH Hamiltonian the stationary point may lie in the complex time plane, and then a surprisingly strong correction to the rotation angle appears. The NH aspects of this rotation can be observed in optical and quantum systems where decay rates can be controlled.
This article is part of a special issue of Journal of Physics A: Mathematical and Theoretical devoted to 'Quantum physics with non-Hermitian operators'.
Export citation and abstract BibTeX RIS
1. Introduction
A general two-level Hermitian Landau–Zener (LZ)-type [1] Hamiltonian has the form

where H0 and H1 are some Hermitian operators and α is a real number. This generic model Hamiltonian describes the simplest scenario of a passage through avoided crossings. As such, it has been studied in various physical systems that can be represented or approximated by a two-level Hamiltonian: a spin in a magnetic field, cold atoms in an optical lattice [2, 3], an atom in a chirped/modulated laser pulse [4], optics [5, 6], superconducting qubits [7] and more. The celebrated LZ result [1] describes the probability of a spin which is an eigenstate of H1 to flip after it has evolved in time from t = −∞ to t = +∞. While investigating various other questions related to some specific Hermitian LZ Hamiltonians, it was observed several times in the literature [8–11] (even though rarely explicitly stated) that in the limit of large α, the spin orientation takes a simple yet non-trivial form at the avoided crossings. The large α limit is very useful in LZ systems that also involve some slow relaxation processes. If the sweep rate α is high, these processes can be ignored and features of the system can be measured using LZ analysis. This technique has been successfully used in energy gap measurement of single-molecule magnets [12, 13]. The analytic observation mentioned before was based on the analysis of the explicit analytical solution of the specific system. The paper has two main goals. The first is to show that this rotation is a general feature of the linear time dependence in the Hamiltonian and that the exact analytical solutions that were used before are not needed. The second goal is to extend this result to a class of non-Hermitian Hamiltonians which are 'asymptotically Hermitian' as will be defined later. Non-Hermitian LZ Hamiltonians have been studied before [6, 14–18], but the effects of non-Hermiticity on the asymptotic azimuthal rotation are studied here for the first time. In particular, we discover two new findings. The first is that the point that dominates the dynamics in the non-Hermitian (NH) case is not the point of the minimal energy gap as in Hermitian systems. The second finding is that in some NH Hamiltonians the correction to the asymptotic rotation value is of order 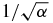 , while in the Hermitian case the leading correction is only of order 1/α.
, while in the Hermitian case the leading correction is only of order 1/α.
NH Hamiltonian systems often appear as an effective compact description of phenomena which are associated with resonances. Resonances describe a leak of population from the state of interest to some continuum which is left out in the compact NH description. In quantum mechanics (QM), such population leaks appear, for example, in tunneling resonances (aka shape resonances), and in optics they can be due to the presence of absorbing/amplifying media. This is fundamentally different from interaction with a bath where momentum/energy exchange is traced out, but the probability in the subsystem is conserved. The interaction with the bath that gives rise to decoherence and other relaxation mechanisms is described by the Lindblad equation for density matrices and not by the Schrödinger equation (SE) for states. Our paper concerns only NH Hamiltonian systems described by the SE. Note that the effect of decoherence, for example, can be avoided in the limit of large α if the whole sweep process is much shorter than the decoherence timescale.
Let |↑1〉 and |↓1〉 be the eigenstates of H1 that correspond to positive (up) and negative (down) eigenvalues of H1. The system is set up to be in one of those eigenstates at t → −∞. In this work, we are interested in the state of the spin at the stationary point of the system. In the Hermitian case, the stationary point corresponds to the avoided crossing of the Hamiltonian. Let  and
and 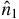 be the directions associated with the positive-valued eigenstates of H0 and H1, respectively. We find that for large α > 0 (Hermitian case), the change in the spin orientation points to the direction:
be the directions associated with the positive-valued eigenstates of H0 and H1, respectively. We find that for large α > 0 (Hermitian case), the change in the spin orientation points to the direction: 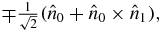 where the '+' ('–') correspond to the spin-up (down) initial state. Stated in terms of spherical coordinates: setting the z axis to be in the
where the '+' ('–') correspond to the spin-up (down) initial state. Stated in terms of spherical coordinates: setting the z axis to be in the 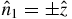 direction and the x axis in the
direction and the x axis in the 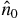 direction, we find that the value of the azimuthal angle of the spin, φ, in the Hermitian case (α > 0) is −3π/4 or π/4 (figure 1(a)). Note that in the adiabatic limit, the spin will be completely oriented in the
direction, we find that the value of the azimuthal angle of the spin, φ, in the Hermitian case (α > 0) is −3π/4 or π/4 (figure 1(a)). Note that in the adiabatic limit, the spin will be completely oriented in the 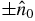 direction. In the fast evolution limit, it is expected that the spin will only slightly deviate from
direction. In the fast evolution limit, it is expected that the spin will only slightly deviate from 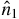 . Yet, it is not straightforward to tell what the direction of this small deviation will be. The NH case is richer and more subtle as will be shown later on. The paper is organized as follows. Section 2 introduces the formalism and defines our points of interest. In section 3, we study the Hermitian case and derive φ at the avoided crossing. Section 4 deals with a certain type of NH Hamiltonian. In section 5, we study more general NH Hamiltonians. We analytically derive the unique NH
. Yet, it is not straightforward to tell what the direction of this small deviation will be. The NH case is richer and more subtle as will be shown later on. The paper is organized as follows. Section 2 introduces the formalism and defines our points of interest. In section 3, we study the Hermitian case and derive φ at the avoided crossing. Section 4 deals with a certain type of NH Hamiltonian. In section 5, we study more general NH Hamiltonians. We analytically derive the unique NH 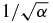 correction to the rotation angle and compare it to numerical results.
correction to the rotation angle and compare it to numerical results.
2. Formalism
The trace of H(t) only affects the global phase of both states, so without loss of generality we consider traceless H0 and H1. We start by transforming the solution of the SE, |ψ〉, to the H1 co-rotating frame via the transformation:  . This transformation contributes only a global phase to the initial eigenstate at t = −∞, and in addition at t = 0: |ψ(t = 0)〉 = |ϕ(t = 0)〉. After writing the state as |ϕ〉 = a(t)|↑1〉 + b(t)|↓1〉 and projecting on the spin-up and spin-down states, the SE takes the form
. This transformation contributes only a global phase to the initial eigenstate at t = −∞, and in addition at t = 0: |ψ(t = 0)〉 = |ϕ(t = 0)〉. After writing the state as |ϕ〉 = a(t)|↑1〉 + b(t)|↓1〉 and projecting on the spin-up and spin-down states, the SE takes the form

where β = αΔ1 and Δ1 = 〈↑1|H1|↑1〉 − 〈↓1|H1|↓1〉 > 0. It is easy to remove the diagonal term by a simple time shift 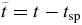 . The shifted Hamiltonian is
. The shifted Hamiltonian is


Now we demand

and obtain

 is traceless so
is traceless so 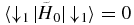 immediately follows from (5). More importantly, it means that there is an avoided crossing at
immediately follows from (5). More importantly, it means that there is an avoided crossing at 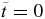 . tsp is always a real number in the Hermitian case, but in the NH case it may be complex. After revising the transformation to
. tsp is always a real number in the Hermitian case, but in the NH case it may be complex. After revising the transformation to 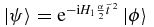 , equations (2) are replaced by
, equations (2) are replaced by


The exponential factors have a stationary phase at 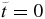 . Had we not made the time shift, the stationary point would have appeared at t = tsp ≠ 0. In what follows, we shall use a superscript ± to denote the solutions for spin-up ('+'), and spin-down ('–') initial conditions. Starting with the '+' initial condition (a+( − ∞) = 1, b+( − ∞) = 0), integration of equation (8) from
. Had we not made the time shift, the stationary point would have appeared at t = tsp ≠ 0. In what follows, we shall use a superscript ± to denote the solutions for spin-up ('+'), and spin-down ('–') initial conditions. Starting with the '+' initial condition (a+( − ∞) = 1, b+( − ∞) = 0), integration of equation (8) from  to
to  yields
yields

In the limit of rapid passage the spin hardly changes its orientation so a+(t) is roughly fixed and close to unity. Using the stationary phase approximation, we obtain
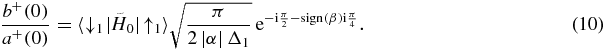
It can easily be shown that the azimuthal angle, φ, of a spin |ϕ〉 = a(t)|↑1〉 + b(t)|↓1〉 with respect to the x axis is given by the phase of b/a :

Therefore, in the limit of large |α| we obtain that the azimuthal angles at the stationary point are

where


These results are shown graphically in figure 1(b). The rotation, Δθ, in the θ coordinate has a simple expression for small angles (which is consistent with rapid passage):

In what follows, we focus on the azimuthal angle φ since it obtains a non-trivial value in the limit of large α, while the angle θ simply approaches zero in this limit. After applying our result to the Hermitian case we shall discuss some features and phenomena that are unique to the NH case.
3. The Hermitian case
In the Hermitian case, 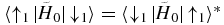 so φ+0 = φ0− and φ+ − φ− = −π, which reflects the fact that the two possible initial spin states remain orthogonal to each other throughout the evolution. Therefore, their spin direction is anti-parallel. To interpret this result geometrically, we point out that the states |↓1〉, |↑1〉 induce a natural choice of axes through the states:
so φ+0 = φ0− and φ+ − φ− = −π, which reflects the fact that the two possible initial spin states remain orthogonal to each other throughout the evolution. Therefore, their spin direction is anti-parallel. To interpret this result geometrically, we point out that the states |↓1〉, |↑1〉 induce a natural choice of axes through the states: 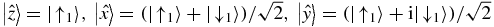 , which are all eigenstates of the standard Pauli matrices
, which are all eigenstates of the standard Pauli matrices 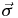 . In this axis system, it is easy to show that in the Hermitian case
. In this axis system, it is easy to show that in the Hermitian case

where ρ is a positive number and φ0 is the azimuthal angle. Thus, the argument in equation (13) gives the angle in the xy plane that corresponds to the direction of 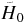 (written before as
(written before as 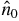 ). Therefore, the spin projections on the xy plane point in the directions
). Therefore, the spin projections on the xy plane point in the directions

where 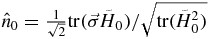 and
and  .
.
The next leading correction to the angle φ for Hermitian 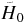 is of the order
is of the order 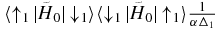 . Figure 2 shows numerically how the azimuthal rotation angle at the avoided crossing approaches the asymptotic value, φ+, as α increases. It is important to note that the faster the passage, the smaller the angle θ becomes (see (15)). Nevertheless, as seen in figure 2 the main effect is apparent even for very moderate α. For example, if the energies of H0 and H1 are comparable and α ∼ 3, θ is about 0.3. The deviation from the asymptotic angle φ+ = −0.75π for this α is just ∼5%. This example shows that the results of the analysis in this paper provide good estimates even very far from the rapid passage limit where Δθ ≪ 1.
. Figure 2 shows numerically how the azimuthal rotation angle at the avoided crossing approaches the asymptotic value, φ+, as α increases. It is important to note that the faster the passage, the smaller the angle θ becomes (see (15)). Nevertheless, as seen in figure 2 the main effect is apparent even for very moderate α. For example, if the energies of H0 and H1 are comparable and α ∼ 3, θ is about 0.3. The deviation from the asymptotic angle φ+ = −0.75π for this α is just ∼5%. This example shows that the results of the analysis in this paper provide good estimates even very far from the rapid passage limit where Δθ ≪ 1.
Figure 1. (a) A spin that is parallel to the z axis and is an eigenstate of H1 (dark blue vector) will slightly rotate (red vector) when it reaches the stationary point of the system. In the limit of fast passage (see equations (12), (17)), the azimuthal angle φ converges to a simple yet non-trivial constant. Specifically, in the Hermitian case, if 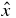 is chosen in the direction of the perturbation H0 denoted by
is chosen in the direction of the perturbation H0 denoted by  and
and 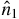 is the direction of the initial spin up, then the projection of the rotated spin on the xy plane (green vector) is as shown in (a). The other initial state will end up in the opposite direction. In the NH case as shown in (b), each initial state has its own reference angle (φ±0). As a result, the spins that correspond to the two initial states do not have to be anti-parallel at the stationary point.
is the direction of the initial spin up, then the projection of the rotated spin on the xy plane (green vector) is as shown in (a). The other initial state will end up in the opposite direction. In the NH case as shown in (b), each initial state has its own reference angle (φ±0). As a result, the spins that correspond to the two initial states do not have to be anti-parallel at the stationary point.
Download figure:
Standard imageFigure 2. Numerical results for the azimuthal angle as a function of the passage rate, α. For the calculation, we used H0 = σx, H1 = σz. The dots show the azimuthal angle of the spin for various α, and the red line shows the predicted asymptotic azimuthal angle, φ+, as given by equation (12). Even for α as small as 3 the deviation from φ+ = −0.75π is just ∼0.037π (about 5%).
Download figure:
Standard image4. The non-Hermitian case
In this section, we focus on NH Hamiltonians which are 'asymptotically Hermitian'. That is, H0 is not Hermitian, but αH1 is still Hermitian. This facilitates the use of the standard Hermitian (Dirac) inner product with the states |↓1〉, |↑1〉. For our first case, we take H0 = iσx, H1 = σz. As mentioned before, in the NH case φ+0 ≠ φ0− (figure 1(b)). From equations (12) and (14), we obtain φ±0 = ±π/2 and φ+ = φ− = −π/4. That is, the two initially orthogonal spin states rotate to the same φ angle, so that they have the same projection on the xy plane (z component is still opposite of course). In NH evolution, two states which are initially orthogonal do not necessarily remain orthogonal. In this particular example, the system traverses two non-Hermitian degeneracies called exceptional points (EPs), or branch points, at 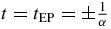 . (For more on EPs, see chapter 9 of [19] and references therein.) The instantaneous energy difference is zero at these points, so supposedly they are the natural analogue of avoided crossing in the Hermitian case. According to our formalism tsp = 0, so t = 0 is the stationary point and not the EPs at
. (For more on EPs, see chapter 9 of [19] and references therein.) The instantaneous energy difference is zero at these points, so supposedly they are the natural analogue of avoided crossing in the Hermitian case. According to our formalism tsp = 0, so t = 0 is the stationary point and not the EPs at 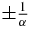 . Yet, our arguments are based on large α, so perhaps this distinction is meaningless, since tEP goes to zero for large α. As it turns out, the distinction between tEP and tsp is important even for large α. Consider the numerical example that appears in table 1. The value of φ is calculated at the stationary point and at the two EPs for three different values of α.
. Yet, our arguments are based on large α, so perhaps this distinction is meaningless, since tEP goes to zero for large α. As it turns out, the distinction between tEP and tsp is important even for large α. Consider the numerical example that appears in table 1. The value of φ is calculated at the stationary point and at the two EPs for three different values of α.
Table 1. Numerical results for a NH case where the Hamiltonian passes through two EPs at t = ±1/α and also through a stationary point at t = 0. At the EPs, the energy gap of the two levels is zero, while at the stationary point it is different from zero. Although the rotation angle converges to the asymptotic angle −0.25π for large enough α at each one of the three points, clearly, it converges much faster at the stationary point. Thus, stationary points should be distinguished from EPs.
 |
 |
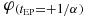 |
|
|---|---|---|---|
| α = 50 | −0.282π | − 0.2479π | −0.210π |
| α = 100 | −0.274π | − 0.2492π | −0.222π |
| α = 200 | −0.267π | − 0.2494π | −0.231π |
As α increases, the rotation speed also increases and therefore the deviation from φ+ at t ≠ tsp becomes more pronounced. Yet, the timescale of the rotation is 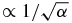 (width of the Gaussian function in (7), or see [20, 11]). Consequently, tEP (∝1/α) goes to zero faster than the rotation time and thus φ(tEP) → φ+ for large enough α. The crucial point here is that as α increases, φ(t = tsp) converges to φ+ much faster than φ(t = tEP) converges to φ+ (see table 1). Hence, we come to the conclusion that the stationary point and the minimal energy gap (EP) points are physically distinguishable entities in the NH case. The asymptotic azimuthal rotation described here is dominated by the stationary point and not by EPs.
(width of the Gaussian function in (7), or see [20, 11]). Consequently, tEP (∝1/α) goes to zero faster than the rotation time and thus φ(tEP) → φ+ for large enough α. The crucial point here is that as α increases, φ(t = tsp) converges to φ+ much faster than φ(t = tEP) converges to φ+ (see table 1). Hence, we come to the conclusion that the stationary point and the minimal energy gap (EP) points are physically distinguishable entities in the NH case. The asymptotic azimuthal rotation described here is dominated by the stationary point and not by EPs.
Our second example has been studied recently in optical lattices [6]. Let H0 be a traceless canonical Jordan block 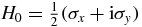 and H1 = σz. This Hamiltonian corresponds to the choice Δ = δ in [6]. The Hamiltonian has an EP at t = 0, which is also the stationary point of the system since tsp = 0. It was found that while one state is being altered by the time evolution, the other state is not affected at all. In [6], it was derived from the analytical solution they found. Here, we offer a simple alternative explanation. The state |↑1〉 = (1, 0) is a right eigenstate of both H0 and H1 (even though H0 and H1 do not commute!). Hence, |↑1〉, is an eigenstate of H(t) which does not depend on t. This is easily seen from the time-independent SE:
and H1 = σz. This Hamiltonian corresponds to the choice Δ = δ in [6]. The Hamiltonian has an EP at t = 0, which is also the stationary point of the system since tsp = 0. It was found that while one state is being altered by the time evolution, the other state is not affected at all. In [6], it was derived from the analytical solution they found. Here, we offer a simple alternative explanation. The state |↑1〉 = (1, 0) is a right eigenstate of both H0 and H1 (even though H0 and H1 do not commute!). Hence, |↑1〉, is an eigenstate of H(t) which does not depend on t. This is easily seen from the time-independent SE:
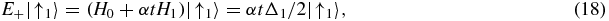
Although the Hamiltonian is time dependent, there is a constant eigenstate with a time-dependent eigenvalue E+ = αtΔ1/2. As a result, this eigenstate/spin does not rotate and the evolution only changes the phase of this state. This can also be seen directly from equation (8). Since the eigenvalue associated with (1, 0) of H0 is zero (the Jordan block is traceless), the matrix element that appears in (8) is also zero. Thus, if the |↓1〉 = (0, 1) state was initially unpopulated, it will remain unoccupied. This does not happen generally when there is an exceptional point at some time t (t = 0 in this case). But for each EP operator H0 there is H1 for which it does happen. We point out that something else happens when H0 and H1 share an eigenstate. The instantaneous eigenvalues of H(t) are analytic in the perturbation parameter (αt in this case) and do not exhibit the typical square root behavior associated with EPs (see equation (18)). This is why the representation in the adiabatic basis [6] does not contain the famous square root which is the hallmark of EPs.
5. Strong NH corrections to the rotation angle
Before concluding our discussion on NH Hamiltonians, we examine the case μ≜Im[〈↑1|H0|↑1〉] ≠ 0 where a surprisingly strong correction to the azimuthal rotation appears. Equation (6) implies that in this case the stationary point is in the complex time plane. Naturally, the time evolution coordinate, t, is a real number, so the stationary point cannot be reached for any value of t. At best, it is possible to be right 'below' this point at t = Re[tsp]. Consequently, the diagonal terms in (2) cannot be completely removed as was possible in the Hermitian case. We make a time shift to the closest point to the EP: ![$\tilde{t}=t-{\rm Re}[t_{{\rm sp}}]$](https://content.cld.iop.org/journals/1751-8121/45/44/444033/revision1/jpa427184ieqn38.gif) (and accordingly
(and accordingly ![$\tilde{H}_{0}=H_{0}+\alpha {\rm Re}[t_{{\rm sp}}]H_{1}$](https://content.cld.iop.org/journals/1751-8121/45/44/444033/revision1/jpa427184ieqn39.gif) ). After some algebra the stationary phase integrals for the '+' and '–' initial conditions are now given by
). After some algebra the stationary phase integrals for the '+' and '–' initial conditions are now given by
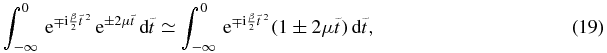
where on the rhs, the small μt approximation was used. However, when μ ≠ 0 a new complication comes into play. Now, the two diabatic states, |↑1〉 and |↓1〉, are associated with gain and loss since


This has a very dramatic and asymmetric effect on the evolution. Recently, this evolution asymmetry was studied in the context of dynamic cycling of EPs [21]. See also [22] for a closely related work. This asymmetry arises due to exponential enhancement of small non-adiabatic couplings. Let us consider the evolution before the energy gap reaches its minimal value. For μ > 0, the |↑1〉 (|↓1〉) will be called the gain (loss) state. The gain state basically grows exponentially as expected. The loss state, on the other hand, will evolve in a completely different manner. In the beginning the loss state decays as expected. Yet, after a short time, tiny non-adiabatic couplings cause the initially unpopulated gain state to get slightly populated. This tiny 'contamination' rapidly grows and may eventually even exceed the population of the loss state. Naturally, when this 'pre-crossing' dynamics takes place, the stationary point cannot account for all the rotation in the system. In contrast, when the gain state evolves, it also 'contaminates' the decay state, but this contamination is not enhanced as before. Thus, for the gain state, the gain only increases the amplitude without changing the population ratio. Hence, the rotation is still generated by the stationary point just as in the μ = 0 case. In summary, only the gain state can be described by the stationary phase method. Using (19), it is found that for α > 0 the azimuthal rotation of the gain state is now given by

where again we emphasize not to apply this formula to both states but only to the gain state (which may be '+' or '–' depending on the sign of μ). The new 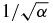 term is unique to NH systems. In the Hermitian case, the leading-order correction is only 1/α. It should be noted that 'gain' appears only because we took the Hamiltonian to be traceless. Often in physical scenarios both states can decay at different rates and the 'gain' state is just the least decaying state. The trace, however, has no effect on the rotation of the states. Table 2 shows a comparison of equation (22) to numerical computation for the already traceless Hamiltonian:
term is unique to NH systems. In the Hermitian case, the leading-order correction is only 1/α. It should be noted that 'gain' appears only because we took the Hamiltonian to be traceless. Often in physical scenarios both states can decay at different rates and the 'gain' state is just the least decaying state. The trace, however, has no effect on the rotation of the states. Table 2 shows a comparison of equation (22) to numerical computation for the already traceless Hamiltonian:

This Hamiltonian is Hermitian for γ = 0. γ ≠ 0 describes a simple scenario where the two diabatic levels have different decay rates (since the trace is set to zero it appears as gain and loss). It is easy to see that the parameter γ is equal to μ in this example. If there is a significant gain and loss in the system, it is important to specify what the initial point of integration (ti) is, since in practice it cannot be −∞. The parameters we chose are α = 100 and ti = 1. This sets the magnitude of the H1 to be roughly hundred times larger than the magnitude of H0 at t = ti.
Table 2. Numerical results for μ = γ ≠ 0. The asymptotic rotation for α → ∞ is −0.75π for the '+' state and +0.25π for the '–' state. In the numerical simulation, we used α = 100. In the Hermitian case, γ = 0, the small numerical deviations from the asymptotic rotations are due to some small 1/α corrections. On the other hand, for γ = ±2, a significant correction to −0.75π and 0.25π appears. This correction, which is unique to NH Hamiltonians, is of order 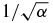 . It is accurately described by our formalism (up to order 1/α). Note that our formula (22) should not be used for the 'loss' states where the norm 〈ϕ|ϕ〉t = 0 is smaller than 1.
. It is accurately described by our formalism (up to order 1/α). Note that our formula (22) should not be used for the 'loss' states where the norm 〈ϕ|ϕ〉t = 0 is smaller than 1.
| φ+calc | φ+num | 〈ϕ|ϕ〉t = 0 | φ−calc | φ−num | 〈ϕ|ϕ〉t = 0 | |
|---|---|---|---|---|---|---|
| γ = 0 | −0.75π | −0.746π | 1 |  |
 |
1 |
| γ = 2 | − 0.699π | − 0.704π | 7.374 | −0.199π | −0.867π | 0.139 |
| γ = −2 | −0.801π | 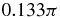 |
0.139 | 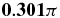 |
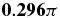 |
7.374 |
The Hermitian case γ = 0 shows that the leading order correction O(1/α) is roughly 0.004π. However, for γ = 2 we see that a very strong correction to the rotation appears. Moreover, as explained before, this correction appears to work only for the '+' initial condition and not for the '–'. Comparing the norm of the state at t = 0, we see that formula (22) agrees well with the numerical result for the state which has the larger norm ('+' in this case). The norm at t = 0 is given by 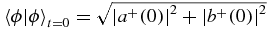 . The small deviation of the numerical results from the calculated value is mostly due to the order α correction which was not taken into account in equation (22). For γ = −2, it is the '–' state that has the larger norm and indeed we see good agreement between equation (22) and the numerical result for the '–' state. To verify the
. The small deviation of the numerical results from the calculated value is mostly due to the order α correction which was not taken into account in equation (22). For γ = −2, it is the '–' state that has the larger norm and indeed we see good agreement between equation (22) and the numerical result for the '–' state. To verify the 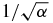 dependence of the NH term in (22), we also calculated the case α = 400,γ = 2. Increasing α by 4 should reduce the NH term by 2, so that φ+calc = −0.725π. The numerical result for this case is φ+num = −0.726π. This validates the
dependence of the NH term in (22), we also calculated the case α = 400,γ = 2. Increasing α by 4 should reduce the NH term by 2, so that φ+calc = −0.725π. The numerical result for this case is φ+num = −0.726π. This validates the 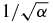 behavior of the NH term in (22). In conclusion, non-Hermitian systems may contain corrections to the rotation which are fundamentally stronger than the corrections that appear in Hermitian systems.
behavior of the NH term in (22). In conclusion, non-Hermitian systems may contain corrections to the rotation which are fundamentally stronger than the corrections that appear in Hermitian systems.
We expect that these non-Hermitian effects could be observed in optics or in quantum systems such as interacting spin ensembles [23] or in accelerated cold atoms [3] where LZ transitions can be observed and the decay can be conveniently controlled.


