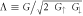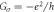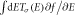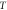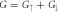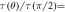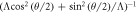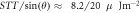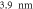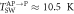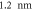Abstract
Based on atomic first principles, we predict enhanced thermal spin transfer (TST) effects and small switching temperature gradient in Fe  MgO
MgO  Fe
Fe  MgO
MgO  Fe double-barrier magnetic tunnel junctions (MTJs). At room temperature, temperature gradient
Fe double-barrier magnetic tunnel junctions (MTJs). At room temperature, temperature gradient  ∼10
∼10  with
with  ∼10 K nm−1 across barriers would be sufficient to switch the magnetic configurations circularly in a junction with 3 MgO atomic layers (L), which is about one order smaller than that in Fe
∼10 K nm−1 across barriers would be sufficient to switch the magnetic configurations circularly in a junction with 3 MgO atomic layers (L), which is about one order smaller than that in Fe  MgO(3L)
MgO(3L) Fe MTJs. This temperature gradient is under the current experimental capability. The resonant quantum-well states in companion with resonant interfacial states are responsible for the enhancement. Moreover, a thermal induced 'off' state is found in a double-barrier MTJ.
Fe MTJs. This temperature gradient is under the current experimental capability. The resonant quantum-well states in companion with resonant interfacial states are responsible for the enhancement. Moreover, a thermal induced 'off' state is found in a double-barrier MTJ.
GENERAL SCIENTIFIC SUMMARY
Introduction and background. Switching the magnetic order parameter thermally is the basis for Spin Caloritronics. Recently, experimental and theoretical studies focusing on thermal spin transfer effect on MgO-based magnetic tunnel junctions (MTJs) have been published in high-profile journals. Switching temperature gradient with order of several tens Kelvin (∼ 60 K with ∼ 100 K/nm) is predicted in a MgO-based MTJs with ultra-thin barrier, which is well beyond the current experimental capacity (∼ 20 K with ∼ 20 K/nm by a femtosecond laser pulses heating). Thus, looking for material with small switching temperature gradient is an urgent and important task in Spin Caloritronics. To the best of our knowledge, material with appropriate switching temperature gradient have been reported both in experiments and theory.
Main results. In this paper, we investigated the thermal spin transfer effects in Fe∣MgO∣Fe∣MgO∣Fe double-barrier tunnel junctions (DMTJs) based on atomic first-principles scattering theory. We predict that a temperature gradient ΔT ∼ 10 K with ΔT ∼ 10 K/nm across barriers can switch the magnetic configurations circularly in a DMTJ with 3 atomic-layer (L) MgO barrier at room temperature, and the needed ΔT and ∇T is about one order smaller than that in Fe∣MgO∣Fe SMTJs with same barrier thickness. The resonant quantum-well states accompanied by the resonant interfacial states are considered to be responsible for the enhanced thermal torque with angular dependency with or close to sine relation. Moreover, a "off" state in a DBMTJ is presented thermally.
Wider implications. By scissoring structure parameters, a material with appropriate switching temperature gradient is predicted, which is under the current experimental capacity. So, we hope experimental scientist can realize our prediction and find more excellent materials to pave the way for Spin Caloritronics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY
Introduction and background. Switching the magnetic order parameter thermally is the basis for Spin Caloritronics. Recently, experimental and theoretical studies focusing on thermal spin transfer effect on MgO-based magnetic tunnel junctions (MTJs) have been published in high-profile journals. Switching temperature gradient with order of several tens Kelvin (∼ 60 K with ∼ 100 K/nm) is predicted in a MgO-based MTJs with ultra-thin barrier, which is well beyond the current experimental capacity (∼ 20 K with ∼ 20 K/nm by a femtosecond laser pulses heating). Thus, looking for material with small switching temperature gradient is an urgent and important task in Spin Caloritronics. To the best of our knowledge, material with appropriate switching temperature gradient have been reported both in experiments and theory.
Main results. In this paper, we investigated the thermal spin transfer effects in Fe∣MgO∣Fe∣MgO∣Fe double-barrier tunnel junctions (DMTJs) based on atomic first-principles scattering theory. We predict that a temperature gradient ΔT ∼ 10 K with ΔT ∼ 10 K/nm across barriers can switch the magnetic configurations circularly in a DMTJ with 3 atomic-layer (L) MgO barrier at room temperature, and the needed ΔT and ∇T is about one order smaller than that in Fe∣MgO∣Fe SMTJs with same barrier thickness. The resonant quantum-well states accompanied by the resonant interfacial states are considered to be responsible for the enhanced thermal torque with angular dependency with or close to sine relation. Moreover, a "off" state in a DBMTJ is presented thermally.
Wider implications. By scissoring structure parameters, a material with appropriate switching temperature gradient is predicted, which is under the current experimental capacity. So, we hope experimental scientist can realize our prediction and find more excellent materials to pave the way for Spin Caloritronics.
1. Introduction
Switching the magnetic order parameter thermally is the basis for spin caloritronic applications such as logic devices and memories [1]. As a easy, efficient, and 'green' method to manipulate the magnetic order parameter, thermal spin transfer (TST) torque has received much attention recently [1–14]. To achieve TST torque (also called thermal torque) comparable to that induced by an electric bias, a large temperature gradient across magnetic elements should be established. Marked TST effect is first reported in a MgO-based magnetic tunnel junctions (MTJs) with ultra-thin barrier [2, 3]. Therein, the skewed TST torque is more favorable to magnetic oscillation rather than switching, a temperature gradient  with
with  K nm−1 is predicted to be needed to switch the magnetic configurations circularly, which is beyond the current experimental capability. The steady-state temperature gradient in MTJs is relatively small, a temperature gradient
K nm−1 is predicted to be needed to switch the magnetic configurations circularly, which is beyond the current experimental capability. The steady-state temperature gradient in MTJs is relatively small, a temperature gradient  with
with  K nm−1 with order of ten picoseconds can be established by femtosecond laser pulses heating [4]. Thus, seeking materials with moderate switching temperature gradient is an urgent and important task in spin caloritronics.
K nm−1 with order of ten picoseconds can be established by femtosecond laser pulses heating [4]. Thus, seeking materials with moderate switching temperature gradient is an urgent and important task in spin caloritronics.
It is resonant interfacial states, widely existed in high quality nanostructures, that to be responsible for the large TST in MgO-based MTJs [3]. Similar to interfacial states, quantum-well (QW) states can lead to resonant tunneling [15–18] and large spin transfer effects. QW states can be engineered easily by the structure parameters such as thickness and materials of barrier and spacer metal, crystal defects and so on [16–19]. Spin transfer torque created by bias voltage in double-barrier MTJs (DBMTJs) is well studied [20–27]. When the QW states calibrate to Fermi energy (EF), thermoelectric effects, including TST, would be enhanced. In DBMTJs, both the resonant QW states and interfacial states can be coexistent. So, larger TST effect and a smaller temperature gradient for magnetic switching would be expected in DBMTJs than those in single-barrier MTJs (SBMTJs). However, as far as we know, few works on this subject have been reported both in experiments and theory.
In this work, we focus on the TST torque in MgO-based DBMTJs in the presence of a nonequilibrium thermal distribution by applying the Landauer–Büttiker formalism with thermal bias [3]. We consider an ultra-thin MgO barrier with thickness of three atomic layers (about 0.6  ) as spin transfer torque (STT) decrease exponentially as barrier thickness increases [3]. Our results show enhanced TST torque in DBMTJs owing to the coexistence of the resonant QW states and the resonant interfacial states. Based on Landau–Lifshitz–Gilbert (LLG) equation, [28] we estimate that a temperature gradient of 10 K nm−1 across barriers would be sufficient to reverse the magnetic configurations circularly at room temperature.
) as spin transfer torque (STT) decrease exponentially as barrier thickness increases [3]. Our results show enhanced TST torque in DBMTJs owing to the coexistence of the resonant QW states and the resonant interfacial states. Based on Landau–Lifshitz–Gilbert (LLG) equation, [28] we estimate that a temperature gradient of 10 K nm−1 across barriers would be sufficient to reverse the magnetic configurations circularly at room temperature.
This paper is organized as follows. In section 2, we give the details of our calculation based on first-principle scattering theory. In section 3, we present our results on Fe  MgO
MgO  Fe
Fe  MgO
MgO  Fe DBMTJs with clean and disordered interfaces. Section 4 is our summary.
Fe DBMTJs with clean and disordered interfaces. Section 4 is our summary.
2. Electronic structure and transport calculations
Considering a DBMTJ as sketched in the inset of figure 1 with temperature and voltage bias across the barriers, the local thermal equilibrium can be depicted by Fermi–Dirac distribution function 
![${[{{\rm{e}}}^{(\epsilon -{\mu }_{{\rm{L}}/{\rm{R}}})/{k}_{B}{T}_{{\rm{L}}/{\rm{R}}}}+1]}^{-1}$](https://content.cld.iop.org/journals/1367-2630/18/6/063012/revision1/njpaa2884ieqn19b.gif) and local chemical potentials
and local chemical potentials  and temperatures
and temperatures  . TST torque transferred to the magnetization
. TST torque transferred to the magnetization  can be estimated by the spin current pumped out of the precessing
can be estimated by the spin current pumped out of the precessing  based on scattering theory [30]
based on scattering theory [30]
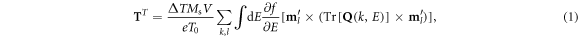
where  with
with  sums all modes over left/right (L / R) lead and
sums all modes over left/right (L / R) lead and  is the scattering matrix that is evaluated at the energy E and k in the two-dimensional Brillouin zone (2D BZ),
is the scattering matrix that is evaluated at the energy E and k in the two-dimensional Brillouin zone (2D BZ),  and
and  are the unit vector along
are the unit vector along  and
and  with respect to saturation magnetization Ms in ferromagnetic region with volume V,
with respect to saturation magnetization Ms in ferromagnetic region with volume V,  is ambient temperature, and
is ambient temperature, and  is temperature bias. Therein, the magnetization dependent parameter
is temperature bias. Therein, the magnetization dependent parameter  is the key to equation (1), which is well-studied by spin pumping theory [31, 32]. By putting TST torque into the phenomenological LLG equation [2], one can estimate thermal induced magnetic dynamics.
is the key to equation (1), which is well-studied by spin pumping theory [31, 32]. By putting TST torque into the phenomenological LLG equation [2], one can estimate thermal induced magnetic dynamics.
Figure 1. Thermal torque in clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs at room temperature. Lower inset: the ratio of the in-plane TST torque to thermocurrent (
Fe DBMTJs at room temperature. Lower inset: the ratio of the in-plane TST torque to thermocurrent ( ). Upper inset: schematic structure of the Fe
). Upper inset: schematic structure of the Fe  MgO
MgO  Fe
Fe  MgO
MgO  Fe DBMTJs. We consider a temperature bias
Fe DBMTJs. We consider a temperature bias  and voltage bias
and voltage bias 
 VR across barriers, and set temperature bias drop within barriers as estimation in [29]. We consider two representable configurations here. S1: the magnetization of the left lead
VR across barriers, and set temperature bias drop within barriers as estimation in [29]. We consider two representable configurations here. S1: the magnetization of the left lead  is fixed along z quantum axis, and both the magnetization of sandwiched Fe M and right lead
is fixed along z quantum axis, and both the magnetization of sandwiched Fe M and right lead  are set free with relative angle
are set free with relative angle  to
to  . S2:
. S2:  is fixed along
is fixed along  quantum axis, and
quantum axis, and  is set free.
is set free.
Download figure:
Standard image High-resolution imageWe consider two stable DBMTJs structures as shown in figure 1. Therein, S1/S2 has one/two magnetization fixed along z quantum axis and two/one free magnetizations, and the magnetic structure of S1 is similar to SBMTJs. In calculations, we neglect the minor lattice mismatch at Fe  MgO interface and fix the interfacial atoms at their bulk positions. For disordered interface, we assume oxygen vacancies (OV) only exist at the first layer of MgO attached to Fe. In the transport calculations, an 800 × 800 k-mesh is used to sample the two-dimensional Brillouin zone (2D BZ) to ensure good numerical convergence. More numerical details of the electronic structure and transport calculations can be found elsewhere [3, 33]. To check the validity of equation (1), a wave-function-matching (WFM) method [34] is used to calculate STT in clean Fe
MgO interface and fix the interfacial atoms at their bulk positions. For disordered interface, we assume oxygen vacancies (OV) only exist at the first layer of MgO attached to Fe. In the transport calculations, an 800 × 800 k-mesh is used to sample the two-dimensional Brillouin zone (2D BZ) to ensure good numerical convergence. More numerical details of the electronic structure and transport calculations can be found elsewhere [3, 33]. To check the validity of equation (1), a wave-function-matching (WFM) method [34] is used to calculate STT in clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs also, where the numbers in the bracket indicate the thickness in atomic layers. We find that the STT obtained by two methods give difference less than 2%, and equation (1) can save calculation cost greatly compared with WFM method.
Fe DBMTJs also, where the numbers in the bracket indicate the thickness in atomic layers. We find that the STT obtained by two methods give difference less than 2%, and equation (1) can save calculation cost greatly compared with WFM method.
3. Thermal torque in Fe  MgO
MgO  Fe
Fe  MgO
MgO  Fe DBMTJs
Fe DBMTJs
Figure 1 shows the angular dependence of the in-plane TST torque ( ) in clean Fe
) in clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs. Therein,
Fe DBMTJs. Therein,  in S2 is symmetric with parameter [35] 4
in S2 is symmetric with parameter [35] 4
 with peak value of
with peak value of  nJ m−2 K−1 at
nJ m−2 K−1 at  , while that in S1 is asymmetric (
, while that in S1 is asymmetric ( ) with peak value of
) with peak value of  nJ m−2 K−1 at
nJ m−2 K−1 at  . The former is nearly double larger than the latter. However, both
. The former is nearly double larger than the latter. However, both  in S1 and S2 structures are larger than that (
in S1 and S2 structures are larger than that ( nJ m−2 K−1 at
nJ m−2 K−1 at  ) in clean Fe
) in clean Fe  MgO(3)
MgO(3) Fe SBMTJs. At the same time, Λ in both S1 and S2 are smaller than that 3.5 in clean Fe
Fe SBMTJs. At the same time, Λ in both S1 and S2 are smaller than that 3.5 in clean Fe  MgO(3)
MgO(3) Fe SBMTJs. It is rather interesting because the larger
Fe SBMTJs. It is rather interesting because the larger  companied with smaller Λ would favor the magnetization switching in DBMTJs than SBMTJs [2]. The out-of-plane part of TST torque (
companied with smaller Λ would favor the magnetization switching in DBMTJs than SBMTJs [2]. The out-of-plane part of TST torque ( ) is about 10% of
) is about 10% of  , and we neglect
, and we neglect  in magnetic dynamic simulations. By putting TST torque into LLG equation [28], we get temperature gradient
in magnetic dynamic simulations. By putting TST torque into LLG equation [28], we get temperature gradient  = 19/9
= 19/9  (
( (
( ,
,  )) and
)) and  16/7.5 K nm−1 to switch between antiparallel (AP) and parallel (P) configurations in S1/S2 structure as shown in table 1, which is considerable smaller than that in SBMTJs with same barrier thickness.
16/7.5 K nm−1 to switch between antiparallel (AP) and parallel (P) configurations in S1/S2 structure as shown in table 1, which is considerable smaller than that in SBMTJs with same barrier thickness.
Table 1.
Thermal torque in clean and dirty (in brackets) Fe  MgO(3)
MgO(3) Fe(8 )
Fe(8 ) MgO(3)
MgO(3) FM DBMTJs at
FM DBMTJs at  and
and  for
for  . For dirty case, we consider 4% OV at Fe
. For dirty case, we consider 4% OV at Fe  MgO interfaces of right side MgO barrier.
MgO interfaces of right side MgO barrier.  and
and  is calculated according to LLG equations [28] with saturation magnetization
is calculated according to LLG equations [28] with saturation magnetization  , uniaxial anisotropy field
, uniaxial anisotropy field  , dimensionless planar anisotropy
, dimensionless planar anisotropy  is the ratio of easy-plane anisotropy energy KP to uniaxial anisotropy energy
is the ratio of easy-plane anisotropy energy KP to uniaxial anisotropy energy  , and magnetic damping coefficient
, and magnetic damping coefficient  . For comparison, we give thermal torque in Fe
. For comparison, we give thermal torque in Fe  MgO(3)
MgO(3) Fe SBMTJs, and we consider 4% OV at both Fe
Fe SBMTJs, and we consider 4% OV at both Fe  MgO interfaces and set thickness of the free magnetization df = 1.2 nm.
MgO interfaces and set thickness of the free magnetization df = 1.2 nm.
| FM | Structure | TMR (%) |
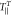 (nJ m−2 K−1) (nJ m−2 K−1) |
Λ |
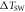 ( ( ) ) |
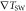 (K nm−1) (K nm−1) |
|---|---|---|---|---|---|---|
| Fe | S1 | 1540 | −220 | 1.5 | 19 | 16 |
| FeCo | S1 | 860 | −125 | 1.0 | 25 | 21 |
| Fe | S2 | 0(110) | −370(−270) | 1.0(1.0) | 9(12) | 7.5(10) |
| FeCo | S2 | 110 | −220 | 1.0 | 14 | 12 |
Fe  MgO(3L) MgO(3L) Fe Fe |
1300(200) | −195(−110) | 3.5(1.5) | 45(33) | 75(55) | |
Fe  MgO(3L) MgO(3L) FeCo FeCo |
420 | −40 | 1.0 | 76 | 126 | |
To check the parameters used in magnetic dynamics simulations, we estimate  in clean Fe
in clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs with S1 structure by taking experimental data, [36] 5
which shows minor difference (
Fe DBMTJs with S1 structure by taking experimental data, [36] 5
which shows minor difference ( ) from that obtained from LLG calculations. So, we conclude that the parameters in magnetic dynamic simulations are reasonable.
) from that obtained from LLG calculations. So, we conclude that the parameters in magnetic dynamic simulations are reasonable.
Huge ratio of the TST torque to thermocurrent  in S1 and S2 structures is found in a large energy range, as shown in the lower inset in figure 1. A saturated
in S1 and S2 structures is found in a large energy range, as shown in the lower inset in figure 1. A saturated  is found at
is found at  in S2 structure. For S1 structure,
in S2 structure. For S1 structure,  at
at  as
as  , this is a 'off' state produced thermally. The small thermocurrent
, this is a 'off' state produced thermally. The small thermocurrent  is responsible to the huge
is responsible to the huge  here, where
here, where ![$T(E)=\mathrm{Tr}[{{tt}}^{\dagger }]$](https://content.cld.iop.org/journals/1367-2630/18/6/063012/revision1/njpaa2884ieqn146.gif) is electronic transmission and t is the transmission part of the scattering matrix. The small
is electronic transmission and t is the transmission part of the scattering matrix. The small  can be understood from the small asymmetry in electronic transmission within thermal energy window
can be understood from the small asymmetry in electronic transmission within thermal energy window  at room temperature, as shown in the upper inset of figure 2(a). The giant spin transfer efficiency in DBMTJs would favor the functional of devices. Furthermore, the 'off' state demonstrated here can be found logic device application.
at room temperature, as shown in the upper inset of figure 2(a). The giant spin transfer efficiency in DBMTJs would favor the functional of devices. Furthermore, the 'off' state demonstrated here can be found logic device application.
Figure 2. (a) Energy-dependent in-plane voltage torkance in ideal Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs with S1 and S2 structures for
Fe DBMTJs with S1 and S2 structures for  . Inset: out-of-plane voltage torkance. (b)
. Inset: out-of-plane voltage torkance. (b)  -resolved in-plane voltage torkance in S1 structure at (left)
-resolved in-plane voltage torkance in S1 structure at (left)  , and (right)
, and (right)  . (c) Energy-dependent in-plane STT in resonant point A (
. (c) Energy-dependent in-plane STT in resonant point A ( 1.03,
1.03,  1.67) in
1.67) in  spin in left panel in (b). (d) Energy-dependent in-plane STT in resonant point B (
spin in left panel in (b). (d) Energy-dependent in-plane STT in resonant point B ( 0.43,
0.43,  0.0) in
0.0) in  spin in right panel in (b).
spin in right panel in (b).
Download figure:
Standard image High-resolution imageTo check the source of the enhancement of TST torque in clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs, we check the energy-dependent voltage torkance
Fe DBMTJs, we check the energy-dependent voltage torkance
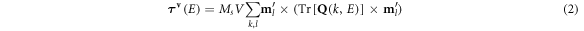
with  and
and  perpendicular to each other. For S1 structure,
perpendicular to each other. For S1 structure,  is along the z axis while
is along the z axis while  and
and  is parallel to the x axis. For S2 structure,
is parallel to the x axis. For S2 structure,  and is along
and is along  while
while  is parallel to x. The processing
is parallel to x. The processing  would pump spin current into both left and right leads, the left-going and right-going spin current are equal for S2 structure, while only left-going spin current existed in S1 structure. When
would pump spin current into both left and right leads, the left-going and right-going spin current are equal for S2 structure, while only left-going spin current existed in S1 structure. When  rotates towards the x/y direction, a in-plane/out-of-plane torkance (
rotates towards the x/y direction, a in-plane/out-of-plane torkance ( ) will be produced. We plot the results in figure 2(a) in the energy range [
) will be produced. We plot the results in figure 2(a) in the energy range [ ,
,  ]. Therein,
]. Therein,  show a striking negative peak with value of
show a striking negative peak with value of  10
10  (
( ) at
) at  and a broaden positive peak with value of
and a broaden positive peak with value of  at
at  in S1/S2 structure. At both peaks,
in S1/S2 structure. At both peaks,  in S2 structure is almost double larger than that in S1 structure due to the double spin transfer process existed in S2 structure, as expressed in equation (2). Both the two peaks contribute to room temperature TST torque. We take S1 structure as an example to analyze the k -resolved contribution to
in S2 structure is almost double larger than that in S1 structure due to the double spin transfer process existed in S2 structure, as expressed in equation (2). Both the two peaks contribute to room temperature TST torque. We take S1 structure as an example to analyze the k -resolved contribution to  . Figure 2(b) plot the k-resolved
. Figure 2(b) plot the k-resolved  at
at  and
and  . The former is dominated by several bright spots in
. The former is dominated by several bright spots in  spin, while the latter is dominated by a bright ring in
spin, while the latter is dominated by a bright ring in  spin.
spin.
The out-of-plane torkance  in DBMTJs shows complicate energy dependency as shown in the lower inset of figure 2(a). Although the out-of-plane TST torques in both S1 and S2 structures are relatively small, the out-of-plane voltage torque are rather considerable. We observe large ratio
in DBMTJs shows complicate energy dependency as shown in the lower inset of figure 2(a). Although the out-of-plane TST torques in both S1 and S2 structures are relatively small, the out-of-plane voltage torque are rather considerable. We observe large ratio  at EF in S1/S2 structure, which is considerable larger than that (∼0.25 at EF) in Fe
at EF in S1/S2 structure, which is considerable larger than that (∼0.25 at EF) in Fe  MgO(3)
MgO(3) Fe SBMTJs.
Fe SBMTJs.
DBMTJ can be considered as two SBMTJs connected in series. The coupling between SBMTJs in DBMTJ can be estimated from the electron transmission. When the electron transmission in DBMTJ (Td) and SBMTJs (Ts) follow /beyond the relation  , the coupling of SMTJs in DBMTJs would be weak/strong. For clean Fe
, the coupling of SMTJs in DBMTJs would be weak/strong. For clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs with S1/S2 structure, Td is 0.012/0.013 at EF, which is close to that (
Fe DBMTJs with S1/S2 structure, Td is 0.012/0.013 at EF, which is close to that ( ) in Fe
) in Fe  MgO(3)
MgO(3) Fe MTJs, indicating strong coupling between SBMTJs. It is noted that the resonant interfacial states in
Fe MTJs, indicating strong coupling between SBMTJs. It is noted that the resonant interfacial states in  spin and resonant QW states in
spin and resonant QW states in  spin that should be responsible to the strong coupling. From the value of Td and Ts, we estimate that the resonant states would contribute to
spin that should be responsible to the strong coupling. From the value of Td and Ts, we estimate that the resonant states would contribute to  of Td in DBMTJs at EF. Moreover, STT can be used to estimate the coupling of SBMTJs in DBMTJ also, which is related with electron transmission by a simple relation [37].
of Td in DBMTJs at EF. Moreover, STT can be used to estimate the coupling of SBMTJs in DBMTJ also, which is related with electron transmission by a simple relation [37].
Due to the strong coupling between SBMTJs in DBMTJ, the energy-dependent torkances for  and
and  at
at  (point A in figure 2(b)) produce three resonant peaks as shown in figure 2(c), which is different from the double peaks scheme in SBMTJs. The energy-dependent torkance share the same shape as the electronic transmission, indicating that the resonant peaks are from interfacial states. Differently, the energy-dependent torkance for
(point A in figure 2(b)) produce three resonant peaks as shown in figure 2(c), which is different from the double peaks scheme in SBMTJs. The energy-dependent torkance share the same shape as the electronic transmission, indicating that the resonant peaks are from interfacial states. Differently, the energy-dependent torkance for  and
and  at
at  (point B in figure 2(b)) give a large resonant peak and two ghost peaks, as shown in figure 2(d). The former is from the resonant QW states, and the latter is from the resonant interfacial states.
(point B in figure 2(b)) give a large resonant peak and two ghost peaks, as shown in figure 2(d). The former is from the resonant QW states, and the latter is from the resonant interfacial states.
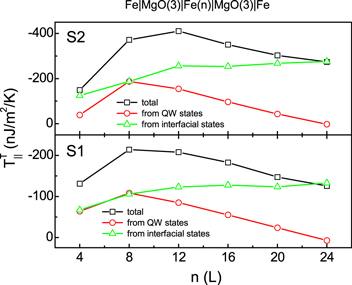
Both the resonant interfacial and QW states contribute to the TST torque in DBMTJs. The position of resonant QW states is sensitive to the thickness of sandwich metal, while the position of resonant interfacial states is stable. Figure 3 shows the contribution of resonant interfacial and QW states to the TST torque in clean Fe  MgO(3)
MgO(3) Fe
Fe  MgO(3)
MgO(3) Fe DBMTJs with respect to the thickness of the sandwiched Fe. Therein, the TST torque in junction with S1/S2 structure increases quickly as n increases, and reaches a saturation value
Fe DBMTJs with respect to the thickness of the sandwiched Fe. Therein, the TST torque in junction with S1/S2 structure increases quickly as n increases, and reaches a saturation value  210
210  nJ m−2 K−1 for n = 12. In addition, the contribution from resonant interfacial states saturate at a value ∼− 130
nJ m−2 K−1 for n = 12. In addition, the contribution from resonant interfacial states saturate at a value ∼− 130  nJ m−2 K−1 for
nJ m−2 K−1 for  12, and the contribution from resonant QW states show a convex curve with peak value of ∼− 110
12, and the contribution from resonant QW states show a convex curve with peak value of ∼− 110  nJ m−2 for n = 8.
nJ m−2 for n = 8.
Figure 3. Thermal torque in clean Fe  MgO(3)
MgO(3) Fe
Fe  MgO(3)
MgO(3) Fe DBMTJs with S1 and S2 structures at room temperature as function of the thickness of the sandwiched Fe.
Fe DBMTJs with S1 and S2 structures at room temperature as function of the thickness of the sandwiched Fe.
Download figure:
Standard image High-resolution imageOwing to the presence of the double spin transfer process, DBMTJs with S2 structure show large TST torque with symmetric angular-dependency, which would favor thermal induced magnetic switching. However, symmetric DBMTJs with S2 structure show zero tunnel magnetoresistance (TMR  with conductance
with conductance  . To achieve observable TMR and large TST at the same time, asymmetric DBMTJs with S2 structure can be devised. Here, we pay attention to the effects of asymmetric interfacial OV and asymmetric leads on
. To achieve observable TMR and large TST at the same time, asymmetric DBMTJs with S2 structure can be devised. Here, we pay attention to the effects of asymmetric interfacial OV and asymmetric leads on  in DBMTJs with S2 structure, as show in figure 4 and table 1 . Firstly, we study the asymmetric interfacial OV, where the Fe
in DBMTJs with S2 structure, as show in figure 4 and table 1 . Firstly, we study the asymmetric interfacial OV, where the Fe  MgO interfaces of left MgO barrier keep clean while that of right MgO barrier is dirty. We find that 4% OV at Fe
MgO interfaces of left MgO barrier keep clean while that of right MgO barrier is dirty. We find that 4% OV at Fe  MgO interfaces of right side MgO can produce TMR ∼110% at zero bias, simultaneously
MgO interfaces of right side MgO can produce TMR ∼110% at zero bias, simultaneously  decreases to −270 nJ m−2 K−1, as shown in table 1. Detail study shows interfacial OV would deteriorate both resonant interfacial and QW states. The resonant interfacial states are more sensitive to OV than the QW ones, as shown in figure 4. Quantitatively,
decreases to −270 nJ m−2 K−1, as shown in table 1. Detail study shows interfacial OV would deteriorate both resonant interfacial and QW states. The resonant interfacial states are more sensitive to OV than the QW ones, as shown in figure 4. Quantitatively,  from resonant interfacial/QW states at energy
from resonant interfacial/QW states at energy  is
is  , show a reduction of 60/20 comparing with that in the clean structure. The asymmetric interfacial OV does not change the symmetry of the angular-dependency of the TST torque, and
, show a reduction of 60/20 comparing with that in the clean structure. The asymmetric interfacial OV does not change the symmetry of the angular-dependency of the TST torque, and 
 with
with  K nm−1 are estimated according to the LLG simulation.
K nm−1 are estimated according to the LLG simulation.
Figure 4. Energy-dependent torkance in DBMTJs with S2 structure at 90 degree in the presence of asymmetric 4% OV at Fe  MgO interfaces of right side MgO, and bcc-Fe0.5Co0.5 alloy as right lead. As comparison, we give torkance in symmetric Fe
MgO interfaces of right side MgO, and bcc-Fe0.5Co0.5 alloy as right lead. As comparison, we give torkance in symmetric Fe  MgO
MgO  Fe
Fe  MgO
MgO  Fe DBMTJs also.
Fe DBMTJs also.
Download figure:
Standard image High-resolution imageWhen the bcc-Co0.5Fe0.5 alloy is used as the right lead, the resonant interfacial states would be quenched completely, while resonant QW states keep stable. The clean asymmetric Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) FeCo DBMTJs with S2 structure show TMR ∼110% at zero bias and symmetric angular-dependent TST torque with peak value of −220 nJ m−2 K−1 at
FeCo DBMTJs with S2 structure show TMR ∼110% at zero bias and symmetric angular-dependent TST torque with peak value of −220 nJ m−2 K−1 at  , and
, and 
 with
with  K nm−1 are estimated from the magnetic dynamic simulation.
K nm−1 are estimated from the magnetic dynamic simulation.
In table 1, we summarize the TST torque in Fe  MgO(3L)
MgO(3L) Fe(8 L)
Fe(8 L) MgO(3L)
MgO(3L) Fe DBMTJs. Therein, DBMTJs with SBMTJ-like magnetic structure (S1) show larger TMR, while those with S2 structure show larger TST torque. By introducing asymmetric OV or asymmetric leads, DBMTJs with S2 structure can give considerable TMR and larger TST torque.
Fe DBMTJs. Therein, DBMTJs with SBMTJ-like magnetic structure (S1) show larger TMR, while those with S2 structure show larger TST torque. By introducing asymmetric OV or asymmetric leads, DBMTJs with S2 structure can give considerable TMR and larger TST torque. 
 with
with  K nm−1 is presented in an asymmetric DBMTJs with S2 structure, which is about one order smaller than that in SBMTJ with same barrier thickness. For same TST torque, the ratio of
K nm−1 is presented in an asymmetric DBMTJs with S2 structure, which is about one order smaller than that in SBMTJ with same barrier thickness. For same TST torque, the ratio of  and
and  in SBMTJs to those in DBMTJs is Λ and
in SBMTJs to those in DBMTJs is Λ and  , respectively. Furthermore. when 4% OV is introduced in Fe
, respectively. Furthermore. when 4% OV is introduced in Fe  MgO(3L)
MgO(3L) Fe SMTJs, the effect of the reduction in Λ cancel that of the reduction in TST torque, leading to smaller
Fe SMTJs, the effect of the reduction in Λ cancel that of the reduction in TST torque, leading to smaller  and
and  comparing with clean junctions, as shown in table 1. It is suggested that, crystal defects such as interfacial OV, may be not always a deleterious factor to magnetic switching.
comparing with clean junctions, as shown in table 1. It is suggested that, crystal defects such as interfacial OV, may be not always a deleterious factor to magnetic switching.
Owing to the involvement of resonant QW states, TST torque in DBMTJs is enhanced. At the same time, the angular-dependency of TST torque gets symmetric or close to symmetric. Both factors lead to considerable reduction in  and
and  comparing with the SBMTJs with the same barrier thickness. So, we predict that MgO-based DBMTJs is more promising in application for thermally induced magnetization switching.
comparing with the SBMTJs with the same barrier thickness. So, we predict that MgO-based DBMTJs is more promising in application for thermally induced magnetization switching.
4. Summary
We predict enhanced TST torque and small switching temperature gradient in Fe  MgO
MgO  Fe
Fe  MgO
MgO  Fe DBMTJs from atomic first principles. Temperature gradient
Fe DBMTJs from atomic first principles. Temperature gradient 
 with
with  ∼ 10
∼ 10  across MgO barriers is predicted to drive the magnetic configurations in a DBMTJs switch circularly at room temperature, which is about one order smaller than that in Fe
across MgO barriers is predicted to drive the magnetic configurations in a DBMTJs switch circularly at room temperature, which is about one order smaller than that in Fe  MgO(3)
MgO(3) Fe MTJs, and under the current experimental capacity. The coexistence of resonant QW states and resonant interfacial states is responsible to the enhancement. The introduction of asymmetry by interfacial OV and different leads would change TMR and TST torque including their angular dependency. Moreover, zero thermocurrent can present at a specific angle in a DBMTJ, indicates that we can produce a 'off' state in the material thermally. Based on these results, we predict that MgO-based DBMTJs is promising in application for heat-flow-induced magnetization switching and logic device.
Fe MTJs, and under the current experimental capacity. The coexistence of resonant QW states and resonant interfacial states is responsible to the enhancement. The introduction of asymmetry by interfacial OV and different leads would change TMR and TST torque including their angular dependency. Moreover, zero thermocurrent can present at a specific angle in a DBMTJ, indicates that we can produce a 'off' state in the material thermally. Based on these results, we predict that MgO-based DBMTJs is promising in application for heat-flow-induced magnetization switching and logic device.
Acknowledgments
JX thanks KX at BNU for his transport codes and valuable discussion, and we gratefully acknowledge financial support from National Natural Science Foundation of China (11274094 and 51332007). JX also acknowledge financial support from Henan Polytechnic University (B2012-021 and T2016-2).
Footnotes
- 4
Slonczewski proposed a asymmetric parameter
 for angular dependent torques with conductance
for angular dependent torques with conductance 
 with
with  is the transmission part of the scatter matrix
is the transmission part of the scatter matrix  and
and  . The parameter would be invalid in case such as 100% spin polarization. In the calculations, we estimate the parameter by supposing the torques following the relation:
. The parameter would be invalid in case such as 100% spin polarization. In the calculations, we estimate the parameter by supposing the torques following the relation: 
 .
. - 5
In a recent experiment
 is needed to switch a
is needed to switch a  CoFe magnetization from P/AP to AP/P configurations. For clean Fe
CoFe magnetization from P/AP to AP/P configurations. For clean Fe  MgO(3)
MgO(3) Fe(8)
Fe(8) MgO(3)
MgO(3) Fe DBMTJs with S1 structure,
Fe DBMTJs with S1 structure,  and
and  is needed to switch a
is needed to switch a  magnetization.
magnetization.