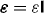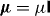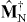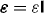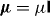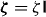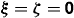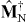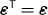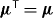Abstract
We formulate macroscopic quantum electrodynamics in the most general linear, absorbing media. In particular, Onsager reciprocity is not assumed to hold. The field quantization is based on the source-quantity representation of the electromagnetic field in terms of the dyadic Green's tensor. For media with a nonlocal response, a description in terms of a complex conductivity tensor is employed. As an alternative description, we introduce the permittivity, permeability and magnetoelectric susceptibilities to obtain an explicitly duality-invariant scheme. We find that duality invariance only holds as a continuous symmetry when nonreciprocal responses are allowed for.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The linear response of a macroscopic material to externally applied electromagnetic fields can go beyond the scope of simple descriptions via electric permittivities and magnetic permeabilities [1]. In particular, cross-susceptibilities naturally arise in chiral (meta-)materials [2], topological insulators [3] or moving media [4]. In the latter case nonlocal responses arise [5] with the additional complication that Onsager reciprocity [6] fails to hold. Onsager reciprocity, the electrodynamic manifestation of time-reversal symmetry, would also be violated in Tellegen media [7], including the recently proposed perfect electromagnetic conductor that continuously interpolates between a perfect conductor and an infinitely permeable material [8].
Chiral metamaterials with cross-susceptibilities have been constructed based on nanoscale chiral objects, such as a helix [9]. This leads to a discriminatory response of the medium to left- and right-circularly polarized light. This central feature of chiral media is important in biological systems due to the prevalence of left-handed objects in the processes crucial to life [10]. Furthermore, chiral meta-materials have been discussed as candidates for repulsive Casimir forces [11]. It should be noted that repulsive forces for magnetoelectric media were originally discussed for dielectric plates interacting with magnetic plates [12]. To implement these effects with metamaterials, the anisotropic response of the medium needs to be taken into account [13].
Topological insulators are a novel class of materials which behave as insulators in their bulk phase but allow for conduction on the surface [14, 15]. Time reversal symmetry is an important feature which ensures an extremely high stability of the surface currents. The latter make topological insulators a promising candidate for quantum computing [16]. It has recently been predicted that topological insulators [3] (or materials with a Chern–Simons interaction [17]) could be used to realize repulsive Casimir forces. A related phenomenon is the fractional quantum hall effect where the Hall current takes fractional values due to electron–electron interactions [18]. This medium can be nonlocal [19] and in contrast to topological insulators it can violate time-reversal symmetry [20] and hence Onsager reciprocity.
The impact of electric versus magnetic material properties can be studied in a systematic way by means of a duality transformation [21]. It has recently been shown that macroscopic QED [22] in isotropic magnetoelectrics obeys a discrete duality symmetry [23]. This has immediate consequences for dispersion forces in free space.
The successes in the realization of the above mentioned novel materials open the perspective on a range of new quantum phenomena related to photon-induced matter interactions, quantum dynamics and (possibly irreversible) quantum-light propagation. To make such studies possible, we will construct a quantum theory of the electromagnetic field in the most general linear absorbing media, including nonlocal, bianisotropic and Onsager reciprocity violating materials. A recent theory based on canonical quantization is a valuable step in this direction [24], which does not yet consider the most general nonlocal media (apart from the above mentioned moving media).
In addition, our theory shall answer the question under which circumstances duality can be realized as a continuous symmetry of the Maxwell equations in media; and it will shed light on the generalizations necessary to discuss moving media and quantum friction.
2. Field quantization in nonlocal media
We begin by recalling a quantization procedure of the electromagnetic field in the presence of an absorbing medium. For alternative methods for the quantization procedure, see [25–27] and references therein. In a linearly responding medium, the effect of an external electromagnetic field on the matter can be given by Ohm's law in its most general form
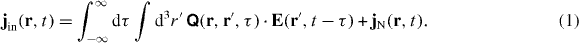
Here, 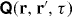 is the conductivity tensor and jN(r,t) is the random noise current required to fulfil the fluctuation–dissipation theorem (17) as given below. Causality requires that
is the conductivity tensor and jN(r,t) is the random noise current required to fulfil the fluctuation–dissipation theorem (17) as given below. Causality requires that 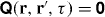 for cτ < |r − r'|, in particular for all τ < 0 [28]. In frequency space, Ohm's law takes the simpler form
for cτ < |r − r'|, in particular for all τ < 0 [28]. In frequency space, Ohm's law takes the simpler form
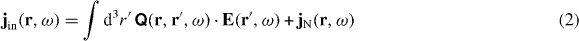
with

As a result of the causality requirement the conductivity obeys the Schwarz reflection principle,

Quantization is achieved by specifying the commutator
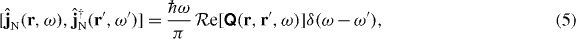
where we have introduced generalized real and imaginary parts of a tensor field according to


They reduce to ordinary real and imaginary parts for orthogonal tensor fields that are reciprocal, i.e.  . The other nontrivial current commutators follow alternatively via the rules
. The other nontrivial current commutators follow alternatively via the rules ![$[\hat {b}, \hat {a}] = - [\hat {a}, \hat {b}]$](https://content.cld.iop.org/journals/1367-2630/14/8/083034/revision1/nj438853ieqn4.gif) or
or ![$[\hat {a}^{\dagger}, \hat {b}^{\dagger}] = - [\hat {a}, \hat {b}]^{\dagger}$](https://content.cld.iop.org/journals/1367-2630/14/8/083034/revision1/nj438853ieqn5.gif) ;
;
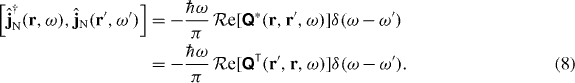
The fact that the right-hand side of this expression is a Hermitian tensor field guarantees the consistency of the commutation relations.
Combining Ohm's law with Maxwell's equations [  ]
]
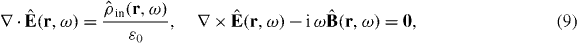
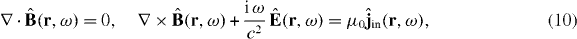
one finds that the electric field obeys a generalized inhomogeneous Helmholtz equation of the form
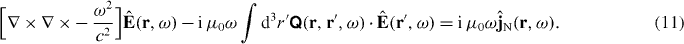
With the help of the Green function  of the Helmholtz equation, defined by
of the Helmholtz equation, defined by
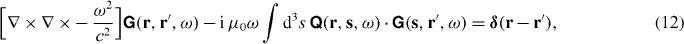
where  for |r − r'| → ∞, the formal solution to the integro-differential equation (11) reads
for |r − r'| → ∞, the formal solution to the integro-differential equation (11) reads

Here, ![$[ \boldsymbol {{\sf {G}}}\star \hat {\mathbf {j}}_{\mathrm {N}}]$](https://content.cld.iop.org/journals/1367-2630/14/8/083034/revision1/nj438853ieqn9.gif) is an abbreviation denoting the spatial convolution
is an abbreviation denoting the spatial convolution
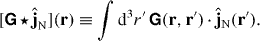
By virtue of its definition (12), the Green tensor inherits the Schwarz reflection principle from the conductivity tensor (4),
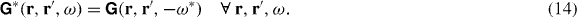
However, as a major departure from previous treatments, we do not require the conductivity to obey reciprocity, i.e. the relation 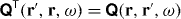 does not necessarily hold. As a consequence, the Green tensor will not obey the Onsager principle, i.e. the relation
does not necessarily hold. As a consequence, the Green tensor will not obey the Onsager principle, i.e. the relation

will not hold in general. Recall that the Onsager principle, applied to electromagnetic field propagation, states a reversibility of optical paths [6]. According to (13), the Green tensor governs the relation between a source current j at r' along a direction e2 and the generated electric field E at r along a direction e1. If (15) holds, then the Onsager principle states that the roles of source and field can be reversed. A source current j at r along a direction e1 would then give rise to an electric field E at r' along a direction e2. In a configuration involving nonreciprocal media, this is not necessarily the case. Despite the extension to nonreciprocal media, it is still possible to derive the useful integral relation (appendix)
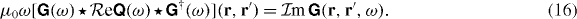
It generalizes the result from [29] to the case where Onsager reciprocity does not hold.
The theory thus far is analogous to classical electromagnetism in an absorbing medium under the assumption of classical fluctuating current sources, 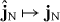 . Their strengths are governed by the fluctuation–dissipation theorem in the classical (high-temperature) limit [30].
. Their strengths are governed by the fluctuation–dissipation theorem in the classical (high-temperature) limit [30].
Introducing the ground state |{0}〉 of the medium-field system according to 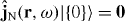 , the currents satisfy the fluctuation–dissipation theorem as an immediate consequence of (5),
, the currents satisfy the fluctuation–dissipation theorem as an immediate consequence of (5),

Combining (5) and (13), one finds that the fluctuations of the electric field are also consistent with the fluctuation–dissipation theorem, as required:
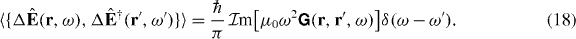
In order to verify the canonical equal-time commutation relations, we introduce the vector potential for the electromagnetic field in the Coulomb gauge,  (⊥: transverse part). Using (5) and (13), one finds
(⊥: transverse part). Using (5) and (13), one finds
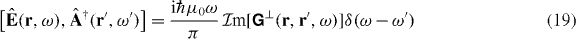
and hence

where the Schwarz reflection principle (14) has been used. Use has been made of the left- and right-sided transverse projections, which are defined, respectively, as

Closing the integration contour in the upper half of the complex ω plane, where the Green's function is analytic, and using the asymptote 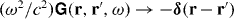 for |ω| → ∞, one finds the canonical commutation relation from free-space QED,
for |ω| → ∞, one finds the canonical commutation relation from free-space QED,

as required. We now introduce the bosonic creation and annihilation operators of the matter-field system,  and
and  according to the prescription
according to the prescription

where 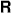 is a square root of the positive definite tensor field
is a square root of the positive definite tensor field ![$\mathcal {R}\mathrm {e}[\boldsymbol {{\sf {Q}}}]$](https://content.cld.iop.org/journals/1367-2630/14/8/083034/revision1/nj438853ieqn18.gif) ,
,

This solution is only unique up to a unitary matrix which does not affect the physical results [29]. Together with equation (5), this ensures bosonic commutation relations,
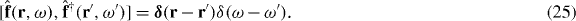
The Hamiltonian of the medium-field system is then
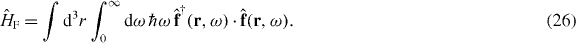
It leads to the free evolution of the dynamical variables as 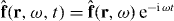 ; hence Maxwell's equations for the electromagnetic-field operators in the Heisenberg picture are valid by construction.
; hence Maxwell's equations for the electromagnetic-field operators in the Heisenberg picture are valid by construction.
3. Field quantization in terms of electric and magnetic response functions
The properties of media with spatially nonlocal or local responses can alternatively be described by their permittivity, permeability and magnetoelectric susceptibilities. To begin, it is convenient to cast the inhomogeneous Maxwell equations (10) into the forms (we drop the spatial and frequency arguments from now on)

with

The polarization and magnetization fields respond linearly to the electric and magnetic fields,
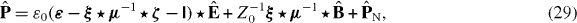
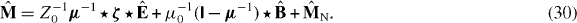
The medium is characterized by its permittivity, ε(r,r',ω), its permeability, μ(r,r',ω) and its magnetoelectric susceptibilities, ξ(r,r',ω) and ζ(r,r',ω). 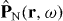 and
and 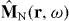 denote the noise polarization and noise magnetization, respectively, and
denote the noise polarization and noise magnetization, respectively, and 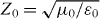 is the vacuum impedance. In the case of nonlocal media the permittivity, permeability and magnetoelectric susceptibilities are functions of two independent spatial variables, whereas in a locally responding media they read ε(r,r',ω) = ε(r,ω)δ(r − r'), μ(r,r',ω) = μ(r,ω)δ(r − r'), ξ(r,r',ω) = ξ(r,ω)δ(r − r') and ζ(r,r',ω) = ζ(r,ω)δ(r − r'). By combining (28)–(30), the constitutive relations can be given in the more familiar form (see [31] for the nonconducting case)
is the vacuum impedance. In the case of nonlocal media the permittivity, permeability and magnetoelectric susceptibilities are functions of two independent spatial variables, whereas in a locally responding media they read ε(r,r',ω) = ε(r,ω)δ(r − r'), μ(r,r',ω) = μ(r,ω)δ(r − r'), ξ(r,r',ω) = ξ(r,ω)δ(r − r') and ζ(r,r',ω) = ζ(r,ω)δ(r − r'). By combining (28)–(30), the constitutive relations can be given in the more familiar form (see [31] for the nonconducting case)
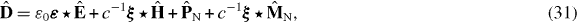

where the notational distinction between locally and nonlocally responding media as given above applies.
In order to distinguish reciprocal magnetoelectric susceptibilities from nonreciprocal ones, as previously discussed in the nondispersive case [32], one commonly writes 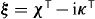 and ζ = χ + iκ. The chirality tensor
and ζ = χ + iκ. The chirality tensor 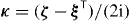 represents the reciprocal magnetoelectric response; whereas the nonreciprocal magnetoelectric tensor
represents the reciprocal magnetoelectric response; whereas the nonreciprocal magnetoelectric tensor 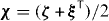 vanishes for a reciprocal medium.
vanishes for a reciprocal medium.
By combining Maxwell's equations with the constitutive relations (31) and (32), we note that the respective Green tensor is the solution to equation (12) with
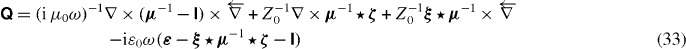
and

where ![$[\boldsymbol {{\sf {T}}}\times \overleftarrow {\mathbf {\nabla }}]_{ij}(\mathbf {r},\mathbf {r}')= \epsilon _{jkl}\partial _l'T_{ik}(\mathbf {r},\mathbf {r}')$](https://content.cld.iop.org/journals/1367-2630/14/8/083034/revision1/nj438853ieqn26.gif) denotes a derivative acting on the second argument of a tensor function. The Green tensor for the electric field (13) solves
denotes a derivative acting on the second argument of a tensor function. The Green tensor for the electric field (13) solves
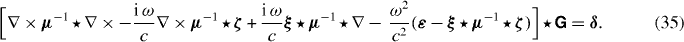
The commutation relations for 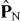 and
and 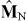 can be deduced by substituting the real parts of (33) and (34) into (5),
can be deduced by substituting the real parts of (33) and (34) into (5),

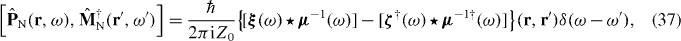
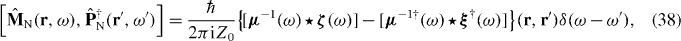
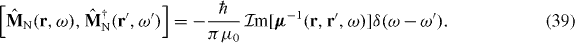
We now introduce the bosonic creation and annihilation operators with commutation relations
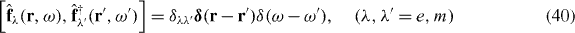
according to

where the (6 × 6)-matrix  is a root of
is a root of
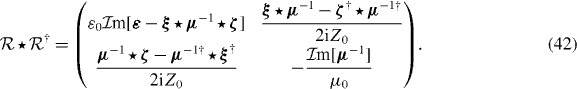
The Hamiltonian of the body–field system is again quadratic and diagonal in the bosonic variables,
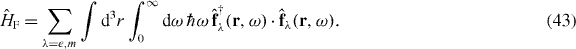
Note that (28)–(30) imply a separation of the internal current density into electric and magnetic parts, 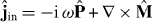 . This separation and the resulting explicit field quantization is not unique in spatially dispersive (i.e. nonlocal) media, as the magnetization field can be absorbed into the transverse part of the polarization field [28]. While a local magnetoelectric medium can always be described in terms of a (nonlocal) conductivity without reference to magnetic properties, the equivalent description in terms of a local permittivity, permeability and cross-susceptibility is much more accessible. These parameters are often known experimentally and they allow for a classification of electromagnetic responses.
. This separation and the resulting explicit field quantization is not unique in spatially dispersive (i.e. nonlocal) media, as the magnetization field can be absorbed into the transverse part of the polarization field [28]. While a local magnetoelectric medium can always be described in terms of a (nonlocal) conductivity without reference to magnetic properties, the equivalent description in terms of a local permittivity, permeability and cross-susceptibility is much more accessible. These parameters are often known experimentally and they allow for a classification of electromagnetic responses.
4. Duality invariance
An electromagnetic system separated into distinct electric and magnetic causes and effects can be subject to a duality transformation operation, that is, a global exchange of the electric and magnetic properties. A system invariant under such an operation is said to possess duality invariance as a symmetry [21]. This symmetry can be exploited in order to simplify the computation of dispersion forces involving, say magnetizable media, from known dispersion forces between polariable media [23].
By introducing dual-pair notation  ,
,  , we may write the Maxwell equations (9) and (27) in the compact form
, we may write the Maxwell equations (9) and (27) in the compact form

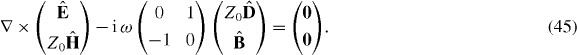
The constitutive relations (31) and (32) in condensed form read
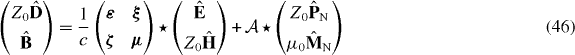
with

Maxwell's equations are invariant under duality transformations
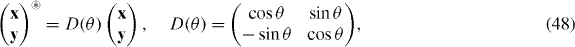
because D(θ) is a symplectic matrix. From the constitutive relations, as shown in (46), we find the transformed medium response functions

with

as well as
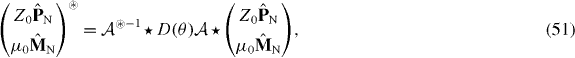
where

It is worth discussing a few special cases of bianisotropic media, their characteristic features and behaviour under duality transformations:
- Local media [ε(r,r',ω) = ε(r,ω)δ(r − r'), similarly for the other response functions]: Convolution operators reduce to ordinary matrix products, compatible with all other special cases below.
- Isotropic media (
 ,
,  ,
,  ): Onsager reciprocity (15) holds;
): Onsager reciprocity (15) holds;  and
and  commute; generalized real and imaginary parts reduce to ordinary ones; discrete duality symmetry.
commute; generalized real and imaginary parts reduce to ordinary ones; discrete duality symmetry. - Bi-isotropic media (
 ,
,  ,
,  ,
,  ): generalized real and imaginary parts in (36) and (39) reduce to ordinary ones; continuous duality symmetry.
): generalized real and imaginary parts in (36) and (39) reduce to ordinary ones; continuous duality symmetry. - Anisotropic media (
 ):
):  and
and  commute; discrete duality symmetry.
commute; discrete duality symmetry. - Reciprocal media (
 ,
,  ,
,  ): (15) holds; generalized real and imaginary parts reduce to ordinary ones; discrete duality symmetry.
): (15) holds; generalized real and imaginary parts reduce to ordinary ones; discrete duality symmetry.
Here, discrete duality symmetry means that the rotation angle is restricted to values θ = nπ/2 with 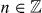 . Note that duality is only realized as a continuous symmetry when Onsager-violation is allowed for. Notably, a reduction in reciprocity symmetry leads to an enhancement of duality symmetry.
. Note that duality is only realized as a continuous symmetry when Onsager-violation is allowed for. Notably, a reduction in reciprocity symmetry leads to an enhancement of duality symmetry.
In order to derive transformation laws for the Green tensor, we combine (9), (11), (28), (30) and (34) to write



where we have introduced the shorthand notations 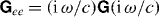 ,
, 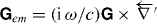 ,
,  and
and 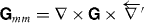 . The transformed Green's tensors follow by applying duality transformations on both sides of this equation,
. The transformed Green's tensors follow by applying duality transformations on both sides of this equation,
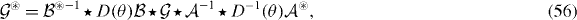
where

In the special case of r and r' being in free space, we have  , so that
, so that  and hence
and hence

The Green tensors then transform like the medium response functions with (50).
5. Conclusion
Based on the general Ohm's law, we have quantized the electromagnetic field in the presence of nonlocal, nonreciprocal media which satisfies (i) the canonical commutation relations from free-space QED; (ii) the linear fluctuation–dissipation theorem; and (iii) the macroscopic Maxwell equations. A key feature of the scheme is the symmetrization of tensor fields via generalized real and imaginary parts, which is necessary whenever Onsager reciprocity does not hold. Their presence in the fluctuation–dissipation theorem is the key to avoiding restrictions on the allowed medium response.
For nonlocal and local bianisotropic media we have shown that quantization can alternatively be performed by the introduction of permittivity, permeability and magnetoelectric susceptibilities. When the latter do not vanish, the noise polarization and magnetization do not commute. We have explicitly determined the behaviour of the fields and response functions under duality transformations. The full continuous transformation group applies for bianisotropic and bi-isotropic media, but reduces to a discrete symmetry for isotropic, anisotropic and/or reciprocal media.
The scheme lays the foundation for exact studies of quantum phenomena such as dispersion forces, Förster energy transfer or environment-assisted molecular transition rates in the presence of motion or novel media with chiral or nonreciprocal properties. Moving media are a prime example for the occurrence of nonreciprocal material properties [28] which have to be thoroughly accounted for in order to understand, e.g. quantum friction. CP violation in atoms or molecules is manifest in their nonreciprocal cross-polarizability. The Curie principle, stating that certain interactions between two partners (atoms, molecules, bodies, etc) require them to possess similar properties, then allows for a detection of CP violation via atom–surface interactions provided the surface exhibits a corresponding nonreciprocity.
Acknowledgment
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC).
Appendix.: Integral relation for the Green tensor
To derive the integral relation (16) for the Green tensor, we write the Helmholtz equation (12) as

where 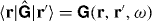 and
and ![$\langle \mathbf {r}|\hat {\boldsymbol {{\sf {H}}}}|\mathbf {r}'\rangle =[\mathbf {\nabla }\times \mathbf {\nabla }\times -\omega ^2/c^2] {\boldsymbol \delta }(\mathbf {r}-\mathbf {r}') -\mathrm {i}\,\mu _0\omega \boldsymbol {{\sf {Q}}}(\mathbf {r},\mathbf {r}',\omega )$](https://content.cld.iop.org/journals/1367-2630/14/8/083034/revision1/nj438853ieqn56.gif) . The Green operator is the right-inverse and, within any group of invertible operators, also the left-inverse of the Helmholtz operator,
. The Green operator is the right-inverse and, within any group of invertible operators, also the left-inverse of the Helmholtz operator,

From this relation and its Hermitian conjugate we find that

In coordinate space this relation reads
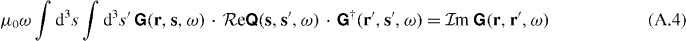
which in convolution notation takes the form of equation (16).