Multipolar second-harmonic emission with focused Gaussian beams

The optical responses of materials are usually described by considering only electric-dipole interactions between light and matter. Such an electric-dipole approximation is justified by the fact that the higher-multipole interactions, most importantly magnetic-dipole and electric-quadrupole interactions, tend to be much weaker [1]. Such interactions, however, need to be considered, e.g., to explain optical activity of chiral materials [2].

For the case of nanostructured materials, one needs to consider two different types of multipole effects. The first arises from the atomic-level light–matter interaction Hamiltonian [3] and the other from Mie scattering theory even when the atomic-level interaction has purely electric-dipole origin [4]. In the latter case, retardation of electromagnetic fields across nanoscale particles gives rise to effective multipole terms in the scattering pattern. Although Mie theory is usually associated with spherical particles, it is possible to show that any scattering pattern outside a finite sphere enclosing the sources can always be expanded in similar multipole terms [1, p 439]. Multipole effects can become considerable when the particle sizes are comparable to wavelength, as recent studies of nanoparticles have shown [5–12]. But a complete understanding of such phenomena is still lacking in order to utilize multipole effects in applications such as in metamaterials or optical antennas [13–15].

Multipole effects have particular importance in nonlinear optics, because second-order nonlinear effects are electric-dipole-forbidden in centrosymmetric materials [16]. A dipole-allowed second-order signal can therefore arise only from the broken symmetry at the material surface or interface [17]. The second-order effects, however, can also occur in the bulk of centrosymmetric materials due to magnetic and quadrupole effects. Separation between the surface and the bulk effects has been notoriously difficult [18–20], only recently achieved in an unambiguous and quantitative way [21, 22]. Effective, Mie-type multipoles can also play a role in nonlinear optics as shown by several nonlinear studies from colloids and arrays of nanoparticles [5–12, 23–28].

Independent of their atomic-level or effective origin, the various multipole sources differ with regard to their far-field radiation patterns and polarization [1]. More specifically, interference between appropriate multipole terms can be used to control the directionality of the radiation pattern [14, 24]. In nonlinear optics, this could lead to nanoscale sources, in other words optical antennas, with emission enhanced in one direction and suppressed in the opposite direction. In traditional nonlinear optics, this is only possible through phase-matching effects, which require samples much larger than wavelength.

In this paper, we show that multipole effects can occur also due to the finite profile of focused Gaussian laser beams. In addition, we show that the multipole effects can even be efficiently controlled in nonlinear optics by using focused Gaussian beams, although the atomic-level light–matter interaction has an electric-dipole origin. The source region is then inhomogeneous and limited by diffraction to the scale of a wavelength. On the other hand, from the viewpoint of far-field radiation, the source region is well confined, implying that the radiation pattern can be expressed as a multipole expansion, where a number of multipoles are expected to contribute to the total radiation pattern. We demonstrate these effects by measuring second-harmonic generation (SHG) from thin films of silicon nitride (SiN), which have the symmetry of an isotropic surface. The experiments are performed using focused Gaussian TEM₀₀ beams at normal incidence. By fully accounting for the vector properties of the spatially varying focal fields and the tensorial character of the nonlinearity, we observe strong differences between the SHG signals emitted in the transmitted and reflected directions. The results are shown to be compatible with the characteristics of the effective multipole moments of the source distribution.

In order to understand qualitatively how focused beams lead to effective multipole effects, we write the second-harmonic (SH) polarization at a frequency ω in the form

$$\begin{equation} \mathbf{P}(\mathbf{r})=\epsilon_0\chi^{(2)}(\mathbf{r}) : \mathbf{E}(\mathbf{r}) \mathbf{E}(\mathbf{r})\, \forall \mathbf{r} \in \mathbb{R}^3 , \end{equation} \tag{ 1 }$$

where E is the field at the fundamental frequency ω/2, χ⁽²⁾_ijk is the second-order susceptibility tensor for SHG and r = (x,y,z) denotes the position vector in the three-dimensional Euclidean space $\mathbb {R}^3$. This form represents the traditional electric-dipole approach to nonlinear optics, where the fields and the nonlinear source polarization are spatially varying [29, 30]. For the case when the fundamental beam is a focused Gaussian beam, the source polarization decays rapidly in space and can be expressed using the Helmholtz decomposition as [1, p 241]

$$\begin{equation} \mathbf{P} = \mathbf{P}_v + \nabla \times \mathbf{P}_p , \end{equation} \tag{ 2 }$$

where ∇ × P_p is the divergence-free and P_v is the curl-free part. In the presence of nonlinear magnetization M, the effective source polarization would be of the form [19]

$$\begin{equation} \mathbf{P}_{\rm eff} = \mathbf{P} + \frac{1 }{\omega^2 \mu} \nabla \times \mathbf{M} , \end{equation} \tag{ 3 }$$

where μ is the permeability. Comparison of equations (2) and (3) thus suggests that the divergence-free part of the polarization is equivalent to a magnetic source term.

The connection between the spatially varying sources and the multipole approach can be made explicit by expressing the electric component of the emitted field at the SH frequency as [1, p 431]

$$\begin{equation} \fl \mathbf{E}_{SH} = \eta \sum_{l=1}^\infty \sum_{m=-l}^l\left[ \frac{{\rm i}}{k}a_{l,m}^E \nabla\times h^{(1)}_l(kr)\mathbf{X}_{l,m} + a_{l,m}^M h^{(1)}_l(kr)\mathbf{X}_{l,m}\right],\quad r=|\mathbf{r}|> R, \end{equation} \tag{ 4 }$$

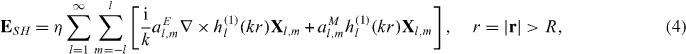
where a^E_l,m and a^M_l,m are electric and magnetic multipole moments, respectively, X_l,m are the vector spherical harmonics (functions of the spherical polar angles), h⁽¹⁾_l are the spherical Hankel functions of the first kind and lth order, η is the intrinsic impedance and k is the wavenumber of the SH field. The sources are required to vanish outside a sphere S of radius R. The time-dependence $\exp (-{\rm i}\omega t)$ is also assumed. Note that the electric (magnetic) moments of successive orders have opposite parity, whereas the electric and magnetic terms of a given order also have opposite parity [1, p 436]. An obvious way to control the directional properties of the emission is therefore to interfere an electric dipole source with a magnetic dipole and/or electric quadrupole. The multipole moments are obtained from the electric-dipole sources as (for the derivation see the supplementary data, available from stacks.iop.org/NJP/14/113005/mmedia)

$$\begin{equation} a_{l,m}^E \propto \int_{S} Y_{l,m}^*\left( -c\nabla \cdot \mathbf{P} \frac{\partial}{\partial r}(rj_l(kr)) \right. + \left.\vphantom{\frac{\partial}{\partial r}} k \omega \mathbf{r}\cdot \mathbf{P}j_l(kr) \right) {\rm d} V , \end{equation} \tag{ 5 }$$

$$\begin{equation} a_{l,m}^M \propto \int_{S} Y_{l,m}^*\mathbf{r}\cdot(\nabla\times \mathbf{P})j_l(kr) {\rm d} V, \end{equation}\noindent \tag{ 6 }$$

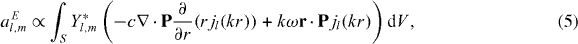
where Y_l,m are the spherical harmonics and j_l are the spherical Bessel functions of the first kind and lth order [1, p 441]. Note that for sources confined to volumes much less than wavelength kr ≪ 1, the second term of the integrand in equation (5) vanishes. For l = 1 the first term becomes ∇·PY*_1,mr, and its integration yields the components of the total dipole moment in the volume. For larger sources, the interpretation is more complicated, because a number of electric and magnetic multipoles can contribute to the emission in the far field. The interpretation of equation (6) is always relatively straightforward, i.e. an effective magnetic moment arises from the curl of the source polarization. Thus we see that in general a non-zero ∇ × P is required to obtain a magnetic response.

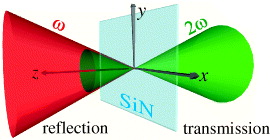
In order to demonstrate these general principles and study the role of ∇ × P in SHG, we use samples with isotropic achiral surface symmetry. Such samples have the highest possible surface symmetry and thus provide a convenient model case to investigate the role of the various multipoles in the nonlinear response. Our samples are thin films (20 and 50 nm thicknesses) of amorphous SiN, prepared by depositing SiN on fused silica substrates using plasma enhanced chemical vapor deposition [33]. Such samples have full rotational symmetry about the film normal. They are therefore equivalent to isotropic surfaces with the non-vanishing components of the electric-dipole susceptibility tensor χ⁽²⁾_ijk as zzz, zxx = zyy and xxz = xzx = yyz = yzy, where z is the film normal (figure 1). In addition, phase matching issues can be neglected because of the small film thickness. The focusing conditions correspond to normal incidence, numerical aperture (NA) of 0.8 and a pupil filling factor of 1. Note that the focusing conditions give rise to longitudinal (z direction) field components required for coupling with the present susceptibility tensor at normal incidence.

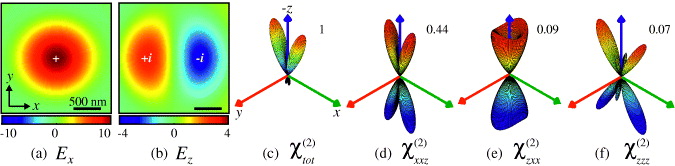
Zoom In Zoom Out Reset image size

For a qualitative understanding, we first consider an x-polarized fundamental beam and calculate the resulting electric field at the waist of the focused beam using an angular spectrum representation (figures 2(a) and (b)). The normal (z) component of the focal field is odd in x, i.e. it consists of two lobes with opposite phases. The other components, on the other hand, are even. It is then easy to see that the nonlinear polarization P due to the zzz or zxx components can never be an odd function (with respect to the x coordinate) [1]. But when the xxz component and the corresponding P are also considered, we see that similarly to E_z, also P_x is now an odd function. This leads to a situation where the contribution from ∇ × P over the interaction volume can be expected to be large.

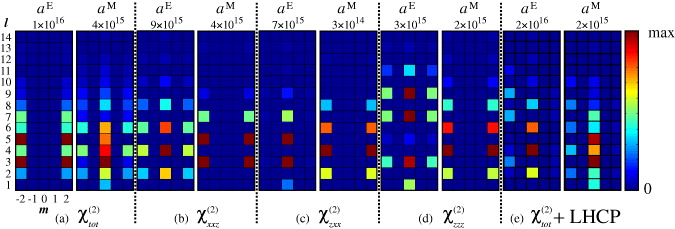
Zoom In Zoom Out Reset image size

Using equation (1), we then calculate the source polarization for SHG at the beam waist (z = 0), and finally the emitted SH powers per unit solid angle using both Green's function approach [31, 32] and the proposed multipole approach. As expected, both approaches led to the same results, which are shown in figures 2(c)–(f). In order to understand the origin of the directionality and the interference effects in the SH emission, we present the results separately for different susceptibility components. In the calculations, we use relative values of zzz = 1, zxx = 0.19 and xxz = 0.2 for the non-zero susceptibility components, corresponding to the recently measured values for the SiN films [33]. For simplicity, only free-space Green's functions are considered, since reflections due to the interfaces cannot explain the measured differences of SH emission and would only improve the quantitative accuracy of the proposed multipolar formalism. Also, the scattered fields at the fundamental frequency are neglected in the calculations since the samples are transparent and thus weakly scattering. Finally, we calculate the normalized multipole moments a^E_l,m and a^M_l,m and find that the only non-zero electric moments occur for m = 0,±2. The non-zero magnetic moments correspond to m = ± 2 and the first seven of the l terms are found to be most dominant. We note that when using isolated tensor components, the non-vanishing moments are such that corresponding multipoles have the same parity. When considering the full tensor, this condition is no longer met and interference can occur.

In our experiments, we measure the transmitted and reflected total radiated SH powers into the far-field while changing the polarization of the input beam (figure 1). The polarization measurements are important because our calculations predict that, in addition to different SH emission strengths in the two directions, their polarization dependences are qualitatively different, allowing key evidence to be obtained even without relying on precise calibration of the signal collection efficiencies in reflection and transmission.

For measurements, a custom-built SHG microscope setup with input femtosecond laser (central wavelength at 1060 nm) providing 200 fs pulses at 82 MHz repetition frequency was used (figure 3). The fundamental beam with an average power of 10 mW was focused onto the samples with an NA = 0.8 microscope objective. The reflected SHG emission was collected by the same focusing objective, and the transmitted SH emission was collected by an additional identical microscope objective placed to the back of the sample. The collected SH emission thus corresponds now to the calculated SH powers per unit solid angle (figures 2(c)–(f)), integrated over the numerical aperture (NA = 0.8) of the collecting objectives. In addition, the use of high-NA collecting objectives is important, since there is no radiation into the strictly forward and backward directions, as can be seen in figure 2(c). The SH emission was then separated from the fundamental beam by dichroic and interference filters, and measured simultaneously by two photomultiplier tubes connected to a photon counting unit. The polarization control of the input beam was done by a rotating QWP, and measurement times of 30 s and angle steps of 5° for the QWP were used. The QWP angles of 0°, 90°, 180°, etc corresponded to linear input polarization and angles of 45°, 135°, 225° and 315° to circular input polarizations.

Zoom In Zoom Out Reset image size

First we measured SHG responses from gold nanodots (radius 75 nm) in order to calibrate the relative detection efficiencies of both detection arms. The collection efficiency for the transmitted SHG was seen to differ from that of reflected SHG by a factor of 2.13, which was used for the mutual calibration of the two SHG signals. We emphasize, however, that the calibration was performed only to increase the accuracy of our measurements, and is not necessary for demonstrating the effect.

After the calibration, we measured the SHG from SiN thin films. Figure 4 shows the measured and calculated SHG responses as a function of the rotation angle of the QWP from the SiN film with a thickness of 50 nm. The average ratio for transmitted and reflected SHG was measured to be 4.06, and more importantly, the polarization dependences of the reflected and transmitted SHG responses clearly differ from each other. The measured SHG responses also correspond surprisingly well with the modeled responses based on both the Green's function and the proposed multipolar approaches (see section 2 for details). For the calculations, no fitting besides normalization to the maximum of transmitted SHG response was performed.

Zoom In Zoom Out Reset image size

We emphasize that our samples are highly transparent and very thin (thickness less than λ/10). Possible phase matching or Fabry–Perot issues can be ruled out due to the sample thickness, because no significant phase accumulation of the fields can occur over such a short distance. Neither can absorption explain the observed differences, since it could not explain the polarization dependences. The samples should therefore emit symmetrically in the transmitted and reflected directions. We also exclude any response from the fused silica substrate as an explanation, since we were not able to get any measurable SHG from the substrate even with input beam powers exceeding 30 mW. The most plausible explanation for the results is thus interference between multipoles of different parities, in particular between electric and magnetic multipoles. We believe that magnetic multipoles play an important role due to non-vanishing ∇ × P. This is also supported by the calculated multipole moments, where the magnetic moments were considerably large as is seen in figure 5.

Zoom In Zoom Out Reset image size

The proposed multipole approach also provides an elegant explanation for the measured polarization dependence of the SH emission. When the input polarization changes from linear to circular, the calculated multipole moments change, respectively. The behavior is seen in figure 5(e), where the calculated multipole moments for left-handed circular input polarization are shown. In essence, the strengths of multipoles with different parities are reduced by changing the input polarization into circular. This leads to reduced interference effects and thus a decreased ratio between the transmitted and the reflected emission as was measured.

Our results provide new insights for understanding the connection between SHG and multipolar effects. Firstly, the results show the power of focused beam geometry and consequent theoretical formalism [32, 34], since SHG is forbidden from our samples at normal incidence and in the limit of plane-wave excitation [16]. Secondly, the results show that electric-dipole interactions can give rise to strong effective magnetic responses, if the source polarization is spatially varying and the condition ∇ × P ≠ 0 is satisfied. In our case, this occurred when the excitation field was a focused TEM₀₀ Gaussian beam and the second-order susceptibility had non-zero xxz component.

Interestingly, our results have similarities to the suggestion of Bethune already in 1981 that multimode beams could enhance the bulk responses of higher-multipole origin in surface SHG [35], as was further studied by Bernal and Maytorena [36]. In our case, however, the higher-multipole responses arise from atomic-level electric-dipole responses, and do not rely on atomic-level higher multipoles. This suggests that the dilemma of differentiating the bulk and surface contributions from each other could be even harder than previously thought, in particular when focused Gaussian beams are used. This problem is due to the fact that the separation of bulk and surface contributions in general relies on measuring either interference effects or different polarization dependences of the SH emission [21, 22, 24]. But our calculations and experimental data show that similar effects can also occur when the source volume is confined.

The results also demonstrate the general principle that the SH emission from confined volumes can be affected by tailoring the excitation, in our case the focusing, conditions. In addition, the introduced multipole approach is expected to facilitate more arbitrary control of SH emission by providing an understanding of how certain types of multipoles could be enhanced, e.g. by utilizing higher-order vector beams.

To conclude, we have shown that traditional electric-dipole-allowed SHG can be interpreted in terms of effective higher-multipole terms when the excitation occurs using focused Gaussian beams. In particular, magnetic terms become important whenever the quantity ∇ × P is non-vanishing. The approach was demonstrated using thin SiN films as the nonlinear source, where the SH emission was strongly asymmetric between the reflected and transmitted directions. Such multipolar approaches provide a way of obtaining directional nonlinear emission from confined and thin source volumes, where traditional phase matching is irrelevant. Nonlinear sources with desired radiation patterns can therefore be tailored by the choice of focal conditions to enable or suppress selected multipoles in the response.

We would like to acknowledge Outi Hyvärinen and Janne Simonen at the Optoelectronics Research Center (Finland) for kindly providing the samples. This work was funded by the Academy of Finland (project 134973). MJH acknowledges support from the Graduate School of Modern Optics and Photonics in Finland and the Emil Aaltonen Foundation. JM acknowledges support from the Graduate School of Tampere University of Technology.