Abstract
The Ring of Fire (RoF) measurement concept to perform on-site experiments of aerodynamic drag for transiting objects is investigated with a study that identifies the main sources of uncertainty.
The main contributors to the uncertainty of the drag measurement are examined for the case of a cyclist riding through the measurement domain. A sensitivity analysis is conducted that assesses how the estimated drag is affected by the choice of particle image velocimetry image processing parameters. The size of the cross-section considered in the control volume formulation is also investigated. It is found that the accuracy of the estimated drag depends on the procedure used to detect the edge of the momentum deficit region in the wake. Moreover imposing mass conservation yields the most accurate drag measurements. The drag estimation has little dependence upon the spatial resolution of the measurement as long as the interrogation window size stays within 5% to 25% of the equivalent diameter of the object cross section. Experiments are conducted in a sport-hall, where the aerodynamic drag estimates from the RoF are compared to a conventional torque power meter installed on the bicycle, and different rider's postures as well as equipment variations are considered. Although the discrepancy in the absolute value of drag can be as high as 20%, power metering and RoF agree within 4% on relative drag variations.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Aerodynamic loads measurements and optimisation are relevant in a broad variety of sectors, including aeronautics and ground transportation, animal flight, and speed sports. Several approaches for measuring the aerodynamic forces, particularly drag, have been proposed in the past, including wind tunnel measurements (Jones 1936, Zdravkovich 1990, Laitone 1997), towing force measurements (von Carmer et al 2008, Tschepe et al 2019), on-site measurements (Le Good et al 1998, Matschke and Heine 2002, Edwards and Byrnes 2007, Usherwood et al 2020) and numerical simulations by Computational Fluid Dynamics (Griffith et al 2014, Khayrullina et al 2015). Wind tunnel experiments often feature scaled models where the aerodynamic loads are measured with a force balance (Watkins et al 1992). Uncertainties typically arise from scaling effects, relative-to-ground motion modelling, model blockage and often interference of the support (Barlow et al 1999, Páscoa et al 2012). Furthermore, some specific cases such as the study of accelerating or decelerating conditions (Coutanceau and Bouard 1977) are difficult to reproduce in the wind tunnel environment. Finally, the development of the wake over a large distance (Scarano et al 2002, Bell et al 2015) or the study of the biomechanics of flight (Spedding and Hedenström 2010, Hedenström and Johansson 2015) are not easily conducted in wind tunnels. In some of the above cases, conducting measurements with the object moving through a quiescent fluid has been pursued. For instance, Henning et al (2016) carried out particle image velocimetry (PIV) measurements in the lateral underfloor region of a full-scale high-speed train transiting at 44 m s−1; in their investigation, the high speed of the train and the corresponding Reynolds number (Re = 9 × 106) were crucial for the so-called ballast projection to occur. When the primary interest of the measurements is not the flow visualisation but rather the evaluation of the aerodynamic drag, the steady state torque test and the coast-down technique are established methods of determining on-road aerodynamic drag of for road vehicles (Passmore and Jenkins 1988) and of cyclists (Debraux et al 2011).
In recent years, the steady state torque test became the most practiced method in cycling. Power meter measurements are carried out to determine the power output of the cyclist, from which the cyclist's aerodynamic drag is retrieved based on the balance of power (Grappe et al 1997). When comparing these on-site techniques with wind tunnel measurements, the advantages of more realistic flow conditions and lower costs are counterbalanced by an increased uncertainty due to additional error sources, such as the less-controlled atmospheric conditions and the physical modelling of non-aerodynamic resistance forces, e.g. due to rolling resistance and drive train losses. Moreover, the on-site techniques adopted so far do provide direct access to the aerodynamic drag, but with no indication of the flow behaviour. The latter is necessary when the physical sources of aerodynamic drag need to be identified and possibly minimised.
In the recent years, a measurement concept has been introduced by the authors' group (Terra et al 2017, 2018, Spoelstra et al 2019), namely the Ring of Fire (RoF), based on large-scale stereoscopic PIV measurements past an object or a vehicle travelling through a quiescent environment. The analysis of the momentum difference between the conditions prior to and after the transit poses the basis to estimate the aerodynamic drag. This measurement approach has been used to estimate the aerodynamic drag of cyclists during outdoor and indoor sport action returning a quantitative visualization of the flow field in the wake (Spoelstra et al 2019).
Knowledge of the drag resolution, or minimum detectable drag variation, is relevant when measurements are intended to perform aerodynamic optimisation. Terra et al (2018) studied the drag resolution of a small-scale RoF system analysing the drag of a towed sphere in a narrow range of velocities, under the assumption of constant drag coefficient. Spoelstra et al (2019) attempted drag estimates from a large-scale RoF. The comparison with literature data could not yield a conclusive assessment, given the large dispersion (approx. 50%) of the data due to many varying parameters, like rider posture, bikes geometries and testing conditions.
Although a number of RoF experiments have returned wake measurements that agree satisfactorily with wind tunnel data, the uncertainty of the measured drag and its dependency upon experimental conditions and the image processing parameters have not yet been addressed. In particular, the errors arising from the set-up of the PIV measurement, the image recording and analysis, as well as the application of the control volume approach require a detailed scrutiny to support best practice of experiments.
In this work, linear error propagation is applied to determine how the uncertainty of the measured velocity field affects the drag calculation. Furthermore, the effect of the above-mentioned PIV parameters is investigated.
The drag resolution of the RoF is studied here during large-scale indoor experiments by comparison with simultaneous power meter measurements. Absolute and relative drag variations are introduced by different cyclist postures, as well as varying garments.
2. Drag evaluation techniques
This section discusses the principles of drag measurement by use of the integrated power meter and from the Ring of Fire velocity measurements. The example of a cyclist is considered here, although the conclusions can be extended to other problems such as ground vehicles and speed sports in general.
2.1. Power meter
A cyclist travelling on a flat, horizontal road imparts a force Fcyclist to sustain the motion contrasted by resistive forces, namely the aerodynamic drag Daero , external (Drolling ) and internal frictional forces (Dfriction for the drive-train and Dbearing for the wheels). Any unbalance between these forces results in acceleration or deceleration of the cyclist (ma).
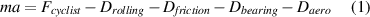
To extract the aerodynamic drag from the total drag value, the other terms are usually modelled by use of semi-empirical expressions. Following the methods described in Martin et al (1998) and Lukes et al (2012), the aerodynamic drag can be obtained by:

Where  is the drivetrain efficiency, Pcyclist
is the mechanical power generated by the cyclist,
is the drivetrain efficiency, Pcyclist
is the mechanical power generated by the cyclist,  is the cyclist velocity in quiescent air,
is the cyclist velocity in quiescent air,  is the rolling friction coefficient, m is the combined mass of rider and bike, g is the gravitational acceleration, rm
is the radius of curvature for the centre of mass trajectory and α is the cyclist's lateral lean angle relative to the horizon. The term
is the rolling friction coefficient, m is the combined mass of rider and bike, g is the gravitational acceleration, rm
is the radius of curvature for the centre of mass trajectory and α is the cyclist's lateral lean angle relative to the horizon. The term  accounts for the case where the cyclist moves along a curvilinear path of the radius of curvature rm
. When the cyclist rides along a straight path, the expression of the aerodynamic drag simplifies to:
accounts for the case where the cyclist moves along a curvilinear path of the radius of curvature rm
. When the cyclist rides along a straight path, the expression of the aerodynamic drag simplifies to:

The drivetrain efficiency varies between 96% and 98% for power outputs in the range 50–200 W (Kyle 2001, Spicer et al
2001). The rolling resistance coefficient is dependent on the tyre-pressure, -loading, -diameter and -temperature, as well as the surface properties of the ground and the steering conditions (Burke 2003). Grappe et al (1997) and Baldissera and Delprete (2016) regard the effect of speed on the rolling coefficient in cycling as negligible and therefore use a speed-invariant  value.
value.
2.2. Ring of Fire measurement principle
The drag evaluation through the Ring of Fire has been described in two previous studies from (Terra et al
2017, Spoelstra et al
2019). Conservation of momentum is invoked for the stationary problem in a control volume around a moving object. The difference of momentum flux results in the drag force D. When the control volume extends sufficiently upstream and downstream of the transiting object, it can be shown that the viscous stresses are negligible (Kurtulus et al
2007) and the drag force can be obtained from the surface integral over the inlet and outlet surfaces as illustrated in figure 1 (Rival and Oudheusden 2017). The measurements are conducted in a fixed frame of reference (that of the laboratory) where the cyclist moves at constant speed  across the measurement region. As discussed in the initial study of the RoF (Spoelstra et al
2019), air prior to the passage of the cyclist features inevitable small chaotic motions due to the disturbances in the environment (atmospheric wind, residual motions from previous passages, as depicted in figure 1). The velocity of such motions is denoted as
across the measurement region. As discussed in the initial study of the RoF (Spoelstra et al
2019), air prior to the passage of the cyclist features inevitable small chaotic motions due to the disturbances in the environment (atmospheric wind, residual motions from previous passages, as depicted in figure 1). The velocity of such motions is denoted as  . After the passage of the cyclist, the flow velocity features a coherent wake with a velocity distribution
. After the passage of the cyclist, the flow velocity features a coherent wake with a velocity distribution  as a result of the air entrainment produced by the cyclist. The variation of momentum written in the cyclist frame of reference, results in the following expression for the instantaneous drag (Terra et al
2017):
as a result of the air entrainment produced by the cyclist. The variation of momentum written in the cyclist frame of reference, results in the following expression for the instantaneous drag (Terra et al
2017):
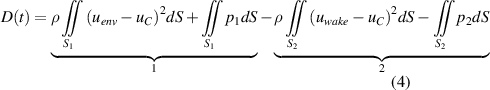
Figure 1. Schematic view of the velocity distribution before and after the passage of the cyclist.
Download figure:
Standard image High-resolution imagewhere  is the air density. This expression is valid at the condition that the mass flow is conserved across surfaces S1 and S2. Time averaging is performed for every single passage with the objective of reducing the effect of the unsteady fluctuations.
is the air density. This expression is valid at the condition that the mass flow is conserved across surfaces S1 and S2. Time averaging is performed for every single passage with the objective of reducing the effect of the unsteady fluctuations.
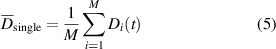
Where M is the total number of time instants composing the measurement. It has been shown in previous works that the unsteady behaviour in the wake of bluff objects typically considered for RoF measurements (Terra et al 2017, Spoelstra et al 2019) prevents the accurate estimate of the aerodynamic drag from one single passage. Therefore, ensemble averaging from multiple passages is required to achieve statistical convergence of the drag estimate.
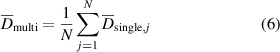
where N is the number of passages.
3. Experimental setup and protocol
3.1. Test facility and subject
Experiments were conducted in a spacious indoor facility (figure 2) 39 m wide and 77 m long, with flat concrete surface. The cyclist rode loops of 190 m length in clockwise direction. The lap can be described as two semi-circles with a radius of 17.8 m, connected by two 39 m long straights. The start point of each lap is located at  = 0 m.
= 0 m.
Figure 2. Isometric view of the testing facility and measurement apparatus layout.
Download figure:
Standard image High-resolution imageThe rider was a professional athlete; his body mass and height were 79 kg and 187 cm, respectively, and his shoulder width was equal to 50 cm. He wore a short leg and short arm time trial skin suit from Team Sunweb. Two helmet types were tested as shown in figure 3. The rider wore over-shoes extending to half of their calves, as well as laser protection goggles.
Figure 3. Riding configurations and helmets used. Upright position with aerodynamic helmet (left). Time trial position with aerodynamic helmet (middle). Time trial position with conventional road helmet (right).
Download figure:
Standard image High-resolution imageA Team Sunweb time trial bike, model Trinity Advanced SL 2018 from Giant was used during experiments of 1.7 m length and 8.8 kg weight. The rear wheel was a PRO Tubular disc. The wheels mounted a Tubular Vittoria Corsa G 23 mm tyre set at 5 bar pressure. The estimated rolling resistance coefficient for this tire and conditions is Crr = 0.0045 (Bierman 2016). The cyclist's velocity was monitored with a magnetic sensor. A magnet was placed on the rear wheel of the bike and scanned by a magnetic sensor to retrieve information about displacement and velocity. The bike GPS device stored these data with a frequency of 1 Hz.
The cyclist maintained a constant speed of 8.3 m s−1, with a normalised pedalling frequency (Crouch et al
2014) of k = 2πrf/uc
= 0.15, where r is the bike crank length,  the cadence and uc
the cyclist velocity. Three different configurations were examined (see figure 3): (1) the cyclist in upright position with an aerodynamic helmet; (2) the cyclist in time trial position with the same helmet and (3) the cyclist in time trial position with a road helmet. For each configuration, measurements were collected during 40 loops to build an ensemble average estimate of the aerodynamic drag from the RoF and gather data from the power meter installed on the bicycle.
the cadence and uc
the cyclist velocity. Three different configurations were examined (see figure 3): (1) the cyclist in upright position with an aerodynamic helmet; (2) the cyclist in time trial position with the same helmet and (3) the cyclist in time trial position with a road helmet. For each configuration, measurements were collected during 40 loops to build an ensemble average estimate of the aerodynamic drag from the RoF and gather data from the power meter installed on the bicycle.
3.2. Power meter measurement system
The bike was equipped with an SRM Road Pro crank-spider-based power, widely regarded as the benchmark for power meter devices (Duc et al 2007, Passfield et al 2017). The device recorded concurrent measurements of the athlete's mechanical power output, ground velocity and cadence in time. Before commencing trials, all units used during testing were calibrated against a zero torque reference, while pedals were stationary and unloaded as indicated by the manufacturer. For the calculation of ground velocity, the measured wheel circumference value of 2096 mm was used. Using an external torque dynamometer, the 95% confidence level uncertainty of the SRM power meter was estimated as 2% of the measured value over a range of 0–4096 W (Bertucci et al 2005). After each complete crank revolution, power and cadence measurements were obtained. Data was recorded by the head unit at a rate of 1 Hz after being linearly interpolated in time (Underwood 2012).
3.3. Ring of Fire measurement system
Velocity measurements upstream and downstream of the cyclist were performed with a large-scale stereoscopic-PIV system based on neutrally buoyant helium-filled soap bubbles (HFSB) of 0.3 mm diameter (Bosbach et al
2009). The tracers were produced by a 200 nozzles rake installed inside the tunnel. A LaVision HFSB fluid supply unit (FSU) controls soap, air and helium flow rates supplied to the seeding rake. A 10 m long tunnel structure of 4 × 3 m2 cross-section was built that confines the tracers around the measurement plane. The tunnel was built out of wooden panels integrated in an aluminium frame. Experiments were performed at a tracer concentration of approximately 13 bubbles/cm3. To quantify the tracing fidelity, the tracer's Stokes number, St
, is considered, which is defined as the ratio of the tracer response time, τp, over the flow characteristic time, τf. Samimy and Lele (1991) showed that a particle is a faithful flow tracer when the condition St
< 0.1 is satisfied. Based on previous studies from our group (Scarano et al
2015, Faleiros et al
2019), the helium-filled soap bubbles feature a tracer response time in the order of 10 to 100 µs, yielding a tracer's Stokes number in the order of 10–3 based on cyclist torso length and velocity. The light source was a Quantel Nd:YAG Evergreen 200 laser (2 × 200 mJ at 15 Hz). A laser sheet thickness of 5 cm was selected to guarantee a sufficient number of tracer particles in each interrogation window, as well as to comply with the one-quarter rule (Raffel et al
2018) when images were recorded with Δt = 2 ms pulse separation. Based on the study of Terra et al (2019), a maximum out-of-plane velocity of 5 m s−1 was expected in the cyclist's wake, thus requiring a laser sheet thickness of at least 4 cm to comply with the one-quarter rule. It should be noted that the selected laser sheet thickness is about 1/40th of the in-plane dimensions of the measurement domain, which is consistent with many PIV experiments conducted at smaller scale (Raffel et al
2018). Two LaVision Imager sCMOS cameras (2560 × 2160 pixels at 50 fps, 16 bit, pixel pitch 6.5 μm) were equipped with AF Nikkor 35 mm objectives and daylight optical filters. A lens-tilt mechanism allowed complying with the Scheimpflug condition for in-focus imaging in stereoscopic conditions. The lens aperture was set to  = 8 ensuring that particles in the illuminated region were imaged in focus. The cameras were placed 5.2 m upstream of the measurement plane at a relative angle of 35 degrees. The field of view captured by both cameras was 2.4 × 1.9 m2, yielding a magnification factor M = 0.0065 and a digital imaging resolution of 1.01 px mm−1. The measurements were synchronised with the transit of the athlete using a photodetector (PHD) placed 20.5 m upstream of the measurement plane, which triggers the PIV system through a LaVision programmable time unit (PTU 9). Image pairs were acquired at a rate of 15 Hz with a pulse separation time of Δt = 2 ms. A detailed sketch of the RoF setup is shown in figure 4.
= 8 ensuring that particles in the illuminated region were imaged in focus. The cameras were placed 5.2 m upstream of the measurement plane at a relative angle of 35 degrees. The field of view captured by both cameras was 2.4 × 1.9 m2, yielding a magnification factor M = 0.0065 and a digital imaging resolution of 1.01 px mm−1. The measurements were synchronised with the transit of the athlete using a photodetector (PHD) placed 20.5 m upstream of the measurement plane, which triggers the PIV system through a LaVision programmable time unit (PTU 9). Image pairs were acquired at a rate of 15 Hz with a pulse separation time of Δt = 2 ms. A detailed sketch of the RoF setup is shown in figure 4.
Figure 4. Schematic representation of the experimental layout of the RoF.
Download figure:
Standard image High-resolution image3.4. Measurement protocol
The PIV system and SRM power meter were calibrated at the beginning of each measurement day. Bubbles production was initiated about two minutes before the start of each run to achieve a uniform tracer distribution with sufficient concentration in the measurement domain. The cyclist started riding from the opposite side of the hall with respect to the measurement region, accelerating to the desired speed of 8 m s−1. At each lap the image acquisition was triggered by the PHD, after which 40 image pairs are recorded and saved to a mass storage device before the next lap (typically 20 s). For all tests, all the doors of the hall were closed to minimise externally generated airflows. However, as the cyclist circled the hall, the induced air entrainment resulted in some systematic tailwind. The latter effect is unwanted, first as it tends to transport the seeding particles out of the RoF-tunnel, and secondly because it introduces larger fluctuations in the air motions prior to the passage of the cyclist. This effect was mitigated by carrying a blanket through the tunnel in the opposite direction after every passage. A movie recorded during the experimental campaign is available online.
4. Data processing
4.1. Power meter
The power output and measured bike velocity of all runs are post-processed to obtain instantaneous drag area values. The power meter data are synchronised with the data recorded from the PIV measurements, including the time stamp of the laser illumination at the cyclist passage. Traces of velocity and power around the track are shown in figure 5 for the individual upright measurements. Besides the individual traces of each loop, the mean value of all loops is included.
Figure 5. Instantaneous (thin lines) and phase-averaged (thick lines) velocity (top) and power (bottom) traces over the circuit. Data from the upright individual test. The RoF measurement plane location is indicated with a green vertical line.
Download figure:
Standard image High-resolution imageThe mean velocity and mean power during the lap vary by approximately 5% and 45%, respectively. The loop-to-loop variations are up to 10% for the velocity and 70% for the power. Olds (2001) and Lukes et al (2012) have discussed the relation between these variations and the movement of the centre of gravity (CG) towards the centre of the track during corners. Due to this movement, the CG travels at lower speed than the tyre contact point. Therefore, the comparison to the RoF is based on the power and velocity data recorded within the straight segment that includes the RoF measurement station (dotted box in figure 5). Within this portion, the relative variation of mean velocity and power stays within 1% and 8% respectively.
An additional correction needed for the power meter needs to account for the velocity of the air ( ). The model as described by equation (3) assumes surrounding air at rest to calculate drag from power and velocity. The relative velocity between cyclist and air is estimated by PIV measurements prior to the cyclist passage.
). The model as described by equation (3) assumes surrounding air at rest to calculate drag from power and velocity. The relative velocity between cyclist and air is estimated by PIV measurements prior to the cyclist passage.
4.2. Ring of Fire: particle image velocimetry
The recorded images are analysed with the LaVision DaVis 8 software. Background light is removed by subtracting an image taken in absence of seeding. Particle intensity is homogenised by a min/max-filter (Westerweel 1993). The two-frame recordings are interrogated with iterative cross-correlation algorithm with window deformation (Scarano 2001). The initial interrogation window (IW) size is at least equal to or larger than ¼ of the particles image displacement (Adrian & Westerweel, 2011), whereas the final interrogation window size is varied to study the effects of spatial resolution (section 5.3). Spurious vectors identification is based on the universal outlier detection method proposed by Westerweel and Scarano (2005). To assess the out-of-plane velocity scales that the PIV system is able to resolve, the dynamic velocity range (DVR, (Adrian 1997)) is determined as the ratio between the maximum velocity in the near wake of the cyclist (≈8 m s−1) and the standard deviation of the velocity distribution in the quiescent flow prior to the cyclist's passage (≈0.03 m s−1). This leads to a DVR of 266.
The results are presented in the coordinate system as shown in figures 1 and 2. Non-dimensional relative velocity and non-dimensional time are defined respectively as:

where c = 0.5m is the shoulder width of the cyclist and t = 0 is the time instant when the rearmost point of the bicycle saddle crosses the laser sheet
4.3. Ring of Fire: control volume approach
4.3.1. Wake identification.
The evaluation of the cyclist drag via the control volume approach requires the flow velocity measurements before and after the passage of the cyclist. In the ideal case when the cyclist is moving through quiescent air and the velocity measurements are noise-free, the drag estimate is not affected by the cross-sectional size of the control volume. However, in practice, environmental flow fluctuations and noise in the velocity measurements affect the estimated drag value and, based on equation (4) and as discussed in more detail in section 5.1, their effect increases with increasing size of the cross-sectional areas S1 and S2. Hence, a dedicated wake contouring approach is applied, which isolates the cyclist's wake from the outer flow region. Several steps are performed to define the wake region behind the cyclist, which are presented in figure 6. The wake is preliminary identified with the flow region where the velocity is below a certain fixed percentage, arbitrarily set to 30%, of the minimum velocity (maximum deficit) in the flow field. Such region is then spatially dilated by a flat disk-shaped structuring element with a specified radius. The dilation length is chosen such that the entire wake and the shear layers are included in the region to be selected for the momentum analysis. The result is the control surface at the outlet S2, recalling equation (4). The procedure for wake contouring is summarised in figure 6.
Figure 6. Flow schematic of wake contouring procedure. Explanatory movie available online.
Download figure:
Standard image High-resolution image4.3.2. Mass conservation.
The control volume analysis is based on the hypothesis that the net mass flow is zero across the side and top boundaries of the domain (Anderson 2011). Therefore, the shape and size of the inlet plane S1 (figure 1) must be adapted to ensure that the mass flow rate across S1 is equal to that across S2. The wake contour at each measurement plane downstream (viz. after the passage) of the cyclist is adapted following the contouring approach discussed above. As initial contour upstream, the projected wake contour at the plane behind the cyclist is taken. The contour of the inlet plane is then narrowed or broadened one row of vectors at the time to reduce the mass flow difference from about 20% to below 0.1%. A graphical representation of this approach is presented in figure 7.
Figure 7. Contour adaptation based on the identification of the wake region (downstream plane) and compliance with the conservation of mass (upstream plane; contour colour corresponds to colour framing of the wake plane).
Download figure:
Standard image High-resolution image5. Results
5.1. A-priori uncertainty estimation
Several error sources can affect the PIV measurements, from noise in the image recordings, to peak locking and through-plane particles motion (Sciacchitano 2019). In this section, the uncertainty of the estimated drag is evaluated based on linear error propagation for the case where the velocity measurements are affected by random errors  , whereas the systematic errors are negligible. The linear error propagation is performed in the wind tunnel frame of reference (frame of reference moving with the model). Furthermore, two simplifying assumptions are made: (a) the upstream and downstream planes are sufficiently far from the object, so that the static pressure in both planes is undisturbed and equal to p∞; (b) there is a uniform inflow. Based on these assumptions, the aerodynamic drag of the cyclist simplifies to:
, whereas the systematic errors are negligible. The linear error propagation is performed in the wind tunnel frame of reference (frame of reference moving with the model). Furthermore, two simplifying assumptions are made: (a) the upstream and downstream planes are sufficiently far from the object, so that the static pressure in both planes is undisturbed and equal to p∞; (b) there is a uniform inflow. Based on these assumptions, the aerodynamic drag of the cyclist simplifies to:
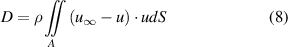
Where  is the freestream velocity seen by the cyclist, and
is the freestream velocity seen by the cyclist, and  is the streamwise velocity component behind the cyclist, in a cross-section of area A. Assuming that the latter velocity component is affected by a (spatially varying) random error
is the streamwise velocity component behind the cyclist, in a cross-section of area A. Assuming that the latter velocity component is affected by a (spatially varying) random error  :
:

being utrue the actual velocity in the wake of the cyclist, the expression of the drag becomes:
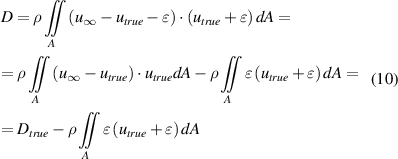
Where Dtrue is the true aerodynamic drag, in absence of measurement errors on the velocity. The expression of the time-averaged drag thus becomes:
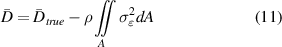
Being  the variance of the velocity error, and having assumed that error and velocity are uncorrelated:
the variance of the velocity error, and having assumed that error and velocity are uncorrelated:  . From equation (11), it follows that a random error in the velocity field leads to an underestimation of the drag. The latter scales with the variance of the random error and with the area of integration. This result clarifies the importance of reducing the region of momentum analysis to the minimum, i.e. only encompassing the region of deficit. It is, however, of great importance that the domain captures the full wake for the entire duration of the measurement, otherwise an even larger underestimation of the drag may occur. For this reason, it is concluded that for the use of the Ring of Fire in an in-vivo environment, the best results in terms of accuracy of the drag evaluation are obtained after applying a dedicated wake contour as described in section 4.3.
. From equation (11), it follows that a random error in the velocity field leads to an underestimation of the drag. The latter scales with the variance of the random error and with the area of integration. This result clarifies the importance of reducing the region of momentum analysis to the minimum, i.e. only encompassing the region of deficit. It is, however, of great importance that the domain captures the full wake for the entire duration of the measurement, otherwise an even larger underestimation of the drag may occur. For this reason, it is concluded that for the use of the Ring of Fire in an in-vivo environment, the best results in terms of accuracy of the drag evaluation are obtained after applying a dedicated wake contour as described in section 4.3.
In order to confirm the results from the a-priori uncertainty estimation, a Monte Carlo simulation is conducted on the flow field around a sphere with diameter d = 10 cm, obtained from a steady-state solver for incompressible, turbulent flow, using the SIMPLE algorithm with the standard k-Omega SST turbulence model (Wilcox 2008). The simulation is performed in a volume of 20 × 20 × 25 sphere diameters (W × H × L). The inlet velocity is set to 2 m s−1, resulting in a Reynolds number of 1.4 × 104. Errors with Gaussian distribution are imposed to the streamwise velocity component in the wake plane 7.5 diameters downstream of the sphere. The relative standard deviation of the random error in the streamwise velocity  is varied in the range from 0 to 3.5%. Consistently with equation (11), figure 8 confirms that the measured drag is underestimated in presence of measurement errors in the velocity, and that the measured drag decreases quadratically with increasing measurement errors in the velocity. Furthermore, the effect of the size of the cross-sectional area is investigated by cropping the original measurement region from all sides. Terra et al (2018) already identified the issue of errors arising from the size of the domain used for the momentum analysis; the authors showed that a reduction in cross-sectional area of the measurement domain could potentially lead to a reduction in the uncertainty of the measured drag by 10%. From the current analysis it is observed that, as expected, the systematic errors scale with the extent of the measurement domain considered for the drag estimation. If however, the domain is cropped so that part of the wake velocity deficit is cut off (area 4 in figure 8), consequently, the drag value is underestimated. In the current case of the sphere, this led to an underestimation of 30% even in absence of any measurement errors in the velocity.
is varied in the range from 0 to 3.5%. Consistently with equation (11), figure 8 confirms that the measured drag is underestimated in presence of measurement errors in the velocity, and that the measured drag decreases quadratically with increasing measurement errors in the velocity. Furthermore, the effect of the size of the cross-sectional area is investigated by cropping the original measurement region from all sides. Terra et al (2018) already identified the issue of errors arising from the size of the domain used for the momentum analysis; the authors showed that a reduction in cross-sectional area of the measurement domain could potentially lead to a reduction in the uncertainty of the measured drag by 10%. From the current analysis it is observed that, as expected, the systematic errors scale with the extent of the measurement domain considered for the drag estimation. If however, the domain is cropped so that part of the wake velocity deficit is cut off (area 4 in figure 8), consequently, the drag value is underestimated. In the current case of the sphere, this led to an underestimation of 30% even in absence of any measurement errors in the velocity.
Figure 8. Uncertainty on drag area propagated from random error in the out-of-plane velocity for different wake plane sizes.
Download figure:
Standard image High-resolution imageAssuming a typical uncertainty of the in-plane velocity components  measured by the Ring of Fire system equal to 0.1 pixel (Westerweel 1993), the uncertainty of the out-of-plane velocity component can be estimated using equation (12) (Prasad 2000), and is equal to 1% and 0.4% of the cyclist's velocity for θ = 20 and 45 degrees, respectively.
measured by the Ring of Fire system equal to 0.1 pixel (Westerweel 1993), the uncertainty of the out-of-plane velocity component can be estimated using equation (12) (Prasad 2000), and is equal to 1% and 0.4% of the cyclist's velocity for θ = 20 and 45 degrees, respectively.

Considering a ratio of measurement area over cyclist frontal area of 47, then, based on the Monte Carlo simulation results, the measured drag is underestimated by 3.5% and 1% for stereoscopic angles of 20 and 45 degrees, respectively.
5.2. Effect of mass conservation
In previous Ring of Fire experiments (Terra et al 2017, 2018, Spoelstra et al 2019), mass conservation in the measurement plane between before and after the passage was only assumed but never imposed. However, such assumption is not generally valid. In the current experiment, due to the rider's motion, an out-of-plane velocity of 2 m s−1 and a 0.4 m s−1 in-plane motion of the surrounding air were induced in the measurement plane. This led to a difference in the mass flow rate before and after passage of the cyclist of the order of 20%. The sensitivity of the drag estimate to the mass conservation is presented hereafter for the cyclist in time trial position with aerodynamic helmet. In literature, the drag area of a cyclist in time trial position is reported to be between 0.2–0.3 m2 (Crouch et al 2017); the value measured via power meter measurements falls in that range, being 0.247 ± 0.008 m2. Without imposing mass conservation, the drag obtained by the Ring of Fire is largely overestimated (0.447 ± 0.015 m2). Instead, when conservation of mass is imposed by applying the approach discussed in section 4.3, the estimated drag area becomes equal to 0.211 ± 0.008 m2, showing much better agreement with the power meter measurement. This same trend is observed for the other two test cases, namely cyclist in time trial position with road helmet the cyclist in upright position: without mass conservation the value of the drag area is overestimated by approximately 100%, whereas when mass conservation is imposed, the estimated drag area agrees with the power meter measurements within 20%.
5.3. Sensitivity to the measurement's spatial resolution
The spatial resolution of the PIV technique is an important parameter characterizing the overall measurement performance. The PIV cross-correlation analysis with a finite interrogation window (IW) size is known to return a spatially filtered velocity field (Raffel et al 2018); the amount of spatial filtering is expected to affect the accuracy of the drag estimate via the control volume approach. Although the simplest way to enhance the spatial resolution is to reduce the interrogation window size, this is accomplished at the cost of increasing uncertainty (Sciacchitano et al 2013). Hence, given the camera resolution, a compromise needs to be found between an image size large enough to capture the full wake and an interrogation window small enough to capture the small scale structures, while still providing an appropriate signal to noise ratio to minimise the number of spurious velocity vectors as well as the uncertainty on the estimated drag. The effects of the IW size on the velocity fields and on the estimated drag are investigated for 30 runs of the baseline case (time trial posture + aerodynamic helmet). The size of the IW is varied from 8 × 8 pixels2 (8 × 8 mm2) to 512 × 512 pixels2 (512 × 512 mm2). The interrogation windows are weighted with a Gaussian function, and the overlap factor between adjacent windows is kept constant at 75% for all cases. The details of the spatial resolution analysis are summarized in table 1.
Table 1. Effect of the interrogation window size on the cross-correlation signal-to-noise ratio (SNR) and the estimated drag area (CdA).
| IW size [mm2] | Image density [particles/IW] | Vector pitch [mm] | Correlation
|
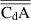 [m2] [m2] |
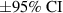 [m2] [m2] |
|---|---|---|---|---|---|
| 8 × 8 | 0.5–1 | 2 | 1.6 | 0.191 | ±0.027 |
| 16 × 16 | 2–5 | 4 | 1.9 | 0.204 | ±0.018 |
| 32 × 32 | 8–20 | 8 | 2.1 | 0.203 | ±0.016 |
| 64 × 64 | 30–70 | 16 | 3.0 | 0.204 | ±0.007 |
| 128 × 128 | 100–300 | 32 | 4 | 0.202 | ±0.007 |
| 256 × 256 | 500–1200 | 64 | 6 | 0.198 | ±0.008 |
| 512 × 512 | 2000–5000 | 128 | 8 | 0.183 | ±0.016 |
The velocity fields reported in figure 9 show that the use of a large interrogation window (512 × 512 mm2) yields an underestimation of the peak entrainment velocity in the cyclist's wake. The latter is caused by spatial modulation whereby the cross-correlation estimation of the convex velocity distribution produces a less-than-average value; conversely, the use of a small interrogation window (16 × 16 mm2) is not visibly affected by spatial modulation, but random errors occasionally appear due to the spurious occurrence of region with a low seeding concentration. The spatial modulation in the velocity field has clear consequences on the drag area: over the first 5 m of the wake, the multi-passage average drag area (red curve in figure 9-right) for the 512 × 512 mm2 IW is lower than that computed with the 64 × 64 and 16 × 16 mm2 windows, especially in the near wake where the peak velocities are higher. The uncertainty of the measured drag area is approximately constant (~0.016 m2, or 7% of the measured value) for interrogation window sizes between 16 × 16 mm2 and 128 × 128 mm2, which indicates the low sensitivity to the PIV spatial resolution in this range of interrogation window sizes. In contrast, higher uncertainty is retrieved for smaller interrogation windows (8 × 8 mm2, uncertainty of 0.018 m2 or ~10% of the measured value) due to the dramatic loss of the cross-correlation signal-to-noise ratio which causes large measurement errors in the velocity fields, as well as for larger interrogation windows (exceeding 256 × 256 mm2) due to spatial modulation effects that cause a larger spread in drag area between the different runs. Hence, the size of IW should be within 0.05 c and 0.25 c, where c is the characteristic length scale representative for the wake topology (shoulder width in this case). Choosing a larger IW leads to errors due to modulation; smaller IW size, on the other hand, leads to an increase in uncertainty due to random errors. This is, however, very dependent on experimental settings such as seeding density and pixel size of the camera. Based on the considerations above, the final interrogation window size value of 64 × 64 mm2 has been selected for the results presented in the remainder of this work as a compromise between high spatial resolution and low measurement errors in the velocity fields.
Figure 9. Dimensionless instantaneous streamwise velocity ( ) at
) at  = 1 (left) and streamwise CdA evolution in the wake (right). Data from the individual test in time trial position with aerodynamic helmet. The black lines represent the wake contours used for the drag analysis. (a) Window size: 16 × 16 [mm2]. (b) Window size: 64 × 64 [mm2]. (c) Window size: 512 × 512 [mm2].
= 1 (left) and streamwise CdA evolution in the wake (right). Data from the individual test in time trial position with aerodynamic helmet. The black lines represent the wake contours used for the drag analysis. (a) Window size: 16 × 16 [mm2]. (b) Window size: 64 × 64 [mm2]. (c) Window size: 512 × 512 [mm2].
Download figure:
Standard image High-resolution image5.4. Comparison to drag estimation from power meter data
The multi-passage average drag  of the three different test cases obtained from the Ring of Fire is compared to the average drag estimated from the power meter data. The measurements were acquired simultaneously, so the average results are obtained from the same set of samples for both the Ring of Fire and the power meter.
of the three different test cases obtained from the Ring of Fire is compared to the average drag estimated from the power meter data. The measurements were acquired simultaneously, so the average results are obtained from the same set of samples for both the Ring of Fire and the power meter.
Firstly, the drag areas obtained from the RoF are considered. As was presented in section 2.2, in order to obtain the multi-passage average drag  per test case, first the drag area in the wake of the single passages needed to be time-averaged to reduce the effect of the unsteady fluctuations. The wake is divided into two regions, namely the near and the far wake. In the near wake region, within five characteristic length scales from the cyclist, pressure effects cannot be disregarded according to Terra et al (2017). Considering as characteristic length the shoulder width of the cyclist c = 0.5 m, it follows that the static pressure in the flow affects the cyclist's drag estimate for the first 2.5 m downstream of the rider. Furthermore, the rider transited the laser sheet with no predefined crank-angle, meaning that the crank-angle at the laser sheet location varied from run to run. Spoelstra et al (2019) report the information of the pedal position is maintained in the near wake, but not in the far wake due to turbulent mixing of the flow. For the upright case, this led to a computed drag area of 0.257 m2, with a 95% confidence level uncertainty of 0.012 m2. For the time-trial position, the drag are reduces to 0.211 m2 when the rider wears a time trial helmet, and to 0.226 m2 when the road helmet is used. The uncertainties of these values are 0.008 m2 and 0.010 m2, respectively, at 95% confidence level.
per test case, first the drag area in the wake of the single passages needed to be time-averaged to reduce the effect of the unsteady fluctuations. The wake is divided into two regions, namely the near and the far wake. In the near wake region, within five characteristic length scales from the cyclist, pressure effects cannot be disregarded according to Terra et al (2017). Considering as characteristic length the shoulder width of the cyclist c = 0.5 m, it follows that the static pressure in the flow affects the cyclist's drag estimate for the first 2.5 m downstream of the rider. Furthermore, the rider transited the laser sheet with no predefined crank-angle, meaning that the crank-angle at the laser sheet location varied from run to run. Spoelstra et al (2019) report the information of the pedal position is maintained in the near wake, but not in the far wake due to turbulent mixing of the flow. For the upright case, this led to a computed drag area of 0.257 m2, with a 95% confidence level uncertainty of 0.012 m2. For the time-trial position, the drag are reduces to 0.211 m2 when the rider wears a time trial helmet, and to 0.226 m2 when the road helmet is used. The uncertainties of these values are 0.008 m2 and 0.010 m2, respectively, at 95% confidence level.
The average drag areas per test cases computed from the power meter data follow the methodology and processing steps explained in sections 2.1 and 4.1. The final values are presented in figure 10 together with the above mentioned values from the RoF.
Figure 10. Comparison between the average drag area from the RoF and Power meter for the different configurations; uncertainty bars for 95% confidence interval.
Download figure:
Standard image High-resolution imageThe results in figure 10 can be analysed in two different ways, namely by assessing the relative difference of the measurement techniques between each test condition, or by evaluating the absolute values of the predicted drag area. Regarding the absolute values, it is observed that the power meter approach on average overestimates the drag by 20% compared to the RoF. Additionally, the drag values obtained with the two techniques do not agree within the respective uncertainty bands. These disagreements can be ascribed to systematic errors in both the RoF approach, as described in section 5.1, and in the power meter measurements due to the simplified power meter model (e.g. flat road) and of the uncertainty in the model constants (e.g. rolling resistance coefficient), as discussed in section 2.1. While the latter error sources affect the absolute drag estimates obtained with the power meter, they cancel out when considering relative drag variations. Therefore, considering the relative performance, the trends of the power meter and the Ring of Fire measurements show good agreement, as a large-scale drag increase from time-trial to upright position is obtained. While the Ring of Fire predicts an increase in drag area of 0.049 m2 (23%), the power meter results increase by 0.066 m2 (27%). Between the two helmet types, a small-scale increase of 0.015 m2 (7%) can be extracted from the Ring of Fire measurements, compared to a delta of 0.020 m2 (8%) for the power meter approach.
6. Conclusions
In this work, large-scale stereo-PIV measurements are conducted to determine the aerodynamic drag of a moving cyclist using the control volume approach. The flow is measured in the wake of a cyclist moving at 8.3 m s−1. The single-passage and multi-passage average aerodynamic drag is evaluated via a control volume approach along the wake behind the cyclist, accounting for the non-uniform flow conditions prior to the cyclist's passage. A sensitivity analysis takes into account key parameters of the PIV technique, namely the interrogation window size and the control volume formulation, specifically determining the boundaries of the control volume. It is found that applying a dedicated wake contour and imposing the conservation of mass results in the most accurate drag measurements. Furthermore, the IW size should be within 0.05 c and 0.25 c, where c is the characteristic length scale representative for the wake topology. Finally, the drag values obtained with the RoF are compared against the drag estimates from simultaneously acquired power meter data. To assess the agreement between the two approaches in different regimes, three individual tests are performed where small drag variations due to different helmets as well as large drag variations due to different cyclist postures are produced. Regardless of the underlying input parameters in the power meter model, both small- and large scale deltas are well captured by both the Ring of Fire technique and the power meter approach and agree with available literature values (Blair et al 2009, Barry et al 2014, Spoelstra et al 2019). The uncertainty on the average drag measurements from the RoF is within 5%. Although such value is considered rather coarse when compared with state-of-the-art force balance measurements conducted in a wind tunnel, it shows great potential for a range of other applications (drones, cars, trains, birds, ...) due to the possibility to determine the aerodynamic drag in-field rather than in the lab environment and simultaneously obtain flow visualization.
Acknowledgments
This research is supported by the Netherlands Organisation for Scientific Research (NWO) Domain Applied and Engineering Sciences (TTW), project 15583 'Enabling on-site sport aerodynamics with the Ring of Fire'. The Team Sunweb provided part of the cycling equipment for both experiments. We thank Albert Timmer and Floortje Mackaij riding a combined 550 laps or 105 km during the experiments. Edoaro Saredi is kindly acknowledged for supporting the CFD simulations.
Data and supplementary movies
The data presented in this publication is available at: doi:10.4121/uuid:c8a6c2a7-7278-43eb-b8aa-7a0fb4b2160d. Supplementary movies are (available online at stacks.iop.org/MST/32/044004/mmedia)











