Plutonium-241 as a possible isotope for neutrino mass measurement and capture

The measurement of the absolute neutrino mass and the detection of the cosmic neutrino background (CNB) are two of the most exciting prospects in neutrino physics for the next two decades. They are closely related. The mass measurement is looking for a deformation of the end of the beta decay spectrum caused by the finite neutrino mass. The CNB search is looking for a small peak from neutrino capture which is separated by twice the lightest neutrino mass from the endpoint. Both measurements require experimental precision and a theoretical understanding of the end of the beta decay spectrum at the level of the neutrino mass, which is of the order of tens of meV.

Candidate nuclides for the mass measurement should first of all have moderate beta decay energy. For isotopes with a decay energy of 10–100 keV, already an experimental precision of 1 ppm is required. A lifetime of 1–20 years is optimal since it leads to a reasonable event rate and relatively stable measurement conditions. Rhenium-187 has the lowest energy of the known beta-decaying isotopes at 2.6 keV, but due to its lifetime of 60 Gyr, there would be no events close to the endpoint within a human lifetime. In addition, the daughter isotope needs to be stable on the timescale of the experiment. Ruthenium-106 for example, does have a significant neutrino capture cross-section, a decay energy of 39.4 keV, and a half-life of 1.48 years, but the daughter isotope Rhodium-106 decays within 30 s with a decay energy of several MeV and the emission of several gammas, making a clean measurement of the endpoint impossible.

For candidate nuclides in the detection of the CNB, there is an additional requirement to have a large neutrino capture cross-section to get an acceptable even rate. The capture cross-section has been evaluated for a large number of isotopes [1]. From this study ³H, which has always been the isotope of choice for mass measurement, is the isotope that best matches the requirements. The KATRIN experiment uses molecular tritium in its current world-best neutrino mass limit [2]. Their current measurement is still dominated by its statistical error, but with more data, it will be limited by the energy spread of the vibrational and rotational excitation spectrum of the daughter molecule ${\left({}^{3}{{\rm{H}}}^{3}\mathrm{He}\right)}^{+}$. The decaying tritium nucleus recoils against the electron and picks up 3.4 eV kinetic energy due to its relatively low mass. The recoil is enough to bring the daughter molecule in one of several of the excited states and leads to an energy spread of 0.36 eV. This is why future experiments, like Project 8 [3], are looking at atomic tritium. The PTOLEMY experiment [4] also plans to use atomic ³H loaded on graphene to measure the mass and, at a later stage, observe the CNB.

A recent study [5] found that the zero-point motion of the ³H bound to the surface of graphene or for that matter any surface leads to an energy spread of ΔE ∼ 0.5 eV. They advocate the investigation of nuclei with A > 100 and define a figure of merit for this effect:

$$\begin{eqnarray}&&\gamma ={\left({Q}^{2}{m}_{e}/{m}_{\mathrm{nucl}}^{3}\right)}^{1/4}\end{eqnarray} \tag{ 1 }$$

and propose ¹⁷¹Tm and ¹⁵¹Sm as candidate isotopes, which have a γ which is an order of magnitude lower than for ³H.

Plutonium-241 is an isotope that is created by double neutron capture on Plutonium-239. About 12% of the plutonium in spent nuclear fuel is ²⁴¹Pu. It mainly undergoes beta decay to ²⁴¹Am with a decay energy of 20.78 ± 0.17 keV [6] and a half-life of 14.33 ± 0.02 years [7], numbers very similar to those of ³H. What makes ²⁴¹Pu interesting for the mass measurement is the large mass of the isotope and as a consequence its low recoil of 47 meV. The γ factor is 25 times smaller than for ³H, which according to [5] should allow for observation of the CNB for neutrino masses of m_ν > 30 meV.

The daughter nuclide ²⁴¹Am decays through α decay to ²³⁷Np with a half-life of 432 years. ²³⁷Np has a half-life of 2 million years and can be considered stable. In addition, ²⁴¹Pu has a small (2.4 × 10⁻⁵) probability to undergo α decay to ²³⁷U. The energies of the α particles, and the subsequent γ's, are well outside the relevant energy window around the endpoint. The biggest challenge comes from the ²³⁷U. It has several β decays to ²³⁷Np with a half-life of 6.7 d and an energy of up to 459 keV. The total rate from the ²³⁷U is about five orders of magnitude smaller than for ²⁴¹Pu  but near the endpoint, the ²⁴¹Pu spectrum is falling rapidly, while ²³⁷U is still on a plateau. Around 20 eV before the endpoint, the rates become similar, and a mass measurement becomes impossible without special measures to remove the ²³⁷U on a timescale much shorter than its lifetime. There are two possible ways to reduce the ²³⁷U background. First, the α decay to ²³⁷U causes a considerable recoil of around 150 keV. In the design of the target, this could conceivably be used to remove part of the ²³⁷U from the active target area. Secondly, the β decay to ²³⁷Np is never to the ground state and is always followed by a γ decay which can be used as a veto.

Given the similar decay energy and half-life, one would expect the experimental setup for atomic ³H to work for ²⁴¹Pu as well. For instance, the Project 8 experiment plans to reach its ultimate precision using an atomic ³H trap and will have to balance statistics, which favors a high density, against the background of recombination of tritium into T₂. ²⁴¹Pu, in the form of gaseous PuF₆ would be an alternative where no such compromise is needed. A recirculation system of the gas in the experiment could be used to remove the ²⁴¹Am and ²³⁷U. For PTOLEMY, the design of the RF system, electromagnetic filter, and calorimeter would be identical. A direct line of sight between the target and calorimeter needs to be avoided, as it is in the current baseline design, on account of gamma radiation from the uranium and americium decays. One requirement is to have a precise reference voltage between the target and the exit of the electromagnetic filter. This in fact is easier using a metallic target like plutonium than for graphene. The back of the target structure could be instrumented to veto gamma rays.

In order to calculate the neutrino capture cross-section for ²⁴¹Pu, we follow a procedure as developed in [8], which we will summarize briefly below. We consider the two related weak processes:

$$\begin{eqnarray}\begin{array}{rcl}{}_{Z}^{A}X & \to & {}_{Z+1}^{A}Y+{e}^{-}+\bar{{\nu }_{e}}\\ \nu {+}_{Z}^{A}X & \to & {}_{Z+1}^{A}Y+{e}^{-}.\end{array}\end{eqnarray} \tag{ 2 }$$

Using Fermi's Golden Rule, we can write the differential beta decay rate dΓ_β and the neutrino capture cross-section as:

$$\begin{eqnarray}\begin{array}{rcl}{\rm{d}}{{\rm{\Gamma }}}_{\beta } & = & \displaystyle \frac{1}{2{\pi }^{3}}\times {p}_{\nu }{E}_{\nu }{E}_{e}{\rm{d}}{E}_{e}\times {W}_{\beta }({p}_{e},{p}_{\nu })\\ {\left(\sigma v\right)}_{\nu } & = & \mathop{\mathrm{lim}}\limits_{{p}_{\nu }\to 0}\displaystyle \frac{1}{\pi }\times {p}_{e}{E}_{e}\times {W}_{\nu }({p}_{e},{p}_{\nu }).\end{array}\end{eqnarray} \tag{ 3 }$$

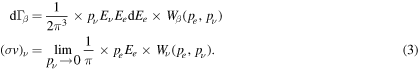
Here W_β (p_e , p_ν ) is the average transition rate for the decay of an atom emitting two leptons in a plane wave with momenta p_e and p_ν and W_ν (p_e , p_ν ) the average transition rate for the capture of a neutrino with momentum p_ν with the emission of an electron with p_e . They are obtained by integrating the transition amplitudes squared over the directions of the leptons, summing over the quantum numbers of the outgoing particles, and averaging over the incoming particles.

For the CNB neutrinos, with p_ν ≪ m_ν we have

$$\begin{eqnarray}&&{W}_{\nu }({p}_{e},0)=\frac{1}{2}\mathop{\mathrm{lim}}\limits_{{p}_{\nu }\to 0}{W}_{\beta }({p}_{e},{p}_{\nu }).\end{eqnarray} \tag{ 4 }$$

Earlier calculations of the neutrino cross-sections [1] have been performed for two kinds of beta decays. Allowed transitions are decays where the parent and daughter isotopes have the same quantum numbers, and no angular momentum is carried away by the lepton pair. In this case, the transition amplitudes can be approximated by a constant and their ratio can be taken as 1, after which it is straightforward to express the capture cross-section in terms of the total decay width of the isotope. This is not true for forbidden decays where the quantum numbers are different for mother and daughter, and there will be a dependency on the momenta.

For a unique forbidden transition, there is only one term contributing. The matrix element and the kinematic factor factorize, and the ratio of the transition rates can be calculated after which the neutrino capture cross-section is again expressed as a function of the total width. For non-unique forbidden transitions, the matrix element contains several terms with each, a unique dependency on the momenta and such a calculation cannot be performed.

For allowed and unique forbidden transitions the approach of [1] extracts the capture cross-section from the half-life of the beta decay, and thus avoids the theory errors associated with the nuclear matrix element. For a light nuclide with an allowed decay like ³H, both methods agree well, but for a heavy, odd mass-number nuclide like ²⁴¹Pu, the calculation of the nuclear matrix element has substantial uncertainties. There is evidence that for heavier nuclides the axial-vector coupling is quenched in the nuclear medium by as much as 40% [9]. Recently, nuclear shell method calculations for forbidden decays with A = 210 – 215 have been performed [10], but the results still show a sizable uncertainty in the calculated half-life of the beta-decaying nuclide. Neutrino capture models based on a local fermi gas [11, 12] cover much higher energies, typically tens of MeV and above, and focus on lighter nuclei.

The decay of ²⁴¹Pu is the first forbidden non-exclusive decay and we cannot make the assumption that the nuclear matrix element is independent of the electron energy. Since the beta half-life involves an integral over the full kinematic range and cosmic neutrino capture takes place at the endpoint of the spectrum the decay and capture transition rates are expected to be different. The novel approach of [8] is using the fact that W_β (p_e , p_ν ) is an analytical function of the momenta, which allows to evaluate the differential decay rate in the same kinematic region as for neutrino capture. For small enough values of p_ν , a linear approximation can be used and (σ v)_ν can be found by extrapolating to p_ν = 0:

$$\begin{eqnarray}&&{(\sigma v)}_{\nu }[1+{\alpha }_{1}{p}_{\nu }/Q+O({p}_{\nu }^{2}/{Q}^{2})]=\frac{{\hslash }^{3}{c}^{2}{\pi }^{2}}{{p}_{\nu }^{2}}\frac{{\rm{d}}{{\rm{\Gamma }}}_{\beta }}{{\rm{d}}{E}_{e}},\end{eqnarray} \tag{ 5 }$$

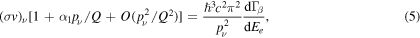
where we put the factors ℏ and c back in. This procedure requires a well-measured decay spectrum.

For the extraction of (σ v)_ν from equation (5) the beta spectrum of ²⁴¹Pu has been measured very precisely[13]. We use a parametrization of this data as our main set. As a cross-check data set, we generate a spectrum using BetaShape [14, 15] with an energy bin width of 0.06 eV. It is useful to point out that the measured spectrum is used as one of the benchmark processes for the BetaShape program.

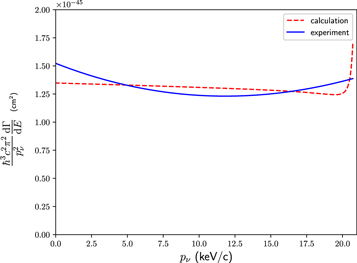
In figure 1 we plot the right-hand side of equation (5) as a function of p_ν . Below p_ν = 5 keV c^–1, the experimental data are well described by a linear function and we extract the capture cross-section from the extrapolation to p_ν = 0 of a linear fit for p_ν < 4 keV c^–1. We find (σ v)_ν = 1.51 ± 0.07 × 10⁻⁴⁵ cm² (statistical error only) The slope is: α₁ = −0.52. Varying the upper fit range between 3 and 5 keV c^–1 and half-life and Q value of the ²⁴¹Pu decay within their known limits gives an additional uncertainty of 0.01 × 10⁻⁴⁵. Using the same method on the calculated spectrum gives a value of (σ v)_ν = 1.34 × 10⁻⁴⁵ cm², which is within 11%.

Zoom In Zoom Out Reset image size

As a cross-check we also evaluate the results for the two isotopes ¹⁵¹Sm and ¹⁷¹Tm. We generate both spectra with BetaShape using energy bins of 0.2 eV and fitted the spectrum, reproducing the values of [8]. These were confirmed in a similar analysis [16]. In addition, we perform the same procedure for the ⁶³Ni isotope and recover the calculated cross-section from [1]. The results are summarized in table 1.

Table 1. Neutrino capture cross-sections for different isotopes. The values for ³H and ⁶³Ni are taken from [1].

Isotope	Q (keV)	t1/2 (yr)	(σ v)ν (10−46cm2)	$\gamma /{\gamma }_{{}^{3}H}$
3H	18.6	12.3	39.2	1.0
63Ni	66.9	100	0.069	0.19
151Sm	76.6	90	0.048	0.10
171Tm	96.5	1.92	1.2	0.11
241Pu	20.8	14.4	15.1	0.039

We have, for the first time, estimated the neutrino capture cross-section on ²⁴¹Pu and found it to be 1.51 · 10⁻⁴⁵. The result from the actual beta spectrum and the BetaShape calculation agree within 11%, which gives confidence in this result. The relevant parameters for ²⁴¹Pu and other candidate isotopes are shown in table 1. If the energy uncertainty for ³H cannot be solved, ²⁴¹Pu seems to be a promising replacement for at least the neutrino mass measurement, provided the ²³⁷U can be removed or its decay vetoed. It has an energy and lifetime similar to ³H, is easily available, and an experiment designed for ³H will also work for ²⁴¹Pu. This is not the case for ¹⁵¹Sm or ¹⁷¹Tm which have substantially larger decay energy. The energy uncertainty for ²⁴¹Pu is more than twice smaller than for these and would, according to [5], allow for a CNB observation for neutrinos with m_ν > 30 meV. The expected rate is lower than for ³H but at least ten times higher than for ¹⁷¹Tm, and the calculation is based on an actual spectrum.

The data that support the findings of this study are available upon reasonable request from the authors.