Study on the security of discrete-variable quantum key distribution over non-Markovian channels

Quantum key distribution (QKD) [1–7] provides a novel way to allow two distant authorized parties, the sender Alice and the receiver Bob, to remotely establish a secret key through quantum and classical channels. Generally, the classical channel needs to be authenticated, i.e. the legitimated parties identify themselves and a third party may listen to the communication but cannot participate in it. However, the quantum channel is open so that the third party can manipulate the communication. The security of QKD originates from the fundamental principles of quantum mechanics. More precisely, the legitimated parties can estimate the security after communication, since the leakage of information in a quantum channel to eavesdropper, Eve, is quantitatively related to the degradation of communication [3].

The unconditional security of QKD schemes with the ideal system [8, 9] and practical system [10] has been proved for several years. However, the ignorance of imperfection of the practical QKD system still exists and limits Eve's attack strategy. So the unconditional security should be reconsidered under more powerful attacks introduced by Eve. To avoid the leakage of information from the loopholes of the imperfect practical QKD system, many potential attacks [11–20] have been proposed recently. The known considerations of the imperfection of the practical QKD system are focused on the practical system devices, and the quantum channels are usually approximately considered to be Markovian, i.e. the correlation time between the system and environment is infinitely short so that the memory effects can be neglected. In practice, the correlations between the system and environment exist for a small finite period of time, which leads to the quantum channel with memory [21]. In recent years, non-Markovian effects have been investigated in the dynamics of entanglement [22–24], quantum correlation [25], quantum channel capacity [26] and the security of continuous-variable QKD [27]. Moreover, the optical non-Markovian signatures in semiconductor quantum wires have been achieved in an experiment [28]. Interestingly, it is shown in [27] that the non-Markovian effects may be exploited to enhance the security of continuous-variable QKD and detect eavesdropping along the transmission line. However, the security analysis is addressed in Gaussian individual attacks, whereas Eve's collective attacks are not being considered.

In this paper, we explore the security of discrete-variable QKD schemes over non-Markovian quantum channels. In particular, we investigate the dynamics of the secret key rates for the six-state protocol [29, 30] by restricting consideration to collective attacks, where the transmission quantum channels are specified as non-Markovian depolarizing channels with coloured noise and the Markovian one with Gaussian white noise [21]. In contrast, we show that the secure secret key rate for the non-Markovian channels may always be larger than the Markovian ones. Moreover, we find that the nosier the channels are, the more effectively the non-Markovian effects will enhance the security of transmission. When the coupling strength of the system with the environment is high enough, the secret key rate fluctuates near the secure point.

This paper is organized as follows. In section 2, we introduce the physical model we will investigate and construct the non-Markovian depolarizing quantum channel with coloured noise. We then briefly introduce the six-state protocol, and calculate and analyse contrastively the dynamics of the secret key rates and quantum bit error rate (QBER) of the six-state protocol under collective attack for the non-Markovian and Markovian depolarizing channels in section 3. Finally, the conclusions are drawn in section 4.

In this section, we introduce the physical model under study, i.e. the non-Markovian depolarizing channel with coloured noise. As known, the evolution of the quantum system can be described as a completely positive map (CPM) [31]. A known depolarizing quantum channel can be expressed as the CPM 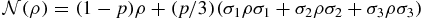$\mathcal {N}(\rho )=(1-p)\rho +(p/3)(\sigma _{1}\rho \sigma _{1}+\sigma _{2}\rho \sigma _{2}+\sigma _{3}\rho \sigma _{3})$, where 0 ⩽ p ⩽ 1, and σ_i for i = 1, 2, 3 are Pauli operators. This CPM defines a depolarizing channel with white noise, which comes from the Markovian master equation. However, the Markovian master equation that describes the time evolution of the quantum system is an approximation, since the correlation time between the quantum system and environment is seen to be infinitely short so that the memory effects can be neglected. In practice, the correlation time is a small finite period of time, which leads to the non-Markovian master equation. In the following, we review the derivation of the depolarizing channel with coloured noise [21].

A prevailing memory kernel master equation can be described by

$$\begin{equation} \dot{\rho }=K\mathcal {L}\rho , \end{equation} \tag{ 1 }$$

where K is an integral operator that depends on time acting as the form 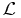$K\mathcal {N}=\int _{0}^{t}k(t-t^{\prime })\mathcal {N}(t^{\prime }){\rm d}t^{\prime }$, $\mathcal {L}$ is a Lindblad superoperator describing the dynamics due to the interaction of the system and environment and ρ is the density operator of the small system of interest. The solution to the master equation (1) defines a completely positive and trace-preserving linear map $\mathcal {N}_{t}:\rho \rightarrow \rho _{t}$ that describes the evolution of a system coupled to an environment.

A master equation of the form of equation (1) arises when considering any two-level quantum system that interacts with an environment possessing random telegraph signal noise. It is possible to write a time-dependent Hamiltonian for this kind of system,

$$\begin{equation} H(t)=\hbar \sum ^{3}_{i=1}\Gamma _{i}(t)\sigma _{i}, \end{equation} \tag{ 2 }$$

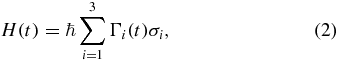
where Γ_i(t) are independent random variables. Each random variable can be defined as Γ_i(t) = a_in_i(t). The random variable n_i(t) has a Poisson distribution with a mean equal to t/2τ_i, while a_i is an independent coin-flip random variable assuming the values ± a_i. A model like this describes, for instance, a spin-1/2 particle in the presence of three orthogonal magnetic fields, each of which has a constant magnitude a_i and inverts randomly in time with a distribution given by n_i.

By using the von Neumann equation $\dot{\rho }=-({\rm i}/\hbar )[H,\rho ]=-{\rm i}\sum _{k}(t)[\sigma _{k},\rho ]$, one can obtain the solution for the density operator of the form

$$\begin{equation} \rho (t)=\rho (0)-{\rm i}\int ^{t}_{0}\sum _{k}\Gamma _{k}(s)[\sigma _{k},\rho (s)]\,{\rm d}s. \end{equation} \tag{ 3 }$$

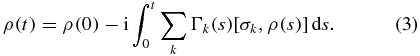
Applying the correlation functions of the random telegraph signal $\langle \Gamma _{j}(t)\Gamma _{k}(t^{\prime })\rangle =a_{k}^{2}e^{-|t-t^{\prime }|/\tau _{k}}\delta _{jk}$, and substituting equation (3) back into the von Neumann equation and performing a stochastic average, one obtains the memory kernel master equation

$$\begin{equation} \dot{\rho }(t)=-\int ^{t}_{0}\sum _{k}{\rm e}^{-(t-t^{\prime })/\tau _{k}}a^{2}_{k}[\sigma _{k},[\sigma _{k},\rho (t^{\prime })]]\,{\rm d}t^{\prime }. \end{equation} \tag{ 4 }$$

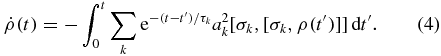
It can be seen from equation (4) that the state of the system at time t depends on its past history. It is known that the Fourier transform of the correlation function gives the power spectrum of the environment. For white noise, the delta-function correlation in time leads to a flat power spectrum for the environment, and the system is equally coupled to all frequencies of environment, while for the coloured noise, the system prefers certain frequencies and a gives the coupling strength of the system with environment while τ determines the most preferred frequencies.

By assuming that the fluctuations τ_i are equal, one can obtain the solution to equation (4) as a linear map $\mathcal {N}_{t}:\rho \rightarrow \rho _{t}$ on $\mathcal {M}_{2}$ [21]. This map is a generalization of the depolarizing channel to the case of coloured noise, which can be written in the form of Kraus decomposition $\mathcal {N}_{t}(\rho )=\sum _{k}A_{k}^{\dag }\rho A_{k}$ with Kraus operators given by 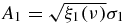$A_{1}=\sqrt{\xi _{1}(\nu )}\sigma _{1}$, $A_{2}=\sqrt{\xi _{2}(\nu )}\sigma _{2}$, $A_{3}=\sqrt{\xi _{3}(\nu )}\sigma _{3}$ and $A_{4}=\sqrt{\xi _{4}(\nu )}I$, provided that the following conditions are all satisfied:

$$\begin{eqnarray} &&\xi _{1}=\case{1}{4}(1+\Lambda _{1}-\Lambda _{2}-\Lambda _{3}),\nonumber \\ &&\xi _{2}=\case{1}{4}(1-\Lambda _{1}+\Lambda _{2}-\Lambda _{3}), \nonumber \\ &&\xi _{3}=\case{1}{4}(1-\Lambda _{1}-\Lambda _{2}+\Lambda _{3}), \nonumber \\ &&\xi _{4}=\case{1}{4}(1+\Lambda _{1}+\Lambda _{2}+\Lambda _{3}), \end{eqnarray} \tag{ 5 }$$

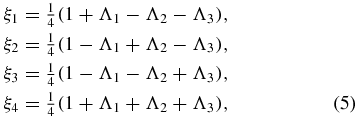
where ν = t/2τ is the dimensionless time and Λ_i(ν) = e^−ν[cos (μ_iν) + sin (μ_iν))/μ_i] are damped harmonic oscillators having frequencies 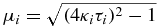$\mu _{i}=\sqrt{(4\kappa _{i}\tau _{i})^{2}-1}$ with κ²_i = a_j² + a²_k for i ≠ j ≠ k. The restrictions in equation (5) assure that the linear map $\mathcal {N}_{t}$ is completely positive. By assuming τ → 0 and a → ∞, the random telegraph signal reduces to a Gaussian white noise and equation (4) becomes $\dot{\rho }(t)=-\int ^{t}_{0}\delta (t-t^{\prime })\sum _{k}2a^{2}_{k}\tau [\sigma _{k},[\sigma _{k},\rho (t^{\prime })]]\,{\rm d}t^{\prime }$. This leads to $\Lambda _{i}(t)={\rm e}^{-\gamma _{{\rm i}}t}$ in equation (5) with inverse lifetimes γ_i = 4κ²_iτ. It should be pointed out that, whether in the case of coloured noise or white noise, there are examples of maps that are positive but not completely [32–34]. The map is completely positive if and only if the linear combinations in equation (5) are non-negative.

The six-state protocol is similar to the well-known BB84 four-state protocol, but with an additional basis [29, 30]. In the six-state protocol, Alice first generates a random bit k = −1, 1 and chooses one basis Θ randomly out of the three bases X, Y and Z. Then Alice prepares and sends over a quantum channel a qubit with the |Θ_k〉 state, which is the eigenstate of the Θ basis with the eigenvalue of k/2. Bob randomly chooses one basis out of the three bases and measures the states along the chosen direction. Alice and Bob compare the bases they used via a public channel, and keep the bit value if the bases match; otherwise they discard it. Lastly, Alice and Bob repeat the above steps and apply bit error correction and privacy amplification to obtain a shared key string.

The unconditional security bounds for the six-state protocol [30] have been found in [35, 36] for the case where the quantum signals are single qubits. As usual, the proof for this prepare-and-measure (P&M) six-state scheme can be performed by an entanglement-based (EB) scheme: Alice produces the state $|\Phi ^{+}\rangle _{AB}=(1/\sqrt{2})(|00\rangle _{AB}+|11\rangle _{AB})$; then she keeps the first qubit and sends the other one to Bob. This state shows perfectly correlated outcomes in the X and Z bases and perfectly anti-correlated outcomes in the Y basis. Bob may flip his results when he measures with Y basis. Without loss of generality, the symmetry of the six-state protocol implies that one can compute the unconditional security bound by restricting the consideration to collective attacks, and even further, to those cases such that the final state of Alice and Bob is Bell diagonal [3, 35, 36],

$$\begin{eqnarray} &&\fl \rho _{AB}=\lambda _{1}|\Phi ^{+}\rangle \langle \Phi ^{+}|+\lambda _{2}|\Phi ^{-}\rangle \langle \Phi ^{-}| +\lambda _{3}|\Psi ^{+}\rangle \langle \Psi ^{+}|\nonumber\\ &&+\,\lambda _{4}|\Psi ^{-}\rangle \langle \Psi ^{-}|, \end{eqnarray} \tag{ 6 }$$

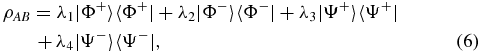
where ∑_iλ_i = 1 and $|\Phi ^{\pm }\rangle _{AB}=(1/\sqrt{2})(|00\rangle _{AB}\pm |11\rangle _{AB})$, $|\Psi ^{\pm }\rangle _{AB}=(1/\sqrt{2})(|01\rangle _{AB}\pm |10\rangle _{AB})$. It should be emphasized that the restriction for calculating the unconditional security bound does not depend on the type of the quantum channel, i.e. whether the quantum channel is with or without quantum memory, the restriction is feasible. In particular, λ_i acts as a function of time for the quantum channel with memory. It can be seen that |Φ^±〉 give perfect correlation in the Z basis, |Φ⁺〉, |Ψ⁺〉 give perfect correlation in the X basis, and |Φ⁺〉, |Ψ⁻〉 show perfect correlation in the Y basis. Thus, the QBER for the three bases are given by

$$\begin{eqnarray} &&\varepsilon _{x}=\lambda _{2}+\lambda _{4},\nonumber \\ &&\varepsilon _{y}=\lambda _{2}+\lambda _{3},\nonumber \\ &&\varepsilon _{z}=\lambda _{3}+\lambda _{4}. \end{eqnarray} \tag{ 7 }$$

Eve's information I_E is given by the Holevo bound

$$\begin{equation} I_{E}=S(\rho _{E})-\sum _{a}p(a)S(\rho _{E|a}), \end{equation} \tag{ 8 }$$

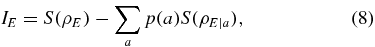
where S is von Neumann entropy, a is a symbol of Alice's classical alphabet distributed with probability p(a), ρ_E = ∑_ap(a)ρ_E|a is Eve's partial state, with ρ_E|a being the corresponding state of Eve's ancilla state. Eve can purify the state of ρ_AB such that S(ρ_E) = S(ρ_AB) = H({λ₁, λ₂, λ₃, λ₄}), and the bit a values 0 or 1 equiprobably in this attack. So we obtain

$$\begin{equation} I_{E}=H(\lbrace \lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4}\rbrace )-\case{1}{2}S(\rho _{E|0})-\case{1}{2}S(\rho _{E|1}). \end{equation} \tag{ 9 }$$

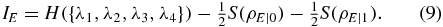
The detailed computation of ρ_E|b [2] shows that S(ρ_E|0) = S(ρ_E|1) = h(ε_z), where h is binary entropy. For the six-state protocol, all the error rates are measured, and equation (9) can be rewritten as

$$\begin{eqnarray} &&\fl I_{E}=\varepsilon _{z}h\bigg (\frac{1+(\varepsilon _{x}-\varepsilon _{y})/\varepsilon _{z}}{2}\bigg )+(1-\varepsilon _{z})\nonumber\\ &&\times \,h\bigg (\frac{1-(\varepsilon _{x}+\varepsilon _{y}+\varepsilon _{z})/2}{1-\varepsilon _{z}}\bigg ). \end{eqnarray} \tag{ 10 }$$

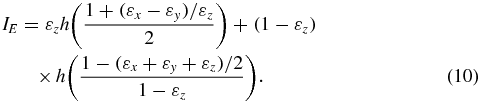
Now we calculate the evolution of the transmission state over the non-Markovian depolarizing channel with coloured noise. Having derived the Kraus operators of the depolarizing channel with coloured noise, the evolution of the state ρ_AB with the second qubit interacting with environment can be written as

$$\begin{equation} \mathcal {N}_{t}(\rho _{AB})=\sum _{k}I^{(A)}\otimes A_{k}^{(B)}\rho _{AB}A_{k}^{(B)\dag }\otimes I^{(A)\dag }. \end{equation} \tag{ 11 }$$

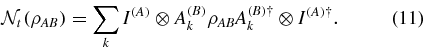
For the case of the non-Markovian depolarizing channel with coloured noise, the error rates can be calculated as

$$\begin{eqnarray} &&\varepsilon _{x}(\nu )=\case{1}{2}[1-\Lambda _{1}(\nu )],\nonumber \\ &&\varepsilon _{y}(\nu )=\case{1}{2}[1-\Lambda _{2}(\nu )],\nonumber \\ &&\varepsilon _{z}(\nu )=\case{1}{2}[1-\Lambda _{3}(\nu )], \end{eqnarray} \tag{ 12 }$$

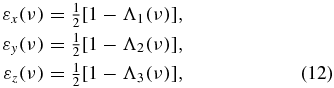
where Λ_i(ν) = e^−ν[cos (μ_iν) + sin (μ_iν))/μ_i]. Now we consider the dynamics of the secret key rates for the non-Markovian case of state evolution. Under the assumption of depolarizing channels, i.e. ε_x(ν) = ε_y(ν) = ε_z(ν) = Q(ν); hence a₁ = a₂ = a₃, the secret key rates for the non-Markovian case can be derived as

$$\begin{eqnarray} &&\fl r^{N}(\nu )=1-Q(\nu )-h[Q(\nu )]-[1-Q(\nu )]\nonumber\\ &&\times \,h\left[\frac{1-3Q(\nu )/2}{1-Q(\nu )}\right], \end{eqnarray} \tag{ 13 }$$

while for the case of the Markovian depolarizing channel with Gaussian white noise, Λ_i(ν) in error rates should be valued as ${\rm e}^{-\gamma _{{\rm i}}t}$, and hence, $Q(t)=\frac{1}{2}[1-{\rm e}^{-\gamma _{{\rm i}}t}]$. The secret key rate for the case of the Markovian channel is denoted as r^M(t). It should be pointed out that the secret key rate here is derived under the assumption of one-way post-processing, no pre-processing and perfect error correction.

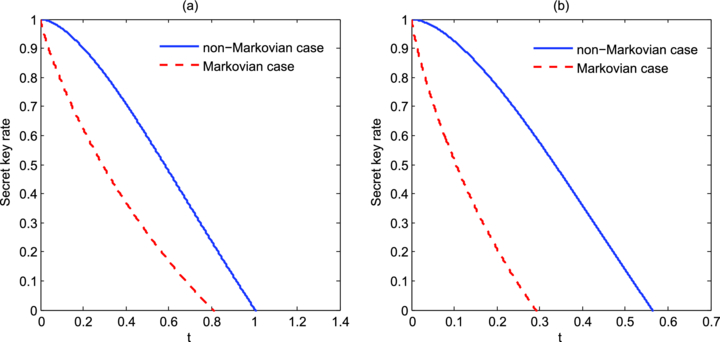
In what follows, we check whether the non-Markovian quantum channel can exhibit higher security of transmission of classical information under the same conditions. In figure 1, we plot the dynamics of the secret key rates for the cases of non-Markovian and Markovian depolarizing quantum channels under the same conditions for some different parameters |a_i|. It can be seen that the secure secret key rate for the non-Markovian case is larger than the Markovian case. Also, the difference between the two cases is much clearer for the more noisy channel, since the secure secret key rate for the Markovian channel is more sensitive to the increase in noise. However, when the coupling strength of the system with the external system, which can be measured by the parameters |a_i|, becomes small, the secure secret key rate for the non-Markovian case will not always be larger than the Markovian case. By setting τ = 1, we find r^N(ν) ⩾ r^M(t) always exists for secure communication in the regime of 0.2282 ⩽ |a_i| ⩽ |a*|, where $|a^{*}|=\sqrt{[(\pi /\ln 3)^{2}+1]/32}$, is the upper bound to keep the linear map $\mathcal {N}_{t}$ completely positive for all times. Figure 2 presents the case that the secure secret key rate for the Markovian depolarizing channel may be larger than the non-Markovian one for some time when |a_i| ⩽ |a*|.

Zoom In Zoom Out Reset image size

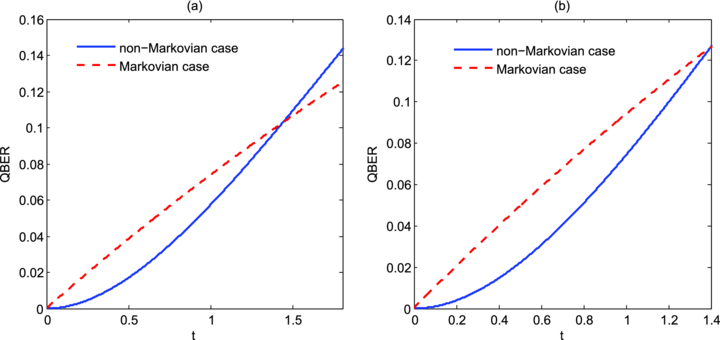
Zoom In Zoom Out Reset image size

It should be mentioned that the time parameter t denotes the duration of the processing of the quantum channel. Thus, to guarantee the absolutely secure communication, one should limit the processing time of the quantum channel. Actually, the control of the processing time corresponds to the restriction of the QBER, and the unconditional security bounds of the QBER for the non-Markovian and Markovian depolarizing channels are equal to 12.61%. However, the dynamics of the QBER for the non-Markovian and Markovian depolarizing channels are different. Correspondingly, we find that the QBER for the Markovian case is always larger than the non-Markovian case under the same conditions in the regime 0.2282 ⩽ |a_i| ⩽ |a*| when setting τ = 1. Figure 3 shows the dynamics of the QBER for two different parameters |a_i|.

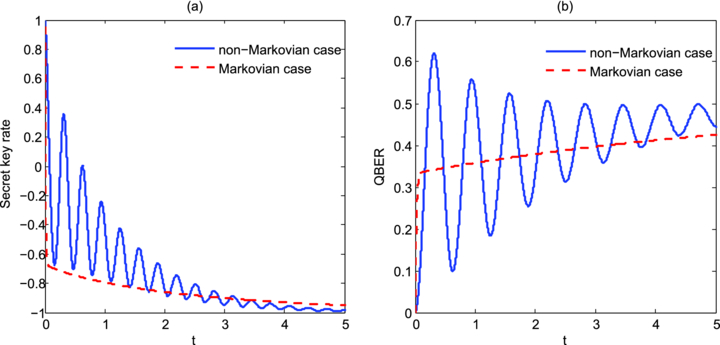
Zoom In Zoom Out Reset image size

Now we extend to the generalized depolarizing channel. Assuming the coupling strengths of the system with the external system in three directions are different, i.e. a_i for i = 1, 2, 3 are not equal, the restriction |a_i| ⩽ |a*| to keep $\mathcal {N}_{t}$ completely positive for all times can be broken. We find that the secret key rate will fluctuate near the secure point along time when the coupling strength of the system with the environment is high enough. This effect originates from the convergent oscillation of the QBER in the case of the non-Markovian depolarizing channel, which has not been found in the case of the Markovian channel. Figure 4 shows this effect when setting a high coupling strength in one direction. Since the secret key rate is positive in only some ranges of time, one application is that the legitimate parties can guarantee security communication by controlling the processing time of the non-Markovian quantum channel. It should be noted that the non-Markovian effects of the constructed quantum channel act along the quantum signals passing through the quantum channel. Moreover, it can be seen from the physical model that the former transmission of the quantum state will not affect the next transmission, i.e. the correlations between the subsequent quantum signals do not exist in this model.

Zoom In Zoom Out Reset image size

Our results for the non-Markovian channel have shown something very different from the Markovian case. The non-Markovian channel has a better performance than the Markovian one to resist the leakage of information with the increasing of noise. Actually, the non-Markovian effects can be useful to enhance the security of quantum communication. This advantage originates from the small period of correlation time between the system and environment of the non-Markovian channel, which leads to a smaller QBER in transmission than the Markovian channel. Therefore, we can combine the application of the non-Markovian and Markovian quantum channel to achieve optimally secure QKD.

We have investigated the dynamics of the secret key rate of the discrete-variable QKD protocol over the quantum channel with non-Markovian effects. In particular, we have introduced the physical model of the non-Markovian depolarizing channel with coloured noise, and calculated the secret key rate for the six-state protocol over non-Markovian and Markovian quantum channels under the same conditions. Moreover, we numerically compare the performances of the information transmissions over these two types of quantum channels. We find that the secure secret key rate will always be larger for non-Markovian channels than Markovian ones when the coupling strength of the system with the environment is strong enough. In particular, we obtain the lower bound of the coupling strength a_i when the parameter τ is specified as τ = 1. It should be mentioned that we focus on the study of the value of the secure secret key rate as the function of processing time of the quantum channel. In practice, the transmission distance for secure QKD is also an important parameter, which is directly related to the transmission speeds of the quantum states over the Markovian and non-Markovian channels. However, the secure transmission distances over the Markovian and non-Markovian channels are out of our discussions.

Since the upper bounds of tolerable QBER for secure QKD are equal over the non-Markovian and Markovian depolarizing channels, we demonstrate that the better performance of the non-Markovian depolarizing quantum channel for the six-state protocol originates from the different dynamics of QBER. Furthermore, we consider the generalized non-Markovian depolarizing channel and show that the secret key rate will fluctuate near the secure point when the coupling strength of the system with the environment is high. This indicates that the coloured noise in the non-Markovian quantum channels can enhance the security of communication. The results demonstrate that the non-Markovian effects of the transmission channel can have a positive impact on the security of discrete-variable QKD.

This work was supported by the National Natural Science Foundation of China (grant nos 61 102 053, 61 170 228, 60 970 109 and 60 801 051).