ABSTRACT
The subject of this paper is the design of practical laser experiments that can produce collisionless shocks mediated by the Weibel instability. Such shocks may be important in a wide range of astrophysical systems. Three issues are considered. The first issue is the implications of the fact that such experiments will produce expanding flows that are approximately homologous. As a result, both the velocity and the density of the interpenetrating plasma streams will be time dependent. The second issue is the implications of the linear theory of the Weibel instability. For the experiments, the instability is in a regime where standard simplifications do not apply. It appears feasible but non-trivial to obtain adequate growth. The third issue is collisionality. The need to keep resistive magnetic-field dissipation small enough implies that the plasmas should not be allowed to cool substantially.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Collisionless shocks are systems in which the properties of colliding plasmas change on spatial scales that are small by comparison with particle–particle collision lengths, in consequence of the interactions of the particles with electromagnetic fields. Such shocks abound in astrophysical systems but remain elusive in the laboratory. Producing them in the laboratory would be of value, as these are complex, three-dimensional systems whose behavior involves the kinetic nature of the particles that are involved. In addition, the opportunities to observe their details are limited, even in the near-Earth space environment. The control offered by laboratory experiments could be essential to developing a clear understanding of their behavior. Many astrophysical collisionless shocks develop in the presence of dynamically important magnetic fields, including, for example, Earth's bow shock (Sagdeev 1966) and (some or all) shocks driven by supernova remnants (Petre 2000). The problem of developing laboratory experiments in this regime, where the magnetization of the ions was important, has been considered by Drake (2000). One has yet to see experimental facilities evolve to the point of accomplishing such experiments, although some work in that direction has been reported (Constantin et al. 2009). Here we consider a different case—systems that are not initially magnetized, so that plasma instabilities must create the electromagnetic fields required to establish the shock.
The second type of astrophysical collisionless shocks, in which the initial magnetic field is not dynamically important, are likely to exist, if less frequently than do the other type. Relativistic shocks of this type may exist in gamma-ray bursts (Medvedev & Loeb 1999). These shocks may also form in outflows that are parallel to the direction of an initially modest field or in supernova remnants if the early dynamics effectively demagnetize the flow (Gargate et al. 2010). Important questions in this case include how the shocks are initiated and what long-term mechanisms sustain the electromagnetic fields that serve to randomize the motion of the incoming particles. When non-magnetized, supersonic flows interpenetrate, the initial ion distribution function is quite anisotropic, having two peaks along the direction of interpenetration. One consequence of this is the electrostatic, two-stream instability, which produces strong fluctuating electric fields. This instability can produce shocks, as was first discussed by Forslund & Shonk (1970) and first simulated for relativistic plasmas by Silva et al. (2004). Some experiments may have observed effects of this process (Bell et al. 1988; Morita et al. 2010; Kuramitsu et al. 2011; Liu et al. 2011). However, this process is limited to fairly small Mach numbers and simulations; Kato & Takabe (2010) show that such shocks may dissipate with time in consequence of their nonlinear saturation dynamics. Another consequence of interpenetration that is potentially more robust as a source of shock formation is the Weibel instability (Weibel 1959) driven by the anisotropic ion distribution function. In the fastest growing unstable mode for this process, a magnetic field is generated in a direction orthogonal to the flow direction, having modulations orthogonal to both the field and the flow. Weibel discussed the instability in the context of anisotropic distributions of electrons, but it can exist for any circumstance in which one or more of the charged species in the plasma is sufficiently anisotropic (Davidson et al. 1972). In many astrophysical contexts, what is required to establish collisionless shocks is a mechanism that can affect the motion of the ions. It was long understood that, through the growth of magnetic fields in response to anisotropy in the ion distribution function, Weibel might contribute to the formation of collisionless shocks (Sagdeev 1966). Medvedev & Loeb (1999) first introduced the hypothesis that Weibel might be responsible for the formation of unmagnetized collisionless shocks in the specific context of gamma-ray bursts, which helped rekindle interest in this mechanism. The Weibel instability has also recently been considered as a possible contributor to cosmological magnetic-field generation (Schlickeiser & Shukla 2003; Miniati & Bell 2011). The Weibel instability is sometimes described as filamentation, and some authors make semantic distinctions related to these two terms. Here, within the context of magnetic-field generation, we make no distinctions between them. In the following, when we refer to Weibel or the Weibel instability without qualification, we are assuming that this process develops in response to anisotropy in the ion distribution function.
Much of what we know now about initially unmagnetized collisionless shocks derives from particle-in-cell (PIC) simulations of interpenetrating plasmas. Recent years have seen a number of papers examining such systems (Silva et al. 2004; Kato 2007; Spitkovsky 2008; Kato & Takabe 2008; Chang et al. 2008; Keshet et al. 2009; Gedalin et al. 2010; Kato & Takabe 2010; Gargate et al. 2010). Kato & Takabe (2008) cite the extensive earlier work with PIC codes on the Weibel instability in counterstreaming relativistic plasmas. The ratio of electron to ion mass creates a significant challenge for PIC simulations in the case of shocks in the electron–ion plasmas of interest here, in which one must resolve the electron timescale but ultimately cares about the ion dynamics. On the basis of simulations of uniform plasmas, Kato & Takabe (2008) suggested that experiments producing plasmas that interpenetrated with a relative velocity above 1000 km s−1 might be expected to produce collisionless shocks by Weibel.
None of the above should be taken to imply that the only mechanism potentially relevant to magnetic-field generation or collisionless-shock formation is the Weibel instability. While Weibel-type instabilities produce primarily magnetic-field fluctuations whose direction and wavevector are both perpendicular to the flow, this is not the only possibility. In analytic theory and magnetohydrodynamic simulations, drifting distributions of ions have been shown to drive unstable fluctuations having a wavevector parallel to the flow (Bell 2004), when the thermal ion velocity is relativistic and is large compared to the drift velocity. PIC simulations of this case confirm this result but suggest that the field cannot be amplified much beyond its initial amplitude (Niemiec et al. 2008). However, in the conditions of interest here the ion drift velocity substantially exceeds the ion thermal velocity. In cases where the anisotropy is introduced by cold, relativistic, electron beams, several mechanisms that could lead to fields producing collisionless shocks are present. Their competition is discussed by Bret (2009), who finds that (electron) Weibel dominates when the magnetization is sufficiently small. In non-relativistic systems, however, the electrons isotropize readily compared to the ions. In practical experiments such as those discussed in the present work, collisions will have this effect. In astrophysical systems, only relatively small fluctuating fields are required to have this same effect. Whenever the electrons are isotropized, the mechanisms that depend on electron anisotropy, such as electron Weibel or Buneman instabilities, will not be present. So long as the ion streaming velocity is smaller than the electron thermal velocity, the electron–ion Buneman instability is also suppressed (Papadopoulos 1988; Ohira & Takahara 2008). In addition, on physical grounds the Weibel instability could be suppressed by a flow-aligned magnetic field, as the instability would then have to overcome the resistance to bending of the field lines. Stockem et al. (2006) find a threshold for this effect and provide other connections with the heliospheric literature. Here, by assumption, such a field is not present. Weibel might also potentially be suppressed by competition with some other concurrent field generation mechanism, such as Biermann-battery effects. We consider this possibility in Section 6. Large-scale astrophysical magnetic fields very likely involve other effects beyond instabilities, such as the dynamo mechanisms discussed in the review by Kulsrud & Zweibel (2008). It may be the case that Weibel is involved in the initial field generation after which post-shock turbulence or other mechanisms further amplify and sustain the field (Ryu et al. 2008). In summary, it would appear that the (ion) Weibel instability should be the dominant, initial, magnetic-field-generation mechanism when ion–electron plasmas interpenetrate under conditions such that the ion thermal velocity is well below the ion drift velocity, which in turn is well below the electron thermal velocity. These are the conditions relevant to the experiments discussed below.
Laser-driven experiments have begun to focus on the challenge of producing collisionless shocks in counterstreaming plasmas that are initially unmagnetized and non-relativistic. The first such experiments, by Borovsky et al. (1984), occurred in the 1980s and were inconclusive, perhaps due to effects of the very energetic electrons produced using the CO2 lasers of that era (Drake 1999). Another paper from the late 1980s reported the observation of density increases in the vicinity of an obstacle to a laser-generated flow, concluding that this was probably due to electrostatic effects (Bell et al. 1988). More recent laser experiments, taking advantage of diagnostic advances since the 1980s, have observed phenomena attributed to the electrostatic two-stream instability (Morita et al. 2010; Kuramitsu et al. 2011) or to other electrostatic dynamics (Romagnani et al. 2008). At present, large research teams are seeking to produce and study Weibel-generated shocks at major laser facilities (Park et al. 2012). This makes a consideration of the design aspects of such systems important and timely.
We consider here the problem of how to produce counterstreaming plasmas that meet the requirements for the generation of well-developed collisionless shocks from initially unmagnetized plasmas, by means of the Weibel instabilty. In the next section, we discuss the geometry of potential experiments. Following that, we consider the problem of obtaining a large-enough and dense-enough plasma that one might hope to produce a collisionless shock, based on the evidence from the PIC simulations regarding the necessary scales. Then we evaluate the instability growth using linear theory, finding that likely experiments are in a regime where simple scaling arguments are problematic. A full evaluation of the kinetic dispersion relation shows when one might expect to amplify the instability into the strongly nonlinear regime. After that, we consider several aspects of collisionality and discuss potential competing mechanisms of field generation in experiments. We then conclude the paper. Throughout the present work we treat a plasma composed of Be ions, although at times we mention how sensitive the results are to the precise ion species. One might prefer to examine systems of H ions, which are of most direct astrophysical relevance. However, the cryogenic technology required to produce H plasmas in laser experiments is sufficiently challenging and time-consuming that basic-science experiments are unlikely to choose to use it. Some experiments may use plastic targets, containing C, H, and perhaps other elements. In this case the H ions may separate from the others and stream out ahead, in a process not unlike the species differentiation that occurs at high elevations in planetary atmospheres. This may prove to be of practical significance in experiments but is not tractable in semi-analytic design calculations like those described here. The physics involved in the H ion separation is discussed by Rambo & Denavit (1994).
2. EXPERIMENTAL GEOMETRY
Figure 1 illustrates the most straightforward way to produce counterstreaming plasmas with lasers. Laser spots of diameter DL create plasma that blows off the irradiated surfaces. One chooses to work with frontside blowoff, as the source temperature can be in the keV range. Rear-surface blowoff produced by laser-driven shock waves, in contrast, has initial temperatures of tens of eV. The resulting, lower, expansion velocities would be insufficient to produce strong Weibel growth. Using two targets and at least two laser beams produces the counterstreaming plasmas. Aside from any laser beams used for diagnostics, one may have a choice whether or not to keep heating the expanding plasma. Doing so has the positive effect of increasing the long-term acceleration of the ions and of reducing collisionality. In contrast, letting the expanding plasma cool increases the anisotropy of the ion velocity distributions, increasing the Weibel growth rate. We will attend to these two effects as our discussion continues.
Figure 1. Sketch of laser-driven experiment.
Download figure:
Standard image High-resolution imageAnother significant consideration is the ratio of target spacing DT to DL. For DT ⩽ DL the expansion will remain approximately planar. As DT increases further, the expansion will become increasingly spherical. Yet access for laser beams and diagnostics tends to imply that DT must be at least several millimeters. We consider two cases. On the Omega laser (Boehly et al. 1995) one can irradiate a planar surface with no more than 5 kJ in 1 ns pulses in 10 beams. Using the available phase plates that produce an 820 μm diameter FWHM laser spot, this means that one can use an irradiance of 9 × 1014 W cm−2 for 1 ns or of 1.9 × 1014 W cm−2 for 5 ns. Either case will produce keV temperatures, but with the indicated laser spot the plasma expansion will be relatively spherical. If one could purchase a set of 2.4 mm FWHM phase plates, one could drive a 2.4 mm diameter area at 1014 W cm−2 for 1 ns, but this irradiance is definitely sub-optimum. In contrast, on the National Ignition Facility (NIF; Hogan et al. 2000) one can irradiate each planar surface with 500 kJ in 3 ns pulses. This means, for example, that one could irradiate a 3.4 mm diameter area at 9 × 1014 W cm−2 for 6 ns. Thus, one could sustain a planar expansion for target separations up to about 7 mm.
An important limitation of laser-ablation plasma flows is that their maximum density is limited to some fraction of the critical density for the laser light. This in turn limits the potential size of the plasma, measured in ion skin depths. Figure 2 shows one approach that might be used on NIF to escape this limitation. Early work with hohlraums on NIF has shown that in some cases a large fraction of the energy of some beams can be converted to the waves driven by stimulated Raman scattering (SRS; Drake et al. 1984; Lindl 1995). When the plasma waves break, the energy that flowed into them, typically about 1/2 of the energy of the scattered light from the SRS, then appears as a distribution of energetic electrons having a characteristic energy of ∼30 keV. One could exploit this by using a target concept having a hohlraum target with some combination of gas fill and early wall blowoff, in order to maximize the production of SRS, and then using the electrons resulting from the SRS to drive a blowoff plasma. One could plausibly irradiate each hohlraum with 500 kJ, converting 300 kJ to SRS and thus 100 kJ to energetic electrons. About 10% of this, or 10 kJ, could then heat and drive expansion of a thin Be endplate. This potentially could produce a flow whose leading behavior corresponded to a planar, isothermal rarefaction from solid density at 30 keV initial temperature.
Figure 2. Sketch of experiment using laser-generated hot electrons in a hohlraum to drive a hotter rarefaction from a higher density maximum.
Download figure:
Standard image High-resolution imageOne could also consider other complex target designs. One might reduce the lateral expansion by creating a plasma jet from a conical surface (Farley et al. 1999). One might produce hotter plasmas using targets in which a CH2 layer was followed by a mid-Z layer that would be heated to a higher temperature by the laser. Simulations suggest that exploding foil targets likewise might be somewhat hotter. One could consider double gas bag targets in which a gas that would be heated to a high temperature was surrounded by a H layer. Or one could consider targets with a collimating tube to reduce the lateral expansion. The difficulty is that any of these options is complex and would require extensive development experiments.
3. OBTAINING THE REQUIRED DENSITY AND LENGTH
We consider first the behavior of a plasma ablated from a single source in order to ultimately draw conclusions about interpenetrating plasmas produced from two such sources. We will consider the available interaction distance to be the distance from the source, from the point of view that the two plasmas will each interact over about half this distance. Several factors, including slowing of the flow and finite total mass ablation, prevent one from expecting much larger effective distances of interaction. The combination of needing density and distance to increase the number of ion skin depths, high velocity of the interacting streams, and a collisionless interaction imposes constraints on the system.
We start with the plasma expansion from some source. The expansion, like most free expansions, will be nearly homologous with fluid velocity u ≃ r/t. This is strictly correct only after expansion cooling has driven the thermal pressure to zero; we discuss more exact descriptions below. Figure 3 shows the implications of such an expansion. Note that an experiment at some distance will last for some time, during which the velocity of each stream will decrease. For example, suppose that the structure of some detectable size becomes unstable (see Section 4) at point A, where the initial velocity of each stream is 1000 km s−1 and the distance from the source is r. The arrow from the left indicates that the initial state of the material will subsequently flow through the location of A from a distance up to r/2. While this happens, the local velocity at r will decrease along the vertical arrow toward point B, reaching half the initial value at some observation time. The growth rate decreases as velocity decreases, which would limit the value of continuing the experiment out to large multiples of the time when the instability exceeds threshold, even if one could sustain the plasma. Because the velocity at threshold will turn out to be a few times 1000 km s−1, and because the target separation must be several miliimeters, the natural timescale for these experiments will be nanoseconds, as opposed to tens of ns or a fraction of an ns. We consider in this section whether one can obtain the required density.
Figure 3. Approximate (homologous) single-stream velocity as a function of space and time. Curves are labeled with velocity, shown for potential positions and times of an experimental interaction.
Download figure:
Standard image High-resolution imageThe required density is related to the size of the interacting plasma measured in ion skin depths. The ion skin depth is
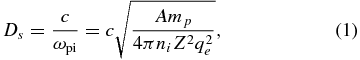
in which the ion density is ni, the speed of light is c, the ion plasma frequency is ωpi, the electron charge is qe = 4.8 × 10−10 statcoulombs for these units, the proton mass is mp, and the ion atomic mass and charge are A and Z, respectively, which for cgs units gives Ds in cm. PIC simulations (Kato & Takabe 2008) indicate that the minimum interaction distance to maintain a shock produced in interpenetrating plasmas is ∼300 Ds. To develop a criterion, for any distance r from one of the targets we find the density at which r = 300 Ds/2. The point of view is that the length of the interaction region will extend a distance r/2 toward each target and that the total density of the interacting streams will equal or exceed this density throughout the interacting region. This then gives the minimum density that must be achieved at that location to meet the interaction–distance criterion. This analysis gives the dashed curve shown in Figure 4. If one has at least this density at each distance, one can in principle obtain the required interaction length.
Figure 4. Plot of ion density against distance. The dashed curve shows the minimum density required for the interaction distance specified to correspond to 300 ion skin depths. Left: the straight lines, on this semilog plot, show density profiles for some planar isothermal rarefactions. The lower two lines are at 3 ns, and the upper line is at 1 ns. Right: the concave downward, red lines, on this semilog plot, show density profiles for some spherical isothermal rarefactions as indicated and discussed in the text.
Download figure:
Standard image High-resolution imageThe density of the interacting plasmas depends more strongly on the experimental details than the velocity does. The largest it can be is the value corresponding to a planar isothermal rarefaction from a thick mass source. One will only actually see this within a distance from the source corresponding to less than a laser spot size while the source is on, so it may be an overestimate of densities that can actually be achieved. Let the ion density in the source material be  , and then we can write the ion density for this case as
, and then we can write the ion density for this case as
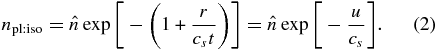
The sound speed cs is
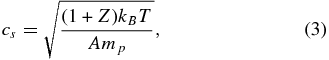
where the average ionization, average atomic weight, proton mass, and Boltzmann constant are Z, A, mp, and kB, respectively. Here we ignore the difference between electron temperature Te and ion temperature Ti, which has a small influence on pressure or sound speed except perhaps for hydrogen. Our typical numbers will correspond to fully ionized Be, which has Z = 4 and A = 9. For this case one has  , where TkeV is T in keV. Laser-irradiated surfaces produce isothermal rarefactions, but from an effective density well below the actual solid density, a consequence of the laser absorption at far below the solid density. Based on simulations, we take
, where TkeV is T in keV. Laser-irradiated surfaces produce isothermal rarefactions, but from an effective density well below the actual solid density, a consequence of the laser absorption at far below the solid density. Based on simulations, we take  cm−3 for UV laser-irradiated Be (the corresponding electron density is
cm−3 for UV laser-irradiated Be (the corresponding electron density is  ). In contrast, for the speculative hohlraum-based target of Figure 2, we take
). In contrast, for the speculative hohlraum-based target of Figure 2, we take  cm−3 for solid-density Be. These assumptions give the profiles shown in Figure 4. The straight (red) lines shown in the figure correspond to an observation time of 3 ns and to temperatures as indicated.
cm−3 for solid-density Be. These assumptions give the profiles shown in Figure 4. The straight (red) lines shown in the figure correspond to an observation time of 3 ns and to temperatures as indicated.
One sees in Figure 4 that planar rarefactions produced by laser ablation and corresponding to temperatures near 2000 eV meet the interaction–distance threshold out to more than 3 mm distance (corresponding to a 6 mm target separation). The figure also shows a curve for the 30 keV expansion from solid density discussed above. Such a plasma would exceed this threshold by several orders of magnitude. Caveats are that the density will be somewhat smaller than shown if the plasma is not heated throughout the expansion, that these plasmas are not homologous out to arbitrarily high velocities, and that lateral flow will tend to reduce the density, especially on experiments on kJ-scale lasers. We address the second and third of these issues next.
These expanding plasmas produce an ion front and are not homologous out to arbitrarily high velocity. As density decreases the electron Debye length, λDe increases, and once it equals the scale length of the density (cst), the decrease of the electric potential becomes more gradual and the ion acceleration effectively ceases (Mora 2003). Correspondingly, there is a maximum velocity, umax. To evaluate umax for the planar isothermal rarefaction, one seeks the solution to
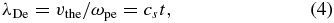
where ωpe is the electron plasma frequency. Using Equation (2) for the ion density and  , and again ignoring any difference in electron and ion temperatures, one finds
, and again ignoring any difference in electron and ion temperatures, one finds
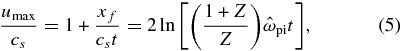
where xf is the front location and  is the ion plasma frequency at density
is the ion plasma frequency at density  . This is 1.2 × 1014 s−1 for fully ionized, laser-ablated Be with
. This is 1.2 × 1014 s−1 for fully ionized, laser-ablated Be with  cm−3 and 5.8 × 1014 s−1 for fully ionized, solid-density Be plasma. Taking
cm−3 and 5.8 × 1014 s−1 for fully ionized, solid-density Be plasma. Taking  , the equation becomes
, the equation becomes
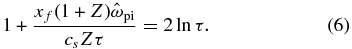
For a laser-ablation plasma at T = 1 keV, observed at xf = 3 mm, this implies τ = 9.2 × 104, so the ion front will arrive at 3 mm at ∼600 ps, moving at 5000 km s−1. We will see in Section 4 that the instability has not typically reached its threshold by this time, so an evaluation based on the full planar rarefaction will be reasonably accurate. For a plasma expanding from solid density at 30 keV, observed at xf = 3 mm, this implies τ = 8.0 × 104, so the ion front will arrive at 3 mm at ∼100 ps, moving at 30,000 km s−1. At that location, the velocity will have dropped to 3000 km s−1 by 1 ns.
A lower limit on the achievable density corresponds to a spherical isothermal rarefaction. The rapidity of thermal heat conduction under these conditions assures an electron temperature that is constant in space. Assuming that one continues to heat the plasma, one can sustain a temperature that is constant in time as well. For this case there is a spatially self-similar solution and the ion density profile, for a total mass M, is
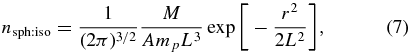
in which L is a time-dependent scale length satisfying the equation  , with ∂t indicating the partial derivative in time and
, with ∂t indicating the partial derivative in time and  being the second partial derivative in time. This has a rather involved solution (Drake 2011), whose results may be approximated (within 7%) as L = 0.95Lo(t/to)1.2, where the scale length is Lo at time to. Here we take to = 1 ns and Lo = csto. The corresponding local fluid velocity is u = 1.2r/t.
being the second partial derivative in time. This has a rather involved solution (Drake 2011), whose results may be approximated (within 7%) as L = 0.95Lo(t/to)1.2, where the scale length is Lo at time to. Here we take to = 1 ns and Lo = csto. The corresponding local fluid velocity is u = 1.2r/t.
It is non-trivial to determine the total mass for this case. Here we note that the ablated mass emerges from the target with  cm−3 throughout the laser irradiation, so that at the end of the laser pulse this must be the maximum density. The implied profiles will have larger densities at small radii and earlier times, which will not be realistic. Here we consider the Omega-relevant case of laser ablation at a temperature of 2 keV for 1 ns, so Lo = 330 μm and the implied value of M is 1.4 × 10−5 g. The corresponding density profiles shown in Figure 4 do not exceed the minimum required values at relevant distances of a few millimeters from the target surface. Although these curves only provide a lower limit, they do suggest that achieving a large-enough interaction distance to produce a well-developed collisionless shock is borderline at best on kJ-class lasers.
cm−3 throughout the laser irradiation, so that at the end of the laser pulse this must be the maximum density. The implied profiles will have larger densities at small radii and earlier times, which will not be realistic. Here we consider the Omega-relevant case of laser ablation at a temperature of 2 keV for 1 ns, so Lo = 330 μm and the implied value of M is 1.4 × 10−5 g. The corresponding density profiles shown in Figure 4 do not exceed the minimum required values at relevant distances of a few millimeters from the target surface. Although these curves only provide a lower limit, they do suggest that achieving a large-enough interaction distance to produce a well-developed collisionless shock is borderline at best on kJ-class lasers.
4. GROWTH
In the context of collisionless shocks, the notion is that one must drive the Weibel instability into a strongly nonlinear state, and that this may establish structure in the plasma that can be identified as a shock wave. The minimum necessary condition for this to occur is that the Weibel instability must be unstable. Beyond that, the instability must be strong enough to reach the nonlinear regime early enough during some specific experiment. To examine the potential for producing the Weibel instability under various experimental circumstances, it is therefore useful to explore the linear theory of the instability.
In a paper in 1972 that we will refer to as DHHW, Davidson, Hammer, Haber, and Wagner provided (Davidson et al. 1972) a treatment of the Weibel instability for arbitrary initial distribution functions. References to the body of work between Weibel's initial paper (Weibel 1959) and 1972 may be found in DHHW. DHHW include the linear theory, the quasi-linear theory, and some simulations. We will be concerned only with the linear theory. There remains the potential for other mechanisms to compete with Weibel, as is discussed in the introduction, although for the specific conditions of interest here the (ion) Weibel instability appears most relevant.
The system of interest includes particles counterstreaming in the y-direction, small-amplitude modulations along the x-direction, and growing magnetic field but no relevant motions in the z-direction, in a standard Cartesian coordinate system. The unperturbed distribution function is formally averaged in the x-direction. The Vlasov and Maxwell equations imply a general dispersion relation for the growth of magnetic modulations. We specialize, as do DHHW, to the case of drifting Maxwellian particle distributions, so that for species j the unperturbed distribution function at time zero,  , is
, is
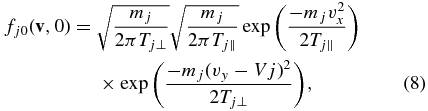
where the mass of the particles of species j is mj, the particle velocities are v with the subscript indicating the direction, the initial drift velocity in the y-direction is Vj, and the temperature of the particle distributions in vx and vy is Tj|| or Tj⊥, respectively. Note that the distribution functions are normalized to unity. With such distributions, the general dispersion relation becomes

where c is the speed of light, k is the wavenumber, Ωk is the complex frequency, with real part ωk and imaginary part (i.e., growth rate) γk, ωpj is the plasma frequency for each species, defined by ω2pj = 4πqj2nj/mj, in which the charge and density of species j are qj and mj, respectively, and the plasma dispersion function is
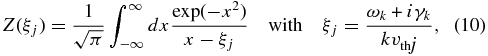
in which  . In the above, temperatures are in energy units and the definition of the plasma frequency is specific to Gaussian cgs units with charge in statcoulombs. Note also the factor of
. In the above, temperatures are in energy units and the definition of the plasma frequency is specific to Gaussian cgs units with charge in statcoulombs. Note also the factor of  in the definition of vth, convenient here but different for electrons than the definition used above.
in the definition of vth, convenient here but different for electrons than the definition used above.
In the experiments of interest, we suppose that two identical ion distributions interpenetrate, in the presence of a stationary electron background of equal temperature, and that other than the drift velocity the distributions are initially isotropic. We use subscripts e, 1, and 2 for these species. The use of a single electron species is justified if, as in the examples here, the electron thermal velocity is large compared to the ion thermal velocity and the drift velocity. Thus,
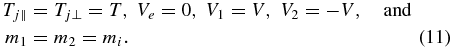
We also take
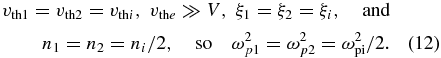
The dispersion relation becomes
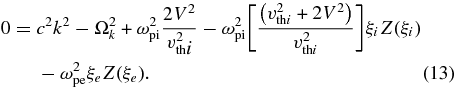
We are interested in purely growing modes, and so we define w = Im(ξi), noting that
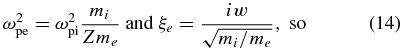
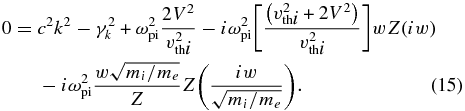
This dispersion relation, including the angular factor that reduces the growth rate for other directions of modulation, is also shown in Kato & Takabe (2010), who consider in addition the impact of evolving ion temperature anisotropy on the linear growth rate. (However, we show below that for realistic experiments the collisions of comoving ions will minimize such anisotropy.)
DHHW discuss the limit where the electrons can be taken to be cold, so ξe → ∞, in which case the rightmost term goes to ω2pe. Then in the event that w is large one can take the large-argument expansion of the dispersion function and find, after some algebra, that
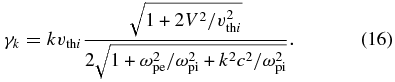
For V ≫ vthi there are interesting limits of this equation. When k is large enough (much larger than an inverse ion skin depth), one has

suggesting that the number of ion skin depths traversed by the interacting plasma is a key parameter. However, when k is of order 10 inverse ion skin depths or smaller, one has

Unfortunately, the cases of interest here span the two regimes just described, and even Equation (16) proves very inaccurate, as we show next. As a result, for these cases one cannot develop a simple, analytic estimate of the range of unstable wavelengths or the integrated linear-theory growth.
We proceed to compare three evaluations of the growth rate for three cases of interest. The general evaluation solves Equation (15) numerically to find γk. For small to moderate |w|, we represented Z(iw) in the equivalent form
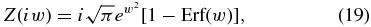
replacing this with the first six terms of the large-argument expansion
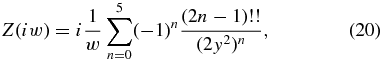
when our numerical evaluation of Equation (19) became unreliable at large |w|. We compare the resulting spectrum with that from an evaluation assuming cold electrons to illustrate when the involvement of the electrons in the dynamics matters. This cold-electron evaluation takes Z(ξe) → −1/(ξe) in Equation (13), corresponding to very large ξe, and then otherwise finds γk as just described. In addition to the spectra from the general and cold-electron evaluations, we show those of Equation (16), which correspond to the limit of both cold electrons and large argument, specifically using the first two terms of the large-argument expansion, so
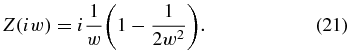
Note that while solving the dispersion relation determines w, we will plot γk/ωpi = kvthiw/ωpi, so that the point of largest growth rate on the plots below is not generally the point of largest argument w.
Table 1 shows the parameters for the three cases of interest. The first of these corresponds to the PIC simulations of Kato & Takabe (2008). The parameters chosen are not uncommon for practical simulations of this type. The second and third correspond to possible Omega and NIF experiments involving interpenetrating Be plasmas.
Table 1. Cases for Weibel Evaluation
| Parameter | Kato | Omega | NIF |
|---|---|---|---|
| A | 1 | 9 | 9 |
| Z | 1 | 4 | 4 |
| mp/me | 20 | 1836 | 1836 |
| V (km s−1) | 30000 | 1000 | 3000 |
| T(eV) | 25 | 100 | 100 |
Download table as: ASCIITypeset image
Figure 5 shows the results. With the degree of anisotropy in the ions that is present in the parameters corresponding to the PIC simulations, the electrons have a relatively small effect on the instability, which is why the solid and short-dashed curves overlap well. In contrast, the analytic result diverges from the other two at large k, where the argument of the plasma dispersion function becomes small. Kato and Takabe observe that structures first appear in the simulations at the scale of the electron skin depth, which corresponds to kc/ωpi ∼ 25 for the mass ratio used in the simulations. This may be coincidence rather than causation: the electron skin depth does not appear naturally in the linear theory, but the growth rate does fall off at smaller spatial scales. Note also that the growth rate approaches 0.1ωpi. If one could achieve the parameters of this case in an experiment, this ought to produce a strongly nonlinear state on a nanosecond timescale.
Figure 5. Plot of ion normalized growth rate γk/ωpi against normalized wavenumber kc/ωpi, for parameters shown in Table 1 for the cases as labeled. The solid curves show the actual growth rate, the short-dashed curves show the growth rate found after assuming cold electrons, and the long-dashed curves show the analytic result that assumes cold electrons and large growth rate.
Download figure:
Standard image High-resolution imageFor a plausible Omega experiment, Figure 5 shows that the electrons play an essential role in the instability, and the analytic result is quite far off, as both dashed curves differ sharply from that corresponding to the solution of the full dispersion relation. The fastest growth occurs for modulations that are a significant fraction of an ion skin depth in spatial scale, but the growth rate is above 10% of the maximum for structures up to about 10 ion skin depths in scale. The normalized growth rate is about 10 times smaller here than in the first case, reflecting primarily the difference in ion velocity. The ion anisotropy itself does not dominate the growth rate. Dropping the temperature T to 10 eV leads to an increased growth rate of less than a factor of two. The use of a non-hydrogenic ion has a modest positive effect. Changing to H ions reduces the growth rate by about a factor of two. Assuming a Be ion density of 1019 cm−3, based on the discussion above, one has ωpi = 6 × 1012 s−1, implying an e-folding time of ∼100 ps. The implication is that the experimental interaction will need to endure for multiples of 1 ns to allow a sustained period of strongly nonlinear dynamics.
For a plausible NIF experiment, assuming that some approach exploiting the energy available on NIF can produce an enduring interaction at higher velocity (and density), Figure 5 shows that the electrons also play an essential role in the instability, and the analytic result is quite far off, as both dashed curves differ sharply from that corresponding to the solution of the full dispersion relation. The fastest growth occurs for modulations that are of order 20% of an ion skin depth in spatial scale, and the growth rate exceeds 0.001ωpi up to about 3 ion skin depths in scale. Assuming that one could achieve a Be ion density of 1021 cm−3, based on the discussion above, one has ωpi = 6 × 1013 s−1, implying an e-folding time of ∼2 ps. This would enable much more nonlinear evolution of the instability.
The discussion above describes the initial behavior of the instability under constant, unchanging conditions. However, in experiments where expanding plasmas interpenetrate, the plasma conditions change during the interaction. For the modes of interest here, which are non-propagating, purely growing modes, the linear theory just discussed will provide a reasonable approximation to the growth rate so long as the spatial scale of the global variations in the plasma properties is large compared to the wavelength of the modulations. This is the case for experiments like those described above. As the plasmas interpenetrate, the density and hence ωpi increase steadily. If one considers the growth of modulations of a given spatial wavelength λ1 at some specific wavenumber k1, the effect of the increasing density is to move these modulations from right to left in Figure 5. Until the density reaches some value, there will be damping rather than growth. Then, as the density increases, the growth rate for structure at λ1 will increase to a maximum and then decrease, but not to zero. To find a reasonable indication of the degree of growth, we will evaluate the number of e-foldings based on the linear-theory growth as

where γk(t) is obtained by an instantaneous solution of Equation (15) and tth is the time when γk reaches zero.
Figure 6 shows the results for laser-driven targets. The targets are taken to be 7 mm apart, and we examine the growth midway between them, at a distance r1 = 3.5 mm from each target. To produce the upper curves, the plasma from each target is assumed to be a planar isothermal rarefaction in fully ionized Be, described by Equation (2) with  cm−3, which, as was discussed above, might be possible to sustain at NIF but not at Omega. Here we assume continuous laser heating so that T = 2000 eV for the expansion and for the interaction. We follow the evolution for 5 ns. Under these conditions, G is 20–80 for wavelengths from about 10 μm to 200 μm. For a wavelength of 100 μm, structure begins to grow at about 1 ns and the growth rate remains substantial for 5 ns but is decreasing steadily by then. The amount of growth shown in the figure is not always large. Depending on the noise level, an amplification of e20 < 109 may not be enough to create a strongly evolved nonlinear state. But an amplification of e40 should be. If instead one assumes that the ions have cooled to T = 100 eV after an initial brief acceleration, one finds a similar spectrum with values of G that are about two times larger. But strengthening the instability in this way comes at the cost of increasing collisionality, as we discuss in the next section.
cm−3, which, as was discussed above, might be possible to sustain at NIF but not at Omega. Here we assume continuous laser heating so that T = 2000 eV for the expansion and for the interaction. We follow the evolution for 5 ns. Under these conditions, G is 20–80 for wavelengths from about 10 μm to 200 μm. For a wavelength of 100 μm, structure begins to grow at about 1 ns and the growth rate remains substantial for 5 ns but is decreasing steadily by then. The amount of growth shown in the figure is not always large. Depending on the noise level, an amplification of e20 < 109 may not be enough to create a strongly evolved nonlinear state. But an amplification of e40 should be. If instead one assumes that the ions have cooled to T = 100 eV after an initial brief acceleration, one finds a similar spectrum with values of G that are about two times larger. But strengthening the instability in this way comes at the cost of increasing collisionality, as we discuss in the next section.
Figure 6. Linear-theory results for the laser-ablation case, for parameters described in the text. The upper curves are for planar isothermal rarefactions; the lower curves are for spherical isothermal rarefactions. Left: linear-theory growth factor from Equation (22) against wavelength in microns. Right: growth rate in s−1 for λ1 = 100 μm against time in ns.
Download figure:
Standard image High-resolution imageThe lower curves in Figure 6 are for a spherical isothermal rarefaction like that described in Section 3. This has a temperature of 2 keV,  cm−3, and M = 1.4 × 10−5 g, as is described there. It represents a very conservative lower limit for an Omega experiment. If the ion density in such an experiment were as low as is assumed here, then there would be only a few e-foldings of Weibel instability growth.
cm−3, and M = 1.4 × 10−5 g, as is described there. It represents a very conservative lower limit for an Omega experiment. If the ion density in such an experiment were as low as is assumed here, then there would be only a few e-foldings of Weibel instability growth.
Figure 7 shows the results for hohlraum-driven targets. The growth rate was evaluated starting at 100 ps, roughly when the ion front reaches the observation location. The targets are taken to be 7 mm apart, and we examine the growth midway between them, at a distance r1 = 3.5 mm from each target. The plasma from each target is assumed to be a planar isothermal rarefaction in fully ionized Be, described by Equation (2) with  cm−3, which, as was discussed above, might be possible to sustain at NIF but not at Omega. Here we assume continuous laser heating so that T = 30 keV for the expansion and for the interaction. We follow the evolution for 5 ns. Under these conditions, G is >50 for wavelengths below about 170 μm. The growth at wavelengths below 20 μm is much larger. If one could achieve a density and velocity even several times less than those described here, this would produce a Weibel instability that was very far into the nonlinear regime.
cm−3, which, as was discussed above, might be possible to sustain at NIF but not at Omega. Here we assume continuous laser heating so that T = 30 keV for the expansion and for the interaction. We follow the evolution for 5 ns. Under these conditions, G is >50 for wavelengths below about 170 μm. The growth at wavelengths below 20 μm is much larger. If one could achieve a density and velocity even several times less than those described here, this would produce a Weibel instability that was very far into the nonlinear regime.
Figure 7. Linear-theory results for the hohlraum-driven case, for a rarefaction from solid density (parameters described in the text). Left: linear-theory growth factor from Equation (22) against wavelength in microns. Right: growth rate in s−1 for λ1 = 100 μm against time in ns.
Download figure:
Standard image High-resolution imageBeyond obtaining enough unstable growth, the interacting region also must be large enough as was discussed in Section 3. Taking the point of view from that discussion that the effective interaction distance extends from the midpoint halfway toward either target, we evaluate the effective number of skin depths Ns as
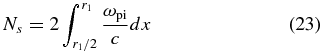
for these model plasmas. Figure 8 shows the result for the laser-ablation case. One sees that Ns reaches 300 at about 3 ns for a planar rarefaction. Whether this would allow time for a collisionless shock to develop is not clear. It is clear in the spherical case that one would be unlikely to see a collisionless shock, as Ns ∼ 40. One would expect this from Figure 4. In contrast, for the hohlraum-driven case Ns exceeds 300 by 400 ps and increases to several thousand after 1 ns.
Figure 8. Effective number of skin depths, Ns, vs. time for the case of Figure 6. The upper curve is for the planar isothermal rarefaction, while the lower curve corresponds to the spherical isothermal rarefaction.
Download figure:
Standard image High-resolution imageOne concludes, from the point of view of density profiles and instability growth rates, that one can produce conditions in which the Weibel instability could plausibly be strong enough to produce collisionless-shock formation, if one is using MJ-class lasers like NIF. This is likely to be possible using laser-ablation targets. It would be more likely if a high-temperature expansion from a solid surface could be produced, for example, using the high-SRS hohlraum target described above. In contrast, experiments on kJ-class lasers are marginal for producing such shocks. Whether or not they would succeed depends in part on the actual density profiles that are produced in real experiments. This could be affected as well, for some target types, by separation of the H ions from the mixed plasma, a topic beyond the scope of the present paper. What remains is to ask whether the collisions can in fact be small enough to allow such shocks to form and also whether they might alter some of the observable quantities in such cases.
5. COLLISIONALITY
The goal of the experiment is to examine the interactions under collisionless conditions, and so one must consider collisionality. There are several aspects to this issue. These include the interactions of the counterstreaming ions, the isotropization of comoving ions, and the dissipation of the Weibel magnetic field in consequence of electron–ion collisions. We consider these in turn. Taking an engineering approach, we work with formulae from the Plasma Formulary for these estimates. Here the densities are in cm−3, energies and temperatures are in eV, and velocities are in cm s−1.
5.1. Scattering of Counterstreaming Ions
One may recall that a collisional shock transition occurs over only a few ion–ion collision lengths. Important context is that the collision length for Coulomb processes is an effective distance for 90° scattering, but that the actual change in the velocity distribution occurs in consequence of many small-angle collisions. As a result, by the time the ions have interpenetrated by one collision length, they in fact will have significantly isotropized and will have begun to form a collisional shock, with a corresponding increase in density, thermal pressure, and transverse temperature. In addition, an interpenetration that occupies a small fraction of a collision length will produce random ion motion involving velocities that are a small fraction of the counterstreaming velocity, which may be large compared to the initial ion thermal velocity. All this implies that to have a clean collisionless-shock experiment, one needs a very large ratio of interpenetration distance to counterstreaming collision length.
We formulate the collision rate for transverse scattering of interpenetrating plasma ions, ν⊥, by treating one plasma as a target at rest, being penetrated by ions from the other plasma, so that
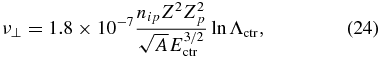
where the target plasma properties are designated by the subscript p; the energy of the counterstreaming ions relative to the target plasma in eV is Ectr = Ampv2d/(2kB), where vd is the relative drift velocity, which for identical plasmas is twice the fluid velocity shown in Figure 3 or identified as V in the discussion of growth rate. We assume here that the ion thermal velocity of the target plasma is less than vd, which is less than the electron thermal velocity. The relevant Coulomb logarithm in this case is
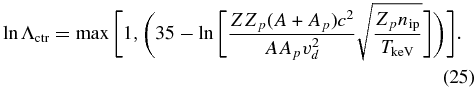
Here and below we approximate the limiting behavior of ln Λ as reaching a minimum value of 1 at high density.
We evaluate the mean-free path for the counterstreaming ions as λctr = vd/ν⊥, and we are interested in the ratio of this distance to the skin depth, χctr = λctrωpi/c, which we would like to be much larger than 300. Then one has
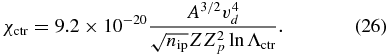
The v4d dependence is striking, and note that the only dependence on Te is through ln Λctr. Figure 9 shows contours of constant χctr, for which one needs to achieve a value of 300 to have one collision per shock formation length. The results are plotted relative to the single-stream velocity, V, discussed above, where vd = 2V. These contours are relatively insensitive to details. They change only slightly for a tenfold change in Te. Surprisingly, they also change little for a pure H interaction as opposed to the Be-on-Be case shown. The change in ln Λctr largely offsets the effect of the changes in mass and charge outside the logarithm. One must bear in mind that the likely ion density where one can achieve enough length is ∼1020 cm−3 for laser-ablation plasmas, and that vd will drop perhaps a factor of two during the interactions of interest. From the discussion just above, one would expect that an experiment located on the contour of χctr = 300 would be well on its way to forming a collisional shock and would exhibit a significant density increase and degree of thermalization of the streams. In contrast, values of χctr above 10,000 would correspond to relatively little thermalization and density increase, and this would be calculable as well by a Fokker–Planck analysis. One concludes that an experiment claiming to detect collisionless-shock formation should be able to show that the entire interaction forming the shock occurs under conditions that are well above χctr = 1000.
Figure 9. Curves of constant ratio, χctr, of the transverse scattering length of counterstreaming Be ions to the ion skin depth, with the value of χctr indicated. The kinks in the bottom two curves correspond to the transition of ln Λctr to 1.
Download figure:
Standard image High-resolution image5.2. Ion–Ion Self-scattering
One also must be aware of the self-scattering of comoving ions. If this rate is large, then the stationary ion population that develops as the shock forms will isotropize rapidly, even if the interactions producing this population are not isotropic. This may or may not have great significance; collisionless PIC simulations to date seem to find that this ion population is relatively isotropic. The transverse scattering rate of ion–ion collisions within each plasma for plasma properties designated by subscript p and for test particles without subscript is
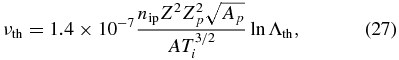
where the relevant Coulomb logarithm is
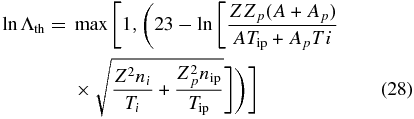
We evaluate the mean-free path for the thermal self-scattering as  , and we are also interested in the ratio of this distance to the skin depth, χth = λthωpi/c. It is less clear how large this needs to be. One has
, and we are also interested in the ratio of this distance to the skin depth, χth = λthωpi/c. It is less clear how large this needs to be. One has
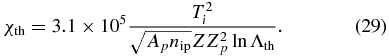
Figure 10 shows contours of constant χth for a Be plasma and for an H plasma. One sees that for the likely densities and temperatures, one will end up with a thermal self-scattering length of about one-tenth of an ion skin depth in a Be plasma. A well-mixed plasma of C and H would be similar. In a H plasma, the scattering length is larger but still small compared to the desired scale of several hundred ion skin depths. One concludes that comoving ion populations will be thermalized and isotropized by collisions under all likely conditions. This would not invalidate a collisionless-shock experiment, so long as one could successfully show that the mechanism that created the comoving, post-shock ion distribution was a collisionless mechanism.
Figure 10. Curves of constant ratio, χth, of the transverse scattering length of thermal ions to the ion skin depth, with the value of χth indicated. Left: Be plasma. Right: H plasma.
Download figure:
Standard image High-resolution image5.3. Magnetic Dissipation
Collisional diffusion of magnetic structures also must be considered. This is frequently characterized in terms of a magnetic Reynolds number, Rm. If Rm were too small, this would imply that the magnetic fields being generated by the particle interactions would become weakened by diffusion and would be resistively dissipated. The standard definition (for Gaussian cgs units) is Rm = UL/(4πη), where the flow velocity is U, the scale length is L, and the kinematic magnetic diffusivity is η. To understand how to evaluate any Reynolds number, however, depends on context. Here we consider the competition of unstable growth and magnetic diffusion in order to arrive at a well-informed evaluation of Rm and a means to evaluate the resistive limits on the Weibel instability. We will seek a result corresponding to the local dynamics of magnetic structures, based on this competition. This would correspond to what is sometimes called an "inner-scale" Reynolds number in viscous flows. Values above 1 are required to be in a regime where growth will occur and values about 10 to make resistive effects negligible.
Before proceeding, we note that for structures within the unstable range, the analytic linear growth rate of DHHW (Equation (16)) was shown above to underestimate the growth rate by a factor of a few. We use the limits of this growth rate here (Equations (17) and (18)), recognizing that this will often overestimate the effects of dissipation.
When the modulations of interest are relatively long wavelength, on the scale of the ion skin depth or larger, Equation (18) is the relevant limit. The rate of magnetic diffusion, from the scaling of the corresponding equation, is that the diffusion rate, νD, is

This enables us, with the identification that k = 2π/L, to write
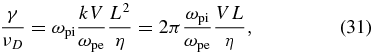
which gives us an expression like the usual magnetic Reynolds number, where L corresponds to the inner-scale size on which structures grow, with a prefactor not so far below 1. For our purposes it is useful to develop this expression further, using the definition of η,

to find
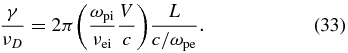
One can note that this is 2π times the ratio of the electron mean-free path to the ion skin depth, multiplied by L/(c/ωpe), the ratio of structure scale to the electron skin depth.
A similar analysis, for the small-scale, large-k limit of Equation (17), gives
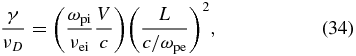
which is the ratio of the electron mean-free path to the ion skin depth, multiplied by the square of the ratio of structure scale to the electron skin depth.
To express these results in practical units for a figure, we note that the electron–ion collision frequency is

where the relevant Coulomb logarithm is
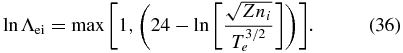
This enables us to find that
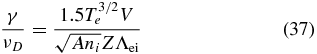
for the small-scale length L = 10c/ωpe and
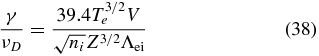
for a large-scale length L = 10c/ωpi. Here we see that the ratio of growth rate to dissipation rate for structures at large scale (∼10c/ωpi) is  times the ratio for structures at small scale (∼10c/ωpe). We plot only the more adverse ratio, for small-scale structures. Figure 11 shows the results. The ratio of growth to dissipation will be a few times larger for hydrogen plasma as compared to Be plasma. One sees that some combination of low density and high temperature within the range shown is required to keep this ratio large. Keeping it above 10 is a reasonable constraint. However, this might be too pessimistic. One might produce a Weibel-mediated shock even if the small-scale structures were collisionally dissipated so long as the structures on the scale of the ion skin depth were not. Even so, allowing the plasma to expand and cool to very low temperature makes the magnetic dissipation significant, and so this issue forces the conclusion that one should keep the plasma warm enough, very likely by continuing to heat it after the initial blowoff is produced.
times the ratio for structures at small scale (∼10c/ωpe). We plot only the more adverse ratio, for small-scale structures. Figure 11 shows the results. The ratio of growth to dissipation will be a few times larger for hydrogen plasma as compared to Be plasma. One sees that some combination of low density and high temperature within the range shown is required to keep this ratio large. Keeping it above 10 is a reasonable constraint. However, this might be too pessimistic. One might produce a Weibel-mediated shock even if the small-scale structures were collisionally dissipated so long as the structures on the scale of the ion skin depth were not. Even so, allowing the plasma to expand and cool to very low temperature makes the magnetic dissipation significant, and so this issue forces the conclusion that one should keep the plasma warm enough, very likely by continuing to heat it after the initial blowoff is produced.
Figure 11. Curves of ratio of Weibel growth rate to magnetic diffusion rate, as indicated, for interpenetrating Be plasmas with a single-stream velocity of V = 2000 km s−1. The results shown are for perturbations at the scale of 10 electron skin depths. Perturbations at the ion skin depth scale or larger grow much more strongly. This ratio scales with V.
Download figure:
Standard image High-resolution image6. COMPETING FIELD GENERATION MECHANISMS
An important question for both the experiments and the astrophysical systems in which initially unmagnetized plasmas interpenetrate is the potential role of competing magnetic-field-generation mechanisms. In principle, one might develop fields that are aligned with the flow or transverse to the flow. These will have rather different effects. Because the instability must bend any flow-aligned field lines, it is clear that flow-aligned fields will weaken the instability. Stockem et al. (2006) find a threshold for instability of roughly V > VA, where VA is the Alfvén velocity. This also has the physically sensible interpretation that instability requires that Alfvén waves cannot escape the region of interaction into the upstream flow. However, for the specific case of interest and the experiments that might study it, we are aware of no mechanisms that would generate flow-aligned fields.
In contrast, there are processes related to the Biermann-battery mechanism that might generate transverse magnetic field, specifically in an azimuthal direction. Physically, such fields would not be expected to limit the instability, but would be expected to organize it so that the fluctuating field was also azimuthal and the associated wavevector was radial. The reason is that fluctuations having these properties would neither bend nor compress the magnetic-field lines. If the quasi-steady, azimuthal, magnetic field were strong enough, this would effectively reduce the Weibel instability to a two-dimensional process. Since PIC simulations in two dimensions still find that Weibel can mediate collisionless shocks, the consequences for shock formation might be modest. Our estimates below find that known sources of this type might produce azimuthal fields comparable to or larger than the fields from Weibel. Even if other sources of azimuthal fields were present, the argument just given would still apply and the Weibel instability might still mediate collisionless shocks. However, magnetic-field measurements might detect such azimuthal fields rather than any fields produced by the Weibel instability, so an evaluation of known effects is important.
For comparison, the energy density in magnetic-field fluctuations produced by Weibel is found in PIC simulations to be ∼1% of the kinetic energy density (Kato & Takabe 2008). This gives

with ni in cm−3 and V in km s−1. However, Kato & Takabe (2008) use simulations with me/mp = 1/20 and A = 1, while Medvedev et al. (2007) argue that the actual saturated field should be proportional to me/(Amp), which would reduce the prefactor in this equation by a factor of about 100.
It is worth noting that there is also an electron Weibel instability generation mechanism that can be effective in plasma expansions where the electrons are collisionless (Thaury et al. 2010). This would not apply to the laser-ablation experiments discussed here but potentially could be important in expansions driven by the production of energetic electrons. Such Weibel fields, if present, could greatly accelerate the process of collisionless-shock formation once two such plasmas met.
For comparisons the Biermann-battery source term (Biermann 1950) is readily derived from Faraday's law and the electron momentum equation, as
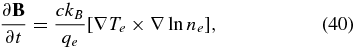
in cgs units with speed of light c, Boltzmann constant kB, electron charge qe, and electron density ne. The first source of azimuthal magnetic field from this source that we consider is near the surface of laser-irradiated targets. Here there is an axial gradient of electron density and the temperature gradient has a radial component. This produces a toroidally shaped, azimuthal field. In general, any system in which heat flow produces a radial temperature gradient while expansion produces an axial density gradient will create such a field.
For irradiation with laser beams having nanosecond pulse length, the field magnitude is typically ∼1 MG (Stamper et al. 1971; Petrasso et al. 2009). This field develops at densities near ∼1021 cm−3, which is ∼10% of the critical density in present-day experiments. The source term weakens as the plasma expands, because rapid heat conduction tends to make the lower-density plasma isothermal (Drake 2011), but the field is also frozen-in as the magnetic Reynolds number is large on the scale of the expanding plasma. In addition, the field may act to inhibit the heat conduction, for which there is some evidence (Montgomery et al. 1994). Here we base our estimate on a field value at the source of 1 MG, with the caveat that differences in source location or scale lengths could alter this field, so it should be considered independently for any given experiment. If a 1 MG field formed at ne = 1021 cm−3 were perfectly frozen in, then its magnitude at lower density would depend on the nature of the expansion. If the toroidal flux tubes expand geometrically, so that their major radius R and minor radius δ are both proportional to r, then the conservation of magnetic flux and of particle number in an expanding flux tube implies that B∝n2/3 while n∝r−3. This gives a magnetic-field estimate of the field propagating from the surface, Bsurf, as
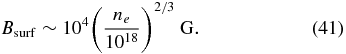
Comparing the two previous equations, one concludes that such a field might approach or exceed the saturated field generated by the Weibel instability.
A second source of direct, Biermann-battery field may be present if a shock front develops. Temperature variations along the shock then produce a source for the field. This is a familiar mechanism in shocks that are quasi-spherical or otherwise have varying obliqueness (Kulsrud et al. 1997); Gregori et al. (2012) claim to have observed this effect. In the present case, the two colliding plasmas will form a planar shock structure, along which there will be a temperature gradient because the radial component of momentum is conserved and so less energy is available for shock heating as the shock becomes increasingly oblique. An upper limit on this source can be found by ignoring electron heat conduction in the shocked plasma. Then the electron temperature of the shocked matter (after the electrons and ions equilibrate), Tsh, based on the energy available for conversion into thermal energy, will be
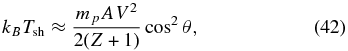
where θ is the angle of the flow relative to the system axis. This gives a temperature gradient
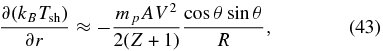
where R is the distance of the shock from the initial target. The scale length of the density gradient should be ∼100 c/ωpi, based on the PIC simulations. The corresponding field source is
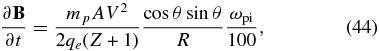
in which all quantities are in Gaussian cps units. For fully ionized Be plasma at R = 3.5 mm with ni = 1020 cm−3, V = 1000 km s−1, and θ = 0.3 radians, one finds a magnetic-field source of about 4 kG ns−1. This also might compete in magnitude with the Weibel-generated source field, again depending on the actual value of the prefactor in Equation 39.
Two other magnetic-field sources are discussed in the literature. Ryutov et al. (2011) show that interpenetrating plasmas of different Z produce a current by collisional current drive. If these plasmas are co-axial and radially symmetric, the resulting field is azimuthal. They consider only uniform plasmas, but we can note that when interpenetrating, homologous plasmas are produced with CH or CH2 targets the hydrogen separation will create a phase when H ions moving in one direction stream through C and H ions moving in the opposite direction. During this phase, current will be driven by this collisional mechanism. The estimated magnitude of the field for relevant parameters is ∼10 kG, and so this mechanism, if present, might also contribute significantly to the total azimuthal field.
7. CONCLUSION
The present paper has considered the problem of designing laser experiments that can produce collisionless shocks through the nonlinear saturation of the Weibel instability between counterstreaming ions. To succeed, such experiments must satisfy the following constraints:
- 1.The two streams must interact over a large-enough distance at a high-enough density. Previous simulations indicate that this distance is of order 300 ion skin depths.
- 2.The interacting plasma must be linearly unstable to the Weibel instability over a sufficient range of experimentally accessible wavelengths and must produce large linear-theory growth factors.
- 3.Collisions of the counterstreaming ions must be so small that their effects cannot produce a partial shock transition.
- 4.Resistive magnetic dissipation must be small enough to allow the Weibel instability to grow.
Any experiment that meets these constraints is likely to involve a nearly homologous expansion having a density that decreases with distance from the source. The largest density will be produced by a planar rarefaction, which might be achieved at NIF. On kJ lasers, however, the rarefaction over the millimeter distances required will be non-planar. A lower limit is that of a spherical rarefaction. This paper considered two types of possible experiments. The first was laser-ablation experiments, in which plasma is driven off the surface of a target in a rarefaction whose maximum density is some fraction of the critical density of the laser light. The second was hot-electron-driven experiments, a more speculative type of system with the potential to produce a rarefaction whose maximum density is the solid density, more than two orders of magnitude larger. This difference is significant; a rarefaction from solid density could produce systems whose size in ion skin depths is far above the minimum required and whose linear-instability growth factors are amply large.
For various model expansions, one can evaluate the linear-instability growth factor, defined as the integral over time of the exponential growth rate for a fixed wavelength. Doing so shows that the growth occurs primarily when the velocity is above 1000 km s−1. Obtaining the needed combination of high velocity and high density is a challenge. One also finds that a spherical expansion from a laser-ablation plasma will not produce sufficient growth to expect any possibility of collisionless-shock development. One concludes that characterization of the density and velocity of actual plasmas is essential to evaluate the growth factor in specific experiments. The combination of needed high velocity, distance scales of millimeters for laser and diagnostic access, and the need to keep the distance small to keep the density up implies that the natural scales of these experiments are millimeters and nanoseconds.
By examining the linear-theory growth rate and the resistive dissipation rate for magnetic field, one concludes that on balance it is better to heat the plasma during the expansion. This significantly reduces the magnetic dissipation without much decrease in growth rate. One also finds that the comoving ion populations will isotropize quite rapidly in any such plasma and that another reason to keep the counterstreaming velocity high is to make sure that the density increase due to collisions, which corresponds to the initial phases of collisional shock formation, is negligible.
It may prove challenging to measure the magnetic field generated by the Weibel process, by comparison to the fields generated by Biermann-battery mechanisms. Measurements or analysis techniques that are sensitive to the field fluctuations may well be necessary.
The work reported here is intended to be of use in planning potential experiments, in interpreting the meaning of design simulations for the plasmas that may be formed, and in interpreting the results of such experiments. One should, for example, be able to turn the Weibel instability on and off by varying the separation of the two plasma sources and the timing of the interaction volume that one probes.
R.P.D. acknowledges a sequence of valuable discussions with Dmitri Ryutov, whose insights substantially impacted the present work, and useful conversations with Youichi Sakawa. G.G. acknowledges illuminating discussions with Brian Reville, Tony Bell, and Francesco Miniati. The authors also acknowledge the work of the entire team involved in the Omega collisionless-shock collaboration, whose exciting work stimulated the analysis shown here. Support for this research for R.P.D. was provided by the US DOE NNSA under the Predictive Science Academic Alliance Program by grant DE-FC52-08NA28616, the Stewardship Science Academic Alliances program by grant DE-FG52-04NA00064, and the National Laser User Facility by grant DE-FG0300SF22021, while the work of G.G. has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement no. 256973.













