ABSTRACT
A rigorous analytical study of the dispersion relations of weakly amplified transverse fluctuations with wavevectors (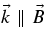 ) parallel to the uniform background magnetic field
) parallel to the uniform background magnetic field 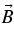 in an anisotropic bi-Maxwellian magnetized electron–proton plasma is presented. A general analytical instability condition is derived that holds for different values of the electron (Ae) and proton (Ap) temperature anisotropies. We determine the conditions for which the weakly amplified left-handed (LH) polarized Alfvén proton cyclotron and right-handed (RH) polarized Alfvén Whistler electron cyclotron branches can be excited. For different regimes of the electron plasma frequency phase speed w = ωp,e/(kc) these branches reduce to the RH- and LH-polarized Alfvén waves, RH-polarized high and low phase speed Whistler, RH-polarized proton, and LH-polarized electron cyclotron modes. Analytic instability threshold conditions are derived in terms of the combined temperature anisotropy A = T⊥/T∥, the parallel plasma beta β∥ = 8 π nekBT∥/B2 and the electron plasma frequency phase speed w = ωp,e/(kc) for each mode. The results of our instability study are applied to the observed solar wind magnetic turbulence at values of 90 ⩽ w ⩽ 330. According to the existence conditions of the different instabilities, only the LH- and RH-polarized Alfvén wave instabilities can operate here. Besides the electron–proton mass ratio μ = 1836, the Alfvénic instability threshold conditions are controlled by the single observed plasma parameter w. The Alfvénic instability diagram explains well the observed confinement limits at small parallel plasma beta values in the solar wind.
in an anisotropic bi-Maxwellian magnetized electron–proton plasma is presented. A general analytical instability condition is derived that holds for different values of the electron (Ae) and proton (Ap) temperature anisotropies. We determine the conditions for which the weakly amplified left-handed (LH) polarized Alfvén proton cyclotron and right-handed (RH) polarized Alfvén Whistler electron cyclotron branches can be excited. For different regimes of the electron plasma frequency phase speed w = ωp,e/(kc) these branches reduce to the RH- and LH-polarized Alfvén waves, RH-polarized high and low phase speed Whistler, RH-polarized proton, and LH-polarized electron cyclotron modes. Analytic instability threshold conditions are derived in terms of the combined temperature anisotropy A = T⊥/T∥, the parallel plasma beta β∥ = 8 π nekBT∥/B2 and the electron plasma frequency phase speed w = ωp,e/(kc) for each mode. The results of our instability study are applied to the observed solar wind magnetic turbulence at values of 90 ⩽ w ⩽ 330. According to the existence conditions of the different instabilities, only the LH- and RH-polarized Alfvén wave instabilities can operate here. Besides the electron–proton mass ratio μ = 1836, the Alfvénic instability threshold conditions are controlled by the single observed plasma parameter w. The Alfvénic instability diagram explains well the observed confinement limits at small parallel plasma beta values in the solar wind.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Kinetic plasma relaxation and turbulence generation processes are responsible for the observed properties of the solar wind plasma which is the only cosmic collision poor plasma accessible to detailed in situ satellite observations (Bale et al. 2009). Although the detailed plasma relaxation processes are not understood, the observed electron and proton distribution functions are close to bi-Maxwellian distributions with different temperatures along and perpendicular to the ordered magnetic field direction. Ten years of Wind/SWE data (Kasper et al. 2002) have demonstrated that the proton and electron temperature anisotropies A = T⊥/T∥ are bounded by mirror and fire-hose instabilities (Hellinger et al. 2006) at large values of the parallel plasma beta β∥ = 8 π nkBT∥/B2 ⩾ 1. In the parameter plane defined by the temperature anisotropy A = T⊥/T∥ and the parallel plasma beta β∥, stable plasma configuration is possible only within a rhomb-like configuration around β∥ ≃ 1, whose limits are defined by the threshold conditions for the mirror and fire-hose instabilities. If a plasma would start with parameter values outside this rhomb-like configuration, it immediately would generate fluctuations via the mirror and fire-hose instabilities, which quickly relax the plasma distribution into the stable regime within the rhomb configuration. The plasma parameters of other dilute cosmic plasmas including the interstellar and intracluster medium (Shekochihin et al. 2005) and accretion disks around compact, massive objects (Sharma et al. 2007) are similar to the solar wind plasma, so that the temperature-anisotropy instabilities should also operate in these systems.
The study of linear electromagnetic instabilities in a collisionless, homogeneous, magnetized, electron–proton plasma with temperature anisotropies has a long history; for reviews we refer the interested reader to chapter 7 of the monograph by Gary (1993), as well as Schwartz (1980), Cuperman (1981), and Marsch (2006). Hellinger et al. (2006) considered linear instability calculations for the oblique mirror, fire-hose, and proton cyclotron instabilities, and represented the approximate threshold conditions from the work of Gary et al. (1994, 2001), Gary & Lee (1994), Samsonov et al. (2001), and Pokhotelov et al. (2004) by analytic relations of the form A = 1 + a(β∥ − β0)−b where a, b, and β0 are fitted parameter values. In order to understand the confinement limits also at small values of the parallel plasma beta β∥ < 1, here we rigorously analyze the full linear dispersion relation in a collisionless homogenous plasma with anisotropic (A ≠ 1) bi-Maxwellian particle velocity distributions of electrons and protons for electromagnetic fluctuations with wavevectors (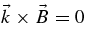 ) parallel to the uniform background magnetic field
) parallel to the uniform background magnetic field 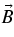 . With a typical solar wind temperature T = 105 T5 K, the thermal particle energy kBT = 8.6 T5 eV is much less than the electron rest mass mec2 = 5.11 · 105 eV, so that the use of the nonrelativistic linearized Vlasov/Maxwell equations is justified. For weakly (γ ≪ ωR) amplified wave solutions, we analytically derive existence and instability conditions. Here, ωR and γ refer to real and imaginary part of the complex frequency ω = ωR + ıγ. Our analysis closely follows the recent study (Schlickeiser 2010) for equal-mass pair plasmas—hereafter referred to as paper S. Our investigation is restricted to weakly amplified (γ ≪ ωR) solutions covering the left-handed (LH) polarized Alfvén proton cyclotron branch and the right-handed (RH) polarized Alfvén Whistler electron cyclotron branch. The corresponding analysis of weakly propagating (ωR ≪ γ) solutions, including mirror, fire-hose, electron cyctronic, and cold magnetized Weibel fluctuations, is the subject of a subsequent paper. As we will demonstrate below, for the case of parallel (
. With a typical solar wind temperature T = 105 T5 K, the thermal particle energy kBT = 8.6 T5 eV is much less than the electron rest mass mec2 = 5.11 · 105 eV, so that the use of the nonrelativistic linearized Vlasov/Maxwell equations is justified. For weakly (γ ≪ ωR) amplified wave solutions, we analytically derive existence and instability conditions. Here, ωR and γ refer to real and imaginary part of the complex frequency ω = ωR + ıγ. Our analysis closely follows the recent study (Schlickeiser 2010) for equal-mass pair plasmas—hereafter referred to as paper S. Our investigation is restricted to weakly amplified (γ ≪ ωR) solutions covering the left-handed (LH) polarized Alfvén proton cyclotron branch and the right-handed (RH) polarized Alfvén Whistler electron cyclotron branch. The corresponding analysis of weakly propagating (ωR ≪ γ) solutions, including mirror, fire-hose, electron cyctronic, and cold magnetized Weibel fluctuations, is the subject of a subsequent paper. As we will demonstrate below, for the case of parallel (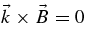 ) wavevectors simple analytical threshold conditions for the two branches can be derived in terms of the combined temperature anisotropy A = T⊥/T∥, the parallel plasma beta β∥ = 8 π nekBT∥/B2, the electron–proton mass ratio, and the electron plasma frequency phase speed w = ωp,e/(kc).
) wavevectors simple analytical threshold conditions for the two branches can be derived in terms of the combined temperature anisotropy A = T⊥/T∥, the parallel plasma beta β∥ = 8 π nekBT∥/B2, the electron–proton mass ratio, and the electron plasma frequency phase speed w = ωp,e/(kc).
2. DISPERSION RELATIONS
For a nonzero background magnetic field strength the nonrelativistic dispersion relations for RH- and LH-polarized fluctuations with wavevectors 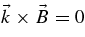 in a thermal electron–proton plasma are (Gary 1993)
in a thermal electron–proton plasma are (Gary 1993)

where we sum over the proton (p) and electron (e) contributions, and where k = |k∥|. ωp,e = (4πe2ne/me)1/2 and ωp,p = (me/mp)1/2ωp,e denote the electron and proton plasma frequencies, respectively. ua,∥ = (kBTa,∥/ma)1/2 is the parallel thermal velocity of component a, Ωa = eaB/(mac) is the nonrelativistic gyrofrequency, and Aa = Ta,⊥/Ta,∥ is the temperature anisotropy of component a, where the directional subscripts refer to directions relative to the background magnetic field. The dispersion relations (1) allow for different values of the proton and electron parallel temperatures and temperature anisotropies.
Z(x) and  denote the plasma dispersion function (Fried & Conte 1961) and its derivative
denote the plasma dispersion function (Fried & Conte 1961) and its derivative
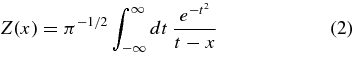
with the well-known properties
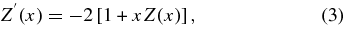
and
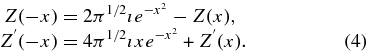
We will frequently use the asymptotic expansions

and
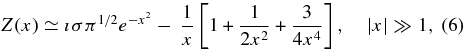
where σ = 0 if ℑ(x)>0, σ = 1 if ℑ(x) = 0, and σ = 2 if ℑ(x) < 0.
Paper S has demonstrated that the analytical analysis is enormously facilitated if we work with phase speeds rather than frequencies. We therefore introduce the complex phase speeds
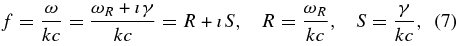
the plasma frequency phase speed

and the absolute value of the electron gyrofrequency phase speed

where |Ωe| = eB/mec is the absolute value of the electron gyrofrequency. We also introduce the mass ratio
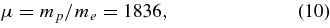
and the dimensionless proton and electron temperatures
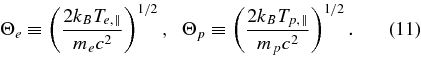
Throughout this work, in the classification of Swanson (1989) we discuss high-density plasmas with ωp,e ≫ |Ωe|, corresponding to w ≫ b which applies to nearly all dilute astrophysical plasmas. These plasmas are dense enough that the electron plasma frequency is much larger than the electron gyrofrequency, but small enough that elastic Coulomb collisions can be neglected.
The two dispersion relations (1) then read
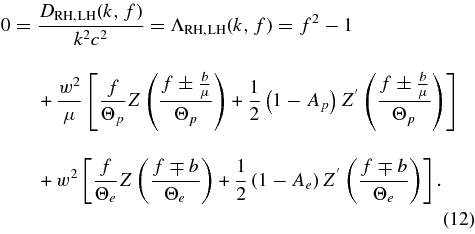
We note the symmetry Λ(−k∥, f) = Λ(k∥, f) of both dispersion relations allowing us to consider only positive values of the wavenumber k>0. In the following, we will simplify the analysis by considering only equal parallel temperature plasmas (Te,∥ = Tp,∥) so that Θe = Θ and Θp = Θ/μ1/2. Bale et al. (2009), reporting on the observations of the solar wind plasma properties, do not provide information on any measured differences of Te,∥ and Tp,∥, so we adopt parallel temperature equality which enormously simplifies the calculations.
The dispersion relations (12) can be separated into real and imaginary parts Λ(R, S) = ℜΛ(R, S) + ıℑΛ(R, S) = 0, implying the two conditions
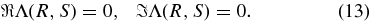
In terms of the complex phase speed f = R + ıS the real and imaginary parts of the two dispersion relations (12) read
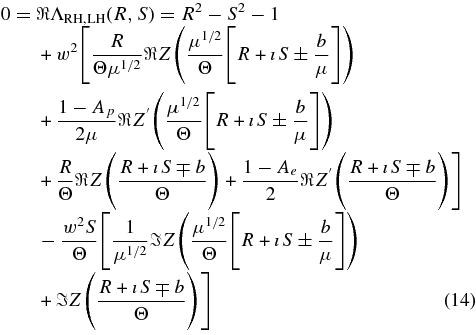
and
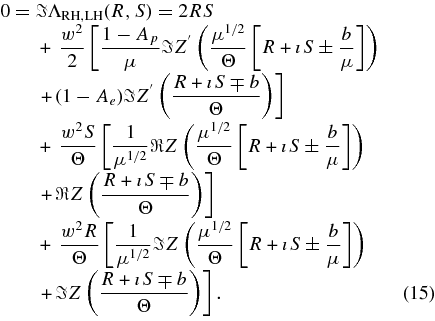
Here, we consider solutions of the dispersion relations in the weak damping/amplification limit |S| ≪ R. As shown in paper S in this limit the real part of the dispersion relation satisfies
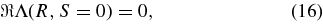
whereas the corresponding imaginary part is given by
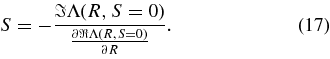
As before we introduce the parallel plasma beta
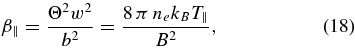
which expresses the magnetic field strength as

in terms of the electron plasma frequency phase speed (w), the parallel temperature (Θ), and the parallel plasma beta β∥. Our restriction to high-density plasmas with ωp,e ≫ |Ωe| or w ≫ b then requires to have parallel plasma betas β∥ ≫ Θ2 ≃ 3.4 × 10−5(Te,∥/105 K) in the solar wind plasma with typical temperatures Te,∥ ≃ 105 K.
3. WEAKLY DAMPED AND AMPLIFIED SOLUTIONS
For weakly damped or amplified fluctuations Equations (14) and (15) read
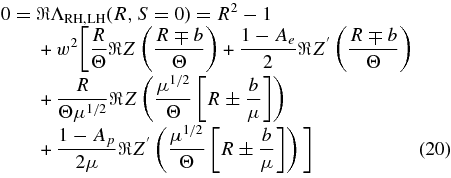
and
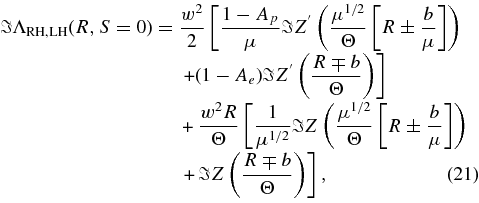
which have to be investigated for positive values of R ⩾ 0.
As noted before, these dispersion relations can be further reduced with the asymptotic expansions (5) and (6), depending on the absolute values of the arguments,
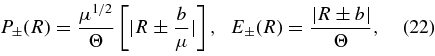
of the plasma dispersion function and its derivative being small or large compared to unity. Scaling R = bx, corresponding to x = ωR/|Ωe|, the absolute values of the arguments (22) in terms of the parallel plasma beta β∥ read
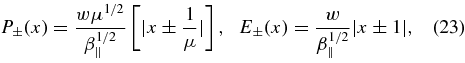
which are shown in Figure 1 as a function of the normalized real frequency x.
Figure 1. Absolute values of the arguments P±(x) and E±(x) of the plasma dispersion function and its derivative in the weak damping/amplification limit as a function of x = R/b.
Download figure:
Standard image High-resolution imageFor parallel plasma beta values β∥ ≪ (w2/μ), we note that P+(x) ≫ 1, E+(x) ≫ 1 for all values of x, whereas P−(x) ≫ 1 for x outside the small interval
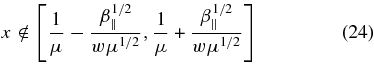
around the proton cyclotron frequency, and E−(x) ≫ 1 for x outside the small interval

around the electron cyclotron frequency.
In the following, we limit our analysis to such values of the parallel plasma beta β∥ ≪ (w2/μ), so that the asymptotic expansion (6) of the plasma dispersion function can be used except near the indicated proton and electron cyclotron frequencies.
Irrespective of the values of P± and E±, we note that both asymptotic expansions (5) and (6) yield the same imaginary part of the dispersion relation
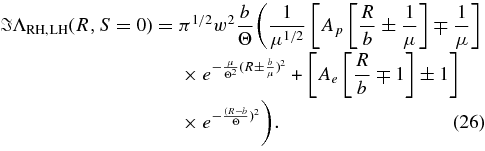
4. ALFVÉN, WHISTLER, CYCLOTRON WAVES, AND ELECTROMAGNETIC WAVES
For parallel plasma beta values β∥ ≪ (w2/μ) the asymptotic expansion (6) yields
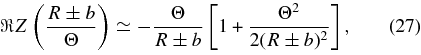
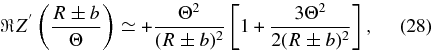
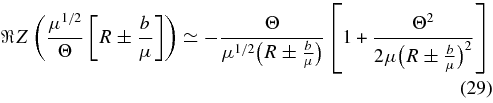
and
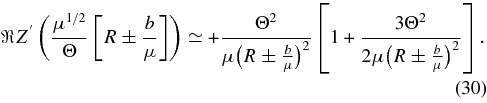
We then obtain for the real part of the dispersion relations (20) to lowest order in Θ2 ≪ 1
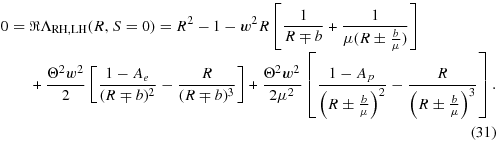
With the scaling R = bx and the parallel plasma beta (18) the dispersion relation (31) reads
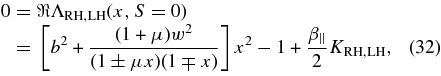
with
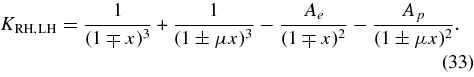
In different limits the solutions of Equations (31) and (32) describe Alfvén waves, Whistler waves, cyclotron waves, and electromagnetic light. We consider each case in the next subsections.
4.1. Alfvén Waves at Phase Speeds R ≪ b/μ for Θ2 ≪ β∥ ≪ w2/μ
For phase speeds R ≪ b/μ the dispersion relation (31) simplifies to
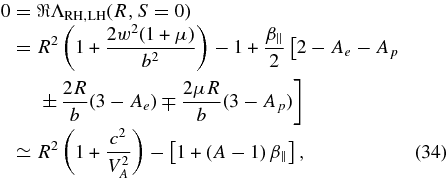
where we introduce the Alfvén speed
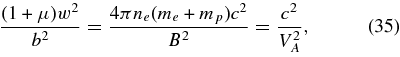
the parallel plasma beta (18), and the combined plasma temperature anisotropy

For high-density plasmas VA ≪ c, the dispersion relation (34) yields the LH- and RH-polarized Alfvén modes with the same phase speed
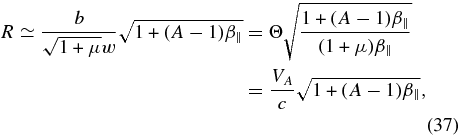
which either can propagate forward and backward. Note that the condition R ≪ b/μ requires (w2/μ) ≫ 1.
Moreover, the four Alfvén modes only exist for temperature anisotropies such that 1 + (A − 1)β∥ ⩾ 0 corresponding to

which includes the isotropic (Ap = Ae = A = 1) plasma temperature case. For small plasma betas (β∥ ⩽ 1) the condition (38) is always fulfilled whereas for large plasma betas (β∥>1) the combined anisotropy A has to be larger than 1 − β−1∥.
Equation (34) also provides

so that for all four modes according to Equations (17) and (26) the growth/damping rate is
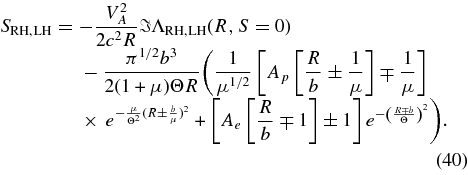
For isotropic (Ap = Ae = 1) plasma temperatures all four Alfvén modes are damped in agreement with Brinca's (1990) general theorem on the electromagnetic stability of isotropic plasma populations. The Alfvén damping rate in the isotropic case is given by
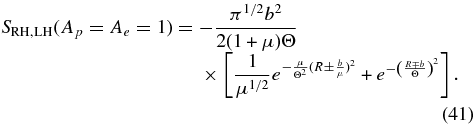
In order to drive the Alfvén modes unstable, the growth rate (40) has to be positive requiring that
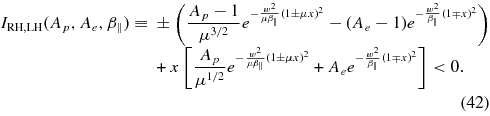
This instability condition is analyzed further in the next section.
4.2. LH-polarized Alfvén Proton Cyclotron and RH-polarized Alfvén Whistler Electron Cyclotron Branches for β∥ ≪ 1
Because we are primarily interested in low plasma beta plasmas for completeness we consider the solutions of the full dispersion relation (32) for subluminal solutions R ≪ 1 and small parallel plasma beta β∥ ≪ 1:
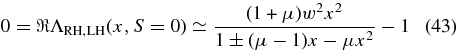
yielding the quadratic equation
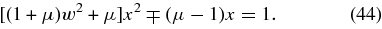
Because μ = 1836 ≫ 1 this equation is well approximated by
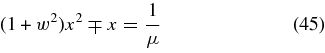
with the solutions
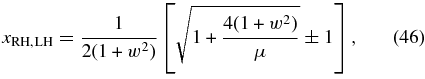
covering the well-known (e.g., Swanson 1989) LH-polarized Alfvén proton cyclotron and RH-polarized Alfvén Whistler electron cyclotron branches for parallel propagation, as the appropriate limits for small and large values of w demonstrate.
For 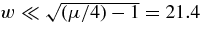 , corresponding to large wavenumbers k ≫ ωp,e/21.4c, we obtain
, corresponding to large wavenumbers k ≫ ωp,e/21.4c, we obtain
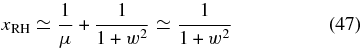
and
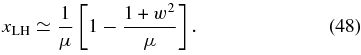
The solution (48), subject to the constraint (24), represents the LH-polarized proton cyclotron waves.
For values of w ≪ 1 the solution (47) represents the RH-polarized electron cyclotron waves subject to the constraint (25) with the dispersion relation

whereas for intermediate values 1 ≪ w ≪ 21.4 the solution (47) reduces to

representing the RH-polarized Whistler waves (R ≃ b/w2).
For large values of 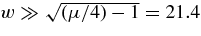 , corresponding to small wavenumbers k ≪ ωp,e/21.4c, we obtain for the solution (46)
, corresponding to small wavenumbers k ≪ ωp,e/21.4c, we obtain for the solution (46)
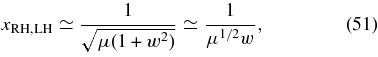
which agrees with the Alfvén wave solutions (37) in the limit β∥ ≪ 1.
Equation (43) for small plasma beta β∥ ≪ 1 also provides
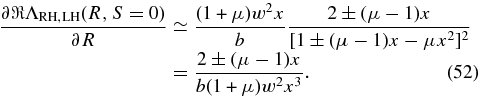
We note that for all solutions (47)–(51), Equation (52) is positive. According to Equations (17) and (26) the growth/damping rate then is
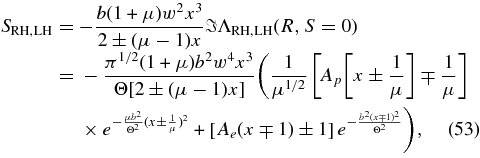
which generalizes the Alfvénic growth/damping rate (40) to non-Alfvénic modes. Apart from the different notation in phase speeds, the rate (53) agrees with Equation (7.1.8) of Gary (1993). For isotropic (Ap = Ae = 1) plasma temperatures all modes of the RH and LH branches, including the cyclotron and Whistler modes, are damped in agreement with Brinca's general theorem. We notice that, in order to drive the cyclotron and Whistler modes unstable, the growth rate (53) has to be positive, requiring again the earlier derived instability condition (42).
4.3. Electromagnetic Waves at Large Frequencies R ≫ b + Θ
For large frequencies R ≫ b + Θ the dispersion relation (31) reduces to
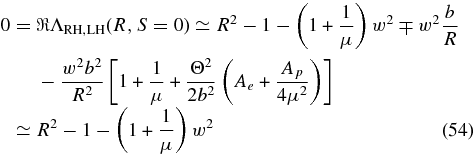
and
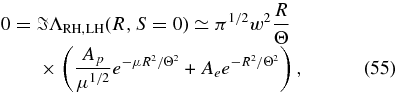
so that for both polarizations to lowest order in (b/R)2 we obtain the dispersion relation of electromagnetic waves
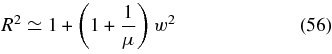
with the same damping rate
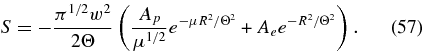
5. INSTABILITY CONDITIONS
In order to drive the LH-polarized Alfvén proton cyclotron and the RH-polarized Alfvén Whistler electron cyclotron branches unstable, the condition (42) has to be fulfilled which, after multiplication with μ3/4, reads
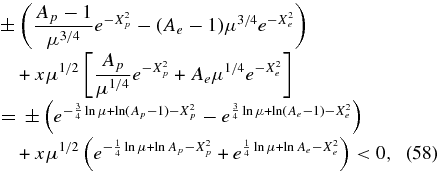
with
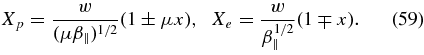
Both brackets in Equation (58) can be further reduced using the identities
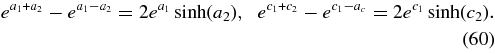
From the first bracket we identify
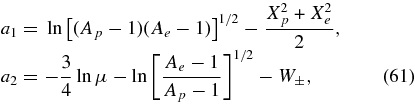
where
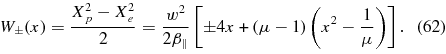
From the second bracket we determine
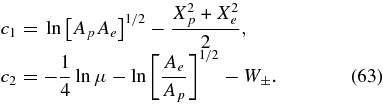
With sinh(−a2) = −sinh(a2) and cosh(−c2) = cosh(c2) condition (58) becomes

which yields the general instability condition for the two branches in the form
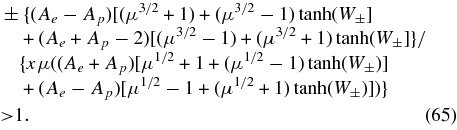
Inserting the general dispersion relation for small plasma betas (46) for x and W±(x) then provides the general instability conditions for the LH-polarized Alfvén proton cyclotron and the RH-polarized Alfvén Whistler electron cyclotron branches, which to the best of our knowledge has not been derived before.
For equal electron and proton temperature anisotropies (Ap = Ae = A0) the condition (65) reduces to
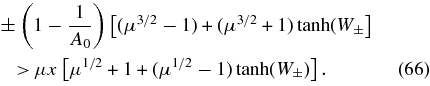
Note that for pair plasmas (μ = 1) the condition (66) reduces to Equation (S-66) in paper S.
Instead of working with the general dispersion relations (46) used in the general instability condition (65), we will discuss different ranges of the plasma frequency phase speed w, where the dispersion relations (46) reduce to simpler limits, as demonstrated in Section 4.2. For w ≫ 21.4 we can use the Alfvenic relation (51), whereas for small values of w ≪ 21.4 we can use the cyclotron and Whistler relations (48)–(50), respectively. We are particularly interested in applying our results to the solar wind observations of Bale et al. (2009), which, as we demonstrate in the next section, cover the phase speed range 90 ⩽ w ⩽ 330.
Before investigating the individual modes, we further inspect the instability condition (66). The instability conditions holds for plasma betas β∥ ≪ w2/μ, implying w2/2β∥ ≫ μ/2 = 918. Consequently, the argument of the tanh -function
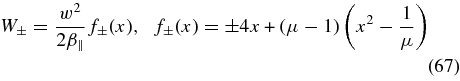
is much larger than unity for f±(x) ≫ 2/μ.
The function f+(x) increases monotonically from its smallest negative value f+(0) = −(1 − μ−1) = −0.9995 and becomes zero at
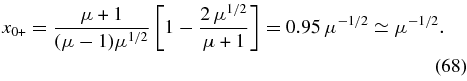
Likewise, the function f−(x) attains its negative minimum value −1.0016 at xE = 2/(μ-1) = 0.0011 and becomes zero at
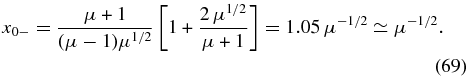
Hence, only for values of x = R/b inside a small interval around μ−1/2, which for RH-polarized fluctuations lies in the Whistler phase speed range, the functions f±(x) are smaller than 2/μ. Both functions are well approximated by
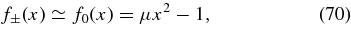
which is negative in the range of Alfvén and proton cyclotron waves and positive in the range of electron cyclotron waves, respectively.
6. OBSERVED SOLAR WIND FLUCTUATIONS
The solar wind magnetic fluctuations measured by Bale et al. (2009) near 1 AU have wavenumbers

with α = 0.56 ± 0.32 and the thermal proton gyroradius ρp = 4.23 × 106 T1/25B−14 cm, where we adopt an interplanetary magnetic field value B = 10−4 B4 G and a temperature T = 105 T5 K. With the solar wind particle density ne = 102n2 cm−3, we find that the plasma frequency phase speed (8)
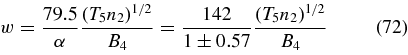
covers the interval

The electron gyrofrequency phase speed (9)
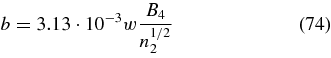
is indeed much smaller than the electron plasma frequency phase speed w justifying the high-density plasma approximation w ≫ b.
Because of the observed large value (72) of the plasma frequency phase speed only the LH- and RH-polarized Alfvén wave instabilities can operate in the w-interval (73). We therefore concentrate our analysis of the instability condition (66) on this case.
In terms of the proton plasma frequency phase speed

the Bale et al. (2009) measurements cover the interval
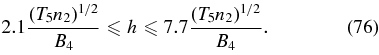
7. ALFVÉN WAVES
In the range of Alfvén waves x ≪ μ−1 the functions f±(x)≃ −1 are negative and practically constant, so that the instability condition (66) becomes
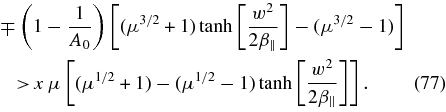
Because β∥ ≪ w2/μ the argument of the tanh -function
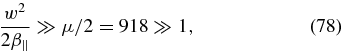
we approximate
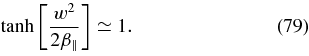
We then find for condition (77)
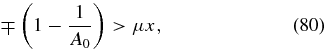
where the parallel plasma beta dependence and additional A0-dependences enter via the solution x(A0, β∥) of the dispersion relation (32).
For b ≪ w and Ap = Ae = A0 the dispersion relation (32) reads
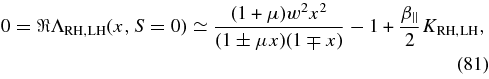
with
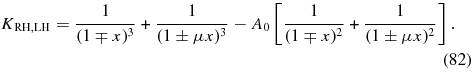
For x ≪ μ−1 we approximate KRH,LH ≃ 2(1 − A0) and
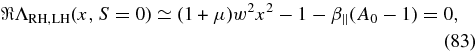
yielding the solution (37) and
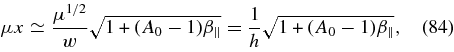
in terms of the proton plasma frequency phase speed (75).
7.1. LH-polarized Alfvén Waves
Inserting Equation (84), we obtain for the instability condition of LH-polarized Alfvén waves (80)
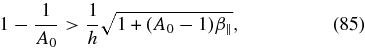
which can only be fulfilled for A0>1. Condition (85) is equivalent to

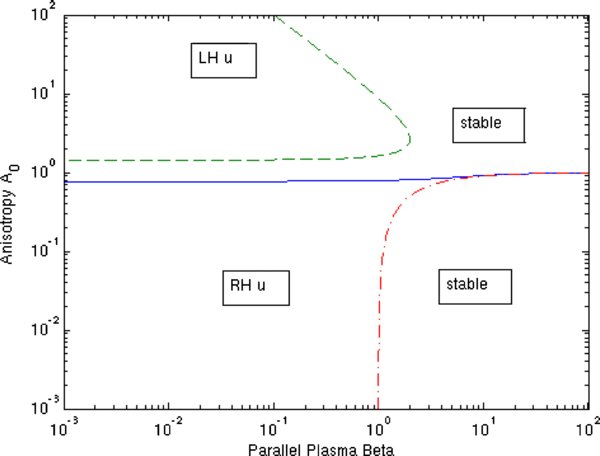
which is shown as the upper dashed curve in Figure 2 calculated for the value w = 142, corresponding to h = 3.3, representing the Bale et al. (2009) measurements.
Figure 2. Anisotropy diagram for LH (dashed curve) and RH (full curve) polarized Alfvén waves for the case of equal electron and proton temperature anisotropies Ae = Ap = A0 and w = 142, corresponding to h = 3.3. The dashed-dotted curve represents the existence condition (38) for Alfvén waves for A0 < 1. Stable and unstable (u) regions are marked.
Download figure:
Standard image High-resolution imageFor values of h>1 the limiting plasma beta value of condition (86) is zero for A0 = h/(h − 1) = 1.43 for h = 3.3. Substituting y = A0/(A0 − 1)>1 yields for the right-hand side of Equation (86)
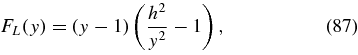
and for its first derivative
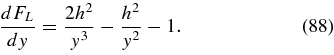
The function FL(y) exhibits one extreme value at yE = ht, where

yielding
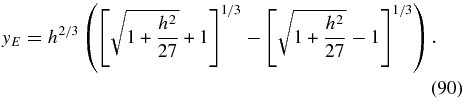
For the case h = 3.3 shown in Figure 2 we obtain yE = 1.61, corresponding to A0 = 2.64, and the maximum plasma beta Fmax = 1.95, which agree with the plot for LH-polarized Alfvén waves shown in Figure 2.
7.2. RH-polarized Alfvén Waves
Likewise, inserting Equation (84) we obtain for the instability condition of RH-polarized Alfvén waves (80)
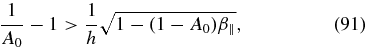
which can only be fulfilled for A0 < 1 and requires the existence condition (38) A0>1 − β−1∥. Condition (91) is equivalent to
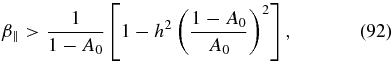
which is shown as the lower full curve in Figure 2 calculated for the value h = 3.3, representing the Bale et al. (2009) measurements.
The limiting plasma beta value of condition (92) is zero for A0 = h/(h + 1) = 0.77 for h = 3.3. Substituting y = A0/(1 − A0)>0 yields for the right-hand side of Equation (92)
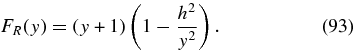
The first derivative
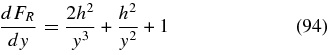
is positive for all values of y, so that the function FR(y) is monotonically increasing, in agreement with the plot for RH-polarized Alfvén waves shown in Figure 2.
The properties of the weakly amplified LH- and RH-polarized Alfvén mode are summarized in Tables 1 and 2, respectively.
Table 1. Properties of Weakly Amplified LH-polarized Alfvén Wave Mode
| Real phase speed range | R ≪ b/μ = wΘ/(μβ1/2∥) |
| Parallel plasma beta range | Θ2 ≪ β∥ ≪ h2 = w2/μ |
| Dispersion relation | 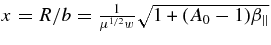 |
| Existence condition | w ≫ μ1/2 = 43 corresponding to h ≫ 1 |
| Instability conditions | A0>1 and ![$\beta _{\parallel }<{1\over A_0-1}\left[h^2\left({A_0-1\over A_0}\right)^2-1\right]$](https://content.cld.iop.org/journals/0004-637X/716/2/1596/revision1/apj345892ieqn11.gif) |
Download table as: ASCIITypeset image
Table 2. Properties of Weakly Amplified RH-polarized Alfvén Wave Mode
| Real phase speed range | R ≪ b/μ = wΘ/(μβ1/2∥) |
| Parallel plasma beta range | Θ2 ≪ β∥ ≪ h2 = w2/μ |
| Dispersion relation | 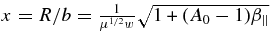 |
| Existence condition | w ≫ μ1/2 = 43 corresponding to h ≫ 1 |
| Instability conditions | A0 < 1 and ![$\beta _{\parallel }>{1\over 1-A_0}\left[1-h^2\left({1-A_0\over A_0}\right)^2\right]$](https://content.cld.iop.org/journals/0004-637X/716/2/1596/revision1/apj345892ieqn13.gif) |
Download table as: ASCIITypeset image
We emphasize that the Alfvenic instability threshold diagram shown in Figure 2 is controlled by a single observed plasma parameter: the proton plasma frequency phase speed h = w/μ1/2. The limiting anisotropy values for small plasma betas β∥ → 0 as well as the maximum plasma beta value for LH-polarized Alfvén waves (see Equation (90)) are fixed by the value of h.
8. PROTON CYCLOTRON WAVES
In the range of LH-polarized proton cyclotron waves x ⩽ μ−1 the functions f−(x) ≃ −1 are negative and practically constant, so that here the instability condition (80) also holds:

where again the parallel plasma beta dependence and additional A0-dependences enter via the solution x(A0, β∥) of the dispersion relation (81). Because x>0 the proton cyclotron instability condition (95) can only be fulfilled for A0>1.
Substituting s = 1 − μx, the condition (95) becomes

We now need solutions of the LH dispersion relation (83) for values of s ≪ 1 but, due to the constraint (24), much larger than s ≫ β1/2∥/h, i.e.,

Because of the smallness of s the LH dispersion relation (83) can be approximated as
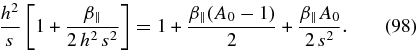
Because of the left inequality in Equation (97), we neglect the second term in the first bracket in Equation (98) to obtain
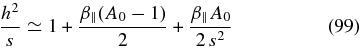
with the solution
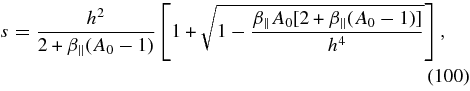
which in the limit β∥ → 0 correctly reproduces solution (48). This solution exists provided that
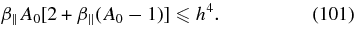
For β∥A0[2 + β∥(A0 − 1)] ≪ h4, which corresponds to the first constraint
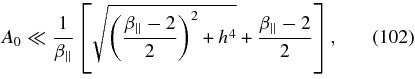
the solution (101) simplifies to

The restrictions (97) on s require two additional constraints
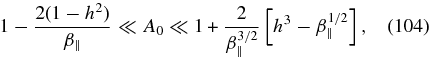
which requires β∥ ≪ h6. Then using the solution (103) we obtain for the instability condition (96)
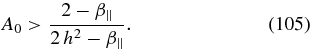
The requirement A0>1 then implies small proton plasma frequency phase speeds h < 1, and consequently also small values of β∥ < h6 ≪ 1. In this case, the left-hand side of the constraint (104) is negative and therefore automatically fulfilled. Its right-hand side yields

Moreover, Equations (102) and (105) simplify to
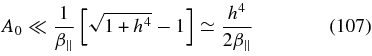
and
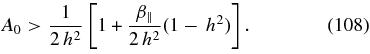
At plasma betas β∥ < h6 the constraint (106) is stronger than the constraint (107), so that we are left with
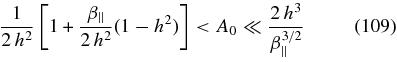
as instability conditions for proton cyclotron waves subject to h < 1 and β∥ < h6 < 1. The final conditions (109) are shown in Figure 3 for a value of h = 2−1/2. Because of the required small value h < 1 this instability cannot operate in the regime (76) observed by Bale et al. (2009).
Figure 3. Anisotropy diagram for LH-polarized proton cyclotron waves for the case of equal electron and proton temperature anisotropies Ae = Ap = A0. The unstable region below the full and above the dashed curve is marked. A value of h = 2−1/2 is adopted so that the results hold for parallel plasma beta values β∥ < h6 = 2−3 = 0.125.
Download figure:
Standard image High-resolution imageThe properties of the weakly amplified proton cyclotron mode are summarized in Table 3.
Table 3. Properties of Weakly Amplified LH-polarized proton Cyclotron Mode
| Real phase speed range | R ≪ b |
| Dispersion relation | ![$x=R/b={1\over \mu }[1-{2\,h^2\over 2+\beta _{\parallel }(A_0-1)}]$](https://content.cld.iop.org/journals/0004-637X/716/2/1596/revision1/apj345892ieqn14.gif) |
| Existence condition | h = w/μ1/2 < 1 |
| Parallel plasma beta range | Θ2 ≪ β∥ ≪ h6 |
| Instability conditions | ![$ {1\over 2\,h^2}\left[1+{\beta _{\parallel }\over 2\,h^2}(1-h^2)\right]<A_0\ll {2\,h^3\over \beta _{\parallel }^{3/2}}$](https://content.cld.iop.org/journals/0004-637X/716/2/1596/revision1/apj345892ieqn15.gif) |
Download table as: ASCIITypeset image
9. ELECTRON CYCLOTRON WAVES
In the range of electron cyclotron waves μ−1/2 ≪ x < 1 the function f+(x) ≃ μx2 ≫ 1 is positive and much larger than unity. The instability condition (66) together with W+ = w2f+(x)/(2β∥) = μw2x2/(2β∥) then becomes
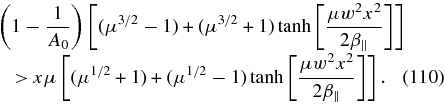
Again the argument of the tanh -function is very large compared to unity so that
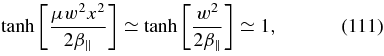
yielding for the instability condition (110)

where again the parallel plasma beta dependence and additional A0-dependences enter via the solution x(A0, β∥) of the dispersion relation (81). Because x < 1 the electron cyclotron instability condition (112) can only be fulfilled for A0>1.
Substituting y = 1 − x we need solutions of the RH dispersion relation (83) for values of y ≪ 1 but, due to the constraint (25), much larger than y ≫ β1/2∥/w, i.e.,

Because of the smallness of y the RH dispersion relation (83) can be approximated as
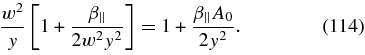
Because of the left inequality in Equation (113), we neglect the second term in the first bracket in Equation (114) to obtain

with the solution
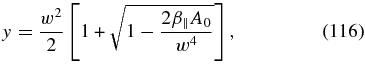
which in the limit β∥ → 0 correctly reproduces solution (49). This solution exists provided that

For

the solution (116) simplifies to
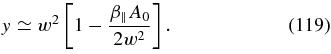
The restrictions (113) on s require w2 ≪ 1 and β∥ ≪ w8. Then using the solution (117) we obtain for the instability condition (112)
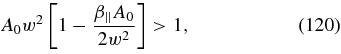
or with β∥ ≪ w6
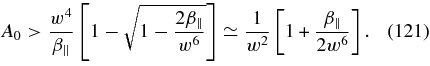
The dual instability requirements subject to w ≪ 1 and β∥ ≪ w6 ≪ 1
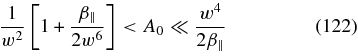
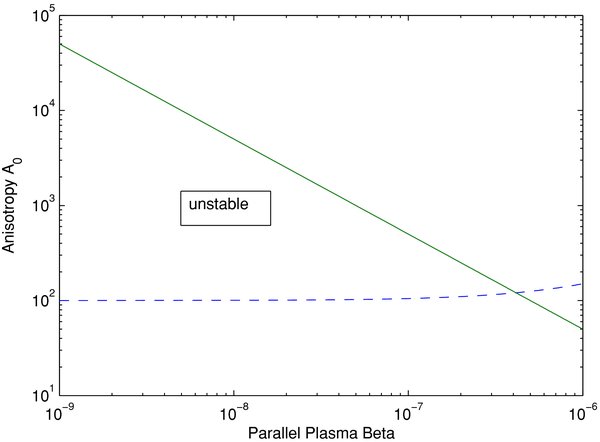
are shown in Figure 4 for a value of w = 0.1. Because of the required small value w ≪ 1 this instability cannot operate in the regime (72) observed by Bale et al. (2009).
Figure 4. Anisotropy diagram for RH-polarized electron cyclotron waves for the case of equal electron and proton temperature anisotropies Ae = Ap = A0. The unstable regions are marked. A value of w = 0.1 is adopted. The results hold for parallel plasma beta values below β∥ < w6 = 10−6.
Download figure:
Standard image High-resolution imageThe properties of the weakly amplified RH-polarized electron cyclotron modes are summarized in Table 4.
Table 4. Properties of Weakly Amplified RH-polarized Electron Cyclotron Mode
| Real phase speed range | bμ−1/2 ≪ R ≪ b |
| Dispersion relation | ![$x=R/b=1-w^2\left[1-{\beta _{\parallel }A_0\over 2w^2}\right]$](https://content.cld.iop.org/journals/0004-637X/716/2/1596/revision1/apj345892ieqn16.gif) |
| Existence condition | w ≪ 1 |
| Parallel plasma beta range | Θ2 ≪ β∥ ≪ w6 |
| Instability condition | ![$ {1\over w^2}\left[1+{\beta _{\parallel }\over 2w^6}\right]<A_0\ll {w^4\over 2\beta _{\parallel }}$](https://content.cld.iop.org/journals/0004-637X/716/2/1596/revision1/apj345892ieqn17.gif) |
Download table as: ASCIITypeset image
10. SUMMARY AND CONCLUSIONS
We rigorously studied the dispersion relations of weakly amplified fluctuations with wavevectors 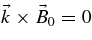 in an anisotropic bi-Maxwellian magnetized proton–electron plasma by the appropriate Taylor expansion of the plasma dispersion function. Apparently for the first time, for equal parallel electron and proton temperatures, a general analytical instability condition (65) is derived that holds for different values of the electron (Ae) and proton (Ap) temperature anisotropies. We determine the conditions for which the weakly amplified LH-polarized Alfvén proton cyclotron and RH-polarized Alfvén Whistler electron cyclotron branches can be excited. For different regimes of the electron plasma frequency phase speed w = ωp,e/(kc) these branches reduce to the RH- and LH-polarized Alfvén waves, RH-polarized proton, and LH-polarized electron cyclotron modes. The properties of the individual modes are summarized in Tables 1–4. Analytic instability threshold conditions are derived in terms of the combined temperature anisotropy A = T⊥/T∥, the parallel plasma beta β∥ = 8 π nekBT∥/B2 and the electron plasma frequency phase speed w = ωp,e/(kc) for each mode.
in an anisotropic bi-Maxwellian magnetized proton–electron plasma by the appropriate Taylor expansion of the plasma dispersion function. Apparently for the first time, for equal parallel electron and proton temperatures, a general analytical instability condition (65) is derived that holds for different values of the electron (Ae) and proton (Ap) temperature anisotropies. We determine the conditions for which the weakly amplified LH-polarized Alfvén proton cyclotron and RH-polarized Alfvén Whistler electron cyclotron branches can be excited. For different regimes of the electron plasma frequency phase speed w = ωp,e/(kc) these branches reduce to the RH- and LH-polarized Alfvén waves, RH-polarized proton, and LH-polarized electron cyclotron modes. The properties of the individual modes are summarized in Tables 1–4. Analytic instability threshold conditions are derived in terms of the combined temperature anisotropy A = T⊥/T∥, the parallel plasma beta β∥ = 8 π nekBT∥/B2 and the electron plasma frequency phase speed w = ωp,e/(kc) for each mode.
For large values of w ≫ 21.4, corresponding to small wavenumbers k ≪ ωp,e/21.4 c, RH- and LH-polarized Alfvén waves are excited in different regions of the temperature anisotropy (A) versus parallel plasma beta (β∥) parameter plane. For appropriate temperature anisotropies, RH-polarized low and high phase speed Whistler waves are excited for intermediate values of 6.5 ≪ w ≪ 21.4 and 1 ≪ w ≪ 6.5, respectively. At values w ≪ 21.4 LH-polarized proton cyclotron waves can be excited, whereas RH-polarized electron cyclotron waves can be excited at small values of w ⩽ 1. In agreement with Brinca's (1990) general theorem on the electromagnetic stability of isotropic plasma populations none of these modes can be excited for isotropic plasma distributions (Ae = Ap = 1).
We apply the results of our instability study to the observed solar wind magnetic turbulence (Bale et al. 2009), corresponding to values of 90 ⩽ w ⩽ 330. According to the existence conditions of the different instabilities, only the LH and RH-polarized Alfvén wave instabilities can operate here. The Alfvénic instability threshold conditions are controlled by a single observed plasma parameter: the proton plasma frequency phase speed h = w/μ1/2. All asymptotic and characteristic values of the threshold anisotropies and the characteristic plasma beta values are solely determined by the value of h. The Alfvénic instability diagram explains well the observed confinement limits at small parallel plasma beta values in the solar wind. It remains to be investigated in future work how weakly propagating and/or obliquely propagating weakly amplified modes add to this diagram.
This work was supported by the Deutsche Forschungsgemeinschaft through grants Schl 201/19-1 and Schl 201/21-1.