ABSTRACT
The study of the origin of irregular satellites remains important in planetary science because it provides constraints on the formation process of giant planets and probes the properties of a now-extinct planetesimal disk that existed at 5-30 AU early in solar system history. While several putative scenarios of irregular-satellite capture around giant planets have been developed, various uncertainties and the lack of an accurate model of the evolutionary history of the solar system usually prevent an assessment of their overall likelihood. Here we study a three-body interaction scenario in which irregular satellites are formed by dissociation of a planetesimal binary in the gravity field of a planet. Within the frame of the Nice model, we determine how many irregular satellites are expected to be formed about each of the giant planets. We pay special attention to a possible capture of Triton via this mechanism. We find that Triton could have been captured via a binary dissociation very soon after Neptune's formation when the planetesimal disk was still dynamically cold. Triton was most likely captured by a dissociation of a binary system where the more massive component was ∼2–5 times heavier than Triton. Our results suggest that Neptune, the formation of Triton's binary, and the capture of Triton around Neptune all occurred within the first ∼5–10 Myr of solar system formation when the gas disk was still present. This would rule out the late formation of ice giants. Our results also indicate that binary dissociation is a highly unlikely process for the origin of small irregular satellites for two reasons. First, the orbital distribution of the captured bodies is inconsistent with that of the observed irregular satellites. Second, the efficiency of the captures is too low to explain the numerous populations of small irregular satellites.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The irregular satellites of giant planets are an important part of the solar system inventory. Their orbital and physical characteristics constrain the evolutionary processes in the early solar system, especially those related to planet formation and their interaction with the residual disk of planetesimals. Various hypotheses of irregular-satellite origin have been discussed in several recent reviews—e.g., Jewitt & Sheppard (2004), Jewitt et al. (2004), Nicholson et al. (2007), or Jewitt & Haghighipour (2007). The origin of Triton, in particular, has recently been addressed in Ćuk & Gladman (2005) and Agnor & Hamilton (2006).
Nicholson et al. (2007) argued that classical capture scenarios for irregular satellites, such as planetesimal collision in the Hill sphere of a planet, capture by aerodynamic drag in an extended gaseous envelope, or sudden growth of the planetary Hill sphere due to rapid mass increase associated with collapsing envelope, all have problems explaining various aspects of the observations. The purely dynamical capture mechanisms that require at least three participating bodies (not including the Sun) seem to offer more promising explanations. In principle, there are two possibilities: (i) planetary encounter with a binary planetesimal that is followed by exchange reaction with one component of the original binary ending on a planet-bound orbit, and (ii) planet–planet close encounter stirring the surrounding disk of planetesimals that might lead to their transfer into planet-bound orbits. The former possibility has long been studied in astrophysics of dense stellar populations, and was only recently applied in planetary science (e.g., Morbidelli & Levison 2004; Agnor & Hamilton 2006). The latter, appropriate to a particular phase of the planetary evolution within the Nice model (see below), has been recently proposed by Nesvorný et al. (2007). In this work we focus on mechanism (i).
Agnor & Hamilton (2006) developed analytic arguments and performed numerical simulations of the model in which Triton is captured by a dissociation of a binary planetesimal in the gravitational field of Neptune. While identifying the true capability of this process, these authors used values of encounter parameters that favor capture. They have not, however, determined how frequent such favorable encounter parameters occur. Therefore, Agnor & Hamilton have not been able to estimate the overall probability of Triton's capture by the proposed process. This prevents a direct comparison with other, possibly competing, mechanisms such as (ii) described above (Nesvorný et al. 2007).
In this paper we develop a self-consistent model of Triton's capture by exchange reactions described in (i). This not only includes considerations of the capture dynamics, but also takes into account the context of the mechanism, namely the precise state of the source population in the planetesimal disk (such as its size distribution, encounter speeds and geometry of the planetesimals approaching planets). This detailed method allows us to estimate the efficiency of the capture process at various stages of planet formation and evolution.
To accomplish the above task, we need to assume something about the early evolution of the solar system. For this we adopt the Nice model (Tsiganis et al. 2005; Morbidelli et al. 2005; Gomes et al. 2005), a new scenario for building the final architecture of the solar system. While not addressing the earliest phase of formation of the giant planets, the Nice model postulates that these planets form in a compact system with four giant planets located between 5 and 18 AU from the Sun. According to the Nice model, the early formation phase left these planets on nearly circular and coplanar orbits in a region largely devoid of planetesimals. A cold disk of planetesimals occupied a zone outside the giant planets up to about ∼30–35 AU, where it had an edge beyond which the accumulation of material into sizable bodies was presumably inefficient or otherwise prevented (see also Levison & Morbidelli 2003). The total initial mass of the disk is not known accurately, but is estimated to be ∼30–50 Earth masses (e.g., Gomes et al. 2005). Planetary gravitational perturbations produced a slow decay of the disk by occasionally releasing some of its planetesimals onto high-eccentricity, planet-crossing orbits. These objects then strongly interacted with the giant planets during close encounters and eventually were ejected from the solar system. In response, giant planets slowly migrated from their initial positions: Jupiter moved inward, while Saturn, Uranus, and Neptune moved outward.
A specific feature of the Nice model is the critical role of Jupiter's and Saturn's passage through their mutual 2/1 mean motion resonance (Tsiganis et al. 2005). During this passage, both gas giants acquired elevated eccentricities and Saturn, residing on a more eccentric orbit, triggered the orbital instability of Uranus and Neptune by its close approaches to these planets. The ice giants were thrown onto mutually-crossing high-eccentricity orbits and deeply penetrated the planetesimal disk. This phase left important fingerprints in solar system history and structure: Gomes et al. (2005) associated a high flux of planetesimals from a destabilized disk with the late heavy bombardment (LHB) of the terrestrial planets and the Moon (e.g., Hartmann et al. 2000; Ryder et al. 2000), while Morbidelli et al. (2005) demonstrated that part of the fleeing disk particles may have produced Jupiter's Trojans with the required orbital characteristics. The association with LHB makes the Jupiter and Saturn passage through the mutual 2/1 resonance constrained in time to ∼0.6–0.7 Gyr after the origin of the solar system. Note that this link to LHB, however, is not logically required by other parts of the Nice model. To make this element clear, we shall speak about the planet-crossing (PC) phase of the Nice model when referring to the period of time when planets were mutually crossing their orbits. Upon leaving the chaotic PC epoch, interaction with the already depleted planetesimal disk made Uranus's and Neptune's orbits migrate outward and reach their final positions at 19.5 AU and 30 AU, respectively. Because of the unpredictable nature of the planetary orbit crossing phase, Uranus's and Neptune's orbits and the magnitude of their residual migration may have varied greatly immediately after this phase. We shall describe and discuss various possibilities in Section 2.1.
In this work, we model the capture of irregular satellites, and Triton specifically, by dissociation of the binary planetesimals after the planets stopped crossing each other within the Nice model. Nesvorný et al. (2007) have shown that any population of irregular satellites captured prior to the PC phase in the Nice model becomes largely depleted by the violent effects of planetary encounters (except, perhaps, at Jupiter). This means the capture mechanism via exchange reactions before the PC phase would have to be extremely efficient to dominate the population created in the post-PC phase (studied here). In Section 4 we argue that this is unlikely. This argument does not apply to Triton, whose orbit may have been circularized close to Neptune prior to the PC phase and was probably immune to mutual planetary perturbations. While understanding Triton's origin is a basic motivation of our work, we also pay separate attention to the efficiency of capture of the overall population of the small irregular satellites by the binary dissociation mechanism.
Section 2 describes our assumptions and numerical model. Results are summarized in Section 3, and their implications are discussed in Section 4.
2. MODEL
Our numerical model consists of three parts: (i) we model the migration of planets within a diluted planetesimal disk during the post-PC phase, (ii) we model the detailed dynamics of exchange reactions, and (iii) we estimate the captured satellite population by a combination of processes (i) and (ii). The last step is done by scaling the assumed initial mass of the disk present in the planetary migration runs and the planetesimal size distribution function. Each of these steps is described in the following sections.
2.1. Selected Migration Runs
Gomes et al. (2005) proposed a new planetary-orbit evolution model to explain LHB (PC phase in our context). Because their numerical simulation contained a planetesimal disk of a limited number of objects, Nesvorný et al. (2007) improved resolution by cloning planetesimals at about 20 Myr before Jupiter and Saturn entered mutual 2/1 mean motion resonance. The starting data of Nesvorný et al. (2007) contained 6868 planetesimal particles, each of ∼1.6 Pluto mass. The advantage of this initial data modification was twofold: (i) the more massive particles in the original disk of Gomes et al. could produce an unrealistically granulated planet migration, and (ii) a variety of planetary migration scenarios can be studied by using different disk clones. It is important to verify the dependence of results on (ii). Our starting orbits of outer planets are those of Nesvorný et al. (2007) and correspond to the situation described by Gomes et al. about 20 Myr before PC: namely, they are near-circular and coplanar at 5.4, 8.4, 12.3, and 18.0 AU (terrestrial planets were not included in our work).
These initial data were propagated using a symplectic integrator SyMBA (Duncan et al. 1998). SyMBA is an efficient numerical integrator that can handle close encounters between massive bodies. While all particles are assumed to be massive in the simulation, only the planets gravitationally interact with each other and gravitationally influence planetesimal disk particles. Planetesimals gravitationally interact with planets, making them migrate, but the code neglects mutual gravitational effects between the planetesimals themselves.
Using 50 initial disk variants, Nesvorný et al. (2007) obtained 14 cases of plausible planetary evolution, each resulting in a solar system architecture approximately matching the current state. Here we selected seven of them and integrated the orbital evolution following the planet-crossing phase of the Nice model (Tsiganis et al. 2005; we used those that best matched the final architecture of the solar system). During this phase, planets no longer undergo close approaches with each other, but slowly migrate to attain their final positions. In each of the selected simulations we recorded parameters of close planetesimal flybys of the planets during a control interval of 100 Myr during this post-PC phase. We believe this time interval is representative enough to characterize such encounters and still be amenable to our computer power (in Section 4 we argue how our results could be extrapolated to later periods of the solar system evolution). In particular, we recorded data for every approach when a planetesimal entered the planetary Hill sphere. At the instant of the closest approach to the planet, we used the relative position and velocity of the planetesimal with respect to the planet to compute three parameters of the hyperbolic-flyby approximation: (i) the orbital pericenter q with respect to the planet, (ii) the velocity of the planetary approach at infinity V∞, and (iii) the inclination of the hyperbolic plane with respect to the ecliptic. This latter parameter was found to be isotropic in space. For purposes of scaling our simulations to the real number of planetesimals in the disk, we also recorded the initial number of disk particles NTP after planets stopped crossing their orbits and the total number of planetesimal encounters Nenc with each of the planets.
Table 1 provides NTP and Nenc values for each of our seven runs (note NTP is different in each of the runs because it gives the number of particles at the moment when planets stopped crossing their orbits). The class designations DE and MA in Table 1 denote the type of planetary evolution defined in Nesvorný et al. (2007): (i) DE stands for "direct emplacement" indicating that both Uranus and Neptune attained their near-final orbits nearly at the end of the mutual-orbit crossing phase, while (ii) MA stands for "Malhotra-class evolution," indicating the post-PC planetary system was still considerably compact and Uranus and Neptune underwent significant migration evolution, similar to that originally proposed by Malhotra (1995) and Hahn & Malhotra (1999). Note, however, that Malhotra (1995) started her planetary migration simulations with zero eccentricity and inclination orbits of both planets and planetesimals in the disk, while in our MA class the orbits have large eccentricity and inclination values after the planet crossing phase. Job no. 4 is somewhat in between these two classes and we designate it MA/DE. Following Tsiganis et al. (2005), we favor DE-type migrations, because MA-type migrations nearly always result in an unrealistic damping of Uranus's and Saturn's orbital eccentricity. For the sake of comparison, though, we keep two MA-type migrations among our selected cases (runs 2 and 7).
Table 1. Parameters of the Selected Planetary Migration Simulations
| Run | Type | NTP | Nenc | |||
|---|---|---|---|---|---|---|
| Jupiter | Saturn | Uranus | Neptune | |||
| 1 | DE | 3583 | 34,582 | 48,143 | 329,971 | 615,985 |
| 2 | MA | 5272 | 83,853 | 95,333 | 461,331 | 782,254 |
| 3 | DE | 3688 | 43,114 | 51,704 | 295,319 | 727,815 |
| 4 | MA/DE | 3816 | 58,540 | 66,131 | 376,177 | 828,050 |
| 5 | DE | 3081 | 33,091 | 43,682 | 233,541 | 522,698 |
| 6 | DE | 3743 | 43,958 | 64,038 | 616,855 | 785,605 |
| 7 | MA | 4600 | 70,421 | 81,706 | 421,333 | 935,985 |
Notes. The second column indicates migration class: DE for direct emplacement scenario of Uranus and Neptune, MA for Malhotra-class scenario of Uranus and Neptune orbital evolution (see the main text for a definition of these migration classes). The third column gives the number of planetesimals left in our simulation after the planet-crossing (post-PC) phase. The next four columns give the total number of planetesimal encounters with planets during the 100 Myr of the post-PC phase.
Download table as: ASCIITypeset image
Figure 1 shows planetary-orbit evolution for two of our simulations (runs 1 and 2). The 100 Myr test interval over which we recorded planetesimal flybys near the migrating planets is denoted by the black arrows. The bottom panel, corresponding to MA-type run 2, indicates that Uranus's eccentricity became effectively zero, in contrast to the currently observed value.
Figure 1. Two cases of migration of major planets: Jupiter (red), Saturn (green), Uranus (blue), and Neptune (purple). The top figure shows results for run 1, the bottom figure shows results for run 2 (see Table 1). A planet-crossing phase occurs at ∼20 Myr in both simulations. The solid lines show the semimajor axes of the planets, the thin lines show their perihelion and aphelion distances, respectively. The black arrows indicate the 100 Myr time interval where we recorded the parameters of the planetesimal encounters to the planets.
Download figure:
Standard image High-resolution imageFigure 2 shows the evolution of the planetesimal disk mass in runs 1 and 2 from the previous figure, as well as the time-resolved number of planetesimal flybys near the four planets (note the initial disk mass before PC phase was ∼25 Earth masses). In both cases, the disk mass dropped by ∼65% during the post-PC interval of 100 Myr; this is because the majority of particles have been swept out of the solar system by encounters with Jupiter, or placed in outer solar system structures, such as the Oort cloud or the scattered disk, by encounters with Jupiter and other planets. As expected, the number of planetary encounters decreases in time roughly proportionally to the overall disk-mass decay. Some fine structures, such as a drop of Uranus encounters in run 1 at about 10 Myr, can be explained by a closer analysis of the simulations. In this case, the decrease of Uranus's eccentricity (Figure 1) decoupled this planet from the denser outer parts of the planetesimal disk.
Figure 2. Time-resolved evolution of the planetesimal disk and the number of planetesimal encounters by the planets in the two simulations from Figure 1 (the top panel is for run 1, the bottom panel is for run 2; see Table 1 and Figure 1). Time in these plots starts at the instant denoted by the first black arrow in Figure 1, i.e., when we started to record parameters of the planetesimal flybys near the planets. The upper bold black curve and the right ordinate shows the time decay of the planetesimal disk mass (in Earth masses). The thin histograms and the left ordinate show the number of planetesimal encounters with the planets in the running 1 Myr window: J stands for Jupiter, S for Saturn, U for Uranus, and N for Neptune.
Download figure:
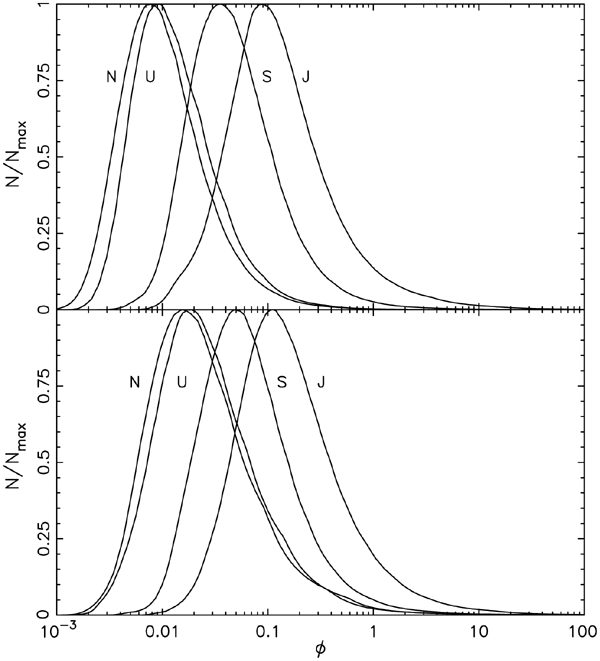
Standard image High-resolution imageFigure 3 shows the distribution of the recorded values of q and V∞ for all planets in two runs 1 and 2. While the overall results are broadly similar in the two cases, there are small differences such as systematically slightly lower encounter speeds V∞ in the MA-type run (run 2). For instance, the distribution maximum of V∞ in the case of Neptune occurs at ∼3 km s−1 (run 1) and ∼2 km s−1 (run 2). The maximum shifts to larger values of V∞ for interior giant planets, up to ∼6 km s−1 (run 1) and ∼5 km s−1 (run 2) for Jupiter. These rather high velocities are due to the fact that the planetesimal disk is highly excited during the post-PC phase within the Nice model (see, e.g., Figure 3 in Nesvorný et al. 2007). Note that small relative velocities (with respect to the planets) that are generally favorable for irregular capture by exchange reactions (e.g., Agnor & Hamilton 2006 assumed encounter speeds ⩽0.5 km s−1) occur for only a very small fraction of recorded flybys.
Figure 3. During migration the disk planetesimals encounter planets on near-hyperbolic orbits centered in the respective planet. The left panels show the distribution of pericenter value q and the right panels show the distribution of encounter velocity at infinity V∞ (note the normalization of each incremental distribution to unity). Labels along the solid lines indicate the planet: J stands for Jupiter, S for Saturn, U for Uranus, and N for Neptune. The top panels show the results for run 1 and the bottom panels show the results for run 2 (see Table 1 and Figure 1).
Download figure:
Standard image High-resolution imageThe distribution of planetocentric pericenter values q is nearly linear up to the Hill radius, with only small variations at the largest values due to details of the migration run (Figure 3). For instance, the drop at ∼0.5 AU for Uranus in run 1 is due to the decrease of the orbital eccentricity at ∼10 Myr (Figure 1) and the lack of interaction with denser regions of the planetesimal disk. Similarly, the decrease of q-distribution for Neptune after ∼0.55 AU in run 2 reflects the variations of the instantaneous Hill radius at different heliocentric distances during the migration of this planet.
The capability to dissociate a given binary planetesimal system is determined mainly by q and V∞. In particular, it is easy to show that the efficiency of exchange reaction is directly related to the quantity ϕ = GM'/(qV2∞), where M' is the mass of the planet (e.g., Agnor & Hamilton 2006). In analytic estimations by Agnor & Hamilton the other two fundamental parameters are q itself and ψ = (M/M')(q/aB); M is the total mass of the binary system and aB is the pre-encounter semimajor axis of the binary orbit (assumed circular). Note that the exchange reaction only weakly depends on the mass ratio of the binary components. We postpone the analysis of ψ to later sections, because ψ depends on additional parameters in the model such as the distribution of aB.
The distributions of q and V∞ characterizing planetary encounters in our migration runs are independent and determined from our migration runs. This makes it easy to construct the expected distribution of ϕ in our model for different planets. Results are shown in Figure 4 for migration runs 1 and 2. The higher the ϕ value is, the higher the planet-intrinsic capability to dissolve the binary.3 Despite systematically larger relative velocities V∞ (Figure 3), we note that Jupiter has about an order of magnitude larger ϕ values. This is due to the larger mass of the planet and the statistically smaller q for planetesimals encountering Jupiter. In the overall statistics of the expected population of irregular satellites created by this mechanism, the larger ϕ values of Jupiter will be compensated by a much smaller number of encounters Nenc (Table 1 and Section 3). It is worth noting that Agnor & Hamilton (2006) only considered encounters with values of ϕ larger than unity in their model of Triton's capture. Figure 4 indicates such values are rarely attained in the post-PC phase.
Figure 4. Distribution of ϕ = GM'/(qV2∞) for planetesimals encountering migrating planets in our simulation runs 1 (top) and 2 (bottom): J stands for Jupiter, S for Saturn, U for Uranus, and N for Neptune.
Download figure:
Standard image High-resolution image2.2. Planetesimal Capture Simulation
Having characterized the planetary migration and encounters within the planetesimal disk, we now describe our approach to modeling the dissociation of binary systems. To handle this problem we constructed a numerical code that propagates a binary system during its approach to a planet and monitors the resulting configuration of the three bodies. In this part of our work we use the three-body problem (planet-binary), neglecting the gravitational tidal field of the Sun in the planet's vicinity. We use a high-accuracy Burlish–Stoer integrator with automatically controlled absolute error (e.g., Press et al. 1992). The initial conditions and model parameters are specified as follows.
- 1.We assume that the two components in the binary system have initially a circular orbit. The orbital plane is chosen to be random in space, while the distribution of their separation, aB, is given by dN ∝ daB/a2B. This distribution corresponds to an uniform distribution of binding energies. We note that compact systems, which favor binary dissociation followed by a satellite capture, are preferred in this way. The minimum and maximum values of aB are set so that (i) the most compact systems correspond to the Roche distance of bodies with a bulk density of 2 g cm−3 (e.g., Bertotti et al. 2003, p. 436), and (ii) the most distant systems are at 0.3 of the Hill radius with respect to the solar tidal forces. The nodal positions of the orbital plane of the binary components relative motion in space are chosen randomly.
- 2.The barycenter of the binary system is initially assumed to approach the planet along a hyperbolic orbit with an isotropic distribution of incoming directions, and q and V∞ parameters are assumed to have distributions identical to those from our migration runs (see, e.g., Figure 3).
- 3.Each simulation uses fixed values of the total mass of the binary system, M, and of the secondary-to-primary mass ratio, μ. In this respect, we consider two different cases for which we conduct two different sets of simulations:
- (a)Origin of numerous populations of small irregular satellites with sizes ≲100 km (note only a few of them are larger than this limit); we probe the capture efficiency by assuming μ = 0 and M spans a large interval of values, such that the secondary component is always massless and the primary component has various values of mass (see Table 2); and
- (b)Origin of Triton such that one of the binary components has a mass of Triton, that sets a minimum value of M ∼ 1.64 Pluto masses, while the second component has again a spectrum of masses from zero to large values (see Table 3).
Table 2. Size Bins Used in Our Simulations of Capture of Small Irregular Satellites
| Bin No. | Dl (km) | Dr (km) | Deff (km) | M (Pluto mass) | Ntrials |
|---|---|---|---|---|---|
| 1 | 50 | 97 | 80.5 | 4.18 × 10−5 | 5 × 1010 |
| 2 | 97 | 188 | 160.0 | 3.04 × 10−4 | 5 × 1010 |
| 3 | 188 | 365 | 302.7 | 2.22 × 10−3 | 5 × 1010 |
| 4 | 365 | 707 | 586.5 | 1.62 × 10−2 | 2.5 × 1010 |
| 5 | 707 | 1371 | 1137.2 | 1.18 × 10−1 | 2.5 × 1010 |
| 6 | 1371 | 2660 | 2206.3 | 8.62 × 10−1 | 1.25 × 1010 |
| 7 | 2660 | 5156 | 4277.0 | 6.28 × 100 | 1.25 × 1010 |
| 8 | 5156 | 10,000 | 8294.7 | 4.58 × 101 | 1.25 × 1010 |
Notes. The second and third columns give the size interval of the considered bin. The fourth column is the effective size of planetesimals used in our simulation (see the main text). The fifth column lists the corresponding mass, given in units of Pluto mass, assuming a bulk density of 2 g cm−3. The last column shows the number of trials Ntrials used in our binary dissociation simulations.
Download table as: ASCIITypeset image
Table 3. Size Bins Used in Our Simulations of Triton's Capture
| Bin No. | Dl (km) | Dr (km) | Deff (km) | M (Pluto mass) | μ |
|---|---|---|---|---|---|
| 1 | 2700 | 3130 | 2931 | 2.02 | 0.2319 |
| 2 | 3130 | 3640 | 3404 | 3.17 | 0.9304 |
| 3 | 3640 | 4220 | 3951 | 4.95 | 0.4953 |
| 4 | 4220 | 4900 | 4585 | 7.74 | 0.2690 |
| 5 | 4900 | 5690 | 5324 | 12.11 | 0.1527 |
| 6 | 5690 | 6600 | 6179 | 18.93 | 0.0949 |
| 7 | 6600 | 7670 | 7175 | 29.64 | 0.0586 |
| 8 | 7670 | 8900 | 8330 | 46.39 | 0.0366 |
| 9 | 8900 | 10,330 | 9668 | 72.51 | 0.0231 |
| 10 | 10,330 | 12,000 | 11,227 | 113.56 | 0.0147 |
Notes. The second and third columns give the size interval of the considered bin. The fourth column is the effective size of planetesimals used in our simulations. The fifth column is its mass, in units of Pluto's mass, assuming a bulk density of 2 g cm−3; this is the total mass of the binary system. The last column gives the ratio of the secondary to primary mass in the binary system; one component is always Triton with 1.64 Pluto masses. In the first two bins Triton is the primary component, otherwise it is the secondary component. In all cases we performed Ntrial = 2.5 × 1010 trial simulations.
Download table as: ASCIITypeset image
We note that the energy and angular momentum excess of the incoming pair of planetesimals, which needs to be overcome to transfer one of the components onto an orbit bound to the planet, depends on the total mass M of the binary, while it is basically independent of their mass ratio μ. Dependence on this latter parameter may start to play a role in a statistically very infrequent case of q comparable to or smaller than aB (note, moreover, that for low-mass binaries, aB is much smaller than the planetocentric distance of regular satellites). As a result, our first set of simulations with a massless secondary (μ = 0) are basically valid for an arbitrary mass ratio. This is important because observations so far indicate that trans-Neptunian binaries have components of comparable mass (or typically within an order of magnitude; e.g., Noll et al. 2007). To verify our conclusions, we also performed a series of simulations for run 1 (Section 3.1) with equal binary components (μ = 0.5) of sizes ranging from 10 to 100 km. None of them provided any captured satellite, even with a large number (1015) of trials. This is consistent with the results of μ = 0 binaries reported below.
In practice, we start our integration at distance 1.5 AU from the planet and compute the state vector of an hyperbolic orbit with respect the planet. This sets the location and speed of the binary's center-of-mass. The motion of the planet and the two components of the binary system are then numerically propagated through the encounter until the planetocentric distance of any of the components reaches a distance of 1.5 AU again. We then determine the relative state vectors of the primary and secondary components with respect to the planet and check if any of them is on a planet-bound orbit. If so, we record its Keplerian orbital elements with respect to the planet.
We conducted the analysis of satellite capture for each of the four giant planets and for each of the selected migration runs listed in Table 1. In each case we performed a large number of trial simulations, Ntrials, changing randomly (but respecting determined distributions) the initial parameters: q, V∞, aB, and angular variables. Each simulation assumed fixed values for M and μ.
The efficiency of satellite capture from low-mass binaries is expected to be very low (e.g., Agnor & Hamilton 2006). On the other hand, these systems may be more abundant in the disk than high-mass binaries due to the steep size distribution. Therefore, we must perform a large number of trial runs. We used Ntrials ≳ 1010 in each simulation. To cope with such a huge number of numerical integrations, we adopt an additional filter and integrate only those configurations that satisfy
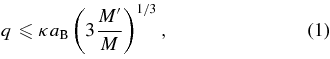
where the coefficient κ is of the order of unity. The condition in Equation (1) means the binary system is at the Hill stability limit when passing through the pericenter q of its orbit relative to the planet. The coefficient κ>1 is a safety parameter. In our simulations we chose κ = 1.5, except for those of Triton capture, where we set κ = 2.5. All trial cases that violate Equation (1) are not integrated and are assumed to fail in producing satellites. They count, however, toward the overall statistics. Using a limited number of simulations, we have verified that cases violating Equation (1) do not really produce captured satellites. Additionally, in all runs we verified that captured orbits have q well below the critical limit 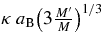 from the right-hand side of Equation (1) for the κ value used.
from the right-hand side of Equation (1) for the κ value used.
The orbital parameters of captured objects recorded by our code are their initial osculating elements. To estimate the long-term stability of these orbits and/or perform comparison with the observed population of irregular satellites, we would ideally need to perform a full-fledged integration of their subsequent evolution. With our large number of trial cases, however, we obtain tens to hundreds of thousands of irregular satellite orbits in each simulation (making in total millions of satellite orbits). Their numerical integration over appropriate time interval would surpass our computer capacity. Therefore, we use an alternative approach to deal with this problem. The main sources of instability for the captured irregular satellites are due to solar perturbations, such as the evection instability and Kozai-cycle instability. Typically, the amplitude of the former is smaller than that of the latter. We thus adopt the simplest approach and compute the minimum and maximum values of the pericenter distance during the Kozai cycle (obtaining thus also minimum and maximum values of the inclination variations). This can be achieved analytically because Kozai dynamics implies two integrals of motion (e.g., Kozai 1962; Kinoshita & Nakai 1999; Carruba et al. 2002; Nesvorný et al. 2003):
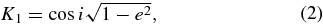
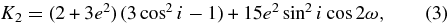
where (a, e, i) are the osculating semimajor axis, eccentricity and inclination, and ω is the osculating argument of the pericenter. In addition to K1 and K2, the semimajor axis a is also conserved by the Kozai dynamics (unless the dissipation effects become important). With the initial orbital parameters (a, e, i) known, and ω statistically modeled, we determine (K1, K2) and compute analytically the minimum/maximum values of e, i, and the orbital pericenter q during the Kozai cycle.4 We then apply the following filters to eliminate unstable or inappropriate orbits.
- 1.Small irregular satellites. We eliminate all orbits whose pericenter during the Kozai cycle becomes smaller than the planetocentric distance of the outermost regular satellite, which turns to be 0.013 AU for Jupiter (Callisto), 0.023 AU for Saturn (Iapetus), 0.004 AU for Uranus (Oberon) and 0.003 AU for Neptune (Triton in this case).
- 2.Capture of Triton. We eliminate all orbits whose pericenter during the Kozai cycle becomes smaller than Neptune's radius. We also eliminate those orbits for which the pericenter is always larger than ∼0.004 AU.
In both cases we also eliminate all satellites whose semimajor axis would exceed the long-term stability zone determined by the numerical experiments of Nesvorný et al. (2003). This typically means a ≳ 0.4 RHill for prograde satellites and a ≳ (0.5–0.6) RHill for retrograde satellites, depending on the time-averaged eccentricity of the orbit (see Figures 9–12 of Nesvorný et al. 2003; RHill is the radius of the Hill sphere for the planet).
The first condition described above is based on the assumption that a population of small irregular satellites crossing the orbits of more massive regular satellites would be destroyed by collisions or would be dynamically eliminated from the system. It basically results in the elimination of orbits in some interval of inclination value around 90° (e.g., Carruba et al. 2002; Nesvorný et al. 2003). The more complicated second condition for Triton's capture is based on the recent orbital evolution model of Ćuk & Gladman (2005). These authors postulate that Triton quickly evolved from its initial (capture) orbit by collisions with a pre-existing population of regular satellites similar to those around Uranus (and thus extending to ∼0.004 AU planetocentric distance). Debris from those satellites produced a massive circum-Neptunian disk that made Triton's orbit evolve into its current orbit in only ∼0.1–1 Myr. In particular, the orbital eccentricity of Triton has shrunk from its initial value to ∼0, while its inclination has not likely undergone significant evolution (Ćuk & Gladman 2005). Note, however, that we do not eliminate captured satellites with inclinations inconsistent with Triton's orbit (∼157° with respect to Neptune's equator). This is because we are interested in the intrinsic efficiency of the capture of satellites with Triton-like orbit by the binary splitting process, of which the actual Triton is just one possible realization.
To evaluate the number Ncap of irregular satellites captured in stable orbits with our method, we must include the value of the argument of the pericenter ω. This angle is random at the moment of capture. For this reason, with each captured orbit, characterized by planetocentric (a, e, i) orbital elements, we associate a statistical weight W by randomly choosing 103 values of ω and evaluating the fraction of (a, e, i; ω) orbits that are stable according to our criteria; in particular, if M such orbits are stable than W = M/103.
To compare the orbits of the captured satellites with those of existing irregular satellites, we use the mean orbital elements rather than the osculating ones (e.g., Nesvorný et al. 2003). This is because the Kozai cycle may significantly change the osculating elements on a timescale of ∼0.1–1 ky. It is possible to determine time-average eccentricity and inclination values over a Kozai cycle semi-analytically (e.g., Kinoshita & Nakai 1999). Such a computation, however, is not straightforward. We thus use a simpler approximate approach by taking an average of minimum and maximum Kozai-cycle values of e and i instead of their true time averages. They are sufficiently close to the time averages of e and i for the purposes of our paper.
2.3. Assumed Size Distribution of Planetesimals
Because of computational limitations, our migration runs in Section 2.1 represented the planetesimal disk by only a few thousands of equal-mass planetesimals (enough, though, to reasonably represent planetary migration and obtain a good statistical description of q and V∞). Thus, the characteristic particle masses in these simulations were ∼1.6 of Pluto mass, or, assuming a bulk density of 2 g cm−3, bodies of ∼2, 920 km in size. In reality, however, the planetesimal disk contains bodies with sizes ranging over the whole spectrum from objects that are very small to objects larger than the ones we used in our migration runs. Bodies in each size range, assuming that some fraction of them are binaries, may be potential sources of irregular satellites. We take this fact into account in the following.
We start with a description of our best guess for the size distribution (SFD) of the planetesimals in the disk. We then assume that the encounter parameters, such as distributions of q or V∞ determined in Section 2.1, are the same for bodies of different sizes (at least at some plausible interval we shall use) and that the captured population of irregular satellites scales with the estimated number of planetesimals of some particular size. This will allow us to quantify the number Nsat of captured irregular satellites from a disk with a realistic size distribution of bodies (Section 2.4).
Both the observational constraints (e.g., Bernstein et al. 2004; Elliot et al. 2005; Petit et al. 2006, 2007) and the evolutionary models (e.g., Stern & Colwell 1997; Gladman et al. 2001) are, to some degree, uncertain and yield only an approximate insight into the SFD of the planetesimal disk prior to or just after the planet-crossing phase. For simplicity, we shall thus assume a broken power law size distribution with a roll-off at size D0 and differential distribution exponents q1 for D ⩾ D0 and q2 for D ⩽ D0. As far as the current population is concerned, Bernstein et al. (2004) found that D0 ∼ 50 km, q1∼ 4–5, and q2∼ 2–3 in the current trans-Neptunian population. While finding nearly the same value of q1, Gladman et al. (2001) and Petit et al. (2006) argue, however, that the roll-off size D0 happens for smaller bodies, perhaps between 10 and 25 km. The robust finding that q1 > 4 and q2 < 4 implies that bodies with diameters D0 dominate the mass of the system. We shall assume that the size distributions of the planetesimals in the trans-Neptunian disk and in the post-PC phase were the same as now, only with their total number scaled to characterize its initial mass in our simulations, which is tied to the assumed 35 Earth mass of the primordial planetesimal disk beyond Neptune.
Our assumptions about SFD mean that the number dN of bodies in each size bin dD is dN ∝ D−q dD. In particular, for D ⩾ D0

and for D ⩽ D0
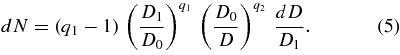
Here D1 is an auxiliary size threshold for which N(D > D1) = 1; we also denote the mass of a body with size D1 to be M1. The total mass, Mdisk, of the planetesimal disk is given by
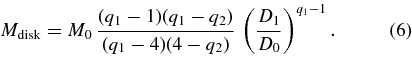
The shape of the assumed size distribution is determined by the (q1, q2, D0) parameters, and the absolute number of objects in the population is defined by the D1 value. The latter parameter is not known a priori, especially in the early post-PC phase. We, however, circumvent this parameter by using Equation (6) that relates D1 to Mdisk known from the initial data of our migration simulations. In particular, we have that
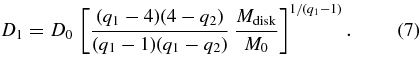
As an example of the (q1, q2, D0; Mdisk) parametrization of the disk we may use Mdisk ∼ 12.4 Earth masses (the case of run 1). To get the feeling how the (q1, q2, D0; Mdisk) parametrization determines our results, we use for definiteness q1 = 4.5, q2 = 2.8 and D0 = 50 km. With these values, Equation (7) yields M1 ≃ 44.6 Pluto masses or about one body of Mars mass in the disk population. We would thus expect, as a result of our mathematical exercise, about one body of that mass in the disk population and about 90 bodies of the Pluto mass.
It is interesting to note that (see Equation [7])

Since q1 > 4, the exponent on the right-hand side of Equation (8) is positive. This means that smaller D0 values would result in smaller D1 for a fixed value of Mdisk. For example, with the same slope exponents as above, Mdisk ∼ 12.4 Earth masses and D0 = 25 km, the disk would hold one body with ∼33 Pluto masses and some 60 bodies of the Pluto mass. In addition, with D0 fixed, larger q1 values result in smaller D1 for a fixed value of Mdisk.
Finally, we note that the size distribution discussed in this section characterizes the total population of disk objects. Our work further considers a fraction of them are binaries. This subpopulation is assumed to obey the same mass distribution as the whole system, or in other words the fraction of binaries is assumed to be roughly constant in the size interval of interest. In further work we actually assume all planetesimals are binaries, and only the final results would eventually be multiplied by the expected binary fraction (e.g., Noll et al. 2007).
2.4. Estimated Population of Captured Irregular Satellites
In the final step, we use all previously collected information to estimate the expected population of the irregular satellites captured by dissociation of the planetesimal binaries. If the equal-mass population of objects in our simulation were to represent the reality, Ncap satellites become captured in stable orbits from Ntrials trial cases (described in Section 2.2), and fbin is the fraction of binaries, we would expect to capture Nsat ∼ fbin Ncap(Nenc/Ntrials) satellites. With a continuum of planetesimal sizes (Section 2.3) such that at each infinitesimal size bin dD we have dN objects (Equations [4] and [5]), we obtain
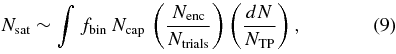
where integration is performed over bodies of all sizes D. Note that Ncap = Ncap(D) depends on the size/mass of the binary system which underwent dissociation in the gravity field of the planet. Similarly, fbin = fbin(D) may likely be a size-dependent parameter.
In practice, we choose finite size/mass bins (D, D + ΔD) and replace integration in Equation (9) with a finite summation:
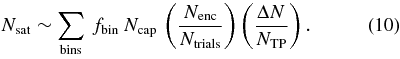
The value ΔN of number of objects in the diameter bin of size ΔD around D is given by Equations (4) and (5).5 Our choice for the size bins is given in Table 2 for experiments with the capture of small (<50 km size) irregular satellites, and in Table 3 for the capture of Triton. In both cases we specify the bins by minimum Dl and maximum Dr diameters. Moreover, since M ∝ D3, we define the effective diameter  and the corresponding mass Meff, assuming a bulk density of 2 g cm−3.
and the corresponding mass Meff, assuming a bulk density of 2 g cm−3.
Our simulations of the capture of small irregular satellites assume a massive primary and massless secondary (thus μ = 0). The number of trials Ntrials in each size bin is given in Table 2. The simulations of Triton's capture must take into account that one component of the binary is a ∼1.64 Pluto mass object. This also sets the minimum total mass of the binary system and fixes the mass ratio μ for each of the bins. For Triton's capture simulations, we used Ntrials = 2.5 × 1010 (Table 3).
In order to verify the robustness of our results on changes of the chosen bin sizes, we also performed a test for run 1 where we took 20 bins for the capture of small irregular satellites and 25 bins for the capture of Triton (the size range between the smallest value of Dl and the largest value Dr was the same). In both cases we also took twice as many trial integrations Ntrial as indicated in Tables 2 and 3.
3. RESULTS
Our plan is to first discuss the results of run 1 in detail and to a lesser extent those of run 2 (Table 1). These will set the stage for what follows. As a third step we summarize overall characteristics of the results for the remaining runs. In this section we strictly use data from the 100 Myr interval following the planet-crossing phase in the Nice model. In Section 4 we extrapolate them to other phases of the solar system evolution. For simplicity, we also assume all disk planetesimals are binary, thus fbin = 1, but more discussion can be found in Section 4.
3.1. Run 1: DE Type
We first analyze the ability to capture small irregular satellites from our runs where the secondary in binary systems was considered massless and the mass of the primary sampled a broad interval of values (Table 2).
Figures 5–8 show the values of the semimajor axis a and the Kozai-cycle mean value of the eccentricity e for captured satellites that meet stability criteria from Section 2.2. We give results for bins 5–8 (i.e., large primary components in the binary systems), because bins 1–4 provide only very limited (or even zero) number of captured satellites, typically with orbits of large a (close to stability limit) and very high e (typically e > 0.8). We nevertheless include them in the statistical analysis below. In all cases, capture from binary systems results in orbits with systematically higher values of the orbital eccentricity than that of the observed satellites (red triangles). The discrepancy is the largest for Jupiter, but even for Neptune the match is not good.
Figure 5. Each of the panels shows mean orbital semimajor axis a and eccentricity e for captured irregular satellites around Jupiter in run 1 (dots) for size bins 5–8 (see Table 2; bin identifier is noted in each panel). The triangles are the mean orbital elements of the observed irregular satellites of Jupiter for comparison.
Download figure:
Standard image High-resolution imageFigure 6. Each of the panels shows mean orbital semimajor axis a and eccentricity e for captured irregular satellites around Saturn in run 1 (dots) for size bins 5–8 (see Table 2; bin identifier is noted in each panel). The triangles are the mean orbital elements of the observed irregular satellites of Saturn for comparison.
Download figure:
Standard image High-resolution imageFigure 7. Each of the panels shows mean orbital semimajor axis a and eccentricity e for captured irregular satellites around Uranus in run 1 (dots) for size bins 5–8 (see Table 2; bin identifier is noted in each panel). The triangles are the mean orbital elements of the observed irregular satellites of Uranus for comparison.
Download figure:
Standard image High-resolution imageFigure 8. Each of the panels shows mean orbital semimajor axis a and eccentricity e for captured irregular satellites around Neptune in run 1 (dots) for size bins 5–8 (see Table 2; bin identifier is noted in each panel). The triangles are the mean orbital elements of the observed irregular satellites of Neptune for comparison.
Download figure:
Standard image High-resolution imageNext we used Equation (10) to obtain the total number Nsat of small irregular satellites by adding captured populations in each of the size bins. Table 4 gives results for selected disk parameters (D0, q1, q2). We also explored (D0, q1, q2) more extensively, namely assuming D0 in the (10, 50) km range, q1 in the (4.1, 4.9) range, and q2 in the (2.3, 3) range. Performing 106 random trials, the maximum number of captured irregular satellites around Neptune (in a statistical sense explained in Section 2.4) was ≃0.25. We also found that a smaller population (by about an order of magnitude) is expected around the other giant planets. This result is in contrast with the finding of Sheppard et al. (2006); see also Jewitt & Sheppard (2004) or Nicholson et al. (2007), who show that the D ⩽ 10 km population of irregular satellites is numerous and broadly similar for each of the giant planets. Our predicted ∼0.01–0.1 captured satellites is about three orders of magnitude below the observed population.
Table 4. Results of Our Simulations
| Run | Nsat | NTrit | |||
|---|---|---|---|---|---|
| Jupiter | Saturn | Uranus | Neptune | ||
| D0 = 50 km | |||||
| 1 | 0.0001 | 0.0000 | 0.0016 | 0.0491 | 0.009 |
| 2 | 0.0002 | 0.0000 | 0.0727 | 1.6882 | 0.034 |
| 3 | 0.0001 | 0.0000 | 0.0035 | 0.1198 | 0.014 |
| 4 | 0.0002 | 0.0000 | 0.0202 | 0.4548 | 0.035 |
| 5 | 0.0001 | 0.0000 | 0.0016 | 0.1198 | 0.007 |
| 6 | 0.0001 | 0.0000 | 0.0095 | 0.0709 | 0.008 |
| 7 | 0.0002 | 0.0000 | 0.0111 | 0.2188 | 0.021 |
| D0 = 25 km | |||||
| 1 | 0.0000 | 0.0000 | 0.0010 | 0.0282 | 0.005 |
| 2 | 0.0001 | 0.0000 | 0.0418 | 0.9697 | 0.019 |
| 3 | 0.0001 | 0.0000 | 0.0020 | 0.0688 | 0.008 |
| 4 | 0.0001 | 0.0000 | 0.0116 | 0.2612 | 0.020 |
| 5 | 0.0000 | 0.0000 | 0.0009 | 0.0688 | 0.004 |
| 6 | 0.0001 | 0.0000 | 0.0055 | 0.0407 | 0.005 |
| 7 | 0.0001 | 0.0000 | 0.0064 | 0.1257 | 0.012 |
| D0 = 10 km | |||||
| 1 | 0.0000 | 0.0000 | 0.0005 | 0.0136 | 0.003 |
| 2 | 0.0001 | 0.0000 | 0.0200 | 0.4558 | 0.009 |
| 3 | 0.0000 | 0.0000 | 0.0010 | 0.0331 | 0.004 |
| 4 | 0.0000 | 0.0000 | 0.0056 | 0.1255 | 0.010 |
| 5 | 0.0000 | 0.0000 | 0.0004 | 0.0330 | 0.002 |
| 6 | 0.0000 | 0.0000 | 0.0026 | 0.0196 | 0.002 |
| 7 | 0.0001 | 0.0000 | 0.0031 | 0.0604 | 0.006 |
Notes. For different migration runs (first column), we give the number of irregular satellites captured in the 100 Myr timespan with D ≲ 50 km and the efficiency to capture Triton at Neptune (the last column; here called NTrit, but computed according to algorithm for Nsat from Equation (10)). All results assume that every disk planetesimal is a binary (fbin = 1). We used three different values of size D0, a parameter that characterizes the inflection point of the disk SFD. We used slope index q1 = 4.8 for D > D0 and q2 = 2.8 for D < D0. In the Saturn case, the captured population of the irregular satellites was always ≃10−5 or smaller.
Download table as: ASCIITypeset image
In order to check how sensitive our results are on the particular choice of 8 size bins from Table 2, we repeated the simulation with 20 size bins that covered the same interval (50–10, 000 km) for the primary size. Secondaries were again massless and we also performed twice as many trial integrations. For a given set of disk parameters (D0, q1, q2) we obtained ≃30% fewer captured satellites Nsat. This difference is not significant. Because of much lower computer time expense, we shall use the 8-bin set in the following.
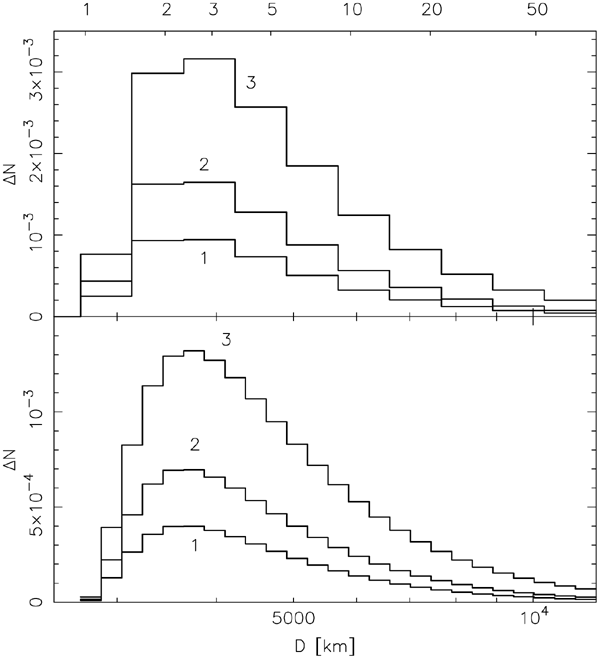
We took advantage of our test run to probe which binary systems contribute most to the population of the captured irregular satellites. Figure 9 shows the contribution ΔNsat = Ncap(Nenc/Ntrials)(ΔN/NTP) of each of the bins in the final value Nsat for all of the planets. Note that much more massive primaries are necessary to provide satellites around Jupiter than around Neptune. The primaries with a peak efficiency for the delivery of small irregular satellites have ∼5, ∼1, ∼0.05, and ∼0.002 Pluto-masses for Jupiter, Saturn, Uranus, and Neptune, respectively. Comparison of ΔNsat for the simulations with 8 and 20 size bins also allows us to understand why the nominal case with 8 bins overestimates the number of captured satellites (Figure 9).
Figure 9. Contribution ΔNsat of individual size bins to expected Nsat for capture of massless irregular satellites in run 1. Data for satellites around different giant planets are the three histograms with appropriate labels: J for Jupiter, U for Uranus and N for Neptune (Saturn satellites would be below the resolution limit in this figure). The top panel for the nominal simulation with 8 size bins (Table 2), the bottom panel for a check simulation with finer grid of 25 size bins. The arrows indicate upper bounds for ΔNsat from the resolution of our integration (in the case of satellites around Jupiter and Saturn these upper bounds are below the minimum value at the ordinate). Note the ΔNsat values for bins in the bottom panels are smaller because they are calibrated to less disk particles ΔN (Equation [10]). The cumulative value ∑ΔNsat of captured satellites is ≃30% less for the finer grid of bins at the bottom part. This is because the capture efficiency steeply rises toward a maximum value in the first few bins. The coarse bins at the top assign too much weight to smaller primaries that in the bottom case already do not contribute to Nsat. The upper abscissa shows mass of the primary in the binary system in masses of Pluto for reference.
Download figure:
Standard image High-resolution image3.1.1. Capture of Triton
Figure 10 shows osculating orbital parameters for satellites meeting the criteria of Triton capture (Section 2.2). Each of the panels corresponds to one individual size bin outlined in Table 3 (the bin identifier is labeled in the right bottom corner). Obviously, a smaller number of Triton-like objects are captured from systems of lower total mass (the initial bins 1, 2, 3...), while much more are captured when the mass of the primary increases (the last bins ..., 9, 10). In the first case the initial eccentricity is systematically very high (≳0.9), while only massive primaries allow lower eccentricity capture orbits. The importance of each of the bins for Triton capture probability depends not only on the number of the captured satellites Ncap, but also on the estimated number ΔN of the binary systems in the planetesimal disk (see Equation [10]). Figure 11 shows the contribution ΔNsat = Ncap(Nenc/Ntrials)(ΔN/NTP) of each of the bins in the final value Nsat for three different values of (D0, q1, q2) triples. Interestingly, bins 2 and 3, corresponding to about 2 to 3 mass ratio between the primary and secondary (Triton), are preferred for the Triton capture. Systems with a lighter primary are more abundant in the disk but provide comparably less captured satellites. On the other hand, very massive binary systems yield a lot of captured satellites, but are very rare in the disk.
Figure 10. For each of the size bins from Table 3, and with adopted capture criteria from Section 2.2, we show the initial osculating orbital semimajor axis a (abscissa) and the eccentricity e (ordinate) of an orbit potentially evolving into the current Triton state. Numbers in the bottom right corner of each panel show the identifier of the bin. The shaded zone shows for the reference pericenter value of the current Triton orbit ±0.001 AU; note that the current orbit of Triton has a ≃ 2.4 × 10−3 AU and e ≃ 2 × 10−5.
Download figure:
Standard image High-resolution imageFigure 11. Contribution ΔNsat of individual size bins to expected Nsat for Triton in run 1. Three different choices of (D0, q1, q2) disk parameters are illustrated: (i) (D0, q1, q2) = (25, 4.8, 2.8) curve 1 (D0 in kilometers), (ii) (D0, q1, q2) = (50, 4.8, 2.8) curve 2 (D0 in kilometers), and (iii) (D0, q1, q2) = (25, 4.5, 2.8) curve 3 (D0 in kilometers). The upper panel is for our nominal set of bins from Table 3. The bottom panel is from a robustness test, where we used 25 bins instead of 10. In both cases ΔNsat peaks between D ∼ 3000–4000 km, when the binary components have the comparable mass of Triton. Note the ΔNsat values for bins in the bottom panels are smaller because they are calibrated to fewer disk particles ΔN (Equation [10]). The cumulative value ∑ΔNsat of captured satellites is, however, the same in both cases (only 7% less in the latter case). The upper abscissa shows the ratio of the total mass of the binary to the mass of Triton (one component).
Download figure:
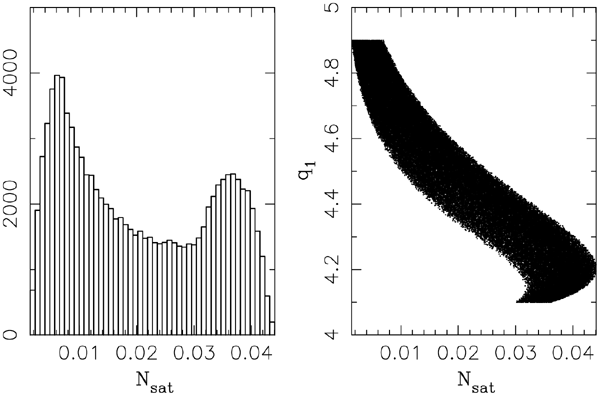
Standard image High-resolution imageFigure 12 shows the expected number of satellites Nsat meeting the criteria of Triton capture (Section 2.2) when the parameters of the planetary-disk distributions are varied in their admissible intervals. In particular, we considered D0 values in the interval (10, 50) km, q1 values in the interval (4.1, 4.9), and q2 values in the interval (2.3, 3). Overall, the chance to capture Triton during the 100 Myr interval during the post-PC phase is less than 2%. The highest values of Nsat are obtained for q1 ∼ 4.1–4.3, while observations tend to prefer higher values of this parameter (e.g., Gladman et al. 2001; Bernstein et al. 2003; Elliot et al. 2005; Petit et al. 2006). The right panel in Figure 12 shows a correlation between Nsat and q1, which is mainly due to the strong influence of q1 on the number of planetesimals ΔN in the size bins used in our simulation. We found that Nsat is significantly less dependent on D0, and nearly independent of q2.
Figure 12. Left: distribution of the Nsat for Triton values in run 1; D0 ranges randomly an interval of values (10, 50) km, q1 ranges randomly in an interval of values (4.1, 4.9), and q2 ranges randomly in an interval of values (2.3, 3) (105 trial cases performed). Right: Nsat vs. q1 exponent used in the trial cases, showing their mutual correlation (Nsat is only weakly correlated with D0, and nearly independent of q2). The variation of Nsat for a fixed q1 values is thus basically given by different D0 values: smaller Nsat for a smaller D0 value.
Download figure:
Standard image High-resolution imageWe have re-run our simulation with 25, instead of 10, size bins and we obtained results that predict only 7% fewer satellites (see Figure 11). This accuracy is enough for our conclusions and it justifies our usage of coarser bins from Table 3 for further runs.
3.2. Run 2: MA Type
The orbits of the captured massless irregular satellites in run 2 indicate the same inconsistency with the observed population, as shown in Figures 5–8 for run 1. In particular, orbits with high eccentricities are preferentially populated leaving the space of low-eccentricity orbits, where the observed satellites reside, depleted or entirely void. As expected, the total number of captured satellites is up to one order of magnitude larger than in run 1. This is especially true for Uranus and Neptune, because these two planets penetrate into a heavier residual disk with less scattered orbits of planetesimals, such that the efficiency factor of capture ϕ is a factor larger than in run 1 (see Figure 4). Nevertheless, Nsat for all planets is still significantly smaller than unity and several orders of magnitude smaller than the observed population. The exception is Neptune, for which we would predict about one captured irregular satellite, obviously not enough to explain its debiased population of small irregular satellites (e.g., Jewitt & Sheppard 2004). Moreover, the predicted population of small irregular satellites at Saturn is more than three orders of magnitude smaller than that at Neptune, contradicting the observations (e.g., Jewitt & Sheppard 2004). In the same way, although our expected likelihood of capturing one Triton-like orbit increases by a factor of a few, yet, at its maximum, it reaches only a few percent.
3.3. Comments on Other Jobs
The planet-crossing phase of the Nice model is violently chaotic. The planetary configuration at its end, the degree of the planetesimal disk depletion, and its dynamical excitation at different heliocentric distances is unknown and strongly dependent on the sequence of planet encounters. As a result, the realistic uncertainty of the irregular satellite capture does not derive only from parameter details of simulations described above (such as the number of size bins, the number of trial integrations, the size-distribution parameters D0, q1, or q2 etc), but is likely dominated by variations in the possible planetary evolution scenarios. To face this fact, we used the results of Nesvorný et al. (2007), who determined 14 different possibilities of the planet evolution after Jupiter and Saturn entered the 2/1 mean motion resonance. Here we selected seven of them and applied our method to estimate the number of captured irregular massless satellites and likelihood of capturing Triton during the first 100 Myr of the post-PC phase.
Table 1 indicates that the mass of the residual trans-Neptunian disk and the number of planetesimal encounters with planets varied by nearly a factor of 2 in these different variants of planetary evolution. Overall, the resulting population of irregular satellites does not deviate from that in runs 1 and 2 (described above) by more than a factor of 2 (see Table 4). In none of the cases did the number of captured satellites come close to the observed population. In addition, the likelihood of Triton's capture remained between 0.1 and 3%. For the small satellites, we also noted in all runs that the eccentricity of the captured satellites is significantly smaller than observed.
4. DISCUSSION AND CONCLUSIONS
Based on the above results we conclude that capture from disk binaries does not seem to be a promising mechanism for the origin of either the overall population of the irregular satellites or Triton during the control interval of time of the post-PC phase within the Nice model (while we have always been working within the frame of this model, we believe our conclusions also apply to the case of the more traditional planet migration model of Malhotra and colleagues; e.g., Malhotra 1995; Hahn & Malhotra 1999). This mechanism lacks necessary efficiency and results in the small irregular satellites captured in orbits having distributions of orbital elements that are incompatible with those of the observed population.
4.1. Inconsistency of the Orbital Distribution
We note this orbital inconsistency occurred in all our simulations and presents, in our opinion, the strongest argument against the capture mechanism. It might, in principle, only be removed by assuming subsequent weak orbital evolution that could pull-down orbital eccentricities while preserving the semimajor axis after satellite capture (e.g., McGleam et al. 2006). However, in our mind, no such universal process has been found as yet. In the absence of gas drag at the late stage of planetary evolution described in this paper, tidal evolution remains the most important long-term effect. This is too weak and it would also primarily drive the evolution along lines of constant pericenter distance q. Another possibility is mutual collisions between the satellites, which may be an interesting evolutionary process yet to be studied in depth, but below we argue that the initially captured population is not populous enough to explain the discrepancy via this mechanism.
4.2. Too Few Satellites Captured
Note that we always assumed fbin = 1, which likely makes our population of captured satellites an overestimate. We purposely avoid closer analysis of how fbin(D) affects our results because too little is known about this function. Current observations suggest a 22+10−5% abundance of binaries in the classical Kuiper belt, with smaller fractions observed in the hot Kuiper belt and the scattered disk (Noll et al. 2007). This fraction might be, however, larger among the largest trans-Neptunian objects (e.g., Brown et al. 2006), and if these objects possess more than one satellite, one may effectively have also fbin ⩾ 1. This would slightly enhance the role of the satellite capture from the population of the largest planetesimals. Another process that might slightly increase the role of satellite captures from these largest planetesimals is that their orbits could be dynamically less excited than those of the smaller disk components, such that their relative encounter velocity with planets might be systematically smaller. We have seen, however, that the largest objects do not contribute dominantly to the overall capture probability. We thus do not expect that these omitted effects would significantly increase the efficiency of irregular satellites production from the exchange reactions that was several orders of magnitude low in our simulations.
4.3. Extrapolation of Our Results
All the above-mentioned conclusions apply to the interval of 100 Myr following the planet-crossing phase of the solar system evolution according to the Nice model. We now argue how they might be extrapolated further in time, but also to the pre-PC phase of the Nice model. First, we comment on the possible satellite population captured during the phase post-dating the 100 Myr analyzed previously in Section 3. In spite of the fact that this phase lasted another ∼3.7 Gyr, we see from Figure 2 that the number of planetesimal encounters with planets decreases very fast. It is not a straightforward exercise to extrapolate this observed trend because a quasi-exponential match of the 100 Myr integrated time interval would provide an unrealistically low-mass trans-Neptunian population today. Clearly, at some time during the late evolution the rapid decay rate of the disk mass (e.g., Figure 2) and the number of planetary encounters had to change into a slower evolution. However, we argue that rather than extrapolating our previous results using a ratio of timespan it makes more sense to use the ratio of mass losses from the planetesimal disk. Indeed, if the number of planetary encounters in Figure 2 decays proportionally to the disk mass, their ratio is constant. So the accumulated number of the planetary encounters during the past ∼3.7 Gyr might be, in the first approximation, proportional to the remaining mass loss from the disk. In run 1, for instance, the final disk mass of ∼4 Earth masses should be next decreased to today's value by another ∼4 Earth masses (note, for the sake of our argument, we do not actually need to know the small residual mass of the trans-Neptunian population today). This is a factor of ∼2 less than what the planetesimal disk lost during the above analyzed 100 Myr interval. As a result, we would expect about half the number of irregular satellites created in this late phase than during the time interval investigated in Section 3. Overall, this would mean a negligible population.
Next, we comment on the pre-PC phase of the Nice model. It is important to note that this interval of time does not include as yet the planetary formation phase during which the giant planets formed within a comparably cold planetesimal disk and were surrounded by a residual gas disk. What we have now in mind is the phase covered by analysis of Gomes et al. (2005), notably starting from a compact configuration of outer planets that already have cleared most of their orbital space. An edge of a ∼35 Earth mass planetesimal disk is located about ∼1–1.5 AU beyond the outer planet, which was found to provide a ∼600–800 Myr long quasi-stable period before LHB takes place. Note, however, that our analysis remains valid even if the PC phase of the Nice model occurred earlier in the evolution of the solar system and was not related to the LHB. During the pre-PC time interval outer planets experience only little migration evolution, preserving their compact configuration until Jupiter and Saturn reach their mutual 2/1 mean motion resonance. This is reflected by the fact that disk particles only occasionally reach the planet zone.
If we apply the disk mass-depletion scaling for the number of planetary encounters, we may expect a comparable number or fewer satellites created during the pre-PC phase than in the 100 Myr interval after planets stopped crossing their orbits (note the initial disk mass had 30 Earth masses and it decreased to about 24 Earth masses before the PC phase). This assumes that the encounter parameters, such as distribution of V∞ or q, are the same as described in Section 3. Indeed, we verified this using two simulations. At first, we started again the initial ∼20 Myr of run 1 (Figure 1), during which the gas giants did not yet reach their mutual 2/1 mean motion resonance. During this time interval we recorded parameters of planetary encounters and verified that distributions in Figure 3 still hold. Moreover, the frequency of the encounters was about two orders of magnitude less than during the post-PC phase, as we expected. We also performed a series of test simulations putting the initial planetary system described by Gomes et al. (2005) interior to massive disks with various surface density profiles. We again integrated the evolution for about 20 Myr and verified that even in this initial phase of Gomes et al. evolution, V∞ and q, with respect to planets, have approximately the same distribution as in Figure 3.
However, we have to point out that a comparable, or even a factor of few larger, captured population of irregular satellites before the PC phase is not enough to explain their observed population today. We recall the results of Nesvorný et al. (2007), who determined that the planet-crossing phase should decimate the pre-existing irregular population by a factor of ∼1000 or more. As a result, the pre-PC captured satellites from binaries should be even much less populous than those created later. This argument does not apply to Triton's capture, because once evolved into its current orbit it would not likely be destabilized during the planetary-encounter phase. Yet, the small factor of increase does not bring the probability of capturing Triton in the pre-PC phase of the Nice model any closer to unity.
We may thus conclude that since the giant planets completed their formation, the surrounding planetesimal disk was cleared, and gas was dissipated from the solar system (the initial moment of the current version of the Nice model), irregular satellite capture from disk binaries is not a viable mechanism to provide the overall populations of irregulars or capture of Triton: the captured orbits are inconsistent with the observed ones and the efficiency is low. It is fair to recall that Jupiter may be a special case, since this planet does not typically participate in close planetary encounters within the current version of the original Nice model (although see a novel route by Morbidelli et al. 2007 that may possibly involve Jupiter's participation in planetary close-encounters and a discussion in Nesvorný et al. 2007). It is possible that its population of irregular satellites was created in part by dissociation of the primordial binary systems in the planetesimal disk very early after (or simultaneously with) Jupiter's formation. A number of Jupiter's irregulars in secular resonances are considered to suggest their early formation in the gaseous environment. Our work, however, suggests that the capture from binaries is likely ineffective in later epochs because of the poor match of orbital characteristics (Figure 5) and a small number of captured satellites.
As far as Triton is concerned, our simulations above make a capture possible onto orbits that could then evolve to the precursor of its currently observed orbit. However, they also indicate that it is unlikely to happen after the planet-crossing phase within the Nice model. In fact we only see a possibility of its capture from a binary system very early after planet formation. In this early phase, orbits of both growing planets and planetesimals in the disk were kept cold by the action of surrounding gas. This means that the relative velocity at the encounters between the planetesimals and the planets was much lower than shown in Figure 3 for the later phase and more consistent with assumptions in Agnor & Hamilton (2006). Whatever formation process of disk-binaries dominated, it is likely that it was operational during this early phase of planet's evolution (in fact, might have been at the peak of its efficiency, e.g., Goldreich et al. 2002; Astakhov et al. 2005). Given the time constraints for this phase, it would be interesting to study constraints on disk parameters (such as its state of excitation, its mass and planetesimal size distribution) to attain an order of unity probability to capture Triton.
Part of this work has been supported by the Grant Agency of the Czech Republic (grant 205/08/0064) and the Research Program MSM0021620860 of the Czech Ministry of Education. Support for D.N. and H.F.L. was provided by the National Science Foundation. We thank an anonymous referee for useful comments.
Footnotes
- 3
Note that the excess of angular momentum of the binary orbit with respect to the planet as a massive center, expressed as its ratio to the the angular momentum of the limiting case of a parabolic orbit, is given by
 .
. - 4
- 5
Since our size bins are not infinitesimal, we use the total (integrated) number of objects between Dl and Dr:
![$\Delta N = (D_1/D_{\rm l})^{q_1-1}\,[1-(D_{\rm l}/ D_{\rm r})^{q_1-1}]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) for Dl, Dr > D0 and
for Dl, Dr > D0 and ![$\Delta N = ((q_1-1)/(q_2-1))\,(D_1/D_0)^{q_1-1}\, (D_0/D_{\rm l})^{q_2-1}\break [1-(D_{\rm l}/D_{\rm r})^{q_2-1}]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) for Dl, Dr < D0.
for Dl, Dr < D0.













![$\Delta N = (D_1/D_{\rm l})^{q_1-1}\,[1-(D_{\rm l}/ D_{\rm r})^{q_1-1}]$](https://content.cld.iop.org/journals/1538-3881/136/4/1463/revision1/aj273799ieqn3.gif)
![$\Delta N = ((q_1-1)/(q_2-1))\,(D_1/D_0)^{q_1-1}\, (D_0/D_{\rm l})^{q_2-1}\break [1-(D_{\rm l}/D_{\rm r})^{q_2-1}]$](https://content.cld.iop.org/journals/1538-3881/136/4/1463/revision1/aj273799ieqn4.gif)