Time integration and differentiation of unipolar pulses of unusual shape

Recently, the possibility of obtaining unipolar electromagnetic pulses with a high-power field burst of the same polarity and a nonzero electric area has been studied (see review [1], papers [2–9] and references therein). The electrical area of the pulse is defined as [10–12]

where E(t) is the electric field strength at a given point in space.

Interest in obtaining such pulses is associated, first of all, with the possibility of efficient and ultrafast control of wave packets in matter [13–15], acceleration of charges [16], and with a number of other applications [1].

The electrical area of subcycle pulses is their important characteristic, since this area determines the degree of impact on quantum objects [13–15]. On the other hand, of fundamental importance is the rule of conservation of the electric area of extremely short pulses in the electrodynamics of continuous media, first proposed in [10] and studied in detail later [8, 11, 12]. This rule is fulfilled in one-dimensional distribution problems and has the form:

This rule is a new law of conservation in physics and should be taken into account in the problems of propagation of extremely short and, in particular, unipolar pulses in matter. From a practical point of view, the issue of obtaining unipolar pulses with a large electric area for affecting quantum objects is important [13–15]. Note that unipolar pulses can exist not only in nature, but also effectively propagate in waveguides [17] and be formed in various systems, for example, in the far zone of a source [18].

In issues related to the use of unipolar pulses and their propagation in various media, the problem of controlling their shape is of great importance. Pakhomov et al. [6, 7] studied the possibility of obtaining unipolar terahertz pulses of unusual shape–rectangular and triangular–due to superradiance of a pulse of stopped polarisation. Rectangular pulses in the terahertz range can also be obtained in the form of precursors as a result of optical rectification in nonlinear crystals [4, 5].

The operations of integration and differentiation of electrical pulses using RC and RL circuits are well known and used in radio electronics. It would seem that in relation to harmonic pulses of optical radiation, which have been obtained in optics for many years and contain tens and hundreds of oscillation cycles, these operations do not make sense, since differentiation and integration of harmonic functions also yields harmonic functions.

However, in recent years, extremely short light pulses have been generated, containing one or even half a cycle of oscillations [2, 3, 19–21], which made it possible to propose methods for obtaining unipolar pulses of nonharmonic shape [1, 6, 7]. For such pulses, the question of their integration and differentiation with respect to time can be raised. As in radioelectronic circuits, this will allow a strong transformation of the pulse shapes, which can be important for various applications. In order to accomplish such tasks in optics, it is necessary to look for systems that are analogues of RC circuits.

Pakhomov et al. [22] constructed a theory of time integration and differentiation of extremely short light pulses in thin metal films. It is important to note that previously such operations were performed only for slowly varying envelopes of ultrashort nano- and picosecond pulses [23–30]. In our paper [22], however, we described for the first time the method of time integration and differentiation of the direct temporal dependence of the electric field strength in extremely short pulses, rather than a slow envelope. In this case, the pulses considered in [22] were mainly bipolar, while the transformation of unipolar pulses was discussed only briefly.

In this paper, on the basis of the theory developed in [22], we study the possibility of integrating and differentiating unipolar pulses. In particular, we consider the transformation of unipolar pulses of unusual shape–rectangular and triangular, the possibility of obtaining which was shown earlier [6, 7] and for which such operations of time integration and differentiation are most obvious. In addition, the conservation of the electrical area in such problems is demonstrated.

Let us consider the problem of propagation of rectangular and triangular unipolar pulses obtained in [6, 7] through thin metal films. As shown in [22], the time integration of extremely short pulses reflected from thin metal films is possible if the condition on the pulse spectrum

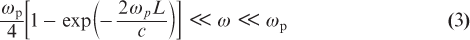
is met, where ω is the circular frequency of the pulse; ω_p is the plasma frequency of the metal in the film; and L is the metal film thickness. In this case, the film thickness for the most efficient pulse integration is chosen as

As can be seen from expression (1), a nonzero area of a unipolar pulse means that the spectrum of such a pulse contains a constant field component. However, inequality (3) does not include near-zero-frequency spectral components, although the expression on the left-hand side of (3) can be made sufficiently small for a small film thickness. Consequently, the spectral range of integration (3) cannot completely cover the spectrum of a unipolar pulse, but it can overlap its significant part. This limitation can be circumvented by using quasi-unipolar pulses, that is, pulses consisting of a unipolar burst and a long tail of opposite polarity, so that the total value of the electrical area of the pulse is zero [1]. In this case, the pulse spectrum has no near-zero-frequency components, and the spectral range of integration (3) can cover the entire spectrum of the pulse.

In the case of time differentiation for transmission, the pulse spectrum must satisfy the inequality [22]

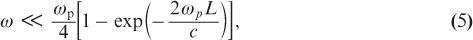
while the optimal film thickness has the form

Condition (6) contains only a limitation on the maximum frequency in the pulse spectrum. Thus, unipolar pulses containing close-to-zero frequencies in the spectrum can easily satisfy inequality (5) with an appropriate selection of the parameters of the metal film.

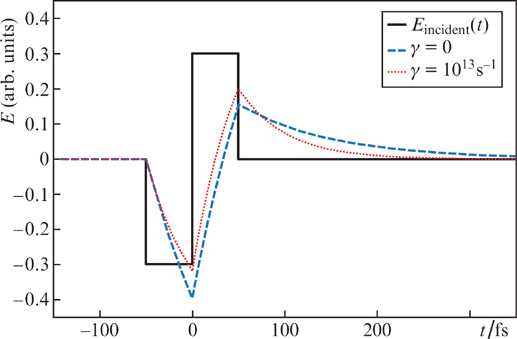
Consider the problem of time differentiation for the case of a triangular unipolar pulse. For a metal film, following formula (6), we take the following parameters: ω_p = 10¹⁶ s⁻¹, and L = 30 nm. Note that the chosen value of the plasma frequency ω_p corresponds to its characteristic values for most common metals. The incident pulse on the film is a 100-fs unipolar linearly polarised triangular pulse with a plane wavefront (see Fig. 1). The passage of a pulse through a metal film is described by the standard wave equation for an electric field:

where P is the macroscopic polarisation of the medium, and z is the longitudinal coordinate. The dispersion properties of the metal in the film were described using the standard Drude–Lorentz model, which for the macroscopic polarisation of the medium has the form:

where γ is the attenuation coefficient. Equations (7) and (8) were solved numerically using the finite-difference time-domain (FDTD) method.

Zoom In Zoom Out Reset image size

Unipolar pulses can propagate in coaxial waveguides, since they lack mode dispersion and cutoff frequency [17]. This leads to the fact that, with an appropriate technological design, a coaxial cable can behave like a waveguide in which the transverse components of unipolar radiation pulses do not change their shape during propagation. This propagation is described by the one-dimensional wave equation (7) for the transverse field components with a zero right-hand side [17, 31]. Thus, the use of a one-dimensional model can be considered justified.

Figure 1 shows the results of numerical simulation of the propagation of a 100-fs triangular unipolar pulse through a metal film with the above parameters for two values of the attenuation coefficient: γ = 0 and 10¹³ s⁻¹. Because the problem in question is linear with respect to the field of the incident pulse, the amplitudes of the incident and transmitted pulses will be expressed in arbitrary units. As can be seen from Fig. 1, at small values of the attenation coefficient γ, when γτ_p ≪ 1, the pulse transmitted through the film is rectangular, that is, the profile of the electric field of the pulse is differentiated in time. At large values of the attenuation coefficient, γτ_p ∼ 1, the shape of the transmitted pulse begins to differ from rectangular, that is, the accuracy of the differentiation operation decreases.

It is of interest to check the fulfilment of the law of conservation of the electric area (2) in the problem under consideration. To this end, in the last case from those shown in Fig. 1, that is, at γ = 10¹³ s⁻¹, the time integration of the electric field strength at each point of the integration region was performed during the entire calculation time. The calculation results are shown in Fig. 2. One can see that the electric area is indeed constant throughout the entire region of integration, and this allows us to draw a number of important conclusions. For example, it is possible to transform a unipolar pulse into a bipolar one or, conversely, with their linear propagation through a layer of a dissipating arbitrary medium. In this case, it is only required that the sum of the electrical areas of the incident and reflected pulses be equal to the electrical area of the pulse transmitted through the layer.

Zoom In Zoom Out Reset image size

Let us now consider the possibility of inverse transformation of a rectangular unipolar pulse into a triangular one by means of time integration. Following estimate (3), in order to effectively integrate unipolar pulses with a duration of tens or hundreds of femtoseconds, the plasma frequency ω_p must be reduced in comparison with the previous example; in what follows, we will take ω_p = 10¹⁵ s⁻¹. Then, in order for the spectral range (3) to include frequencies ω ∼ 10¹³−10¹⁴ s⁻¹, it is necessary that the left-hand side of inequality (4) be at least two to three orders of magnitude smaller than the right-hand side. For further calculations, we will take a metal film 3 nm thick and consider the reflected field when a rectangular pulse propagates through such a film in one-dimensional geometry. Figure 3 shows both the incident rectangular pulse and the reflected pulses for γ = 0 and 10¹³ s⁻¹. It can be seen that the reflected pulse has a triangular shape with a nonzero electric area (1), that is, the profile of the incident pulse field is integrated in time. Even in the case γ = 0, due to the finite thickness of the metal film and the presence of the lower boundary of the spectral range of integration (3), the integration accuracy turns out to be limited, and noticeable extended tails of reflected pulses with opposite field polarity are formed.

Zoom In Zoom Out Reset image size

As in the previously considered example of time differentiation, we also checked the fulfilment of the law of conservation of the electric area (2); it again turned out to be constant, in full agreement with the conservation law (2).

Thus, the obtained results show that, by combining metal films with certain parameters that satisfy conditions (3)–(6), it is possible to carry out mutual transformations of rectangular and triangular unipolar pulses with durations of tens and hundreds of femtoseconds. In this case, rectangular pulses are transformed into triangular ones due to the integration of the time dependence of the electric field strength of the incident pulse during reflection, while the inverse transformation of triangular pulses into rectangular ones is due to the differentiation of the time dependence of the electric field strength during propagation through the film. The accuracy of both operations in this case strongly depends on the value of the attenuation coefficient γ. In those cases when the attenuation turns out to be significant at times of the order of the duration of the incident pulse, the shapes of the obtained pulses can differ markedly from the results of the exact time integration/differentiation of the incident pulse, which is also accompanied by the formation of extended tails at the trailing edge of the pulses.

We have considered the propagation of rectangular and triangular unipolar pulses through thin metal films. We have shown that with an appropriate choice of the parameters of the incident unipolar pulse and the film thickness, it is possible to perform time transformations of the shape of these pulses, such as time integration (reflection) and differentiation (transmission). In this case, as a result of time integration of rectangular pulses, triangular pulses are formed, and as a result of time differentiation of triangular pulses, rectangular ones are generated. Thus, depending on the choice of the configuration of the system in question, pulses of a similar shape can be converted into each other. It is important to note that the described time transformations of pulses relate directly to the time dependence of the electric field strength in the pulse E(t) rather than to the slowly varying pulse envelope, as in many other works.

The obtained results demonstrate new approaches to controlling the shape of extremely short pulses. In particular, femtosecond unipolar pulses can be of great interest for controlling various ultrafast processes in matter, including the dynamics of electrons, ions, and excitation of atoms and molecules. The possibility of controlled transformations of the temporal shape of such ultrashort unipolar pulses becomes one of the key difficulties in this case. The described operations of time integration and differentiation of unipolar pulses provide one of the possible ways to control the pulse profile within a fairly wide range.

This work was supported by the Russian Science Foundation (Grant No. 21-72-10028).