Fiscal Consequences of Missing an Inflation Target

Abstract

The European Central Bank is unique in setting monetary policy for several sovereign states with heterogeneous debt levels and different maturity structures. The monetary–fiscal nexus is central to the functioning of the euro area. We focus on one particular aspect of that nexus, the effect of the reliability of the European Central Bank monetary policy on public debt burdens. We show that when the ECB misses its inflation target this has large heterogeneous fiscal consequences for Euro Area countries.

Appendices

Data Construction

We compiled a dataset with debt to GDP from the OECD. We used general government debt securities to GDP, this excludes loans and other types of non-marketable debts.³³ We exclude these other categories as we do not have detailed duration information. By this token, our results are a lower bound on the effects of missing inflation targets as we focus only on a subset of the government liabilities. The duration of government debt data comes the FTSE WGBI Data. We used Macaulay duration.

These data are subject to a number of caveats. First of all, the OECD securities debt-to-GDP excludes holding by government entities, say social security and most importantly the central bank. A second caveat is that the FTSE WGBI data computes the duration measure on bonds (so excludes t bills, and other debt). This implies that the measure is an upper bound as for public debt we use all bonds. To give a comparison for these two measures, overall General government securities debt-to-GDP (so not only Federal) in the USA in 2019 was about 99 percentage of GDP. All outstanding Federal bonds (so no t bills or other debt) were around 70 percentage, and the bond publicly held were 55 percentage. Clearly the last one is too conservative, but the first one might be too high. As a comparison, in this paper dataset for the USA in 2019 we have Duration-to-GDP at 6.4 percentage of GDP (the increase in the market value of public debt in GDP units in case there is a 1 percentage decrease in interest rates across the yield curve), Andreolli (2022) computes the same measure from bond-by-bond data and finds 3.1 percentage of debt to GDP in case of bonds only held by the general public and four percentage of debt to GDP when including the FED holdings. This gives an idea of the degree of differences in magnitude for Duration-to-GDP depending on the source of the data. On the other hand, Macaulay duration for the USA is quite similar when computed bond-by-bond and when computed with the FTSE WGBI index.

A second caveat pertains to countries under an IMF or Troika programme. In these cases, non-marketable loans become a significant part of public debt, and therefore, the Macaulay duration of bonds becomes less informative of the duration risk of public liabilities. This is why we do not report Greek numbers and the numbers for other countries under these programmes should be discounted for the programme periods.

ECB reports the weighted average maturity (WAM) of its debt holdings in the context of the PSPP portfolio holdings (QE). We complement this with the average life for the overall stock of bonds from the FTSE WGBI data. Both these measures compute the maturity by taking the weighted years the principal of bond is due, weighted by amount outstanding (for the overall measure) or by ECB holdings of this bond (for the ECB holding measures).

Inflation-linked swap data comes from ICAP, downloaded from Datastream and the break-even inflation rated for the USA comes from the Fed and is based on Gürkaynak, Sack, and Wright (2010). In the computational exercise, we use 10-year benchmark rates on sovereign debt to measure interest rates. The data source is Refinitiv.

1.1 Additional Figures

In this subsection, we add additional figures with a larger number of countries to provide a broader picture of the main results. In Figure 6, we present Duration-to-GDP and its components (Macaulay duration and Public Securities Debt) for all the countries in the dataset.

Fig. 6

Duration-to-GDP for all countries. Notes: The time series presents Duration-to-GDP (in the blue solid line), Macaulay duration (in the red short dashed line), and government debt securities (in the green long dashed line) for all the countries in the dataset. Macaulay duration data are FTSE WGBI. Debt data are government debt securities over GDP from the OECD. The sample goes from 1999Q1 to 2022Q1

Comparison of Inflation Expectation Measures

First, in Figure 7 we present the same inflation expectation figure for the USA as we did for the Euro Area in Figure 2. We can see the same pattern, with debt-embedded inflation expectations being close to the long run expectation and short inflation expectations being closer to inflation realisation.

In the baseline exercise, we use the survey of professional forecasters (SPF) measures for long run inflation expectations due to their coverage and ability to forecast inflation (see Ang, Bekaert, and Wei 2007). Moreover, these metrics directly measure inflation expectations and do not need a structural model to disentangle expectations from risk premia, liquidity premia, or convenience yields as market-based metrics. However, it is important to show how this measure compares other metrics for long run inflation expectations. Grishchenko, Mouabbi, and Renne (2019) combined several inflation survey sources to fit a yield curve of inflation expectations for the USA and the Euro Area. Similarly, Aruoba (2020) does a similar exercise for the USA. For the USA, we also present the Cleveland Fed Expected Inflation Term Structure by Haubrich, Pennacchi, and Ritchken (2012) which fits a structural model with data from inflation swap rates, nominal Treasury rates, and survey forecasts of inflation. Finally, we also present row market-based metrics: forwards on inflation liked swaps (for the Euro Area and the US) and on break-even inflation rates from nominal and inflation-linked treasuries (for the US). These metrics should not be used as inflation expectations directly as they incorporate inflation risk premia, liquidity premia, and convenience yields. However, they are still useful to look at, as they are based on market prices and we show robustness in our results to employing them directly.

Figures 8 and 9 present the results of this comparison for the Euro Area and for the USA, respectively. We can see that most survey-based metrics track quite closely the SPF, and the market-based metrics are a bit more volatile but still track the SPF and yield large mispricing as in the baseline.

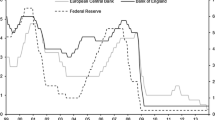
Moreover, to understand the inflation expectations embedded in bond prices, long run inflation expectations are the key expectations given the relatively long maturity of public debt. However, it is important to see how they are related to shorter horizon expectations. For this reason, in Figure 10, we plot the mean inflation expectations in the ECB and Fed SPF. From this picture, we can see that the stability of long run inflation expectations does not carry through to the shorter horizon metrics, as they track variation in inflation more closely.

With respect to inflation embedded in bond prices, we take a issuance weighted average of inflation rates and use the following formula:

$$\begin{aligned} \sum _{j=1}^{J-1}\mathbb {E}_{t-j}(\pi ^{a}_{t|t-j})\frac{1}{\text{Mat}_{t}}\left( 1-\frac{1}{\text{Mat}_{t}}\right) ^{j-1} + \mathbb {E}_{t-J}(\pi ^{a}_{t|t-J})\left( 1-\frac{1}{\text{Mat}_{t}}\right) ^{J} \end{aligned}$$

where $\pi ^{a}_{t|t-j}$ is the annualised inflation rate from period $t-j$ to t, $\text{Mat}_{t}$ is the annualised maturity of public debt, measured with average life from the WGBI FTSE data. J is the maximum inflation expectation horizon we have available (we set J to 10 years). This formula comes directly from the theoretical framework, with a constant fraction of debt being repaid each period.³⁴ The formula implies that we assign the long-term inflation expectation $\pi ^{a}_{t|t-J}$ in period $t-J$ to all debt issued before period $t-J$.³⁵ We use j to be an annual horizon, as we have annual inflation expectations in the ECB SPF. This means that $\mathbb {E}_{t-1}(\pi ^{a}_{t|t-1})$ is the average, next year inflation expectation prevailing in the past four quarters, $\mathbb {E}_{t-2}(\pi ^{a}_{t|t-2})$ is the 2 years head inflation expectations on average in the past five–eight quarters, and so on.

In the baseline debt-embedded inflation expectations we study in the empirical exercise, we use the raw SPF data with the following assumptions: for $\mathbb {E}_{t-1}(\pi ^{a}_{t|t-1})$ we use 1 year head inflation expectations, for $\mathbb {E}_{t-2}(\pi ^{a}_{t|t-2})$ we use 2 years head inflation expectations, and for any $\mathbb {E}_{t-j}(\pi ^{a}_{t|t-j})$ with $j>2$ we use the long run inflation expectation. We are implicitly assuming that all inflation expectations above 2 years are the long run ones. In order to assuage concerns about this assumption, we also employ the inflation expectations of Grishchenko, Mouabbi, and Renne (2019), Aruoba (2020) who provide a full term structure of inflation expectations computed from surveys. Additionally, for the USA we also compute the same metric with the inflation expectations from Haubrich, Pennacchi, and Ritchken (2012), who combine market-based data with surveys in a term structure model. Furthermore, we compute the same metric with the yield curve from inflation-linked swaps which also embed risk and term premia. Finally, for the USA, where we have a long time series of TIPS and nominal yield curves, we also computed the debt-embedded inflation expectations using break-even inflation rates from the Fed (based on Gürkaynak, Sack, and Wright 2010). We follow the Fed practice and start the sample in 2004q1 due to illiquidity in the TIPS market in the first years in which these securities were introduced and for comparability with the inflation-linked swaps which also start in 2004q1. Moreover, we do not use the data for the last two quarters of 2008 (but use the value of 2008q2), when the financial crisis created affected the functioning of the TIPS market due to very high illiquidity (this phenomenon was also highlighted by Reis 2020) and therefore made the break-even inflation even a worse predictor of inflation. Moreover, we exploit the all the break-even rates provided by the Fed, going from 2 years ahead to 20 years ahead. As we do not have 1-year-ahead break-even inflation we use the 2 years ahead metric. We plot the comparison in Figure 11, together with actual inflation and the current long run inflation expectations from the SPF. All these metrics are very close to each other, implying we can use directly the SPF data. Moreover, the conclusion from Section 3 remains: all inflation expectations embedded in debt are very close to the current long run inflation expectations, as proof of the credibility of the inflation target in the past two decades. The inflation risk premium embedded in swaps tends to be positive in most of the sample, except in the last part of the disinflationary period (the mean 5 years by 5 years forward computed from swaps is 2.16 percentage for the Euro Area and 2.64 percentage for the USA in the 2004q1 to 2022q2 sample, in both cases higher than realised inflation and long run expected inflation from the SPF).

Figure 12 and Table 6 show the inflation forecast errors. Figure 12 shows the time series of the inflation forecast errors for all Euro Area countries and for the USA measured with expectations embedded in current debt and with the naive inflation expectation: 1.9 percentage in the Euro Area and 2.0 percentage in the USA. Table 6 shows the average inflation forecast errors in the Euro Area and in the USA for various samples and different expectations: in addition to the aforementioned expectations on debt and naive ones, it shows the forecast errors on short run inflation expectations. We can see that in the low inflation decade forecast errors on debt have been large at $-0.59$ and $-0.71$ percentage points in the Euro Area and in the USA, respectively. Both these numbers are statistically different from zero. Whereas, when we measure short run inflation expectations, with lagged (one quarter) inflation expectations on current year inflation, the forecasts errors are $-0.04$ and $-0.13$ percentage points and not statistically different from zero. That is, short run inflation expectations tracked inflation much more than long run expectations and debt-embedded inflation expectations.

Next, we replicate the results on the fiscal costs of missing the inflation target also with a metric that incorporate the risk premium for debt-embedded inflation expectations. The reason is that, if the inflation risk premium had been negative in the sample we might have overestimated our results on the cost of newly issued debt. A negative inflation risk premium can happen if inflation is low when the marginal utility consumption is high (in recessions, so when business cycles are mainly demand driven) and this hedge mechanism (the negative covariance of inflation with the SDF in asset pricing terms) is stronger than the effect that inflation uncertainty at long horizons has on increasing the risk premium (the variance of inflation).³⁶ We do so by using directly inflation-linked swaps to compute debt-embedded inflation expectations. Table 8 shows exactly this. In the first two set of columns shows the baseline (SPF) and Grishchenko, Mouabbi, and Renne (2019) metrics with survey-based inflation expectations (no risk premium) and the last set of columns shows the same cost with the inflation-linked swap (with the risk premium). We can see that the order of magnitude is the same across all columns. Additionally, for each Euro Area country the market-based metric embedding the inflation risk premium is higher than the baseline metric. The reason is that, despite the period after 2015 when the inflation risk premium was negative, most debt was issued and priced before that and overall the premium was positive in our sample (remember than long debt allows to smooth-out short run variations in funding conditions). For the USA, it is a little lower, but of the same order of magnitude.

Additionally, we replicate the results on the fiscal costs of missing the inflation target for the USA with also additional metrics for debt-embedded inflation expectations. The reason is that for the USA we have a long time series for many inflation expectations metrics: pure survey ones, term structure model ones, and pure market-based ones. In Table 9, we replicate Table 2 with all the debt-embedded inflation expectations presented in Figure 11. We can see that except with the naive forecast (2% always), all the metrics yield a statistically significant costs (the Cleveland Fed one only marginally). Crucially, the order of magnitude is similar in all the strongly significant results. Even in the case where we use the break-even inflation rate directly to compute inflation expectation the cost is 1.7 percentage of GDP. For the Euro Area, the results with using the Grishchenko, Mouabbi, and Renne (2019) are virtually identical for each country to the baseline ones with the SPF and are available upon request.

Next, we ask what is the implication of assuming that Euro Area bond markets are integrated in the pricing of government bonds. To achieve this, we replicate the results for the France, Germany, Italy, and Spain with country specific information. As we do not have country specific surveys, we use the inflation-linked swaps on country specific inflation to compute debt-embedded inflation expectations (with the inflation risk premium) and realised country specific inflation. The results are presented in Table 10. The first set of columns shows the baseline (SPF), the second set the integrated inflation-linked swaps data, and the last set of columns the country specific results with inflation-linked swaps.³⁷ We can see the order of magnitude is the same across each column for each country. For Italy the number is a little lower, for the other three is a bit higher, but the magnitude is overall the same. This means that market segmentation across Euro Area countries cannot overturn our results.

Moreover, we check the robustness of excluding Central Banks holdings of government debt in the context of Quantitative Easing policies. QE reduces the maturity of outstanding public debt as swaps long securities for short reserves in the consolidated balance sheet of the public sector. For countries with their own central bank, it is conceptually easy as one should exclude the entirety of the securities holding; however, for the Euro Area countries there is an additional hurdle as there a limited amount of risk sharing across countries in the bond holdings of the ECB. This penalised more countries with longer debt in the low inflation period than countries with shorter debt, as the risk-shared capital gains for the ECB are allocated according to the capital key. For this reason, we do not use as a baseline the debt net of ECB holding, but show robustness to this metric. One should bear in mind that the number would be a lower bound due to risk sharing. In Table 11, we present the results of this experiment. In columns 4 and 5, we compute Duration-to-GDP where we subtract from securities debt the Central Bank holdings of the two major ECB QE programmes on public debt: the Public Sector Purchase Programme (PSPP) and the Pandemic Emergency Purchase Programme (PEPP). This calculation assumes that the ECB bought securities at a maturity not too dissimilar to that of the overall amount of outstanding securities in the market, which is the case in the data. We can see that numbers are a little lower but of the same order of magnitude and with the same relative magnitude across countries. The results are robust to excluding QE holdings.³⁸

In our baseline results, we focus on marketable debt as we have good maturity data for this debt and we know that most sovereign bonds are fixed rate (either nominally or inflation linked). However, many countries borrow also with non-marketable loans. It is therefore important to look also at this debt type. The key challenge is that we do not have widespread maturity measures and do not know what fraction of this debt is variable rate. If we are willing to assume that non-marketable loans have the same maturity and interest payment structure as marketable debt, we can construct Duration-to-GDP and with the same methodology. Table 12 presents the results of missing the inflation target on the debt burdens. We can see that the costs are even larger for every country but of the same order of magnitude.

Finally, we discuss how our approach relates to that proposed by Chiang and LaBelle (2022); their work is related but they ask a different question which is why they get a different result. We ask what the ex-post real burden of debt is given the inflation expectations embedded in debt at issuance and what the effect of a strongly anchored inflation target is. For us the long run expectations are the most important ones and are those that give us the highest inflation shocks given that they are closely aligned with the target thanks to the credibility of the Central Bank, while realised inflation is away from the target. This is true both in the disinflationary period and in the inflation burst of today. They ask a different question: they ask how much people updated from last year to today their inflation expectations at different horizons (so how much one was expecting to get in real terms on an investment in a nominal bond issued in 2021 in 2021 vs how much one is expecting to get in 2022 on the same bond issued in 2021). Their metric puts a strong weight on short run inflation expectations and realised inflation has a stronger effect on short horizons. In that metric, the inflation shock at a 30 years horizon is the smallest from 2021 to 2022; that is, one does not update strongly the expected inflation rate from 2021 to 2051 (given the credibility of central banks).

Fig. 7

Inflation Expectations and Inflation in the USA. Notes: This graph presents long run inflation expectations, short run inflation expectations for the current year, the inflation expectations embedded on outstanding public debt at issuance, and realised inflation. The source of inflation expectations is the Philadelphia Fed Survey of Professional Forecasters (SPF) Inflation and its expectations pertain to the headline Consumer Price Index (Headline CPI). The sample goes from 1999Q1 to 2022Q2

Fig. 8

Long Run Inflation Expectations Comparison and Inflation in the Euro Area. Notes: This graph presents long run inflation expectation measures and realised inflation for the Euro Area. The SPF series is the 4/5 years ahead YoY inflation from the ECB Survey of Professional Forecasters (SPF). Ten (5)-year GMR is the 10 (5)-year-ahead inflation expectation from the Grishchenko, Mouabbi, and Renne (2019) measure. The 5-year by 5-year forward from inflation-linked swap is computed from inflation-linked swaps. Inflation and its expectations pertain to the Harmonised Index of Consumer Prices (HICP). The sample goes from 1999Q1 to 2022Q2. The 5-year by 5-year forward inflation liked swap sample starts in 2004Q1

Fig. 9

Long Run Inflation Expectations Comparison and Inflation in the USA. Notes: This graph presents long run inflation expectation measures and YoY CPI realised inflation for the USA. The SPF series is the 10-year average inflation from the Philadelphia Fed Survey of Professional Forecasters (SPF). Cleveland is the Cleveland Fed 10-year-ahead expected inflation, ATSIX is the mean inflation expectation 10-year ahead from Aruoba (2020). GMR is the 10-year-ahead inflation expectation from the Grishchenko, Mouabbi, and Renne (2019) measure. Five-year, 5-year forward inflation rate is measured with nominal and inflation-linked treasury rates. The 5-year by 5-year forward from inflation-linked swap is computed from inflation-linked swaps. The sample goes from 1990q1 to 2022Q2. The 5-year, 5-year forward inflation Rate sample starts in 2003q1 and the 5 years by 5 years forward inflation liked swap sample starts in 2004Q1

Fig. 10

SPF Inflation Expectations Comparison and Inflation. Notes: This graph presents all the Survey of Professional Forecasters (SPF) inflation expectations across horizons for the Euro Area (inflation is HCPI) in the first panel and for the USA (inflation is CPI) in the second panel. The sample goes from 1999q1 to 2022Q2

Fig. 11

Inflation Expectations on Debt Comparison and Inflation in the Euro Area and in the USA. Notes: This graph presents debt-embedded inflation expectations and YoY inflation for the Euro Area (HCPI) and for the USA (CPI). The long run inflation expectations are the Survey of Professional Forecasters (SPF) series, the 4/5 years ahead YoY inflation from the ECB for the Euro Area and the 10-year average inflation from the Philadelphia Fed for the USA. Cleveland is the Cleveland Fed model, ATSIX is the mean inflation expectation from Aruoba (2020). GMR is the inflation expectation from the Grishchenko, Mouabbi, and Renne (2019) measure. Inflation-linked swaps uses the term structure of inflation-linked swaps from ICAP. Break-even inflation uses the break-even inflation from the difference between Nominal and TIPS Treasuries. The sample goes from 1990q1 to 2022Q1

Fig. 12

Inflation Forecasts Errors for All Euro Area Countries and for the USA. Notes: This graph presents the forecast error on debt-embedded inflation expectations. Inflation expectations come from the ECB (for the Euro Area on HICP inflation) and Philadelphia Fed (for the USA on Headline CPI) Surveys of Professional Forecasters (SPF). The naive approach assumes an inflation expectation of 1.9 percentage for the Euro Area and 2 percentage for the USA. The vertical axis units are percentage points. The sample goes from 1999Q1 to 2022Q2

Fig. 13

Fiscal Consequences of Missing Inflation Targets for All Euro Area Countries and for the USA. Notes: This figure shows the fiscal costs of missing the inflation targets on public debt. The “Misses” lines show the multiplication between Duration-to-GDP and the forecast error on debt-embedded inflation expectations with SPF, OECD, and FTSE WGBI data. The “Misses - Naive” show the same multiplication, but with the naive inflation forecast. The vertical axis units are per cent of GDP. A positive number implies that inflation is below its forecast and a negative number that inflation is above its forecast. The sample goes from 1999Q1 to 2022Q1

Table 6 Inflation Forecasts Errors

Table 7 Fiscal Consequences of Missing Inflation Targets—With the Recent Inflation Increase

Table 8 Fiscal Consequences of Missing Inflation Targets—Metrics Comparison

Table 9 Fiscal Consequences of Missing Inflation Targets—Additional Metrics Comparison for the USA

Table 10 Fiscal Consequences of Missing Inflation Targets—Comparison with Market Segmentation Case

Table 11 Fiscal Consequences of Missing Inflation Targets—No ECB QE

Table 12 Fiscal Consequences of Missing Inflation Targets—Also Non-marketable Debt

Theoretical Results Derivation

In this appendix, we present the detailed derivations for the theoretical results in section 5. We start with the first experiment, where we highlight the costs on legacy debt, with the government refinancing only the maturing debt. This is equivalent in having $L_{t+j}=\delta ^{d} D_{t+j} = \delta ^{d} D_{t}$. The system we study becomes:

$$\begin{aligned} L_{t}&= \delta ^{d} D\\ R^\text{ave}_{t}&= \left( 1-\frac{L_{t}}{D}\right) R^\text{ave}_{t-1} + \frac{L_{t}}{D}R^\text{new}_{t}\\ S_{t}&=R^\text{ave}_{t-1} D\\ \frac{1}{(\delta ^{d} +R^\text{new}_{t})}&= \mathbb {E}_{t}\sum _{j=1}^{\infty }\left[ \frac{1}{\prod _{k=1}^{j}\pi _{t+k}}\beta ^{j}(1-\delta ^{d})^{j-1}\right] \end{aligned}$$

First, let us show the effect of changes inflation expectations in this framework. We establish the effect of a changing the expectations of inflation at some future horizon on newly issued bonds:

$$\begin{aligned} \frac{\partial R^\text{new}_{t+l}}{\partial \mathbb {E}_{t+l}(\pi _{t+l+m})}&= (\delta ^{d}+R)^{2}\sum _{j=m}^{\infty }\pi ^{-j-1}\beta ^{j}(1-\delta ^{d})^{j-1}\\&= (\delta ^{d}+R)^{2}\pi ^{-1}(1-\delta )^{-1}\beta \sum _{j=m}^{\infty }\pi ^{-j}\beta ^{j}(1-\delta ^{d})^{j}\\&= (\delta ^{d}+R)^{2}\pi ^{-1}(1-\delta )^{-1}\frac{\left( \frac{\beta (1-\delta )}{\pi }\right) ^{m}}{1-\frac{\beta (1-\delta )}{\pi }}\\&= (\delta ^{d}+R)^{2}\pi ^{-1}(1-\delta )^{-1}\frac{\left( \frac{1-\delta }{1+R}\right) ^{m}}{1-\frac{1-\delta }{1+R}}\\&= \frac{\delta ^{d}+R}{1+R}\pi ^{-1}(1-\delta )^{-1}\left( \frac{1-\delta }{1+R}\right) ^{m} \end{aligned}$$

With this result we can highlight the effect of next period expectations only:

$$\begin{aligned} \frac{\partial R^\text{new}_{t +l }}{\partial \mathbb {E}_{t+l}(\pi _{t+l+1})}&= \frac{\delta ^{d}+R}{1+R}\pi ^{-1}(1-\delta )^{-1}\left( \frac{1-\delta }{1+R}\right) ^{1}\\&= \frac{1+R}{\pi }\frac{\delta ^{d}+R}{1+R} \end{aligned}$$

That is, the interest rate changes by one over duration, when only short run expectation move. Similarly, we can compute the effect of shifting all future inflation expectation at the same time.

$$\begin{aligned} \frac{\partial R^\text{new}_{t +l}}{\{\partial \mathbb {E}_{t+l}(\pi _{t+l+m})\}_{m=1}^{\infty }}&= (\delta ^{d}+R)^{2}\sum _{j=1}^{\infty }j \pi ^{-j-1}\beta ^{j}(1-\delta ^{d})^{j-1}\\&= (\delta ^{d}+R)^{2}\pi ^{-2}\beta \sum _{j=0}^{\infty }j \left( \frac{\beta (1-\delta ^{d})}{\pi }\right) ^{j-1} \\&= (\delta ^{d}+R)^{2}\pi ^{-2}\beta \frac{1}{\left( 1-\frac{\beta (1-\delta ^{d})}{\pi }\right) ^{2}} \\&= (\delta ^{d}+R)^{2}\pi ^{-2}\beta \frac{(1+R)^2}{\left( R+\delta ^{d}\right) ^{2}} \\&=\pi ^{-2}\beta (1+R)^2\\&= \frac{1+R}{\pi } \end{aligned}$$

If we have a parallel shift in inflation expectations, the change in interest rates is one to one irrespective of maturity. Next we show the effect of a change in newly issued debt from period $t+1$ on average interest rates in the future.

$$\begin{aligned} \frac{\partial R^\text{ave}_{t+k}}{\{\partial R^\text{new}_{t+l}\}_{l=0}^{k}}&= \sum _{l=0}^{k}(1-\delta ^{d})^{k-l}\frac{1}{\prod _{m=l}^{k}\pi _{t+m}g_{t+m}}\frac{l_{t+l}}{d_{t+k}}\\ \end{aligned}$$

From steady state:

$$\begin{aligned} \frac{\partial R^\text{ave}_{t+k}}{\{\partial R^\text{new}_{t+l}\}_{l=0}^{k}}&= \sum _{l=0}^{k}\left( 1-\delta ^{d}\right) ^{k-l}\delta ^{d}\\&= \frac{1-\left( 1-\delta ^{d}\right) ^{k+1}}{1-(1-\delta ^{d})}\delta ^{d}\\&= 1-\left( 1-\delta ^{d}\right) ^{k+1} \end{aligned}$$

Next, solve for the effect of a change in newly issued rates on the fiscal burden.

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{ \{\partial R^\text{new}_{t+l}\}_{l=0}^{\infty } }&= \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k} \frac{\partial s_{t+j}}{\partial R^\text{ave}_{t+j-1}} \frac{\partial R^\text{ave}_{t+j-1} }{\{\partial R^\text{new}_{t+l}\}_{l=0}^{k}} \\&= \sum _{j=1}^{\infty }\left( \beta \frac{1}{\pi } \right) ^{j} D \left( 1-\left( 1-\delta ^{d}\right) ^{j}\right) \\&=D \left( \frac{\frac{1}{1+R}}{1-\frac{1}{1+R}} - \frac{\frac{1-\delta ^{d}}{1+R}}{1-\frac{1-\delta ^{d}}{1+R}}\right) \\&=D \left( \frac{1}{R} - \frac{1-\delta ^{d}}{\delta ^{d}+R}\right) \\&=D\frac{\delta ^{d}}{R} \frac{1+R}{\delta ^{d}+R} \end{aligned}$$

We find the effect of inflation expectations on the fiscal burden. Notice that the effect of a change in expectations in a given future horizon is the same irrespective of the period we are in, therefore, the expression simplifies. We consider two cases, first if only inflation expectations on next period adjust:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j} }{\{\partial \mathbb {E}_{t+l}(\pi _{t+l+1})\}_{l=0}^{\infty }}&= \sum _{l=0}^{\infty }\frac{\sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j} }{\partial R^\text{new}_{t+l}}\frac{\partial R^\text{new}_{t+l} }{\partial \mathbb {E}_{t+l}(\pi _{t+l+1})}\\&=D\frac{\delta ^{d}}{R} \frac{1+R}{\delta ^{d}+R} \frac{1+R}{\pi }\frac{\delta ^{d}+R}{1+R} \\&= \frac{D}{\pi } \frac{1+R}{R} \delta ^{d} \end{aligned}$$

And then if all future expectations adjust:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\{\partial \mathbb {E}_{t+l}(\pi _{t+l+m})\}_{m=1}^{\infty }\}_{l=0}^{\infty }}&= \sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial R^\text{new}_{t+l}}\frac{\partial R^\text{new}_{t+l} }{ \{\partial \mathbb {E}_{t+l}(\pi _{t+l+m})\}_{m=1}^{\infty } }\\&=\sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial R^\text{new}_{t+l}}\frac{1+R}{\pi } \\&=D\frac{\delta ^{d}}{R} \frac{1+R}{\delta ^{d}+R} \frac{1+R}{\pi }\\&= \frac{D}{\pi } \frac{1+R}{R} \delta ^{d} \frac{1+R}{\delta ^{d}+R} \end{aligned}$$

We can see that even in the case in which all future expectations adjust the debt burden varies by less in the long debt case, as the legacy debt has its interest rate fixed. Moreover, if no expectation adjusts at all, whether short or long, interest rates would not move at all. In the next step, we show the effect of inflation on the debt burden. First, we show that inflation does not have a direct effect on average interest rates. We can simply see that by substituting the issuance policy of refinancing only maturing debt in the law of motion of average interest rates:

$$\begin{aligned} R^\text{ave}_{t}&= \left( 1-\frac{L_{t}}{D}\right) R^\text{ave}_{t-1} + \frac{L_{t}}{D}R^\text{new}_{t}\\ R^\text{ave}_{t}&= \left( 1-\delta ^{d}\right) R^\text{ave}_{t-1} + \delta ^{d}R^\text{new}_{t} \end{aligned}$$

As interest rate on newly issued debt is not affected by realised inflation, holding expectation constant, then also average rates will not be as they are only a function of these new rates. With this result, we find the effects of future inflation at any horizon on primary surpluses:

$$\begin{aligned} \frac{\partial s_{t+j}}{\{\partial \pi _{t+l}\}_{l=1}^{\infty }}&= \sum _{l=1}^{\infty } \frac{\partial s_{t+j}}{\partial \pi _{t+l}}\\&= - R^\text{ave}_{t+j-1} D \frac{1}{\prod _{k=1}^{j} g_{t+k}\pi _{t+k}}\sum _{l=1}^{j}\frac{1}{\pi _{t+l}} \\&= - R D \frac{1}{\pi } j \left( \frac{1}{\pi g}\right) ^{j} \end{aligned}$$

Next, let us study what happens if inflation increases from tomorrow $t+1$ onward on the fiscal burden.

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+l}\}_{l=1}^{\infty } }&= \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k} \frac{\partial s_{t+j}}{\{\partial \pi _{t+l}\}_{l=1}^{\infty }}\\&= -\sum _{j=1}^{\infty }\left( \beta g\right) ^{j} R D \frac{1}{\pi } j \left( \frac{1}{\pi g}\right) ^{j}\\&= - \frac{D}{\pi }R \sum _{j=1}^{\infty }\left( \frac{1}{1+R}\right) ^{j} j \\&= - \frac{D}{\pi }\frac{R}{1+R} \sum _{j=0}^{\infty }\left( \frac{1}{1+R}\right) ^{j-1} j \\&= - \frac{D}{\pi }\frac{1+R}{R} \end{aligned}$$

Finally, we combine the inflation and the expectations results to study the overall effect on the fiscal burden. We start with the scenario when all inflation expectations adjust.

$$\begin{aligned}&\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\{\partial \pi _{t+1+l},\mathbb {E}_{t+l}(\pi _{t+l+m})\}_{l=0}^{\infty }\}_{m=1}^{\infty }}\\&\quad \equiv \sum _{l=1}^{\infty } \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \pi _{t+l}} \\&\qquad + \sum _{l=0}^{\infty }\sum _{m=1}^{\infty } \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \mathbb {E}_{t+l}(\pi _{t+l+m}) } \\&\quad = - \frac{D}{\pi }\frac{1+R}{R} + \frac{D}{\pi } \frac{1+R}{R} \delta ^{d} \frac{1+R}{\delta ^{d}+R} \\&\quad = - \frac{D}{\pi }\frac{1+R}{R} \frac{R+\delta ^{d} - \delta ^{d}-R\delta ^{d}}{\delta ^{d}+R} \\&\quad = - \frac{D}{\pi }\frac{1+R}{\delta ^{d}+R} (1 - \delta ^{d}) \end{aligned}$$

Next when only short run expectations adjust:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+1+l},\mathbb {E}_{t+l}(\pi _{t+l+1})\}_{l=0}^{\infty }}&\equiv \sum _{l=1}^{\infty } \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \pi _{t+l}} \\&\quad + \sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \mathbb {E}_{t+l}(\pi _{t+l+1}) } \\&= - \frac{D}{\pi }\frac{1+R}{R} + \frac{D}{\pi } \frac{1+R}{R} \delta ^{d} \\&= - \frac{D}{\pi }\frac{1+R}{R+\delta ^{d} } \frac{R+\delta ^{d} }{R}(1- \delta ^{d}) \end{aligned}$$

1.1 Solution when the Central Bank Fixes Interest Rates

In this section, we show the same experiment but, in a case, where no inflation expectation adjusts following the permanent change in inflation. Notice that this experiment is observationally equivalent to a case where the central bank keeps nominal rates constant at any horizon, starting from steady state. First, we show that, in the proposed framework, no inflation expectation adjusting implies that interest rates are constant, both on the proposed model and on hypothetical zero-coupon bonds at various horizons. We can see by looking at the Euler equation on newly issued bonds and notice that it depends only on inflation expectations and two parameters $\beta$ and $\delta ^{d}$. If inflation expectations do not move, neither interest rates will. The same argument holds also for hypothetical zero-coupon bonds.

$$\begin{aligned} \frac{1}{(\delta ^{d} +R^\text{new}_{t})}&= \mathbb {E}_{t}\sum _{j=1}^{\infty }\left[ \frac{1}{\prod _{k=1}^{j}\pi _{t+k}}\beta ^{j}(1-\delta ^{d})^{j-1}\right] \\ \frac{1}{1 +R^{\text{zero}\ \text{coupon}}_{t,t+j}}&= \mathbb {E}_{t}\left[ \frac{1}{\prod _{k=1}^{j}\pi _{t+k}}\beta ^{j}\right] \end{aligned}$$

With this result, we can easily find the effect on the fiscal burden by looking at the result on realised inflation only:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+1+l}\}_{l=0}^{\infty }}&= - \frac{D}{\pi }\frac{1+R}{R} \end{aligned}$$

When debt is long ($\delta ^{d}$ low) the effect is quite close to that where only short run expectations adjust, as it differs only by a factor of $1-\delta ^{d}$:

$$\begin{aligned} \frac{\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+1+l},\mathbb {E}_{t+l}(\pi _{t+l+1})\}_{l=0}^{\infty }}}{\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+1+l}\}_{l=0}^{\infty }}}&= 1-\delta ^{d} \end{aligned}$$

Under reasonable calibrations $1-\delta ^{d}$ is close to one.³⁹ Table 13 summarises the effects on the fiscal burden with no expectation moving (central bank fixes interest rates), with only short expectations moving, and with all expectations moving. As we argued, with empirically plausible debt maturity, the effect of the central bank fixing all rates is very close to the effect when short run expectations move and long run do not, similar to what we see in the data. The reason is debt owed one quarter ahead does not constitute a sizeable part of public debt (only a fraction $\delta ^{d}$ of the principal). On the other hand, when debt is short we see the full effect of inflation if all interest rates are fixed. This is an interesting theoretical point; however, it is empirically implausible and highlights the need for incorporating maturity in discussions on debt sustainability and monetary regimes.

Table 13 Inflation, Maturity, Central Bank Interventions, and the Fiscal Burden on Legacy Debt

1.2 Solution under Constant Debt to GDP

In this subsection, we show the same derivations under the second exercise we perform, a constant debt-to-GDP scenario. The system we study becomes:

$$\begin{aligned} f_{t}&= (R^\text{ave}_{t-1} + \delta ^{d}) \frac{1}{g_{t}\pi _{t}}d\\ d&= (1-\delta ^{d})\frac{1}{g_{t}\pi _{t}}d + l_{t}\\ R^\text{ave}_{t}&= \left( 1-\frac{l_{t}}{d}\right) R^\text{ave}_{t-1} + \frac{l_{t}}{d}R^\text{new}_{t}\\ f_{t}&=s_{t} + l_{t}\\ \frac{1}{(\delta ^{d} +R^\text{new}_{t})}&= \mathbb {E}_{t}\sum _{j=1}^{\infty }\left[ \frac{1}{\prod _{k=1}^{j}\pi _{t+k}}\beta ^{j}(1-\delta ^{d})^{j-1}\right] \end{aligned}$$

Some key steady state relationships:

$$\begin{aligned} R&= R^\text{new} = R^\text{ave}= \frac{\pi }{\beta }-1\\ R+\delta ^{d}&= \frac{\pi }{\beta }\left( 1- (1-\delta ^{d})\frac{\beta }{\pi }\right) \\ d&= \frac{1}{\left( 1-\frac{1-\delta ^{d}}{\pi g}\right) }l\\ d&= s \frac{\frac{\pi g}{1+R}}{1- \frac{\pi g}{1+R}} \end{aligned}$$

First establish the effect of a change in interest rates on newly issued debt an average interest rates:

$$\begin{aligned} \frac{\partial R^\text{ave}_{t+k}}{\{\partial R^\text{new}_{t+l}\}_{l=0}^{k}}&= \sum _{l=0}^{k}(1-\delta ^{d})^{k-l}\frac{1}{\prod _{m=l}^{k}\pi _{t+m}g_{t+m}}\frac{l_{t+l}}{d_{t+k}} \end{aligned}$$

From steady state:

$$\begin{aligned} \frac{\partial R^\text{ave}_{t+k}}{\{\partial R^\text{new}_{t+l}\}_{l=0}^{k}}&= \sum _{l=0}^{k}\left( \frac{1-\delta ^{d}}{\pi g}\right) ^{k-l}\left( 1-\frac{1-\delta ^{d}}{\pi g}\right) \\&= \frac{1-\left( \frac{1-\delta ^{d}}{\pi g}\right) ^{k+1}}{1-\frac{1-\delta ^{d}}{\pi g}}\left( 1-\frac{1-\delta ^{d}}{\pi g}\right) \\&= \left( 1-\left( \frac{1-\delta ^{d}}{\pi g}\right) ^{k+1}\right) \end{aligned}$$

Next look at the effect of changing interest rates on newly issued rates on the fiscal burden.

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{ \{\partial R^\text{new}_{t+l}\}_{l=0}^{\infty } }&= \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k} \frac{\partial s_{t+j}}{\partial R^\text{ave}_{t+j-1}} \frac{\partial R^\text{ave}_{t+j-1} }{\{\partial R^\text{new}_{t+l}\}_{l=0}^{k}} \\&= \sum _{j=1}^{\infty }(\beta g)^{j} \frac{1}{g\pi }d \left( 1-\left( \frac{1-\delta ^{d}}{\pi g}\right) ^{j}\right) \\&=d\frac{1}{g\pi } \left( \frac{\frac{\pi g}{1+R}}{1-\frac{\pi g}{1+R}} - \frac{\frac{1-\delta ^{d}}{1+R}}{1-\frac{1-\delta ^{d}}{1+R}}\right) \\&=d\frac{1}{1+R} \frac{1}{\left( 1-\frac{\pi g}{1+R}\right) }\frac{1 - \frac{1-\delta ^{d}}{\pi g}}{\left( 1-\frac{1-\delta ^{d}}{1+R}\right) } \\&=\frac{d}{1+R} \frac{1}{\left( 1-\frac{\pi g}{1+R}\right) } \frac{1+R}{\delta ^{d}+R} \left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \end{aligned}$$

The first term of this expression simply scales the change by the steady state values of the fiscal burden and of the interest rate. Notice that, as we care about the effect as a percentage of GDP, the debt level d shows how big it will be. The second term shows that the effect is permanent as it is one over one minus the discount factor. Maturity matters chiefly as the third element is duration. The last term also depends on maturity and scales duration by the fact that with positive nominal growth legacy nominal debt will not have an effect as large as in a no growth economy.

We now combine the effect of a change in the inflation expectation on interest rates with the effect of the change in interest rates on the fiscal burden to find the effect of inflation expectations on the fiscal burden. Notice that the effect of a change in expectations in a given future horizon is the same irrespective of the period we are in, therefore the expression simplifies. We consider two cases, first if only inflation expectations on next period adjust:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j} }{\{\partial \mathbb {E}_{t+l}(\pi _{t+l+1})\}_{l=0}^{\infty }}&= \sum _{l=0}^{\infty }\frac{\partial d_{t}}{\partial R^\text{new}_{t+l}}\frac{\partial R^\text{new}_{t+l} }{\partial \mathbb {E}_{t+l}(\pi _{t+l+1})}\\&=\sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j} }{\partial R^\text{new}_{t+l}}\frac{1+R}{\pi }\frac{\delta ^{d}+R}{1+R} \\&= \frac{d}{1+R} \frac{1}{\left( 1-\frac{\pi g}{1+R}\right) } \frac{1+R}{\delta ^{d}+R} \left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \frac{1+R}{\pi }\frac{\delta ^{d}+R}{1+R} \\&= \frac{d}{\pi } \frac{1}{\left( 1-\frac{\pi g}{1+R}\right) }\left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \end{aligned}$$

And then if all future expectations adjust:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\{\partial \mathbb {E}_{t+l}(\pi _{t+l+m})\}_{m=1}^{\infty }\}_{l=0}^{\infty }}&= \sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial R^\text{new}_{t+l}}\frac{\partial R^\text{new}_{t+l} }{ \{\partial \mathbb {E}_{t+l}(\pi _{t+l+m})\}_{m=1}^{\infty } }\\&=\sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial R^\text{new}_{t+l}}\frac{1+R}{\pi } \\&=\frac{d}{1+R} \frac{1}{\left( 1-\frac{\pi g}{1+R}\right) } \frac{1+R}{\delta ^{d}+R} \left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \frac{1+R}{\pi } \\&= \frac{d}{\pi } \frac{1}{\left( 1-\frac{\pi g}{1+R}\right) } \frac{1+R}{\delta ^{d}+R} \left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \end{aligned}$$

We can see that even in the case in which all future expectations adjust the debt burden varies by less in the long debt case, as the legacy debt has its interest rate fixed. We now move to the effect of inflation on the debt burden. As a first step, find the effects of inflation on primary surpluses:

$$\begin{aligned} \frac{\partial s_{t+j}}{\partial \pi _{t+j}}&= \frac{\partial f_{t+j}}{\partial \pi _{t+j}} - \frac{\partial l_{t+j}}{\partial \pi _{t+j}}\\&= -(R^\text{ave}_{t+j-1} + \delta ^{d}) \frac{1}{g_{t+j}\pi _{t+j}^{2}}d + \frac{1}{g_{t+j}\pi _{t+j}}d\frac{\partial R^\text{ave}_{t+j-1}}{\partial \pi _{t+j}} - (1-\delta ^{d})\frac{1}{g_{t+j}\pi _{t+j}^{2}}d \\&= -(R^\text{ave}_{t+j-1} + 1) \frac{1}{g_{t+j}\pi _{t+j}^{2}}d + \frac{1}{g_{t+j}\pi _{t+j}}d\frac{\partial R^\text{ave}_{t+j-1}}{\partial \pi _{t+j}}\\&= -(R^\text{ave}_{t+j-1} + 1) \frac{1}{g_{t+j}\pi _{t+j}^{2}}d \end{aligned}$$

where the last step uses the fact that average interest rates prevailing in the last period are not affected by inflation in the current period, again holding expectation constant. Next, we show that changes in inflation do not have an effect also on the contemporaneous average interest rate if we are evaluating the change from steady state.

$$\begin{aligned} \frac{\partial R^\text{ave}_{t+j}}{\partial \pi _{t+j}}&= \left( 1-\frac{l_{t}}{d}\right) \frac{\partial R^\text{ave}_{t+j-1}}{\partial \pi _{t+j}}+ \frac{l_{t}}{d}\frac{\partial R^\text{new}_{t+j}}{\partial \pi _{t+j}} + \frac{1}{d} \left( R^\text{new}_{t+j}- R^\text{ave}_{t+j-1} \right) \frac{\partial l_{t+j}}{\partial \pi _{t+j}}\\&= \frac{1}{d} \left( R- R \right) \frac{\partial l_{t+j}}{\partial \pi _{t+j}}\\&= 0 \end{aligned}$$

Inflation rates in the past will not affect average interest rates as they have an effect on average interest rates today through their effect on contemporaneous average interest rates, which we just showed to be zero. Armed with these results, we can show the effect of inflation on the surplus at any horizon following the shock:

$$\begin{aligned} \frac{\partial s_{t+j}}{\{\partial \pi _{t+l}\}_{l=1}^{\infty }}&= \sum _{l=1}^{\infty } \frac{\partial s_{t+j}}{\partial \pi _{t+l}}\\&=\frac{\partial s_{t+j}}{\partial \pi _{t+j}}\\&= - (R^\text{ave}_{t+j-1} + 1) \frac{1}{g_{t+j}\pi _{t+j}^{2}}d + \frac{1}{g_{t+j}\pi _{t+j}}d\frac{\partial R^\text{ave}_{t+j-1}}{\partial \pi _{t+j}}\\&= \frac{1+R}{\pi }\frac{1}{g\pi }d \end{aligned}$$

Next, let us study what happens if inflation increases from tomorrow $t+1$ onward on the fiscal burden.

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+l}\}_{l=1}^{\infty }}&= \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k} \frac{\partial s_{t+j}}{\{\partial \pi _{t+l}\}_{l=1}^{\infty }}\\&= -\sum _{j=1}^{\infty }\left( \beta g\right) ^{j} \frac{1+R}{\pi }\frac{1}{g\pi }d\\&=-\frac{\beta g}{1-\beta g} \frac{1+R}{\pi }\frac{1}{g\pi }d\\&=-\frac{\frac{\pi g}{1+R}}{1-\frac{\pi g}{1+R}} \frac{1+R}{\pi }\frac{1}{g\pi }d\\&=-d\frac{1}{\pi }\frac{1}{1-\frac{\pi g}{1+R}} \end{aligned}$$

Finally, we combine the effects to study the joint effect of inflation and expectations under the two scenarios. Start with the case when all inflation expectations adjust to the new level of inflation.

$$\begin{aligned}&\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\{\partial \pi _{t+1+l},\mathbb {E}_{t+l}(\pi _{t+l+m})\}_{l=0}^{\infty }\}_{m=1}^{\infty }} \\&\quad \equiv \sum _{l=1}^{\infty } \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \pi _{t+l}} + \sum _{l=0}^{\infty }\sum _{m=1}^{\infty } \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \mathbb {E}_{t+l}(\pi _{t+l+m}) } \\&\quad = -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}}\left[ 1-\frac{1+R}{\delta ^{d}+R} \left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \right] \\&\quad = -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}}\left[ \frac{(\delta ^{d}+R)\pi g - (1+R)(\pi g -1 +\delta ^{d})}{(\delta ^{d}+R)\pi g} \right] \\&\quad = -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}}\left[ \frac{\delta ^{d}\pi g - R( -1 +\delta ^{d}) - (\pi g -1 +\delta ^{d})}{(\delta ^{d}+R)\pi g} \right] \\&\quad = -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}}\left[ \frac{(1-\delta ^{d})\left( \frac{1+R}{\pi g}-1\right) }{\delta ^{d}+R} \right] \\&\quad = -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}}\frac{1+R}{\delta ^{d}+R}\frac{1-\delta ^{d}}{\pi g}\left( 1- \frac{\pi g}{1+R}\right) \\&\quad = -d\frac{1}{\pi }\frac{1+R}{\delta ^{d}+R}\frac{1-\delta ^{d}}{\pi g} \end{aligned}$$

Next when only short run expectations adjust:

$$\begin{aligned} \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\{\partial \pi _{t+1+l},\mathbb {E}_{t+l}(\pi _{t+l+1})\}_{l=0}^{\infty }}&\equiv \sum _{l=1}^{\infty } \frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \pi _{t+l}} \\&\quad + \sum _{l=0}^{\infty }\frac{\partial \sum _{j=1}^{\infty }\beta ^{j}\prod _{k=1}^{j}g_{t+k}s_{t+j}}{\partial \mathbb {E}_{t+l}(\pi _{t+l+1}) } \\&= -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}}\left[ 1-\left( 1 - \frac{1-\delta ^{d}}{\pi g}\right) \right] \\&= -d\frac{1}{\pi }\frac{1}{1-\frac{g\pi }{1+R}} \frac{1-\delta ^{d}}{\pi g} \\&= -d\frac{1}{\pi }\frac{1}{R + 1-g\pi }\frac{1+R}{\delta ^{d}+R}(\delta ^{d}+R) \frac{1-\delta ^{d}}{\pi g} \\&= -d\frac{1}{\pi }\frac{R+\delta ^{d}}{R - (g\pi -1)}\frac{1+R}{\delta ^{d}+R}\frac{1-\delta ^{d}}{\pi g} \end{aligned}$$

These results are summarised in Table 14. In the first row we show the effect under any arbitrary maturity, and in the second row we show the same effect under short debt. Overall, the same pattern emerges. When debt is short, it does not matter if the inflation target is missed or not, the fiscal burden does not vary. When debt is long there are potentially large variations in the fiscal burden. When all expectations adjust the variation is approximately Duration-to-GDP. With long debt $\frac{1-\delta ^{d}}{\pi g}$ is close to one. When only short run inflation expectation moves, the fiscal burden varies a lot more. The multiplicative factor $\frac{R+\delta ^{d}}{R - (g\pi -1)}$ is larger than in the legacy debt only case as we are subtracting the net nominal growth rate of the economy $g\pi -1$ from net nominal interest rates R.

Table 14 Inflation, Maturity, and Fiscal Burdens with Debt Stabilisation

Data Fit of Geometric Approximation Model

The proposed geometric approximation model has the benefit of fully characterising public debt and its law of motion with a small number of state variables. This allows to prove a number of results, as the market value to interest rate saving mapping that Duration-to-GDP allows and to avoid the curse of dimensionality that models with unrestricted maturity choices face. However, an important question that arises from this model is how good it is as an approximation for actual public debt promises. We cannot answer this question with the dataset used in this paper, as we have only information on averages: Macaulay duration and average life. However, we can use the results from Andreolli (2022) on US data with bond-by-bond data. He shows that the model has a high fit on actual public debt promises: he computes the $R^2$ in each period of his US estimation sample on annual model predicted principal debt promises on actual promises. The average R2 is high at 0.9001 and its standard deviation is low at 0.0306. He uses bond-by-bond data, which are nominally fixed rate, marketable bonds held by the public. The full description of the data construction can be found in Appendix A of Andreolli (2022). Figure 14 shows on a given period (December 2007) the model predictions vis-à-vis the data. The key take away is that this model does a good job in approximating the actual maturity choices of the US treasury, so that we do not lose much in precision but we gain in tractability and in being able to use average maturity data.

Fig. 14

Geometric Approximation Fit. Notes: The figure presents the fraction of principal debt promises in the data and in the geometric approximation model for the USA in December 2007. The data come from bond-by-bond data which are nominally fixed rate, marketable bonds held by the public. The model fits this data with the maturity parameter

Time Varying Maturity and Recursive Formulation

In order to fit the quantitative model to the data, we need to accommodate for the existence of a time varying maturity structure. In this appendix, we show how to extend the framework from first principles while retaining a recursive structure under a first-order approximation. Let us assume that in each period the government issues new debt $L_{t}$ with a geometrically decaying principal with an interest rate $R^\text{new}_{t}$ and a maturity parameter $\delta ^\text{new}_{t}$. With this formulation, each bond vintage has a geometric structure, but the overall debt stock does not as we do not have a unique discounting parameter. However, we show that for a small deviation from steady state the overall debt stock retains a geometric structure with the average principal repayment. Let us start by defining the non-approximated stock of debt, average principal due, average interest rate on debt:

$$\begin{aligned} {\tilde{D}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}L_{t-j}\\ {\tilde{\delta }}^\text{ave}_{t}{\tilde{D}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}L_{t-j}\delta ^\text{new}_{t-j}\\ {\tilde{R}}^\text{ave}_{t}{\tilde{D}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}L_{t-j}R^\text{new}_{t-j} \end{aligned}$$

Divide by real GDP ($Y_{t}$) and the price level ($P_{t}$) at various horizons and define cumulative growth: $g_{t|t-j}\equiv \frac{Y_{t}}{Y_{t-j}}$ and cumulative inflation: $\pi _{t|t-j}\equiv \frac{P_{t}}{P_{t-j}}$. Lower case letters define issuance and debt over nominal GDP ($l_{t}\equiv \frac{L_{t}}{Y_{t}P_{t}}$ and ${\tilde{d}}_{t}\equiv \frac{{\tilde{D}}_{t}}{Y_{t}P_{t}}$).

$$\begin{aligned} {\tilde{d}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}\\ {\tilde{\delta }}^\text{ave}_{t}{\tilde{d}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}\delta ^\text{new}_{t-j}\\ {\tilde{R}}^\text{ave}_{t}{\tilde{d}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}R^\text{new}_{t-j} \end{aligned}$$

We are going to guess a recursive formulation for the three variables:

$$\begin{aligned} d_{t}&= l_{t} + \frac{1-\delta ^\text{ave}_{t-1}}{\pi _{t|t-1}g_{t|t-1}}d_{t-1} \end{aligned}$$

(7)

$$\begin{aligned} \delta ^\text{ave}_{t}d_{t}&= l_{t} \delta ^\text{new}_{t} + \frac{1-\delta ^\text{ave}_{t-1}}{\pi _{t|t-1}g_{t|t-1}}\delta ^\text{ave}_{t-1}d_{t-1} \end{aligned}$$

(8)

$$\begin{aligned} R^\text{ave}_{t}d_{t}&= l_{t} R^\text{new}_{t} + \frac{1-\delta ^\text{ave}_{t-1}}{\pi _{t|t-1}g_{t|t-1}}R^\text{ave}_{t-1}d_{t-1} \end{aligned}$$

(9)

Notice that in steady state the two formulations are equivalent with ${\tilde{\delta }}^\text{ave}=\delta ^\text{ave}=\delta ^\text{new}=\delta$, ${\tilde{d}}=d=l\frac{1}{1-\frac{1-\delta }{\pi g}}$ (with no nominal growth $\pi g=1$, this simplifies to $d=l/\delta$), and ${\tilde{R}}^\text{ave}=R^\text{ave}=R^\text{new}=R$, where a variable without subscript indicates the steady state value. Start by taking a first-order Taylor approximation of the recursive formulation, where we linearize debt, issuance, interest rates and the decaying parameter and log-linearize growth, and inflation. ${\hat{x}}_{t}\equiv x_{t}-x$ for l, d, R, and $\delta$ and ${\hat{x}}_{t}\equiv \frac{x_{t}-x}{x}$ for $\pi$ and g. The law of motion of the debt stock:

$$\begin{aligned} {\hat{d}}_{t}&= {\hat{l}}_{t} + \frac{1-\delta }{\pi g} {\hat{d}}_{t-1} - \frac{1-\delta }{\pi g}d ({\hat{\pi }}_{t|t-1}+{\hat{g}}_{t|t-1}) - \frac{1}{\pi g}d {\hat{\delta }}^\text{ave}_{t-1} \end{aligned}$$

The law of motion of the average fraction of debt to be repaid:

$$\begin{aligned} d{\hat{\delta }}^\text{ave}_{t} + \delta {\hat{d}}_{t}&= l{\hat{\delta }}^\text{new}_{t} + \delta \left[ {\hat{l}}_{t} + \frac{1-\delta }{\pi g} {\hat{d}}_{t-1} - \frac{1-\delta }{\pi g}d ({\hat{\pi }}_{t|t-1}+{\hat{g}}_{t|t-1}) - \frac{1}{\pi g}d {\hat{\delta }}^\text{ave}_{t-1}\right] \\&\quad + \frac{1-\delta }{\pi g}d {\hat{\delta }}^\text{ave}_{t-1}\\ d{\hat{\delta }}^\text{ave}_{t}&= l{\hat{\delta }}^\text{new}_{t} + \frac{1-\delta }{\pi g}d {\hat{\delta }}^\text{ave}_{t-1}\\ {\hat{\delta }}^\text{ave}_{t}&= \left( 1-\frac{1-\delta }{\pi g }\right) {\hat{\delta }}^\text{new}_{t} + \frac{1-\delta }{\pi g} {\hat{\delta }}^\text{ave}_{t-1}\\ \end{aligned}$$

The law of motion of the average interest rate:

$$\begin{aligned} d{\hat{R}}^\text{ave}_{t} + R {\hat{d}}_{t}&= l{\hat{R}}^\text{new}_{t} + R\left[ {\hat{l}}_{t} + \frac{1-\delta }{\pi g} {\hat{d}}_{t-1} - \frac{1-\delta }{\pi g}d ({\hat{\pi }}_{t|t-1}+{\hat{g}}_{t|t-1}) - \frac{1}{\pi g}d {\hat{\delta }}^\text{ave}_{t-1}\right] \\&\quad + \frac{1-\delta }{\pi g}d {\hat{R}}^\text{ave}_{t-1}\\ {\hat{R}}^\text{ave}_{t}&= \left( 1-\frac{1-\delta }{\pi g }\right) {\hat{R}}^\text{new}_{t} + \frac{1-\delta }{\pi g} {\hat{R}}^\text{ave}_{t-1} \end{aligned}$$

We now move to the variables without the recursiveness guess. Start again with the law of motion of the stock of debt.

$$\begin{aligned} {\tilde{d}}_{t}&=\sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}\\ {\tilde{d}}_{t}&=\sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{\prod _{k=0}^{j-1}g_{t-k|t-k-1} \pi _{t-k|t-k-1}}l_{t-j}\\ \hat{{\tilde{d}}_{t}}&=\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} {\hat{l}}_{t-j} - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \sum _{k=0}^{j-1}\left( {\hat{g}}_{t-k|t-k-1} + {\hat{\pi }}_{t-k|t-k-1}\right) \\&\quad - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } j {\hat{\delta }}^\text{new}_{t-j} \end{aligned}$$

Use this expression in the law of motion of the average principal repayment.

$$\begin{aligned} {\tilde{\delta }}^\text{ave}_{t}{\tilde{d}}_{t}&= \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{\prod _{k=0}^{j-1}g_{t-k|t-k-1} \pi _{t-k|t-k-1}}l_{t-j}\delta ^\text{new}_{t-j}\\ {\tilde{d}}\hat{{\tilde{\delta }}}^\text{ave}_{t} + \delta \hat{{\tilde{d}}}_{t}&= \delta \Bigg [\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} {\hat{l}}_{t-j} - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \sum _{k=0}^{j-1}\left( {\hat{g}}_{t-k|t-k-1} + {\hat{\pi }}_{t-k|t-k-1}\right) \\&\quad - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } j {\hat{\delta }}^\text{new}_{t-j}\Bigg ] + \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{\delta }}^\text{new}_{t-j} \\ {\tilde{d}}\hat{{\tilde{\delta }}}^\text{ave}_{t}&= \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{\delta }}^\text{new}_{t-j} \\ {\tilde{d}}\hat{{\tilde{\delta }}}^\text{ave}_{t}&= l {\hat{\delta }}^\text{new}_{t} + \left( \frac{1-\delta }{\pi g}\right) {\tilde{d}}\hat{{\tilde{\delta }}}^\text{ave}_{t-1}\\ \hat{{\tilde{\delta }}}^\text{ave}_{t}&= \left( 1- \frac{1-\delta }{\pi g} \right) {\hat{\delta }}^\text{new}_{t} + \left( \frac{1-\delta }{\pi g}\right) \hat{{\tilde{\delta }}}^\text{ave}_{t-1}\\ \end{aligned}$$

This last expression shows that $\hat{{\tilde{\delta }}}^\text{ave}_{t}$ has a recursive structure and it is equal to the expression for ${\hat{\delta }}^\text{ave}_{t}$. We are going to use this result back in the last term of the debt stock formula:

$$\begin{aligned} \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } j {\hat{\delta }}^\text{new}_{t-j}&=\sum _{k=1}^{\infty } \sum _{j=k}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } {\hat{\delta }}^\text{new}_{t-j}\\&=\frac{1}{1-\delta }\sum _{k=1}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{k} \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{\delta }}^\text{new}_{t-k-j}\\&=\frac{1}{1-\delta }\sum _{k=1}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{k} {\tilde{d}}\hat{{\tilde{\delta }}}^\text{ave}_{t-k}\\&=\frac{1}{1-\delta }\frac{1}{1-\frac{1-\delta }{\pi g}}\sum _{k=1}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{k} l\hat{{\tilde{\delta }}}^\text{ave}_{t-k}\\&=\frac{1}{1-\delta }\frac{ \frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\sum _{k=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{k} l\hat{{\tilde{\delta }}}^\text{ave}_{t-1-k}\\ \end{aligned}$$

Use a similar method to express the cumulative inflation and growth:

$$\begin{aligned}&\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \sum _{k=0}^{j-1}\left( {\hat{g}}_{t-k|t-k-1} + {\hat{\pi }}_{t-k|t-k-1}\right) =\\&\quad =0 + l \left( \frac{1-\delta }{\pi g}\right) ({\hat{g}}_{t|t-1} + {\hat{\pi }}_{t|t-1}) + l \left( \frac{1-\delta }{\pi g}\right) ^2 ({\hat{g}}_{t|t-1} + {\hat{\pi }}_{t|t-1} + {\hat{g}}_{t-1|t-2} + {\hat{\pi }}_{t-1|t-2})\\&\qquad + l \left( \frac{1-\delta }{\pi g}\right) ^{3} ({\hat{g}}_{t|t-1} + {\hat{\pi }}_{t|t-1} + {\hat{g}}_{t-1|t-2} + {\hat{\pi }}_{t-1|t-2}+ {\hat{g}}_{t-2|t-3} + {\hat{\pi }}_{t-2|t-3})+\dots \\&\quad = l \frac{\frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\left( \frac{1-\delta }{\pi g}\right) ^{0}({\hat{g}}_{t|t-1} + {\hat{\pi }}_{t|t-1}) + l \frac{\frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\left( \frac{1-\delta }{\pi g}\right) ^{1}({\hat{g}}_{t-1|t-2} + {\hat{\pi }}_{t-1|t-2})\\&\qquad + l \frac{\frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\left( \frac{1-\delta }{\pi g}\right) ^{2}({\hat{g}}_{t-2|t-3} + {\hat{\pi }}_{t-2|t-3})+\dots \\&\quad = l \frac{\frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\sum _{j=0}^{\infty }\left( \frac{1-\delta }{\pi g}\right) ^{j}({\hat{g}}_{t-j|t-j-1} + {\hat{\pi }}_{t-j|t-j-1}) \\ \end{aligned}$$

Plug these results in the debt expression and obtain in a recursive formulation:

$$\begin{aligned} \hat{{\tilde{d}}_{t}}&=\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} {\hat{l}}_{t-j} - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \sum _{k=0}^{j-1}\left( {\hat{g}}_{t-k|t-k-1} + {\hat{\pi }}_{t-k|t-k-1}\right) \\&\quad - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } j {\hat{\delta }}^\text{new}_{t-j}\\ \hat{{\tilde{d}}_{t}}&=\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} {\hat{l}}_{t-j} -l \frac{\frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\sum _{j=0}^{\infty }\left( \frac{1-\delta }{\pi g}\right) ^{j}({\hat{g}}_{t-j|t-j-1} + {\hat{\pi }}_{t-j|t-j-1}) \\&\quad - \frac{1}{1-\delta }\frac{ \frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l\hat{{\tilde{\delta }}}^\text{ave}_{t-1-j}\\ \hat{{\tilde{d}}_{t}}&={\hat{l}}_{t} -l \frac{\frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}}({\hat{g}}_{t|t-1} + {\hat{\pi }}_{t|t-1}) - \frac{1}{1-\delta }\frac{ \frac{1-\delta }{\pi g}}{1-\frac{1-\delta }{\pi g}} l\hat{{\tilde{\delta }}}^\text{ave}_{t-1} + \left( \frac{1-\delta }{\pi g}\right) \hat{{\tilde{d}}}_{t-1}\\ \hat{{\tilde{d}}_{t}}&={\hat{l}}_{t} -\frac{1-\delta }{\pi g}{\tilde{d}}({\hat{g}}_{t|t-1} + {\hat{\pi }}_{t|t-1}) - \frac{1}{\pi g}{\tilde{d}}\hat{{\tilde{\delta }}}^\text{ave}_{t-1} + \left( \frac{1-\delta }{\pi g}\right) \hat{{\tilde{d}}}_{t-1}\\ \end{aligned}$$

Which has the same recursive structure and it is equal to ${\hat{d}}_{t}$. We can show with similar steps the same result for the average interest rate:

$$\begin{aligned} {\tilde{R}}^\text{ave}_{t}{\tilde{d}}_{t}&= \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}R^\text{new}_{t-j}\\ {\tilde{R}}^\text{ave}_{t}{\tilde{d}}_{t}&= \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{\prod _{k=0}^{j-1}g_{t-k|t-k-1} \pi _{t-k|t-k-1}}l_{t-j}R^\text{new}_{t-j}\\ {\tilde{d}}\hat{{\tilde{R}}}^\text{ave}_{t} + R \hat{{\tilde{d}}}_{t}&= R \Bigg [\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} {\hat{l}}_{t-j} - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \sum _{k=0}^{j-1}\left( {\hat{g}}_{t-k|t-k-1} + {\hat{\pi }}_{t-k|t-k-1}\right) \\&\quad - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } j {\hat{\delta }}^\text{new}_{t-j}\Bigg ] + \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{R}}^\text{new}_{t-j} \\ {\tilde{d}}\hat{{\tilde{R}}}^\text{ave}_{t}&= \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{R}}^\text{new}_{t-j} \\ \hat{{\tilde{R}}}^\text{ave}_{t}&= \left( 1- \frac{1-\delta }{\pi g} \right) {\hat{R}}^\text{new}_{t} + \left( \frac{1-\delta }{\pi g}\right) \hat{{\tilde{R}}}^\text{ave}_{t-1}\\ \end{aligned}$$

This means that the recursive formulation works up to a first-order approximation even if the time varying maturity does not yield an exact recursive structure.

1.1 Note on Secondary Market Price

We can show that the secondary market price of the overall debt stock behaves as in the constant maturity case in the linearized equilibrium. First of all, define the secondary market price of the overall stock of public debt the price that multiplies the book value of debt such that the product equal to the issuance weighted sum of secondary market prices of various debt vintages ($q^{t-j}_{t}$ is the price at time t of debt issued in period $t-j$).

$$\begin{aligned} {\tilde{q}}^{D}_{t}{\tilde{D}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}L_{t-j}q^{t-j}_{t} \end{aligned}$$

In GDP units:

$$\begin{aligned} {\tilde{q}}^{D}_{t}{\tilde{d}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}q^{t-j}_{t} \end{aligned}$$

As long as no-arbitrage across vintages holds, then Euler equation, for an arbitrary unique stochastic discount factor is:

$$\begin{aligned} q^{t-j}_{t}&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M_{t+k|t}}{\pi _{t+k|t}}\left( (1-\delta ^\text{new}_{t-j})q^{t-j}_{t+1} + R^\text{new}_{t-j} + \delta ^\text{new}_{t-j}\right) \right] \\ q^{t-j}_{t}&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M_{t+k|t}}{\pi _{t+k|t}}(1-\delta ^\text{new}_{t-j})^{k-1}\left( R^\text{new}_{t-j} + \delta ^\text{new}_{t-j}\right) \right] \end{aligned}$$

In state state:

$$\begin{aligned} \frac{1}{R+\delta }&= \left[ \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^k}(1-\delta )^{k-1}\right] \end{aligned}$$

where M(k) is the steady state stochastic discount factor k periods ahead. Notice that we do not assume an exponential form for the stochastic discount factor, so that we allow for any arbitrary yield curve shape in steady state.

Take a first-order Taylor approximation around the steady state of the above expression:

$$\begin{aligned} \frac{q^{t-j}_{t}}{ R^\text{new}_{t-j} + \delta ^\text{new}_{t-j}}&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M_{t+k|t}}{\pi _{t+k|t}}(1-\delta ^\text{new}_{t-j})^{k-1}\right] \\ {\hat{q}}^{t-j}_{t}\frac{1}{ R+ \delta } - \frac{1}{(R+ \delta )^2} ( {\hat{R}}^\text{new}_{t-j} + {\hat{\delta }}^\text{new}_{t-j})&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-1} ({\hat{M}}_{t+k|t} - {\hat{\pi }}_{t+k|t}) \right] \\&\quad - \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-2}(k-1){\hat{\delta }}^\text{new}_{t-j} \\ {\hat{q}}^{t-j}_{t}\frac{1}{ R+ \delta } - \frac{1}{(R+ \delta )^2} ( {\hat{R}}^\text{new}_{t-j} + {\hat{\delta }}^\text{new}_{t-j})&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-1} ({\hat{M}}_{t+k|t} - {\hat{\pi }}_{t+k|t}) \right] \\&\quad - {\hat{\delta }}^\text{new}_{t-j}\frac{d}{d(1-\delta )}\sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-1} \\ {\hat{q}}^{t-j}_{t}\frac{1}{ R+ \delta } - \frac{1}{(R+ \delta )^2} ( {\hat{R}}^\text{new}_{t-j} + {\hat{\delta }}^\text{new}_{t-j})&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-1} ({\hat{M}}_{t+k|t} - {\hat{\pi }}_{t+k|t}) \right] \\&\quad - {\hat{\delta }}^\text{new}_{t-j}\frac{d}{d(1-\delta )}\frac{1}{R+\delta } \\ {\hat{q}}^{t-j}_{t}\frac{1}{ R+ \delta } - \frac{1}{(R+ \delta )^2} ( {\hat{R}}^\text{new}_{t-j} + {\hat{\delta }}^\text{new}_{t-j})&= \mathbb {E}_{t} \left[ \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-1} ({\hat{M}}_{t+k|t} - {\hat{\pi }}_{t+k|t}) \right] \\&\quad - {\hat{\delta }}^\text{new}_{t-j}\frac{1}{(R+\delta )^2} \\ {\hat{q}}^{t-j}_{t}&= \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t-j}+ (R+ \delta )\mathbb {E}_{t}\\&\quad \left[ \sum _{k=1}^{\infty }\frac{M(k)}{\pi ^{k}}(1-\delta )^{k-1} ({\hat{M}}_{t+k|t} - {\hat{\pi }}_{t+k|t}) \right] \end{aligned}$$

where $\frac{d}{d(1-\delta )}$ is the derivative with respect to $1-\delta$. Notice that the last term of the final expression is equal across vintages j. We can use this result together with the fact that the price of the current vintage ($j=0$) is always zero, as the interest rate on newly issued debt $R^\text{new}_{t}$ adjusts to express the price only in terms of vintage interest rates compared to the current one:

$$\begin{aligned} {\hat{q}}^{t-j}_{t}&= \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t-j} - \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t} \end{aligned}$$

Armed with this last result, we can linearize the expression for secondary market price of overall debt:

$$\begin{aligned} {\tilde{q}}^{D}_{t}{\tilde{d}}_{t}&\equiv \sum _{j=0}^{\infty } (1-\delta ^\text{new}_{t-j})^{j}\frac{1}{g_{t|t-j} \pi _{t|t-j}}l_{t-j}q^{t-j}_{t} \\ {\tilde{d}}\hat{{\tilde{q}}}^{D}_{t} + q \hat{{\tilde{d}}}_{t}&= q \Bigg [\sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} {\hat{l}}_{t-j} - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \sum _{k=0}^{j-1}\left( {\hat{g}}_{t-k|t-k-1} + {\hat{\pi }}_{t-k|t-k-1}\right) \\&\quad - \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \frac{1}{1-\delta } j {\hat{\delta }}^\text{new}_{t-j}\Bigg ] + \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{q}}^{t-j}_{t} \\ {\tilde{d}}\hat{{\tilde{q}}}^{D}_{t}&= \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l {\hat{q}}^{t-j}_{t} \\ {\tilde{d}}\hat{{\tilde{q}}}^{D}_{t}&= \sum _{j=0}^{\infty } \left( \frac{1-\delta }{\pi g}\right) ^{j} l \left( \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t-j} - \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t}\right) \\ {\tilde{d}}\hat{{\tilde{q}}}^{D}_{t}&= {\tilde{d}}\left( \frac{1}{(R+ \delta )} {\hat{R}}^\text{ave}_{t} - \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t}\right) \\ \hat{{\tilde{q}}}^{D}_{t}&= \frac{1}{(R+ \delta )} {\hat{R}}^\text{ave}_{t} - \frac{1}{(R+ \delta )} {\hat{R}}^\text{new}_{t} \end{aligned}$$

Which says that the secondary market price will be higher if the average interest rate is with respect to the interest rate on newly issued debt. Notice that this is the same expression as under fixed maturity, and variation in maturity does not affect the secondary market price up to a first-order approximation.

Counterfactual Experiments Details

In this appendix, we describe how we fit the data in the theoretical model and perform additional experiments.

We use the same dataset as in the empirical exercises. for the main three state variables, bond debt-to-GDP $d_{t}$, average interest rates at book value $R^\text{ave}_{t}$, and average fraction of bond debt due in each period $\delta ^\text{ave}_{t}$, we use seasonally adjusted government securities debt over GDP from OECD data, government bonds average coupon from WGBI data, and (one over) government bonds average life from WGBI data. We adjust all data to quarterly frequency. Real GDP growth $g_{t}$ (OECD data for European Countries and Fred for the US) and inflation $\pi _{t}$ (HICP for the Euro Area and CPI for the US) are QoQ rates. With respect to inflation expectations in the baseline, we use raw SPF data and we assign forecasts in the following way. For the Euro Area expectations, we use current year expectations for the following two quarters, 1-year-ahead expectation for three and four quarters ahead, 2 years ahead expectations for five to eight quarters ahead, and long run expectations from nine quarters ahead onwards. For the USA, we use the same data, but as 2 years ahead expectations are not recorded in the SPF we use inflation in two calendar years from now for five to eight quarters ahead when available and QoQ inflation four quarters ahead when not available.

We measure the interest rate on newly issued debt $R^\text{new}_{t}$ with the benchmark interest rate on a 10-year government bond, we use this rate as it is the most liquid and it is available for all countries in the sample for the all sample. We compute issuance over GDP $l_{t}$ and (one over) maturity on newly issued debt $\delta ^\text{new}_{t}$ from equations (7) and (8). As this is “flow” derived data from “stock” original data, it is imprecise. Therefore, we filter $\delta ^\text{new}_{t}$ with a HP filter with a low smoothing parameter (10) and keep the trend component.⁴⁰ We ensure that the maximum average maturity for newly issued debt is 20 years (that is, we allow for longer debt, up to consoles, but the average maturity of debt issued in a quarter does not exceed that threshold, as in the data).

The only parameter we calibrate is $\beta$ as 0.995. With this parameter, inflation expectation data, maturity on newly issued debt, and interest rates on newly issued debt we compute the convenience yield $c_{t}$ (or term premium or liquidity premium or risk premium) as the difference between interest rates on newly issued debt and the interest rate that would prevail under risk neutral pricing from the Euler equation with the calibrated $\beta$. Finally, we also find the net resource needs $s_{t}$ from equations (7), (8), (9), and the budget constraint. The following equations summarise the system here for convenience:

$$\begin{aligned} f_{t}&= (R^\text{ave}_{t-1} + \delta ^\text{ave}_{t-1}) \frac{1}{g_{t}\pi _{t}}d_{t-1}&\Leftarrow \text {Debt Payments}\\ d_{t}&= (1-\delta ^\text{ave}_{t-1})\frac{1}{g_{t}\pi _{t}}d_{t-1} + l_{t}&\Leftarrow \text {Debt Law of Motion (LoM)} \\ R^\text{ave}_{t}&= \left( 1-\frac{l_{t}}{d_{t}}\right) R^\text{ave}_{t-1} + \frac{l_{t}}{d_{t}}R^\text{new}_{t}&\Leftarrow \text {Average Interest Rate on Debt LoM}\\ \delta ^\text{ave}_{t}&= \left( 1-\frac{l_{t}}{d_{t}}\right) \delta ^\text{ave}_{t-1} + \frac{l_{t}}{d_{t}}\delta ^\text{new}_{t}&\Leftarrow \text {Average Debt Maturity LoM}\\ f_{t}&=s_{t} + l_{t}&\Leftarrow \text {Govt Budget Constraint} \\ \frac{1}{(\delta ^\text{new}_{t} +R^\text{new}_{t} - c_{t})}&= \mathbb {E}_{t}\sum _{j=1}^{\infty }\left[ \frac{1}{\pi _{t+j|t}}\beta ^{j}(1-\delta ^\text{new}_{t})^{j-1}\right]&\Leftarrow \text {Bond Euler} \\ \end{aligned}$$

Table 4 shows the results of this exercise in the baseline sample. Additionally, Table 15 shows the same results in the whole sample, from 2000Q1 to 2022Q1. The results are very similar.

In our baseline exercise, we use Euro Area wide HICP inflation for each Euro Area country for inflation realisations. We do this as this maps directly to the Survey of Professional Forecasters inflation expectations. However, an important question is how using country specific inflation can affect results, as country specific inflation is finally what affects debt dynamics. In Table 16, we rerun the baseline exercise (short-vs-long debt) under country specific HICP in columns 4 and 5 and under the country specific GDP deflator in columns 6 and 7. We can see how the numbers are very similar across the various scenarios and therefore conclude that the results are not strongly affected by the inflation measure we employ.

In Table 17, we rerun the same exercise where we exclude the debt held in the context of the ECB QE programmes that bought public sector bonds: the Public Sector Purchase Programme (PSPP) as part of the broader Asset Purchase Programme (APP) and in the Pandemic Emergency Purchase Programme (PEPP). The numbers are lower but not strongly so, as the ECB QE started relatively late and until recently did not own a significant share of outstanding public debt.

In Table 18, we ask how long it would take for the results to be overturned by the high inflation episode. Specifically, we run the model forward in the future with the most recent values for the exogenous variables. This implies that realised inflation would be high, with short run inflation expectation being relatively high, but long run inflation expectation being still anchored to the inflation target, making long-term debt much cheaper ex-post than short debt. We run the baseline model and the counterfactual model with one period debt. We ask how long it takes until the short debt profile produces a higher debt level than the baseline model. We can see that this ranges between 2024Q4 for the USA to 2034Q4 for Belgium, with most countries in the 2026/2027 range. This shows that, even the unexpected high inflation we recently observed takes a while to overturn the debt burden results, as the long low inflation regime accumulated to high differential debt burdens.

Table 15 Counterfactual Exercises—With Recent Period

Table 16 Counterfactual Exercises—Alternative Inflation Measures

Table 17 Counterfactual Exercises—No ECB QE

Table 18 Counterfactual Exercises—How Long Until Results Reverse

Fig. 15

Fiscal Consequences of Missing Inflation Targets—Extended Country Sample. Notes: This figure shows the results under the counterfactual exercise. It shows the path of debt, interest payments, and debt-embedded inflation expectations for the Belgium, Spain, the Netherlands, and Austria. The blue solid line shows the path of these variables under the actual maturity structure $\delta ^\text{ave}_{t}$, the red dot-dashed line shows the path under a counterfactual short debt ($\delta ^\text{ave}_{t}=1$). The sample goes from 2001Q1 to 2021Q1