Introduction

Evolutionary game theory works if an individual's performance not only depends on its own type, but also on the type of individuals with whom they interact. It links the neutral drift theory1 with survival of the fittest in evolutionary theory2,3,4,5. Evolutionary game theory can also be used to study cultural dynamics including human strategic behavior and updating6,7,8. Interesting questions in this field include: i) based on what knowledge, do individuals update their strategies? ii) how do individuals update their strategies?

It is important to understand how humans behave. Yet, it is still an open question to be studied, since various updating mechanisms have been supported experimentally in humans9,10,11,12. It is a great challenge, which is mainly because of a lack of verifiable constraint of human behaviors. Recent experimental investigation paves the way for tackling such questions. It is found that the cooperation level does not change in spatial structures compared with a well-mixed population12,13,14. This contradicts previous theoretical results based on imitation rules which show that spatial structure promotes cooperation. Here imitation means that players update their strategies after the comparison between their own payoffs via the game and another individual's15,16,17. It provides a constraint on searching for the updating rules of humans. Those that do not change the cooperation level in spatial populations may likely be candidates. Progress along this line is fruitful. One of the key findings is that self-evaluation based updating can result in the invariance of cooperation level in different population structures12,18,19. While simulation results are abundant, analytical investigation is rare.

Here we analytically show that the aspiration dynamics makes the cooperation level invariant in different population structures. In aspiration-driven updating, players switch strategies if an aspiration level is not met, where the level of aspiration is an intrinsic property of the focal individual20,21,22,23,24. Aspiration-driven dynamics are often observed in studies of animal and human behavioral ecology. For example, fish would ignore social information when they have relevant personal information25. Experienced ants hunt for food based on their own previous chemical trails rather than imitating others26. Aspiration also plays a key role in the individual behaviors in rat populations27. These examples clearly show that the idea behind aspiration dynamics, i.e., self-evaluation, is present in the animal world. In behavioral sciences, the view that individuals value their payoffs by comparing them with an aspiration level has a long tradition28,29. It is also studied as in the domain of human decision-making under risk30,31. Aspiration levels are frequently incorporated when predicting behaviors in interactive situations21,32,33,34,35,36.

We study the statistical mechanics of a simple case of aspiration-driven self-learning dynamics in various structured populations of finite size. For regular graphs, under weak selection approximation, we show that the favored strategy by aspiration dynamics is the same as that of a well-mixed population. For irregular graphs, simulations suggest the same result in random networks. Simulations also extrapolate our weak selection results to stronger selection cases. Our results foster the understanding of aspiration dynamics in structured population. And it may trigger the studies in behavior experiments.

Results

Model definition

We consider stochastic evolutionary game dynamics with two strategies in a structured population of finite size, N. A focal player can be of type A, or B and interact with all of its neighbors according to the underlying population structure. In the model, each individual occupies a vertex of a graph. The edges denote connections between players in terms of interaction of game. Here we only consider that the interaction graph and the replacement graph are identical, although they need not be the same37. In individual encounters, players obtain their payoffs from simultaneous actions. Based on all the interactions, an average payoff of an individual is calculated based on the payoff matrix as follows

For example, a B player, which encounters k other individuals and i of those are type A, obtains payoff [ci+d(k − i)]/k. An A player connected with i other A player and k − i B players obtains payoff [ai + b(k − i)]/k.

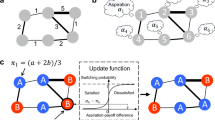
In the following, we introduce an update rule based on a global level of aspiration. This allows us to define a Markov chain describing the inherently stochastic dynamics in a finite population: probabilistic change of the composition of the population is driven by the fact that each individual compares its actual payoff with an imaginary value that it aspires to. Note here that we are only interested in the simplest way to model such a complex problem and do not address any learning process that may adjust such an aspiration level as the system evolves. For a sketch of the aspiration-driven evolutionary game, see Fig. 1.

Figure 1
figure 1

Evolutionary game dynamics in structured populations driven by global aspiration.

In our mathematical model of strategy updating driven by self-learning, players in the finite population are assigned on a graph structure to play the game. According to this, players calculate and obtain their actual payoffs. They are more likely to switch strategies if the payoffs they aspire to are not met. On the other hand, the higher the actual payoffs compared with the aspiration level α are, the less likely they switch their strategies. Besides, strategy switching is also determined by a selection intensity ω. For vanishing selection intensity, switching is entirely random irrespective of payoffs and the aspiration level. For increasing selection intensity, the self-learning process becomes increasingly more “optimal” in the sense that for high ω, individuals tend to always switch when they are dissatisfied and never switch when they are tolerant. We examine the simplest possible setup, where the level of aspiration α is a global parameter that does not change with the dynamics. We show that, however, the average abundance of a strategy does not depend on α under weak selection.

Full size image

Aspiration-level-driven stochastic dynamics

We consider the simplest case of an entire population having a certain level of aspiration. Players needn't see any particular payoffs but their own, which they compare with an aspiration value. This level of aspiration, α, is a variable that influences the stochastic strategy updating. The probability of switching strategy is random when individuals' payoffs are close to the level of aspiration, reflecting the basic degree of uncertainty in the population. When payoffs exceed the aspiration, strategy switching is unlikely. At high values of aspiration compared with payoffs, switching probabilities are high.

Note that although the level of aspiration is a global variable and does not differ individually, owing to payoff inhomogeneity there can always be a part of the population that seeks to switch more often due to dissatisfaction with the payoff distribution.

In our microscopic update process, we randomly choose an individual, x, from the population and assume that the average payoff of the focal individual is πx. To model stochastic aspiration-driven switching, we can use the following probability function

which is similar to the Fermi-rule20,38, but replaces a randomly drawn opponent's payoff by the aspiration level. The wider the positive gap between aspiration and payoff, the higher the switching probability. Reversely, if payoffs exceed the level of aspiration individuals become less active with increasing payoffs. The aspiration level, α, provides the benchmark used to evaluate how “greedy” an individual is. Higher aspiration levels mean that individuals aspire to higher payoffs. In addition, when modeling human strategy updating, one typically introduces another global parameter, the intensity of selection, ω, which provides a measure for how important individuals deem the impact of the actual game on their update. Irrespective of the aspiration level and the frequency dependent payoff distribution, vanishing values of ω refer to nearly random strategy updating. For large values of ω, individuals' deviations from their aspiration level have a strong impact on the dynamics. In the case of ω → ∞, individuals are strict in the sense that they either switch strategies with probability one if they are not satisfied, or stay with their current strategy if their aspiration level is met or overshot.

In the analysis process (see Methods and Supplementary Information ), we are interested in the limit of weak selection, and its ability to predict the success of cooperation in evolutionary games in structured populations. The weak selection, which has a long standing history in population genetics and molecular evolution1, also plays a role in social learning and cultural evolution. Recent experimental results suggest that the intensity with which humans adjust their strategies might be low8. Although it has been unclear to what degree and in what way human strategy updating deviates from random11,39, the weak selection limit is of importance to quantitatively characterize the evolutionary dynamics. In the limiting case of weak selection, we are able to analytically classify strategies with respect to the neutral benchmark, ω → 015,17,40,41,42. We note that a strategy is favored by selection, if its average abundance under weak selection is greater than one half. In order to come to such a quantitative observation, we need to calculate the stationary distribution over the abundance of strategy A.

Results and conclusions

We analytically derive a unified condition, a + b > c + d, for one strategy to be favored over the other in regular graphs, which is the same with that in a well-mixed population. The analytical derivation process is detailed in Methods and Supplementary Information . Further by simulation, we verify that under the limit of weak selection, the criteria of strategy dominance for aspiration dynamics with various population structures are the same (see Fig. 2). Particularly, this criterion is the well-known condition for risk dominance. Thus the risk-dominant strategy which has the bigger basin of attraction always dominates the population for any population structures. For random networks, we maintain that the criterion holds for different population sizes and average degrees via simulation. The results are depicted in Fig. 3.

Figure 2
figure 2

Simulations for aspiration dynamics confirm the criterion a + b > c+d.

We study a payoff matrix of a = 1, −1 ≤ b ≤ 1, −0.5 ≤ c ≤ 1.5 and d = 0. The change trends of the abundance of strategy A for different structures are shown. According to the linear inequality σ a + b > c + σ d in [43], the equilibrium condition is σ = c − b, which is shown as the fitting (red dash dot) line in each panel. Below the line strategy A is favored. For the structures considered, the simulation results fit for the theoretical prediction σ = 1. (a) A well-mixed population with N = 8. (b) A cycle with N = 8. (c) A regular graph with k = 3 and N = 8. (d) A lattice with k = 4 and N = 9. (e) A star with N = 8. (f) A random graph with N = 8 and average degree . For all the simulations, we use selection intensity ω = 0.01. Each point is an average over 2 × 108 runs.

Full size image
Figure 3
figure 3

Numerical simulations confirm the criterion a + b > c + d for random graphs with different population sizes and average degrees.

Entries in the payoff matrix are a = 1, −1 ≤ b ≤ 1, 0 ≤ c ≤ 2 and d = 0. The fitting red line is the equilibrium condition c = b + σ. Below this line A is favored. The network structures are generated with population size N = 10, 50 and 100. Random graphs are generated in much the same way as random regular graphs, but relaxing the constraint that every node has the same number of links to having k links on average. Here, we first need to make sure that the graph is connected, thus every node is first linked to a random node of the already connected ones. In a second step two randomly drawn nodes are linked. The second step is repeated until the desired average connectivity is reached. For various N and average degree , 3 and 4, the simulation results fit for the theoretical prediction σ = 1. For all the simulations, we use selection intensity ω = 0.01. Each simulation point is an average over 2 × 108 runs.

Full size image

For our aspiration-driven update rule, the transition probabilities are differentiable at ω = 0; and it is symmetric for the two strategies. Considering the concept of structural dominance43,44, for a population structure and an update rule satisfying above conditions, strategy A is favored over B for weak selection if σ a + b > c + σ d. Here a, b, c, d are the entries of the payoff matrix (1) and σ is the structure coefficient, which depends on the model and the dynamics, such as population structure and update rule, but not on the entries of the payoff matrix. For death-birth process, birth-death process and imitation process43,44,45, the corresponding σ varies for different population sizes and structures (see Fig. 4). Taking DB updating for example, in a well-mixed population, σ = (N − 2)/N; in a cycle, σ = (3N − 8)/N; in a regular graph, σ = [(k + 1)N − 4k]/[(k − 1)N]; and in a star, σ = 1. Compared with former referred update process, the structure coefficient for aspiration dynamics is always σ = 1 under weak selection limit (simulation results see Fig. 2). It is worth noting that this is true for graphs of any population size. This reduces structural dominance to the well-known concept of risk dominance, a + b > c + d, as if the population was well mixed. This means that the population structure never leads to a clustering of strategies in such dynamics. Individuals treat counterparts of different strategies alike without distinction when interacting. This explains why the aspiration dynamics does not alter the cooperation level. It is shown that under weak selection, the favored strategy is invariant for different structures. Moreover, for the aspiration dynamics, strategy selection in structured populations share the same favored strategy with well-mixed populations. It suggests that population structures have little relevance as a cooperation promoter or inhibitor among humans on this aspiration-driven behavioral rule.

Figure 4
figure 4

Comparison of different dynamics in various structures.

For update rules satisfying the assumptions in [43], the condition that strategy A is favored over B reads σ a + b > c + σ d. Under weak selection, the structure coefficient σ for aspiration dynamics in various graphs is compared with those in birth-death updating, death-birth updating and pair-wise comparison process of different population sizes. As shown in [43,44], the structure coefficient for those updating rules is in well-mixed populations. For BD updating and pair-wise comparison on a wide class of homogeneous graphs, , which is the same as that in well-mixed populations; while on a star . For DB updating, for a regular graph of degree k (including cycle and lattice); while on a star σ = 1. In particular, most of the results for Moran-like process in structured populations depend on the mutation rate, thus the theoretical σ is obtained under low mutation limit.

Full size image

We study the equilibrium strategy distribution in a finite population and make a weak selection approximation for the average strategy abundance for any population size with two strategies, which turns out to be independent of the level of aspiration. This is different from the aspiration dynamics in infinitely large populations, where the evolutionary outcome crucially depends on the aspiration level46. Numerical Simulations not only verify the analytical results, but also extrapolate weak selection results to stronger selection cases (see Fig. 5). It turns out that our weak selection predictions also hold for strong selection in these examples.

Figure 5
figure 5

Fraction of strategy A for aspiration dynamics of various population structures.

The common parameters are a = 1, d = 0, population size N = 8 and aspiration level α = 0.3, 0.6. In all the panels, cases of b = 0.5, c = 1.2 and b = 0.5, c = 2 are depicted, which represents a + b > c + d and a + b < c + d respectively. Panel (a) shows the mean fraction of strategy A as a function of selection intensity for a well-mixed population. Panel (b) shows that for a cycle. Panel (c) shows that for a regular graph of k = 3. Panel (d) shows that for a random graph of average degree . For all the simulations, each point is an average over 2 × 108 runs.

Full size image

Discussion

Recent experiments reveal that human cooperation level may not change for different population structures. This motivates us to theoretically investigate what kind of updating rules satisfy this constraint. It is known that population structures can dramatically alter the evolutionary outcome. This is true for the well-studied pair-wise comparison process, Moran-like process, especially for Death-birth (DB) process and Birth-death (BD) process43,44,45. It seems unlikely to have such an updating rule to make the evolutionary outcome robust to all the structures. Here, surprisingly, we find that aspiration-driven dynamics can make the cooperation level unchanged in respect to population structures, which agrees with the recent experimental results. This suggests that humans may update strategies based on aspiration. The next question is whether or not this aspiration dynamics is the only dynamics that keep the invariance of strategy abundance? If not, what else can be there? Are there any similarities among those candidate updating rules? These questions will foster the understanding of the human updating.

Our analytical results hold for weak selection, which might be a useful framework in the study of human interactions, where it is still unclear with what role model individuals compare their payoffs and with what strength players update their strategies. Although weak selection approximations are widely applied in the study of frequency-dependent selection, it is not clear whether the successful spread of human behavioral traits operates in this parameter regime. Owing to that selection intensity can have crucial effects on the evolutionary outcome47, it will be interesting to derive analytical results that either hold for any intensity of selection or at least for the limiting case of strong selection in finite populations. On the other hand, further theoretical results for all the structures will be essential to our fundamental understanding of human behaviors and may guide insights to the effective functioning of the human mind.

Compared with imitation (pairwise comparison) dynamics, our self-learning process, which is essentially an Ehrenfest-like Markov chain, has some different characteristics. Without the introduction of mutation or random strategy exploration, there exists a stationary distribution for the aspiration-driven dynamics. Even in a homogenous population, there is a positive probability that an individual can switch to another strategy owing to the dissatisfaction resulting from payoff-aspiration difference. This facilitates the escape from absorbing states in the pairwise comparison process and other Moran-like evolutionary dynamics. Hence there exists a nontrivial stationary distribution of the Markov chain satisfying detailed balance.

Our model illustrates that aspiration-driven self-learning dynamics alone, irrespective of any discrepancy of population structure, may be sufficient to alter the expected strategy abundance. The weak selection criterion under aspiration dynamics that determines whether a strategy is more abundant than the other, differs from the criterion under imitation dynamics, especially when the population size is not too large. Based on this, a strategy favored under imitation dynamics can be disfavored under aspiration dynamics. This highlights the intrinsic difference between imitation and aspiration dynamics.

Methods

Analysis for a well-mixed population

The expected payoffs for any A or B in a finite well-mixed population of size N with i players of type A and N − i players of type B, are given by πA(i) and πB(i).

The spread of successful strategies is modeled as follows in discrete time. In one time step, three events are possible: the abundance of A, i, can increase by one with probability , decrease by one with probability , or stay the same with probability . All other transitions occur with probability zero. The transition probabilities can be obtained (see Supplementary Information ). Based on the probabilities, we can obtain and . In the limit of weak selection (ω → 0), we have , , , , and , when we denote the following equivalent payoffs, and .

In each time step, a randomly chosen individual obtains its payoff in the evolutionary game and compares it with the level of aspiration. Individual changes strategy with probability lower than 1/2 if its payoff exceeds the aspiration. Otherwise, it switches with probability greater than 1/2, except when the aspiration level is exactly met, in which case it switches randomly (note that this is very unlikely to ever be the case).

The Markov chain satisfies the detailed balance condition , where () is the stationary distribution over the abundance of A in equilibrium48,49. Considering , we find the exact solution by recursion, given by

where is the probability of successive transitions from j to k. The analytical solution Eq. (3) allows us to find the exact value of the average abundance of strategy A,

for any strength of selection.

To better understand the effects of selection intensity, aspiration level and payoff matrix on the average abundance of strategy A, we further analyze which strategy is more abundant based on Eq. (3). For a fixed population size, under weak selection, i.e. ω → 0, the stationary distribution ψj(ω) can be expressed approximately as

where the neutral stationary distribution is simply given by and the first order term of this Taylor expansion amounts to

Interestingly, in the limiting case of weak selection, the first order approximation of the stationary distribution of A does not depend on the aspiration level. For higher order terms of selection intensity, however, ψj(ω) does depend on the aspiration level.

Based on the approximation (5), with two strategies of normal form (1), we can calculate a weak selection condition such that in equilibrium A is more abundant than B. As for neutrality, holds and thus 〈XA〉(0) = 1/2, it is sufficient to consider positivity of the sum of jω [∂ω ψj(ω)]ω= 0/N over all . Under weak selection, strategy A is favored by selection, i.e., 〈XA〉(ω) > 1/2, if

It is similar to the concept of risk-dominance translated to finite populations40. For a detailed derivation of this analytical result, see Supplementary Information .

Analysis for general regular graphs

We can calculate the average abundance of strategy A for any two-strategy game on a regular graph by using pair approximation22,50,51,52 (see Supplementary Information ). We still show that if a + b > c + d, strategy A is favored in abundance for any degree k. Therefore, it implies that under weak selection, aspiration dynamics does not alter the average abundance of a strategy in a pairwise game, irrespective of the aspiration and the degree of a regular graph.