Introduction

Cooperative behavior is extremely important, both in the animal world as well as across human societies1,2,3,4. Yet it is also an evolutionary puzzle, as it is costly but has no immediate individual benefits, except in rare exceptions, for example when cooperation is agreed upon as a risk-sharing mechanism. How cooperation evolved amongst selfish and unrelated individuals is therefore still ardently investigated, as evidenced by recent reviews5,6,7,8,9,10.

Evolutionary game theory11,12,13 provides an apt theoretical framework to address the subtleties of the evolution of cooperation. One of the most popular games that is representative for situations constituting a social dilemma is the prisoner's dilemma game1. It can be summarized succinctly. Two individuals have to decide simultaneously whether they wish to cooperate or not. Cooperator pays a cost c towards the mutual benefit b where b > c > 0, while defector contributes nothing. This yields the temptation to defect T = b, reward for mutual cooperation R = b – c, punishment for mutual defection P = 0 and the sucker's payoff S = –c, which for the prisoner's dilemma game thus satisfy T > R > P > S and 2R > T + S. Evidently, for an individual it is best to defect regardless of what the opponent does. As rational players are aware of this, they both defect, in turn obtaining P rather than R, hence the social dilemma14.

Several mechanisms that facilitate the evolution of cooperation are known. Nowak summarizes five rules6, which are kin selection15, direct reciprocity16, indirect reciprocity17, group selection18 and network reciprocity19. Networks in particular, have received substantial attention in the recent past7. While scale-free networks appear to provide the best environment for the evolution of cooperation20,21,22,23,24,25,26,27, small-world28,29,30,31,32 and hierarchical networks33,34,35 also received ample attention. Largely motivated by the discovery that complex networks facilitate the evolution of cooperation, heterogeneity in general has emerged as an important property that may help keep defectors in the minority36,37,38,39. Coevolutionary games10, where the structure of the network was subject to evolution just as the strategies of players have been studied thoroughly too40,41,42,43,44,45,46,47,48,49,50,51,52,53,54, with the prevailing conclusion being that this may give rise to robust cooperative states and lead to socially preferable interaction networks in a spontaneous manner. Quite remarkably, this has recently been confirmed empirically55, although very extensive experiments also indicate that the human behavior may suppress network reciprocity56,57.

In fact, how human decision-making affects the evolution of cooperation is of particular relevance for the present work. Szabó et al.58 have recently considered a special type of strategy updating. Instead of players exclusively caring only about their own payoffs when updating their strategies, they investigated what happens when a pair of randomly chosen neighboring players tries to maximize their collective income by simultaneously updating their two strategies. It was reported that the proposed strategy update rule produces the antiferromagnetic ordering structure of cooperators and defectors on the square lattice at sufficiently low noise intensities and that this favors the evolution of cooperation more than the traditional pairwise imitation updating. Human decision-making dynamics has also been investigated experimentally, whereby we are particularly interested in the so called “social influence” effect reported by Lorenz et al.59. As stated in their paper, social influence among group members plays an important role in individual decision-making.

One may then ask how this affects the evolution of cooperation? To address this question, we propose an adaptive strategy-adoption rule in which the social influence is taken into account. In particular, as a proxy for the social influence we assume that the decisions the players make are affected by all their neighbors, not just a single randomly selected or the most successful neighbor. Players can collect information from their neighbors and moreover, their decision-making is more likely to be affected by the circle of “close friends” rather than the whole social environment. We introduce this so-called local influence to the strategy updating simply so that, before a potential update, each player considers the average performance of its own strategy and that of the other strategy, if present, within its neighborhood. As we will show in what follows, this introduces a qualitatively different evolutionary dynamics that is able to support the stable existence of very small cooperative clusters, which in turn supports the survivability of cooperative behavior even under very unfavorable conditions. Besides simulation results60, we will also present results obtained with pair approximation methods, which are, along with the game theoretical model, accurately described in the Methods section.

Results

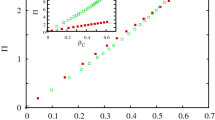
We begin by presenting the fraction of cooperators ρC as a function of the cost-to-benefit ratio r = c/b at two temperatures, namely at K = 0.1 and K = 0.83. The usage of the latter value is motivated by recent empirical research from behavioral science61, although essentially, as we will show in what follows, the temperature, i.e., the level of uncertainty by strategy adoptions, does not play a decisive role. Results for both the pairwise and locally influenced strategy updating are presented in Fig. 1(a,c). It can be observed that for K = 0.1 the evolution of cooperation is promoted across the whole applicable span of r if the traditionally used pairwise strategy updating is replaced by the proposed local influence based strategy updating. For K = 0.83, however, the outcome is a bit less clear-cut. While pairwise imitation fails to sustain cooperative behavior at such high values of r as locally influenced strategy updating, it is nevertheless more apt for achieving complete cooperator dominance. As we will show in what follows, it is indeed the case that locally influenced strategy updating often fails to completely eliminate defectors at small values of r, yet it opens up the possibility of survival of cooperators even under harsh defector-friendly conditions.

Figure 1
figure 1

Fraction of cooperators ρC as a function of the cost-to-benefit ratio r, as obtained for K = 0.1 [panels (a) and (b)] and K = 0.83 [panels (c) and (d)].

Results presented in panels (a) and (c) were obtained by means of Monte Carlo simulations, while those presented in panels (b) and (d) were obtained by means of pair approximation (see Methods section for details). Figure legend indicates whether pairwise or locally influenced strategy updating was used.

Full size image

These simulation results can be corroborated by results of pair approximations (see Methods for details), which we present in Fig. 1(b,d). The general trends are predicted correctly, although as expect, the beneficial effect of network reciprocity19 at low values of r are underestimated. It is worth mentioning that the pair approximation is in general more accurate for larger values of K62 and indeed it can be observed that the agreement with simulation results is better for K = 0.83 than it is for K = 0.1. In particular, for K = 0.83 the pair approximation method correctly predicts the occurrence of an intersection point [compare panels (c) and (d)]. Altogether, results of pair approximations corroborate the conclusion that the survivability of cooperators, especially at high values of r, is substantially promoted by locally influenced strategy updating.

Further adding to the robustness of this conclusion are results presented in Fig. 2(a,c), where we present full K – r phase diagrams for both considered updating rules. It can be observed that the positive impact of local influence on the evolution of cooperation persists across large regions of K. On the other hand, the presented phase diagrams also evidence more clearly the failure of the proposed updating rule to lead to an absorbing C phase. Moreover, there is a notable qualitative difference in the critical behavior that is evoked by the updating rule. By focusing on the D → C+ D phase boundaries, it can be observed that for pairwise strategy updating there exists an optimal value of K at which cooperators thrive best. Note that the D → C + D phase boundary is bellshaped, indicating that K ≈ 0.3 is the optimal temperature at which cooperators are able to survive at the highest value of r. For strategy updating based on local influence, however, this feature is absent. The D → C + D phase boundary is in fact an inverted bell, indicating the existence of the worst rather than an optimal value of K. Notably, the results for pairwise strategy updating are in agreement with previous works62,63,64, where it was shown that the lack of overlapping triangles, as is the case for the square lattice as well as for random regular graphs, introduces an optimal uncertainty for the evolution of cooperation. Conversely, the results obtained by considering local influence suggest that the system is behaving as if overlapping triangles were in fact present in the interaction network. Note that in the latter case an optimal K for the evolution of cooperation does not exist. This leads us to the conclusion that the interaction network is effectively altered when the local influence is taken into account. In particular, triplets of players that are not connected by means of the original interaction graph (the square lattice) become effectively connected through the joint participation of players in the same local groups (neighborhoods) that are subject to the same local influence. An identical effect was indeed observed by the study of the public goods game65, where triplets also became effectively connected because of the participation of players in the same groups. Below, we will provide further evidence concerning the effective linkage of triples of players, which is essentially a side effect of locally influenced strategy updating. Another interesting observation is that the parameter region of the mixed C + D phase in general widens as K increases, which is in contract to the results obtained by means of pairwise strategy updating.

Figure 2
figure 2

Full K – r phase diagrams, as obtained by means of Monte Carlo simulations [panels (a) and (c)] and by means of pair approximation [panels (b) and (d)].

Upper red (lower blue) lines denote the boundaries between the mixed C + D and homogeneous D (C) phases.

Full size image

We have also constructed full K – r phase diagrams by means of pair approximations. Figure 2(b,d) features the obtained results, from which it follows that qualitative features, compared to the simulation results, are again captured fairly accurately, although the extent of the parameter region of the mixed C + D phase is overestimated. Expectedly, the predictions are also less accurate near the phase boundaries, which is because the pair approximation does not take into account loops nor does it take into account long-range correlations, which however, have a noticeable effect especially in the vicinity of critical transitions66.

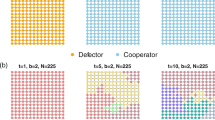
In order to obtain an understanding of the reported observations, we proceed with the presentation of characteristic spatial patterns, as obtained for both pairwise and locally influenced strategy updating, in Fig. 3. Regardless of which update rule is applied, cooperators form compact clusters by means of which they are able to exploit the mechanism of network reciprocity19. If the value of r is small, the clusters are larger and more compact than for higher values of r. On the other hand, the spatial patterns emerging under the two update rules also have noticeable dissimilarities. Foremost, given a value of r, pairwise strategy updating yields larger clusters than locally influenced strategy updating, even if the density of cooperators is approximately the same [compare panels (a) and (c)]. Nearer to the extinction threshold the stationary densities differ, yet the difference in the spatial patterns the two rules generate becomes most apparent [compare panels (b) and (d)].

Figure 3
figure 3

Characteristic snapshots of spatial patterns formed by cooperators (blue) and defectors (red) under pairwise imitation [(a) r = 0.004, (b) r = 0.019] and under strategy updating based on local influence [(c) r = 0.004, (d) r = 0.221].

The size of the square lattice was 100 × 100 and K = 0.83. (a) In this snapshot there are 77 clusters, ranging in size from a single cooperator to 3042 cooperators, with a weighted average size of 1925.21. The stationary fraction of cooperators is ρC ≈ 0.52. (b) In this snapshot there are 99 clusters, ranging in size from a single cooperator to 162 cooperators, with a weighted average size of 70.01. The stationary fraction of cooperators is ρC ≈ 0.19. These characteristics are significantly different in the bottom two snapshots. (c) In this snapshot there are 439 clusters, ranging in size from a single cooperator to 427 cooperators, with a weighted average size of 137.69. The stationary fraction of cooperators is ρC ≈ 0.52. (d) In this snapshot there are 164 clusters, ranging in size from a single cooperator to 19 cooperators, with a weighted average size of 6.63. The stationary fraction of cooperators is ρC ≈ 0.05. Note that in snapshots (a) and (c) the densities of cooperators for both update rules are practically identical, while nearer to the extinction thresholds [panels (b) and (d)] they differ quite significantly.

Full size image

The visual inspection of the characteristic spatial patterns invites a quantitative analysis of the exposed differences, the results of which are presented in Fig. 4 separately for both updating rules. It can be observed that, in general, as r increases, the cluster size decreases. The number of clusters, on the other hand, is maximal at an intermediate value of r. Concrete r values, however, differ significantly for the two considered strategy updating rules. In particular, by pairwise strategy updating both the clusters size and the number of clusters are shifted significantly towards lower values of r. One reason is obviously that pairwise strategy updating simply does not support the survivability of cooperators by as high values of r as locally influenced strategy updating. Nonetheless, the fact that for any given value of r, where comparisons are possible, the typical cluster size obtained with pairwise strategy updating is much larger than the one obtained with locally influenced strategy updating begets the conclusion that there are significant differences in the way cooperators cluster to withstand being wiped out by defectors. Note that for cooperators to survive under pairwise updating the minimally required cluster size is ≈ 76.18, while for locally influenced updating it is only 6.61. Moreover, for pairwise strategy updating the cluster size decreases much faster, which speaks in favor of the increased stability of the clusters under locally influenced strategy updating.

Figure 4
figure 4

Macroscopic properties of cooperative clusters in the dependence on the cost-to-benefit ratio r.

Cluster size (a) and cluster count (b) are depicted for pairwise and locally influenced strategy updating. In both cases the cluster size decreases as r increases, while the cluster count reaches a maximum at a certain value of r and then decreases. Note that for pairwise imitation a minimum cluster size of about 76.18 is required for cooperators to survive. Taking into account the local influence of the neighbors reduces this to 6.61. The depicted results were determined in the stationary state on 100 × 100 square lattices and by using K = 0.83. Error bars indicate the standard deviation.

Full size image

To confirm these conjectures, we present in Fig. 5 two typical C-cluster configurations and analyze the survivability of cooperators separately for each particular case. For the sake of simplicity but without loss of generality, we consider for the following analysis only the K → 0 limit. Then if the payoff of each cooperator along the boundary is larger than that of each defector in its neighborhood, we are allowed to conclude that such a C-cluster will survive. For the left C-cluster pattern in Fig. 5 under pairwise updating, the payoffs of a cooperator C (PC) and defector D (PD) along the boundary are

respectively. For locally influenced updating, however, the average payoff of cooperators () and the average payoff of defectors () along the boundary are given by

respectively. Thus for such a C-cluster pattern to survive, both update rules lead to r < –0.25. Indeed, neither locally influenced nor pairwise strategy updating support the survivability of such a pattern. Performing the same analysis for the configuration on the right, however, yields a different outcome. The payoff of a cooperator C2 () on the boundary and that of the two types of defectors D1 and D2 ( and ) are

respectively. For locally influenced updating the corresponding payoffs are

Accordingly, we find that under pairwise updating the condition for survivability is r < –0.25, while under locally influenced updating it is only . Hence, locally influenced strategy updating can warrant the survivability of cooperators when grouped in this way, while pairwise updating can not. Note also that the C-cluster configuration on the right of Fig. 5 is the smallest one which can persist in the population under the most hostile conditions under locally influenced strategy updating. Based on this analysis, we can in fact estimate the extinction threshold in the limit K → 0 and indeed we find excellent agreement between this analytical approximation and the simulation results presented in Fig. 2(c).

Figure 5
figure 5

Schematic presentation of two representative cooperative (blue) clusters surrounded by defectors (red).

The cluster depicted left has no chances of survival under pairwise or locally influenced strategy updating. The cluster on the right, however, cannot prevail under pairwise imitation, but can do so under locally influenced strategy updating. This is because the core of the cooperative cluster (C1 in the figure) is quarantined from defectors in case imitation proceeds according to local influence (see main text for details).

Full size image

With these insights, we argue that local influence based strategy updating can support the survivability of cooperative behavior only if the core of the C-cluster is isolated from defectors (compare left and right configuration of Fig. 5), because cooperators along the boundary can then gain a higher level of support from the cluster and thus protect themselves against being exploited by defectors. In previous works, where only pairwise strategy updating was considered, individual players were concerned only with their own payoffs when updating their strategies. However, if individuals are exposed to the local influence, i.e., they care about the average performance of the strategies in their neighborhood, cooperators can benefit not only from their own payoffs, but also from the payoffs of their cooperative neighbors. In this sense, locally influenced strategy updating further strengthens the linkage between cooperators within cooperative clusters and so cooperators can reciprocate with each other on a profounder and altogether more effective level.

In terms of the robustness of the described mechanism to variations of the interaction network, our preliminary investigations indicate that cooperation is always promoted on regular small-world networks with different rewiring probabilities67, as well as on scale-free networks68 provided the payoffs are normalized with the number of neighbors25. If the payoffs on scale-free networks are not normalized with the number of neighbors20, the promotion of cooperation due to local influence, compared to the traditional pairwise strategy updating, may be compromised. Additional research is needed, however, to clarify conclusively the potential negative impact of strongly heterogeneous degree distributions on the newly identified mechanism for the promotion of cooperation. It would also be of much interest to clarify the role of zero-determinant strategies69,70, which point to major paradigm shifts in the resolution of social dilemmas.

Discussion

Summarizing, we have analyzed the impact of “local influence” on the evolution of cooperation in the spatial prisoner's dilemma game. Instead of the performance of a single neighbor, players considered the average performance of the two strategies within their neighborhoods. We have shown that by going beyond the traditionally assumed pairwise strategy updating, the evolution of cooperation can be promoted. We have determined full K – r phase diagrams by means of simulations and pair approximation methods, which both indicate that this effect is robust against uncertainty by strategy adoptions. Moreover, the phase separation lines indicate that the consideration of local influence effectively changes the interaction network as an optimal K is no longer inferable. This is characteristic for interaction networks with overlapping triangles62,64, which are obviously not part of the square lattice topology that we have employed. By analyzing the macroscopic features of emerging spatial patterns as well as the survivability of typical cooperative clusters, we have provided further insights as to how the consideration of local influence changes the evolutionary dynamics.

Lastly, it is worth relating the presently considered strategy updating rule to previous gametheoretical models. By the win-stay-lose-shift rule32,71,72,73,74, for example, each individual has an aspiration according to which it judges whether or not to change strategy. The aspiration, however, is traditionally assumed to be constant. In our case, on the other hand, we relax this assumption by considering the aspiration as a dynamical quantity. Note that the average payoff of the strategy that is not adopted by the focal player can in fact be regarded as the aspiration level. This in turn implies that here the aspiration depends on the outcome of the game and hence is subject to change. Moreover, the present rule can be regarded as a learning rule. The difference from the traditional single role model learning rule is that in the present case the strategy update depends not on the comparison of a pair of individuals, but on the comparison of two groups of individuals, each involving several individuals adopting the same strategy. Overall, we hope that these considerations and in particular the consideration of local influence and the “wisdom of crowds”59,75,76, will motivate further research aimed at promoting our understanding of the evolution of cooperation.

Methods

Mathematical model

Players are located on the vertices of a L × L square lattice with periodic boundary conditions. Each individual is initially designated either as a cooperator C or defector D with equal probability. For the pairwise imitation strategy updating rule77 (we use the label “pairwise” in the figure legends when applying this rule), Monte Carlo simulations of the game are carried out comprising the following elementary steps. First, a randomly selected player x collects its payoff Px by interacting with its four nearest neighbors. For the purpose of payoff evaluation, it is worth introducing unit vectors S = [1, 0]T and [0, 1]T for cooperators and defectors, respectively. The payoff matrix is

where is the cost-to-benefit ratio. The payoff of player x is thus

where Γ(x) represents its neighborhood. Subsequently, one randomly chosen neighbor y of player x also acquires its payoff Py identically as previously player x.

After the evaluation of payoffs, players consider changing their strategies. In particular, player x adopts the strategy Sy of the randomly selected neighbor with the probability

where K is the uncertainty by strategy adoptions7. If the local influence is taken into account (we use the label “local” in the figure legends when applying this rule), however, the elementary steps are as follows. First, we randomly choose a player x with the strategy Sx. Next, we evaluate the average payoff of those players who adopt the same strategy Sx, as well as the average payoff of those players who adopt the opposite strategy of player x, if any, within the neighborhood. In particular, we have

where the Dirac delta function δ(x) satisfies

Lastly, player x will adopt the strategy with the probability

where K is, as by pairwise imitation, the uncertainty by strategy adoptions.

The presented simulation results were obtained by using L = 100 – 400 depending on the proximity to phase separation lines and the size of the emerging spatial patterns. In accordance with the random sequential update, each full Monte Carlo step, which consists of repeating the elementary steps L×L times corresponding to all players, gives a chance once on average for every player to alter its strategy. The stationary frequency of cooperators ρC is determined by averaging over 104 Monte Carlo steps in the stationary state after sufficiently long relaxation times. In general, the stationary state has been considered to be reached when the average of the cooperation level becomes time-independent. To further increase the accuracy of our simulations, we have averaged the final outcome over 50 independent initial conditions.

Pair approximations

Let pC and pD = 1 – pC denote the frequencies of cooperators and defectors, respectively and let pCC, pCD, pDC and pDD represent the frequencies of CC, CD, DC and DD pairs, respectively. Then qX|Y = pXY/pY with specifies the conditional probability to find an X-player given that the neighboring node is occupied by an Y-player. Note that here X, Y and Z denote either C or D. Instead of the first-order approximation considering the frequency of strategies as in the well-mixed population, the pair approximation tracks the frequencies of strategy pairs . The probabilities of larger configurations are approximated by the frequencies of configurations not more complex than pairs. Based on the compatibility condition pX = ΣYpXY, the symmetry condition pXY = pYX and closure conditions, pC and pCC can fully determine the dynamics of the system. While the pair approximation for pairwise imitation is well-known and can be looked up for example in the Appendix of7 or more recently78, for the imitation based on local influence the derivations are as follows.

A defector is selected for strategy updating with the probability pD. Let kC and kD denote the number of cooperators and defectors amongst the neighbors on a regular lattice with degree k, respectively. The frequency of such a configuration is

and the payoff of the defector is PD(kC, kD) = (1 + r) · kC + r · kD. The configuration probability with which a neighboring cooperator has cooperators and defectors as its neighbors is

where qX|YZ gives the conditional probability that a player next to the YZ pair is in state X. The payoff of the neighboring cooperator is . Similarly, the configuration probability with which a neighboring defector has cooperators and defectors as its neighbors is

and the payoff of the neighboring defector is . Thus, the average payoff of cooperators that are neighbors of the focal defector is

The average payoff of defectors that are neighbors of the focal defector, on the other hand, is

Consequently, pC increases by 1/N where N = L2, with probability

where is the individual transition probability given by Eq. 10. The number of CC pairs increases by kC and thus pCC increases by 2kC/(kN) with probability

A cooperator, on the other hand, is selected for strategy updating with the probability pC. The frequency of a configuration that there are kC cooperators and kD defectors in the neighborhood of the focal cooperator is

and the payoff of the focal cooperator is PC(kC, kD) = kC. The configuration probability with which a neighboring cooperator has cooperators and defectors as its neighbors is

and the payoff of the neighboring cooperator is . Similarly, the configuration probability with which a neighboring defector has cooperators and defectors as its neighbors is

and the payoff of the neighboring defector is . Thus the average payoff of cooperators in the neighborhood of the focal cooperator is

while, the average payoff of defectors in the neighborhood of the focal cooperator is

Thus pC decreases by 1/N with probability

Moreover, the number of CC pairs decreases by kC and thus pCC decreases by 2kC/(kN) with probability

These derivations lead us to the master equations

and

Although these equations are per derivation exact, they do depend on the density of triplet configurations which are outside their scope. Thus, in order to “close” the system of differential equations, the triplet configuration probabilities have to be approximated by probabilities of configurations that are not more complex than pairs. Note that by using different closure conditions, we can in general obtain different pair approximations. Here we employ the so-called ordinary pair approximation method, where only the first-order pair correlations are considered. We thus have qX|YZ ≈ qX|Y.