Quiet point engineering for low-noise microwave generation with soliton microcombs

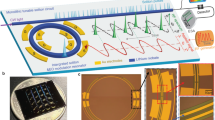
Abstract

Low-noise microwave signals can be efficiently generated with microresonator-based dissipative Kerr solitons (microcombs). However, the phase noise level in integrated microcombs is presently several orders of magnitude above the limit imposed by fundamental thermorefractive noise, resulting from residual pump laser frequency noise transduction to the soliton repetition rate. This effect can be substantially reduced by accessing a quiet point (QP) in the parameter space, where the transduction is compensated by the dispersive wave (DW) recoil, which conventionally relies on accidental mode crossings. Here we present a method to deterministically engineer the QP, both in terms of spectral width and position, and we discover a continuum of possible QPs within the soliton existence region. Using two controlled mode crossings, we obtain regions where the QPs interact with each other, extending the noise suppression range. Our work demonstrates a promising way to reach the fundamental limit of low-noise microwave generation in integrated microcombs.

Introduction

The discovery of dissipative Kerr solitons (DKS)¹ in driven dissipative Kerr nonlinear resonators, has heralded a new method to synthesize coherent and broadband optical frequency combs, with compact form factor, wafer scale manufacturing compatible techniques, and mode spacings that can access the microwave to THz. The dynamics of such DKS in microresonators is described by the Lugiato-Lefever equation (LLE)². It is by now well understood that microcombs give rise to a plethora of coherent nonlinear dynamical states, i.e., “dissipative structures”, including platicons, zero dispersion solitons, and solitons in unusual dispersion landscapes^3,4, that challenge the understanding of “classical” bright solitons. DKSs can crucially be generated in photonic integrated microresonators based on silicon nitride⁵, a foundry level, mature photonic integrated circuit technology, that has been the basis of numerous system level demonstrations, including massively parallel⁶, dual-comb ⁷ and chaotic LiDARs⁸, neuromorphic computing^9,10, as well as optical frequency synthesis¹¹ and optical clocks¹².

Microcombs also enable low-noise microwave generation by detecting the repetition rate of the soliton pulse stream. Such optically generated microwaves are attractive due to the low input power¹³ and potentially low phase noise that can be generated. More broadly, microcombs can be employed in a variety of applications, such as microwave photonics, Radar¹⁴, 5G/6G¹⁵ or wireless communications¹⁶. In contrast to optical frequency division, which employs phase stabilized femtosecond laser frequency combs, the phase noise of the generated microwaves in the case of microcombs is determined primarily by transduction of laser phase noise to the soliton group velocity. There have been numerous demonstrations of the soliton stream-based low-noise microwave generation ^{17,18,19,20,21,22,23,24}, ranging from sources in the K and X microwave band using integrated Si₃N₄ microresonators²⁵ to the THz domain²⁶. Despite achieving phase noise on par with mid-range commercial microwave generators based on quartz oscillators, the fundamental limit of the repetition rate noise, as given by thermorefractive noise (TRN)^24,27,28, is still several tens of decibels below the best experimentally demonstrated noise performance photonic chip-scale microcombs. While soliton microcombs have achieved lower noise, this has so far only been possible in bulk polished crystalline resonators, that have significantly lower TRN levels, and do not show Raman self-frequency shifts²⁹. In contrast, for chip-integrated microcomb platforms, such as those based e.g., on silica, silicon nitride, etc. the presence of the Raman self-frequency shift-related transduction noise limits achieving the fundamental thermodynamical limit^24,27,28. One way to reduce this noise has been the observation of quiet points^21,30, which exploit a cancellation due to the interplay of the Raman self-frequency shift and the recoil from the DW generation via avoided mode crossing (AMX) induced soliton Cherenkov radiation^5,31,32. However, this technique relies on accidental AMXs and therefore is fixed to a certain mode number μ and shift Δ_μ by design. The strength of the AMX is a fixed parameter that is usually not controlled^21,22. Moreover, the width of the QP has been reported to be substantially narrower than the linewidth of the microresonator cavity, implying possible second-order transduction effects.

In this work, we report on a deterministic approach (i.e., precise control over the AMX position) to QP engineering and demonstrate a substantial increase in noise suppression bandwidth. We predict that with such improvements it is possible to reach the fundamental thermodynamical limit of phase noise, and thereby substantially improve the ability to synthesize low-noise microwaves directly from optical integrated microresonators. Our approach is directly realizable within currently demonstrated silicon nitride integrated microresonator technology using the Vernier configuration^33,34 or by corrugating the microresonator circumference which enables the mode-by-mode dispersion control³⁵.

Results

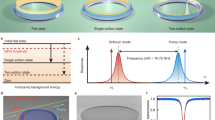
To understand the transduction of phase noise to the soliton (i.e., DKS repetition rate ω_rep) we consider Raman scattering and the DW recoil as the main noise transfer mechanisms (cf Fig. 1a), and aim to reduce the repetition rate susceptibility to the laser detuning fluctuations δω, i.e., minimize $| \frac{\partial {\omega }_{{{{{{{{\rm{rep}}}}}}}}}}{\partial \delta \omega }| \propto | \frac{\partial }{\partial \delta \omega }({\Omega }_{{{{{{{{\rm{Raman}}}}}}}}}+{\Omega }_{{{{{{{{\rm{DW}}}}}}}}})|$²². To introduce the presence of a DW, we consider a simplified model of AMX, characterized by a single-mode displacement at position $\bar{\mu }$ and strength ${\Delta }_{\bar{\mu }}$, in the integrated dispersion profile, as shown in Fig. 1b. As expected, the corresponding spectrum of the generated DKS has a typical ${{{{{{{{\rm{sech}}}}}}}} }^{2}$ shape, frequency shifted by Ω and with spectral enhancement at $\bar{\mu }$, due to the DW (Fig. 1c). To qualitatively explain the noise reduction mechanism, we start by separately analyzing the Raman and DW contributions to the DKS repetition rate response. We consider the simplest case of sinusoidal frequency modulation of the pump detuning around a constant value δω as presented in Fig. 1d–i. In the presence of the Raman effect only, the DKS’s group velocity is in-phase with the detuning change (c.f. Fig. 1d). In the nonlinear dispersion relation (NDR) representation³⁶, the DKS dynamics has a butterfly-shaped profile, revealing the transfer of the laser detuning modulation to the DKS group velocity v_g (i.e., the tilt of the DKS line in Fig. 1e) that directly reflects the repetition rate change³⁷. Equally, the NDR representation clearly shows the comb-line dependent frequency noise multiplication mechanism induced by the repetition rate variation^38,39 (i.e., phase noise multiplication). In the presence of an AMX, the laser detuning dependence of the DKS’s group velocity can exhibit the opposite sign as shown in Fig. 1f. Represented in the NDR, the soliton forms a similar butterfly shape with enhanced photon occupancy at the displaced mode (Fig. 1g). These two effects, combined together, can then counteract due to the opposite dependence, resulting in the reduction of the detuning noise transfer (Fig. 1h, i). In the following, we identify a QP by reconstructing the group velocity manifold v_g as a function of δω and parameters of the AMX i.e., mode index $\bar{\mu }$ and its displacement from the unperturbed dispersion profile ${\Delta }_{\bar{\mu }}$, further computing its extrema along the laser detuning direction. In general, this problem does not have an analytical solution, but we can efficiently reconstruct the desired dependence using a semi-analytic approach based on the Newton-Raphson method, which we describe in detail below.

Fig. 1: The concept of the quiet point engineering using coupled resonators.

a Schematic of the phase-noise reduction in a microresonator. The auxiliary cavity is required to control the DW recoil in order to balance the effect of Raman scattering. The active control can be established by adding a heater or actuator to the auxiliary cavity. b Example of the considered integrated dispersion profile with shifted resonance for a single spatial mode (i.e., localized AMX); the shifted mode number is $\bar{\mu }=15$ and the resonance is shifted from the perfect parabolic profile by ${\Delta }_{\bar{\mu }}=-4$. c Power spectral density of stable soliton solution both in the presence of Raman scattering and AMX for the integrated dispersion given in (b); the presence of Raman scattering and AMX results in a detuning-dependent frequency shift Ω of the soliton spectrum responsible for the pump phase noise transduction. The modification of the integrated dispersion profile by AMX leads to the generation of DWs via the soliton Cherenkov radiation. Real-space (d, f, h) and Fourier-space (e, g, i) soliton dynamics driven with a sinusoidal detuning (${\zeta }_{0}(t)=4+0.4\,\cos (\alpha t+\varphi ),\alpha =0.0033,\varphi =-200$) in presence of Raman scattering only (left), AMX (center) and both (right) for the dispersion profile in (b).

Mean-field model for noise transduction

We model the DKS dynamics in the microresonator using the LLE with a modified dispersion profile and a Raman scattering term. In the normalized units, the generalized LLE takes the form:

$$\frac{\partial \psi }{\partial t}= -(1+i{\zeta }_{0})\psi +\frac{i}{2}{\partial }_{\theta }^{2}\psi +i| \psi {| }^{2}\psi +f\\ +{v}_{g}{\partial }_{\theta }\psi -i{\Delta }_{\bar{\mu }}{\psi }_{\bar{\mu }}{e}^{i\bar{m}\theta }-i\tau \psi {\partial }_{\theta }| \psi {| }^{2}.$$

(1)

Here we use a standard normalization of the LLE¹ (see “Methods” for further details) which rescales fast time (intracavity angle ϕ) term as $\theta =\sqrt{\kappa /2{D}_{2}}\varphi$. In this way, the mode index becomes non-integer $m=\mu \sqrt{2{D}_{2}/\kappa }$, where μ –is an integer mode index, κ is the total loss rate, and D₂ is the second-order integrated dispersion. Terms in the second line of Eq. (1), that extend the conventional form of the LLE, represent group velocity change v_g, modification of the D_int by the AMX at the mode $\bar{\mu }$, and the Raman scattering, respectively. This formulation of the LLE is essential for the stationary solution search with the Newton-Raphson algorithm, as explained in “Methods”.

QP achieved with a single-mode displacement

To investigate the DKS group velocity response to the detuning variations ζ₀, we look for a single-soliton equilibrium solution ψ_DKS and its relative group velocity v_g for the parameter set $(f,{\zeta }_{0},\bar{\mu },{\Delta }_{\bar{\mu }})$ using the Newton-Raphson approach for Eq. (1) described in details in “Methods”. To reduce the dimensionality of the parameter space, we fix the pump power f² = 6, $| \bar{\mu }| =21$, and sweep the detuning value within the soliton existence range (given by π²f²/8¹ in the unperturbed case) and the ${\Delta }_{\bar{\mu }}$ in the vicinity of the DW resonance. As a result, we obtain a soliton solution and the corresponding group velocity v_g for every point on the $({\Delta }_{\bar{\mu }},{\zeta }_{0})$-subspace, both for blue- ($\bar{\mu } < 0$) and red-side ($\bar{\mu } > 0$) mode shifts (cf. Fig. 2).

Fig. 2: Quiet point identification via group velocity detection and dynamics in the 2D space of detuning-mode crossing strength.

a–d Simulation results obtained with the Newton-Raphson algorithm for $({\Delta }_{\bar{\mu }},{\zeta }_{0};\bar{\mu }=-21,{f}^{2}=6,\tau =5\cdot 1{0}^{-3})$, i.e., in presence of Raman scattering and single-mode resonance shift. a Single-soliton solution for $({\Delta }_{\bar{\mu }}=-5,{\zeta }_{0}=4.73)$ (blue star). The single-mode shift leads to a periodic modulation of the constant background with period $\frac{2\pi }{| \bar{\mu }| }$. b single-soliton group velocity v_g in $({\Delta }_{\bar{\mu }},{\zeta }_{0})$-plane. The black area indicates the region of parameters where the method does not converge. The white dashed line highlights the existence range of the single DKS solution. The colormap shows how the soliton existence range is reduced in the presence of a higher value of the group velocity related to the increasing intensity of the DW that perturbs the DKS state. c $10\,{\log }_{10}| \frac{\partial {v}_{g}}{\partial {\zeta }_{0}}|$ as a measure of the DKS repetition rate susceptibility to the variation of laser detuning. The smallest value of the susceptibility is obtained for a continuous line of operating point in the $({\Delta }_{\bar{\mu }},{\zeta }_{0})$-plane, here called the QP line (dark blue). d Comparison of the susceptibility (solid) and group velocity (dashed) profiles for two different sections of the QP line [green and light blue lines in subplot (c)]. e–h Similar results for opposite mode displacement, i.e., $({\Delta }_{\bar{\mu }},{\zeta }_{0};\bar{\mu }=21,{f}^{2}=6,\tau =5\cdot 1{0}^{-3})$.

First, we focus on the blue-sided displacement (i.e., $\bar{\mu } < 0$). The presence of the shifted mode results in the generation of the DW (see Fig. 2a), whose strength depends on the phase matching condition with the DKS. The acquired group velocity due to the recoil increases in the vicinity of the DW resonance as shown in Fig. 2b. After a given value of detuning, the DW destabilizes the DKS and the equilibrium state cannot be achieved anymore (the absence of the soliton solution is depicted in black in Fig. 2b).

Increasing the normalized mode shift strength ${\Delta }_{\bar{\mu }}$, we observe that the effect of the DW on the soliton is substantially reduced and the soliton existence range approaches the value estimated for the unperturbed LLE (see white dashed line in Fig. 2b). Next, we compute the group velocity directional derivative ${\partial }_{{\zeta }_{0}}{v}_{g}$ shown in Fig. 2c. As a result, we observed a family of solutions with ${\partial }_{{\zeta }_{0}}{v}_{g}=0$ that correspond to the QPs. Crucially, due to the lack of control, prior experimental works have reported only a slice (vertical line cut) of the map for the fixed ${\Delta }_{\bar{\mu }}$ as depicted in Fig. 2d. Dashed lines represent the interpolated group velocity as a function of detuning ζ₀ for two values ${\Delta }_{\bar{\mu }}=-6.85,-5$ while the solid lines represent the response ${\partial }_{{\zeta }_{0}}{v}_{g}$ on a logarithmic scale (directly reflecting the noise transduction). For both values ${\Delta }_{\bar{\mu }}$ there are two points with zero derivative ${\partial }_{{\zeta }_{0}}{v}_{g}$. We followed the same procedure for the red-side mode displacement $\bar{\mu } > 0$ (same side as for the Raman frequency shift) and observed similar behavior for the soliton states, group velocity, and its derivative (Fig. 2e–h). Qualitatively, the soliton profile and its existence range remain the same as in the previous case, but the QP line is shifted now toward the higher mode-displacement amplitudes where the soliton existence range is narrowed.

Two-mode displacement for enhanced QP engineering

Next, we investigate the region where the two QPs (for displaced modes on the blue and the red side of the pump) can co-exist and interact. First, we fix the displaced mode index $\bar{\mu }=-21$ and the displacement strength ${\Delta }_{\bar{\mu }}=-5.00$ scanning the displacement ${\Delta }_{-\bar{\mu }}$, of the mode ${\bar{\mu }}^{{\prime} }=-\bar{\mu }$ for different detunings ζ₀. The Newton-Raphson results for the single DKS state are shown in Fig. 3a–d. As in the case of a single-mode displacement, the DKS coexists with a single-period DW background (the periodicity is given by $| \bar{\mu }|$). In this case, we discovered that the single-soliton solution exists for ${\Delta }_{-\bar{\mu }} < -7$. For large negative displacements (${\Delta }_{-\bar{\mu }}\approx -20$), ${\bar{\mu }}^{{\prime} }$ is out of resonance and the QP detuning value corresponds to the one in Fig. 2c. Reducing the displacement $| {\Delta }_{-\bar{\mu }}|$, the soliton starts being resonant also to mode ${\bar{\mu }}^{{\prime} }$ resulting in an effective bending of the QP line, converging to the single-mode one for red-shifted mode (Fig. 2f). While in the case of a single-mode displacement, the QP line is always tilted (see Fig. 2c, g) which narrows down the noise suppression region for a fixed value of ${\Delta }_{\bar{\mu }}$, displacing two modes, we are crucially able to engineer a flat susceptibility over a wide range of laser detunings ζ₀. We refer to this state of the system as engineered QP (EQP). The flat susceptibility region is achieved at ${\Delta }_{-\bar{\mu }}=-12.52$ (cf. Fig. 3c). In Fig. 3d, we compare v_g and its susceptibility ${\partial }_{{\zeta }_{0}}{v}_{g}$ for the single-mode displacement (green lines in Fig. 2d) with the case in Fig. 3c (gray lines). The latter clearly shows a flatter response profile that can be practically beneficial for accessing the QP regime. The effect of this is depicted in Fig. 3d, which shows an order of magnitude broadening of the QP detuning bandwidth. We repeat the same procedure, fixing the mode $\bar{\mu }=21$ with ${\Delta }_{\bar{\mu }}=-10.7$ and shifting the mode ${\bar{\mu }}^{{\prime} }=-\bar{\mu }$ by ${\Delta }_{-\bar{\mu }}$. Simulation results in Fig. 3e–h show qualitatively similar behavior, with shorter DKS existence range (defined by the fixed mode $\bar{\mu }=21$, see Fig. 2f). However, in this case, we find two QP families for a single DKS solution. The flattest response is achieved at ${\Delta }_{-\bar{\mu }}=-3.74$ (see Fig. 3g, h). In this way, we observe that careful control over the two-mode displacement can extend the noise suppression region of the QP in the parameter space.

Fig. 3: Quiet point engineering.

a–d Newton-Raphson simulations for a dispersion profile with two modes displaced: $\bar{\mu }$ and ${\bar{\mu }}^{{\prime} }=-\bar{\mu }$, i.e., $({\Delta }_{-\bar{\mu }},{\zeta }_{0};\bar{\mu }=-21,{\Delta }_{\bar{\mu }}=-5,{f}^{2}=6,\tau =5\cdot 1{0}^{-3})$. a Equilibrium DKS solution for the EQP, i.e., $({\Delta }_{-\bar{\mu }}=-12.52,{\zeta }_{0}=5.41)$ (blue star). b Value of the group velocity in the subspace of parameters $({\Delta }_{-\bar{\mu }},{\zeta }_{0};{f}^{2},\tau ,{\Delta }_{\bar{\mu }})$ and (c) its detuning directional derivative $(10{\log }_{10}| \frac{\partial {v}_{g}}{\partial {\zeta }_{0}}| )$. d Comparison of detuning response between single-mode displaced quiet point QP1 (green line, see Fig. 2c) and engineered quiet point (EQP1) with second mode displaced (gray line in subplot c). e–h Similar plots for the case for $\bar{\mu }=21$, ${\Delta }_{\bar{\mu }}=-10.7$, ${\bar{\mu }}^{{\prime} }=-21$, ${\Delta }_{-\bar{\mu }}=-3.74$.

Linear stability of the solutions

Having derived above the equilibrium value of the DKS group velocity and its relative soliton state, for different mode shifts and having observed QP lines in various configurations using the Newton-Raphson method, a crucial question arises that we answer next: are the observed states stable and/or is there any additional instability region? To estimate the stability of the equilibrium solutions, we perform linear stability analysis, numerically investigating the eigenvalues λ of the Jacobian operator associated with (1) for each particular soliton state found in the previous section (see “Methods”). In particular, we focus on the eigenvalues with the greatest real part, since, if positive, those are responsible for the linear growth of any perturbation around the equilibrium. The real part of the latter ($\max \Re \{\lambda \}$) are plotted in Fig. 4a–d. We observe that the soliton solutions are linearly stable almost everywhere in the considered subspace, and in particular at the QPs. We observed instability regions close to the area where the soliton solution does not exist. In those regions there exists at least one eigenvalue with a positive real part. From the actual structure of the spectrum of the Jacobian, computed for the quiet point states (Fig. 4e–h) we find that these instabilities are due to the transition to the Hopf bifurcation. In this region of parameter space, those will be responsible for the transition from stable solitons to breathing states.

Fig. 4: Linear stability of the quiet points.

a–d Value of the real part of the Jacobian eigenvalue (λ) with highest real part, in the parameters subspaces considered in Figs. 2b, f and 3b, f respectively. The analysis shows there are regions within the DKS existence range in which the soliton solutions are linearly unstable (colored regions) but those do not include the analyzed QP that is consequently considered stable. e–h Detail on the spectrum of the Jacobian for the cases in (a–d). The spectrum shows that the instabilities arising in the colored regions are due to the Hopf bifurcation, considered the presence of pairs of conjugated modes approaching ℜ{λ} = 0.

Dynamical simulation of the phase noise transfer

To compare the phase noise performance of different operating points, the dynamical evolution has been simulated with the step-adaptative Dormand-Prince Runge-Kutta method of Order 8(5,3)⁴⁰. We perform the direct dynamical simulations of the LLE adding a realistic noise to the detuning term measured experimentally from the Toptica CTL 1550 laser having a standard deviation of 5 kHz (standard deviation of the phase noise δϕ is 0.1 rad, see “Methods”). In this way, we simulate two DKS operating points: QP1 (see Fig. 2b) and EQP1 (see Fig. 3b). The difference between the phase noise transfer performance at different operating points can be clearly seen in Fig. 5a, b and from the calculated δϕ: for the former, we obtain δϕ = 4.26 ⋅ 10⁻⁷ rad, while for the latter the computed value is δϕ = 2.93 ⋅ 10⁻⁷ rad. A series of numerical experiments confirm the conclusion obtained with the stationary solver analysis.

Fig. 5: Dynamical simulations of the noise transfer for different operating points.

PM2PM coefficient (ratio between the microwave phase noise and the pump laser phase noise) at 10 kHz offset frequency in the vicinity of QP1 (green crosses in a) and EQP1 (gray crosses in b) as defined in Figs. 2b and 3b, respectively. c Phase noise plot for exact laser detuning corresponding to QP1 and EQP1 as well as a deviation of 3Δ = 3 ⋅ 10⁻³κ. d Spatiotemporal diagram of the DKS evolution under the influence of amplified pump phase noise. e Nonlinear dispersion relation, for different operating points. The noise transduction to the soliton repetition rate is greatly reduced in the presence of two engineered mode-crossings.

We estimate the transduction of the phase modulation (PM) noise from the pump to the DSK repetition rate as PM2PM = ${S}_{\phi }/{S}_{\phi }^{{{{{{{{\rm{in}}}}}}}}}$ at 10 kHz offset, where S_ϕ is the phase noise power spectral density of the soliton and ${S}_{\phi }^{{{{{{{{\rm{in}}}}}}}}}$—the phase noise power spectral density of the pump laser. Changing the central frequency of the pump by the value of 10⁻³κ, we clearly observe that the overall EQP1 performance increases by 0.5 dB for 3 ⋅ 10⁻³κ (δϕ = 3.00 ⋅ 10⁻⁷ rad), while in the case of QP₁, we observe > 28 dB of the transduction enhancement (δϕ = 33.63 ⋅ 10⁻⁷ rad). Corresponding single-sideband (SSB) phase noise power spectral density is depicted in Fig. 5c. As one can see, the fluctuations of the central frequency of the pump laser do not visibly affect the performance of the system at EQP1.

Next, we verify that in the case of the noisy pump lasers (standard deviation of 8% κ/2) EPQ leads to a significant noise reduction due to the larger noise suppression region. We employed the same phase noise data, scaling it to obtain the detuning fluctuation of the order of the width of the standard QP, i.e., 8% κ/2. In the parameter regime outside of the QP region the influence of the pump fluctuations on the DKS dynamics is visible directly from the spatiotemporal diagram (see Fig. 5d). To distinguish the performance of QP1 and EQP1, we can use the NDR to represent its effect (Fig. 5e). We observe a clear suppression of the noise multiplication in the case of EQP1. This confirms our predictions based on the group velocity variation obtained with the stationary solution solver.

Conclusions

In summary, we have demonstrated a method to increase the effectiveness of QPs, that are central to achieving low phase noise soliton microcombs for microwave generation. Our work shows that engineering QP introduced via two dedicated and controllable AMX enables one to create broader regions of enhanced noise suppression. Our work is directly implementable using current technology and provides an approach to the enduring challenge of obtaining thermal noise-limited micro-wave generation from integrated soliton microcombs, which in contrast to crystalline resonators employ materials such as silicon nitride or silica, that do exhibit a Raman self-frequency shift.

These results were obtained via a semi-analytical approach, based on the Newton-Raphson method, which studied the phenomenology of QP in the presence of Raman scattering, DW, and detuning noise, within a simplified model of AMX. This allowed us to obtain several insights (1) QPs can be achieved by placing AMX on both blue- and red-detuned sides of the pump. This highlights the fact that not the absolute value of the frequency shift must be compensated, but its derivative over the laser detuning. (2) By controlling the mode displacement, QP can be placed at an arbitrary laser detuning within the soliton existence range. (3) Engineering the interaction of two QPs leads to the increased bandwidth of the noise suppression and in the case of a noisy pump laser to further reduction of the noise transfer. (4) The EQPs predicted in this work are linearly stable and characterized by more than 28 dB reduction of the PM2PM coefficient with respect to a generic QP described in the literature when a detuning deviation of the order of 0.03% of κ is introduced. We anticipate that other arrangements of the mode displacements can lead to similar or better performance of the EQP. We also believe that the detuning-dependent variation of the repetition rate can be completely eliminated by further controlling the integrated dispersion profile for example by corrugating the microresonator circumference³⁵, which is however outside the scope of this work.

Methods

Mean field model

The modified LLE, presented in the main text, which accounts for the Raman scattering and effect induced by the AMX:

$$\frac{\partial \psi }{\partial t}= -(1+i{\zeta }_{0})\psi +\frac{i}{2}{\partial }_{\theta }^{2}\psi +i| \psi {| }^{2}\psi +f\\ +{v}_{g}{\partial }_{\theta }\psi -i{\Delta }_{\bar{\mu }}{\psi }_{\bar{\mu }}{e}^{i\bar{m}\theta }-i\tau \psi {\partial }_{\theta }| \psi {| }^{2},$$

(2)

where $t={t}^{{\prime} }/2{\tau }_{{{{{{{{\rm{ph}}}}}}}}}$ is the time normalized to photon lifetime τ_ph = 1/κ, κ = κ₀ + κ_ex is the total linewidth of the cavity composed of the internal linewidth κ₀ and the coupling to the bus waveguide κ_ex. The normalized laser-cavity detuning is ζ₀ = 2δω/κ, the fast time is defined as $\theta =\sqrt{\kappa /2{D}_{2}}\varphi$ with D₂ as the GVD and φ ∈ [−π, π] as the azimuthal coordinate inside the cavity. $\bar{\mu }$ indicates the shifted mode number and ${\psi }_{\bar{\mu }}$ is the amplitude of the displaced mode. We point out that, due to the normalization of the fast time coordinate, the mode numbers m are not integers, however, they are related to the actual comb line index μ by a simple multiplication factor, i.e., $m=\mu \sqrt{2{D}_{2}/\kappa }$. Thus, referring to an integer $\bar{\mu }$, we imply the comb line index $\bar{\mu }$ is associated with the displaced mode. The normalized pump power is $f=\sqrt{8{\kappa }_{{{{{{{{\rm{ex}}}}}}}}}{g}_{0}/{\kappa }^{3}}{s}_{{{{{{{{\rm{in}}}}}}}}}$ where g₀ is single photon Kerr frequency shift and ${s}_{{{{{{{{\rm{in}}}}}}}}}=\sqrt{{P}_{{{{{{{{\rm{in}}}}}}}}}/\hslash \omega }$ and where ∣s_in∣² is the laser photon flux. The last two terms in Eq. (1) describe the single-mode AMX and the Raman scattering respectively. The normalized mode displacement is defined as ${\Delta }_{\bar{\mu }}{\delta }_{\mu ,\bar{\mu }}=2({D}_{{{{{{{{\rm{int}}}}}}}}}(\mu )-{D}_{2}{\mu }^{2}/2)/\kappa$, with ${\delta }_{\mu ,\bar{\mu }}$ as Kronecker delta, and the normalized Raman shock time is $\tau ={\tau }_{{{{{{{{\rm{R}}}}}}}}}{D}_{1}\sqrt{\kappa /2{D}_{2}}$.

The single-mode AMX term comes directly from the modified dispersion profile (e.g., Fig. 1b) as follows from:

$${{{{{{{{\mathcal{F}}}}}}}}}^{-1}\left[(\frac{{\mu }^{2}}{2}+{\Delta }_{\bar{\mu }}{\delta }_{\mu ,\bar{\mu }}){\psi }_{\mu }\right]=-\frac{1}{2}{\partial }_{\theta }^{2}\psi +{\Delta }_{\bar{\mu }}{\psi }_{\bar{\mu }}{e}^{i\bar{m}\theta },$$

where ${{{{{{{{\mathcal{F}}}}}}}}}^{-1}[...]$ stands for the inverse Fourier transform. We simulate a system with the following parameters: κ/(2D₂) = 76.923, τ_RD₁ = 0.0006.

Newton-Raphson method for the QP

The stationary solitons state and their respective value of group velocity have been computed from Eq. (1) applying the Newton-Raphson method. This method is used to compute the solutions of a nonlinear (in principle vectorial) equation of the form of:

$${{{{{{{\bf{F}}}}}}}}({{{{{{{\boldsymbol{\Phi }}}}}}}})=0,$$

(3)

by applying the following iterative scheme:

$$\left\{\begin{array}{l}{{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{k+1}={{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{k}-{\underline{\underline{J}}}^{-1}({{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{k}){{{{{{{\bf{F}}}}}}}}({{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{k})\quad \\ {{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{0}:{{{{{{{{{\rm{Initial}}}}}}}\,{{{{{{\rm{guess}}}}}}}}}}\quad \hfill\end{array}\right.$$

(4)

where ${\underline{\underline{J}}}^{-1}$ is the inverse of the Jacobian matrix of the function F^41,42, i.e.:

$${J}_{i,j}=\frac{\partial {F}_{i}}{\partial {{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j}}$$

(5)

If the initial condition has been chosen correctly and the Jacobian remains invertible, the algorithm will converge to the desired solution Φ^⋆, fixed point of (4), i.e.:

$${{{{{{{{\boldsymbol{\Phi }}}}}}}}}^{\star }={{{{{{{{\boldsymbol{\Phi }}}}}}}}}^{\star }-{\underline{\underline{J}}}^{-1}({{{{{{{{\boldsymbol{\Phi }}}}}}}}}^{\star }){{{{{{{\bf{F}}}}}}}}({{{{{{{{\boldsymbol{\Phi }}}}}}}}}^{\star })$$

(6)

and so characterized by F(Φ^⋆) = 0.

In our case, we exploit the method to find stationary single-soliton solutions, ψ, of Eq. (1) and the corresponding group velocity v_g by adding it explicitly as an optimization variable. In this case Eq. (3) is set as the following:

$${{{{{{{\bf{F}}}}}}}}(\psi ,{\psi }^{* },{v}_{g}):= \left[\begin{array}{c}g(\psi ,{\psi }^{* },{v}_{g})\\ {g}^{* }(\psi ,{\psi }^{* },{v}_{g})\\ \Re \{{\partial }_{\theta }\psi \}{| }_{\theta = {\theta }_{max}}\end{array}\right]=0$$

(7)

where g(ψ, ψ^*, v_g) is the r.h.s of Eq. (1). To implement the iterative algorithm from Eq. (4) for Eq. (7), we define Ψ ≔ (ψ, ψ^*, v_g) and rewrite the function F(Ψ) as a formal matrix product:

$${{{{{{{\bf{F}}}}}}}}({{{{{{{\boldsymbol{\Psi }}}}}}}})=\underline{\underline{\widetilde{{{{{{{{\rm{F}}}}}}}}}}}({{{{{{{\boldsymbol{\Psi }}}}}}}}){{{{{{{\boldsymbol{\Psi }}}}}}}}\equiv \left[\begin{array}{ccc}{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,1}&{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,2}&{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,3}\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{2,1}&{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{2,2}&{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{2,3}\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{3,1}&{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{3,2}&{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{3,3}\\ \end{array}\right]\left[\begin{array}{c}\psi \\ {\psi }^{* }\\ {v}_{g}\end{array}\right]$$

(8)

where $\underline{\underline{\widetilde{{{{{{{{\rm{F}}}}}}}}}}}({{{{{{{\boldsymbol{\Psi }}}}}}}})$ is a 3 × 3 matricial operator defined by the following equations :

$$\begin{array}{c}{\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,1}=-1-i({\zeta }_{0}-\frac{1}{2}{\partial }_{\theta }^{2}+{\Delta }_{\bar{\mu }}{e}^{i\bar{\mu }\theta }{\hat{{{{{{{{\mathcal{F}}}}}}}}}}_{\bar{\mu }})\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,2}=i{\psi }^{2}(1-\tau {\partial }_{\theta })-i\tau \psi {\partial }_{\theta }\psi \\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,3}={\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{2,3}={\partial }_{\theta }\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{2,2}={({\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,1})}^{* }\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{2,1}={({\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{1,2})}^{* }\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{3,1}={\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{3,2}=\frac{1}{2}{\int}_{{{{{{{{\mathcal{R}}}}}}}}}d\theta \delta (\theta -{\theta }_{{{{{{\rm{max}}}}}}}){\partial }_{\theta }\\ {\widetilde{{{{{{{{\rm{F}}}}}}}}}}_{3,3}=0\\ \hat{{{{{{{{\mathcal{F}}}}}}}}}\psi =\int\,d\theta \psi {e}^{-i\mu \theta }={\psi }_{\mu }\\ {\hat{{{{{{{{\mathcal{F}}}}}}}}}}^{-1}{\psi }_{\mu }={\sum }_{\mu }{\psi }_{\mu }{e}^{i\mu \theta }=\psi \\ {\hat{{{{{{{{\mathcal{F}}}}}}}}}}_{\bar{\mu }}\psi ={\sum }_{\mu }{\delta }_{\mu ,\bar{\mu }}\hat{{{{{{{{\mathcal{F}}}}}}}}}\psi ={\psi }_{\bar{\mu }}\end{array}$$

In this way, the iterative equation in (4) can be rewritten as:

$$\underline{\underline{J}}{{{{{{{{\boldsymbol{\Psi }}}}}}}}}_{k+1}=(\underline{\underline{J}}-\underline{\underline{\widetilde{{{{{{{{\rm{F}}}}}}}}}}}){{{{{{{{\boldsymbol{\Psi }}}}}}}}}_{k}$$

(9)

that can be numerically solved for Ψ_k+1.

Thus, the Jacobian in the rotating frame takes form:

$$\underline{\underline{{{{{{{{\rm{J}}}}}}}}}}({{{{{{{\boldsymbol{\Psi }}}}}}}})=\underline{\underline{\widetilde{{{{{{{{\rm{F}}}}}}}}}}}({{{{{{{\boldsymbol{\Psi }}}}}}}})+\left[\begin{array}{ccc}\hat{\Delta }({{{{{{{\boldsymbol{\Psi }}}}}}}})&0&0\\ 0&{\hat{\Delta }}^{* }({{{{{{{\boldsymbol{\Psi }}}}}}}})&0\\ 0&0&0\end{array}\right]$$

(10)

where:

$$\hat{\Delta }(\Psi ):= 2i| \psi {| }^{2}+{v}_{g}{\partial }_{\theta }-i\tau ({\partial }_{\theta }| \psi {| }^{2}+| \psi {| }^{2}{\partial }_{\theta }+\psi {\partial }_{\theta }{\psi }^{* }).$$

(11)

We implement the differential operators appearing in the matrices entries using the discrete Fourier transform matrix (DFT matrix⁴³), which allows us to express those operators in the Fourier space where they are represented algebraically.

To control the numerical convergence of the algorithm, we use the standard measure:

$$\sqrt{\frac{\parallel {{{{{{{{\boldsymbol{\Psi }}}}}}}}}_{k+1}-{{{{{{{{\boldsymbol{\Psi }}}}}}}}}_{k}{\parallel }_{2}^{2}}{\parallel {{{{{{{{\boldsymbol{\Psi }}}}}}}}}_{k}{\parallel }_{2}^{2}}} < 1{0}^{-6}$$

(12)

where ∥ ⋅ ∥₂ is the L²-norm. To avoid discretization problems, (especially for the computation of the correct spectrum of the Jacobian), we discretized the envelop function ψ in N_ψ = 2¹⁰ number of points.

Finally, some comment on the choice of the initial condition Ψ₀ is required. Despite its power, this method, being the simplest of its kind, suffers from a small convergence radius. That means the initial condition must be already very close to the actual one. To overcome the problem, we used a numerical DKS solution from dynamical simulations as a guess solution with zero group velocity. For the subsequent points, we used instead as seeds the converged solution from the closest point in the detuning direction.

Dynamical simulation of the noise transduction

The dynamical simulations have been carried out with the step-adaptative Dormand-Prince Runge-Kutta method of Order 8(5,3)⁴⁰, hard seeded an approximate DKS solution. The input pump phase noise has been obtained from a linearization of the data of the power spectral density data of Toptica CTL 1550 Laser, ${S}_{\phi }^{{{{{{{{\rm{in}}}}}}}}}$. In particular, it has been implemented through a detuning noise term ζ₀(t) obtained as:

$${\zeta }_{0}(t)=\alpha \hat{{{{{{{{{\mathcal{F}}}}}}}}}_{t}}(\sqrt{{\nu }^{2}{S}_{\phi }^{{{{{{{{\rm{in}}}}}}}}}(\nu )}{e}^{ix(\nu )}),$$

(13)

where a uniformly distributed random phase x(ν) has been added to each frequency to obtain a random realization of the detuning noise and coefficient α normalizes the standard deviation of the pump detuning. We used the following simulation parameters¹: n₀ = 1.9, n₂ = 2.4e−19, m²/W, FSR = 95.4 GHz, ω₀/2π = 192 THz, waveguide dimensions: 1.5 × 0.85 μm, κ₀/2π = 100 MHz, κ_ex/2π = 100 MHz, τ_R = 1 fs, D₂/2π = 1.3 MHz.

Output field in real units for the case of critical coupling (κ_ex = κ₀):

$${P}_{{{{{{{{\rm{out}}}}}}}}}(\phi ,t)=\hslash {\omega }_{0}\frac{{\kappa }_{{{{{{{{\rm{ex}}}}}}}}}^{2}}{{g}_{0}}| f-\psi {| }^{2}$$

(14)

Spectrogram:

$${P}_{\mu }(t)={\hat{{{{{{{{\mathcal{F}}}}}}}}}}_{\mu }{P}_{{{{{{{{\rm{out}}}}}}}}}$$

(15)

where ${\hat{{{{{{{{\mathcal{F}}}}}}}}}}_{\mu }$ is the operator taking the μth Fourier component of a function (the power in this case), as defined in the previous section. The phase of the first comb line (repetition rate phase):

$$\phi (t)=\arg \left[{P}_{1}(t)\right],$$

(16)

where $\arg \left[{P}_{1}(t)\right]$ denotes the phase of the first complex Fourier component of the detected optical power. The spectrum of phase noise:

$${S}_{\phi }(\nu )=| {\hat{{{{{{{{\mathcal{F}}}}}}}}}}_{\nu }\phi (t){| }^{2}$$

(17)

The transduction coefficient has been computed as:

$${{{{{{{\rm{PM2PM}}}}}}}}=10{{{{{{\rm{log}}}}}}}_{10}\frac{{S}_{\phi }}{{S}_{\phi }^{{{{{{{{\rm{in}}}}}}}}}}$$

(18)

We point out, in this analysis we assume an ideal photodetector, neglecting its actual response function. As for the Newton-Raphson method, we discretized the fast time axis (i.e., azimuthal coordinate) in N_ψ = 2¹⁰ points while the slow time in N_t = 20,000 points. In addition, in order to obtain a sensitivity of the order of the kHz, we simulate the soliton dynamics for 1 ms. TRN phase noise limit is calculated using methods and parameters presented in studies of Si₃N₄ microresonators²⁷. The comparison of the phase noise performance of different DKS states and calculated TRN noise limit is shown in Fig. 6.

Fig. 6: Phase noise performance of the soliton microcomb.

Phase noise plot of a DKS outside of the quiet point (Δ₋₂₁ = −15,  ζ₀ = 5.9 in Fig. 2b, c) and at QP1 (defined in Fig. 2b) compared to pump laser phase noise and thermorefractive (TRN) phase noise limit.