Interference, diffraction, and diode effects in superconducting array based on bismuth antimony telluride topological insulator

Abstract

It is well-known in optics that the spectroscopic resolution of a diffraction grating is much better compared to an interference device having just two slits, as in Young’s famous double-slit experiment. On the other hand, it is well known that a classical superconducting quantum interference device (SQUID) is analogous to the optical double-slit experiment. Here we report experiments and present a model describing a superconducting analogue to the diffraction grating, namely an array of superconducting islands positioned on a topological insulator film Bi_0.8Sb_1.2Te₃. In the limit of an extremely weak field, of the order of one vortex per the entire array, such devices exhibit a critical current peak that is much sharper than the analogous peak of an ordinary SQUID. Therefore, such arrays can be used as sensitive absolute magnetic field sensors. A key finding is that the device acts as a superconducting diode, controlled by magnetic field.

Introduction

Topological insulator (TI) films can be made superconducting, using the proximity effect, by placing superconducting electrodes on the TI surface^1,2. Such hybrid structures provide a testing ground for topological superconductivity³. They continue to be a hot topic in condensed matter physics due to the predicted and, to some extent, observed signatures of Majorana zero modes⁴. Although single junctions and SQUIDs have been previously studied in great depth, topological superconductor arrays, and superconducting quantum interference filters (SQIFs) have not been sufficiently investigated. Various SQUIF systems^5,6 are interesting for applications since they contain many interfering superconducting loops and thus enable absolute magnetic field sensitivity⁷. Moreover, arrays can provide room for multiple interacting vortices, which may be subjected to quantum braiding manipulations. These are sought after due to the promise of topologically protected quantum computation.

Another phenomenon that has attracted attention recently is the superconducting diode effect^{8,9,10,11,12,13}. A magnetically controllable superconducting diode has been demonstrated in, [Nb/V/Ta]_n, an artificial superlattice without a center of inversion¹⁴. Previously, superconducting rectifiers have been realized in asymmetric superconducting nanowire loops^15,16. It was also reported that Mo-Ge perforated films could be patterned using a conformal mapping approach in order to create superconducting diodes¹⁷. Recently, a theoretical model was proposed, predicting that Majorana bound states, if present, can generate a parity-protected diode effect, due to their exotic current-phase relationship¹⁸.

Generally speaking, nonreciprocal phenomena are well-known in relation to semiconductor diodes, which are based on p-n junctions. They exhibit either a high or low resistance, depending on the current polarity. The diode effect is used in a number of very important electronic components, including photodetectors, ac rectifiers, and frequency multipliers. But, due to their finite resistance, Joule heating and energy losses are inevitable in such devices. Therefore, a superconducting rectifier or a diode, characterized by zero resistance, remains highly desired for computational, sensing, and communication applications with ultralow power consumption. Such a device should have zero resistance at one current polarity and a nonzero resistance at the opposite polarity. Correspondingly, in the fully superconducting regime, the kinetic inductance would be dependent on the supercurrent polarity.

The focus of our study is a square array of superconducting Niobium islands overlaying an intrinsic topological insulator film Bi_0.8Sb_1.2Te₃ (BST)². There are theoretical predictions suggesting that BST can be used to build superconducting qubits for topologically protected quantum computers¹⁹. Yet, previous reports² suggested that it is very difficult, if not impossible, to introduce a significant proximity superconductivity into the intrinsic topological insulator, BST². In our work, we demonstrate that it is possible to establish high critical current and good contact, hence stronger proximity. We find that such a proximitized array acts as a superconducting analog of the optical diffraction grating. Constructive interference of the supercurrents in multiple parallel superconducting nanowires has been discussed theoretically previously²⁰. We observe an extreme sensitivity of the array to perpendicular external magnetic fields, which is explained in terms of the diffraction-grating-style interference of supercurrents in many parallel junctions. The interference peak is so narrow that it allowed us to distinguish magnetic fields which differ by about 8 nT, using a simple dc technique. The zeroth-order critical current interference peak is significantly sharper and taller than all other maxima, thus allowing absolute magnetic field measurements. By contrast, regular superconducting quantum interference devices^21,22 are characterized by a periodic dependence on the external field and thus do not allow absolute field measurements. Another key finding: We demonstrate that topological insulator-superconductor arrays can behave as efficient superconducting rectifiers. It is observed that the system of proximity-coupled Nb islands acts as a superconducting diode, i.e., it exhibits a dependence of the critical current on the polarity of the bias current, at nonzero magnetic fields. A model is presented to explain the observed diode effect.

Results

Sample description

Our samples are based on high-quality topological insulator thin films (40 nm thick) having a nominal composition Bi_0.8Sb_1.2Te₃, grown by molecular beam epitaxy². Similar films were used in a previous study of the superconducting proximity effect in which it was shown that this composition provided undoped topological insulators without bulk carriers or an accumulation layer caused by band bending. The only free carriers in this material are the topological surface carriers due to the inter-band Dirac cone that exhibits spin-momentum locking. There it was shown that the proximity effect was restricted to the surface in contact with the superconductor².

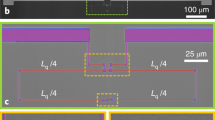
Our Nb-BST-Nb arrays consist of Niobium square islands arranged into a square lattice deposited on top of the TI-BST film (Fig. 1a). The thickness of the islands is 30 nm and the lattice constant is w + d = 1.3 μm (Fig. 1). The array is fabricated by electron beam lithography and plasma sputtering of the Nb film and contains 23 × 23 Nb islands (see “Methods” for further details). The gap between neighboring islands, as estimated from the scanning electron microscope (SEM) images, equals d ≈ 150 nm (Fig. 1b). So, the width of each island is ~w ≈ 1.15 μm.

Fig. 1: Sample configuration.

a Autocad-generated design file of the device. A square array of square Niobium islands is placed over the surface of a topological insulator epitaxial film, Bi_0.8Sb_1.2Te₃ (BST). The blue color illustrates the Nb leads and the square Nb islands. The black color represents the BST film. The yellow color is where the BST film was milled off to expose the sapphire substrate underneath, thus creating trenches to isolate devices from each other. The bias current is applied horizontally between the I⁺ and I⁻ leads and the magnetic field is oriented perpendicular to the surface of the sample. The voltage is probed on the V⁺ and V⁻ contact pads. b An scanning electron microscope (SEM) image of the Nb array.

Initial characterization of the sample

All measurements except the last have been performed at the base temperature of T = 0.3 K. The resistance versus temperature (R–T) curve (Fig. 2a) shows that a superconducting transition takes place in the Nb islands first, at T ≈ 8 K. Due to the proximity effect, the surface of the topological insulator becomes superconducting near the islands. Consequently, the resistance drops to zero at T ≈ 0.4 K. Global superconductivity of the array is evident from the voltage–current (V–I) curves (Fig. 2b), which show a critical current below which the voltage is zero. So, V–I curves exhibit sharply defined critical currents (Fig. 2b). Note that in order to obtain such V–I curves, it was necessary to apply a small magnetic field to compensate for the Earth’s field. The symmetric curve (black) is presumed to occur at zero magnetic field (Fig. 2b). A zoomed-in version of these three V–I curves is shown in Fig. 2b, inset. The V–I curve was measured four times at each magnetic field. Such repeated measurements demonstrate the same switching current. The fluctuations are less than 0.1%, indicating, among other things, that noise, thermal phase slips, as well as quantum tunneling of phase slips do not contribute significantly to cause premature switching events.

Fig. 2: Evidence of the global superconductivity of the topological array.

a Resistance versus temperature (R–T) curve. b Examples of voltage–current (V–I) curves, taken at different (weak) magnetic field values: B = 0T—black line, B = 0.93 μT—blue line, B = −0.87 μT—red line. The temperature was T = 0.3 K. The V–I curve measured at zero field is presumed symmetric, while the others are not. The curves illustrate the strong sensitivity of the array to the magnetic field. b, inset: A zoomed-in version of (b). Each curve is measured four times. The curves illustrate the fact that the switching current does not change from one measurement to the next one if the magnetic field is fixed.

Magnetic field effects

A typical resistance versus magnetic field (R–B) curve is shown in Fig. 3. The horizontal axis represents the external magnetic field, B, applied perpendicular to the sample plane. The field is normalized as

$$f=AB/{\phi }_{0},$$

(1)

where f is the flux per unit cell of the array, A = (w + d)² = 1.69 μm² is the area of the unit cell of the square lattice, and ϕ₀ = 2.067 × 10⁻¹⁵ Wb is the magnetic flux quantum in superconductors. Thus, the oscillation period, defined as f = 1, corresponds to the theoretical value ΔB = 1.22 mT. The experimental value, ΔB = 1.23 mT, was used when normalizing the field. The resistance is measured by calculating the slope of the best linear fit to the V–I curve. The V–I curve is measured using a low-frequency ac signal, the amplitude of which is indicated on the graph. The V–I is nonlinear, thus explaining why the resistance is generally larger for larger amplitudes of the bias current (I_bias).

Fig. 3: Resistance versus magnetic field (R–B) curves.

Three curves were taken at different amplitudes of the ac bias current amplitudes: I_bias = 80 nA—gray line, I_bias = 250 nA— red line, I_bias = 850 nA—black line. The temperature was T = 320 mK.

Sharp minima of the resistance at integer values of the magnetic flux per unit cell

A pronounced feature of the R–B plot is the presence of sharp minima of the resistance at f = 0 and f = 1 and a well-pronounced minimum at f = 3. However, the expected minimum at f = 2 is missing (see, e.g., the black curve in Fig. 3). Such suppression is probably related to a strong Fraunhofer diffraction effect, which causes the critical current of each junction to go close to zero if the flux in a single junction equals the flux quantum. Note in passing that the complete suppression of the supercurrent provides a testing ground for the search of Majorana fermions. In the ideal case, when the flux per junction equals one flux quantum, the critical current is zero unless Majorana states are present, as they have a different current-phase relationship⁴.

The existence of such sharp resistance minima can be understood as a result of vortices, which, in the range of the relatively weak fields considered here, are localized in the N-regions of the SNS junctions of the array. Here “S” stands for superconductor (Nb), and “N” represents the conducting normal surface states of the topological insulator. These surface states are, in fact, also weakly superconducting due to the proximity effect. Generally speaking, the resistance is defined by the level of dissipation in the array, which is proportional to the concentration of vortices and their mobility. Thus, the minimum at f = 0 is explained by the lack of vortices in the array at zero magnetic field. On the other hand, the minima f = 1 and f = 3 correspond to cases where the number of vortices per unit cell is an integer (equal f). In the cases of f being an integer, the vortex lattice is commensurate with the Nb islands lattice. Such commensurability ensures strong pinning of the vortices, corresponding to low mobility of the vortex lattice, which corresponds to low dissipation and low resistance.

Possible arrangement of vortices at integer values of the magnetic flux per unit cell

Recently, it has been demonstrated explicitly that vortices in SNS junctions possess normal cores²³. We suggest that in the case of perfect commensurability, f = 1, each vortex core is located between the corners of four neighboring squares (Fig. 4a), where the proximity-induced superfluid density is the lowest. Thus, each vortex is located at the very minimum of its potential energy, and so has a very low mobility. Interestingly, a weaker but still prominent commensurability-related suppression of the resistance occurs also at fractional frustration values, namely f = 1/3, 1/2, 2/3 (see the black curve in Fig. 3). This is a clear sign that vortices form an ordered lattice, even when they occupy every second or every third cell of the array, while the other cells are free of vortices.

Fig. 4: Schematic of the sample, which illustrates the possible distribution of fluxoids at different values of the magnetic field.

The Nb squares are shown as blue. A unit cell is shown by a dashed line. Due to the proximity effect, the Nb squares induce superconductivity into the underlying topological insulator film (yellow). Since the entire array is globally superconducting, we expect that Josephson supercurrents are looping between neighbor Nb squares if a magnetic field is applied. a The centers of supercurrent loops are shown, schematically, as swirls, for the case f = 1. Note that the edges of the Nb squares are colored green to illustrate the regions when the Meissner effect is incomplete. b Josephson vortex centers are shown as swirls, for the case f = 2. In this case, each junction has one quantum of magnetic flux, so the Josephson vortex is located in the center of each junction between each pair of neighbor islands.

Missing resistance minimum at frustration f = 2

The missing minimum at f = 2 (see the definition Eq. (1)) can be explained by a qualitatively different arrangement of the vortices. With two flux quanta per unit cell (f = 2), each junction receives one vortex. Such a conclusion stems from the fact that in the square array, there are exactly two junctions per unit cell (Fig. 4), the vertical one and the horizontal one. Thus, at f = 2 the flux per junction equals one flux quantum. According to the Fraunhofer formula, the critical current of a single junction is ${I}_{c1}({f}_{1})={I}_{c1}(0)\sin (\pi {f}_{1})/(\pi {f}_{1})$, where f₁ is the magnetic flux in the junction, normalized by the flux quantum, and I_c1(0) is the critical current of one junction at zero field. So, the critical current of each junction should approach zero at f = 2 since, geometrically, f₁ ≈ f/2. Therefore the resistance of each junction has a maximum at f = 2 or a slightly higher field. This maximum negates the expected resistance minimum, related to the matching of the vortex lattice and the lattice of the Nb islands. To explain a zero or a very low critical current, we suggest that at f = 2, the cores of the vortices enter the junctions (Fig. 4b). In such arrangements, the vortices are located at the maxima of their potential energy, so they can easily slide under the influence of the Lorentz force related to the bias current.

Effect of the magnetic field on the critical current

So far we have presented the multiple-island interference and the Fraunhofer diffraction effects, as they appear on the R–B curve. The same phenomena can be distinguished on the critical current versus magnetic field (I_c–B) curve (Fig. 5a). The most pronounced feature is the extra sharp peak at zero field. It reflects a coherent addition of the condensate transmission coefficients on all columns of the array. This is in analogy with the optical diffraction grating, which shows a high transmission at zero angle because the waves diffracted by all the slits arrive in phase. We can use the peak narrowing factor to evaluate the accuracy of the analogy. For a 23-slit diffraction grating, its I_c–B curve can be calculated from Eq. (4), and the full width at half maximum (FWHM) of the central peak is 0.052. Thus the peak narrowing factor is 1/0.052 =  19.2. For the array device, according to Fig. 5a, FWHM of the central peak is 0.096, so the peak narrowing factor is 2/0.096 = 20.8, which is close to the expected value. The factor 2 is introduced since the unit cell contains four junctions, so one needs a twice larger flux to generate the same phase bias per junction as in ordinary superconducting quantum interference devices (SQUID), which contain two junctions per loop. (Since we know that B = 1.23 mT corresponds to one vortex per unit cell, i.e., 23 × 23 = 529 vortices in the entire array, the field corresponding to the FWHM condition represents 23 vortices in the arrays, i.e., ≅ 2.2 fluxons per each row of Nb islands. The vortices occur only in BST, i.e., between Nb islands but not inside Nb film.) The similarity of the observed and the calculated peak narrowing factors supports the analogy of the superconducting array and the optical diffraction grating. The fact that the peak at zero field is different than the other peaks suggests that such arrays can be used as sensitive detectors of the absolute magnetic field. A calculated curve (to be discussed below) is shown in Fig. 5b.

Fig. 5: Critical current versus normalized flux per unit cell, f.

a The critical current shows sharp peaks coinciding with integer values of f. The peak f = 2 is suppressed. b Blue line: theoretical dependence ${I}_{C}^{+}(\tilde{f})$ obtained by numerical solution of Eqs. (2) and (7)). Red dashed line: the dependence ${I}_{C}^{(1)}(\tilde{f})$ for a single junction Eq. (5) multiplied by N = 23.

Superconducting array as an absolute magnetic field sensor

The superconducting diffraction-grating effect, presented above, enables sensitive detection of the absolute magnetic field, as illustrated in Fig. 6. There, each point is obtained by measuring 1000 V–I curves, over a time span of 100 s, and subsequent averaging of the corresponding critical currents. The closest separation between the points we could resolve, using a simple dc-current measurement of the critical current, is about 8 nT. If, as in this case, the critical current is used to monitor the magnetic field then it is important to realize a sample with a small fluctuation of the switching current. Our array shows a very low fluctuation, as is evident from Fig. 2b, inset, where each curve is measured four times. The standard deviation of the critical current was about 2.8 nA, which is about 0.1% of the critical current value. (For comparison, the fluctuation of the switching current was close to 1% in the experiments on superconducting nanowires having critical currents of the order of 20 micro-Apmps²⁴. A possible explanation is that quantum tunneling of vortices across the entire array is very unprobable since the array is much wider.) Note that the central peak of the critical current versus B plot of the array is much taller and sharper than the other critical current maxima. Therefore the superconducting array sensor can detect the absolute zero of the magnetic field, which is an advantage compared to ordinary SQUIDs, which are periodic with the magnetic field.

Fig. 6: Magnetic field sensitivity test.

Each red dot represents the mean value of N₁ = 1000 critical current measurements taken at a rate of 10 point per second, at a constant magnetic field. The measurements are taken to the left of the I⁻(B) peak, where the slope is the largest. The error bars represent the standard errors, which are calculated from each ensemble of N₁ = 1000 points, by first finding the standard deviation (SD) and then calculating the standard error as SD/$\sqrt{{N}_{1}}$.

Asymmetry and the diode effect at various temperatures

As we zoom in on the central peak of the critical current (see Fig. 7a), we find a shift of the point of the maximum away from the zero field point. Note that the point of zero field is defined through the equality of the two critical currents with the opposite polarity, i.e., ${I}_{c}^{+}(0)={I}_{c}^{-}(0)$. The strongest asymmetry, which amounts to $\eta ={I}_{c}^{-}/{I}_{c}^{+}\approx 1.2$, takes place at B₀ ≅ 5.05 μT. (This field represents about 2.2 fluxons in the entire arrays of 23 × 23 Nb islands.) At B = B₀, the critical currents are ${I}_{c}^{-}=2.78 \, \upmu$A and ${I}_{c}^{+}=2.3\, \upmu$A. Such 20% strong asymmetry of the critical current constitutes a field-controlled superconducting diode effect. It can be used to rectify ac-signals if the amplitude of the applied ac current is larger than the critical current of one polarity but lower than the critical current of the opposite polarity. We demonstrate the diode effect directly by applying an ac current (10 Hz) with an amplitude that is lower than ${I}_{c}^{-}$ but larger than ${I}_{c}^{+}$. The result, a clear rectification effect, is shown in Fig. 7 by the black curve.

Fig. 7: Superconducting diode effect.

a The critical current on positive (blue line) and negative (red line) branches is plotted as a function of the magnetic field. The black curve represents the rectification effect. It is the mean value of the voltage measured as the bias current is set such that it exceeds the lower critical current but remains lower than the other critical current. b Theoretical dependencies ${I}_{C}^{+}({B}_{z})$ (blue line) and ${I}_{C}^{-}({B}_{z})$ (red line), which are obtained by numerical solution of Eqs. (2) and (7) with $\tilde{f}={B}_{z}(d+w)(d+0.3537w)/{\phi }_{0}$ and other parameters given in the caption of Fig. 5.

Temperature effect

Experimentally (see Fig. 8), as the temperature increases the asymmetry, η, decreases rapidly. We observed η = 1 when the temperature exceeds 0.52 K, i.e., the superconducting diode effect vanishes at T > 0.52 K. Note that the critical current decreases only by 15% as we warm up from 0.3 to 0.52 K. A similar I_c versus T dependence has been observed in a recent experiment²⁵. It has been interpreted in terms of the two parallel conducting channels for the supercurrent: ballistic states on the surface of the topological insulator and also some diffusive channels. The diffusive transport can be associated with a high normal state sheet resistance and can be associated with the diode effect as we explained in the Model section. According to this interpretation, at temperature T₀ the supercurrent in the diffusive channel gets suppressed by thermal fluctuations. Therefore, at T > T₀ only the ballistic surface states, which do not induce the diode effect, contribute to the Josephson current. Thus, these observations support our model, which is based on the high resistance per square in the normal state.

Fig. 8: The effect of temperature on the superconducting diode effect.

a The dependence of the negative ${I}_{c}^{-}$ (red triangles) and positive ${I}_{c}^{+}$ (blue circles) critical currents on temperature, measured at the magnetic field of −5 μT. At temperature T₀ = 0.52 K the diode effect disappears, i.e., $\eta ={I}_{c}^{-}/{I}_{c}^{+}$ = 1 for T > T₀. b The ratio of the negative and positive critical currents versus the temperature. The horizontal axis in (a) and (b) is the same.

Scale of fields needed to induce diode effect

It might be instructive to compare these results to previously published observations of superconducting diode phenomena. Recently, a superconducting diode was realized using a noncentrosymmetric superlattice. The lattice was made of alternating epitaxial films of tantalum, vanadium, and niobium¹⁴. In their study, the inversion symmetry was broken in the vertical direction. Thus, in order to break the time-reversal symmetry, a precisely aligned in-plane magnetic field, applied perpendicular to the current, was required. Our superconducting array, based on topological Bi_0.8Sb_1.2Te₃ films, requires much weaker fields in order to act as a superconducting rectifier. The magnetic field needs to be applied perpendicular to the plane of the sample but does not require any fine alignment. Note that to identify the exact physical mechanisms for the observation of the low-field supercurrent rectification in this proximity-coupled superconducting array, in particular, whether intrinsic or extrinsic, further study is necessary. From the point of view of possible applications, our design might be superior, in some aspects, to previously published designs. For example, our system requires only very small magnetic fields, about 5 μT, for the occurrence of the diode effect. The scale of this field is such that only three fluxoids are induced in the entire array. Such fields are orders of magnitude lower than those used in a previously reported system¹⁷.

Model

To explain the results we propose a model which takes into account the high kinetic inductance of surface states of the topological insulator. Another key ingredient of the model is the naturally occurring variation in the Nb-BST junction parameters. We model the system as a two-dimensional array of wide Josephson junctions between square Nb islands of the size w × w separated by the gaps of width d. The Josephson current flows through the proximitized BST layer, which has a small induced superconducting gap Δ under the islands and no gap between the islands. Yet, the pair amplitude between the islands differs from zero, so global superconductivity is possible. The physics of Josephson arrays is very rich. For example, they exhibit superconductor-insulator phase transitions^26,27,28,29, and at finite magnetic field a vortex lattice is formed in the array³⁰. For these reasons, the full theoretical description of such systems is complicated^31,32,33. To keep the analysis tractable, here we adopt a simple model, which is formally valid at small magnetic fields. Despite its simplicity, the model captures the main effect we study—Josephson current rectification.

In the experiment, we observe ac bias current rectification at small but finite magnetic fields, see Fig. 7. This effect may be caused by several reasons: It might be due to Majorana modes, as was recently predicted¹⁸. It may be a simple self-field effect earlier observed in asymmetric SQUIDs^{15,34,35,36,37} and asymmetric wide junctions³⁸ with high critical currents. The rectification may be caused by spin–orbit interaction in BST, which requires the presence of the two field components: parallel (B_y) and perpendicular (B_z) to the BST plane. This effect has been previously demonstrated in junctions made on GaAs¹² and Bi₂Se₃³⁹ substrates. Most of these phenomena cannot explain our observations because, in our experiments, both applied and induced magnetic fields are very small. Thus, our experiment resembles recent studies of NbSe₂ nanowires⁴⁰ and of thin metallic films⁴¹, where the rectification has been observed in the presence of only the B_z field component. We attribute the rectification effect in our sample to the finite kinetic inductance of the proximized BST layer under the Nb islands, as will be explained below. However, we cannot exclude an additional contribution from the edge states or even Majorana states in BST, which may effectively form asymmetric SQUID loops with a non-sinusoidal current-phase relation^10,18.

To develop a model, we need to emphasize that there are two important properties of the array. The first is peak sharpening. This property will be explained using the analogy with the optical diffraction grating, which requires multiple parallel junctions interfering with each other. The second property is the diode effect. This one will be explained by approximating the array by a single large junction of width W equal to the width of the entire array.

Let us consider the gap between two neighboring rows of Nb islands in the middle of the array, namely the gap between the rows with the numbers i and i + 1. We express the Josephson current as an integral along the line going through the middle of this gap,

$${I}_{J}=\int\nolimits_{0}^{W}dy\,{j}_{C}(y)\sin [\phi (y)].$$

(2)

Here W = N(w + d) is the total width of the array, N is the number of islands in one row (N = 23 in our sample), y is the coordinate along the line, j_C(y) is the coordinate-dependent critical current density, and ϕ(y) is the gauge invariant phase difference across the Josephson junctions. Here we assume the usual sinusoidal current-phase relation for the junctions. The current density j_C(y) equals zero in the segments confined between four corners of four neighbor Nb islands. In Eq. (2), the gauge invariant phase ϕ(y) is expressed as

$$\phi (y)=\varphi (y)-\frac{2\pi {B}_{z}d}{{\phi }_{0}}y,$$

(3)

where φ(y) = φ_i+1(y) − φ_i(y) is the difference between the phases of the superconducting order parameters in the two adjacent islands belonging to the rows i + 1 and i, and ϕ₀ is the magnetic flux quantum.

To elucidate the well-known relation between Eq. (2) and the diffraction phenomenon in optics, we consider an ideal sample with constant current density j_C(y) within the junctions and j_C(y) = 0 in the gaps between them. We also assume that superconducting leads are bulky and the magnetic field is fully expelled from them. In this case, the integral Eq. (2) can be solved analytically. Maximizing the Josephson current over the coordinate independent phase difference φ, one arrives at the familiar diffraction-grating-like dependence of the critical current on f,

$${I}_{C}(f)={I}_{C}^{(1)}(f)\left\vert \frac{\sin (\pi Nf)}{\sin (\pi f)}\right\vert ,$$

(4)

where

$${I}_{C}^{(1)}(f)=\frac{{I}_{C}}{N}\left\vert \frac{w+d}{\pi fw}\sin \left(\frac{\pi fw}{w+d}\right)\right\vert$$

(5)

is the critical current versus flux dependence for a single junction, and I_C is the critical current of the whole array at f = 0. In Eqs. (4) and (5) f = B_z(w + d)d/ϕ₀, where B_z is the field in the gaps between the bulk islands. Due to flux focusing, this field is larger than the external field created by the magnet. Flux conservation ensures that one can equivalently express the parameter f by Eq. (1), in which B is the external field. While this simple model well describes a single wide Josephson junction²², it loses accuracy for a 2d array above a certain value of the magnetic field where vortex penetration becomes important.

To find the rectification effect, we start with the expression for the current density in the proximized BST layer under a single square Nb island. Adopting the disordered superconductor model, we obtain j = (πΔ/2eR_□)( ∇ φ − 2eA/ℏc). Here φ is the phase and Δ is the absolute value of the induced superconducting order parameter in BST and A is the vector potential with the components A_x = B_zy, A_y = A_z = 0. We assume that the current flows along the x-axis, and we also fully ignore the screening of the field by thin Nb islands. Since ∇ j = 0 and ∇ A = 0, the phase under the island satisfies the equation ∇²φ(x, y) = 0 with the boundary conditions derived from the conditions for the current components ${j}_{x}(0,y)={j}_{x}(w,y)={j}_{C}(y)\sin [\phi (y)]$, j_y(x, 0) = j_y(x, w) = 0. Solving the equations for the phase φ(x, y) under the two neighboring Nb islands from the rows i and i + 1 and taking the difference between the phases at the edges of these islands, we arrive at the self-consistent equation for the gauge invariant phase Eq. (3) in the form

$$\phi (y)\, = \, {\varphi }_{0}-\int\nolimits_{0}^{w}\frac{d{y}^{{\prime} }}{2\pi }\ln \frac{\left(\cosh \pi -\cos \frac{\pi (y-{y}^{{\prime} })}{w}\right)\left(\cosh \pi -\cos \frac{\pi (y+{y}^{{\prime} })}{w}\right)}{\left(1-\cos \frac{\pi (y-{y}^{{\prime} })}{w}\right)\left(1-\cos \frac{\pi (y+{y}^{{\prime} })}{w}\right)}\\ \times \,\left(\frac{2e{R}_{\square }}{\pi {{\Delta }}}{j}_{C}({y}^{{\prime} })\sin [\phi ({y}^{{\prime} })]+\frac{2\pi {B}_{z}}{{\phi }_{0}}{y}^{{\prime} }\right)-\frac{2\pi {B}_{z}d}{{\phi }_{0}}y.$$

(6)

Here φ₀ is an arbitrary constant phase shift. Assuming further that the current density ${j}_{C}({y}^{{\prime} })\sin [\phi ({y}^{{\prime} })]$ slowly varies with the coordinate ${y}^{{\prime} }$, one can re-write Eq. (6) in the simplified form

$$\phi (y)\approx {\tilde{\varphi }}_{0}-\frac{2e{R}_{\square }w}{\pi {{\Delta }}}{j}_{C}(y)\sin [\phi (y)]-\frac{2\pi \tilde{f}}{d+w}y.$$

(7)

Here ${\tilde{\varphi }}_{0}$ is independent of the y part of the phase and $\tilde{f}={B}_{z}(d+w)(d+0.3537w)/{\phi }_{0}.$ This parameter slightly differs from the normalized flux f defined in Eq. (1) due to field penetration in the leads. Equation (7) is valid in the limit $| \tilde{f}| \ll 1$, where one can assume that the current densities at both edges of a square island perpendicular to the bias current are equal, and at the edges parallel to the bias current—equal to zero. At higher fields local currents in the array flow in all directions and the field dependence of the critical current should be determined by f, i.e., in the limit ∣f∣ ≳ 1 we expect $\tilde{f}=f$. We plot the critical current versus the flux, in Fig. 5b. The calculation shows sharp peak at integer values of the normalized flux, as expected from the basic analogy with the diffraction-grating formula given in Eq. (4).

The Eq. (7) can be extended to the whole width of the array 0 < y < W, while Eq. (6) is valid only for a single junction, i.e., for 0 < y < w. The second term in Eq. (7) may be interpreted as the kinetic inductance contribution to the phase difference. It is equal to the phase drop across a single island. If this term is independent of y it can be absorbed into the phase ${\tilde{\varphi }}_{0}$ and, therefore, has no effect on the value of the critical current. However, for the asymmetic current distribution j_C(y) the kinetic term acts as the effective self-induced field ${B}_{z}^{{{{{{{{\rm{eff}}}}}}}}}\propto {j}_{C}(y-W/2)-{j}_{C}(W/2-y)$. The effective field ${B}_{z}^{{{{{{{{\rm{eff}}}}}}}}}$ changes sign depending on the direction of the bias current and in this way causes the rectification effect. Indeed, the maxima of the curves ${I}_{C}^{\pm }(\tilde{f})$ shift from zero in the opposite directions. The maxima occur at $\tilde{f}={f}_{0}$ for ${I}_{C}^{+}$ and at $\tilde{f}=-{f}_{0}$ for ${I}_{C}^{-}$ with ${f}_{0}\propto {B}_{z}^{{{{{{{{\rm{eff}}}}}}}}}$.

Evaluating the Josephson current Eq. (2) with ϕ(y) obtained from Eq. (6) requires extensive numerical simulations. However, one can estimate the rectification effect on the basis of the simplified equation Eq. (7). First, we consider the limit of small sheet resistance such that

$$\begin{array}{r}\alpha =\frac{2e{I}_{C}{R}_{\square }}{\pi N{{\Delta }}}\ll 1.\end{array}$$

(8)

In this limit, one can derive a general expression for the shift of the critical current maximum f₀ for an arbitrary critical current distribution j_C(y),

$${f}_{0}=\frac{e{R}_{\square }w(w+d)}{{\pi }^{2}{{\Delta }}}\frac{\int\nolimits_{0}^{W}d{y}_{1}d{y}_{2}{j}_{C}({y}_{1}){j}_{C}({y}_{2})[{j}_{C}({y}_{1})-{j}_{C}({y}_{2})]({y}_{1}-{y}_{2})}{\int\nolimits_{0}^{W}d{y}_{1}d{y}_{2}{j}_{C}({y}_{1}){j}_{C}({y}_{2}){({y}_{1}-{y}_{2})}^{2}}.$$

(9)

One can verify that f₀ ≠ 0 only if the distribution j_C(y) is asymmetric, i.e., j_C(y − W/2) ≠ j_C(W/2 − y). The critical current versus flux dependence in this approximation becomes

$${I}_{C}^{\pm }(\tilde{f})={I}_{C}-\frac{{\pi }^{2}{(\tilde{f}\mp {f}_{0})}^{2}}{{(d+w)}^{2}{I}_{C}}\int\nolimits_{0}^{W}d{y}_{1}\int\nolimits_{0}^{W}d{y}_{2}\,{j}_{C}({y}_{1}){j}_{C}({y}_{2}){({y}_{1}-{y}_{2})}^{2}.$$

(10)

As a model, we choose the simplest asymmetric critical current density distribution of the form

$${j}_{C}(y)=\frac{{I}_{C}}{W}\left[1+\beta \left(\frac{y}{W}-\frac{1}{2}\right)\right],$$

(11)

This formula provides the definition for the dimensionless asymmetry parameter, β. The meaning of this formula is that the critical current density increases linearly, from the value on the left side of the sample, where it is ${j}_{C}(0)=\frac{{I}_{C}}{W}[1-\beta /2]$ to the maximum value on the right side of the sample, where it is ${j}_{C}(W)=\frac{{I}_{C}}{W}[1+\beta /2]$. The parameter β is an unknown and an adjustable parameter, which can be extracted, indirectly, from the shape of the V–I curves, which is explained below, where we compare the model to the experiment.

With such model of the asymmetric critical current distribution one gets

$${f}_{0}=\frac{e{R}_{\square }{I}_{C}w\beta }{{\pi }^{2}{N}^{2}{{\Delta }}(w+d)},$$

(12)

$${I}_{C}^{\pm }(f)={I}_{C}\left[1-\frac{{\pi }^{2}{N}^{2}}{6}\left(1-\frac{{\beta }^{2}}{12}\right){(\tilde{f}\mp {f}_{0})}^{2}\right].$$

(13)

We note for clarity that the distribution Eq. (11) ignores the gaps between the islands because in our sample d ≪ w. Thus, in this approximation, the array is essentially replaced by a single junction with the width W. From Eq. (13), one can estimate the asymmetry parameter introduced earlier,

$$\eta =\frac{{I}_{C}^{-}(-{f}_{0})}{{I}_{C}^{+}(-{f}_{0})}={\left[1-\frac{2}{3{\pi }^{2}}{\left(\frac{e{R}_{\square }{I}_{C}w}{N{{\Delta }}(w+d)}\right)}^{2}{\beta }^{2}\left(1-\frac{{\beta }^{2}}{12}\right)\right]}^{-1}.$$

(14)

Let us check if Eq. (12) is consistent with the experiment. From the experimental ${I}_{C}^{\pm }({B}_{z})$ curves presented in Fig. 7, we estimate f₀ ≈ 4 × 10⁻³. Some of the experimental parameters are known from the sample design and from independent measurements, namely, we can take N = 23, w = 1.15 μm, d = 150 nm, I_C = 2.7 μA, R_□ = 1.135 kΩ. The asymmetry parameter β can be roughly estimated from the spread of the re-trapping currents visible on the I-V curves presented in Fig. 2b. Indeed, the difference in the re-trapping currents of individual junctions should roughly correspond to the difference in their critical currents. Assuming further that the junctions with the highest and the lowest critical currents are located close to the opposite edges of the array, one can roughly approximate the distribution j_C(y) by Eq. (11) with the asymmetry parameter β ≈ 0.15. With these parameters, Eq. (12) gives the experimentally observed value f₀ ≈ 4 × 10⁻³ if one chooses the gap in the BST layer as Δ = 19 μeV. This value is ~18 times smaller than previously reported one in similar structures⁴², but it is consistent with the data from angle-resolved photoemission spectroscopy, which show strong suppression of the proximity effect in the BST². Moreover, the value of the gap is consistent with the ${I}_{C}^{{{{{{{{\rm{jct}}}}}}}}}{R}_{{{{{{{{\rm{norm}}}}}}}}}^{{{{{{{{\rm{jct}}}}}}}}}$-product for a single junction, where ${I}_{C}^{{{{{{{{\rm{jct}}}}}}}}}={I}_{C}/N$ is the critical current and ${R}_{{{{{{{{\rm{norm}}}}}}}}}^{{{{{{{{\rm{jct}}}}}}}}}$ is the normal state resistance of the junction. Indeed, ${I}_{C}^{{{{{{{{\rm{jct}}}}}}}}}={I}_{C}/N=0.117\,$ μA and the resistance of a single junction should be equal to the resistance of the whole square array at high temperatures, where Nb is superconducting but the proximity effect is negligibly weak (at about 6 K). In this way, from Fig. 3 we estimate ${R}_{{{{{{{{\rm{norm}}}}}}}}}^{{{{{{{{\rm{jct}}}}}}}}}\approx 225\,{{\Omega }}$. With these parameters, we obtain ${I}_{C}^{{{{{{{{\rm{jct}}}}}}}}}{R}_{{{{{{{{\rm{norm}}}}}}}}}^{{{{{{{{\rm{jct}}}}}}}}}\approx 26.4\,$ μV, which is indeed close to the gap value Δ = 19 μeV obtained above. With these numbers the asymmetry parameter (14) takes the value η = 1.062, which is a bit lower than the observed one, η = 1.2.

Although the simple Eqs. (12) and (13) explain the data reasonably well, they have been derived under the assumption α ≪ 1. However, with the parameters outlined above one finds α ≈ 4. For this reason, we have lifted the restrictions on α and have solved Eq. (7) numerically to find the coordinate dependence of the phase ϕ(y). For α > 1 this equation has multiple solutions with possible jumps between them. We choose one of these solutions for every value of y, with phase jumps to another solution happening at certain values of this coordinate where the previous solution ceases to exist. Such jumps correspond to the centers of the Josephson vortex cores, which are formed in the array. In addition, we assume constant critical current density, j_C,n, within the n − th junction, and assume that these values follow Eq. (11),

$${j}_{C,n}=\frac{{I}_{C}}{W}\left[1+\beta \left(\frac{n-1}{N}-\frac{1}{2}\right)\right].$$

(15)

To get a better agreement with the experiment, we have slightly adjusted the critical current of the whole array choosing I_C = 2.88 μA, and have also changed the value of the gap taking Δ = 59 μeV. In Fig. 5, we plot the dependence ${I}_{C}^{+}(\tilde{f})$, numerically obtained from Eqs. (2) and (7), for the wide range of the normalized fluxes $| \tilde{f}| \le 2.5$. We observe qualitative agreement between the theory and the experiment in spite of the simplicity of the model, which does not properly describe the complicated process of vortex formation. In particular, both in the theory and in the experiment the peaks occurring at $\tilde{f}=1/2$, $\tilde{f}=1/3$ and $\tilde{f}=2/3$ are clearly visible.

The experiment shows a clear jump at B = 25 μT (Fig. 7a). This might not be the first vortex entering. The first vortex entrance seems to be associated with a massive and sharp drop of the critical current observed at about B ≈ 6 μT. This magnetic field is close to the estimated value. Indeed, since the field required to populate each unit cell with exactly one vortex is 1.23 mT, and the number of unit cells is 23 × 23 = 529, the field needed to put just one vortex in the array is 2.3 μT. The experimental field at which a vortex can enter (≈6 μT) is somewhat larger, probably due to some non-negligible screening.

If one further examines Fig. 5, one finds an interesting distinction between experiment (a) and model (b). Namely, the model predicts that at various values of the magnetic flux, the critical current should approach zero. Yet the experiment shows that in the entire range of fields, the critical current is never zero. This could be due to some inhomogeneity that is qualitatively different from the one included in the model. Alternatively, this could be an instance of a node lifting, which might indicate that vortices carry Majorana zero modes that contribute to the measured critical current⁴. A qualitatively different experiment will be needed to confirm or reject this interesting possibility. For example, applications of microwave pulses may be able to push vortices around and entangle them, thus producing braiding and the corresponding modifications of the critical current. This will be the subject of future work.

To reveal the rectification effect, in Fig. 7, we analyze small magnetic fields, ∣B_z∣ ≤ 40 μT, which correspond to $| \tilde{f}| \le 0.0113$. The maxima of the theoretical curves ${I}_{C}^{+}({B}_{z})$ and ${I}_{C}^{-}({B}_{z})$ occur at B_z = ± 4 μT (Fig. 7b), which is close to the experimental values ± 5 μT. The asymmetry parameter estimated from the theoretical curves is again somewhat lower than in the experiment, η = 1.045. The theoretical curves differ from the experimental ones in shape. To reproduce the experimental ${I}_{C}^{\pm }({B}_{z})$ curves more accurately one should precisely know the distribution of the critical current densities j_C,n. Considering these uncertainties, we conclude that our model describes the experimental data reasonably well.

Conclusions

We observe both the interference and the diffraction effects on a superconducting array involving an intrinsic topological insulator. The square array is analogous to the optical diffraction grating. The interference, originating from multiple superconducting islands, produces a very sharp peak of the critical current. The diffraction effect causes the second matching peak to disappear. We develop a model which captures the main features of the experiment. One aspect in which the model differs from the experiment is that the model predicts that at many various values of the magnetic flux, the critical current should return to zero due to either interference or diffraction. Yet the experiment demonstrates that the critical current does not approach zero at any magnetic field. This so-called node lifting could be a sign that a more advanced model of the disorder is needed. It is also consistent with a more exotic phenomenon of node lifting caused by Majorana zero modes⁴. More advanced experiments will be needed to distinguish these two possibilities.

The sample also exhibits a superconducting diode effect. Our model explains it based on the assumption of a significant kinetic inductance of the topological surface states combined with some inhomogeneity. The rectification appears at very lower fields of the order of a few micro-Tesla.

Finally, we find that the devices can be used as sensitive absolute magnetic field detectors due to the interference phenomenon analogous to optical diffraction gratings.

The critical current peak sharpening and the diode efficiency can be improved via array geometry engineering. The peak sharpening is an interference effect between multiple parallel islands. In the general sense, it is analogous to the diffraction grating. In latter case, it is known that the diffraction peaks become sharper when the number of scattering groves is increased, provided that the spacing between the groves is constant. The implication for our case is that the peak sharpening can be made stronger if the number of islands is increased, provided that the islands and the spacing between them are uniform with sufficiently high precision. Sharper current peaks will lead to even higher sensitivity of the device to the magnetic field. In order to maximize the diode effect, the optimal geometry is a wide sample with strong asymmetry factor β, generated artificially by, for example, changing the spacing between the islands in a systematic manner, in order to produce a stronger gradient of the critical current.

Methods

Topological insulator growth

The substrate for TI growth is a single-side polished c-plane sapphire (MTI Corp) that was annealed in oxygen at 1100 °C for several hours for atomic-level flatness and large crystalline terraces. The unpolished side was coated with 100-nm titanium to allow for accurate measurements of substrate temperature using a pyrometer, as sapphire is transparent in the infrared spectrum. The substrate was clamped onto a tantalum holder using tantalum wire at its four corners and allowed to outgas in the load lock for several hours before being introduced into the growth chamber for high-temperature outgassing. The growth chamber base pressure was at a low 10⁻⁸ torr level.

The composition of the film was controlled by the flux ratio of Bismuth/Antimony from Knudsen effusion cells with an excess Tellurium flux to compensate for tellurium losses from the surface. A Te/(Bi+Sb) ratio greater than 6 is sufficient. Two quartz crystal microbalance (QCM) measurements of the Bi and Sb fluxes were taken to ensure the fluxes are stable. The substrate was heated to the growth temperature of 200–215 °C on the pyrometer (260 °C on a thermal couple placed on the backside of the substrate), and the tellurium shutter was opened for 10 s to ensure the starting layer of the quintuple stacked Te-(Bi+Sb)-Te-(Bi+Sb)-Te structure is tellurium. Then the Bi and Sb shutters were opened and shut simultaneously for periods of time calculated using their flux measurements. A two-stage growth method was used, where the first three quintuple layers (QLs) are grown and annealed in excess of Te flux for an hour before growing the remaining 37 QLs. At the end of film growth, the film was annealed for 4 h at around 260–265 °C on the pyrometer (330 °C on the thermal couple), but with a lowered Te flux to prevent excess Te buildup. Once the annealing was completed, the tellurium flux was cut off. The film was then moved into the load lock and allowed to fully cool down before being removed from the vacuum. To prevent oxidation from happening at the exposed film surface due to exposure to the atmosphere, polymethyl methacrylate (PMMA) was dropped onto the film immediately when it was removed and allowed to dry. The PMMA layer was completely removed prior to device fabrication by dissolving the protective PMMA film in acetone and rinsing the sample in isopropyl alcohol.

Device fabrication

For device fabrication, a two-session electron beam (e-beam) lithography method was used. In the first session, the film was coated with PMMA 950 A4 and exposed under a 10kV e-beam to define the array structure, electrodes, and alignment markers. The sample was developed in Methyl isobutyl ketone (MIBK): IPA 1:3 solution for 25 s and immediately loaded into a plasma sputtering system for metal deposition. A 2-s ion milling was applied to briefly clean the BST surface, followed by 30 nm Nb sputtering. Lift-off was done by placing the sample into acetone at room temperature for 2 h and sonicating it for 5 s. In the second lithography session, the trenches are aligned and exposed. After developing in MIBK: IPA 1:3 solution, a 60-s ion milling session was applied to completely remove the TI in the trenches. The trenches serve to separate the samples and to define the electrodes for the current injection and the voltage probing.

Device measurements

The sample was placed in a cryogen-free cooler with a base temperature of 0.3 K. The cooler involves RDK-101DL from Sumitomo and a He-3 stage supplied by Chase Cryogenics. The current bias for the sample was set by taking an ac voltage, U, from a National Instrument data acquisition card NI-DAQ USB-6216 output and applying it to the sample connected in series with a known standard resistor R_st. Typically, R_st = 10 kOhm. The same NI-DAQ card was used to measure the voltage on the sample, V, and on the standard resistor V_st, at a high data acquisition rate of the order of 100,000 points per second (Fig. 9). Then we plot the voltage on the sample, V, versus the bias current, I = V_st/R_st, in LabVIEW environment and thus get a complete V–I curve on the screen of the computer. (The bias current is calculated from the voltage measured on the standard resistor by Ohm’s law, I = V_st/R_st.) This way we can take V–I curves at different current-bias amplitudes by adjusting the voltage amplitude, U, supplied by the NI-DAQ card. To get a complete V–I curve where the critical current is visible, the amplitude of the voltage, U, should be sufficiently large so the maximum bias current in the circuit exceeds the critical current of the sample. On the contrary, if a linear resistance measurement is desired, then U is chosen such that the bias current is much lower than the critical current and the V–I curve is linear. Then a simple linear fit of the V–I curve, performed in the LabView software, provides the exact value of the electrical resistance of the sample.

Fig. 9: Schematic of the electrical circuit.

An ac voltage U is supplied from a National Instrument data acquisition card (NI-DAQ). The bias current in the sample is set by a high-value standard resistor connected in series with the sample. The same NI-DAQ card is equipped with an analog-digital converter. So, it is used to measure the voltage on the sample, V, and the voltage, V_st, on the standard resistor, R_st. The measurement is done in real time, as the bias current sweeps up and down. The resulting array of data points is plotted on the screen of the computer in the V versus/format, where the bias current is calculated as I = V_st/R_st.

Filtering of electromagnetic noise

The voltage and the current leads were carefully filtered against electromagnetic noise and well thermalized. The filtering was done by winding a highly resistive twisted pair of constantan wires around a copper cold finger and coating them with stycast epoxy filled with Cu particles, which efficiently absorb parasitic electromagnetic noise. For the purpose of thermalization, varnish-coated Cu wires have been squeezed between two Cu bars maintained at 0.3 K. All electrical signals were passed through such cold Cu wire segments to ensure that all leads attain the base temperature. In addition to the above measures, 1.9 MHz π-filters were installed at the top of the cryostat. Also, a 100 kOhm resistor was placed right at the BNC input leading to the current biasing connection of the sample. This resistor served to further reduce the interference of the external noise. The high efficiency of our filters was confirmed by the fact that the observed fluctuations of the critical current were very low, only about 0.1%.