Introduction

Following the early demonstration of ultrafast demagnetization in ferromagnets1, the optical manipulation of spin degrees of freedom emerged as an effective strategy for steering electronic properties in quantum materials2. Over the years, light excitation protocols evolved from purely thermal effects to more sophisticated optical excitations involving Zeeman interaction3, nonlinear phonon excitation4,5, or the renormalization of local interactions6,7. While most of these experimental efforts aim to manipulate magnetic orders, driving fluctuating spins with light could represent an effective dynamical control strategy for superconductivity in strongly correlated electron systems.

In the copper oxides, experimental8,9,10 and theoretical works11,12,13,14,15,16,17 suggest that spin fluctuations around the antiferromagnetic (AFM) wavevector QAF = (π, π) could contribute to the pairing interaction and determine the superconducting critical temperature Tc. Whether optically driving these spin fluctuations may explain the recent observation of light-induced superconductivity in certain copper oxides18,19,20,21 or be conducive to further optimized light-induced coherence is an open question.

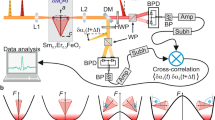
Directly probing the effect of ultrafast light pulses on spin fluctuations at finite momentum q requires a tool beyond optical probes, which are only sensitive to long-wavelength (q ~ 0) dynamics22,23,24,25. Resonant inelastic X-ray scattering (RIXS) at transition-metal L-edge with cross-polarized incident and scattered X-rays (see Fig. 1a) is sensitive to magnetic excitations and able to map their dispersion thanks to the high photon momentum26,27,28. Pioneering time-resolved RIXS (trRIXS) experiments in the hard X-ray regime provided first snapshots of pseudospin dynamics near QAF in layered iridates29,30 and future soft X-ray experiments at the Cu and Ni L-edges will further expand the reach of this new ultrafast technique. Based on these developments, it becomes critical to theoretically, and possibly experimentally, investigate how dispersive spin fluctuations and superconducting pairing evolve in a prototypical correlated system driven far from equilibrium.

Fig. 1: Probing light-driven spin fluctuations with resonant inelastic X-ray scattering.
figure 1

a Sketch of a pump–probe resonant inelastic X-ray scattering (RIXS) experiment with π–σ polarization. b Magnon dispersion in the 2D Hubbard model in (blue solid line) and out of equilibrium (red dashed line, pump field amplitude A0 = 0.6) as determined through the linear spin-wave and Floquet linear spin-wave (FLSW) theory [see Eqs. (7)]. The gray shaded region indicates momenta that are kinematically inaccessible to Cu L-edge RIXS.

Full size image

In this work, we present a trRIXS calculation of finite-momentum spin fluctuations in the paradigmatic single-band Hubbard model. We calculate the full trRIXS cross-section for a direct L3-edge absorption for π–σ polarizations and for two different hole doping levels. We show that an ultrafast resonant pump induces a prompt softening of the short-ranged spin excitation spectrum, compatible with a light-induced renormalization of the exchange interaction [sketched in Fig. 1b], and a simultaneous suppression of d-wave pairing correlations. Our findings in a canonical Hubbard model demonstrate that light pulses can be used to tailor finite-momentum spin fluctuations and pave the way to novel strategies for the light control of unconventional superconductors.

Results and discussion

Microscopic model

With a particular focus on the high-Tc cuprates, we consider valence and conduction electrons described by the 2D single-band Hubbard model and for two different hole dopings (x = 0 and x = 0.167). Since the X-ray scattering process explicitly involves an intermediate core level, the full Hamiltonian reads as

$${{{{{{{\mathcal{H}}}}}}}}= -\mathop{\sum}\limits_{{{{{{{{\bf{i}}}}}}}}{{{{{{{\bf{j}}}}}}}}\sigma }\,{t}_{h}^{{{{{{{{\bf{i}}}}}}}}{{{{{{{\bf{j}}}}}}}}}({d}_{{{{{{{{\bf{j}}}}}}}}\sigma }^{{{{\dagger}}} }{d}_{{{{{{{{\bf{i}}}}}}}}\sigma }\,+\,h.c.)\,+U\mathop{\sum}\limits_{i}{n}_{{{{{{{{\bf{i}}}}}}}}\uparrow }^{(d)}{n}_{{{{{{{{\bf{i}}}}}}}}\downarrow }^{(d)}\\ +\mathop{\sum}\limits_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }{E}_{{{{{{{{\rm{edge}}}}}}}}}(1-{n}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }^{(p)})-{U}_{c}\mathop{\sum}\limits_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma {\sigma }^{\prime}}{n}_{{{{{{{{\bf{i}}}}}}}}\sigma }^{(d)}(1-{n}_{{{{{{{{\bf{i}}}}}}}}\alpha {\sigma }^{\prime}}^{(p)})\\ +\lambda \mathop{\sum}\limits_{\genfrac{}{}{}{}{i\alpha {\alpha }^{\prime}}{\sigma {\sigma }^{\prime}}}{p}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }^{{{{\dagger}}} }{\chi }_{\alpha {\alpha }^{\prime}}^{\sigma {\sigma }^{\prime}}{p}_{{{{{{{{\bf{i}}}}}}}}{\alpha }^{\prime}{\sigma }^{\prime}}.$$
(1)

Here, diσ (\({d}_{{{{{{{{\bf{i}}}}}}}}\sigma }^{{{{\dagger}}} }\)) annihilates (creates) a \(3{d}_{{x}^{2}-{y}^{2}}\) electron at site i with spin σ, while piασ (\({p}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }^{{{{\dagger}}} }\)) annihilates (creates) a 2pα electron (α = x, y, z). \({t}_{h}^{{{{{{{{\bf{i}}}}}}}}{{{{{{{\bf{j}}}}}}}}}\) is the hopping integral between site i and j, \({n}_{{{{{{{{\bf{i}}}}}}}}}^{(d)}\,=\,{\sum }_{\sigma }{d}_{{{{{{{{\bf{i}}}}}}}}\sigma }^{{{{\dagger}}} }{d}_{{{{{{{{\bf{i}}}}}}}}\sigma }\) and \({n}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }^{(p)}\,=\,{p}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }^{{{{\dagger}}} }{p}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }\) are the valence and core-level electron density operators, respectively. The nearest-neighbor hopping amplitude is set to th = 300 meV, the next-nearest neighbor hopping to \({t}_{h}^{\prime}\,=\,-0.3\ {t}_{h}\), and the on-site repulsion to U = 8th31,32. The core–hole potential Uc is instead fixed at 4th and regarded identical for all 2p orbitals31,32,33. Eedge = 938 eV represents instead the Cu L-edge absorption energy, i.e., the energy difference between the 3d and 2p orbitals without spin–orbit coupling. Finally, the spin–orbit coupling with the X-ray-induced core hole in the degenerate 2p-orbitals is accounted for by the last term in Eq. (1) with λ = 13 eV 33,34.

The trRIXS cross-section at a direct absorption edge can be written as35,36 (see Supplementary Note 1 for further details)

$${{{{{{{\mathcal{I}}}}}}}}({{{{{{{\bf{q}}}}}}}},{\omega }_{{{{{{{{\rm{s}}}}}}}}},{\omega }_{{{{{{{{\rm{in}}}}}}}}},t)\,= \,\iint\iint {e}^{i{\omega }_{{{{{{{{\rm{in}}}}}}}}}({t}_{2}-{t}_{1})-i{\omega }_{{{{{{{{\rm{s}}}}}}}}}({t}_{2}^{\prime}-{t}_{1}^{\prime})}g({t}_{1};t)g({t}_{2};t)\\ \times \left\langle \right.{\hat{{{{{{{{\mathcal{D}}}}}}}}}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{i}}}}}}}}}{{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}_{{{{{{{{\rm{i}}}}}}}}}}^{{{{\dagger}}} }({t}_{2}){\hat{{{{{{{{\mathcal{D}}}}}}}}}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{s}}}}}}}}}{{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}_{{{{{{{{\rm{s}}}}}}}}}}({t}_{2}^{\prime}){\hat{{{{{{{{\mathcal{D}}}}}}}}}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{s}}}}}}}}}{{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}_{{{{{{{{\rm{s}}}}}}}}}}^{{{{\dagger}}} }({t}_{1}^{\prime}){\hat{{{{{{{{\mathcal{D}}}}}}}}}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{i}}}}}}}}}{{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}_{{{{{{{{\rm{i}}}}}}}}}}({t}_{1})\rangle \\ \times l({t}_{1}^{\prime}-{t}_{1})l({t}_{2}^{\prime}-{t}_{2})d{t}_{1}d{t}_{2}d{t}_{2}^{\prime}d{t}_{1}^{\prime}\,$$
(2)

where q = qi − qs is the momentum transfer between the incident and scattered photons with energies ωin and ωs, respectively, and \(l(\tau )\,=\,{e}^{-\tau /{\tau }_{{{{{{{{\rm{core}}}}}}}}}}\theta (\tau )\) the core–hole lifetime decay, with \({\tau }_{{{{{{{{\rm{core}}}}}}}}}\,=\,0.5\ {t}_{h}^{-1}\) as its characteristic timescale. For a direct transition (e.g., Cu L-edge), the dipole operator is explicitly given by \({{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\bf{q}}}}}}}}{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}={\sum }_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }{e}^{-i{{{{{{{\bf{q}}}}}}}}\cdot {{{{{{{{\bf{r}}}}}}}}}_{{{{{{{{\bf{i}}}}}}}}}}({A}_{\alpha {{{{{{{\boldsymbol{\varepsilon }}}}}}}}}{d}_{{{{{{{{\bf{i}}}}}}}}\sigma }^{{{{\dagger}}} }{p}_{{{{{{{{\bf{i}}}}}}}}\alpha \sigma }+h.c.)\), where Aαε is the matrix element of the dipole transition associated with a ε-polarized photon. As shown in Fig. 1a, we employed the π–σ polarization configuration (εi parallel and εs perpendicular to the scattering plane) and fixed αin + αout = 50°. This probe condition maximizes the spin-flip response in presence of the spin–orbit coupling term26,31. Calculations for the π–π polarization configuration are reported in Supplementary Note 2 for completeness. Due to the \(O({N}_{t}^{4})\) complexity of the trRIXS calculation, we adopt the 12D Betts cluster as a compromise between complexity and finite size.

In our calculations, the vector potential of the optical pump field is

$${{{{{{{{\bf{A}}}}}}}}}^{({{{{{{{\rm{pump}}}}}}}})}(t)={A}_{0}\ {e}^{-{t}^{2}/2{\sigma }_{t}^{2}}\cos ({{\Omega }}t)\ {\hat{{{{{{{{\bf{e}}}}}}}}}}_{{{{{{{{\rm{pol}}}}}}}}},$$
(3)

with frequency Ω = 10th ~ 3.0 eV (above the Mott gap ~4–5th) and duration \(6{\sigma }_{t}=18\ {t}_{h}^{-1}\approx 39.49\) fs, while the probe has a Gaussian envelope \(g(\tau ;t)={e}^{-{(\tau -t)}^{2}/2{\sigma }_{{{{{{{{\rm{pr}}}}}}}}}^{2}}/\sqrt{2\pi }{\sigma }_{{{{{{{{\rm{pr}}}}}}}}}\) with \({\sigma }_{{{{{{{{\rm{pr}}}}}}}}}\,=\,1.5\ {t}_{h}^{-1}\). A0 is measured in natural units ea0E0/Ω, where A0 = 0.1 corresponds to a E0 = 79 mV/Å peak electric field. The pump polarization \({\hat{{{{{{{{\bf{e}}}}}}}}}}_{{{{{{{{\rm{pol}}}}}}}}}\) is linear along the x-direction.

Here, we numerically calculate the trRIXS cross-section at each time step t by scanning the full four-dimensional hyperplane defined by the time-integration variables in Eq. (2) at zero temperature. We first determine the equilibrium ground-state wavefunction with the parallel Arnoldi method37,38 and, then, calculate the time evolution of the system through the Krylov subspace technique39,40.

trRIXS and transient spin fluctuations

In Figure 2, we show selected snapshots of the cross-polarized trRIXS spectrum at q = (π/2, π/2), where the magnon dispersion is maximized [see Supplementary Note 3 for a comparison with q = (0, 2π/3)]. At resonance (ωin ~ 931 eV for Cu L3-edge in Fig. 2), the loss spectra below the Mott gap are dominated by a single intense peak at ω ~ 2J = 0.3 eV, where \(J=4{t}_{h}^{2}/U\) is the exchange interaction. The energy and shape of this peak reflect the distribution of spin excitations: for an undoped Hubbard model, these manifest as a coherent magnon due to the strong antiferromagnetic (AFM) order; in contrast, in the x = 0.167 case, the spin excitations damp into a short-ranged paramagnon41,42,43,44,45. Negative time delays, when the system is close to equilibrium, our calculations reveal a splitting of the resonance along the ωin axis at x = 0.167 doping. This reflects the presence of two different chemical environments, as the valence states can be either half-occupied or empty.

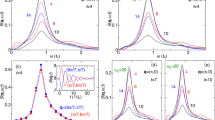
Fig. 2: Snapshots of the time-resolved resonant inelastic X-ray scattering signal.
figure 2

Cross-polarized time-resolved resonant inelastic X-ray scattering (trRIXS) spectra for selected pump–probe time delays as a function of the incident photon energy ωin for a x = 0 and b x = 0.167 hole doping. ω = ωin − ωs indicates the energy loss, while the momentum transfer is kept fixed at q = (π/2, π/2). The peak at ω ~ 0.3 eV corresponds to the collective spin fluctuations of the system. The red arrow marks the center of mass of the resonance along the ωin axis. The color bar indicates the spectral intensity in arbitrary units (a.u.).

Full size image

At the center of the pump pulse, the resonance undergoes (i) an overall suppression, and (ii) a redshift along the energy loss axis for both compositions. Since the center of the absorption peak does not exhibit a pump-induced shift along ωin, one can fix ωin = 931.5 eV and examine the time evolution of the magnon/paramagnon peak at q = (π/2, π/2) [see Fig. 3a, b]. The intensity drop and the peak shift closely follow the pump envelope and then persist long after the pump arrival due to the lack of dissipation. The photoexcited RIXS spectrum is visibly broadened at x = 0 and to a lesser extent at x = 0.167. Next, we analyze the dependence of the spin fluctuation peak as a function of the pump field strength A0 up to a maximum value of 1. This physical regime is relevant to recent experiments on Sr2IrO429 and Sr3Ir2O730, which employed fields strengths A0 up to 0.35 and 0.52, respectively. As A0 increases, the peak position for both x = 0 and x = 0.167 shifts monotonically to lower energies [see Fig. 3c, d] by 80% and 50%, respectively. At the same time, the magnon/paramagnon peak broadens due to the generation of high-order fluctuations beyond simple spin-wave excitations and of photo-doped carriers which perturb the spin background. These observations imply that optical laser pulses with negligible momentum have tangible effects on the spin fluctuations at large momenta.

Fig. 3: Time-dependent renormalization of the spin fluctuations.
figure 3

a, b Time evolution of the cross-polarized time-resolved resonant inelastic X-ray scattering (trRIXS) spectra for pump energy Ω = 10th and amplitude A0 = 0.6 at a x = 0 and b x = 0.167 doping. The momentum transfer is fixed at q = (π/2, π/2). The thin dashed line tracks the instantaneous peak positions of the spin fluctuation peak. The color bar indicates the spectral intensity in arbitrary units (a.u.). trRIXS spectra at t = 0 (center of the pump pulse) for variable pump amplitudes at c x = 0 and d x = 0.167 doping. Spin excitation energy ωq (the peak of the trRIXS intensity) as function of the pump amplitude at e x = 0 and f x = 0.167 doping. The energy width of these spectra includes a broadening due to the finite X-ray probe duration. The dashed line denotes pure photodoping effects (\(\gamma {\omega }_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{eq}}}}}}}}}\), where \({\omega }_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{eq}}}}}}}}}\) is the numerically evaluated magnon energy at equilibrium and γ is the instantaneous local moment defined in the text), while the solid line represents a Floquet linear spin-wave prediction of the magnon energies (including photodoping effects) (\(\gamma {\omega }_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{FLSW}}}}}}}}}\)).

Full size image

Magnon/paramagnon energy renormalization

While we report here an exact calculation of the full trRIXS cross-section, it is useful to discuss the microscopic physics at play in more intuitive terms. The magnon/paramagnon energy softening in our single-band Hubbard model can be attributed to photodoping, a dynamical Floquet-type renormalization of the spin-exchange interaction J46,47, or a combination of the two. Other experimentally relevant mechanisms, such as magnetophononics4,48,49, would require extending the Hubbard Hamiltonian through the inclusion of additional degrees of freedom.

We first consider the photodoping contribution. Due to the light-induced holon-doublon excitations, the local spin moment \(\langle {m}_{z}^{2}\rangle\) is diluted. In the simplest linear spin wave picture, this will induce a homogeneous softening of the spin structure factors across the entire Brillouin zone. To quantify this effect, we calculate the instantaneous local moment at t = 0, defined as \(\gamma =\sqrt{\frac{\langle {{{{{{{{\bf{S}}}}}}}}}^{2}(t=0)\rangle }{\langle {{{{{{{{\bf{S}}}}}}}}}^{2}(t=-\infty )\rangle }}\), and plot the renormalized magnon/paramagnon peak energy \(\gamma {\omega }_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{eq}}}}}}}}}\) as dashed lines in Fig. 3e, f. Here, \({\omega }_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{eq}}}}}}}}}\) is the numerically evaluated magnon energy at equilibrium. As visible from the comparison, the local photodoping effect, i.e., the dilution of the local spin moment, is too small to account for the observed energy softening.

The other possible mechanism to explain the peak shift hinges on a light-induced renormalization of the effective Hamiltonian. It has been demonstrated that for an ideal system driven by an infinitely long, nonresonant pump, the effective spin exchange energy J is modified by a Floquet dressing of the intermediate doubly occupied states47. In order to quantitatively understand our trRIXS spectrum, we apply Floquet linear spin-wave (FLSW) theory at different pump field amplitudes. In this framework, we assume the system at the center of the pump pulse to be in a steady-state, thus leading to a closed form for the spin excitations dispersion \({\omega }_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{FLSW}}}}}}}}}\) (see “Methods” section.)

By including both the Floquet renormalization and photodoping effects, we calculate the transient magnon/paramagnon energy \(\gamma {\omega }_{{{{{{{{\bf{q}}}}}}}} = (\pi /2,\pi /2)}^{{{{{{{{\rm{FLSW}}}}}}}}}\) and multiply it by a constant factor to match the equilibrium peak positions (see Fig. 3e, f). The scale factors are 1.15 for x = 0 and 1.02 for x = 0.167. At x = 0, the FLSW prediction tracks the magnon softening for weak pump fields but grossly deviates at higher pump strength. This is likely due to mobile photo-carriers which frustrate the AFM ground state50 and lower the energy cost of spin-flip events. At x = 0.167 hole-doping, however, FLSW theory closely aligns with the trRIXS calculation for all pump strengths. We tentatively attribute the difference between these two trends to intrinsic three-site correlated hopping. In the low-energy projection of the Hubbard Hamiltonian, holes can hop to next- and next-next-nearest neighbors (and thus lower the total energy) provided that the middle site has an opposite spin configuration51,52,53, which is otherwise inhibited. At equilibrium, this term partially cancels the doping-induced energy softening31,54 and is essential to reproduce the spin excitation spectrum of copper oxides. Active at x = 0.167, these correlations are silent in the AFM ground state and build up too slowly to compensate for the spin frustration. While both Floquet and linear spin-wave theories over-simplify the nonequilibrium many-body physics at play, their agreement with the paramagnon energy shift provides evidence of an ultrafast modification of effective model parameters beyond pure photodoping.

This striking light-induced softening represents a genuine emergent phenomenon, which is quantitatively distinct from the behavior of magnons/paramagnons at equilibrium. Short-range spin excitations in La2CuO4 show negligible dispersion changes for temperature changes well above their Néel temperature55, while hole-doped cuprates exhibit at most a redshift of order 20–30% for a doping change Δx = 0.4 (undoped to the overdoped regime)41,42,43,44,45. For a direct comparison, we compute the transient hole concentrations 〈nh(t = 0)〉 [see Fig. 4a and Supplementary Note 4], defined as nh = ∑i(1 − ni↑)(1 − ni↓)/N. Due to the presence of quantum fluctuations, the 〈nh〉 at equilibrium is 0.06 higher than the nominal hole concentration (0.167). Out of equilibrium at t = 0, the strongest pump gives only an extra 0.07 holes per site. In both the doped and undoped systems, the number of photoinduced holes is less than the full doping excursion between underdoped and overdoped regimes, and yet produces a larger softening than what is observed in cuprates at equilibrium.

Fig. 4: Pump-induced modification of spin excitation energy and pairing correlations.
figure 4

a Equilibrium (gray) and maximal transient (colored) change of hole concentration and spin excitation energy (extracted from time-resolved resonant inelastic x-ray scattering spectral peaks) for the pump conditions in panel Fig. 3 at half-filling and 16.7% hole doping, respectively. b Corresponding dynamics of the d-wave pairing correlations.

Full size image

d-wave pairing correlations

Since spin fluctuations have been discussed as a possible source of pairing in the cuprates11,12,13,14,15,16,17,56, we examine whether the paramagnon energy renormalization affects the superconducting pairing. We calculate the d-wave pairing correlation function \({P}_{d}=\langle {{{\Delta }}}_{d}^{{{{\dagger}}} }{{{\Delta }}}_{d}\rangle\) at x = 0.167 for various pump strengths [see Fig. 4b], with the factor Δd defined as \({{{\Delta }}}_{d}=\frac{1}{\sqrt{N}}{\sum }_{{{\bf{k}}}}{d}_{{{\bf{k}}}\uparrow} {d}_{-{{{{{{{\bf{k}}}}}}}}\downarrow }\left[\cos {k}_{x}-\cos {k}_{y}\right]\). At the pump arrival, Pd undergoes a rapid suppression, thus indicating a decrease of pairing in the d-wave channel. The drop in Pd is found to be monotonic with the increase of the pump strength A0. Intuitively, the value of Pd is determined by both the quasiparticle density and the pairing interaction strength. In our calculations, the pump simultaneously increases quasiparticles via photodoping and reduces the spin excitation energy. While the former effect is favorable for superconductivity, it is the latter that dominates and reduces the nonequilibrium pairing correlations.

Conclusions

We studied the light-induced dynamics of finite-momentum spin excitations in the prototypical 2D Hubbard model through a full calculation of the π–σ polarized trRIXS spectrum. By exciting a Mott insulator with an ultrashort pump pulse, we find that magnons and paramagnons undergo a dramatic light-induced softening, which cannot be exclusively explained by photodoping. Paramagnon excitations are quantitatively described by a Floquet renormalization of the effective exchange interactions, while magnons at high field strengths deviate from this picture. At optimal doping, we also observe a sizeable reduction of d-wave pairing correlations. While here we explore a paradigmatic optical excitation at the Mott gap, alternative mechanisms such as phonon Floquet57, ligand manipulation7, multi-band dynamical effects58,59, and coupling to cavities60,61 might lead to harder spin fluctuations and increased pairing47,62. Future polarization-dependent trRIXS experiments and theoretical calculations will be key to investigate these photoinduced spin dynamics in a wide variety of quantum materials63,64.

Methods

Floquet Linear-Spin-Wave Theory

To describe the evolution of magnetic excitations at finite momentum, we generalize the local Floquet renormalization of the spin-exchange interaction46,47 through FLSW theory. This approach is based on the assumption that the driven system can be instantaneously approximated by an effective Hamiltonian \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{F}}}}}}}}}\) and a steady state wavefunction \(\left|{\psi }_{F}\right\rangle\). In the Floquet framework, the hopping tij in the effective Hamiltonian \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{F}}}}}}}}}\) is renormalized by a factor \({{{{{{{{\mathcal{J}}}}}}}}}_{m}({{{{{{{\bf{A}}}}}}}}\cdot {{{{{{{{\bf{r}}}}}}}}}_{ij})\), where \({{{{{{{{\mathcal{J}}}}}}}}}_{m}(x)\) is the Bessel function of the first kind and A is the vector potential of an infinitely long driving field. Following second-order perturbation theory, the effective spin-exchange interaction between two coordinates is renormalized into47

$${J}_{ij}^{{{{{{{{\rm{eff}}}}}}}}}=\frac{4{t}_{ij}^{2}}{U}\mathop{\sum }\limits_{m=-\infty }^{\infty }\frac{{{{{{{{{\mathcal{J}}}}}}}}}_{m}{({{{{{{{\bf{A}}}}}}}}\cdot {{{{{{{{\bf{r}}}}}}}}}_{ij})}^{2}}{1+m{{\Omega }}/U}.$$
(4)

Then, through the standard Holstein-Primakoff transformation and large-S expansion, one can obtain the linearized bosonic Hamiltonian

$${{{{{{\mathcal{H}}}}}}}_{FLSW}=\mathop{\sum}\limits_{{{{{{\bf{q}}}}}}}\sqrt{{A}_{{{{{{\bf{q}}}}}}}^{2}-{B}_{{{{{{\bf{q}}}}}}}^{2}}\ {a}_{{{{{{\bf{q}}}}}}}^{{{\dagger}} }{a}_{{{{{{\bf{q}}}}}}}=\mathop{\sum}\limits_{{{{{{\bf{q}}}}}}}{\omega }_{{{{{{\bf{q}}}}}}}^{{{{{{\rm{FLSW}}}}}}}{a}_{{{{{{\bf{q}}}}}}}^{{{\dagger}} }{a}_{{{{{{\bf{q}}}}}}},$$
(5)

where aq is the magnon annihilation operator and the coefficients Aq and Bq in the two-dimensional plane are65

$${A}_{{{{{{{{\bf{q}}}}}}}}}= \,{J}_{x}^{{{{{{{{\rm{eff}}}}}}}}}+{J}_{y}^{{{{{{{{\rm{eff}}}}}}}}}-{J}_{xy}^{{{{{{{{\rm{eff}}}}}}}}}\left[1-\cos ({q}_{x}+{q}_{y})\right]\\ -{J}_{yx}^{{{{{{{{\rm{eff}}}}}}}}}\left[1-\cos ({q}_{x}-{q}_{y})\right],$$
(6)
$${B}_{{{{{{{{\bf{q}}}}}}}}}={J}_{x}^{{{{{{{{\rm{eff}}}}}}}}}\cos {q}_{x}+{J}_{y}^{{{{{{{{\rm{eff}}}}}}}}}\cos {q}_{y}.$$
(7)

Here, unlike the equilibrium counterpart, the coefficients are anisotropic due to the electric field polarization

$${J}_{x/y}^{{{{{{{{\rm{eff}}}}}}}}}=\frac{4{t}_{h}^{2}}{U}\mathop{\sum }\limits_{m=-\infty }^{\infty }\frac{{{{{{{{{\mathcal{J}}}}}}}}}_{m}{({{{{{{{\bf{A}}}}}}}}\cdot {{{{{{{{\bf{e}}}}}}}}}_{x/y})}^{2}}{1+m{{\Omega }}/U},$$
(8)
$${J}_{xy/yx}^{{{{{{{{\rm{eff}}}}}}}}}=\frac{4{t}_{h}^{^{\prime} 2}}{U}\mathop{\sum }\limits_{m=-\infty }^{\infty }\frac{{{{{{{{{\mathcal{J}}}}}}}}}_{m}{({{{{{{{\bf{A}}}}}}}}\cdot ({{{{{{{{\bf{e}}}}}}}}}_{x}\pm {{{{{{{{\bf{e}}}}}}}}}_{y}))}^{2}}{1+m{{\Omega }}/U}.$$
(9)

This derivation can be extended to higher-order following the strategy of equilibrium LSW theory65.