Main

The basic laws of thermodynamics dictate that any system in contact with an environment eventually relaxes to the temperature of its surroundings as a result of irreversible flows that drive the system to thermodynamic equilibrium. If the difference between the initial temperature of the system and that of the surroundings is small, that is the system is initially ‘close to equilibrium’1, the relaxation is typically assumed to evolve quasi-statically through local equilibrium states, an assumption that is justifiable only a posteriori1,2. However, if the temperature contrast is such that it pushes the system far from equilibrium, the assumption breaks down and the relaxation path is no longer unique but depends strongly on the initial conditions. This gives rise to counter-intuitive phenomena, such as anomalous relaxation (also known as the Mpemba effect)3,4,5,6,7,8,9, in which a system reaches equilibrium faster upon a stronger temperature quench, and the so-called Kovacs memory effect10,11,12,13,14, in which there is a non-monotonic evolution towards equilibrium.

Intriguingly, thermal relaxation was recently predicted to depend also on the sign of the temperature change. Namely, considering two thermodynamically equidistant (TE) temperatures (one higher and the other lower than an intermediate temperature selected such that the initial free energy difference with the equilibrium state is the same), then heating from the colder temperature was predicted to be faster than cooling from the hotter one15,16. This prediction challenges our understanding of non-equilibrium thermodynamics as it compares reciprocal relaxation processes elusive to classical thermodynamics. The initially hotter system must dissipate into the environment an excess of both energy and entropy, whereas in the colder system, energy and entropy must increase15,17. Moreover, this comparison of heating and cooling provokes an even more fundamental question relating to reciprocal relaxation processes between two fixed temperatures. According to the ‘local equilibrium’ paradigm1, the system relaxes quasi-statically and, thus, traces the same path along reciprocal processes. We show, however, that this is not the case: heating and cooling are inherently asymmetric and evolve along distinct pathways.

In this work, we used colloidal particles in temperature-modulated optical traps to interrogate the relaxation kinetics upon temperature quenches (Fig. 1). We unveiled three fundamental asymmetries between heating and cooling. We experimentally confirmed the prediction that heating is faster than cooling in three complementary situations: (1) that heating from a colder temperature towards an intermediate target temperature is faster than cooling from the corresponding TE hotter temperature15. Unexpectedly, we also show (2) that the reverse process, that is heating from the intermediate temperature to a hotter temperature, is faster than cooling to the corresponding TE colder temperature. Most surprisingly, we show (3) that between a fixed pair of temperatures, heating is faster than the reciprocal cooling. In all cases, we provide mathematical proofs that establish these asymmetries as a general feature of systems with (at least locally) quadratic energy landscapes.

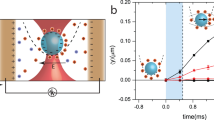
Fig. 1: Set-up for probing the heating–cooling asymmetry.
figure 1

a, Schematic representation of the experiment. A charged dielectric microparticle dispersed in water is confined in a parabolic trap generated by a tightly focused infrared laser. Its effective temperature is controlled by an electric field that shakes the particle, mimicking a thermal bath at a higher temperature than the water. An arbitrary signal generator feeds a noisy signal with a white Gaussian spectrum into a pair of gold microelectrodes immersed in the liquid, thus producing the required electric field. Therefore, the particle exhibits Brownian motion inside the trap. This motion has a Gaussian distribution whose variance is determined by the effective temperature. b, In the experiments, we tracked the evolution of the position distribution upon quenches of the effective thermal bath during heating (red arrows) or cooling (blue arrows). c, Schematic representation of the respective protocols. In the forward protocol, the system is initially prepared at equilibrium with the thermal bath at a temperature higher (Th) or lower (Tc) than the target (Tw) temperature. Th and Tc are chosen to be TE from Tw with Th > Tw > Tc. During the backward protocol, the system relaxes at the respective TE temperatures Th and Tc, starting from a common initial condition that is the equilibrium at Tw. In a third situation, only two temperatures are compared, and the evolution of the system upon heating and cooling between them is assessed. In b and c, solid and dashed arrows stand for the forward and backward process, respectively, and thick lines indicate faster evolution than thin ones.

Full size image

A key result is that the production of entropy within the system during heating is more efficient than heat dissipation during cooling. Asymmetries (2) and (3) further imply that the microscopic relaxation paths during heating and cooling are distinct. Moreover, whereas a system prepared at TE temperatures is by construction equally far from equilibrium in terms of free energy, we show that the colder system is, in fact, statistically farther from equilibrium and yet heating from the said colder temperature is faster. We have developed a new framework that we call ‘thermal kinematics’ to explain the asymmetry using the propagation in the space of probability distributions. This propagation is intrinsically faster during heating.

Heating and cooling under TE conditions

Thermal relaxation kinetics beyond the ‘local equilibrium’ regime can be quantified using stochastic thermodynamics18,19,20, which requires knowing the statistics of all slow, mesoscopic degrees of freedom. In the present work, in which we use a colloidal particle with a diameter of 1 μm trapped with a tightly focused laser (Fig. 1), the overdamped regime ensures that only the position has to be analysed20,21,22. Due to the symmetry of the tweezers set-up, it suffices to follow a single coordinate of the particle as a function of time, which we denote by xt. We consider two different initial conditions. By the nature of the set-up (Fig. 1), xt is initially in equilibrium in the optical potential U(x) at either the ‘hot’ Th or ‘cold’ Tc temperature, with a probability density \({P}_\mathrm{eq}^{\,\,j}(x)=\exp({({F}_{j}-U(x))/{k}_{{{{\rm{B}}}}}{T}_{\,j}})\), where \({F}_{j}\equiv -{k}_{{{{\rm{B}}}}}{T}_{j}\ln \int\nolimits_{-\infty }^{\infty }\exp({-U(x)/{k}_{{{{\rm{B}}}}}{T}_{\,j}})\,\mathrm{d}x\) is the equilibrium free energy at temperature Tj and kB is the Boltzmann constant. In the following, equilibrium probability densities are denoted by \({P}_{{{{\rm{eq}}}}}^{\,\,j}(x)\), where j = h, w or c refers to the bath temperature Tj. Observables with both a subscript i = h, w or c and a superscript f = h, w or c, for example, \({A}_{i}^{\,f}\), denote transient observables, where the subscript refers to the initial and the superscript to the target state. The state of the system at any time is fully specified by, \({P}_{i}^{\,\,f}(x,t)\), the probability density of the particle’s position at time t.

We first focus on the forward protocol in which relaxation occurs at the ‘warm’ temperature Tw and i = h or c. The dynamics is ergodic and, therefore, \({P}_{i}^\mathrm{w}(x,t)\) relaxes towards \({P}_\mathrm{eq}^\mathrm{w}(x)\). We use \({\langle \ldots \rangle }_{i}^{\rm{w}}\) to denote averages over \({P}_{i}^\mathrm{w}(x,t)\), and quantify the instantaneous displacement from the equilibrium distribution \({P}_{{{{\rm{eq}}}}}^\mathrm{w}(x)\) with the generalized excess free energy given by15,23,24 \({{{{\mathcal{D}}}}}_{i}^\mathrm{w}(t)={\langle U({x}_{t})\rangle }_{i}^{\rm w}-{T}_\mathrm{w}{S}_{i}^\mathrm{w}(t)-{F}_\mathrm{w}={k}_{{{{\rm{B}}}}}{T}_{\rm w}\tilde{D}[{P}_{i}^\mathrm{w}(x,t)\|{P}_{{{{\rm{eq}}}}}^\mathrm{w}(x)]\) for i = h or c, where \({S}_{i}^\mathrm{w}(t)=-{k}_{{{{\rm{B}}}}}{\langle \ln {P}_{i}^\mathrm{w}({x}_{t},t)\rangle }_{i}^\mathrm{w}\) is the Gibbs entropy and \(\tilde{D}[P\|Q]=\int{P}\ln (P/Q)\,\mathrm{d}x\) is the relative entropy between the probability distributions P and Q. This generalizes the canonical free energy F = U − TS to instantaneous non-equilibrium configurations with a probability density P(x,t). Temperatures Th and Tc are said to be TE from Tw when the initial excess free energies are equal, that is, \({\mathcal{D}}_\mathrm{h}^\mathrm{w}(0)={\mathcal{D}}_\mathrm{c}^\mathrm{w}(0)\). The unexpected prediction was made in ref. 15 that \({\mathcal{D}}_\mathrm{c}^\mathrm{w}(t) < {\mathcal{D}}_\mathrm{h}^\mathrm{w}(t)\) at all times t > 0. That is, the system heats up to the temperature of its surroundings faster than it cools down. Albeit an asymmetric relaxation is counter-intuitive, our experiments quantitatively corroborate this prediction to be true (Fig. 2).

Fig. 2: Experimental evolution of the generalized excess free energy during heating and cooling under TE conditions.
figure 2

Thick red arrows stand for heating, whereas thin blue arrows represent cooling. a,b, Time evolution of the generalized excess free energy for a characteristic time τ = γ/κ = 0.1844(3) ms, Tc/Tw = 0.11(1) and Th/Tw = 3.56(1) for the forward protocol (a) and the backward protocol (b). Red circles stand for heating and blue squares stand for cooling. Solid lines correspond to the theoretical predictions without fitting parameters. Insets represent the initial value of the relative entropy \({\mathcal{D}}_{i}^\mathrm{w}(0)/{k}_\mathrm{B}{T}_\mathrm{w}\) (y axis) as a function of the temperature (x axis) on the logarithmic scale. The arrows represent the evolution direction along the master curve \(f(\rho )=(\rho -1-\ln \rho )/2\). The data are estimated as the mean over ten independent measurements, whereas error bars are the s.e.m. (see Methods for further details). c,d, Generalized excess free energy \({\mathcal{D}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)/{k}_\mathrm{B}{T}_\mathrm{w}\) as a function of \({\varLambda }_{i/\mathrm{w}}^{\mathrm{w}/i}(t)\), along the master curve f(ρ), for several different TE conditions for the forward protocol (c) and the backward protocol (d). The corresponding time series (data and error bars) are included in Extended Data Fig. 3. Here, error bars have been omitted for clarity.

Full size image

Even more surprising is that the heating also turns out to be faster along the reversed, backward protocol. That is, we prepared the system in equilibrium at the warm temperature Tw and tracked the relaxations to Th or Tc. We again quantified the kinetics with the relative entropy \({\mathcal{D}}_\mathrm{w}^{i}(t)\equiv {k}_{{{{\rm{B}}}}}{T}_\mathrm{w}\tilde{D}[{P}_\mathrm{w}^{i}(x,t)\|{P}_{{{{\rm{eq}}}}}^\mathrm{w}(x)]\), such that \({\mathcal{D}}_\mathrm{w}^\mathrm{h}(t)\) and \({\mathcal{D}}_\mathrm{w}^\mathrm{c}(t)\) evolve from zero and asymptotically converge to \({\mathcal{D}}_\mathrm{w}^\mathrm{h/c}(\infty )={\mathcal{D}}_\mathrm{h/c}^\mathrm{w}(0)\). Although \({\mathcal{D}}_\mathrm{w}^{i}(t)\) sensibly quantifies the departure from \({P}_{{{{\rm{eq}}}}}^\mathrm{w}(x)\), it is strictly speaking not an excess free energy, in contrast to \({\mathcal{D}}_{i}^\mathrm{w}(t)\) defined above, because Tw and \({P}_{\rm{eq}}^\mathrm{w}(x)\) no longer refer to the target equilibrium, that is because \({\mathcal{D}}_\mathrm{w}^{i}(t)={\langle U\,\rangle }_\mathrm{w}^{i}-{T}_\mathrm{w}{S}_\mathrm{w}^{i}(t)-{F}_\mathrm{w}\ne {\langle U\rangle }_\mathrm{w}^{i}-{T}_{i}{S}_\mathrm{w}^{i}(t)-{F}_\mathrm{w}\), where the latter would correspond to an excess free energy. We observe in Fig. 2 that \({\mathcal{D}}_\mathrm{w}^\mathrm{h}(t) > {{{{\mathcal{D}}}}}_\mathrm{w}^\mathrm{c}(t)\) for all times t > 0, that is the system heats up to the new equilibrium at Th faster than it cools back to Tc. This observation is remarkable, as it shows that heating is inherently faster than cooling under TE conditions. Further experimental results demonstrating the asymmetry for both the forward and backward protocols under different experimental conditions are shown in Extended Data Fig. 3.

To confirm these observations theoretically, we assume that the particle’s dynamics evolve in a parabolic potential with stiffness κ, such that U(x) = κx2/2, according to the overdamped Langevin equation \(\mathrm{d}{x}_{t}=-(\kappa /\gamma ){x}_{t}\,\mathrm{d}t+\mathrm{d}{\xi }_{t}^{i}\) with friction constant γ given by Stokes’ law γ = 6πrη, where η is the viscosity of the suspending medium and r is the particle’s radius. The thermal noise \(\mathrm{d}{\xi }_{t}^{i}\), where i = h, w or c denotes the temperature of the reservoir, vanishes on average and obeys the fluctuation–dissipation theorem \(\langle \mathrm{d}{\xi }_{t}^{i}\,\mathrm{d}{\xi }_{{t}^{{\prime} }}^{i}\rangle =2({k}_{\rm{B}}{T}_{i}/\gamma )\,\delta (t-{t}^{{\prime} })\,\mathrm{d}t\,\mathrm{d}{t}^{{\prime} }\). Under these assumptions, we determine the TE temperatures Th and Tc(Th), that is, we calculate Tc after we arbitrarily set Th (Supplementary equation (6)). So, \({\mathcal{D}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)\) then reads

$${\mathcal{D}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)=\frac{{k}_{\rm{B}}{T}_\mathrm{w}}{2}[{\varLambda }_{i/\mathrm{w}}^{\mathrm{w}/i}(t)-1-\ln {\varLambda }_{i/\mathrm{w}}^{\mathrm{w}/i}(t)],$$
(1)

where \({\varLambda }_{i}^\mathrm{w}(t)=1+({T}_{i}/{T}_\mathrm{w}-1)\,{\rm{e}}^{-2(\kappa /\gamma )t}\) and \({\varLambda }_\mathrm{w}^{i}(t)={T}_{i}/{T}_\mathrm{w}+\left(\right.1-{T}_{i}/\)\({T}_\mathrm{w}\left.\right){\rm{e}}^{-2(\kappa /\gamma )t}\). We consider \({\mathcal{D}}_{i}^\mathrm{w}(t)\) during the forward protocol and \({\mathcal{D}}_\mathrm{w}^{i}(t)\) during the backward protocol. According to equation (1), by plotting \({\mathcal{D}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)/{k}_{\rm{B}}{T}_\mathrm{w}\) as a function of \(\rho ={\varLambda }_{i/\mathrm{w}}^{\mathrm{w}/i}(t)\), all data should collapse onto the master curve \(f(\rho )=(\rho -1-\ln \rho )/2\), which is indeed what we observe in Fig. 2. Having established the validity of the model, we prove (Supplementary Theorem 1) that our observations hold for all TE temperatures and for any κ and γ, that is

$${\mathcal{D}}_{\mathrm{c}}^{\mathrm{w}}(t) < {\mathcal{D}}_{\mathrm{h}}^{\mathrm{w}}(t)\quad {{{\rm{and}}}}\quad {\mathcal{D}}_{\mathrm{w}}^{\mathrm{h}}(t) > {\mathcal{D}}_{\mathrm{w}}^{\mathrm{c}}(t),\;{\text{for all}}\;0 < t < \infty .$$
(2)

Our observations in Fig. 2 and the inequalities (equation (2)) establish rigorously that under TE conditions, heating is faster than cooling.

Notwithstanding, these results are still unsatisfactory for two reasons. First, \({\mathcal{D}}_\mathrm{w}^{i}(t)\), unlike \({\mathcal{D}}_{i}^\mathrm{w}(t)\), lacks a consistent thermodynamic interpretation and, in particular, is not an excess free energy. Second, neither the relative entropy \(\tilde{D}[P\|Q]\) nor \(\sqrt{\tilde{D}[P\|Q]}\) is a true metric; they are not symmetric, \(\tilde{D}[P\|Q]\ne \tilde{D}[Q\|P]\) and do not satisfy triangle inequalities. The latter in particular implies that although a Pythagorean theorem holds (this theorem is discussed in ref. 25; see the Supplementary Information for an experimental validation), \(\tilde{D}[{P}_{{{{\rm{eq}}}}}^{i}(x)\|{P}_{{{{\rm{eq}}}}}^\mathrm{w}(x)]\ge \tilde{D}[{P}_\mathrm{eq}^{i}(x)\|{P}_\mathrm{w}^{i}(x,t)]+\tilde{D}[{P}_\mathrm{w}^{i}(x,t)\|{P}_{\rm{eq}}^\mathrm{w}(x)]\), where we used \({P}_\mathrm{w}^{i}(x,0)={P}_{\rm{eq}}^{i}(x)\). Thus, the triangle inequality does not hold. That is, in general \(\sqrt{\tilde{D}[{P}_{{{{\rm{eq}}}}}^{i}(x)\Vert{P}_{\rm{eq}}^{\mathrm{w}}(x)]}\)≰ \(\sqrt{\tilde{D}[{P}_{\rm{eq}}^{i}(x)\Vert {P}_{\mathrm{w}}^{i}(x,t)]}+\sqrt{\tilde{D}[{P}_{\mathrm{w}}^{i}(x,t)\Vert{P}_{\rm{eq}}^{\mathrm{w}}(x)]}\). As a result, \({\mathcal{D}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)\) does not measure the ‘distance’ from equilibrium and \({\partial }_{t}{\mathcal{D}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)\) is therefore not a ‘velocity’, which seems to preclude a kinematic description of relaxation. In the following sections, we show that combining stochastic thermodynamics with information geometry26 makes it possible to devise a formulation of thermal kinematics.

Towards thermal kinematics

Immense progress has been made in recent years in understanding non-equilibrium systems. The discovery of thermodynamic uncertainty relations27,28,29,30 and ‘speed limits’25,26,31,32 revealed that the entropy production rate, which quantifies irreversible local flows in the system, universally bounds fluctuations and the rate of change in a non-equilibrium system. Closely related is the so-called Fisher information from information geometry, which quantifies how local flows change in time and can be used to define a statistical distance26,33,34,35.

In our context of thermal relaxation, an infinitesimal statistical line element may be defined as follows. As \(\tilde{D}[{P}_{i}^{\,f}(x,t+\mathrm{d}t)\|{P}_{i}^{\,f}(x,t)]\) \(={I}_{i}^{\,f}(t)\,\mathrm{d}{t}^{2}+{{{\mathcal{O}}}}(\mathrm{d}{t}^{3})\) (Supplementary Information), where we introduced the Fisher information \({I}_{i}^{\,f}(t)\equiv \langle {({\partial }_{t}\ln {P}_{i}^{\,\,f}(x,t))^{2}}\rangle_{i}^{\;f}\), we can define the line element as \(\mathrm{d}l\equiv \sqrt{\tilde{D}[{P}_{i}^{\,\,f}(x,t+\mathrm{d}t)\|{P}_{i}^{\,\,f}(x,t)]}\) \(=\sqrt{{I}_{i}^{\,f}(t)}\,\mathrm{d}t\), and thus, \({v}_{i}^{\,f}(t)\equiv \sqrt{{I}_{i}^{\,f}(t)}\) is the instantaneous statistical velocity of the system26 as it relaxes from \({P}_{\rm{eq}}^{i}(x)\) at temperature Tf towards \({P}_{\rm{eq}}^{\,f}(x)\). The statistical length traced by \({P}_{i}^{\,f}(x,\tau )\) until time t is \({\mathcal{L}}_{i}^{f}(t)=\int\nolimits_{0}^{t}{v}_{i}^{\,f}(\tau )\,\mathrm{d}\tau\). The distance between the initial and the final states is, thus, given by \({\mathcal{L}}_{i}^{f}(\infty )\), which does not depend on the direction. That is, \({\mathcal{L}}_{a}^{b}(\infty )={\mathcal{L}}_{b}^{a}(\infty )\), for two different temperatures Ta and Tb. To establish a kinematic basis for quantifying thermal relaxation kinetics, we define the degree of completion \({\varphi }_{i/\mathrm{w}}^{\mathrm{w}/i}(t)\equiv {\mathcal{L}}_{i/\mathrm{w}}^{\mathrm{w}/i}(t)/{\mathcal{L}}_{i}^\mathrm{w}(\infty )\), which increases monotonically between 0 and 1.

Assuming that the system evolves according to overdamped Langevin dynamics in a parabolic potential, we find (Supplementary Information) that \({\mathcal{L}}_{i}^\mathrm{w}(\infty )=| \ln ({T}_{i}/{T}_\mathrm{w})| /\sqrt{2}\) and

$${\varphi }_{i/\mathrm{w}}^{\mathrm{w}/i}(t)=1-\frac{\ln (1+({T}_{i/\mathrm{w}}/{T}_{\mathrm{w}/i}-1)\,{\rm{e}}^{-2(\kappa /\gamma )t})}{\ln ({T}_{i/\mathrm{w}}/{T}_{\mathrm{w}/i})}.$$
(3)

Moreover, we prove (Supplementary Theorem 2) for any pair of TE temperatures Th and Tc that \({\mathcal{L}}_\mathrm{c}^\mathrm{w}(\infty ) > {\mathcal{L}}_\mathrm{h}^\mathrm{w}(\infty )\) and yet

$${\varphi }_\mathrm{c}^\mathrm{w}(t) > {\varphi }_\mathrm{h}^\mathrm{w}(t)\quad {{{\rm{and}}}}\quad {\varphi }_\mathrm{w}^\mathrm{h}(t) > {\varphi }_\mathrm{w}^\mathrm{c}(t)\quad \,{{\mbox{for all}}}\,\,0 < t < \infty .$$
(4)

That is, the colder system is statistically farther from equilibrium than the hotter system. Nevertheless, heating is faster than cooling. On the one hand, equation (4) confirms the asymmetry (equation (2)) from a kinematic point of view. On the other hand, it reveals something more striking; during heating in the forward protocol, the system traces a longer path in the space of probability distributions but it does so faster. The reason lies in the propagation speed \({v}_{\mathrm{w}/i}^{i/\mathrm{w}}(t)\), which at short times is intrinsically larger during heating than during cooling. This speed-up is because entropy production in the system during heating is more efficient than the heat flow from the system to the environment during cooling (see also ref. 15). These predictions have been fully confirmed by experiments (Fig. 3 and Extended Data Figs. 4–6). The results show that an initial overshoot of \({v}_\mathrm{c}^\mathrm{w}(t)\) or \({v}_\mathrm{w}^\mathrm{h}(t)\) ensures that under TE conditions, heating is, for both protocols, at all times faster than cooling according to the inequalities (equation (4)). As both processes relax to the same equilibrium, \({v}_\mathrm{c}^\mathrm{w}(t)\) and \({v}_\mathrm{h}^\mathrm{w}(t)\) must eventually cross. Analogously, the crossing of the corresponding velocities is observed in the background process.

Fig. 3: Thermal kinematics of heating and cooling processes under TE conditions.
figure 3

All data correspond to the series shown in Fig. 2. As in previous figures, red arrows stand for heating whereas blue ones represent cooling, solid and dashed arrows refer to the forward and backward protocols, respectively, and thicker lines indicate a faster evolution than thin ones. a, Initial value of the relative entropy \({\mathcal{D}}_{i}^\mathrm{w}(0)/{k}_\mathrm{B}{T}_\mathrm{w}\) as a function of the temperature. b, Total traversed statistical distance \({\mathcal{L}}_{i}^\mathrm{w}(\infty )={\mathcal{L}}_\mathrm{w}^{i}(\infty )={\mathcal{L}}(\infty )\) as a function of the temperature. c,e, Temporal evolution of the instantaneous statistical velocity \({v}_{i}^{f}(t)\) for the forward protocol (c) and the backward protocol (e). d,f, Temporal evolution of the degree of completion \({\varphi }_{i}^{f}(t)\) for the forward protocol (d) and the backward protocol (f). Red circles stand for heating, whereas blue squares correspond to cooling. Solid lines are theoretical predictions without fitting parameters. The data are estimated as the mean over ten independent measurements, whereas error bars are the s.e.m. (see Methods for further details).

Full size image

Between pairs of temperatures, heating is faster than cooling

We now take our thermal kinematics approach one step further and consider two arbitrary fixed temperatures T1 < T2 and observe heating, that is relaxation to T2 in a temperature quench from an equilibrium prepared at T1, and the reverse cooling, that is relaxation to T1 in a temperature quench from the equilibrium at T2. By construction, the distances between the initial and final states for the reciprocal processes are the same, \({\mathcal{L}}_{2}^{1}(\infty )={\mathcal{L}}_{1}^{2}(\infty )\). Nevertheless, according to our model, in particular equation (3), we have for any T1 < T2 (Supplementary Theorem 3) that

$${\varphi }_{1}^{2}(t) > {\varphi }_{2}^{1}(t)\quad \,{{\mbox{for all}}}\,\quad 0 < t < \infty .$$
(5)

That is, between any pair of temperatures, heating is faster than cooling, which is a much stronger statement. Notice that it was not possible to make such a statement based on the generalized excess free energy, since in this case, the description of the backward process lacked physical consistency. This result highlights that heating and cooling are inherently asymmetric processes, which is neither limited to the TE setting nor to strong quenches. The asymmetry (equation (5)) has been fully corroborated by experiments (Fig. 4 and Extended Data Figs. 4–6). As before, the asymmetry emerges due to an initial overshoot in \({v}_{1}^{2}(t)\). However, in this case, the difference in the velocities implies that the pathway taken during heating is fundamentally different from the pathway followed during the reciprocal cooling process. Note that this goes beyond ‘hysteresis’-type asymmetries that occur during the heating and cooling of macroscopic systems through phase or glass transitions.

Fig. 4: Thermal kinematics of heating and cooling between any pair of temperatures.
figure 4

The data shown correspond to T1 = 302(3) K and T2 = 2753(7) K and a characteristic time τ = γ/κ = 0.1844(3) ms. a, Instantaneous statistical velocity v(t) as a function of time. b, Degree of completion φ(t) as a function of time. Red circles stand for heating, whereas blue squares correspond to cooling. Solid lines are theoretical predictions without fitting parameters. The data are estimated as the mean over ten independent measurements, whereas error bars are the s.e.m. (see Methods for further details).

Full size image

Near equilibrium, heating and cooling become symmetric

Finally, we show that for quenches near equilibrium, heating and cooling are indeed almost symmetric, in agreement with linear non-equilibrium thermodynamics1. First, for Th = (1 + ε)Tw with 0 < ε ≪ 1, we find that \({T}_\mathrm{c}({T}_\mathrm{h})=(1-\varepsilon +{{{\mathcal{O}}}}({\varepsilon }^{2})){T}_\mathrm{w}\) (Supplementary Information). That is, near equilibrium, TE temperatures are approximately equidistant from the ambient temperature Tw. Second, \({\partial }_{t}{\mathcal{D}}_{i}^\mathrm{w}{| }_{t = 0}=[2-{T}_{i}/{T}_\mathrm{w}-{T}_\mathrm{w}/{T}_{i}]\) \({k}_\mathrm{B}{T}_\mathrm{w}\kappa /\gamma\) (Supplementary Information), from which, for small ε, we obtain \(({\partial }_{t}{\mathcal{D}}_\mathrm{c}^\mathrm{w}{| }_{t = 0}-{\partial }_{t}{\mathcal{D}}_\mathrm{h}^\mathrm{w}{| }_{t = 0})\gamma /\kappa {k}_\mathrm{B}{T}_\mathrm{w}={\mathcal{O}}({\varepsilon }^{3})\), such that heating and cooling in terms of \({\mathcal{D}}_{i}^\mathrm{w}\) become symmetric. Third, we find in this limit (Supplementary Corollary 4) that \({\varphi }_\mathrm{w}^{i}(t)={\varphi }_{i}^\mathrm{w}(t)=1-{\rm{e}}^{-2(\kappa /\gamma )t}+{\mathcal{O}}(\varepsilon )\) and

$${\varphi }_\mathrm{w}^\mathrm{c}(t)={\varphi }_\mathrm{w}^\mathrm{h}(t)+{\mathcal{O}}(\varepsilon )\quad {{{\rm{and}}}}\quad {\varphi }_\mathrm{h}^\mathrm{w}(t)={\varphi }_\mathrm{c}^\mathrm{w}(t)+{\mathcal{O}}(\varepsilon ).$$
(6)

Thus, for near-equilibrium quenches, that is for Th,c − Tw ≪ Tw, heating and cooling in terms of both \({\mathcal{D}}\) and φ are approximately symmetric, and the asymmetry is a genuinely far-from-equilibrium phenomenon, as claimed. Actually, even for values of (Th,c − Tw)/Tw of the order of 1, heating and cooling are virtually symmetric within the experimental error (Extended Data Fig. 3, lower row, and Supplementary Information).

Discussion

Detailed experiments on colloidal particles corroborated by analytical theory have revealed a fundamental asymmetry in thermal relaxation upon a rapid change of temperature. For TE temperature quenches as well as between two fixed temperatures, heating is always faster than cooling. Moreover, the microscopic pathways followed by a system during heating and cooling are fundamentally different. Therefore, except very near to thermodynamic equilibrium, thermal relaxation, in general, does not evolve quasi-statically through quasi-equilibria even for systems with a single energy minimum. We, therefore, witness a breakdown of the ‘near equilibrium’ paradigm of classical non-equilibrium thermodynamics1.

Namely, when the system is brought rapidly out of equilibrium, such as upon a temperature quench, the probability density of the system cannot follow the temperature change quasi-statically and a lag develops between the instantaneous \({P}_{i}^\mathrm{w}(x,t)\) and the new equilibrium \({P}_{\rm{eq}}^\mathrm{w}(x)\) (ref. 24). This lag, which here corresponds to \(\tilde{D}\left[{P}_{i}^\mathrm{w}(x,t)\|\right.\)\(\left.{P}_{\rm{eq}}^\mathrm{w}(x)\right]\), is nominally smaller during heating than during cooling. This is so because for short times, heating essentially corresponds to a free expansion15, which is materialized as an overshoot of the statistical velocity and is characterized by a smaller amount of dissipated work. The latter, in turn, bounds from above the maximal lag that can develop24. The initial free expansion during heating also explains the faster departure from the initial equilibrium within the backward protocol, as well as for heating and cooling between any two fixed temperatures.

During heating, this initial free expansion leads to a rapid increase in the system entropy and, therefore, to a decrease in the generalized excess free energy, \({\mathcal{D}}(t)=\langle U\rangle (t)-{T}_\mathrm{w}S(t)-{F}_\mathrm{w}\). Cooling is dominated by the decrease in 〈U〉, which is, however, less efficient than the decay of the system entropy during cooling. In turn, this causes the asymmetry for TE quenches15. Another intuitive argument for faster heating follows from spectral theory. Namely, the spectral representation of localized initial distributions nominally requires more eigenfunctions, in turn implying, since the initial distribution is normalized, that there is a larger weight on the higher, faster-decaying modes36,37. Since the colder system is more localized, one would expect a faster relaxation during heating. The faster heating between any two temperatures, established here, may further be rationalized as follows. Microscopically, diffusion is driven by collisions between molecules in the medium. Since heating evolves at a higher temperature of the medium, collisions occur at a higher rate, in turn facilitating faster relaxation38.

Our work further underscores that there is a fundamental difference between equidistant temperatures, TE temperatures and kinematically equidistant temperatures. The existence of a zero temperature and the e−1/T-dependence of Boltzmann–Gibbs equilibrium statistics readily imply that raising and lowering the temperature by the same amount pushes the system far from equilibrium in different ways. However, even when the temperatures are chosen to be TE, the colder system is kinematically farther from equilibrium than the hotter one, yet it reaches equilibrium faster.

Thermal relaxation, therefore, seems to be much more complex than originally thought, and our results only scratch at the surface. In systems with several energy minima3,8,15,16, time-dependent potentials21,22,39,40,41,42 and driven relaxation processes43,44 and in the presence of time-irreversible, detailed-balance-violating dynamics30,45,46,47, relaxation remains poorly understood, which calls for a systematic analysis through the lens of thermal kinematics.

Methods

Experimental set-up

Silica microspheres of diameter d = 1 μm were dispersed in deionized and filtered water at a concentration of a few spheres per millilitre. The dispersion was injected into a custom-made electrophoretic fluid chamber in which two parallel, gold-coated wires acted as a pair of parallel electrodes. A white, Gaussian, noise signal, which was composed of a sample of 500,000 independent Gaussian values of zero mean and unit variance, was generated by an arbitrary waveform generator (RSPro, RSDG2082X with 80 MHz bandwidth), thus producing a voltage output signal V(t) that was fed into the pair of electrodes. The repetition frequency of the cited signal was chosen to minimize correlations, and the time of noise persistence was just 0.04 ms, which is much shorter than any characteristic time of the studied processes (these covered a range between 0.1 and 0.5 ms).

Our experiment used an optical tweezers set-up, which consisted of a commercial device from JPK-Bruker (NanoTracker 2). The optical potential was generated by a near-infrared laser with a wavelength of 1,064 nm, which was used for both trapping and detection. The forward scattered light was analysed using a quadrant position detector operating at a rate of 50 kHz. The trap stiffness depended linearly on the laser power and could be adjusted by controlling the latter with the software provided by the manufacturer.

The noisy signal was modulated by a square signal with a period of 10 ms (Extended Data Fig. 1). This period was chosen as it was a multiple of the sampling time of 0.02 ms to enhance the accuracy of data processing. The heights of the square signal were set to ensure equidistant quenches between the heating and cooling processes. As only the ratio between the initial and final temperatures was important, it was not necessary to set the high level of the heating process equal to the low level of the cooling process as long as the initial values of the relative entropy coincided for both heating and cooling.

In Extended Data Fig. 1, we show an example of the evolution in time of the variance of the modulated noisy signal for both heating and cooling processes. Note the ‘ramp’ with a finite slope and length tr = 0.10 ms linking the initial and final values, instead of an instantaneous change. However, this ramp did not prevent the studied phenomena from occurring, as our results seem to corroborate the theory even though the ramp time was, in some situations, of the order of the characteristic time of the considered relaxation processes.

Effective heating by an external random force

The applied noisy electric field \(\mathrm{d}{\xi }_{t}^{\rm{ext}}\) mimics an additional, independent source of thermal fluctuations in the particle dynamics, due to the electric charges all over the particle surface48. When the field is applied, the position xt along the considered direction obeys the Langevin equation \(\gamma\,\mathrm{d}{x}_{t}=-\kappa {x}_{t}\,\mathrm{d}t+\mathrm{d}{\xi }_{t}^{\rm{th}}+\mathrm{d}{\xi }_{t}^{\rm{ext}}\), where \(\mathrm{d}{\xi }_{t}^{\rm{th}}\) follows \(\langle \mathrm{d}{\xi }_{t}^{\rm{th}}\,\mathrm{d}{\xi }_{{t}^{{\prime} }}^{\rm{th}}\rangle =\) \(2\gamma {k}_\mathrm{B}T\,\delta (t-{t}^{{\prime} })\,\mathrm{d}t\,\mathrm{d}{t}^{{\prime} }\). If the spectrum of the external noise is also white and of amplitude σ2, then the particle is subjected to an effective white noise \(\mathrm{d}{\xi }_{t}^{\rm{eff}}\) of zero mean and autocorrelation \(\langle \mathrm{d}{\xi }_{t}^{\rm{eff}}\,\mathrm{d}{\xi }_{{t}^{{\prime} }}^{\rm{eff}}\rangle =\) \(2\gamma {k}_\mathrm{B}{T}_{\rm{eff}}\,\delta (t-{t}^{{\prime} })\,\mathrm{d}t\,\mathrm{d}{t}^{{\prime} }\), where

$${T}_{\rm{eff}}=T+\frac{{\sigma }^{2}}{2{k}_\mathrm{B}\gamma }.$$
(7)

Hence, the position of the particle along the selected axis fluctuates corresponding to an effective temperature Teff, which is always higher than the temperature of the thermal bath. These fluctuations did not affect the dissipation at all. This effective temperature can be estimated from the equipartition theorem, \(\kappa \langle {x}_{t}^{2}\rangle ={k}_\mathrm{B}{T}_{\rm{eff}}\), which must continue to hold.

In our case, \({\sigma }^{2}={q}^{2}{V}_{0}^{2}/{d}^{2}\), where \({V}_{0}^{2}\) is the variance of the noisy voltage output. The previous expression shows that the effective temperature increases linearly with \({V}_{0}^{2}\), whose slope can be estimated from several realizations of the particle position for different amplitudes. Extended Data Fig. 2 shows two examples of power spectral densities (PSDs) for the position of the sphere with and without the electric field, as well as an example of a calibration curve of Teff versus \({V}_{0}^{2}\). The effective temperatures were estimated with the equipartition theorem.

Data analysis

We collected M = 24,000 trajectories, with each trajectory comprising values for the position of the particle at N = 250 different time instants, \({{{{\boldsymbol{x}}}}}^{(k)}=({x}_{1}^{(k)},\ldots ,{x}_{N}^{(k)})\), k = 1, …, M. From the M trajectories, the N histograms (one for each time instant) were calculated and properly normalized, \({\{p(x,{t}_{j})\}}_{j = 1}^{N}\). A total of Nb = 80 equidistantly distributed bins separated by a fixed length \(\Delta x=({\max }_{jk}{x}_{j}^{k}-{\min }_{jk}{x}_{j}^{k})/{N}_\mathrm{b}\) were used.

The values of the relative entropy calculated throughout our work were computed directly from the definition:

$$\tilde{D}[P\|Q]=\int\,\mathrm{d}x\,P\log \frac{P}{Q}.$$
(8)

The previous integral was discretized as usual from the histograms:

$$\tilde{D}[P\|Q]\approx \Delta x\mathop{\sum }\limits_{k=1}^{{N}_\mathrm{b}}P({x}_{k})\log \frac{P({x}_{k})}{Q({x}_{k})}.$$
(9)

The convention \(0\log 0=0\) was employed. Finally, to smooth out the results, the presented series were estimated from an average of ten different temporal series. Subsequent uncertainties were estimated as the standard error of the mean (s.e.m.).

The number of counts n in each bin of the histogram was assumed to follow a Poisson distribution since the spatial interval Δx associated with each bin was small and the total number N of measured values of the position was high enough. Consequently, the uncertainty associated with each of the heights could be fairly well approximated by \(\sqrt{n}\), as it corresponds to the standard deviation of the cited probability distribution.

We estimated the Fisher information from its definition, which directly involves the relative entropy: \(\tilde{D}[P(x,t+\Delta t)\|P(x,t)]=\) \(I(t)\Delta {t}^{2}+{{{\mathcal{O}}}}(\Delta {t}^{3})\). An appropriate choice of Δt had to be made to reduce the numerical noise and to smooth the resulting curves. In our case, we chose Δt = 0.04 ms. We further took an average of ten different temporal series. Subsequent uncertainties were estimated as the s.e.m.

Finally, to calculate the statistical length \({\mathcal{L}}(t)\), we used a first-order numerical algorithm to calculate the corresponding integrals. If t = nΔt, then n ≥ 0 is a multiple of the sampling time, and \(v(t)\equiv \sqrt{I(t)}\) is the instantaneous velocity introduced in the main part, so that

$${\mathcal{L}}(t)\approx \Delta t\sum_{i=0}^{n-1}v(i\Delta t).$$
(10)

Transient evolution during a ramp thermal protocol

As we showed earlier, the thermal quench that our particle underwent was not completely instantaneous. The noise variance (as shown in Extended Data Fig. 1) exhibited a ramp connecting its initial and final values. Although the time interval for this ramp was expected to be small compared to the relaxation times τ = γ/κ explored in this work, this may not have been the case for higher values of this parameter.

We denote the time duration for the ramp as tr. The parameter δ ≡ tr/τ determines the strength of the driving protocol into the thermal relaxation processes being studied. In this section, we will show that from the time instant in which the bath reaches its target temperature, the evolution law for \(\langle {x}_{t}^{2}\rangle\) coincides in shape with that corresponding to an instantaneous quench.

Thus, let us consider a non-instantaneous quench protocol determined by the bath temperature profile:

$$T(t)=\begin{cases}{T}_{0}+\lambda t,& 0\le t\le {t}_\mathrm{r}, \\ {T}_\mathrm{f},& t\ge {t}_\mathrm{r}, \end{cases}$$
(11)

where λ ≡ (Tf − T0)/tr and T0,f are the initial and final temperatures, respectively. If the initial distribution follows a Gaussian profile

$$P(x,0)=\sqrt{\frac{\kappa }{2\pi {k}_\mathrm{B}{T}_{0}}}\operatorname{e}^{-\kappa {x}^{2}/2{k}_\mathrm{B}{T}_{0}},$$
(12)

the solution of the Fokker–Planck equation

$${\partial }_{t}P=\frac{\kappa }{\gamma }{\partial }_{x}(xP)+\frac{{k}_\mathrm{B}T(t)}{\gamma }{\partial }_{x}^{2}P$$
(13)

also follows a Gaussian profile of zero mean and variance:

$$\langle {x}_{t}^{2}\rangle =\frac{{k}_\mathrm{B}{T}_{0}}{\kappa }\operatorname{e}^{-2(\kappa /\gamma )t}+\,2\int\nolimits_{0}^{t}\mathrm{d}s\,\frac{{k}_\mathrm{B}T(t)}{\gamma }\operatorname{e}^{-2(\kappa /\gamma )(t-s)}.$$
(14)

The preceding integral takes a different expression if the considered time instant t is greater or less than tr. On the one hand, when 0 ≤ t ≤ tr, it takes the form:

$$\langle {x}_{t}^{2}\rangle =\frac{{k}_\mathrm{B}{T}_\mathrm{f}}{2\delta \kappa }\left[(1-\tilde{T})\operatorname{e}^{-2(\kappa /\gamma )t}+\tilde{T}-1+2\delta \tilde{T}+2\frac{\kappa }{\gamma }(1-\tilde{T})t\right],$$
(15)

where we define \(\tilde{T}\equiv {T}_{0}/{T}_\mathrm{f}\). On the other hand, when t ≥ tr:

$$\langle {x}_{t}^{2}\rangle =\frac{{k}_\mathrm{B}{T}_\mathrm{f}}{\kappa }\left[1+\frac{\operatorname{e}^{2\delta }-1}{2\delta }(\tilde{T}-1)\operatorname{e}^{-2(\kappa /\gamma )t}\right].$$
(16)

The previous expression, thus, takes the same form as the one corresponding to an instantaneous quench, but with a parameter that acts as a relative temperature:

$${\tilde{T}}_{\rm{eff}}\equiv \frac{\operatorname{e}^{2\delta }-1}{2\delta }(\tilde{T}-1)+1.$$
(17)

All the theoretical curves plotted over the experimental data shown throughout this article assume the previous expression for \(\langle {x}_{t}^{2}\rangle\).

To accurately observe the phenomena addressed in our study, we adopted the closest situation to ideality, which meant maintaining the value of δ at or below one, as this aligns with the original theoretical model and ensures that the effects of the temperature ramp do not overpower the observations. However, our findings indicate that the phenomenology studied is relatively robust to the presence of a non-zero response time in the generator. Moreover, our theoretical predictions are undoubtedly substantiated by our experimental results, even when δ exceeds unity (see Extended Data Figs. 3–6). Future examinations of all the phenomenology derived from the protocol analysed in this section will be necessary to fully understand the limits of the validity of our predictions.