Abstract
Significant efforts have focused on the magnetic excitations of relativistic Mott insulators, predicted to realize the Kitaev quantum spin liquid (QSL). This exactly solvable model involves a highly entangled state resulting from bond-dependent Ising interactions that produce excitations which are non-local in terms of spin flips. A key challenge in real materials is identifying the relative size of the non-Kitaev terms and their role in the emergence or suppression of fractional excitations. Here, we identify the energy and temperature boundaries of non-Kitaev interactions by direct comparison of the Raman susceptibility of α-RuCl3 with quantum Monte Carlo (QMC) results for the Kitaev QSL. Moreover, we further confirm the fractional nature of the magnetic excitations, which is given by creating a pair of fermionic quasiparticles. Interestingly, this fermionic response remains valid in the non-Kitaev range. Our results and focus on the use of the Raman susceptibility provide a stringent new test for future theoretical and experimental studies of QSLs.
Similar content being viewed by others
Introduction
Exotic excitations with fractional quantum numbers are a key characteristic of QSLs,1,2,3,4 which result from the long range entanglement of these non-trivial topological phases.5,6,7 Originating from frustrated magnetic interactions, the fractional nature inspires an overarching goal of studying QSLs, realizing topological quantum computing immune to decoherence, with high operating temperatures from large exchange interactions.8,9 The last decade has seen great progress towards identifying the fractional excitations of QSLs.10,11,12,13,14,15,16,17,18 Attention has focused on relativistic Mott insulators that are close to the exactly solvable Kitaev model with a QSL ground state. In materials such as A2IrO3 (A = Cu, Li, or Na)4,8,19,20,21,22,23 and α-RuCl3,24,25,26,27 the large spin–orbit coupling and Coulomb repulsion result in jeff = 1∕2 moments on a honeycomb lattice.2,9,28,29,30,31,32,33,34,35 According to the pure Kitaev model, in these materials spin flips could produce Z2 gauge fluxes and dispersive Majorana fermions.14,36
In these materials, as with other QSL candidates, the presence of additional symmetry allowed terms (Heisenberg and bond-dependent off-diagonal interactions in this case), produces long-range magnetic order.10,10,29,37 Despite extensive studies and evidence for fractional particles,11,34,38,39 the relative size of the non-Kitaev terms and the range over which they are relevant remains controversial.37,40 In α-RuCl3, these non-Kitaev terms lead to a magnetically ordered phase below 7 K, which could be destroyed by an in-plane magnetic field.41,42,43,44,45 The exact nature of the field induced QSL state remains unclear27,38,42 as the zero field Hamiltonian is still unresolved. In particular, non-Kitaev interactions dominant energy and temperature ranges, have not yet been experimentally established. Additionally, there is a need to determine if excitations in these ranges maintain their fractional nature.
Raman scattering is a powerful probe of magnetic materials, revealing the presence of long-range order, symmetry and statistics of the excitations, as well as the strength and nature of the exchange, even in single 2D atomic layers.3,46,47,48,49,50,51,52,53 Indeed, Raman scattering was the first to reveal the continuum from magnetic excitations in α-RuCl3.11 However, a careful study of the Kitaev term’s temperature and energy dependence is still a challenge, as one requires a very high temperature and energy resolution to show the spectral change and directly compare the spectra with theoretical calculations.54 Previously, Raman efforts relied on spectral integration over a certain energy range which averaged out the energy dependence of the excitations, and the low scattering intensity made it difficult to directly compare the spectra with theoretical calculations from the exact Kitaev model. As such, the role of the non-Kitaev terms, and their size, could not be identified in previous efforts. Furthermore, demonstration of the fractional nature relied on the integrated Raman intensity and thus required subtraction of a bosonic background, without justification. This approach also meant fitting the data with an average energy in the Fermi function, further limiting the ability to uncover if the non-Kitaev terms affected the statistical response of the excitations.26,34
Here, we overcome all these previous limitations with new Raman spectra with dramatically improved signal levels, high temperature, and energy resolution. Firstly, having improved the optics, our Raman measurements now obtain a signal level 18 times larger than before11 (see supplemental). This high signal level provides enough anti-Stokes response to ensure the temperature is correct and allows us to directly extract the Raman susceptibility by taking the difference between Stokes and anti-Stokes intensities, after the dark counts have already been removed. In this way, the role of the non-Kitaev terms is revealed via a direct comparison of the full temperature and energy dependence of the α-RuCl3 Raman susceptibility with a QMC calculation for the pure Kitaev model. Furthermore, we provide compelling evidence for the fermionic nature of the excitations without the need to subtract a bosonic background. Our results show that the Raman susceptibility of α-RuCl3 is consistent with QMC calculations at higher temperatures and energies (>40 K and >6 meV). The deviation between them in the low temperature and energy range (<40 K and <6 meV) results from the non-Kitaev terms. Via these temperature and energy boundaries, we directly measure the ratio of JK and Γ interactions in the Hamiltonian. Moreover, the high temperature (>150 K) difference between the Raman susceptibility and the QMC indicates the presence of quasi-elastic scattering (QES) induced by thermal fluctuations in the system, commonly observed in frustrated systems.7,11,26 With our enhanced signal the anti-Stokes spectra for all temperatures can be compared with the Stokes response to prove the sample is in detailed balance without laser heating (Fig. 2d). To further explore the effect of non-Kitaev interactions, we fit the Raman susceptibility with a Fermi function containing half the measured energy. The very good overlap shows the excitations are governed by Fermi statistics even beyond the Kitaev dominant range.55 We also checked that the susceptibility integration is governed by a Fermi function with half energy, which further confirms each fractional particle holds one half of the scattering energy in both Kitaev and non-Kitaev dominant regimes. Interestingly this is revealed without the need to subtract the bosonic background.
Results and discussion
In inelastic light scattering, the measured intensity is determined by symmetry, Fermi’s golden rule, and from the fluctuation-dissipation theorem, is proportional to the Raman susceptibility (\({\rm{Im}}(\chi [\omega ,T])\)) times a Bose function.56,57 In magnets this can produce peaks from single magnons, broad features reflecting the two-magnon joint density of states (JDos), or QES from thermal fluctuations.11,13 For the Kitaev QSL, Raman predominantly excites pairs of fractional particles in the energy range considered here (≈0.5JK < ℏω < ≈2JK), leading to the energy loss (IS[ω, T]) and gain (IaS[ω, T]) intensities:34,58
where nB∕F[ω, T] are the Bose/Fermi distributions and JDos[ω, T] is approximately given by the JDos from the fractional particles. For responses from non-fractional excitations, for example phonons, we expect an additional term to be added to the susceptibility, without contributions from the Fermi function.
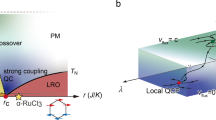
As shown in Fig. 1a, we collected both the Stokes and anti-Stokes spectra of bulk α-RuCl3 from 10 K to 300 K. Our Rayleigh scattering half width is 2.3 meV, enabling measurement down into the low energy regime. The temperature dependent spectra show a clear magnetic excitation continuum (2.3 meV ~ 10 meV) below the first phonon, which mostly results from the Kitaev interaction and is consistent with previous predictions and measurements.11,26,34,39 Since the measured Raman intensity contains a Bose factor, it is best to investigate the Raman susceptibility \({\rm{Im}}[\chi [\omega ,T]]\).13,50,52,56 Using our new anti-Stokes spectra, we directly determine the susceptibility from the difference between the Stokes and anti-Stokes intensities (\({I}_{S}[\omega ,T]-{I}_{aS}[\omega ,T]={\rm{Im}}[\chi [\omega ,T]]\)). This new data set, combined with minimizing the rise in temperature due to the laser, reveals the regimes in which non-Kitaev terms are relevant. Specifically, Fig. 1b shows the comparison of the QMC results for the pure Kitaev limit and the Raman susceptibility at 10 and 40 K. While excellent agreement is seen at 40 K, the data at 10 K only matches the model between 6 and 10 meV. Noting that this temperature is still above the magnetic ordering temperature of 7 K, this additional susceptibility results from non-Kitaev terms, as recently suggested by exact diagonalization (ED) calculations.40
a Temperature dependent Raman intensity of α-RuCl3 in XY polarization. Both Stokes and anti-Stokes data are collected from 10 K to 300 K with 5 K steps below 120 K and 10 K steps above. the gray shade is indicates the magnetic continuum excitation. b The measured Raman susceptibility in XY polarization of α-RuCl3 at 10 K (blue line) compared with the calculated result of the pure Kitaev limit (purple line) at the same temperature. The enhanced signal at low energies results from the non-Kitaev interactions in the system. By 40 K there is nearly perfect agreement between the Raman data (yellow line) and the QMC calculation (red line), indicating the non-Kitaev terms are not relevant in this energy and temperature range. c The temperature and energy dependent map of χδ (χδ = χmeasured − χQMC). χδ at low temperature and low energy range shows the temperature and energy boundary of non-Kitaev (NK) interactions in the system. χδ at the high temperature and low energy range indicates the quasi-elastic scattering (QES) in the system.
To further investigate the temperature and energy dependence of the non-Kitaev interactions, we consider the energy and temperature dependent colormap in Fig. 1c. Here χδ = χmeasured − χQMC is the difference between the measured Raman susceptibility and that of the pure Kitaev model (determined by the QMC calculation). The green color indicates the measured susceptibility is higher than the QMC results and the blue color indicates regions of very good overlap between the measurement and the calculation. The black dots suggest the temperature and energy boundaries where the system perfectly resembles the pure Kitaev QSL. Specifically, there is a large χδ in the quarter circle area below 6 meV and 40 K, which can be explained as the region where non-Kitaev interactions become dominant in the response. The deviation above 150 K and below 8 meV results from the QES induced by thermal fluctuations in the system, which is well known in frustrated magnets.7,11,26,48,59 The high energy deviation (>12 meV) is from the low energy tail of the phonon. Nonetheless, the low energy and temperature deviation from the pure Kitaev model is consistent with the calculated intensities of recent ED results for a model with only Γ and Kitaev terms in the system (K-Γ model)40 with −JK∕Γ = 5. Furthermore, the ED results suggest enhanced response over that expected for the pure Kitaev limit for ωΓ ~ 2.5Γ. As shown in our colormap, when the temperature is low, the disagreement occurs for ωΓ < 6 meV. based on the K-Γ model, this suggests Γ ≈ 2.4 meV, where the Heisenberg interaction and terms beyond nearest neighbors are neglected. We note that regardless of the specific non-Kitaev terms, this can be interpreted as an upper bound on the ratio of Kitaev to non-Kitaev terms in this system. Furthermore, we find the best agreement for the pure Kitaev limit with JK = 10 meV (Supplementary Fig. 4), consistent with our observed bandwidth of the continuum (Fig. 1a) of 30 meV.11,58 The Γ ≈ 2.4 meV we obtained here is also consistent with the results obtained from neutron scattering (2.5 meV),29 from thermal Hall measurements (2.5 meV),60 and from THz measurements (2.4 meV).61
Having established the size and extent of the non-Kitaev terms, we examine the statistics of the excitations in α-RuCl3 to see if they are truly fractional. As the statistics depends on both temperature and energy, one should make sure the system is in detailed balance56 and that laser heating is negligible, which was not quantitatively shown before. As discussed in the supplemental, the fermionic response written above is consistent with the fluctuation-dissipation theorem with the presence of time-reversal symmetry, requiring \({I}_{S}[\omega ,T]/{I}_{aS}[\omega ,T]={e}^{\frac{\hslash \omega }{{k}_{B}T}}\).50,56 Previously, the discrepancy between the prediction of the Bose factor and the measured intensity at low temperatures was attributed to fractional statistics.26,34 However, these works did not exclude the possibility that laser induced heating kept the measured area at a fixed temperature, while the bulk was cooled. This is not unlikely, given the small specific heat and thermal conductivity of RuCl3 at low temperatures.55,62,63,64,65 Furthermore, as described in the supplemental, previous uses of the anti-Stokes responses were unreliable due to the low signal levels.11 Most importantly, unless the temperature is well known, it is difficult to directly compare with the theoretical prediction for fractional statistics. In our current work we have made substantial improvements to the thermal anchoring and collection efficiency to allow for much higher temperature resolution and lower Raman frequency. In this way, we can observe the spectra change between different temperatures and directly compare it with the QMC results. Most importantly, due to enhanced signals and lower probing frequencies, we have been able to collect anti-Stokes response at lower temperatures to ensure that laser induced heating is not an issue. Returning to the actual sample temperature, in Fig. 2d, we compare the anti-Stokes intensity and Stokes intensity times a Boltzmann factor with the measured temperature. The excellent agreement between them reveals that there is nearly no heating in the laser spot and thus we can use the measured crystal temperature. Unlike previous studies,11,26 our new quantitative comparison between Stokes and anti-Stokes limits the possibility of laser heating to explain the low temperature upturn and confirms the sample is in detailed balance.
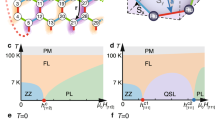
a Raman susceptibility of RuCl3, \(\Delta {\rm{Im}}[\chi (\omega ,T)]={\rm{Im}}[\chi (\omega ,T)]-{\rm{Im}}[\chi (\omega ,150\,{\rm{K}})]\)). The curves with black outlines are the contour plots of the Fermi function (ΔnF(ω∕2, T) = nF(ω∕2, 150) − nF(ω∕2, T)). Both data and the prediction are normalized to their maximum values. The agreement between the two confirms that Raman creates magnetic excitations that are made of pairs of fermions. The upturn of the Raman intensity in the high temperature and low energy range results from thermal fluctuations of the magnetism (quasi-elastic scattering). b Raman susceptibility of a similar magnet, Cr2Ge2Te6, where, opposite to α-RuCl3, ΔIm[χ(ω, T)] is negative and does not match nF(ω∕2, T). c Comparison of nF(ω∕2, T) and \(\Delta {\rm{Im}}[\chi (\omega ,T)]\) of RuCl3 at fixed temperatures. The agreement further confirms the excitations are fermionic. d The excellent agreement between Stokes and anti-Stokes spectra of α-RuCl3 when normalized by the Boltzmann factor demonstrates the absence of laser heating.
We explore the possibility that the Raman susceptibility results from purely fermionic excitions in Fig. 2a. If the excitation is fractional, one expects \({\rm{Im}}[\chi (\omega ,T)]\propto JDos(\omega ,T)* (1-2{n}_{F}(\omega /2,T))\). This results from the particle-hole symmetry of these excitations, and that we are probing creation/annihilation processes. To cancel the constant term and focus only on the fermionic part, we show the difference of susceptibility: \(\Delta Im(\chi [\omega ,T\le 150\,{\rm{K}}])={\rm{Im}}(\chi [\omega ,T])-{\rm{Im}}(\chi [\omega ,150\,{\rm{K}}])\). The utility of such an analysis is quite clear: the energy and temperature extent of the continuum can be directly observed – without contributions from high temperature QES fluctuations or phonons. To test the predicted fermionic response from fractional particles, we plot ΔnF[ω∕2, T] = nF[ω∕2, T] − nF[ω∕2, 150 K], as contour lines on top of the data. The agreement is quite good and is further confirmed in Fig. 2c via constant temperature cuts of the data shown in Fig. 2a, along with the calculated ΔnF[ω∕2, T]. The good agreement between the data and Fermi functions with half of the scattering energy provides strong evidence for the presence of pairs of fractional particles. We note this is done without any artificial subtraction of a bosonic background.
The approach described above, relies on a nearly temperature and energy independent JDos[ω, T], which is expected from the numerical calculations for the Kitaev system at temperatures above the flux gap.55 This assumption appears to generally hold in our data, whose temperature and energy evolution are generally described by a Fermi function. Nonetheless, at the lowest temperatures, there is some deviation of the data for energies above 6 meV. The origin of this discrepancy is not clear, but likely results from the temperature and energy dependence of the JDos[ω, T]. Additionally, we find poor agreement if the full scattering energy (nF[ω, T]) is used (not shown). We additionally performed the same analysis on another honeycomb system Cr2Ge2Te6 (Fig. 2b), which was grown by established methods and which is ferromagnetic below 60 K with a similar Curie-Weiss temperature as α-RuCl3.59,66 The behavior of Cr2Ge2Te6 is the exact opposite of α-RuCl3, namely, \(\Delta {\rm{Im}}(\chi [\omega ,T])\) is negative throughout the whole measured range and decreases upon cooling.
Returning to Fig. 2a, we have also drawn the boundary of the non-Kitaev contributions determined from the analysis in Fig. 1c. We find the Fermi function matches the susceptibility very well, suggesting the Fermi statistics hold even when the agreement with the pure Kitaev model (Fig. 1b) does not. However, given the relatively large size of the Kitaev term relative to the non-Kitaev contributions, this may not be surprising and suggests the excitations in α-RuCl3 are primarily fractionalized. Our analysis presented in Fig. 1c and Fig. 2a also reveals the crossover from spin liquid-like behavior (i.e. fractional continuum) to a standard paramagnet. Indeed, \(\Delta {\rm{Im}}(\chi [\omega ,150\,{\rm{K}}\le T\le 200\,{\rm{K}}])\) is nearly constant, as expected for a paramagnet in this range. As discussed later, the response at higher temperatures is consistent with quasi-elastic scattering. We note that the exact temperature at which the response will set in, depends on the energy scale at which it is measured. As such the integrated response investigated in Fig. 3C, appears to have a higher onset temperature for the QES due to the inclusion of higher energy scales. Specifically, a Lorentzian at zero energy results from thermal fluctuations of the magnetism that confirm the magnetic specific heat is consistent with a standard paramagnet at high temperatures. Lastly, this analysis also provides new insights into the phonons overlapping the continuum. Specifically, consistent with previous works we also find the phonons have a low energy tail due to their coupling with the continuum (Fig. 1c and Supplementary Fig. 4b). However, via our new comparison with the pure Kitaev limit, it is clear the influence of the two lowest energy phonons on the continuum is limited to ≈12 → 14 meV, and ≈15 → 19 meV, respectively. Interestingly, the response in these regions still follows the prediction of the Fermi function (2a), showing the mixing of the phonons with the fractional excitations does not significantly influence them.
a The continuum in α-RuCl3 due to fractional particles is removed by taking the difference between XY and XX intensities. This confirms the continuum is consistent with predictions of the Kitaev model, and the high temperature response is from quasi-elastic scattering (i.e. Lorentzian times a Bose factor). b The integration of the Raman susceptibility (3 meV–8 meV) with only the quasi-elastic scattering response, reveals a linear T behavior above 150 K and temperature independent behavior below. c, d Integrated spectral weight(3 meV–8 meV) of \({\rm{Im}}[\chi (\omega ,T)]\), reveals Fermi statistics in α-RuCl3 below ≈100 K (solid red line) in XX and XY polarizations. Above 150 K the response is linear in temperature due to the quasi-elastic scattering (yellow lines). The spectral weight (3 meV–8 meV) from Cr2Ge2Te6 (e, f) is enhanced up to TC (blue dashed line) but the temperature dependence above does not fit that expected for fermions (solid red line).
To ensure our approach is self-consistent, it is worthwhile to also analyze the integrated Raman response, as done previously in α-RuCl3 and Li2IrO3.11,26,34 Likewise, it is also crucial to find a reliable method to separate the QES response from the continuum such that it can be independently studied for further confirmation of the presence of Fermi statistics. This is now possible using both the polarization and Stokes minus anti-Stokes spectra (\({\rm{Im}}[\chi [\omega ,T]]\)). Since the continuum has equal weight in both polarizations11,58 it can be removed via their difference: \(\Delta {I}_{S/aS}[\omega ,T]={I}_{S/aS}^{{\mathrm{XX}}}[\omega ,T]-{I}_{S/aS}^{{\mathrm{XY}}}[\omega ,T]\). We also note the isotropic response of the continuum implies an isotropic Kitaev interaction.34,58 As seen in Fig. 3a, ΔIS∕aS[ω, T] is consistent with thermal fluctuations (i.e. QES),13,48,52 namely a Lorentzian whose amplitude is given by the magnetic specific heat (Cm[T]) times the temperature and appropriately weighted Bose factors (i.e. greater Stokes than anti-Stokes intensity). We now calculate the QES amplitude via the spectral weight (SW) of the Raman susceptibility: \({\mathrm{S}}{\mathrm{{W}}}_{{\mathrm{QES}}}[T]=\int {\chi }_{{\mathrm{XX}}}^{{\mathrm{QES}}}[\omega ,T]-{\chi }_{{\mathrm{XY}}}^{{\mathrm{QES}}}[\omega ,T]{\mathrm{d}}\omega =\int {\mathrm{d}}E\Delta \chi\). Here, the integration energy range is 3–8 meV. Consistent with direct fits of the ΔIS∕aS[ω, T] (see supplemental) and robust to the limits of integration (as long as phonons are not included), we find SWQES[T] ∝ T (see Fig. 3b). This suggests the magnetic specific heat is nearly temperature independent, as expected for a classical paramagnet at high temperatures. Since the QES signal is nearly zero in χ[ω, T < 150 K], this confirms the Raman susceptibility (and not the intensity) naturally separates the QES from the continuum. Thus our new measurements reveal the energy and temperature range over which the excitations are fractional without contamination from other contributions.
Having isolated the QES and identified its temperature dependence, we can independently check the temperature bounds of the Fermi statistics. Specifically, we investigate the difference between the Stokes and anti-Stokes SW in a given polarization (ΔSW[T] = ∫(IS[ω, T] − IaS[ω, T])dω), which includes the integrated Fermi function from the fractional excitations and the QES contribution (see supplemental). As shown in Fig. 3c, d for two different polarizations, the integrated weight follows the expected response for pairs of fermionic excitations (∫(1 − 2nf(ω∕2, T))dω) until T ≈ 150 K where it crosses over to a linear temperature dependence from the QES. The fermionic response is equal in both polarization configurations and covers the Kitaev ranges. Thus with just three parameters, one fixed by the lowest temperature, we fully explain the SW for all energy ranges, temperatures, and polarizations. To further confirm this, we tried the same analysis on our new Cr2Ge2Te6 data. As shown in Fig. 3e, f, the difference between the Stokes and anti-Stokes of Cr2Ge2Te6 cannot be fit with a Fermi function at all. Thus the results presented in Fig. 3c, d provide a quantitative confirmation of the presence of fractional excitations up to high temperatures.
To conclude, our higher quality data and anti-Stokes spectra provide direct comparison of the Raman susceptibility energy and temperature dependence with QMC calculations. At higher temperatures and energies, these results are consistent with QMC calculations for the pure Kitaev limit. Consistent with ED calculations, the Raman susceptibility is enhanced over the Kitaev QSL only at low energies and temperatures due to additional non-Kitaev terms. Thus our results reveal the temperature and energy boundary of non-Kitaev interactions becoming dominant. Furthermore, via comparison of the measured Raman susceptibility and the Fermi function, the data provide concrete evidence that the magnetic excitations in α-RuCl3 are fractional and follow Fermi statistics. Interestingly, these fractional excitations follow Fermi statistics even in the ranges where non-Kitaev terms become dominant. It remains to be answered whether, and how, different non-Kitaev terms compete with each other in the low temperature and energy range. Nonetheless, our approach enables a new means to extract the size and influence of non-frustrating terms in QSLs, and could be applied at finite magnetic field to confirm the fractional nature of excitations in the field induced QSL state of α-RuCl3.
Methods
RuCl3 crystal growth, handling, and characterization
Single crystals of α-RuCl3 were prepared using high-temperature vapor-transport techniques from pure α-RuCl3 powder with no additional transport agent. Crystals grown by an identical method have been extensively characterized via neutron scattering techniques39,42,63 revealing behavior consistent with what is expected for a relativistic Mott insulator with a large Kitaev interaction.16,24,25,29,30,32,33,41,43,45,65,67,68 The crystals have been shown to consistently exhibit a single dominant magnetic phase at low temperature with a transition temperature TN ≈ 7 K, indicating high crystal quality with minimal stacking faults.63 Care was taken in mounting the crystals to minimize the introduction of additional stacking faults, as evidenced by the high reproducibility of the spectra across different crystals and experimental setups. Characterization was consistent with previous studies.24,27,44,69,70,71
Raman spectroscopy experiments
Since Raman scattering involves a photon in and photon out, it allows one to measure both the symmetry and energy change of an excitation. Furthermore, one can choose an energy and/or symmetry channel to separate the magnetic, electronic, and lattice responses.11,13,26,34,52,56,59 The majority of the Raman experiments were performed with a custom built, low temperature microscopy setup.72 A 532-nm excitation laser, whose spot has a diameter of 2 μm, was used with the power limited to 30 μW to minimize sample heating while allowing for a strong enough signal. The sample was mounted by thermal epoxy onto a copper xyz stage. At both room and base temperature the reported spectra were averaged from three spectra in the same environment to ensure reproducibility. The spectrometer had a 2400-g/mm grating, with an Andor CCD, providing a resolution of ≈1 cm−1. Dark counts are removed by subtracting data collected with the same integration time, but with the laser off. To minimize the effects of hysteresis from the crystal structural transition, data was taken by first cooling the crystal to base temperature, and once cooled to base temperature, spectra were acquired either every 5 or 10 K by directly heating to that temperature. The absence of hysteresis effects was confirmed by taking numerous spectra at the same temperature after different thermal cycles (100 K in the middle of the hysteresis region). In addition, recent studies of the Raman spectra of RuCl3 suggest an effect of the surface structure upon exposure to air.49,69 To minimize this, crystals were freshly cleaved and immediately placed in vacuum within 3 min. Lastly, a recently developed wavelet based approach was employed to remove cosmic rays.72,73
Quantum Monte Carlo calculations
The Hamiltonian of the Kitaev model on the honeycomb lattice is given by14
where Sj represents an S = 1∕2 spin on site j, and \({\langle {J}_{K}\rangle }_{\gamma }\) stands for a nearest-neighbor (NN) γ(=x, y, z) bond. In the calculation for the spectrum of the Raman scattering we adopt the Loudon-Fleury (LF) approach. The LF operator for the Kitaev model is given by
where ϵin and ϵout are the polarization vectors of the incoming and outgoing photons and dα is the vector connecting a NN α bond.47,58 Using this LF operator, the Raman spectrum is calculated as
where \({\mathcal{R}}(t)={e}^{i{\mathcal{H}}t}{\mathcal{R}}{e}^{-i{\mathcal{H}}t}\) is the Heisenberg representation. The temperature dependence of I(ω) is numerically evaluated using the Monte Carlo simulation in the Majorana fermion representation without any approximation.16 In the following we show the details of the calculation procedure.34
Using the Jordan-Wigner transformation, the Hamiltonian is mapped onto the Majorana fermion model as
where \({(jj^{\prime} )}_{\gamma }\) is the NN pair satisfying \(j\ <\ j^{\prime}\) on the γ bond, and ηr is a Z2 conserved quantity defined on the z bond (r is the label for the bond), which takes ±1. This Hamiltonian is simply written as
using the Hermitian matrix Ajk({ηr}) depending on the configuration of {ηr}. The LF operator shown in Eq. (4) is also given by the bilinear form of the Majorana fermion:
where B({ηr}) is a Hermitian matrix. To evaluate Eq. (5), we separate the sum over the states into {cj} and {ηr} parts:
with
where \(Z=\sum _{\{{\eta }_{r}\!=\!\pm 1\}}{e}^{-\beta {F}_{f}(\{{\eta }_{r}\})}\) and \({Z}_{f}(\{{\eta }_{r}\})={e}^{-\beta {F}_{f}(\{{\eta }_{r}\})}={{\rm{Tr}}}_{\{{c}_{j}\}}{e}^{-\beta {\mathcal{H}}(\{{\eta }_{r}\})}\). By applying Wick’s theorem to Eq. (10), we calculate the Raman spectrum at ω(≠0) for a given configuration {ηr} as
where f(ε) = 1∕(1 + eβε) is the Fermi distribution function with zero chemical potential, {ελ} is the set of the positive eigenvalues of A with the eigenvectors {uλ}, and the matrices C and D are given by \({C}_{\lambda \lambda ^{\prime} }=2{{\boldsymbol{u}}}_{\lambda }^{\dagger }B{{\boldsymbol{u}}}_{\lambda ^{\prime} }\) and \({D}_{\lambda \lambda ^{\prime} }=2{{\boldsymbol{u}}}_{\lambda }^{\dagger }B{{\boldsymbol{u}}}_{\lambda ^{\prime} }^{* }\). In the Monte Carlo simulations, we generate a sequence of configurations of {ηr} to reproduce the distribution of \({e}^{-\beta {F}_{f}(\{{\eta }_{r}\})}\), and hence the finite-temperature spectrum is simply computed as \(I(\omega )={\langle \bar{I}(\omega ;\{{\eta }_{r}\})\rangle }_{{\rm{MC}}}\) with 〈⋯ 〉MC being the Monte Carlo average.
Correction for optical constants
According to the Beer-Lambert Law, the intensity of the laser decreases exponentially with the depth: I[z] = I0e−αz, where d is the depth and α is the attenuation constant, which is a function of laser frequency and dielectric constant of the material (\(\alpha =\frac{\omega }{c}{\rm{Im}}[\tilde{n}(\omega )]=-\frac{4\pi E[{\omega }_{0}]}{hc}k[{\omega }_{0}]\)). Alternatively one can express this in terms of a penetration depth indicating the length scale relevant to absorption: \(\delta =\frac{1}{\alpha }\). Applying this to our experiment, for a certain depth d, we find the incident laser intensity as a function of distance from the surface, \({I}_{in}[{\omega }_{0},z]={I}_{0}{e}^{-\frac{4\pi E[{\omega }_{0}]}{hc}k[{\omega }_{0}]z}\). Here, ω0 is the frequency of the excitation laser, I0 is the initial incoming laser power in front of the sample,and δ (≈140 nm) is much shorter than the thickness of α-RuCl3 bulk crystal. To properly account for the temperature dependence of the optical constants on the measured Raman signal, it is crucial to account for these absorption losses. Specifically, the measured intensity is reduced by the absorption of the outgoing Raman photons, (i.e. \({I}_{out}[\omega ,{\omega }_{0},z]={I}_{in}[{\omega }_{0},z]{e}^{-\frac{4\pi E[\omega ]}{hc}k[\omega ]z}\)) where ω is the frequency of the scattered light. Furthermore, one should also consider the probability of transmission at the surface of α-RuCl3 (T[ω]), which also depends on the Raman light frequency. Applying the transmission rate to the Raman signal, we obtain the Raman intensity coming out of the sample at each point IRaman [ω, ω0, z] = Iout[ω, ω0, z] × T[ω]. Finally, one obtains the signal intensity by integrating the attenuated intensity of scattering point at each depth via \({I}_{{\mathrm{corrected}}}[{\omega }_{0},\omega ]={\int }_{0}^{{d}_{{\mathrm{max}}}}{I}_{{\mathrm{Raman}}}[\omega ,{\omega }_{0},z]{\mathrm{d}}z\).72 All presented Raman data in this paper are corrected by this method using the previously published optical constants.25
Data availability
The data that support the findings of this study are available in figshare with the identifier(s) data DOI(s) https://doi.org/10.6084/m9.figshare.11774793.v1.
References
Wen, X.-G. Colloquium: zoo of quantum-topological phases of matter. Rev. Mod. Phys. 89, 041004 (2017).
Nussinov, Z. & van den Brink, J. Compass models: theory and physical motivations. Rev. Mod. Phys. 87, 1–59 (2015).
Burch, K. S., Mandrus, D. & Park, J.-G. Magnetism in two-dimensional van der waals materials. Nature 563, 47–52 (2018).
Takahashi, S. K. et al. Spin excitations of a proximate Kitaev quantum spin liquid realized in Cu2IrO3. Phys. Rev. X 9, 031047 (2019).
Lee, P. A. An end to the drought of quantum spin liquids. Science 321, 1306–1307 (2008).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2016).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a Kagome lattice antiferromagnet. Nature 492, 406–410 (2012).
Kitagawa, K. et al. A spin-orbital-entangled quantum liquid on a honeycomb lattice. Nature 554, 341–345 (2018).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Catuneanu, A., Yamaji, Y., Wachtel, G., Kim, Y. B. & Kee, H.-Y. Path to stable quantum spin liquids in spin-orbit coupled correlated materials. npj Quant. Mater. 3, 23 (2018).
Sandilands, L. J., Tian, Y., Plumb, K. W., Kim, Y.-J. & Burch, K. S. Scattering continuum and possible fractionalized excitations in α−RuCl3. Phys. Rev. Lett. 114, 147201 (2015).
Banerjee, A. et al. Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 15, 733–740 (2016).
Wulferding, D. et al. Interplay of thermal and quantum spin fluctuations in the Kagome lattice compound herbertsmithite. Phys. Rev. B 82, 144412 (2010).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Vojta, M., Mitchell, A. K. & Zschocke, F. Kondo impurities in the Kitaev spin liquid: Numerical renormalization group solution and gauge-flux-driven screening. Phys. Rev. Lett. 117, 037202 (2016).
Nasu, J., Udagawa, M. & Motome, Y. Vaporization of Kitaev spin liquids. Phys. Rev. Lett. 113, 197205 (2014).
Becker, M., Hermanns, M., Bauer, B., Garst, M. & Trebst, S. Spin-orbit physics of \(j=\frac{1}{2}\) mott insulators on the triangular lattice. Phys. Rev. B. 91, 155135 (2015).
Seifert, U. F. P., Meng, T. & Vojta, M. Fractionalized fermi liquids and exotic superconductivity in the Kitaev-Kondo lattice. Phys. Rev. B 97, 085118 (2018).
Singh, Y. & Gegenwart, P. Antiferromagnetic mott insulating state in single crystals of the honeycomb lattice material Na2IrO3. Phys. Rev. B 82, 064412 (2010).
Abramchuk, M. et al. Cu2IrO3: a new magnetically frustrated honeycomb iridate. J. Am. Chem. Soc. 139, 15371–15376 (2017).
Matern, S. & Hermanns, M. Entanglement in 3D Kitaev spin liquids. J. Stat. Mech. Theory Exp. 2018, 063101 (2018).
Comin, R. et al. Na2IrO3 as a novel relativistic mott insulator with a 340-mev gap. Phys. Rev. Lett. 109, 266406 (2012).
Modic, K. A. et al. Realization of a three-dimensional spin-anisotropic harmonic honeycomb iridate. Nat. Commun. 5, 4203 (2014).
Plumb, K. W. et al. α−RuCl3: a spin-orbit assisted mott insulator on a honeycomb lattice. Phys. Rev. B 90, 041112 (2014).
Sandilands, L. J. et al. Optical probe of Heisenberg-Kitaev magnetism in α−RuCl3. Phys. Rev. B 94, 195156 (2016).
Glamazda, A., Lemmens, P., Do, S.-H., Kwon, Y. S. & Choi, K.-Y. Relation between Kitaev magnetism and structure in α−RuCl3. Phys. Rev. B 95, 174429 (2017).
Zheng, J. et al. Gapless spin excitations in the field-induced quantum spin liquid phase of α−RuCl3. Phys. Rev. Lett. 119, 227208 (2017).
Kim, H.-S. & Kee, H.-Y. Crystal structure and magnetism in α−RuCl3: an ab initio study. Phys. Rev. B 93, 155143 (2016).
Winter, S. M. et al. Breakdown of magnons in a strongly spin-orbital coupled magnet. Nat. Commun. 8, 1152 (2017).
Do, S.-H. et al. Majorana fermions in the Kitaev quantum spin system α − RuCl3. Nat. Phys. 13, 1079–1084 (2017).
Sandilands, L. J. et al. Spin-orbit excitations and electronic structure of the putative Kitaev magnet α − RuCl3. Phys. Rev. B 93, 075144 (2016).
Zhou, X. et al. Angle-resolved photoemission study of the Kitaev candidate α − RuCl3. Phys. Rev. B 94, 161106 (2016).
Koitzsch, A. et al. Jeff description of the honeycomb mott insulator α − RuCl3. Phys. Rev. Lett. 117, 126403 (2016).
Nasu, J., Knolle, J., Kovrizhin, D. L., Motome, Y. & Moessner, R. Fermionic response from fractionalization in an insulating two-dimensional magnet. Nat. Phys. 12, 912–915 (2016).
Yan, S., Huse, D. A. & White, S. R. Spin-liquid ground state of the s = 1/2 Kagome Heisenberg antiferromagnet. Science 332, 1173–1176 (2011).
Knolle, J., Kovrizhin, D. L., Chalker, J. T. & Moessner, R. Dynamics of a two-dimensional quantum spin liquid: Signatures of emergent majorana fermions and fluxes. Phys. Rev. Lett. 112, 207203 (2014).
Chaloupka, J. c. v., Jackeli, G. & Khaliullin, G. Kitaev-Heisenberg model on a honeycomb lattice: possible exotic phases in iridium oxides A2IrO3. Phys. Rev. Lett. 105, 027204 (2010).
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018).
Banerjee, A. et al. Neutron scattering in the proximate quantum spin liquid α − RuCl3. Science 356, 1055–1059 (2017).
Rousochatzakis, I., Kourtis, S., Knolle, J., Moessner, R. & Perkins, N. B. Quantum spin liquid at finite temperature: Proximate dynamics and persistent typicality. Phys. Rev. B 100, 045117 (2019).
Leahy, I. A. et al. Anomalous thermal conductivity and magnetic torque response in the honeycomb magnet α − RuCl3. Phys. Rev. Lett. 118, 187203 (2017).
Jansa, N. et al. Observation of two types of fractional excitation in the Kitaev honeycomb magnet. Nat. Phys. 14, 786–790 (2018).
Yadav, R. et al. Kitaev exchange and field-induced quantum spin-liquid states in honeycomb α − RuCl3. Sci. Rep. 6, 37925 (2016).
Wang, Z. et al. Magnetic excitations and continuum of a possibly field-induced quantum spin liquid in α − RuCl3. Phys. Rev. Lett. 119, 227202 (2017).
Jansa, N. et al. Observation of two types of fractional excitation in the Kitaev honeycomb magnet. Nat. Phys. 14, 786–790 (2018).
Reiter, G. F. Light scattering from energy fluctuations in magnetic insulators. Phys. Rev. B 13, 169–173 (1976).
Fleury, P. A. & Loudon, R. Scattering of light by one- and two-magnon excitations. Phys. Rev. 166, 514–530 (1968).
Kim, K. et al. Suppression of magnetic ordering in XXZ-type antiferromagnetic monolayer NiPS3. Nat. Commun. 10, 345 (2019).
Zhou, B. et al. Possible structural transformation and enhanced magnetic fluctuations in exfoliated α − RuCl3. J. Phys. Chem. Solids 128, 291–295 (2019).
Misochko, O. V., Tajima, S., Urano, C., Eisaki, H. & Uchida, S. Raman-scattering evidence for free spinons in the one-dimensional spin-1∕2 chains of Sr2 CuO3 and SrCuO2. Phys. Rev. B 53, R14733–R14736 (1996).
Kuroe, H. et al. Spin fluctuations in CuGeO3 probed by light scattering. Phys. Rev. B 55, 409–415 (1997).
Nakamura, Y., Kato, R. & Kishida, H. Study of magnetic excitation in Pd(dmit)2 salts by raman scattering spectroscopy. J. Phys. Soc. Jpn 84, 044715 (2015).
Gretarsson, H. et al. Two-magnon raman scattering and pseudospin-lattice interactions in Sr2IrO4 and Sr3Ir2O7. Phys. Rev. Lett. 116, 136401 (2016).
Winter, S. M., Riedl, K., Kaib, D., Coldea, R. & Valentí, R. Probing α − RuCl3 beyond magnetic order: Effects of temperature and magnetic field. Phys. Rev. Lett. 120, 077203 (2018).
Nasu, J., Udagawa, M. & Motome, Y. Thermal fractionalization of quantum spins in a Kitaev model: Temperature-linear specific heat and coherent transport of majorana fermions. Phys. Rev. B 92, 115122 (2015).
Devereaux, T. P. & Hackl, R. Inelastic light scattering from correlated electrons. Rev. Mod. Phys. 79, 175–233 (2007).
Butcher, P. N. & Ogg, N. R. Fluctuation-dissipation theorems for driven non-linear media at optical frequencies. Proc. Phys. Soc. 86, 699–708 (1965).
Knolle, J., Chern, G.-W., Kovrizhin, D. L., Moessner, R. & Perkins, N. B. Raman scattering signatures of Kitaev spin liquids in A2IrO3 iridates with a = Na or Li. Phys. Rev. Lett. 113, 187201 (2014).
Tian, Y., Gray, M. J., Ji, H., Cava, R. J. & Burch, K. S. Magneto-elastic coupling in a potential ferromagnetic 2D atomic crystal. 2D Materials 3, 025035 (2016).
Kasahara, Y. et al. Unusual thermal hall effect in a Kitaev spin liquid candidate α − RuCl3. Phys. Rev. Lett. 120, 217205 (2018).
Wu, L. et al. Field evolution of magnons in α − RuCl3 by high-resolution polarized terahertz spectroscopy. Phys. Rev. B 98, 094425 (2018).
Majumder, M. et al. Anisotropic Ru3+4d5 magnetism in the α − RuCl3 honeycomb system: susceptibility, specific heat, and zero-field nmr. Phys. Rev. B 91, 180401 (2015).
Cao, H. B. et al. Low-temperature crystal and magnetic structure of α − RuCl3. Phys. Rev. B 93, 134423 (2016).
Lee, J.-U., Yoon, D., Kim, H., Lee, S. W. & Cheong, H. Thermal conductivity of suspended pristine graphene measured by raman spectroscopy. Phys. Rev. B 83, 081419 (2011).
Hirobe, D., Sato, M., Shiomi, Y., Tanaka, H. & Saitoh, E. Magnetic thermal conductivity far above the néel temperature in the Kitaev-magnet candidate α − RuCl3. Phys. Rev. B 95, 241112 (2017).
Ji, H. et al. A ferromagnetic insulating substrate for the epitaxial growth of topological insulators. J. Appl. Phys. 114, 114907 (2013).
Wellm, C. et al. Signatures of low-energy fractionalized excitations in α − RuCl3 from field-dependent microwave absorption. Phys. Rev. B 98, 184408 (2018).
Figgis, B. N., Lewis, J., Mabbs, F. E. & Webb, G. A. Magnetic properties of some iron(iii) and ruthenium(iii) low-spin complexes. J. Chem. Soc. A 422–426 (1966).
Mashhadi, S. et al. Electrical transport signature of the magnetic fluctuation-structure relation in α − RuCl3 nanoflakes. Nano Lett. 18, 3203–3208 (2018).
Majumder, M. et al. Breakdown of magnetic order in the pressurized Kitaev iridate β−Li2IrO3. Phys. Rev. Lett. 120, 237202 (2018).
Little, A. et al. Antiferromagnetic resonance and terahertz continuum in α − RuCl3. Phys. Rev. Lett. 119, 227201 (2017).
Tian, Y. et al. Low vibration high numerical aperture automated variable temperature raman microscope. Rev. Sci. Instrum. 87, 043105 (2016).
Tian, Y. & Burch, K. S. Automatic spike removal algorithm for raman spectra. Appl. Spectrosc. 70, 1861–1871 (2016).
Acknowledgements
We are grateful for numerous discussions with Natalia Perkins, Joshua Heath, Kevin Bedell and Ying Ran. The Raman experiments at 532 nm were performed by Y.W. with support from the National Science Foundation, Award No. DMR-1709987. G.B.O. assisted in the analysis with support from the U.S. Department of Energy (DOE), Office of Science, and Office of Basic Energy Sciences under Award No. DE-SC0018675. Raman experiments performed at 720 nm (T.G. and J.Y.) were achieved by support from the National Science Foundation, Award No. ECCS 1509599. The crystal growth and characterization of α-RuCl3 (P.L.K. and D.M.) with the Gordon and Betty Moore Foundation EPiQS Initiative through Grant GBMF4416. A.B. and S.E.N. were supported by the US DOE Basic Energy Sciences Division of Scientific User Facilities. The work on Cr2Ge2Te6 (H.J. and R.J.C.) at Princeton University is sponsored by an ARO MURI, grant W911NF1210461. The numerical simulations were performed by J.N. with support from Grants-in-Aid for Scientific Research (KAKENHI) (numbers JP15K13533, JP16H02206, JP16K17747, and JP18H04223). Parts of the numerical calculations were performed in the supercomputing systems in ISSP, the University of Tokyo.
Author information
Authors and Affiliations
Contributions
Y.W. performed the Raman experiments, with assistance from G.B.O., T.G., and J.Y. Analysis was done by Y.W., J.N., J.K., and G.B.O. The crystal growth and initial characterization were done by P.L.K., A.B., and D.M. The design of the experiments and conception of the study were achieved by K.S.B, S.E.N., and J.K. The theoretical calculations were performed by J.N., J.K., and Y.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Osterhoudt, G.B., Tian, Y. et al. The range of non-Kitaev terms and fractional particles in α-RuCl3. npj Quantum Mater. 5, 14 (2020). https://doi.org/10.1038/s41535-020-0216-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0216-6