Compact description of quantum phase slip junctions

Abstract

Quantum circuit theory is a powerful tool to describe superconducting circuits. In its language, quantum phase slips (QPSs) are considered to be the exact dual to the Josephson effect. This duality renders the integration of QPS junctions into a unified theoretical framework challenging. As we argue, different existing formalisms may be inconsistent, and the correct inclusion of time-dependent flux driving requires introducing a large number of auxiliary, nonphysical degrees of freedom. We resolve these issues by describing QPS junctions as inductive rather than capacitive elements, and reducing the Hilbert space to account for a compact superconducting phase. Our treatment provides an approach to circuit quantization exclusively in terms of node-flux-node variables, and eliminates spurious degrees of freedom. Finally, the inductive treatment reveals the possibility of a voltage-dependent renormalization of the QPS amplitude, by accounting for spatial variations of the electric field built up across the junction.

Introduction

Given the enormous potential of superconducting circuits for realizing large scale quantum computers^1,2, it is of utmost importance to provide a concise, yet powerful tool for their theoretical description. The paradigm of circuit quantum electrodynamics (cQED)^3,4,5,6,7 seems to provide just that: circuits are straightforwardly reduced to lumps, described by the canonically conjugate pair of total Cooper pair number N and superconducting phase φ, whose operators satisfy $[\widehat{N},\widehat{\varphi }]=i$.

Despite its widespread use, quantum circuit theory is still not quite without occasional teething troubles. For instance, it was very recently argued that a proper, realistic description of circuits driven via time-varying magnetic fields – an important means for addressing and manipulating superconducting quantum information hardware – requires going way beyond a simple lumped-element picture^8,9,10. One key insight of ref. ⁹ will be of particular relevance here: for devices involving Josephson junctions, the precise form of the electromotive force is not dominated by the junction self-capacitances (as was prior consensus), but depends on the device geometry and distribution of the magnetic field. As a consequence, loop constraints do not work as simply as commonly expected. The same school of thought has subsequently given rise to the notion of voltage-dependent renormalization of circuit parameters^10,11, which provides a nontrivial complication in the circuit quantization procedure¹⁰.

Deeply related to the above is the issue of charge quantization, respectively the compactness of the superconducting phase. Charge and phase being canonically conjugate, the quantization unit of N fixes the periodicity (compactness) of φ. While phase compactness and possible consequences of it are themes that have been studied long time ago^12,13,14, they have seen a revival in recent years in various contexts¹⁵, such as to understand charge noise sensitivity of quantum circuits^{16,17,18,19,20}, quantum dissipative phase transitions^{21,22,23,24,25,26,27,28}, the validity of the spin-boson paradigm²⁹, geometric aspects of current measurements³⁰ or flux-driving^9,10, as well as in topological phase transitions defined in the transport degrees of freedom^{31,32,33,34,35,36,37,38,39,40,41,42}. In particular, while symmetries and constraints are equivalent for a closed quantum system⁶, the community seems to be still divided on that subject for open quantum systems^26,27,28.

In this work, we take the above developments and persisting controversies as a context to revisit a particularly important and widely studied type of circuit element: the quantum phase slip (QPS) junction^{43,44,45,46,47,48,49,50,51,52,53}. In their influential work, Mooij and Nazarov⁴⁸ put forth the idea that QPS junctions can be described as a nonlinear capacitor $\sim \cos (2\pi N)$ and thus be considered as exact duals of regular JJs, $\sim \cos (\varphi )$. QPS junctions are now an integral part of the zoo of elements which may enter any quantum circuit diagram. Their understanding as a nonlinear capacitor was used to explain observed interference patterns with respect to applied gate voltages, interpreted as the circuit version of the Aharonov-Casher effect, a recurrent and important theme in superconducting circuits^51,54,55. Very recently, it gave rise to the prediction, that the Gottesman-Kitaev-Preskill (GKP) code⁵⁶ may be realized using only transport degrees of freedom⁵⁷.

However, there are some important issues with this simple description, especially when including non-linear capacitors into a cQED framework. Its standard formulation^4,5,7 is based on distinguishing between inductive and capacitive elements, whose respective energy contributions to the Lagrangian are treated as potential and kinetic energy terms, respectively. However, nonlinear capacitors give generally rise to nonconvex kinetic energy functions with non-invertible charge-voltage relationships. To cure such problems, an alternative formulation was given in ref. ⁶, based on loop charges (time-integral of loop currents). Here, the roles of inductive and capacitive elements are reversed (the former now being of kinetic nature). In alignment with the terminology of ref. ⁶, we refer to these two approaches as the node-flux and the loop-charge formalisms. However, in order for Josephson junctions (nonlinear inductors) and QPS junctions (nonlinear capacitors) to coexist, this formalism requires the combined use of node flux and loop charge variables.

In our work, we derive a description of QPS junctions different from existing approaches in three main points. First of all, instead of a capacitive treatement, we show that QPS junctions can be described as inductive elements with an intrinsic degree of freedom. This renders the description of QPS junctions compatible with node flux quantization without the need of loop charges, and as a consequence, allows for the inclusion of the aforementioned recent insights concerning time-dependent flux drive⁹. In particular, this significantly reduces the number of auxiliary degrees of freedom needed to describe a general circuit. Second, we derive a combined constraint on the phase and intrinsic QPS degrees of freedom consistent with the generalized requirement of charge quantization outlined in ref. ³⁰. This constraint limits the possible inductive couplings to a generic electromagnetic environment, and renders the predictions of basic thermodynamic quantities (such as the thermodynamic energy, entropy and heat capacity) consistent. Third, the combination of the two above innovations allows to take into account voltage-dependent renormalization of the QPS parameters similar in spirit to refs. ^10,11, which significantly changes the predicted energy spectrum of already quite simple circuits. Overall, our approach is able to account for both the Aharonov-Bohm and Aharonov-Casher effects in a unified picture, and provides important information on the available computational space for quantum information applications. Based on the latter, we refine the necessary conditions for the proposition by ref. ⁵⁷ to use QPS junctions for a realization of the GKP code. Finally, as outlined in the outlook, our approach is likely the starting point for an entire series of further revisions on the subject of QPS physics.

Results

Open issues in the state of the art and their solution

Circuit quantization is the leading paradigm to derive the Hamiltonian of an in principle arbitrary quantum circuit network. In its standard formulation^4,5,7,9, referred to as node flux quantization⁶, it considers the superconducting phases of the circuit nodes and the corresponding voltages, φ_j and ${\dot{\varphi }}_{j}$, and constructs a Lagrangian of the general form

$$L=T(\{{\dot{\varphi }}_{j}\})-V(\{{\varphi }_{j}\})\,,$$

(1)

where the energy stored in capacitive elements (whose energy depends on the voltage ${\dot{\phi }}_{j}$) is added to the kinetic energy, T, and elements of inductive nature (with an energy depending on the phase ϕ_j) are added to the potential energy V. To get to the Hamiltonian, one performs a Legendre transformation $H={\sum }_{j}{\dot{\varphi }}_{j}{N}_{j}-L$ with the canonically conjugated charge, ${N}_{j}={\partial }_{{\dot{\varphi }}_{j}}L$ (which, incidentally, provides the charge-voltage relationships of the involved capacitances) and subsequently promoting the variables to operators, ${\varphi }_{j},{N}_{j}\to {\widehat{\varphi }}_{j},{\widehat{N}}_{j}$, satisfying the charge-phase quantization condition $[{\widehat{\varphi }}_{j},{\widehat{N}}_{{j}^{{\prime} }}]=i{\delta }_{j{j}^{{\prime} }}$. Another important aspect is the treatment of externally applied time-varying fluxes – an indispensable tool for controlling quantum hardware. Only recently it was noticed^8,9 that care has to be taken with respect to gauge transformations. In the most general case, a convenient approach consists of computing the vector potential A in the so-called irrotational gauge, satisfying B = ∇ × A and ${{{{\bf{E}}}}}_{\dot{{{{\rm{B}}}}}}=-{\partial }_{t}{{{\bf{A}}}}$, where ${{{{\bf{E}}}}}_{\dot{{{{\rm{B}}}}}}$ is the part of the electric field induced by the time-dependent driving of the magnetic field (the electromotive force) satisfying the Maxwell-Faraday equation ∇ × E = − ∂_tB (where the device geometry fixes the boundary conditions for the fields). This vector potential enters inside the inductive elements connecting, e.g., nodes ϕ_j and ϕ_k as the equivalent of a Peierls phase, ${V}_{ik}({\phi }_{j}-{\phi }_{k})\to {V}_{ik}({\phi }_{j}-{\phi }_{k}+{\phi }_{{{{\rm{ext}}}}}^{ik})$ with ${\phi }_{{{{\rm{ext}}}}}^{ik}=2\pi /{{{\Phi }}}_{0}{\int}_{{{{{\mathcal{L}}}}}_{jk}}d{{{\bf{l}}}}\cdot {{{\bf{A}}}}$, where ${{{{\mathcal{L}}}}}_{jk}$ denotes the path Cooper pairs have to take to travel from note k to node j and Φ₀ is the flux quantum. For circuit elements with intrinsic degrees of freedom, it has already been shown for the example of Majorana-based junctions^10,11, that the electromotive force leads to the renormalization of the junction parameters depending on the voltage ${\dot{\phi }}_{j}-{\dot{\phi }}_{k}$. These terms modify the charge-voltage relationship in a nontrivial way, and give, e.g., rise to significant changes in the quantum charge fluctuations¹⁰.

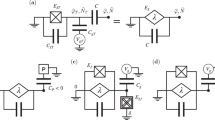
It has already been understood, that the above node flux approach is problematic for quantum phase slip (QPS) junctions. As argued by Mooij and Nazarov⁴⁸, the physics of a QPS junction can be regarded as the exact dual to the Josephson effect, and captured in an energy term resembling a nonlinear capacitor, $-{E}_{{{{\rm{S}}}}}\cos (2\pi {N}_{j})$. One therefore would have to find a corresponding kinetic energy as a function of the voltage ${\dot{\phi }}_{j}$, which, after the Legendre transformation, results in exactly this $\sim \cos (2\pi {N}_{j})$ term. Such a candidate function was proposed in⁵⁷, but it turns out to be a nonconvex function, such that the Legendre transformation is not defined, and the charge-voltage relationship cannot be inverted (unless a parallel shunt with a linear capacitance with sufficiently high charging energy is added⁵⁷). Ulrich and Hassler proposed an alternative circuit quantization procedure relying on loop charges ${N}_{j}^{\circ }$, respectively on loop currents, ${\dot{N}}_{j}^{\circ }$ (throughout this work, we use the notation X^∘ for quantitites X that are specific to the loop-charge quantization procedure). For a given circuit, one identifies its loops instead of its nodes (see Fig. 1c, d), and assigns the corresponding energy contributions from each element, to add it to a Lagrangian L^∘ which is now a function of ${N}_{j}^{\circ }$ and ${\dot{N}}_{j}^{\circ }$. Here, inductive and capacitive elements play inversed roles compared to Eq. (1), i.e., the former (latter) now contributes to the kinetic (potential) energy. Likewise, the canonical loop phase is defined as ${\varphi }_{j}^{\circ }={\partial }_{{\dot{N}}_{j}^{\circ }}{L}^{\circ }$ (flux-current relationships), and quantization is achieved in the same manner, $[{\widehat{\varphi }}_{j}^{\circ },{\widehat{N}}_{{j}^{{\prime} }}^{\circ }]=i{\delta }_{j{j}^{{\prime} }}$. In the loop charge picture, there is now no more issue regarding the nonlinear capacitor, as the energy term ${E}_{{{{\rm{S}}}}}\cos (2\pi {N}_{j}^{\circ })$ can directly enter the potential energy of L^∘ and is unaffected by the Legendre transformation (up to a change of the minus sign). But due to the duality between quantum phase slips and the Josephson effect, solving the nonlinear capacitor problem comes at the expense of difficulties to describe regular Josephson junctions and other nonlinear inductor elements. Reference⁶ showed that it is possible to include both QPS and Josephson junctions in a mixed picture involving both loop charges and node fluxes, see Fig. 1c, d. Note however, that in order for this mixed approach to work, the junction self-capacitances must be nonzero – otherwise one encounters divisions by zero on the way to the Hamiltonian (in the form of noninvertible charge-voltage relationships).

Fig. 1: Issues related to time-dependent flux control, exemplified with the dc-SQUID.

Conventionally, the dc-SQUID is represented as in (a), where each Josephson junction has a finite self-capacitance. However, as shown in ref. ⁹, the capacitively shunted Josephson junction picture does not hold in general for time-varying magnetic fields, and external fluxes have instead to be attached to the bare junctions (b), while there is only a single bulk capacitance C_tot. The loop-charge based quantization procedure⁶ can only include Josephson junctions in a mixed node/loop picture, requiring extra capacitive shunts for each junction as well as auxiliary inductances. Depending on whether the dominant island capacitance is distributed between the junctions C₁ and C₂ (c), or described as the single bulk capacitance C_tot = C₁ + C₂ (d), the number of auxiliary degrees of freedom changes. The version with a lower number of degrees of freedom (c) may suffer from spurious instabilities due to the fact that effective junctions capacitances (either C₁ or C₂) may be negative⁹.

This last point already brings us to the first issue, related to external fluxes and their connection to loop constraints. Prior to the work of ref. ⁹, it was common to assign to each junction (or generally to each inductive element) a nonzero self-capacitance. In particular for the problem of the dc-SQUID, this self-capacitance, in conjunction with a pure lumped element treatment of externally applied time-varying fluxes, led to the prediction by You, Sauls and Koch⁸, that the electromotive force term depends on the relative strength of the self-capacitances of the two junctions in the dc-SQUID. As pointed out in ref. ⁹, this statement is only true for a subset of device geometries. If the electrostatics is dominated by the bulk (which is, e.g., commonly the case in transmons⁵⁸) then, this result breaks down. In the most general case, there is only a physically meaningful capacitive energy between different bulk charge islands, and the total resulting bulk capacitance cannot be distributed among the different inductive elements connecting to the given bulk island – unless one introduces effective junction self-capacitances, which can be either negative, time-dependent or even momentarily singular⁹. As we show in more detail later, this has significant impact on the concept of the mixed loop charge/node flux formalism introduced by ref. ⁶. In short, within this formalism, we might choose to stick to effective junction capacitances, which however fails for negative effective capacitances, as they create problematic bosonic Hamiltonians with no lower bound, and a generally complex eigenspectrum. This problem can be avoided by introducing dominant bulk capacitances, which provide regular, bounded Hamiltonians. However, due to the aforementioned division-by-zero problem, one needs to keep finite self-capacitances for Josephson junction elements within the construction of the Lagrangian, which can only be set to zero at the very end on the Hamiltonian level. Therefore, one has to carry around a large amount of auxiliary degrees of freedom to describe the circuit, leading to a significant theoretical overhead (see, e.g., Fig. 1d).

The other main issue concerns the relationship between discrete symmetries and compact constraints on wave functions. In particular, if the superconducting phase φ is constrained to be compact, it follows that the canonically conjugate charge N is integer. Specifically for QPS junctions, the capacitive treatment with an energy term $\sim \cos (2\pi N)$ can only provide nontrivial dynamics if the charge N is allowed to assume noninteger values. One therefore has to wonder, how charge quantization, understood to be a fundamental property of non-relativistic quantum field theory^{30,59,60,61,62,63,64}, can be reconciled with it. This issue can likewise be illustrated without the explicit involvement of QPS junctions. Take the example of the well-known charge qubit Hamiltonian⁶⁵,

$${H}_{{{{\rm{C,J}}}}}={E}_{{{{\rm{C}}}}}{\left(\widehat{N}+{N}_{{{{\rm{g}}}}}\right)}^{2}-{E}_{{{{\rm{J}}}}}\cos (\widehat{\varphi })\,,$$

(2)

with $[\widehat{N},\widehat{\varphi }]=i$. The capacitive energy is E_C = 2e²/C_tot (C_tot = C + C_g, with the junction self-capacitance C and the gate capacitance C_g) and the Josephson energy E_J = I_c/2e (where ℏ = 1), proportional to the junction’s critical current I_c. The parameter N_g represents the gate-induced offset charge on the island, N_g = C_gV_g/2e, where V_g is the applied voltage.

The symmetry H_C,J(φ + 2π) = H_C,J(φ) expresses the fact that the junction transports Cooper-pairs in integer portions. But if this discrete symmetry was the only relevant ingredient, we would find (according to Bloch’s theorem) continuous energy bands with a wave vector k as a quantum number, that is, ${H}_{{{{\rm{C,J}}}}}\left\vert {\psi }_{n}(k)\right\rangle ={E}_{n}(k)\left\vert {\psi }_{n}(k)\right\rangle$. Related to that, any stationary contribution to the gate-induced offset charge N_g could be gauged away by means of a time-independent unitary transformation. In order to correctly predict the experimentally well-established N_g-dependence^66,67,68,69, and discrete energies instead of energy bands, one needs to impose an additional symmetry constraint on the wave function itself, $\left\vert \psi (\varphi +2\pi )\right\rangle =\left\vert \psi (\varphi )\right\rangle$; with this constraint we obtain the eigenenergies E_n(N_g) instead of E_n(k)⁶⁵. This can be understood as an inverted Bloch theorem. The additional constraint on the wave function selects out the k vector which is consistent with having N_g as the equivalent of the vector potential. The latter is no longer a gauge degree of freedom: when progressing in φ-space by 2π the system returns to the same state (because φ now lives on the circle), and thus self-interferes while picking up the phase ${e}^{i2\pi {N}_{{{{\rm{g}}}}}}$.

In the literature, there however persists a lack of consensus with regard to symmetries versus constraints, which has not yet been resolved in spite of it being an old and well-known problem^13,14. In ref. ⁶ it was argued that the discrete symmetry in the Hamiltonian and the symmetry constraint on the wave function can be considered equivalent. This statement is valid for closed quantum systems in the following sense. Namely, one can fix a given Bloch vector at some initial time t₀ → − ∞, which must stay the same throughout the whole time-evolution. Thus, one could in principle identify the constant k vector as the external parameter N_g without having to explicitly impose boundary conditions on the wave function. Crucially, however, a realistic account of any type of quantum hardware requires an understanding of the system including an environment. Therefore, let us here first point out that for open quantum systems, constraints and symmetries are not interchangeable. We illustrate this point for the example Hamiltonian in Eq. (2) in two different ways: first, by considering an explicit inductive coupling to an external electromagnetic environment, and second by means of general thermodynamic considerations. For the inductive coupling, consider both the extended and the compact version of the charge qubit, which can be understood as a particle moving on an extended 1D line in a cosine potential, or respectively, as a pendulum subject to earth’s gravity, see Fig. 2. The presence of an external electromagnetic field coupling to the circuit can now be visualized by means of a generic additional force field acting on the particle. Crucially, if we impose no constraints on the force field, then the two systems behave diametrically different. Namely, in the extended system, the force field can in general break the discrete symmetry of the cosine potential, and thus break the conservation of the aforementioned Bloch vector. In particular, a generic ac drive of the external force can drive intraband transitions, such that the response function of the circuit would have continuous bands. If we insist on the 2π-periodic constraint on the other hand, the force field cannot break 2π-periodicity, as there is simply not enough available Hilbert space. The response to an ac drive here reveals a discrete spectrum.

Fig. 2: Different perspectives on the phase space representation of the charge qubit Hamiltonian.

a describes the 2π-periodic phase space, where we consider the Hamiltonian to be analogous to a particle in a cosine potential. b considers the Hamiltonian to be the analogous to a pendulum in a gravitational field, which corresponds to the compact phase space representation. The difference between the two representations becomes apparent if we consider an external force field F_e. In case (a) F_e can break the 2π-periodicity, where in case (b) the same is not possible, since the periodicity is a property of the system itself.

The same fact can be expressed equivalently in terms of generic thermodynamic considerations. For this purpose, take the partition function $Z={{{\rm{tr}}}}[{e}^{-\beta H}]$, where β = 1/k_BT is the inverse thermal energy and T is the temperature. Well-known thermodynamic quantities derived from Z are, e.g., the Helmholtz free energy $A={\beta }^{-1}\ln Z$, the entropy S = −∂_TA or the heat capacity C_ν = T∂_TS. The partition function is distinctly different for the compact and the extended system, either yielding ${Z}_{{{{\rm{c}}}}}({N}_{{{{\rm{g}}}}})={\sum }_{n}{e}^{-\beta {E}_{n}({N}_{{{{\rm{g}}}}})}$ or $Z=\int\,dk{\sum }_{n}{e}^{-\beta {E}_{n}(k)}$ (where the subscript c indicates the compact version of Z). In particular, the former depends on N_g, contrary to the latter, which does not. The two results are per se compatible only if we assume that N_g fluctuates slowly (such that after each change of N_g the system has time to relax to thermal equilibrium), and that thermodynamic quantities can only be measured over times slower than the fluctuations of N_g. Then, if on average all values of N_g are equally likely, we get $\sim {\int} dN_{g} Z_{c}(N_{g})\,=\,Z$. Note that we have omitted the fact that if we take an average over N_g by means of a normalized probability distribution, the time-averaged Z_c and Z are equivalent only up to a divergent prefactor. This is however unproblematic, as for all relevant thermodynamic quantities (Helmholtz energy, heat capacity, changes in entropy) this prefactor cancels.

If the thermodynamic quantities are measured on shorter time-scales than the fluctuations of N_g, then, we cannot obtain the correct partition function with symmetries only. As a last resort, one might try to invoke a breaking of ergodicity, observed in a variety of different systems^{70,71,72,73,74,75}, by which the charge qubit could not explore the entire (noncompact) phase space (keeping the k fix even for the open system). Such sophisticated arguments are however not required: for the charge qubit, the island can at low temperatures only host integer number of Cooper pairs – a result that follows from basic field theoretic considerations without the need of invoking ergodicity breaking^30,60. The compact constraint on the wave function is thus the simplest possible approach to make correct, generic predictions about the circuit coupled to an environment, without requiring detailed knowledge about the latter.

While charge quantization in integer portions of the Cooper pair for an island coupled via a Josephson junction is straightforward to derive, more complicated circuit elements provide a more sophisticated picture, and in particular, may add intrinsic degrees of freedom, which do not live within the superconducting bulk but at the interface between two superconductors, see, e.g., Majorana-based junctions^10,11,76. However, even for these circuits, there must generally exist a basis choice with compact φ as long as there exists a condensate with an integer number of Cooper pairs^30,76. Changing between different basis choices (which may be necessary to truncate to the low-energy degrees of freedom) was shown to give rise to the aforementioned $\dot{\varphi }$-dependent renormalization of circuit parameters^10,10, and thus adds a nontrivial component to the charge operator following from canonical quantization¹⁰.

In this work, we revisit quantum phase slip junctions under exactly this light, that is, by taking into account quantization of the local charge operator, and including an intrinsic junction degree of freedom counting the number of phase slips. Overall, we accomplish the following.

• (i) We establish a pure node flux treatment of a QPS junction, viewing it as an inductor with intrinsic freedom rather than a nonlinear capacitor.

• (ii) We derive the correct constraint on the wave function, fixing the available degrees of freedom at a microscopic level.

• (iii) We identify a renormalization of the QPS amplitude due to a nontrivial coupling with a capacitive shunt.

As already indicated above, (i) is important when including time-dependent flux driving. In particular, our proposed node flux picture allows minimizing the number of degrees of freedom required to accurately describe a time-dependently driven circuit. (ii) allows us to derive a generalized constraint for the wave function describing circuits involving QPS junctions, paramount to provide unambiguous predictions for the device as an open quantum system, crucially without the need for a detailed description of the environment. Moreover, we will show that the constraint is also important to accurately predict the available computational space if the device is used for quantum information processing purposes. (iii) allows us to take into account details on how (with what spatial resolution) a capacitance in parallel to the QPS junction, or any other field or measurement device couples to the transported charge across the junction. As already stated, this effect stems from a dynamically renormalized amplitude for quantum phase slips (an effect similar to what has recently been predicted in Majorana-based junctions^10,11). The treatment presented in this work is valid for a weak renormalization. The correct quantization procedure for strong renormalization goes beyond the scope of the current work, and will be tackled in the future.

As a final note, while dissipative quantum phase transitions are not the main focus of our work, our treatment nonetheless allows to comment on certain aspects which are currently hotly debated for Josephson junctions²⁶, and how they might be related to QPS junctions. In particular, in ref. ²⁶ some tentative arguments are presented, as to why the observed absence of the transition in Josephson junctions could be related to whether the normal metal bath preserves or violates phase compactness. We note that this work was not received without controversy^27,28, and has spurred a number of follow-up works with differing results, both on the theoretical⁷⁷ and the experimental⁷⁸ side. At any rate, we expect (ii) to be important to limit the allowed forms of a generic inductive coupling to an environment for circuits involving QPS junctions. Future works will shed more light on possible repercussions of this observation for predictions regarding Ohmic dissipation.

Inductive treatment of the QPS junction

We now derive the low-energy physics of the QPS junction within a purely inductive picture, and compare its features with other currently accepted treatments. While QPS wires may be realized in a number of ways, our discussion is aimed at features which are the same, irrespective of the experimental realization.

Consider the isolated QPS junction, which is only contacted to two superconducting lumps. We assume that one of the lumps has phase zero (ground), and the other phase φ (Fig. 3a, b). In principle, one might write down a full microscopic Hamiltonian description of the wire by means of a Hamiltonian H_QPS(φ), where H_QPS could, e.g., be derived from the Gor’kov Greens function⁷⁹. However, such an approach would be obviously unfeasible, which is why a suitable low-energy approximation has to be found. Inspired by existing treatments, we revisit this path step by step. In this revision, we want to keep two properties which are commonly neglected. First, the full microscopic Hamiltonian H_QPS is 2π-periodic in φ, due to fundamental charge quantization in the bulk. Secondly, while the wire has intrinsic physics, the bulk phase φ stays constant, unless the wire is integrated into a larger circuit.

Fig. 3: Compact versus extended descriptions of quantum phase slips along a QPS junction.

The two ends are phase biased by φ (the left contact is the ground with phase 0). The extended phase profile in (a) can be projected to a 2π-periodic profile in (b). While it seems that picture (a) is the one motivating the standard Hamiltonian description by Mooij and Nazarov, we argue in the main text that an extended picture for the phase may lead to too large a Hilbert space including spurious states which are represented in neither (a) nor (b). Depiction of two possible measurements of charges transported across the QPS junction in (c), the quantized charge N and the continuous charge $\widetilde{N}$. While the quantized charge N is effectively eliminated in the course of the low-energy approximation, its presence is nonetheless felt as a topological constraint on the Hilbert space.

First, in the absence of actual phase slips, it is understood that the connecting wire has a spatially varying local phase profile, linearly ramping the phase up from zero to φ, see Fig. 3. This linear profile is the classical solution minimizing the internal energy of the wire, on top of which there may be local fluctuations. For a continuous wire, the frequency of local fluctuations can be estimated by means of the parameters of the Nambu-Goldstone mode⁷⁹, which (in 1D) can be interpreted as a capacitive and an inductive density c and l of the wire. For Josephson junction arrays, this minimization works in a very similar way (see, e.g., ref. ¹⁸), where the densities l and c can be related to the junction energies, respectively, the capacitances in the array (mostly the capacitance to ground for sufficiently long arrays⁸⁰). Neglecting local fluctuations is therefore justified when considering energies below the superconducting plasmon frequency ${\omega }_{{{{\rm{p}}}}} \sim \sqrt{lc}d$, where d is the wire length. Within the same framework, we can estimate also the energy associated to the strain due to the linear phase profile, which provides us with an inductive energy of the wire, ~ E_Lφ², with E_L = 1/(8e²dl). The following low-energy description of QPS junctions is in particular justified when E_L ≪ ω_p (we remind that ℏ = 1).

As for quantum phase slips, they have been historically first understood as a quantum analogy of the classical, thermally activated phase-slips described by means of Ginzburg-Landau theory, see ref. ⁴³ (and references therein). Within Ginzburg-Landau, the superconducting phase profile inside the wire, φ(x), is by construction compact for each x, such that there is not one unique solution to the minimization profile of the phase inside the wire but many distinct (in a field-theoretic sense local) minimum solutions, which can be parametrized as $f\in {\mathbb{Z}}$ kinks in the phase profile (see Fig. 3b). In order to arrive at the current state-of-the art description of quantum phase slips^6,48, the phase profile with kinks is mapped to a new, extended phase profile, where the phase value of φ is copied by multiple integers of 2π (see Fig. 3a). We note that while the former picture can be obtained from the latter via a projection (taking the phase modulo 2π), the two pictures strictly speaking do not conserve the size of the Hilbert space, since the local phase is either compact or not. Throughout our work, we show that compact and extended representations of the physics of QPS junctions can to a certain degree be mapped into one another, but for a variety of question, care has to be taken not to introduce spurious states into the description.

In the quantum regime the system may now coherently jump between these different minima, to which we assign the energy E_S. In the existing literature, a lot of effort went into finding accurate predictions for the value of E_S, especially for Josephson junction arrays^81,82, including off-set charge fluctuations within the array, which give rise to a temporally fluctuating value for E_S⁵⁵, or in a very large array limit, where off-set charge disorder was argued to lead to strong values for E_S⁸⁰. In the presence of offset charges, the QPS energy becomes in general complex, ${E}_{{{{\rm{S}}}}}\cos (2\pi N)\to ({E}_{{{{\rm{S}}}}}{e}^{i2\pi N}+{{{\rm{h.c.}}}})/2$ with⁵⁵

$${E}_{{{{\rm{S}}}}}=\mathop{\sum}\limits_{j}{E}_{{{{\rm{S}}}}}^{(j)}{e}^{i2\pi {N}_{{{{\rm{g}}}}}^{(j)}}\,,$$

(3)

where ${E}_{{{{\rm{S}}}}}^{(j)}$ is the local QPS amplitude for junction j within the array, and ${N}_{{{{\rm{g}}}}}^{(j)}$ is the local offset charge added to island j. We here focus on revisiting the topology and size of the Hilbert space, while assuming E_S (for the most part) as a given value, or a fitting parameter. Nonetheless, the above equation will reappear in our considerations later, to provide an example of a voltage-induced renormalization of E_S, which naturally occurs in our formalism.

As we show now, there are subtle, but important differences, depending on whether the compact or extended picture is deployed. While our main goal is to remain in the compact picture, let us first summarize the currently accepted state of the art description by means of the extended picture (Fig. 3a). Here, one obtains the capacitive interpretation of the phase slip processes: jumps of φ by 2π are naturally expressed in terms of the jump operator ${e}^{-2\pi {\partial }_{\varphi }}$. Given that [N, φ] = i is satisfied by N = i∂_φ, and summing over quantum jumps in both directions, we get the $\cos (2\pi N)$ energy term discussed above. The energy penalty due to the strain in the phase profile, giving rise to the inductive energy E_L is accounted for by putting a linear inductor in series with the ideal QPS junction⁴⁸. Following the loop charge quantization procedure⁶, this circuit is described by the Lagrangian ${L}^{\circ }={\left({\dot{N}}^{\circ }\right)}^{2}/(4{E}_{{{{\rm{L}}}}})+{E}_{{{{\rm{S}}}}}\cos (2\pi {N}^{\circ })$, which, after Legendre transformation ${\dot{N}}^{\circ }{\partial }_{{\dot{N}}^{\circ }}{L}^{\circ }-L$, results in the Hamiltonian

$${H}_{{{{\rm{QPS}}}}}^{\circ }={E}_{{{{\rm{L}}}}}{\left({\varphi }^{\circ }\right)}^{2}-{E}_{{{{\rm{S}}}}}\cos (2\pi {N}^{\circ })\,,$$

(4)

with the canonically conjugate loop phase ${\varphi }^{\circ }={\partial }_{{\dot{N}}^{\circ }}{L}^{\circ }={N}^{\circ }/(2{E}_{{{{\rm{L}}}}})$. Already on this level, we can observe a peculiarity: as stated at the outset, the superconducting phase φ is in principle an externally fixed parameter (which, if we close the two contacts into a loop, can be controlled by an externally applied flux), whereas in the above loop charge Hamiltonian, it is a dynamic quantity (due to the 2π jumps). However, just like in the charge qubit Hamiltonian, Eq. (2), there is a discrete symmetry, ${H}_{{{{\rm{QPS}}}}}^{\circ }({N}^{\circ }+1)={H}_{{{{\rm{QPS}}}}}^{\circ }({N}^{\circ })$, which gives rise to a conserved Bloch vector. According to the argument provided by ref. ⁶, this Bloch vector can in the closed system be interpreted as the externally applied flux, or simply the fixed phase bias across the QPS junction. But as we have already argued in the previous section, this is only true for the closed system.

Let us therefore now rederive the low-energy approximation of the QPS Hamiltonian keeping phase compactness, according to Fig. 3b. Here, the phase difference φ does not change as a consequence of the intrinsic physics inside the wire, justifying the inductive treatment of the QPS junction. In fact, an early version of the Hamiltonian we are after was already present in ref. ⁴⁸. Taking f as the number of kinks in the phase profile and associating to each local minimum the quantum state $\left\vert f\right\rangle$, the low-energy Hamiltonian description can instead be given as

$$\begin{array}{ll}{H}_{{{{\rm{QPS}}}}}\,=\,-\frac{{E}_{{{{\rm{S}}}}}}{2}\mathop{\sum}\limits_{f}\left(\left\vert f\right\rangle \left\langle f-1\right\vert +\left\vert f-1\right\rangle \left\langle f\right\vert \right)\\ \qquad\quad\;\;\;\;+\,{E}_{{{{\rm{L}}}}}\mathop{\sum}\limits_{f}{\left(\varphi +2\pi f\left\vert f\right\rangle \left\langle f\right\vert \right)}^{2}\,,\end{array}$$

(5)

where the quantum coherent phase slips are included in the E_S-term.

For a constant value of φ, the Hamiltonian in Eq. (5) provides the correct low-energy spectrum, and contains directly the right size of the Hilbert space (without requiring symmetry arguments), as there is only the discrete degree of freedom f. Crucially, however, an important detail has so far been missing in Eq. (5), which becomes relevant once we start varying φ (i.e., once the QPS junction is integrated into a larger circuit). Namely, if we allow for a Hilbert space where the discrete quantum number f coexists with a noncompact φ ($\varphi \in {\mathbb{R}}$), shifting φ by 2π (and keeping f constant) would actually give rise to a state distinct from the one where we leave φ constant and instead shift f by 1. However, given the phase profile in Fig. 3b we understand that this cannot be. For distinct f, φ can only meaningfully assume values within a 2π-periodic interval (e.g., φ ∈ [ −π, π)).

To continue, we fix the Hamiltonian, such that it does not overcount the available low-energy states. In the compactified picture, the reduction of the Hilbert space can be readily performed by endowing the basis $\left\vert f\right\rangle$ with a phase dependence $\left\vert f\right\rangle \to {\left\vert f\right\rangle }_{\varphi }$, such that

$${\left\vert f\right\rangle }_{\varphi \pm 2\pi }={\left\vert f\pm 1\right\rangle }_{\varphi }\,.$$

(6)

As a matter of fact, this φ-dependence of the phase slip states could have been derived also on the level of the minimization problem of the wire phase profile. Namely, if we understand $\left\vert f\right\rangle$ as a representation of the wave function of the phase profile inside the wire, then it becomes clear that the wave function must be φ-dependent in exactly the way we just stated (see also the Supplementary Material, where we discuss this fact for a discrete realization of the QPS junction via Josephson junction arrays). If we now want to cast the physics related to f into the framework of canonically conjugate charge and phase variables, we have to explicitly keep the φ-dependence in the notation – at least initially. As we show in a moment, there is a particular way in which the basis dependence can be dealt with. For now, we therefore get

$${H}_{{{{\rm{QPS}}}}}^{{{{\rm{c}}}}}=-{E}_{{{{\rm{S}}}}}\cos \left({\widehat{S}}_{\varphi }\right)+{E}_{{{{\rm{L}}}}}{\left(\varphi +2\pi {\widehat{f}}_{\varphi }\right)}^{2}\,.$$

(7)

Note that ${e}^{i\widehat{S}}={\sum }_{f}\left\vert f\right\rangle \left\langle f-1\right\vert$ and $\widehat{f}={\sum }_{f}f\left\vert f\right\rangle \left\langle f\right\vert$ still fulfill the ordinary commutation relations $[{e}^{i\widehat{S}},\widehat{f}]=-{e}^{i\widehat{S}}$, in spite of the φ-dependent basis. For φ externally fixed, the Hamiltonians H_QPS and ${H}_{{{{\rm{QPS}}}}}^{{{{\rm{c}}}}}$, given in Eqs. (5, 7), provide the same energy spectrum as a function of φ, see Fig. 4a–d. Without phase slips (E_S = 0, see Fig. 4a, b), the eigenenergies are simply given by the parabolas due to the ordinary kinetic term ( ~ E_L). With finite E_S, the parabolas hybridize, inducing a gapped spectrum (Fig. 4c, d). One of the crucial differences between the two Hamiltonians is that Eq. (5) allows for the creation of spurious extra states, by copy-pasting the spectrum to an extended phase φ (Fig. 4a, c). In Eq. (7), only the spectrum for a compact φ exists. The other central difference is the φ-dependence of the basis. While of course both of these differences are immaterial for an externally fixed φ, they matter as soon as φ becomes dynamical, as we show now.

Fig. 4: Comparison between compact and noncompact node-flux descriptions of the physics of QPS junctions.

The noncompact energy spectrum, Eq. (5), is shown either for E_S = 0 (a) or E_S ≠ 0 (c). In (b, d) we depict the spectrum of our proposed compact description, Eq. (7), for the same set of parameters. Locally, both Hamiltonians provide the same spectrum. Globally however, the noncompact picture yields periodically repeated copies of the same spectrum with extended φ. When shunting the QPS junction with a linear capacitance, see Fig. 5b, the phase becomes dynamical, leading to various possible trajectories, represented by the red arrows. For E_S = 0 (a, b) the dynamics of the compact and noncompact description are equivalent, because the system simply stays within the same parabola. Matters are different for finite E_S (c, d). Here, the compact description predicts trajectories where the system state can self-interfere (marked with a yellow star). Such trajectories do not exist in the noncompact description. As a consequence, the offset charge N_g can no longer be removed by a gauge transformation (see main text). For a single QPS junction with a capacitive coupling, the physical picture of the compact node-flux formalism and the standard loop-charge formalism are the same: the latter follows from the former by means of a decompactification of the φ-space. The compact and noncompact description are related by an inverted Bloch theorem, where for the continuous Bloch band, see (e), the Bloch wave vector gets replaced by the external parameter N_g, see (f). For the latter, there can only be discrete excitations.

In particular, we now aim to provide a quantizable theory where there is a meaningful way to integrate the QPS Hamiltonian into a larger circuit, and provide a Hamiltonian for the full circuit with [N, φ] = i. In this regard, the conservation of the size of the Hilbert space, came at a cost of a considerable complication: the explicit φ-dependence of the f-basis. Therefore, the next crucial step is to understand how to correctly quantize with respect to φ, for a generic circuit including QPS junctions. In order to tackle this problem, we rely on a technique recently also deployed in other circuit elements^10,11,83, where the explicit phase-dependence of the basis is first transformed away within a unitary transformation $U(\phi )={\sum }_{f}\vert \widetilde{f}\rangle {\left\langle f\right\vert }_{\varphi }$ to a new basis $\vert \widetilde{f}\rangle$ which is constant in φ. This has the following consequences. First of all, the full QPS Hamiltonian receives an extra correction term due to $\dot{\varphi }$ being nonzero, ${H}_{{{{\rm{QPS}}}}}\to U{H}_{{{{\rm{QPS}}}}}{U}^{{\dagger} }-i\dot{\varphi }U{\partial }_{\varphi }{U}^{{\dagger} }$. The effect of this term has to be included in the low energy approximation. For the concrete realization with Josephson junction arrays, this can be done explicitly. Namely, the unitary transformation here gives rise to voltage dependent shift of the offset charges reaching into the QPS wire (the array), i.e., ${N}_{{{{\rm{g}}}}}^{j}\to {N}_{{{{\rm{g}}}}}^{j}+{\alpha }_{j}\dot{\varphi }$ (for details see the the Supplementary Material). Based on Eq. (3), it is now evident, that we receive a dynamical renormalization of the QPS energy scale ${E}_{{{{\rm{S}}}}}\to {E}_{{{{\rm{S}}}}}(\dot{\varphi })$. In fact, the prefactors α_j depend on where within the full microscopic H_QPS the phase difference φ is allocated – that is, they depend on how the electric field is distributed across the QPS junction, when separating charges. Related effects have recently been studied for Josephson junction arrays subject to an external, classical flux drive, see ref. ⁸⁴. Our treatment is a significant generalization of this principle, because within the circuit quantization paradigm the dynamics of φ is not necessarily governed by a classical external drive, but by the quantum dynamics of the phase due to a capacitive coupling. For a capacitive coupling, the prefactors α_j express the spatial profile which which the capacitance measures the charge transported across the QPS junction. Two extremal scenarios are depicted in Fig. 3c. If the capacitor couples to the charge that has a finite blurry support reaching linearly within the wire, there is no renormalization (all α_j = 0). Interpreting the spatial profile as a probability distribution, ref. ³⁰ proposes a Rényi entropy measure, by which this charge is maximally blurry, in the sense that it maximizes this entropy. If on the other hand, the capacitor couples to a different spatial charge profile, then a renormalization is present. For instance, if the capacitor couples to the charge sharply localized at the right contact, then we find α_j ~ j/J where J is the total number of Josephson junctions comprising the QPS junction (see the Supplementary Material). Given the generality of the above discussion, we expect that this feature is present not only for junction arrays, but also if the QPS junction is made of a thin superconducting wire. However, to the best of our knowledge there currently exists no feasible microscopic theory, by which this renormalization could be quantitatively evaluated for bulk superconductors. Future research shall be dedicated to answer this question. At any rate, the renormalization is, e.g., experimentally observable in a voltage-biased QPS junction, as it modifies the Landau-Zener probability at the phase slip degeneracy points (e.g., where the states f and f ± 1 have the same inductive energy). Later, we show how this renormalization changes the energy spectrum of a capacitively shunted QPS junction.

The second important consequence of the unitary transformation has to do with the size of the low-energy Hilbert space. Namely, the transformation can be understood as a local flattening of the basis. Note however, that we are yet again at risk of creating spurious states in the Hilbert space, because the global 2π-periodic property, Eq. (6), would be lost in the new basis, if we just naively continued to flatten indefinitely. Therefore, we need to reinsert this constraint on the level of the circuit’s low-energy wave function. We do so by defining an arbitrary interval with length 2π for φ, e.g., φ ∈ ( − π, π], at the boundaries of which states with neighbouring f are stitched together, according to Eq. (6). The details of wave function constraint will be given explicitly in a moment. The constraint can be understood as follows: if some circuit element induces dynamical changes to the phase difference across the QPS junction (e.g., a capacitive shunt), changes of φ by multiples of 2π must necessarily come with a winding of the wire’s phase profile, and thus changes f by an integer.

We are thus finally at the point where we can combine all ingredients. Given a general circuit Lagrangian in Eq. (1), a QPS junction connecting nodes φ_j and φ_k, the low-energy QPS Hamiltonian

$${H}_{{{{\rm{QPS}}}}}=-{E}_{{{{\rm{S}}}}}({\dot{\varphi }}_{j}-{\dot{\varphi }}_{k})\cos (\widehat{S})+{E}_{{{{\rm{L}}}}}({\varphi }_{j}-{\varphi }_{k}+2\pi \widehat{f})\,,$$

(8)

is added to the potential energy V. The additional global constraint is included as a boundary condition on the wave function of the total circuit. Let us denote the wave function as ψ_f({φ_j}), where the discrete index f is written as an index instead of an argument (interpreting the number of kinks f as a kind of pseudo-spin). For a single QPS junction connecting two nodes j and k, it can be given as

$${\psi }_{f}({\varphi }_{j}-{\varphi }_{k}+2\pi )={\psi }_{f+1}({\varphi }_{j}-{\varphi }_{k})\,,$$

(9)

This constraint guarantees that a progression of the phase difference by 2π automatically results in a jump of f by + 1, i.e., winding of the phase profile inside the QPS junction, without the need of creating auxiliary states. If there are two QPS junctions in parallel connecting one and the same pair of nodes (j and k), then they have in general two QPS degrees of freedom f₁ and f₂, whose boundary constraints are however connected, that is,

$${\psi }_{{f}_{1},{f}_{2}}({\varphi }_{j}-{\varphi }_{k}+2\pi )={\psi }_{{f}_{1}+1,{f}_{2}+1}({\varphi }_{j}-{\varphi }_{k})\,,$$

(10)

and so on for a higher number of QPS junctions in parallel. This modified constraint comes from the fact that when the phase difference progresses by 2π, the phase profiles inside the two parallel QPS junctions follows the phase instantaneously, such that the winding of φ goes hand in hand with an increase of both f₁ and f₂ at the same time. With respect to charge-phase quantization, the constraint Eq. (9) can be understood as follows. Consider for simplicity a circuit with a single node φ. Moreover, let us choose to represent φ on the interval ( − π, π], such that φ = ± π are the boundaries of the compact phase. In phase space, the condition [N, φ] = i is equivalent to stating that N acts on the wave function as the derivative i∂_φ. While this derivative is obviously well-defined on the extended real line, one has to explicitly define it for a compact φ, i.e., how it acts on the wave function at the boundaries. The above constraint is equivalent to fixing the derivative across the boundary as

$${\left.{\partial }_{\varphi }{\psi }_{f}(\varphi )\right\vert }_{\varphi = \pi }\equiv \mathop{\lim }\limits_{\delta \to 0}\frac{{\psi }_{f+1}(-\pi +\delta )-{\psi }_{f}(\pi -\delta )}{2\delta }\,,$$

(11)

for the right end of the Brillouin zone, and

$${\left.{\partial }_{\varphi }{\psi }_{f}(\varphi )\right\vert }_{\varphi = -\pi }\equiv \mathop{\lim }\limits_{\delta \to 0}\frac{{\psi }_{f}(-\pi +\delta )-{\psi }_{f-1}(\pi -\delta )}{2\delta }\,,$$

(12)

for the left end. As we show below, the problem can often be simplified, such that the compact phase φ and intrinsic QPS degree of freedom f can be combined into a decompactified phase $\widetilde{\varphi }$, that is, a phase without 2π-periodic constraint. The corresponding decompactified charge operator $\widetilde{N}$ now takes again the form of a regular derivative in an extended phase space. This procedure preserves the size of the Hilbert space, and may be useful for explicit computations, and in some cases, allows for an explicit comparison between the Hamiltonian we receive in the node flux picture and the one obtained from loop charge quantization. Note however, that the details of decompactification depend on the model at hand, and cannot be given generally. At any rate, this concludes the formal part, and constitutes our proposed treatment of QPS junctions within the node flux picture.

We now move on to applying this circuit to a number of device examples to make testable predictions. Overall, we will be able to show that an inductive treatment of QPS junctions is not only advantageous (reducing number of degrees of freedom) but in the most general case actually a necessity: the renormalization effect could not possibly have been included within the loop charge picture on a basic conceptual level, because it is a true nonlinear capacitive effect, whereas the nonlinear capacitive treatment of the quantum phase slips themselves arises only due to a mapping onto an extended space with too large a Hilbert space. This distinction can only be made within an inductive approach.

Capacitively shunted QPS junction and renormalization effects

Let us first consider a QPS junction with a capacitive shunt, see Fig. 5. Such a device could for instance serve as a realization of a qubit, thanks to the nonlinearity introduced by the QPS junction. Here, the Lagrangian of the circuit is given as

$$L=\frac{C}{2}{\left(\frac{\dot{\varphi }}{2e}\right)}^{2}-{E}_{{{{\rm{L}}}}}{\left(\varphi +2\pi \widehat{f}\right)}^{2}+{E}_{{{{\rm{S}}}}}\left(\dot{\varphi }\right)\cos \left(\widehat{S}\right).$$

(13)

As stated above, if the capacitor C couples to the maximally fuzzy charge (reaching linearly into the wire, see Fig. 3c), then E_S is simply a constant, and the Legendre transformation can be performed without any problems. We here however want to make predictions which are valid also for the case where the capacitor couples to the charge with a different spatial support (for instance, the charge which is sharply defined at the island, see Fig. 3c). Here, we have to include the aforementioned $\dot{\varphi }$-dependent renormalization of E_S. Assuming a weak $\dot{\varphi }$-dependence, we expand ${E}_{{{{\rm{S}}}}}\left(\dot{\varphi }\right)$ for low values of $\dot{\varphi }$, that is, ${E}_{{{{\rm{S}}}}}\left(\dot{\varphi }\right)\approx {E}_{{{{\rm{S}}}}}+\lambda \dot{\varphi }$. The approximate Lagrangian is then

$$\begin{array}{ll}L\,\approx \,\frac{C}{2}{\left(\frac{\dot{\varphi }}{2e}\right)}^{2}-{E}_{{{{\rm{L}}}}}{\left(\varphi +2\pi \widehat{f}\right)}^{2}\\\,\,\,\qquad +\,{E}_{{{{\rm{S}}}}}\cos \left(\widehat{S}\right)+\lambda \dot{\varphi }\cos \left(\widehat{S}\right),\end{array}$$

(14)

where Legendre transformation is again possible, since the linear term in $\dot{\varphi }$ preserves the convexity of the Lagrangian and merely gives rise to a $\widehat{S}$-dependent shift of the parabola $\sim {\dot{\varphi }}^{2}$. This approximation is valid if the correction of E_S up to second order in $\dot{\varphi }$ is smaller than 1/E_C, with E_C ≡ 2e²/C. The resulting Hamiltonian is

$$\begin{array}{ll}{H}_{{{{\rm{C}}}},{{{\rm{QPS}}}}}\,=\,{E}_{{{{\rm{C}}}}}{\left[N+{N}_{{{{\rm{g}}}}}-\lambda \cos \left(\widehat{S}\right)\right]}^{2}\\\qquad \qquad \,\,\,\,+\,{E}_{{{{\rm{L}}}}}{\left(\varphi +2\pi \widehat{f}\right)}^{2}-{E}_{{{{\rm{S}}}}}\cos \left(\widehat{S}\right)\,.\end{array}$$

(15)

Assuming that the charge island is subject to an additional gate voltage, we have included a corresponding offset charge in N, that is, N → N + N_g.

Fig. 5: Measurable effect of the renormalization of E_S on the energy spectrum.

a Depending on whether the capacitance C couples to the maximally blurry charge (left), or a more localized charge, such as the the charge localized on the charge island (right), the amplitude E_S is either constant or depends on the voltage $\dot{\varphi }$ built up at the capacitor (b). The energy spectrum for the bare and the renormalized case differ (c). In particular, the renormalization induces a distinct asymmetry in the charge dispersion.

According to the rules layed out above, this Hamiltonian is supplemented with a boundary condition for the wave function of the form ψ_f(φ + 2π) = ψ_f+1(φ). To understand the effect of the constraint consider first the case of zero phase slips, that is, E_S = 0 and λ = 0 (see Fig. 4b). The boundary condition defines a Brillouin zone in the space of φ with width 2π. The kinetic term, proportional to E_C, gives rise to a finite quantum dynamics of the phase φ. These quantum fluctuations of the phase are best understood if we consider again the spectra of the Hamiltonian as a function of φ, in Fig. 4. The compact constraint ensures that if the phase exits the interval on one end, it reenters it from the other end, while switching the value of f to f ± 1, depending on whether the phase exits the Brillouin zone on the right or the left end (see the trajectory shown with the red arrow in Fig. 4b). This statement is equivalent to the above definition of the charge operator defined on the compact φ space, Eqs. (11, 12). Without the constraint, we would have the extended picture, see Fig. 4a. Here, all values of φ are allowed, such that the capacitively induced dynamics result in the system moving along a single parabola (red arrow in Fig. 4a). We note however, that due to E_S = 0, the two versions of the system (extended and compact) have the exact same dynamics, and the exact same spectrum (that of a regular LC resonator, as shown in Fig. 4e, f). This is due to the fact that the extended system can only explore the parabola for a single, fixed f. That is, for E_S = 0 the extended system can be considered nonergodic. Here, the difference between the extended and the compact system is merely the question of whether one prefers to regard the parabola on an extended line, or to fold it back onto an interval of width 2π.

However, for nonzero E_S, this is no longer true. Here, the two systems differ, in that the extended system would explore a much larger Hilbert space than the compact system, which however has no physical representation within the circuit. Apart from producing spurious states, the role of N_g is fundamentally different. For the extended system, N_g is an irrelevant quantity that can be gauged away. This is not so in the compact system: with a finite E_S, the system has the possibility to return to its original state when progressing φ by 2π (red arrow in Fig. 4d), and can thus self-interfere while picking up the phase ${e}^{i2\pi {N}_{{{{\rm{g}}}}}}$. The compact system thus resembles to some degree the pendulum representation of the regular charge qubit (based on a simple Josephson junction), see Fig. 2b, except that it has the additional degree of freedom f. Consequently, we arrive at a similar reversed Bloch wave vector argument. The system without constraints has continuous Bloch bands (Fig. 4e) whereas the compact system selects out the Bloch wave vector consistent with N_g (Fig. 4f). As already stated previously, for the closed system, the extended and compact models are equivalent, because here, the Bloch vector can be considered a conserved quantity. But as we pointed out already, if the system is subject to an external drive or coupled to an external bath, one has to keep the correct size of the Hilbert space. For instance, a generic ac drive for the compact system provides a finite response for discrete frequencies (indicated by the wiggly arrow in Fig. 4f), whereas the extended system would predict a continuous response.

Next, let us use the decompactification procedure $\varphi +2\pi f\to \widetilde{\varphi }$, where $\widetilde{\varphi }$ is extended to the entire ${\mathbb{R}}$. Its conjugated variable will then be $N\to \widetilde{N}$ and the $\cos \left(S\right)$ will become $\cos(2\pi \widetilde{N})$. Thus we arrive at the Hamiltonian

$$\begin{array}{ll}{H}_{{{{\rm{C}}}},{{{\rm{QPS}}}}}\,=\,{E}_{{{{\rm{C}}}}}{\left[\widetilde{N}+{N}_{g}-\lambda \cos \left(2\pi \widetilde{N}\right)\right]}^{2}\\\qquad\qquad\,\,\,+\,{E}_{{{{\rm{L}}}}}{\left(\widetilde{\varphi }\right)}^{2}-{E}_{{{{\rm{S}}}}}\cos \left(2\pi \widetilde{N}\right)\,.\end{array}$$

(16)

This Hamiltonian has the advantage that we no longer require special definitions of the charge operator at the boundaries, Eqs. (11, 12). Moreover, we can make an explicit comparison to the Hamiltonian predicted by the loop-charge formalism of ref. ⁶. This formalism yields the Hamiltonian (for details, see ref. ⁶ and the Supplementary Material),

$$\begin{array}{rr}{H}_{{{{\rm{C}}}},{{{\rm{QPS}}}}}^{\circ }\,=\,{E}_{{{{\rm{C}}}}}{\left({\widehat{N}}^{\circ }+{N}_{{{{\rm{g}}}}}\right)}^{2}+{E}_{{{{\rm{L}}}}}{\left({\widehat{\varphi }}^{\circ }\right)}^{2}\\\qquad\qquad\,\,-\,{E}_{{{{\rm{S}}}}}\cos (2\pi {\widehat{N}}^{\circ })\,.\end{array}$$

(17)

We see right away that the Hamiltonians of Eqs. (16, 17) are structurally the same (up to the renormalization effect ~ λ). In particular, we note that for the QPS junction closed by a loop, Eq. (4), the loop charge quantization procedure used too large a Hilbert space. Or more precisely, it used one and the same variable to represent the actual dynamical degree of freedom (the phase slips inside the wire) and external parameter (the externally applied flux). The capacitively shunted QPS junction on the other hand has in both formalisms a Hilbert space of the same size.

There is however one crucial difference between the two models: the dynamical renormalization of E_S (the term ~ λ). As already stated in the node flux formalism developed above, the renormalization is a consequence of the fact that electrostatically, the capacitive shunt C may couple in general to a different charge (that is, a different spatial resolution of the charge) transported across the QPS junction, see Fig. 5a, b. A nonzero λ significantly changes the eigenenergy spectra, see Fig. 5c. In particular, it gives rise to an energy spectrum which has a distinct saw-tooth dependence in N_g. This concludes our discussion on the renormalization of E_S. For the remainder of this work, we assume λ = 0, and focus on other ramifications of our approach, which do not depend on the details of E_S.

Inclusion of time-dependent flux driving

We now discuss with a concrete example how flux driving is included into our formalism, and show how our approach resolves issues present within the loop charge approach. For illustration purposes, consider a circuit where a single QPS junction is shunted by a dc-SQUID, the latter being externally controlled by an applied flux, see Fig. 6. This model will provide an explicit example of the complications already outlined in Fig. 1.

Fig. 6: Different number of degrees of freedom needed to describe the same circuit with different formalisms.

When deploying loop-charge quantization, the minimal circuit model involves four degrees of freedom, two loops and two auxiliary nodes for the two Josephson junctions involved (a). However, this representation runs into issues for negative partial capacitances, which were predicted in ref. ⁹. These issues are circumvented by introducing a dominant bulk capacitance, resulting in 5 degrees of freedom due to the additional loop (b). In contrast, with the here proposed compact node flux procedure, we only require two degrees of freedom, one phase node and the intrinsic QPS degree of freedom f (c).

In our node flux formalism, we proceed just like in the previous section, with the Lagrangian as defined in Eq. (13) and adding the Josephson energies of the two junctions forming the SQUID. After the Legendre transformation, we obtain the Hamiltonian

$$\begin{array}{r}{H}_{{{{\rm{SQUID}}}},{{{\rm{QPS}}}}}\,=\,{E}_{{{{\rm{C}}}}}{\left(\widehat{N}+{N}_{{{{\rm{g}}}}}\right)}^{2}+{E}_{{{{\rm{L}}}}}{\left(\widehat{\varphi} +2\pi \widehat{f}\right)}^{2}-{E}_{{{{\rm{S}}}}}\cos (\widehat{S})\\\qquad \qquad\qquad+\,{E}_{{{{\rm{J}}}}1}\cos (\widehat{\varphi} +{\phi }_{{{{\rm{ext}}}},1})+{E}_{{{{\rm{J}}}}2}\cos (\widehat{\varphi} +{\phi }_{{{{\rm{ext}}}},2}),\end{array}$$

(18)

where E_J1,2 represent the respective Josephson energies of the junctions forming the SQUID. The externally applied flux has been included along the lines of ref. ⁹, that is, the vector potential A expressing the applied magnetic field gives rise to the external phases ϕ_ext,1,2, see also the beginning of the “Results” section. We here assume for simplicity that there is no external phase drop attaching to the QPS junction. This assumption is justified if the surface charges screening the induced electric field due to a time-dependent flux drive are not localized at the QPS junction (in accordance with ref. ⁹). The model could of course be generalized to the case where screening surface charges reach the QPS junction. In that case, the inductive energy term ~ E_L would receive a similar phase shift term, and depending on how the electro-magnetic field is spatially distributed along the QPS wire (similar in spirit to ref. ⁸⁴), there could even be a renormalization of E_S due to the voltage drop induced by the electro-motive force (as already pointed out above).

Here, we we discard these details, and instead compare the above formalism to currently available treatments. In particular, we note that in the above Hamiltonian the time-dependence was implemented in a straightforward slender fashion, directly using the result of ref. ⁹. Moreover, we needed to use only two degrees of freedom, the compact phase φ and the integer f. In analogy to Eq. (16), these two degrees of freedom could furthermore be combined to an extended phase $\widetilde{\varphi }$. Had we resorted to loop-charge quantization instead, the combination of QPS junctions and regular Josephson junctions would have required us to use the mixed representation using loop charges and auxiliary phase nodes for each Josephson junction. Hence for the considered circuit, we would have had to use at least four circuit degrees of freedom, see Fig. 6a. However, this circuit representation only works if two assumptions are true. One, that the self-capacitance of the Josephson junctions are the dominant contributions to the total capacitance between ground and charge island, and that both capacitances are positive and well-defined for all times. Especially the latter assumption is not correct in general, as pointed out in ref. ⁹. Namely, in order to correctly take into account time-dependent flux driving of the SQUID while insisting on representing the circuit by means of dominant junction self-capacitances is in general only possible if accepting partially negative or even time-dependent capacitances. Here, we show why especially the first case, negative partial capacitances, leads to an ill-defined Hamiltonian. To this end, we derive the Hamiltonian based on loop-charge quantization for the SQUID. Since it is not necessary to include the QPS junction explicitly, we focus on the pure SQUID circuit within the single loop representation shown in Fig. 1c. Its Hamiltonian is (see the Supplementary Material for the derivation)

$$\begin{array}{ll}H\,=\,\frac{{\left(2e\right)}^{2}}{2{C}_{1}}{\left({N}_{1}-{N}^{\circ }\right)}^{2}+\frac{{\left(2e\right)}^{2}}{2{C}_{2}}{\left({N}_{2}+{N}^{\circ }\right)}^{2}\\\qquad\quad-{E}_{{{{\rm{J}}}}1}\cos \left({\varphi }_{1}\right)-{E}_{{{{\rm{J}}}}2}\cos \left({\varphi }_{2}\right)+{E}_{{{{\rm{L}}}}}{\left(\frac{{\varphi }^{\circ }}{2e}\right)}^{2}\,,\end{array}$$

(19)

where N^∘ represents the loop charge, and φ_1,2 are the auxiliary phases. Note that in order to emphasize the role of the junction capacitances C_1,2, we refrain from making the replacement ${E}_{{{{{\rm{C}}}}}_{\alpha }}\equiv 2{e}^{2}/{C}_{\alpha }$ (which was, e.g., used in Eq. (15)). Importantly, for the coupling between loop and auxiliary node variables to work without a hitch, the introduction of an extra inductive element ( ~ E_L) connecting the two junctions is necessary (see also ref. ⁶). If the device geometry, or the magnetic field distribution, is asymmetric, then only the sum of the capacitances C = C₁ + C₂ can be guaranteed to be positive, whereas either C₁ or C₂ individually can be (and in general are) negative. The fact that this leads to an instability can be seen most easily when assuming large Josephson junctions, such that the cosines can be approximated by a parabolic potential, $\cos ({\varphi }_{\alpha })\approx 1-{\varphi }_{\alpha }^{2}/2$ (see also the Supplementary Material). Then, the eigenspectrum of the Hamiltonian can be obtained by means of a regular Bogoliubov transformation for noninteracting bosons. Some of the eigenmodes will turn out to be imaginary if either C₁ or C₂ are negative. Note that this instability could be mended by taking the E_L → ∞ limit (neglecting the time it takes for Cooper pairs to travel between the two junctions of the SQUID), such that only the sum of capacitances emerges. However, the entire sequence of steps before taking this limit, the formulation of the Lagrangian, the Legendre transformation and subsequent quantization, are done in a regime where they are ill-defined, thus questioning the validity of the entire procedure.

In order to circumvent this problem, the loop charge formalism requires adding a separate bulk capacitance, see Fig. 6b, or relatedly, Fig. 1d. The idea here is that the bulk capacitance takes care of the actual, electrostatic capacitance between ground and charge island (which is by the way also the physical picture deployed in ref. ⁹). Nonetheless, the formalism still requires adding nonzero auxiliary self-capacitances for each junction (which are not required in the node flux approach, see Fig. 6c), as otherwise, the Legendre transformation and subsequent computation of the Hamiltonian would result in singularities. Only in the very last step, the self-capacitances can be put to zero. At any rate, this approach requires at a minimum 5 degrees of freedom, and thus a significant (and in the end redundant) mathematical overhead compared to the node flux approach proposed in this work.

Aharonov-Casher versus Aharonov-Bohm effect

We now consider a circuit containing two QPS junctions. Such circuits have already been studied and found to give rise to the so-called Aharonov-Casher effect^50,51, i.e., an interference of QPS processes between the wires sensitive to the offset charge N_g. This phenomenon is considered the dual of the Aharonov-Bohm effect present, e.g., in a dc-SQUID, as illustrated in Fig. 7.

Fig. 7: Aharonov-Bohm effect versus Aharonov-Casher effect in circuit-QED.

While the Aharonov-Bohm effect is present and measurable as a sensitivity of the dc-SQUID (left) eigenspectrum of the applied external flux Φ_ext, the experimentally observed N_g-dependence of a circuit connecting two QPS junctions in series (right) is the dual Aharonov-Casher effect. In this work, we provide an alternative picture for the latter, not requiring duality.

For the circuit shown in Fig. 8, applying our node flux formalism yields the Hamiltonian

$$\begin{array}{l}{H}_{{{{\rm{C}}}},2{{{\rm{QPS}}}}}^{{{{\rm{c}}}}}={E}_{{{{\rm{C}}}}}{\left(\widehat{N}+{N}_{{{{\rm{g}}}}}\right)}^{2}-{E}_{{{{\rm{S}}}}1}\cos ({\widehat{S}}_{1})-{E}_{{{{\rm{S}}}}2}\cos ({\widehat{S}}_{2})\\ \qquad\qquad +{E}_{{{{\rm{L}}}}1}{\left(\widehat{\varphi }+2\pi {\widehat{f}}_{1}\right)}^{2}+{E}_{{{{\rm{L}}}}2}{\left(\widehat{\varphi }+2\pi {\widehat{f}}_{2}-{\phi }_{{{{\rm{ext}}}}}\right)}^{2}\,.\end{array}$$

(20)

In accordance with the principles we developed above, we have yet again to include a periodicity constraint. As already pointed out, for the two coupled QPS junctions, the wave function ${\psi }_{{f}_{1},{f}_{2}}(\varphi )$ now needs to satisfy the constraint given in Eq. (10). Since we have only one active phase node, this condition simplifies to

$${\psi }_{{f}_{1},{f}_{2}}(\pm \pi )={\psi }_{{f}_{1}\pm 1,{f}_{2}\pm 1}(\mp \pi )\,.$$

(21)

Crucially, note that without the constraint, the above Hamiltonian would merely have a discrete symmetry: it is invariant upon shifting φ by + 2π while at the same time shifting f_1,2 by − 1. Relatedly, N_g would vanish as a pure gauge term, and thus, strictly speaking, the system would actually not predict the Aharonov-Casher effect. Again, one could invoke the argument made by ref. ⁶ and interpret the resulting conserved Bloch wave vector as the externally applied N_g, which however does not apply for a generic open system. Only with the constraint, the Bloch bands truly disappear in favour of a discrete energy spectrum, depending on both the gate-induced offset charge N_g and the externally applied flux ϕ_ext. Our formalism thus reproduces both the Aharonov-Casher and the Aharonov-Bohm effects within one formalism, without having to rely on symmetry arguments. To show why this aspect matters, we compare this Hamiltonian to the one obtained from the loop charge formalism.

Fig. 8: Node flux and loop charge approaches to a circuit with two QPS junctions.

The loop-charge formalism (right) predicts an Aharonov-Casher effect, but the Aharonov-Bohm effect can only be inferred through constants of motion. The here proposed node-flux treatment (left) directly reproduces both effects.

But to facilitate this comparison, we first cast the above Hamiltonian into a decompactified form, similar in spirit to Eq. (16). To that end, take Eq. (20) and perform the transformation,

$$\widehat{f}=\frac{{\widehat{f}}_{1}+{\widehat{f}}_{2}}{2}\,\,\,\,\,\,\,\,\widehat{S}={\widehat{S}}_{1}+{\widehat{S}}_{2}$$

(22)

$$\delta \widehat{f}={\widehat{f}}_{1}-{\widehat{f}}_{2} \,\,\,\,\,\,\,\, \delta\widehat{S}=\frac{{\widehat{S}}_{1}-{\widehat{S}}_{2}}{2}\,.$$

(23)

We arrive at

$$\begin{array}{ll}{H}_{{{{\rm{C}}}},2{{{\rm{QPS}}}}}^{c}={E}_{{{{\rm{C}}}}}{\left(\widehat{N}+{N}_{g}\right)}^{2}-{E}_{{{{\rm{S}}}}1}\cos \left(\widehat{S}/2+\delta \widehat{S}\right)+{E}_{{{{\rm{L}}}}1}{\left(\widehat{\varphi }+2\pi \widehat{f}+\pi \delta \widehat{f}\right)}^{2}\\ \qquad\qquad\;\;\;-\,{E}_{{{{\rm{S}}}}2}\cos \left(\widehat{S}/2-\delta \widehat{S}\right) +{E}_{{{{\rm{L}}}}2}{\left(\widehat{\varphi }+2\pi \widehat{f}-\pi \delta \widehat{f}-{\phi }_{{{{\rm{ext}}}}}\right)}^{2}\,.\end{array}$$

(24)

We can now safely decompactify without changing the size of the Hilbert space. Due to the nontrivial boundary conditions, the capacitively induced progression of φ across the boundaries of the Brillouin zone provokes a simultaneous slip of f₁ and f₂ by ± 1, see Eq. (21). In terms of the new variables, this changes f by ± 1, whereas δf stays the same. We can thus combine the compact φ ∈ [π, π) with the f index to an extended $\widetilde{\varphi }$, and replace the operator $\widehat{S}$ with $2\pi \widehat{N}$. Hence, we arrive at the Hamiltonian

$$\begin{array}{ll} {H}_{{{{\rm{C}}}},2{{{\rm{QPS}}}}}^{c}={E}_{{{{\rm{C}}}}}{\left(\widetilde{N}+{N}_{g}\right)}^{2}-{E}_{{{{\rm{S}}}}1}\cos \left(\pi \widetilde{N}+\delta \widehat{S}\right)+{E}_{{{{\rm{L}}}}1}{\left(\widetilde{\varphi }+\pi \delta \widehat{f}\right)}^{2}\\\qquad\qquad\;\;\;-\,{E}_{{{{\rm{S}}}}2}\cos \left(\pi \widetilde{N}-\delta \widehat{S}\right)+{E}_{{{{\rm{L}}}}2}{\left(\widetilde{\varphi }-\pi \delta \widehat{f}-{\phi }_{{{{\rm{ext}}}}}\right)}^{2}\,.\end{array}$$

(25)

This Hamiltonian is computationally easier to handle, because the constraint of Eq. (21) is already explicitly worked in. The conjugate pair of operators $\widetilde{N}$ and $\widetilde{\varphi }$ are here truly extended, whereas δf remains an integer. In fact, it is exactly the integer nature of δf which guarantees that the energy spectrum of this Hamiltonian includes a finite dependence on ϕ_ext. If we would allow δf to assume any real value, ϕ_ext could be gauged away.

With the loop-charge quantization approach on the other hand, we arrive at the Hamiltonian (see the Supplementary Material)

$$\begin{array}{l}{H}_{{{{\rm{C}}}},2{{{\rm{QPS}}}}}^{\circ }={E}_{{{{\rm{C}}}}}{\left({\widehat{N}}_{1}^{\circ }-{\widehat{N}}_{2}^{\circ }+{N}_{{{{\rm{g}}}}}\right)}^{2}-{E}_{{{{\rm{S}}}}1}\cos (2\pi {\widehat{N}}_{1}^{\circ })\\\qquad\qquad\,\,\,+\,{E}_{{{{\rm{L}}}}1}{\widehat{\varphi}}_{1}^{\circ 2}-{E}_{{{{\rm{S}}}}2}\cos (2\pi {\widehat{N}}_{2}^{\circ })+{E}_{{{{\rm{L}}}}2}{\widehat{\varphi }}_{2}^{\circ 2}\,.\end{array}$$

(26)

Up to discrete symmetries (respectively constraints) the Hamiltonians of Eqs. (20, 26) are equivalent. To see this, perform in Eq. (26) the coordinate transformations ${N}^{\circ }={N}_{1}^{\circ }-{N}_{2}^{\circ }$ and $\delta {N}^{\circ }=({N}_{1}^{\circ }+{N}_{2}^{\circ})/2$, and equate 2πδN to δS. With our treatment, we directly arrive at the correct quantization of the flux, since δf is defined as an integer right from the get-go. In the loop charge formalism, this quantization is not present, but instead has to be inferred from the fact that the Hamiltonian is invariant upon shifting ${N}_{1}^{\circ }\to {N}_{1}^{\circ }\pm 2\pi$ and ${N}_{2}^{\circ }\to {N}_{2}^{\circ }\mp 2\pi$ – yet another discrete symmetry. But as established in this work, we want to consider the possibility of coupling the circuit to an external drive or environment, where symmetries and constraints are not equivalent. Thus, from the point of view of a generic open quantum system, the two formalisms are not equivalent. In particular, while the Aharonov-Casher effect is present in both formalisms, the Aharonov-Bohm effect follows in the loop-charge formalism only by means of a discrete symmetry, which has to be assumed unbroken even in the presence of a generic external force field. Thus, our formalism unifies both the Aharonov-Casher and Aharonov-Bohm effects on a fundamental level, by means of a microscopic derivation of constraints on the Hilbert space. We summarise this result in Fig. 9. If we were to take the node-flux treatment, Eq. (20), but discarding the constraint of Eq. (21), we would arrive at a Hamiltonian that reproduces the Aharonov-Bohm effect, but fails to predict the N_g-dependence of the energy spectrum (instead predicting Bloch bands due to a symmetry in phase space), see Fig. 9a. The loop-charge approach reproduces the Aharonov-Casher effect, but yields Bloch bands instead of the ϕ_ext-dependent energy levels, due to a discrete symmetry in charge space, see Fig. 9b. Only when explicitly including the constraint of Eq. (21), we get a discrete spectrum (without continuous bands), depending on both N_g and ϕ_ext, see Fig. 9c. That being said, let us note that while it should be theoretically expected that the device considered in Fig. 8 should exhibit both an Aharonov-Casher and an Aharonov-Bohm effect, to the best of our knowledge, existing measurements^50,51 have so far only explicitly varied N_g, but not ϕ_ext. While the data in said experiments is indicative of the presence of discrete energy spectra, an experiment varying both parameters could unequivocally confirm the above prediction.

Fig. 9: Different predictions depending on whether symmetries or constraints are used.

We here show different possible energy spectra of the circuit with a central island, coupled to two QPS junctions and a central gate, see Fig. 8, subject to a gate-induced offset charge N_g and an externally applied flux ϕ_ext. The non-compact approach predicts a spectrum with continuous bands, depending explicitly on ϕ_ext but not on N_g. The reverse is true for the loop-charge formalism. Our compact node-flux approach removes the bands and predicts discrete energy levels, due to the topological constraint in the Hilbert space, relying on charge quantization. The spectrum depends on both N_g and ϕ_ext, and thus unifies the Aharonov-Bohm and Aharonov-Casher effects.

Finally, let us point out that our approach provides an alternative understanding of the Aharonov-Casher effect. Instead of seeing it as an interference of quantum phase slips of QPS junctions in series, we can understand the oscillations of the energy spectrum as function of N_g on the exact same footing as for a regular charge qubit, Eq. (2). Namely, the interference effect comes from the very same type of trajectory of the node phase φ, that is, the progression of the phase by 2π, returning to its original state, while picking up the phase ${e}^{i2\pi {N}_{{{{\rm{g}}}}}}$. This type of trajectory was explicitly shown above for a single QPS junction (red arrow in Fig. 4d), and exists analogously for the circuit with two QPS junctions. Overall, our work demonstrates that one can use a pure node flux procedure (which is to some degree asymmetric with respect to the role of charge and phase variables) to reproduce seemingly dual physical effects.

Reduced computational space and dual frustration

While the above discussion focused on the effect that constraints have on the energy spectrum, in this final section, we want to show that determining the correct Hilbert space size is also crucial to correctly assess the computational space, and how to manipulate and measure it, when examining the utility of circuits for potential qubit realizations. In particular, we pick up on an interesting recent proposal⁵⁷ to use QPS junctions for the realization of the Gottesman-Kitaev-Preskill (GKP) code⁵⁶. The proposed device is equivalent to the one shown in Fig. 6, except that it requires only one Josephson junction instead of two. The authors of ref. ⁵⁷ derive the following Hamiltonian for this device

$$\begin{array}{ll}{H}_{{{{\rm{C}}}},{{{\rm{QPS,J}}}}}\,=\,-{E}_{{{{\rm{S}}}}}\cos \left(2\pi {\widehat{N}}_{{{{\rm{S}}}}}\right)+{E}_{{{{\rm{L}}}}}{\left({\widehat{\varphi }}_{{{{\rm{S}}}}}-\widehat{\varphi }\right)}^{2}\\\,\,\quad\qquad\qquad+\,{E}_{{{{\rm{L}}}}}{\left(\widehat{N}+{N}_{g}\right)}^{2}-{E}_{{{{\rm{J}}}}}\cos \left(\widehat{\varphi }-{\varphi }_{e}\right)\,.\end{array}$$

(27)

Note that this is one of the few cases, where the non-linear capacitor treatment within a node-flux approach works (see above mentioned issues about non-convexity of the kinetic energy term), and the authors find a Hamiltonian equivalent to our node-flux approach, again up to constraints. At any rate, the picture deployed by the authors of ref. ⁵⁷ thus closely follows the picture advocated by Mooij and Nazarov⁴⁸, whereby the QPS junction can be described by an auxiliary node variable φ_S, i.e., in our case the discrete variable f, see also Fig. 5. Indeed, Eq. (27) corresponds to the Hamiltonian we provide in Eq. (18), which can be seen by setting one of the Josephson junctions to zero (e.g., E_J2 = 0), and replacing the operators $2\pi {\widehat{N}}_{S}\to \widehat{S}$ and ${\widehat{\varphi }}_{S}\to 2\pi \widehat{f}$. There are however several crucial differences and additions within our formalism (some of which have already been discussed above for other examples). We here explain their relevance for the idea of using QPS-based circuits for the GKP code.

Let us begin by the most fundamental ingredient. Namely, our formalism brought forth the symmetry constraint in (φ, f)-space on the wave function for one QPS junction, given in Eq. (9). In the previous sections, this constraint merely fixed the Bloch vector, and thus replaced Bloch bands by discrete energy spectra. Here, the compactification of φ has another profound consequence. Namely, the goal of ref. ⁵⁷ is to arrive at a regime where the effects of the parasitic capacitance ( ~ E_C) and inductance ( ~ E_L) are negligible, arriving at a pure double-cosine Hamiltonian. Especially with respect to the inductive term, disregarding the constraint would suggest that the regime of interest would be for small inductances, such that E_L → ∞. A naive application of this limit would suggest that the phases φ_S and φ are perfectly coupled (the inductive energy term would act as a Lagrange multiplier), such that the auxiliary charge and phase, N_S, φ_S, could be promoted to the physical charge and phase N, φ. Crucially, our proposed constraint forbids taking such a problematic limit, since there is simply not enough available Hilbert space to reach this limit. The effect can be thought of as a dual frustration: in reality f is integer, and φ is restricted to an interval of size 2π. Hence, the two cannot be coupled by rendering E_L large, because they are fundamentally incompatible. Instead, for E_L ≫ E_S, QPS are simply suppressed, and the circuit begins to work like a regular fluxonium¹⁶.

Consequently, if one strives to realize a double-cosine Hamiltonian one has to search in the opposite regime, where E_L is small compared to E_S. We expect that this first of all a significant experimental hurdle, as E_S cannot always be tuned to large values for all physical implementations of QPS wires. Note furthermore, that for E_L, E_C → 0, strictly speaking, the operators inside the two cosines are not even the actual canonically conjugate pair of operators. The operator $\widehat{S}$ knows about the phase slip state inside the wire, and φ represents the phase inside the island. This problem in and of itself can, at least in principle, be solved by the above introduced decompactification procedure, see Fig. 3. We thus eliminate again the S, f degrees of freedom and end up with a single pair of N, φ where φ is now no longer compact. This seems to salvages the idea of realising a GKP code.

But at this stage, the other insights of our above developed microscopic picture become important. In particular, note how the new (non-compact) phase and charge variables are defined: they extend linearly into the wire, see Fig. 3c. Let us stress, that the central idea behind the GKP code as a quantum error correction code is to track random external shifts (here in N_g and ϕ_ext) by appropriate nonlocal measurements in the respective spaces of the conjugate observables, without destroying the quantum information. That is, merely looking at the Hamiltonian lures one into the false impression that the analysis of the qubit state can be performed by measurements of charge and phase on the island. The physical picture we develop demonstrates to the contrary, that we instead need to measure the state inside the QPS wire. Measuring the local charge on the island on the other hand, would propel the system out of the low-energy computational space, since (as stated above) the local, quantized charge has been eliminated from the low-energy description of the QPS junction. The above represent important caveats, significantly complicating the idea of an experimental implementation of quantum error correction strategies by using QPS junctions.

The above illustrates the importance of the inductive treatment of QPS junctions and the resulting constraints on the Hilbert space, not only to predict the correct energy spectrum, but to accurately assess the correct size of the available computational space of a given device, and how a more sophisticated picture can shed light on important details regarding state control and measurement, which are of importance for quantum information applications.

Discussion

We demonstrate that it is possible to regard QPS junctions as purely inductive elements, thus rendering them compatible with regular node-flux quantization. We derive an important constraint on the wave function, based on charge quantization, which explicitly reduces the Hilbert space, and eliminates spurious degrees of freedom. As we show, this has profound consequences on how the circuit can interact with externally applied electric and magnetic fields, and allows us to unify the Aharonov-Bohm and Aharonov-Casher effects within one formalism. Furthermore, the reduction of the Hilbert space is an important principle when examining the utility and feasibility of possible qubit architectures involving QPS junctions.

We note that the constraint can be regarded as a minute, but decisive breaking of the exact duality between the Josephson effect and quantum phase slips. This is due to the fundamental difference with respect to how charge and phase degree of freedoms enter the Hamiltonian (in particular, the latter enters always in the exponent, e^iϕ). To predict the correct physics, it appears crucial that the theory retains a possibility for the phase to be represented on a compact manifold, even when charge quantization is not explicitly present (or removed within the low-energy sector of the state space).

Our treatment of QPS physics furthermore uncovered new QPS-related physics, such as a renormalization of the phase slip energy E_S. We have examined this phenomenon for weak renormalization, where it gave rise to an asymmetry of the energy spectrum as a function of the offset charge. Strong renormalization effects are expected to massively increase the complexity of the overall circuit dynamics. This effect will be explored in more detail in the future. Moreover, it will be interesting to bring topological superconductors into the mix, where the presence of Majorana bound states could potentially change the width of the Brillouin zone, i.e., φ may live on an interval of size 4π instead of 2π. A dedicated work tackling that particular question is underway, where we expect to see competing effects of 2π- versus 4π-periodicity. Moreover, the physics of 1D superconducting structures (such as Josephson junction arrays) are often mapped onto the sine-Gordon model^80,82, where disorder may lead to interesting renormalization effects^80,85. However, the sine-Gordon equation has extended quantum fields. We are so far unaware of theoretical studies examining the possibility of a modified sine-Gordon model with compact quantum fields – which we believe to be of relevance to model superconducting structures, and (since charge quantization is a fundamental property) possibly even beyond.