Introduction

The availability of big data analyzed and exploited with machine learning methods is one of the main traits of the present information era and the search for enhanced data processing capabilities is spurring research also in quantum approaches1,2,3. Recent quantum machine learning implementations have been reported ranging from NMR platforms4 to noisy quantum computers5,6, and many proposals7,8,9,10,11 promise an advantage in the performance with respect to classical approaches. Still, dealing with quantum systems for machine learning poses new challenges not only to preserve fragile quantum coherence from the action of the environment12 but also to efficiently access the processed information through measurement13, being these related issues. In particular, a first distinctive aspect of quantum measurements is that expectation values require an ensemble of copies of the system. Indeed, in most quantum technologies including computation14, sensing15,16, or communications17,18,19, different approaches to optimize and reduce the number of measurements have been recently reported20,21 also including classical machine learning tools22,23,24,25. A second distinctive aspect to deal with is that a measurement performed on a quantum system generally alters its state26,27,28,29. This measurement back-action has deep consequences when monitoring a system, beyond a single input-output setup and has been addressed for instance in feedback control13 or in quantum error correction30,31. Our goal here is to introduce a quantum measurement framework for temporal series processing considering both accuracy and back-action.

Many prominent tasks in the context of (classical) machine learning deal with time-series processing, like speech recognition, stock market forecasting or climate prediction. In contrast to classification tasks32, temporal ones require continuous data monitoring and the temporal order within the data sequence to be processed plays a key role33. Among classical approaches to time-series processing34,35,36,37, reservoir computing38 has been successful in recognizing spoken words39,40 and human activity41 or in forecasting chaotic dynamical systems42,43, with appealing features such as easy training and energy efficiency. In this scheme, data are continuously injected into a reservoir system, processed, and extracted, without requiring an external memory avoiding the von Neumann bottleneck44. The reservoir itself can be either an artificial recurrent neural network45 or even a physical substrate46, providing a high dimensional phase space, a non-linear input-output transformation and a fading memory47.

Recently, reservoir computing has been extended to the quantum regime considering several ideal models ranging from qubits to fermions and bosons, in photonic, atomic and solid-state platforms48,49. Theoretical proposals display successful performances of quantum reservoir computing (QRC) in genuine temporal tasks50,51,52,53,54,55 and in generalization and classification ones49,56,57,58,59,60,61, an approach known as extreme learning machine. QRC is indeed a burgeoning alternative approach in quantum machine learning, but continuous monitoring for sequential time series processing poses a major challenge. A first experimental implementation of a static classification task has been realized with NMR of a nuclear spin ensemble in a solid62, while the first exploration of temporal series processing with QRC was recently reported on a quantum digital computer52. The potential of exploiting present NISQ devices3,63 is indeed one of the motivations for QRC50. Still, the monitoring issue is unsolved. In order to establish the most promising avenues towards quantum approaches a daunting question is how to efficiently monitor and extract meaningful information in such experimental platforms, when including the effect of quantum measurement. The scope of this work is to address this point by proposing different measurement protocols and to identify the most promising ones for implementation, also addressing the crucial issue of the required resources.

Continuous time-series processing needs to be not only efficient in terms of time and energy resources (repetitions, ensemble size) but also reliable in spite of measurement back-action, being these often competing requirements. The presence of noise due to finite ensembles is common to most quantum technologies and has also been considered in proposals of QRC56,57,64,65. In time-series processing, the back-action of measurement for continuous monitoring (i.e. introducing the measurement map for each processing time step) becomes a further crucial factor for realistic implementations, still to be addressed. Here, we will explore protocols based either on repeating (part of) the reservoir dynamics or on weak measurements66,67, known to be noisier and less informative than projective ones, but with the advantage to perturb less the state, therefore preserving time information in the system. In this work, we analyze the effect of quantum measurement for realistic QRC, assessing the required resources for temporal series processing (considering both finite ensemble and back-actions issues) with analytical and numerical methods. Considering different protocols based on both projective and weak measurements and taking into account their accuracy, we will identify successful strategies leveraging performance and resource efficiency. We illustrate these aspects for time series processing in tasks requiring respectively memory or forecasting capabilities.

Results

Restarting, rewinding and online protocols

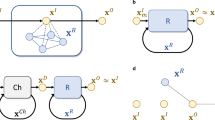
All QRC architectures48 for time series processing proposed so far share the common feature of information extraction based on quantum measurement at the output layer, Fig. 1a. In this section, we present three different measurement protocols of a quantum system driven by a sequence of (classical or quantum) inputs, as illustrated in Fig. 1b–d, being most considerations generally valid for any monitored quantum system, also beyond QRC. We formally describe the evolution of a quantum system state in discrete time steps, with k = t/Δt labeling the input injection sequence, by means of the recurrence relation

$${\rho }_{k}^{{{{\rm{u}}}}}={{{{\mathcal{L}}}}}_{k}\left[{\rho }_{k-1}^{{{{\rm{u}}}}}\right]$$
(1)

for the unperturbed (u) state dynamics, i.e., in the absence of any measurement process. The superoperator \({{{{\mathcal{L}}}}}_{k}\) can account both for a unitary evolution as well as for the interaction with an additional external environment. The input, sk in Fig. 1, can be introduced either through the sequential update of part of the system state50 or by means of a control Hamiltonian or dynamical parameter52,68.

Fig. 1: Quantum reservoir computing and measurement protocols.
figure 1

a Schematic representation of QRC, in input, reservoir and output layers. b–d Measurement restarting, rewinding and online protocols (RSP, RWP and OLP) for consecutive measurements at time steps k + 1 and k + 2 in one ensemble realization. For the RSP (b), at each output time step, all the sequence processing is repeated (Nt time steps to gather the output k + 1, Nt + 1 time steps to gather k + 2, etc.). For the RWP (c), Nwo steps of the sequence are repeated for each output time step. For the RWP the choice of the reset state at tk − τwo has no effect on the output (here we set it to ρ0). For the OLP with weak measurement (d), the evolution is continuously monitored without repeating any part of the reservoir evolution.

Full size image

In an ideal case, at each time step, information is extracted through the expectation value of any observable operator \(\hat{{{{\mathcal{O}}}}}\) over an infinite ensemble

$${\langle \hat{{{{\mathcal{O}}}}}\rangle }_{{\rho }_{k}^{{{{\rm{u}}}}}}^{\infty }\equiv {{{\rm{Tr}}}}(\hat{{{{\mathcal{O}}}}}{\rho }_{k}^{{{{\rm{u}}}}}).$$
(2)

In any implementation, however, the expectation value can be inferred only from a finite number, Nmeas, of identical copies of the quantum system and the estimated value suffers from a statistical error that represents a first major experimental limitation. The second issue of paramount relevance is represented by the disturbance introduced by a quantum measurement, which modifies the “unperturbed” dynamics of Eq. (1) at each time step k. A common way to circumvent this back-action issue, –where the effect of quantum measurement is not accounted for– is through the reinitialization of the dynamics after each measurement, as usually implicit in QRC proposals so far48. As a drawback, one would need to repeat the experiment Nmeas times for each of the time steps tk of the input time series to be processed. This scheme, which we will refer to as the restarting protocol (RSP), is sketched in Fig. 1b. It was used in the quantum digital computer implementation in ref. 52.

A significant improvement with respect to the RSP can be attained in reservoir computing considering its dynamical features, and in particular the echo state property, that is its ability to process time series independently on the initial state ρ0 of the reservoir69. We introduce the washout time τwo, as the time necessary for the dynamical system to lose any information from initial conditions, so that the reservoir computer depends effectively on the input recent history, a property also known as fading memory (Fig. 1b). This suggests that a more efficient strategy than the RSP is to limit the repetition time to the shorter washout time, restarting the dynamics from tk − τwo instead of t052. This rewinding protocol (RWP) is devised to optimize the resources needed to overcome the measurement feedback by re-initialization and is characterized by a sliding repetition time interval τwo with an associated number of input injections Nwo ≡ τwo/Δt (Fig. 1c).

In both RSP and RWP, the measurement outcomes, Vk l, at each time step k and for several realizations l = 1, …, Nmeas, allow one to approximate the expectation value of the observables as an average over a large number of measured values \({\langle \hat{{{{\mathcal{O}}}}}\rangle }_{{\rho }_{k}^{{{{\rm{u}}}}}}^{{N}_{{{{\rm{meas}}}}}}\) with a precision proportional to \(1/\sqrt{{N}_{{{{\rm{meas}}}}}}\). In other words, the statistical uncertainty limits the approximation to the ideal expectation values as \({\langle \hat{{{{\mathcal{O}}}}}\rangle }_{{\rho }_{k}^{{{{\rm{u}}}}}}^{{N}_{{{{\rm{meas}}}}}}={\langle \hat{{{{\mathcal{O}}}}}\rangle }_{{\rho }_{k}^{{{{\rm{u}}}}}}^{\infty }+O\left({N}_{{{{\rm{meas}}}}}^{-\frac{1}{2}}\right)\). These protocols are designed so that the measurement back-action does not need to be taken into account, but require to repeat, for each input injection, part or all of the processing sequence, thus requiring the storage of these inputs in an external memory. An important question arises in this context: is there a way to avoid restarting (or rewinding) the process after each output extraction? For this purpose, we consider the possibility of continuously monitoring the quantum trajectories of the evolving QRC by introducing weak quantum measurements.

If information is extracted at the output layer through projective measurements of all the reservoir physical units, then most coherence is lost also erasing information of previous inputs. As a strategy to overcome this extreme back-action effect, the QRC can be monitored by preserving part of its fading memory either considering weak measurements or projectively measuring only part of the reservoir nodes (indirectly measuring the rest of the reservoir)66,70, being both approaches actually related13. Weak measurements have been considered for instance in the context of quantum metrology and quantum physics foundations (see Supplementary Methods II B), and experimentally implemented in diverse settings, including optical71, superconducting qubits70,72, and traped ions73 platforms. Then, alternating input injection and output extraction –as in classical RC– we propose an online time series processing protocol based on weak measurement, as represented in panel (d) of Fig. 1.

For a single realization of the online protocol (OLP), the monitored state \({\rho }_{{{{{\bf{V}}}}}_{k}}\) (for which we drop the apex ‘u’) evolves following a quantum trajectory characterized by the (stochastic) measurement outcomes Vk:

$${\rho }_{{{{{\bf{V}}}}}_{k}}=\frac{\left({{{{\mathcal{M}}}}}_{{{{{\bf{V}}}}}_{k}}\circ {{{{\mathcal{L}}}}}_{k}\right)[{\rho }_{{{{{\bf{V}}}}}_{k-1}}]}{{{{\rm{Tr}}}}\left(\left({{{{\mathcal{M}}}}}_{{{{{\bf{V}}}}}_{k}}\circ {{{{\mathcal{L}}}}}_{k}\right)[{\rho }_{{{{{\bf{V}}}}}_{k-1}}]\right)},$$
(3)

where the effect of the measurements on the system is determined by the form of the superoperator \({{{{\mathcal{M}}}}}_{{{{{\bf{V}}}}}_{k}}\) (see Methods). The mixed state that accounts for all possible measurement outcomes at time step k, assuming an infinite ensemble of realizations, is given by (see Supplementary Methods II A):

$${\rho }_{k}=\int\nolimits_{-\infty }^{\infty }d{{{{\bf{V}}}}}_{k}{\rho }_{{{{{\bf{V}}}}}_{k}}P({{{{\bf{V}}}}}_{k})=\int\nolimits_{-\infty }^{\infty }d{{{{\bf{V}}}}}_{k}\left({{{{\mathcal{M}}}}}_{{{{{\bf{V}}}}}_{k}}\circ {{{{\mathcal{L}}}}}_{k}\right)[{\rho }_{k-1}],$$
(4)

The expectation values of operators in the OLP can be immediately generalized by replacing the unperturbed state \({\rho }_{k}^{{{{\rm{u}}}}}\) of the RSP and RWP with the monitored state ρk, accounting for the measurement back-action.

We employ indirect measurements already implemented experimentally in diverse platforms49,70,72,73,74,75,76,77 (see Methods). For instance, the state of a superconducting qubit coupled to a cavity is indirectly measured by probing the cavity typically with a microwave signal70,72,74,75,76, or in the trapped ion experiment in73, the information about the electronic states is extracted from their interaction with the vibrational motion.

Within our measurement framework for a system of N qubits, we find that Eq. (4) is simplified to (see Supplementary Methods II A):

$${\rho }_{k}=M\odot {{{{\mathcal{L}}}}}_{k}[{\rho }_{k-1}],$$
(5)

where ⊙ represents the element-wise product and M is defined as

$$M\equiv {\tilde{M}}^{\otimes N},\quad \tilde{M}=\left(\begin{array}{cc}1&{e}^{-\frac{{g}^{2}}{2}}\\ {e}^{-\frac{{g}^{2}}{2}}&1\end{array}\right).$$
(6)

The measurement strength, g, allows us to quantify the increasing decoherence introduced by sharp measurements (g ≫ 1), while for g ≪ 1 the state is weakly perturbed. The parameter g depends on the coupling between the probe and the indirectly measured system and the properties of their mutual interaction (see Methods and Supplementary Methods II B).

An interesting question is about the possible effect of measurement as a further nonlinearity source for QRC. In order to address this point more clearly, let us specialize on the framework of QRC introduced in ref. 50, which will be also used in the following sections. The reservoir consists of a qubit network unitarily evolving under the disordered transverse-field Ising Hamiltonian50,53, while the input is injected into the system by rewriting a node state \({\rho }_{k}^{{{{\rm{in}}}}}\). The system parameters are chosen in such a way that the reservoir is found in the ergodic dynamical phase, which has been shown to guarantee optimal QRC performances53. Different realizations of the reservoir produce similar results. Full details are given in Methods and Supplementary Results I A. By using Eqs. (5) and (6), we find that the explicit dependence on the input and on g of the components of ρk is translated to the observables as (see Supplementary Methods II A):

$${\langle \hat{{{{\mathcal{O}}}}}\rangle }_{{\rho }_{k}}^{\infty }=\mathop{\sum }\limits_{n=1}^{N}{e}^{-\frac{N-n}{2}{g}^{2}}\left({A}_{n}+{B}_{n}{s}_{k}+{C}_{n}{r}_{k}\right),$$
(7)

where sk is the kth input injected, \({r}_{k}\equiv \sqrt{{s}_{k}(1-{s}_{k})}\), and the matrices An, Bn, and Cn depend on the state ρk−1, as it was found in the absence of measurement in Ref. 78. Iterating these relations, it is then found that no further nonlinearities beyond the polynomials of rk and sk with different k are introduced in the measurement process. The exponential factors of Eq. (7) effectively determine the amount of measurement-induced back-action introduced in the system, being all equal to 1 in the unperturbed case.

Measurement accuracy

In the previous discussion, we have anticipated two main experimental limiting factors to the detection of the expected values of the system observables: (i) the finite number of stochastic measurements in the ensemble, affecting all the protocols of Fig. 1, and (ii) the measurement weakness, which preserves better the state but limits the amount of information that can be extracted and is particularly relevant for the OLP.

Within our measurement framework, for single-qubit observables, these two sources of statistical uncertainty combine together to give an error up to (see Supplementary Methods II B):

$${\bar{s}}_{\langle \hat{\sigma }\rangle }=\sqrt{\frac{{g}^{2}+1}{{g}^{2}{N}_{{{{\rm{meas}}}}}}},$$
(8)

while for two-qubit observables the statistical uncertainty reads:

$${\bar{s}}_{\langle \hat{\sigma }\otimes \hat{\sigma }\rangle }=\sqrt{\frac{{g}^{4}+2{g}^{2}+1}{{g}^{4}{N}_{{{{\rm{meas}}}}}}}.$$
(9)

The fact that more information is extracted with sharper measurements (g ≫ 1) is reflected in a reduction in the statistical uncertainty in the observables when increasing g, for a fixed number of measurements. For the RSP and the RWP, this justifies the use of strong measurements, approximately projective (e.g. g = 10). However, for the OLP a careful assessment is needed, taking into account that measurement back-action in general leads to deviations from the unperturbed dynamics, erasing information. Equations (8)-(9) also tell us that the degree of precision depends on the kind of observable chosen. Indeed, taking a weak value g ≪ 1, the same uncertainty obtained with Nmeas ~ g−2 for single-qubit observables would require Nmeas ~ g−4 in the case of two-qubit observables. In the following, we consider weak measurements with g = 0.3 and strong measurements with g = 10, which are well within experimentally accessible values (see Supplementary Methods II B).

In order to appreciate the way back-action and the two sources of statistical uncertainty (i) and (ii) affect the OLP, we plot in Fig. 2 the dynamics of some observables and compare them with the ideal quantities. The finite number of measurements is responsible for small deviations (not visible in the plot), namely, \({\bar{s}}_{\langle \hat{\sigma }\rangle }\approx 2\cdot 1{0}^{-3}\) in panels (a) and (c), and \({\bar{s}}_{\langle \hat{\sigma }\rangle }\approx 8\cdot 1{0}^{-4}\) in (b) and (d). Actually, as we will show below, these seemingly small fluctuations have an important impact for machine learning purposes. The most apparent discrepancies are due to measurement back-action and are shown in Fig. 2d, between the (OLP) measured and the (RSP and RWP) unperturbed values. Back-action impact is rooted in the reservoir state features and finally in its operation regime: In the z-direction, in panels (a) and (b), this effect is less important because the qubits are mostly aligned along z due to the reservoir parameter choice53. If the measurements are done in a different direction, i.e. to gather \(\langle {\hat{\sigma }}_{i}^{{{{\rm{x}}}}}\rangle\) and are sharp (Fig. 2d), they introduce strong decoherence leading to the strong deviation with respect to the unperturbed state. Only with sufficiently weak measurements, as in Fig. 2c, the (unperturbed) dynamics is qualitatively and approximately preserved with the OLP. A similar discussion also applies to more general observables, like two-qubit observables (see Supplementary Results I B). These analytical and numerical findings hint at the fact that a weak measurement is the only viable option for the OLP.

Fig. 2: Qubits dynamics.
figure 2

Single-qubit observables of the first three qubits of the system with N = 6 in the (a, b) z and (c, d) x directions. Solid lines correspond to the ideal values (Nmeas → ∞) with (black) the effect of measurements on the system (OLP) and (grey) the unperturbed case (RSP and RWP), respectively. In symbols, the values obtained by numerically simulating the measurement process with Nmeas = 1.5 ⋅ 106 in the OLP. Panels (a), (c) correspond to a weak measurement strength, g = 0.3; whereas in panels (b), (d) strong measurements, g = 10, are performed. The input is encoded into the state of qubit 0 (see Methods).

Full size image

An important consequence of Eq. (6) is that, for g ≪ 1, the ideal state (monitoring an infinite ensemble) is weakly perturbed, as M approaches the unity matrix with all components 1. Intuitively, the disturbance introduced by such measurement is so weak that almost no information is lost during online processing. With finite measurement ensembles Nmeas, the error associated with this unsharp measurement is larger than in the unperturbed state (e.g. \({\bar{s}}_{\langle \hat{\sigma }\rangle }\) in Eq. (8) is larger than \(1/\sqrt{{N}_{{{{\rm{meas}}}}}}\)). Interestingly, in the ideal case (infinite resources) information would still be extracted with a limit vanishing error \({\bar{s}}_{\langle \hat{\sigma }\rangle }\). Building on this analysis, the estimation of observables experimentally accessible with finite measurements can be numerically emulated by adding the proper Gaussian noise to the ideal ones, \({\langle \hat{{{{\mathcal{O}}}}}\rangle }_{{\rho }_{k}}^{\infty }\). The comparison between either performing numerically an ensemble over Nmeas independent trajectories or adding Gaussian noise to an ideal infinite ensemble (with standard deviation given by either Eq. (8) or (9)) will also be verified below.

Short-term memory capacity

In the previous sections, we have analytically assessed measurement effects and we are now applying this framework to QRC assessing its memory (this section) and forecasting (next section) capabilities. In order to identify the accuracy limitations and back-action effects of measurements, we consider the short-term memory (STM) task. This allows us to establish the reservoir efficiency in storing past information, that is, the fading memory crucial for effective reservoir computing. Given the input sequence {sk} of random numbers generated from a uniform distribution, the task is to reproduce the target values

$${y}_{k}={s}_{k-\tau },$$
(10)

where τ is the delay. The predictions are obtained with different measured observables (for instance \(\langle {\hat{\sigma }}_{i}^{{{{\rm{x}}}}}\rangle\), or \(\langle {\hat{\sigma }}_{i}^{{{{\rm{z}}}}}{\hat{\sigma }}_{j}^{{{{\rm{z}}}}}\rangle\)) for all qubits i, j = 1, N and comparing RSP, RWP and OLP. As usual, the performance is quantified comparing predictions, \(\tilde{{{{\boldsymbol{y}}}}}=\{{\tilde{y}}_{k}\}\), and target values, y = {yk}, through the normalized correlation, namely the capacity C(τ) ∈ [0, 1]. Perfect STM at delay τ corresponds to C(τ) = 1. More details in Methods.

The STM capacity for increasing delays is shown in Fig. 3a, for single-qubit observables in the output layer. The performance when neglecting any perturbation introduced by measurement (black line) progressively decays, showing the ability of the reservoir to store past information up to about six previous steps (consistently with the network size N = 679). This STM capacity can be achieved with the RWP and the RSP with high accuracy for Nmeas = 1.5 ⋅ 106. We remark that values of Nmeas ranging from 104 to 106 are in accordance with experiments of quantum computation14 and quantum machine learning5. When continuously monitoring the system in the OLP, the effect of measurement back-action becomes critical and for sharp measurement (g = 10) the performance is significantly hindered. Remarkably, this limitation is overcome with weak measurements and the STM capacity achieved for g = 0.3 is approaching the unperturbed case. Therefore, weak measurements preserve short memory performing this online temporal task, sequentially injecting new inputs and continuously extracting information. The explanation of the hindered performance for strong measurement (g = 10) is shown to be due to both back-action and statistical noise, with C decaying strongly for τ = 2. Assuming infinite accuracy (ideal case of infinite Nmeas, green continuous line in Fig. 3a), the capacity instead reaches larger delays (τ = 4). Therefore, the ideal OLP with g = 10 does not achieve the memory obtained with the other protocols due to back-action: continuous sharp measurements erase reservoir information encoded in quantum coherences and correlations (Fig. 2d).

Fig. 3: Short-term memory capacity.
figure 3

a STM capacity from single-qubit observables depending on the delay τ obtained with the different protocols and Nmeas = 1.5 ⋅ 106 measurements (symbols). The ideal capacities (Nmeas → ∞), are represented with a solid line in the corresponding color; the unperturbed situation is in black. The dashed green line corresponds to estimated values obtained from the observables in the limit Nmeas → ∞ but adding Gaussian noise. Indices of label \(\langle {\hat{\sigma }}_{i}^{\alpha }\rangle\) refer to i = 0, …, N = 6 and α = x, y, z. In (b) and (c), target values (grey filled circles) are shown with predictions (colored unfilled symbols) for the STM task at τ = 2 obtained with the OLP and weak measurements (b), and strong measurements (c), both with single-qubit observables. All data shown correspond to the test data set.

Full size image

The input sequence to the QRC and the ability to reproduce past inputs in the OLP are shown in more detail in Fig. 3b and c, for the STM capacity at delay τ = 2. For weak measurement (b), all qubits observables (\({\hat{\sigma }}^{{{{\rm{x}}}}},{\hat{\sigma }}^{{{{\rm{y}}}}},\) and specially \({\hat{\sigma }}^{{{{\rm{z}}}}}\)) contribute to the capacity C(τ = 2), while sharp measurements (large g) hinder the ability of the output to reproduce the target. On the one hand, Fig. 3b also tells us that, despite the state being mostly aligned in the z direction53, the reservoir is far from approaching the classical regime, where quantum coherences would be negligible. Indeed, significant contributions to the capacity come from all the qubit directions (more details are given in Supplementary Results I C). Intuitively, even though such coherences are small with respect to the populations (see also Fig. 2), they still provide significant richness to the reservoir output (being larger than the statistical uncertainty of the measurement process). On the other hand, we see in Fig. 3c that if such coherences are further hindered by stronger back-action (falling below the statistical noise, then the capacity reached with \({\hat{\sigma }}^{{{{\rm{z}}}}}\) (C = 0.21) does not improve when also considering \({\hat{\sigma }}^{{{{\rm{x}}}}}\) and \({\hat{\sigma }}^{{{{\rm{y}}}}}\).

The overall performance of the STM task is quantified in Fig. 4 by the sum capacity accounting for the total memory at all delays (equivalent to truncating at 10 as C(τ > 10) ~ 0)

$${C}_{\Sigma }\equiv \mathop{\sum}\limits_{\tau }C(\tau ),$$
(11)

as a function of g, considering both single-qubit and two-qubit observables. In the infinite-measurements limit, the OLP (solid lines) in Fig. 4a displays maximum memory CΣ for g → 0+, when the system becomes effectively unperturbed (no back-action effect, see Eq. (15)). However, in realistic implementations with a finite number of measurements, the statistical uncertainty diverges in this extremely weak (non-informative) measurement limit as shown in Eq. (8). Then, the optimum sum capacity is achieved at a larger g value, depending on Nmeas, where the output expectation values are more accurate but at the same time the back-action is not too strong. Indeed the larger Nmeas, the weaker the measurement that maximizes the capacity. With Nmeas = 1.5 ⋅ 106, the optimal measurement strength is found around g = 0.3 for one-qubit observables (black diamonds).

Fig. 4: Total memory capacity and experimental resources.
figure 4

a STM sum capacity depending on g for different kinds of observables. For the OLP, solid lines represent the values when Nmeas → ∞ associated to the unfilled symbols in the same color for the Nmeas = 1.5 ⋅ 106 case. Vertical dashed lines represent the values of g = 0.3 (red), g = 0.5 (orange), and g = 10 (green). The capacities of the RWP and the RSP are nearly identical. This figure has also been reproduced for 100 realizations of the random couplings of the Hamiltonian (see Supplementary Fig. 1). In (b), CΣ is plotted as a function of the number of measurements; in (c), depending on the experimental time required. Single-qubit observables, \(\langle {\hat{\sigma }}_{i}^{\alpha }\rangle\), are used in (b) and (c), with α = x, y, z and i = 1, …, N = 6. All data shown correspond to the test set.

Full size image

Two-qubit correlations can also be exploited for QRC, and, in the ideal limit (solid purple line in Fig. 4a) they reach a larger memory capacity than single-qubit ones, as expected for a larger number of observables. However, these correlations are smaller and subject to a more significant statistical uncertainty. Therefore, with a finite number of measurements, the performance is actually worse than for single qubit observables (symbol lines). Of course, we also see that in this case there is further room for improvement by increasing Nmeas. This is a key point in view of experimental implementations as, beyond the performance achievable in QRC when considering quantum measurements, it is critical to quantify the amount of needed resources. In Fig. 4b, we represent the sum capacity as a function of the number of measurements, showing that with the OLP limited to weak measurements (red line), as well as with the RSP and the RWP, the sum capacity increases as soon as the statistical uncertainties become negligible and until the corresponding upper bound is approached. Indeed, while for ensemble sizes Nmeas ~ 104, reset protocols perform better, all the RSP, the RWP and the OLP with g = 0.3 reach ideal capacities for Nmeas ~ 106. In contrast, the use of strong measurements with the OLP leads to a slow convergence of the capacity (green line in Fig. 4b), which seems to saturate to a lower value than the one corresponding to the Nmeas → ∞ limit.

In order to analyze the real amount of resources demanded by each protocol, it is meaningful to quantify the time needed for each experimental realization (see Supplementary Results I D, Supplementary Eqs. (1)–(3)) and not only the ensemble size Nmeas. The required experimental time for each measurement protocol is shown in Fig. 4c for the case of a single-observable output layer. As expected, the RSP is not efficient, while both the OLP and the RWP achieve a good performance with the same resources, if the measurement is weak in the online approach (OLP with g = 0.3). Indeed it is interesting to compare the OLP and the RWP by finding the value of g such that \({t}_{\exp }^{{{{\rm{OLP}}}}}\le {t}_{\exp }^{{{{\rm{RWP}}}}}\) while also imposing the same statistical uncertainty in both cases. This leads to finding a criterion to determine the minimum measurement strength for online processing to be advantageous with respect to rewinding. The relevant quantity to this aim is the number of washout steps Nwo, (see Supplementary Results I D) that, as shown before, defines the finite memory of the reservoir. For single-qubit observables we find

$$g\ge \sqrt{\frac{1}{{N}_{{{{\rm{wo}}}}}-1}}.$$
(12)

This is a necessary condition to be successful in online processing (with less resources than the RWP), while it will be sufficient if the corresponding measurement is weak enough to have negligible back-action effects in the OLP. For instance, if the washout steps amount to Nwo = 20, the measurement strength in Eq. (12) is g ≳ 0.23 producing negligible back-action. Indeed the red line of Fig. 4c of best capacity corresponds to g = 0.3. The bound in g for efficient OLP also depends on the kind of observables considered. The analogous condition for two-qubit observables is more restrictive, i.e. a stronger measure is needed, as described in Supplementary Results I D and further discussed in Supplementary Results I B.

Chaotic time series forecasting

After the analysis of the STM task, we quantify the capacity of the QRC system to make forward predictions on the Santa Fe laser time series, corresponding to a NH3 laser in a chaotic dynamical state80. This benchmark dataset originates from a time-series forecasting competition held at the Santa Fe Institute in the 1990s81 and it has been used extensively ever since. Formally, our target is written as

$${y}_{k}={s}_{k+\eta },$$
(13)

where η labels the number of steps forward to make the predictions. The original values of the Santa Fe series were shifted and normalized such that {sk} ∈ [0, 1] (see Methods).

In Fig. 5a and b, we illustrate the performance of the QRC for one-step forward predictions with the unperturbed system. By considering together both single-qubit and two-qubit observables, a remarkable capacity of C = 0.98 is reached. A similar accuracy can be obtained with the RSP or the RWP. The prediction of the Santa Fe time series is particularly challenging when there is a jump from large to low amplitude oscillations, see t/Δt ~ 1500 in Fig. 5a. Accordingly, the most appreciable differences in Fig. 5b between the target and the predicted values are found when there are sudden changes in the amplitude of the signal, which are nevertheless mostly captured by the predicted values.

Fig. 5: Forecasting capacity.
figure 5

a One-step forward predictions and (b) prediction errors on the Santa Fe time series for a part of the test data when the observables of the unperturbed quantum reservoir are employed. In panel (a), target values correspond to grey-filled circles and predictions to black unfilled circles. c Capacity of predictions, C, depending on the number of time steps forward η. In panel (c), the OLP with g = 0.3 and g = 10 is used, respectively, to estimate the observables with Nmeas = 1.5 ⋅ 106 measurements at each time step. The limit case for g = 0.3 with Nmeas → ∞ is represented with a solid red line; the unperturbed situation is in black. The dashed red and green lines correspond to estimated values obtained in the limit Nmeas → ∞ but adding Gaussian noise to the observables. The values of the capacities correspond to the test data.

Full size image

The quality of further future predictions (η ≥ 1) is shown in Fig. 5c, where we have concentrated on the study of the results obtained with the OLP in comparison to the unperturbed situation (ideally retrieved by the RSP and the RWP). The prediction task becomes more complicated as the prediction distance η increases. Accordingly, the goodness of the predictions decreases with increasing η. As an exception, there are local maxima in the capacity due to the quasi-periodicity in the Santa Fe laser time series, i.e. at η ≈ 7 and η ≈ 14. As shown in the previous section for the STM task, the perturbative nature of a sharp quantum measurement (e.g. g = 10) erases part of the QRC memory on the input history. The results presented in Fig. 5c illustrate that such a memory loss also impacts the forecasting capabilities of the QRC, with the prediction capacity for g = 10 falling below the one for g = 0.3. Interestingly, in the limit of infinite measurements, the capacity for the weak measurement matches the one of the unperturbed system and there is no significant back-action effect on future predictions. The considerably good capacity obtained with the simulated experimental data with weak measurements in Fig. 5c (red symbols) could be improved with more measurements to eventually approach the upper bound (solid red line).

Discussion

The potential advantage in processing temporal data sequences with quantum systems in reservoir computing is rooted in the large processing capability opened by their Hilbert space48,50. Here, we provide the first evidence that this advantage can still be achieved beyond ideal situations, when including the effect of quantum measurement, paving the way to experimental demonstrations of sequential data processing both in memory and forecasting tasks. We have analyzed protocols where after each detection the reservoir dynamics is repeated for the whole past input sequence52,55 (named restarting protocol, RSP) or for the last part of it, exploiting the fading memory of the reservoir (rewinding protocol, RWP). The latter achieves a linear instead of a quadratic scaling with the injection steps. An alternative proposal is based on weak measurements, allowing for online data processing (OLP) without storing any inputs externally.

For time series processing, the impact on the task accuracy (i) of statistical noise (ensemble size), (ii) of measurement weakness, and (iii) of the back-action for continuous monitoring, need to be taken into account to design a quantum reservoir computer with a good compromise between performance and resource cost. Optimum performance has been shown to be reachable beyond ideal assumptions both in the RSP and RWP, with projective measurements and buffering input data, as well as in the OLP with (weak) monitoring. The distinctive feature of the OLP is the online operation, without storing any input, either classical or quantum. This is particularly advantageous in platforms where system ensembles can be measured at the output layer, at each input injection, as for atomic/molecular ensembles82 or in multimode (pulsed) photonics83, where fully online time series processing with weak measurements could be realized.

Online weak measurements enable us to partially preserve quantum coherences in the OLP. They can be implemented for different reservoirs, with a prominent example of superconducting qubits and trapped ions, where the strength of the measurement can be tuned through the interaction time between the system and measurement apparatus73,75, or through the reflectivity in the photonic memristor set-up in ref. 49. Alternative strategies for continuous monitoring time series could be considered depending on the choice of the physical reservoir, as for instance detection based on quantum jumps, while quantum non-demolition measurements could be used but are typically limited in the number of accessed observables. In general quantum trajectories have been successfully implemented in a variety of contexts72,84,85,86,87 laying the grounds for monitored QRC experiments, as recently proposed for non-temporal tasks56.

A further crucial aspect in view of experimental implementations of high-performance QRC is the efficiency in terms of experimental resources. Energy efficiency is actually a major feature of reservoir computing88. Here, we have estimated time (and therefore energy) resources relative to these different measurement protocols. We stress that the potential advantage of QRC, given by the exponential size of the Hilbert state, requires the use of higher-order terms \(\langle {\hat{\sigma }}_{i}^{{\alpha }_{i}}\otimes \cdots \otimes {\hat{\sigma }}_{j}^{{\alpha }_{j}}\otimes {\hat{\sigma }}_{l}^{{\alpha }_{l}}\rangle\) that are typically of small magnitude and actually necessitate more resources to be accurately determined. Depending on the reservoir fading memory and the performing task, we find that the OLP with measurements of the proper strength could exceed the performance of the RWP being efficient even for higher-order moments (ultimately exploiting the full size of the Hilbert space).

Quantum models suited for QRC as the one studied here are realized in state-of-the-art experiments, such as in superconducting qubits89 and trapped ions90,91. Besides our particular scheme, this realistic measurement framework establishes the advantage of quantum reservoirs beyond ideal scenarios. Furthermore, it is expected to pave the way to efficient experimental implementations involving continuous monitoring as time-series processing with quantum systems52,53,54,55 –also with time multiplexing50–, temporal quantum tomography51, quantum recurrent neural networks and quantum neuromorphic computing92, among others.

Methods

Monitored qubit system

In order to account for the measurements during the dynamics of the system with the OLP, we introduce in Eq. (3) the following measurement superoperator:

$${{{{\mathcal{M}}}}}_{{{{{\bf{V}}}}}_{k}}[\rho ]={\hat{{{{\boldsymbol{\Omega }}}}}}_{{{{{\bf{V}}}}}_{k}}\rho {\hat{{{{\boldsymbol{\Omega }}}}}}_{{{{{\bf{V}}}}}_{k}}^{{\dagger} }.$$
(14)

Given a system of N qubits, single-qubit measurements in a single realization are described by the Kraus operators \({\hat{{{{\boldsymbol{\Omega }}}}}}_{{{{{\bf{V}}}}}_{k}}={\hat{\Omega }}_{{V}_{k}^{(0)}}\otimes \,\cdots \,\otimes {\hat{\Omega }}_{{V}_{k}^{(N-1)}},\) which give a set of measurement results \({{{{\bf{V}}}}}_{kl}=\{{V}_{k\,l}^{(i)}\}\), with i = 0, …, N − 1, where the indices k and l label the time step and the experimental realization, respectively.

Indirect measurements in the z direction can be modeled by means of the following operator (see Supplementary Methods II B):

$${\hat{\Omega }}_{V}^{{{{\rm{z}}}}}=\frac{1}{\root 4 \of {2\pi }}\left({e}^{-\frac{{\left(V-g\right)}^{2}}{4}}\left\vert 0\right\rangle \left\langle 0\right\vert +{e}^{-\frac{{\left(V+g\right)}^{2}}{4}}\left\vert 1\right\rangle \left\langle 1\right\vert \right),$$
(15)

where g is the tunable strength of the measurement and V is the measurement outcome, both normalized with the width of the two Gaussians. Particularly, this operator is implemented in superconducting qubit experiments, where the value of g depends on the coupling between the cavity probe and the qubit and is tuned by varying the measurement duration70,72,74,75. Measurements in the x and y directions can be obtained by means of rotations (see Supplementary Methods II B). From Eq. (15), the probability distribution for an outcome V, when we measure a qubit in the reduced state ω, \({P}_{{{{\rm{z}}}}}(V)={{{\rm{Tr}}}}({\hat{\Omega }}_{V}^{{{{\rm{z{\dagger} }}}}}{\hat{\Omega }}_{V}^{{{{\rm{z}}}}}\omega )\), is:

$${P}_{{{{\rm{z}}}}}(V)={\omega }_{00}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{\left(V-g\right)}^{2}}{2}}+(1-{\omega }_{00})\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{\left(V+g\right)}^{2}}{2}},$$
(16)

where ω00 = 〈0∣ω∣0〉, and whose outcomes are sampled from a weighted sum of two Gaussian distributions (at distance 2g) depending on the state before the measurement. Therefore, in the limit of large g, the projective case is approached and most outcomes V can be unambiguously assigned to one of the two distributions. However, if g is small, the measurement is weak and the two distributions largely overlap making the measurement less informative (see Supplementary Methods II B, Supplementary Fig. 6). With the outcomes obtained from indirect measurements, we can compute the expectation values of the observables. For instance, when we measure a single qubit with state ω in the z direction, we have \({\langle V\rangle }_{\omega }^{{{{\rm{z}}}}}=\int\nolimits_{-\infty }^{\infty }V\,{P}_{{{{\rm{z}}}}}(V)\,dV=g{\langle {\hat{\sigma }}^{{{{\rm{z}}}}}\rangle }_{\omega }\). The expectation values of two-qubit observables are computed in a similar way, as shown in Supplementary Methods II B 2.

Quantum reservoir based on a disordered transverse Ising model

Reservoir computing38,46,47 is a supervised machine learning method based on the three-layer scheme: (i) input, (ii) reservoir, and (iii) output, depicted in Fig. 1a. The main enabling features of reservoir computing are the ability to differentiate any pair of inputs, known as separability93, the fading memory in the past and the independence of the reservoir initialization (echo state or convergence property)69. This guarantees that after a transient time the reservoir output depends only on the recent input sequence. Recent proposals for quantum reservoir computing have been reviewed in48.

The quantum reservoir computer considered in this work consists of a qubit network evolving in time under the action of the disordered transverse-field Ising Hamiltonian50,53:

$$\hat{H}=\frac{1}{2}\mathop{\sum }\limits_{i=0}^{N-1}h{\hat{\sigma }}_{i}^{{{{\rm{z}}}}}+\mathop{\sum }\limits_{i < j}^{N-1}{J}_{ij}{\hat{\sigma }}_{i}^{{{{\rm{x}}}}}{\hat{\sigma }}_{j}^{{{{\rm{x}}}}}.$$
(17)

In all the numerical simulations, we used N = 6 qubits and randomly generated a single set of qubit-qubit couplings Jij from a uniform distribution in the interval [ − Js/2, Js/2], where Js is set as a reference unit. Actually, the scope of our analysis is valid beyond the specific choice of the reservoir. We have checked that the deviations introduced by different coupling realizations90 are not relevant, as can be seen in the example of Supplementary Results I A. The external magnetic field and the time interval, respectively, are fixed at h = 10Js and Δt = 10/Js so that the reservoir is in an appropriate dynamical regime where the system tends to thermalize53. The input is represented by a sequence {s0, s1, …, sk, … } and is injected into the system by rewriting a node state \({\rho }_{k}^{{{{\rm{in}}}}}\) every time step k. In particular, we consider encoding a real input sk ∈ [0, 1] in one qubit (labeled by 0) by setting it at each time into a pure state \(\left\vert {\psi }_{k}\right\rangle =\sqrt{1-{s}_{k}}\left\vert 0\right\rangle +\sqrt{{s}_{k}}\left\vert 1\right\rangle\)78. The resulting evolution after input injection is given by the completely positive trace-preserving map \({{{{\mathcal{L}}}}}_{k}[\rho ]=\hat{U}\left({\rho }_{k}^{{{{\rm{in}}}}}\otimes {{{{\rm{Tr}}}}}_{{{{\rm{in}}}}}\left[\rho \right]\right){\hat{U}}^{{\dagger} }\)50,53. This fully defines the unperturbed state dynamics in the case of the RSP and the RWP, as given by Eqs. (1) and (3).

QRC training and test

For task resolution, the QRC systems are trained in a supervised manner. Given the target output yk for the input sk in the training examples, a linear weighted combination of the reservoir observables that constitute the output feature space is constructed to minimize the prediction error with a least-squares method34. More precisely, the form of the predictions is

$${\tilde{y}}_{k}=\mathop{\sum }\limits_{m=1}^{L}{w}_{m}{\langle \hat{{{{\mathcal{O}}}}}\rangle }_{k,(m)}+{w}_{L+1},$$
(18)

where wm are the free parameters (weights) to be optimized, including the bias term wL+1. The total number of weights employed, L, depends on our particular choice for the observable set. For instance, when we consider the expectation values of \({\hat{\sigma }}_{i}^{{{{\rm{x}}}}}\), \({\hat{\sigma }}_{i}^{{{{\rm{y}}}}}\), and \({\hat{\sigma }}_{i}^{{{{\rm{z}}}}}\) for all qubits, then the dimension of the feature space is L = 3N.

For the STM task, we consider a total dataset of Nt = 1000 time steps. The initial Nwo = 20 instants within the washout time are discarded. This value, in agreement with previous results79, is long enough to guarantee a nearly identical performance between the RSP and the RWP. It is also valid for the OLP even if a shorter time could be enough, as the memory of the system is reduced for increasing values of g due to back-action. The weights in Eq. (18) are optimized using the following 735 time instants and the last 245 time steps constitute the test set, where the learned weights are used to evaluate the accuracy of the QRC system.

For the Santa Fe task, the data set is comprised of Nt = 2000 time steps. The first Nwo = 20 time steps are again discarded. The following 70% instants are used to train the weights, while the test prediction error is evaluated for the last 30% steps.

The QRC performance is quantitatively evaluated through the capacity

$$C\equiv \frac{{{{{\rm{cov}}}}}^{2}\left({{{\boldsymbol{y}}}},\tilde{{{{\boldsymbol{y}}}}}\right)}{{{{\rm{var}}}}({{{\boldsymbol{y}}}}){{{\rm{var}}}}(\tilde{{{{\boldsymbol{y}}}}})},$$
(19)

where \({{{\rm{cov}}}}\left({{{\boldsymbol{y}}}},\tilde{{{{\boldsymbol{y}}}}}\right)\) indicates the covariance between the two series and var(y) is the variance. C ∈ [0, 1] and perfect predictions are obtained with C = 1.