Practical quantum tokens without quantum memories and experimental tests

Abstract

Unforgeable quantum money tokens were the first invention of quantum information science, but remain technologically challenging as they require quantum memories and/or long-distance quantum communication. More recently, virtual “S-money” tokens were introduced. These are generated by quantum cryptography, do not require quantum memories or long-distance quantum communication, and yet in principle guarantee many of the security advantages of quantum money. Here, we describe implementations of S-money schemes with off-the-shelf quantum key distribution technology, and analyse security in the presence of noise, losses, and experimental imperfection. Our schemes satisfy near-instant validation without cross-checking. We show that, given standard assumptions in mistrustful quantum cryptographic implementations, unforgeability and user privacy could be guaranteed with attainable refinements of our off-the-shelf setup. We discuss the possibilities for unconditionally secure (assumption-free) implementations.

Introduction

Quantum tokens, also called quantum money, were invented by Wiesner¹ in 1970. In Wiesner’s original quantum token scheme Bob (the bank) secretly and securely generates a classical serial number s and a quantum state $\left|\psi \right\rangle$ of N qubits, prepared from a set of different bases, gives s and $\left|\psi \right\rangle$ to Alice, and stores s and the classical description of $\left|\psi \right\rangle$ in a database. Alice presents the token by giving s and $\left|\psi \right\rangle$ back to Bob, and Bob validates or rejects the token after measuring the received quantum state in the basis in which $\left|\psi \right\rangle$ was prepared. In refinements of this scheme^{2,3,4,5,6,7,8,9,10}, Alice can present the token to Bob or to one of a set of verifiers, by communicating the classical outcomes of quantum measurements applied on $\left|\psi \right\rangle$, as requested by Bob or the verifier. Alternatively, Alice presents the token by giving s and $\left|\psi \right\rangle$ to the verifier, who applies quantum measurements on $\left|\psi \right\rangle$. The verifier communicates with Bob to validate or reject the token.

There exist quantum token schemes satisfying unforgeability, i.e., they guarantee that a token cannot be validated more than once, with unconditional security, i.e., based only on the laws of physics without restricting the technology of dishonest Alice^{2,3,4,5,6,7,8,9,10}. Intuitively, this follows from the no-cloning theorem, stating that it is impossible to perfectly copy unknown quantum states^11,12. Unforgeable quantum token schemes based on computational assumptions have also been investigated (e.g., ^13,14,15,16), with some of these schemes not requiring communication with the bank for token validation (e.g., ^15,16).

However, there exist purely classical token schemes that can also guarantee unforgeability with unconditional security. For example, the token may comprise a classical serial number s and a classical secret password x that Bob gives Alice and that Alice presents by giving to one of a set of verifiers; validation of the token comprises cross-checking; for example, the verifier communicates with Bob and validates the token if this has not been presented before and if the given serial number and password correspond to each other.

In addition to unforgeability, some important properties of quantum token schemes are the following. First, quantum tokens can be transferred while keeping Bob’s database static. On the other hand, since classical information can be copied perfectly, in order to satisfy unforgeability, when a purely classical token with serial number s is transferred from Alice to another party Charlie, Bob must change the classical data associated to s; for example, Bob must change x to another value $x^{\prime}$ and give s and $x^{\prime}$ to Charlie in the example above².

Second, some quantum token schemes satisfy instant validation. This means that the schemes do not require communication between the verifiers and Bob for validation after Alice presents the token⁴. This implies in particular that the token can be presented by Alice at one of a set of different spacetime points that can be spacelike separated without validation delays by the verifier due to cross-checking with Bob and/or with other verifiers.

Third, quantum token schemes satisfy future privacy for the user or simply user privacy. That is, neither Bob, nor the verifiers, can know where and when Alice will present the token.

It is not difficult to construct purely classical token schemes that satisfy with unconditional security any two of unforgeability, instant validation, and user privacy. For example, the classical token scheme above satisfies unforgeability and user privacy with unconditional security, but not instant validation. To the best of our knowledge, no purely classical token scheme has been shown to satisfy all three properties simultaneously with unconditional security. Classical variations of the quantum token schemes we consider here, based on classical relativistic bit commitments, whose security is hypothesized but not proven, were proposed in ref. ¹⁷, which considers their potential advantages and disadvantages. As far as we are aware, aside from these, there are no known classical schemes that plausibly satisfy all three properties simultaneously with unconditional security.

Among plausible future applications of quantum token schemes are very high value and time-critical transactions requiring very high security, such as financial trading, where many transactions take place within half a millisecond¹⁸, or network control, where semi-autonomous teams need authentication as fast as possible. A reasonable assumption for such applications is that tokens may be transferred a relatively small number of times among a relatively small set of parties—the tokens may be valid for a relatively short time, for example. In this context, Bob having a static database does not seem to be a great advantage of quantum token schemes over classical schemes whose databases must be updated after each transaction, given that processing classical information is much easier and cheaper than processing quantum information. Furthermore, for very high-value transactions one might expect that the communication network among Bob and the verifiers is sufficiently protected that communication among them is very rarely (if ever) interrupted. So, in this context, it appears to be a major advantage of quantum token schemes over classical token schemes that a quantum token can be presented at one of a set of spacelike separated points with near-instant validation without time delays due to cross-checking, while satisfying unforgeability and user privacy with unconditional security.

Standard quantum token schemes satisfying unforgeability, user privacy and instant validation with unconditional security require to store quantum states in quantum memories and/or to transfer quantum states over long distances in order to give Alice enough flexibility in space and time to present the token^{1,2,3,4,5,6,7,8,9,10,13,14,15,16}. Recently, a quantum memory of a single qubit with a coherence time of over an hour has been experimentally demonstrated^19,20. However, storing large quantum states for more than a fraction of a second remains challenging^21,22. Furthermore, the transmission of quantum states over long distances in practice comprises the transmission of photons through optical fiber or through the atmosphere via satellites. In both cases a great fraction of the transmitted photons is lost. For these reasons, standard quantum token schemes are impractical for most purposes at present.

Recently, experimental investigations of quantum token schemes have been performed^{23,24,25,26,27}. References^23,27 investigated the experimental implementation of forging attacks on quantum token schemes. Reference²⁴ presented a simulation of a quantum token scheme in IBM’s five-qubit quantum computer. References^25,26 reported proof-of-principle experimental demonstrations of the preparation and verification stages of quantum token schemes, by transmitting quantum states encoded in photons over a short distance—for example, ref. ²⁶ reports optical fiber lengths of up to 10 m. A full experimental demonstration of a quantum token scheme that includes storing quantum states in a quantum memory and/or transmitting quantum states over long distances remains an important open problem.

“S-money”¹⁷ is a class of quantum token schemes, which is designed for the settings described above comprising networks with relativistic or other trusted signaling constraints. These schemes can guarantee many of the security advantages of standard quantum token schemes—in particular, instant validation, unforgeability, and user privacy—without requiring either quantum state storage or long-distance transmission of quantum states. Furthermore, S-money tokens that can be transferred among several parties and that give the users great flexibility in space and time to present the token are also possible²⁸. In this paper, we begin to investigate how securely S-money schemes can be implemented in practice with current technology.

Our results are twofold. First, we introduce quantum token schemes that extend the quantum S-money scheme of ref. ²⁹ in practical experimental scenarios that consider losses, errors in the state preparations and measurements, and deviations from random distributions; and, in photonic setups, photon sources that do not emit exactly single photons, and single-photon detectors with non-unit detection efficiencies and with nonzero dark count probabilities, which are threshold detectors, i.e., which cannot distinguish the number of photons in detected pulses. In our schemes, Alice can present the token at one of 2^M possible spacetime presentation points, which can have arbitrary timelike or spacelike separation, for any positive integer M. Our schemes satisfy instant validation and comprise Bob transmitting N quantum states to Alice over a distance which can be arbitrarily short, Alice measuring the received quantum states without storing them, and further classical processing and classical communication over distances which can be arbitrarily large. Thus, our schemes are advantageous over standard quantum token schemes because they do not need quantum state storage or transmission of quantum states over long distances. We use the flexible versions of S-money defined in ref. ²⁸, giving Alice the freedom to choose her spacetime presentation point after having performed the quantum measurements. We show that our schemes satisfy unforgeability and user privacy, given assumptions that have been standard in implementations of mistrustful quantum cryptography to date (see Table 6) but are nonetheless idealizations.

Second, we performed experimental tests of the quantum stage of one of our schemes for the case of two presentation points, which show that with refinements of our setup our schemes can be implemented securely, giving guarantees of unforgeability and user privacy, based on the standard assumptions in experimental mistrustful quantum cryptography mentioned above.

Results

Preliminaries and notation

We present below two quantum token schemes that do not require quantum state storage, are practical to implement with current technology, and allow for experimental imperfections. We show that for a range of experimental parameters our token schemes are secure.

In the token schemes below, Bob (the bank) and Alice (the acquirer) agree on spacetime regions Q_i where a token can be presented by Alice to Bob, for i ∈ {0, 1}^M and for some agreed integer M ≥ 1. Bob has trusted agents ${{{\mathcal{B}}}}$ and ${{{{\mathcal{B}}}}}_{i}$ controlling secure laboratories, and Alice has trusted agents ${{{\mathcal{A}}}}$ and ${{{{\mathcal{A}}}}}_{i}$ controlling secure laboratories, for i ∈ {0, 1}^M. The agent ${{{{\mathcal{A}}}}}_{i}$ can send messages to ${{{{\mathcal{B}}}}}_{i}$ in the spacetime region Q_i, for i ∈ {0, 1}^M. All communications among agents of the same party are performed via secure and authenticated classical channels, which can be implemented with previously distributed secret keys. Alice’s agent ${{{\mathcal{A}}}}$ and Bob’s agent ${{{\mathcal{B}}}}$ perform the specified actions in a spacetime region P that lies within the intersection of the causal pasts of all Q_i, unless otherwise stated.

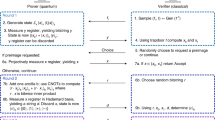
The token schemes comprise two main stages. Stage I includes the quantum communication between ${{{\mathcal{B}}}}$ and ${{{\mathcal{A}}}}$, which can take place between adjacent laboratories, and must be implemented within the intersection of the causal pasts of all the presentation points. In particular, this stage can take an arbitrarily long time and can be completed arbitrarily in the past of the presentation points, which is very helpful for practical implementations. Stage II comprises only classical processing and classical communication among agents of Bob and Alice, and must be implemented very fast in order to satisfy some relativistic constraints. A token received by ${{{{\mathcal{B}}}}}_{b}$ from ${{{{\mathcal{A}}}}}_{b}$ at Q_b can be validated by ${{{{\mathcal{B}}}}}_{b}$ near-instantly at Q_b, without the need to cross-check with other agents. We note that Alice chooses her presentation point in stage II, meaning in particular that it can take place after her quantum measurements have been completed. This is basically the application of the refinement of flexible S-money tokens discussed in ref. ²⁸, which gives Alice great flexibility in spacetime to choose her presentation point. See Tables 1–3 for details.

In stage I, ${{{\mathcal{B}}}}$ generates quantum states randomly from a predetermined set and gives these to ${{{\mathcal{A}}}}$. ${{{\mathcal{A}}}}$ measures the received states in bases from a predetermined set. ${{{\mathcal{A}}}}$ sends some classical messages to ${{{\mathcal{B}}}}$, mainly to indicate the set of states that she successfully measured. For all i ∈ {0, 1}^M, ${{{\mathcal{A}}}}$ communicates her classical outcomes to ${{{{\mathcal{A}}}}}_{i}$; ${{{\mathcal{B}}}}$ sends classical messages to ${{{{\mathcal{B}}}}}_{i}$, indicating mainly the labels of the states reported by ${{{\mathcal{A}}}}$ to be successfully measured.

In stage II, Alice chooses the label b ∈ {0, 1}^M of her chosen presentation point in the intersection of the causal pasts of the presentation points. Further classical communication steps among agents of Alice and Bob take place. The token schemes conclude by Alice giving a classical message x (the token) to Bob at her chosen presentation point Q_b and Bob validating the token at Q_b if x satisfies a mathematical condition.

The main difference between the first and second token schemes below (either in their idealized or realistic version) is that, in the first one, Alice measures each received qubit randomly in one of two predetermined bases, while in the second one Alice measures large sets of qubits in the same basis, which is chosen randomly by Alice from two predetermined bases. The first token scheme is more suitable to implement with setups used for quantum key distribution. The second token scheme requires a slightly different setup.

We say a token scheme satisfies instant validation if, for any presentation point Q_i, an agent of Bob receiving a token from Alice at Q_i can validate or reject the token nearly instantly at Q_i, without the need to wait for any messages from other agents at spacetime points spacelike separated from Q_i.

We say a token scheme is:

• ϵ_rob − robust if the probability that Bob aborts when Alice and Bob follow the token scheme honestly is not greater than ϵ_rob, for any b ∈ {0, 1}^M;

• ϵ_cor − correct if the probability that Bob does not accept Alice’s token as valid when Alice and Bob follow the token scheme honestly is not greater than ϵ_cor, for any b ∈ {0, 1}^M;

• ϵ_priv − private if the probability that Bob guesses Alice’s bit-string b before she presents her token to Bob is not greater than $\frac{1}{{2}^{M}}+{\epsilon }_{{{\mathrm{priv}}}}$, if Alice follows the token scheme honestly, for b ∈ {0, 1}^M chosen randomly from a uniform distribution by Alice;

• ϵ_unf − unforgeable, if the probability that Bob accepts Alice’s tokens as valid at any two or more different presentation points is not greater than ϵ_unf, if Bob follows the token scheme honestly.

We say a token scheme using N transmitted quantum states is:

• robust if it is ϵ_rob − robust with ϵ_rob decreasing exponentially with N.

• correct if it is ϵ_cor − correct with ϵ_cor decreasing exponentially with N.

• private if it is ϵ_priv − private with ϵ_priv approaching zero by increasing some security parameter.

• unforgeable if it is ϵ_unf − unforgeable with ϵ_unf decreasing exponentially with N.

Note that our definition of privacy is different because it depends on different parameters: see Lemma 4 below. In our schemes each of the N quantum states is a qubit state with probability 1 − P_noqub, and a quantum state of arbitrary Hilbert space dimension greater than two with probability P_noqub, where P_noqub = 0 in ideal schemes and P_noqub > 0 in practical schemes. In photonic implementations, each pulse transmitted by Bob is either vacuum or one-photon with probability 1 − P_noqub, and multi-photon with probability P_noqub.

Below we present token schemes for two presentation points (M = 1) that satisfy instant validation and that are robust, correct, private, and unforgeable. The extension to 2^M presentation points for any $M\in {\mathbb{N}}$ is given in Supplementary Note VIII. For clarity of the presentation, we first present the ideal quantum token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$ where there are not any losses, errors, or any other experimental imperfections. These are given in Table 1. More realistic quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ that allow for various experimental imperfections are presented in Tables 2 and 3, respectively. A summary of the used notation is given in Table 4. An illustration of implementation in a token scheme for the case of two spacelike separated presentation points is given in Fig. 1. A diagram of the schemes is given in Fig. 2.

Table 1 Ideal quantum token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$ for two presentation points. Steps 1 to 8 in ${{{{\mathcal{IQT}}}}}_{1}$, and 1 to 5 in ${{{{\mathcal{IQT}}}}}_{2}$, take place within the intersection of the causal pasts of the presentation points.

Table 2 Practical quantum token scheme ${{{{\mathcal{QT}}}}}_{1}$ for two presentation points. Steps 1 to 9 take place within the intersection of the causal pasts of the presentation points. See Table 4 for a summary of the notation and Fig. 2 for an illustration of the scheme.

Table 3 Practical quantum token scheme ${{{{\mathcal{QT}}}}}_{2}$ for two presentation points. See Table 4 for a summary of the notation and Fig. 2 for an illustration of the scheme.

Table 4 Summary of notation used for ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$.

Fig. 1: Illustration of implementation in a quantum token scheme.

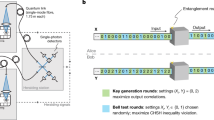
A case of two presentation points in a Minkowski spacetime diagram in 1 + 1 dimensions is illustrated. Bob has laboratories B, B₀, and B₁, controlled by agents ${{{\mathcal{B}}}}$, ${{{{\mathcal{B}}}}}_{0}$, and ${{{{\mathcal{B}}}}}_{1}$ (yellow rectangles), and Alice has laboratories A, A₀, and A₁, controlled by agents ${{{\mathcal{A}}}}$, ${{{{\mathcal{A}}}}}_{0}$, and ${{{{\mathcal{A}}}}}_{1}$ (green rectangles), adjacent to Bob’s laboratories. The quantum communication stage takes place within B and A, can take an arbitrarily long time and can be completed arbitrarily in the past of the presentation points (Q₀ and Q₁). Alice’s classical measurement outcomes x are kept secret by Alice and communicated to her laboratories A₀ and A₁ via secure and authenticated classical channels. In this illustrated example, Alice sends classical messages to Bob at laboratory B, and either at B₀ or B₁. The messages sent to B can take place anywhere in the past of Q₀ and Q₁ after the quantum communication stage and includes a message indicating the labels of the quantum states successfully measured by Alice. These messages are communicated from B to B₀ and B₁ via secure and authenticated classical channels. Alice chooses to present her token at Q_b within the intersection of the causal pasts of Q₀ and Q₁. The message at either B₀ or B₁ is the bit c = b ⊕ z, effectively committing Alice to present her token at Q_b. Alice presents the token by giving Bob x at Q_b. The case b = 1 is illustrated. The small black box represents a fast classical computation performed at Bob’s laboratory receiving the token, to validate or reject Alice’s token, as described in step 12 of the scheme ${{{{\mathcal{QT}}}}}_{1}$ (see Table 2), for instance. As illustrated, this would require this computation to be completed within a time shorter than the time that light takes to travel between the locations of laboratories B₀ and B₁, which could be 10 μs if B₀ and B₁ are separated by 3 km, for example. This is because, as discussed in the introduction, we require presentation and acceptance to be completed within spacelike separated regions in order to achieve an advantage over purely classical token schemes.

We use the following notation. We use bold font notation a for strings of bits. The bit-wise complement of a string a is denoted by $\bar{{{{\bf{a}}}}}$. The kth bit entry of a string a is denoted by a_k. We define the set [N] = {1, 2, …, N}. The symbol “⊕” denotes bit-wise sum modulo 2 or sum modulo 2 depending on the context. We write the Bennett-Brassard 1984 (BB84) states³⁰ as $\left|{\phi }_{00}\right\rangle =\left|0\right\rangle$, $\left|{\phi }_{10}\right\rangle =\left|1\right\rangle$, $\left|{\phi }_{01}\right\rangle =\left|+\right\rangle$ and $\left|{\phi }_{11}\right\rangle =\left|-\right\rangle$, where $\left|\pm \right\rangle =\frac{1}{\sqrt{2}}\left(\left|0\right\rangle \pm \left|1\right\rangle \right)$, and where ${{{{\mathcal{D}}}}}_{0}=\{\left|0\right\rangle ,\left|1\right\rangle \}$ and ${{{{\mathcal{D}}}}}_{1}=\{\left|+\right\rangle ,\left|-\right\rangle \}$ are qubit orthonormal bases, called the computational and Hadamard bases, respectively. The Hamming distance is denoted by d( ⋅ , ⋅ ).

Fig. 2: Diagram of the quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$.

Alice’s (Bob’s) steps are indicated with the blue (red) arrows. The differences between ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are shown. b The steps perfomed by Alice’s and Bob’s agents ${{{\mathcal{A}}}}$ and ${{{\mathcal{B}}}}$ in ${{{{\mathcal{QT}}}}}_{1}$ are illustrated. a The steps of Alice’s and Bob’s agents ${{{{\mathcal{A}}}}}_{i}$ and ${{{{\mathcal{B}}}}}_{i}$ in ${{{{\mathcal{QT}}}}}_{1}$ are shown, for i ∈ {0, 1}. The case i = b represents Alice’s token presentation and Bob’s validation/rejection.

The quantum token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$ given in Table 1 have the following properties.

First, the token schemes are correct. Since we assume there are not any errors in the state preparations and measurements, if Alice and Bob follow the token scheme honestly then Bob validates Alice’s token at her chosen presentation point Q_b with unit probability. If Alice and Bob follow ${{{{\mathcal{IQT}}}}}_{1}$ honestly, ${\tilde{d}}_{b,k}={d}_{b,k}\oplus c={d}_{k}\oplus b\oplus c={y}_{k}\oplus z\oplus b\oplus c={y}_{k}$, for k ∈ [N]. Thus, ${\tilde{{{{\bf{d}}}}}}_{b}={{{\bf{y}}}}$, which means that y_k = u_k for all k ∈ Δ_b, hence, Alice measures in the same basis of preparation by Bob for all states $\left|{\psi }_{k}\right\rangle$ with labels k ∈ Δ_b. Therefore, Alice obtains the correct outcomes for these states: x_b = t_b. Similarly, if Alice and Bob follow ${{{{\mathcal{IQT}}}}}_{2}$ honestly then we have that ${\tilde{{{{\bf{d}}}}}}_{b}$ has bit entries ${\tilde{d}}_{b,k}=b\oplus c=z={y}_{k}$, for k ∈ [N]. Thus, as above, ${\tilde{{{{\bf{d}}}}}}_{b}={{{\bf{y}}}}$, i.e., ${\tilde{{{{\bf{d}}}}}}_{b}$ corresponds to the string of measurement basis implemented by Alice. Therefore, in both token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$, Alice obtains x_b = t_b and Bob validates Alice’s token at Q_b with unit probability.

Second, the token schemes are robust. More precisely, neither Bob nor Alice have the possibility to abort. This is because we assume there are not any losses of the transmitted quantum states and that Alice successfully measures all the received quantum states. Thus, Alice does not need to report to Bob any labels of states that she successfully measured, in contrast to the extended token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ discussed below.

Third, the token schemes are private, i.e., Bob cannot obtain any information about b in the causal past of Q_b. This is because the messages Alice sends Bob in the causal past of Q_b carry no information about b and we assume that Alice’s laboratories and communication channels are secure.

Fourth, the token schemes are unforgeable. This follows from the following lemma, which is shown in Supplementary Note IV. Alternative proofs are given in ref. ³¹, based on quantum state discrimination tasks. We have chosen the proof given in Supplementary Note IV because an extension of it allows us to prove Theorem 1 too.

Lemma 1

The quantum token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$ are ϵ_unf − unforgeable with

$${\epsilon }_{{{\mathrm{unf}}}}={\left(\frac{1}{2}+\frac{1}{2\sqrt{2}}\right)}^{N}.$$

(1)

Fifth, the token schemes satisfy instant validation. We note from step 11 of ${{{{\mathcal{IQT}}}}}_{1}$ that a token received by Bob’s agent ${{{{\mathcal{B}}}}}_{b}$ from Alice’s agent ${{{{\mathcal{A}}}}}_{b}$ at a presentation point Q_b can be validated by ${{{{\mathcal{B}}}}}_{b}$ near-instantly at Q_b. In particular, ${{{{\mathcal{B}}}}}_{b}$ does not need to wait for any signals coming from other agents of Bob.

Finally, the token schemes above can be modified in various ways. For example, in ${{{{\mathcal{IQT}}}}}_{1}$, step 3 can be discarded, and step 10 can be replaced by the following: after choosing b, ${{{\mathcal{A}}}}$ sends x to ${{{{\mathcal{A}}}}}_{b}$ and ${{{{\mathcal{A}}}}}_{b}$ presents the token x to ${{{{\mathcal{B}}}}}_{b}$ in Q_b. In another variation, step 5 in ${{{{\mathcal{IQT}}}}}_{1}$ can be modified so that ${{{\mathcal{B}}}}$ computes d_i and sends it to ${{{{\mathcal{B}}}}}_{i}$; in both versions of step 5, ${{{{\mathcal{B}}}}}_{i}$ must have d_i in the causal past of Q_i, for i ∈ {0, 1}. In another variation, the step 9 in ${{{{\mathcal{IQT}}}}}_{1}$ is performed only by Bob’s agent ${{{{\mathcal{B}}}}}_{b}$ receiving a token from Alice. The version we have chosen for step 9 allows ${{{{\mathcal{B}}}}}_{b}$ to reduce the computation time after receiving a token, hence, allowing faster token validation. Further variations of the token schemes can be devised in order to satisfy specific requirements; for example, some steps might need to be completed within very short times, which might require reducing the computations within these steps, which can be achieved by delegating some computations within some other steps, for instance.

Practical quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ for two presentation points

The quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ presented in Tables 2 and 3 extend the quantum token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$ to allow for various experimental imperfections (see Table 5), and under some assumptions (see Table 6). ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ can be implemented in practice with the photonic setups of Fig. 3. The token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ can be modified in various ways, as discussed for the token schemes ${{{{\mathcal{IQT}}}}}_{1}$ and ${{{{\mathcal{IQT}}}}}_{2}$.

Fig. 3: Photonic setups to implement the quantum stage of ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$.

In both ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$, the setup of honest ${{{\mathcal{B}}}}$ comprises an approximate single-photon source and a polarization state modulator, encoding the quantum state $\left|{\psi }_{k}\right\rangle$ in the polarization degrees of freedom of a photon pulse labeled by k, for k ∈ [N]. a In ${{{{\mathcal{QT}}}}}_{1}$, the setup of honest ${{{\mathcal{A}}}}$ comprises a 50:50 beam splitter, a wave plate, two polarizing beam splitters (PBS₀₁ and PBS₊₋), and four threshold single-photon detectors D₀, D₁, D₊, and D₋. In order to counter multi-photon attacks by ${{{\mathcal{B}}}}$,${{{\mathcal{A}}}}$ implements the following reporting strategy that we call here reporting strategy 1: ${{{\mathcal{A}}}}$ assigns successful measurement outcomes in the basis ${{{{\mathcal{D}}}}}_{0}$ (${{{{\mathcal{D}}}}}_{1}$) with unit probability for the pulses in which at least one of the detectors D₀ and D₁ (D₊ and D₋) click and D₊ and D₋ (D₀ and D₁) do not click. As follows from ref. ⁵³, this reporting strategy offers perfect protection against arbitrary multi-photon attacks, given assumption F (see Table 6, and Lemma 5 in Methods). b In ${{{{\mathcal{QT}}}}}_{2}$, the setup of honest ${{{\mathcal{A}}}}$ comprises a wave plate set in one of two positions, according to the value of her bit z, a polarizing beam splitter, and two threshold single-photon detectors D₀ and D₁. In order to counter multi-photon attacks by ${{{\mathcal{B}}}}$, ${{{\mathcal{A}}}}$ implements the following reporting strategy that we call here reporting strategy 2: ${{{\mathcal{A}}}}$ reports to ${{{\mathcal{B}}}}$ as successful measurements those in which at least one of her two detectors click. As follows from ref. ⁵³, this reporting strategy offers perfect protection against arbitrary multi-photon attacks, given assumption F (see Table 6, and Lemma 5 in Methods).

Regarding correctness, we note in the token scheme ${{{{\mathcal{QT}}}}}_{1}$ that if Alice follows the token scheme honestly and chooses to present the token in Q_b, then we have that ${\tilde{{{{\bf{d}}}}}}_{b}$ has bit entries ${\tilde{d}}_{b,j}={d}_{b,j}\oplus c={d}_{j}\oplus b\oplus c={d}_{j}\oplus z={y}_{j}$, for j ∈ [n]. Thus, ${\tilde{{{{\bf{d}}}}}}_{b}={{{\bf{y}}}}$, i.e., ${\tilde{{{{\bf{d}}}}}}_{b}$ corresponds to the string of measurement bases implemented by Alice on the quantum states reported to be successfully measured. Similarly, in the token scheme ${{{{\mathcal{QT}}}}}_{2}$ if Alice follows the token scheme honestly and chooses to present the token in Q_b, then we have that ${\tilde{{{{\bf{d}}}}}}_{b}$ has bit entries ${\tilde{d}}_{b,j}=b\oplus c=z={y}_{j}$, for j ∈ [n]. Thus, as above, ${\tilde{{{{\bf{d}}}}}}_{b}={{{\bf{y}}}}$, i.e., ${\tilde{{{{\bf{d}}}}}}_{b}$ corresponds to the string of measurement bases implemented by Alice on the quantum states reported to be successfully measured. Therefore, in both token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$, if Alice can guarantee her error probability to be bounded by E < γ_err then with very high probability she will make less than ∣Δ_b∣γ_err bit errors in the ∣Δ_b∣ quantum states that she measured in the basis of preparation by Bob.

Let P_det be the probability that a quantum state $\left|{\psi }_{k}\right\rangle$ transmitted by Bob is reported by Alice as being successfully measured, with label k ∈ Λ, for k ∈ [N]. Let E be the probability that Alice obtains a wrong measurement outcome when she measures a quantum state $\left|{\psi }_{k}\right\rangle$ in the basis of preparation by Bob; if the error rates E_tu are different for different prepared states, labeled by t, and for different measurement bases, labeled by u, we simply take $E=\mathop{\max }\nolimits_{t,u}\{{E}_{tu}\}$.

The robustness, correctness, privacy, and unforgeability of ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are stated by the following lemmas, proven in Supplementary Note V, and theorem, proven in Supplementary Note VII. These lemmas and theorem consider parameters γ_det, γ_err ∈ (0, 1), allow for the experimental imperfections of Table 5, and make the assumptions of Table 6. A diagram presenting the conditions under which robustness, correctness, and unforgeability are satisfied simultaneously is given in Fig. 4.

Fig. 4: Illustration of security conditions for ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$.

A diagram presenting the conditions under which robustness, correctness, and unforgeability of the quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are satisfied simultaneously is illustrated (see Lemmas 2 and 3 and Theorem 1). The function f is defined by (8). If all the conditions are satisfied (filled area) then there exist a sufficiently large integer N such that ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are ϵ_rob-robust, ϵ_cor-correct and ϵ_unf-unforgeable, for desired values of ϵ_rob, ϵ_cor, ϵ_unf > 0.

Lemma 2

If

$$0\, < \,{\gamma }_{{{\mathrm{det}}}}\, < \,{P}_{{{\mathrm{det}}}},$$

(2)

then ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are ϵ_rob − robust with

$${\epsilon }_{{{\mathrm{rob}}}}={e}^{-\frac{{P}_{{{\mathrm{det}}}}N}{2}{\left(1\,-\,\frac{{\gamma }_{{{\mathrm{det}}}}}{{P}_{{{\mathrm{det}}}}}\right)}^{2}.}$$

(3)

Lemma 3

If

$$\begin{array}{l}0\, < \,\frac{{\gamma }_{{{\mathrm{err}}}}}{2}\, < \,E\, < \,{\gamma }_{{{\mathrm{err}}}},\\ 0\, < \,{\nu }_{{{\mathrm{cor}}}}\, < \,\frac{{P}_{{{\mathrm{det}}}}(1-2{\beta }_{{{\mathrm{PB}}}})}{2},\end{array}$$

(4)

then ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are ϵ_cor − correct with

$${\epsilon }_{{{\mathrm{cor}}}}={e}^{-\frac{{P}_{{{\mathrm{det}}}}(1-2{\beta }_{{{\mathrm{PB}}}})N}{4}{\left(1-\frac{2{\nu }_{{{\mathrm{cor}}}}}{{P}_{{{\mathrm{det}}}}(1-2{\beta }_{{{\mathrm{PB}}}})}\right)}^{2}}+{e}^{-\frac{E{\nu }_{{{\mathrm{cor}}}}N}{3}{\left(\frac{{\gamma }_{{{\mathrm{err}}}}}{E}-1\right)}^{2}}.$$

(5)

Lemma 4

${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are ϵ_priv − private with

$${\epsilon }_{{{\mathrm{priv}}}}={\beta }_{{{\mathrm{E}}}}.$$

(6)

Theorem 1

Consider the constraints

$$\begin{array}{l}0\, < \,{\gamma }_{{{\mathrm{err}}}}\, < \,\lambda (\theta ,{\beta }_{{{\mathrm{PB}}}}),\\ 0\, < \,{P}_{{{\mathrm{noqub}}}}\, < \,{\nu }_{{{\mathrm{unf}}}}\, < \,\min \left\{\,2{P}_{{{\mathrm{noqub}}}},{\gamma }_{{{\mathrm{det}}}}\left(1-\frac{{\gamma }_{{{\mathrm{err}}}}}{\lambda (\theta ,{\beta }_{{{\mathrm{PB}}}})}\right)\right\},\\ 0\, < \,{\beta }_{{{\mathrm{PS}}}}\, < \,\frac{1}{2}\left[{e}^{\frac{\lambda (\theta ,{\beta }_{{{\mathrm{PB}}}})}{2}{\left(1-\frac{\delta }{\lambda (\theta ,{\beta }_{{{\mathrm{PB}}}})}\right)}^{2}}-1\right].\end{array}$$

(7)

We define the function

$$\begin{array}{l}f({\gamma }_{{{\mathrm{err}}}},{\beta }_{{{\mathrm{PS}}}},{\beta }_{{{\mathrm{PB}}}},\theta ,{\nu }_{{{\mathrm{unf}}}},{\gamma }_{{{\mathrm{det}}}})\\ =({\gamma }_{{{\mathrm{det}}}}-{\nu }_{{{\mathrm{unf}}}})\left[\frac{\lambda (\theta ,{\beta }_{{{\mathrm{PB}}}})}{2}{\left(1-\frac{\delta }{\lambda (\theta ,{\beta }_{{{\mathrm{PB}}}})}\right)}^{2}-\ln (1+2{\beta }_{{{\mathrm{PS}}}})\right]\\ \quad -\,\left(1-({\gamma }_{{{\mathrm{det}}}}-{\nu }_{{{\mathrm{unf}}}})\right)\ln \left[1+h({\beta }_{{{\mathrm{PS}}}},{\beta }_{{{\mathrm{PB}}}},\theta )\right],\end{array}$$

(8)

where

$$\begin{array}{l}h({\beta }_{{{\mathrm{PS}}}},{\beta }_{{{\mathrm{PB}}}},\theta )\,=\,2{\beta }_{{{\mathrm{PS}}}}\sqrt{\frac{1}{2}+2{\beta }_{{{\mathrm{PB}}}\,}^{2}+\left(\frac{1}{2}-2{\beta }_{\,{{\mathrm{PB}}}\,}^{2}\right)\sin (2\theta )},\\ \qquad \qquad\quad\,\,\delta \,=\,\frac{{\gamma }_{{{\mathrm{det}}}}{\gamma }_{{{\mathrm{err}}}}}{{\gamma }_{{{\mathrm{det}}}}-{\nu }_{{{\mathrm{unf}}}}}.\end{array}$$

(9)

There exist parameters satisfying the constraints (7), for which f(γ_err, β_PS, β_PB, θ, ν_unf, γ_det) > 0. For these parameters, ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ are ϵ_unf − unforgeable with

$${\epsilon }_{{{\mathrm{unf}}}}={e}^{-\frac{{P}_{{{\mathrm{noqub}}}}N}{3}{\left(\frac{{\nu }_{{{\mathrm{unf}}}}}{{P}_{{{\mathrm{noqub}}}}}-1\right)}^{2}}+{e}^{-Nf({\gamma }_{{{\mathrm{err}}}},{\beta }_{{{\mathrm{PS}}}},{\beta }_{{{\mathrm{PB}}}},\theta ,{\nu }_{{{\mathrm{unf}}}},{\gamma }_{{{\mathrm{det}}}})}.$$

(10)

We note in step 0 of ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ that Alice and Bob agree on parameters N, β_PB, γ_det, and γ_err. As follows from Lemmas 2–4, in order for Alice to obtain a required degree of correctness, robustness, and privacy, she must guarantee her experimental parameters P_det, E, and β_E to be good enough. This is independent of any experimental parameters of Bob, except for the previously agreed parameter β_PB, which plays a role in correctness but not in robustness or privacy. Additionally, Alice must choose a suitable mathematical variable ν_cor to compute a guaranteed degree of correctness, as given by the bound of Lemma 3.

On the other hand, as follows from Theorem 1, in order for Bob to obtain a required degree of unforgeability, he must guarantee his experimental parameters P_noqub, θ, β_PB, and β_PS to be good enough. This is independent of any experimental parameters of Alice. Additionally, Bob must choose a suitable mathematical variable ν_unf to compute a guaranteed degree of unforgeability, as given by the bound of Theorem 1.

Furthermore, as follows from Lemma 4, in order for Alice to obtain a required degree of privacy, she must guarantee her experimental parameter β_E to be small enough.

The parameters N, β_PB, γ_det, and γ_err agreed by Alice and Bob must be good enough to achieve their required degrees of robustness, correctness, and unforgeability. But they must also be achievable given their experimental setting.

Extension of ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ to 2^M presentation points

Extensions of the quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ to 2^M presentation points, for any integer M ≥ 1, and the proof of the following theorem are given in Supplementary Note VIII.

Theorem 2

For any integer M ≥ 1, there exist quantum token schemes ${{{{\mathcal{QT}}}}}_{1}^{M}$ and ${{{{\mathcal{QT}}}}}_{2}^{M}$ extending ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ to 2^M presentation points, in which Bob sends Alice NM quantum states, satisfying instant validation and the following properties. Consider parameters β_PB, β_PS, β_E, P_det, P_noqub, E, and θ satisfying the constraints (2), (4), (7) of Lemmas 2 and 3 and Theorem 1, for which the function f(γ_err, β_PS, β_PB, θ, ν_unf, γ_det) defined by (8) is positive. For these parameters, ${{{{\mathcal{QT}}}}}_{1}^{M}$ and ${{{{\mathcal{QT}}}}}_{2}^{M}$ are ${\epsilon }_{\,{{\mathrm{rob}}}\,}^{M}-$robust, ${\epsilon }_{\,{{\mathrm{cor}}}\,}^{M}-$correct, ${\epsilon }_{\,{{\mathrm{priv}}}\,}^{M}-$private, and ${\epsilon }_{\,{{\mathrm{unf}}}\,}^{M}-$unforgeable with

$$\begin{array}{l}{\epsilon }_{\,{{\mathrm{rob}}}\,}^{M}\,=\,M{\epsilon }_{{{\mathrm{rob}}}},\\ {\epsilon }_{\,{{\mathrm{cor}}}\,}^{M}\,=\,M{\epsilon }_{{{\mathrm{cor}}}},\\ \!\!{\epsilon }_{\,{{\mathrm{priv}}}\,}^{M}\,=\,\frac{1}{{2}^{M}}\left[{(1+2{\epsilon }_{{{\mathrm{priv}}}})}^{M}-1\right],\\ \!{\epsilon }_{\,{{\mathrm{unf}}}\,}^{M}\,=\,C{\epsilon }_{{{\mathrm{unf}}}},\end{array}$$

(11)

where C is the number of pairs of spacelike separated presentation points, and where ϵ_rob, ϵ_cor, ϵ_priv, and ϵ_unf are given by (3), (5), (6), and (10).

Quantum experimental tests

We performed experimental tests for the quantum stage of the ${{{{\mathcal{QT}}}}}_{1}$ scheme for the case of two presentation points (M = 1), using the photonic setup of Fig. 3 and reporting strategy 1 (see Methods for details). Using a photon source with Poissonian distribution of average photon number μ = 0.09, and a repetition rate of 10 MHz, we generated a token of N = 4 × 10⁷ photon pulses, with detection efficiency of η = 0.21, detection probability of P_det = 0.019, and error rate of E = 0.058. We obtained deviations from the random distributions for the basis and state generation of β_PB = 2.4 × 10⁻³ and β_PS = 3.6 × 10⁻³, respectively. In order to guarantee unforgeability using Theorem 1, we need to improve some experimental parameters (see Fig. 5).

Fig. 5: Numerical example.

The plots denote the maximum value ${\beta }_{\max }$ for β_PB and β_PS that our bounds can allow to guarantee correctness, robustness, and unforgeability simultaneously in a numerical example with the allowed experimental imperfections of Table 5 and under the assumptions of Table 6 for our quantum token schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$. The region below the plotted curves denotes the secure region in which we have set ϵ_rob = ϵ_cor = ϵ_unf = 10⁻⁹ in Lemmas 2 and 3 and in Theorem 1. The plotted values keep all parameters fixed to the experimental values reported above, except for the deviations from the random distributions for basis and state generation, β_PB and β_PS, the uncertainty θ on the Bloch sphere in the state generation, and the error rate E. The blue curve denotes the values obtained for the experimentally obtained value E = 0.058. The red square denotes the assumed upper bound for our experimental values of θ ≤ 10^∘, and corresponds to a value of ${\beta }_{\max }=6\times 1{0}^{-6}$, which is about 400 and 600 times smaller than the obtained experimental values of β_PB = 2.4 × 10⁻³ and β_PS = 3.6 × 10⁻³, respectively. The orange and gray curves plot the values of ${\beta }_{\max }$ assuming E = 0.03 and E = 0.01, respectively. In an ideal case in which θ = 0^∘ and E = 0.01, the value for ${\beta }_{\max }$ would be ~6 × 10⁻⁴, which is about four and six times smaller than our obtained experimental values for β_PB and β_PS, respectively. In a more realistic case, with θ = 5^∘ and E = 0.03, our numerical example gives approximately ${\beta }_{\max }=2.3\times 1{0}^{-4}$; meaning that with these experimental values, by reducing our obtained experimental values for β_PB and β_PS by respective factors of ~10 and 16, we could guarantee correctness, robustness, and unforgeability simultaneously in our schemes.

Guaranteeing privacy in our schemes ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ can be satisfied with good enough random number generators, as follows from Lemma 4. Due to the piling-up lemma, by using a large number of close-to-random bits, we can guarantee ϵ_priv to be arbitrarily small in practice.

Discussion

We have presented two quantum token schemes that do not require either quantum state storage or long-distance quantum communication and are practical with current technology. Our schemes allow for losses, errors in the state preparations and measurements, and deviations from random distributions; and, in photonic setups, photon sources that do not emit exactly single photons, and threshold single-photon detectors with non-unit detection efficiencies and with nonzero dark count probabilities (see Table 5).

Our analyses follow much of the literature on practical mistrustful quantum cryptography (e.g., ^{32,33,34,35,36}) in making the assumptions of Table 6. Under these assumptions, we have shown that there exist attainable experimental parameters for which our schemes can satisfy instant validation, correctness, robustness, unforgeability, and user privacy. Importantly, Theorem 2 shows that this holds, in principle, for 2^M presentation points with arbitrary M. As in the schemes of ref. ²⁸, our schemes allow the user to choose her presentation point Q_b after her quantum measurements are completed, as long as she chooses Q_b within the intersection of the causal past of all the presentation points. This means that the quantum communication stage of our schemes can take an arbitrarily long time and can be implemented arbitrarily in the past of the presentation points, which is very convenient for practical implementations.

We note that the security of our quantum token schemes does not rely on any spacetime constraints. In principle, all presentation points could be timelike separated, for example. However, as discussed in the introduction, in order for our quantum token schemes to have an advantage over purely classical schemes, some spacetime presentation points need to be spacelike separated.

In practice, this means that some classical processing and classical communication steps in our schemes must be implemented sufficiently fast. This is in general feasible with current technology (for example, using field programmable gate arrays), if the presentation points are sufficiently far apart, as demonstrated by previous implementations of relativistic cryptographic protocols^{33,34,37,38,39}. Furthermore, Alice’s and Bob’s laboratories must be synchronized securely to a common reference frame with sufficiently high time precision. This can be implemented using GPS devices and atomic clocks^{33,34,37,38,39}, for example. A detailed analysis of these experimental challenges is left for future work.

Using quantum key distribution for secure communications in our quantum token schemes can be useful, but it is not crucial. As discussed, Alice’s and Bob’s agents must communicate via secure and authenticated classical channels, which can be implemented with previously distributed secret keys. In an ideal situation where Alice’s and Bob’s agents have access to enough quantum channels, for example in a quantum network^40,41,42,43 or in the envisaged quantum internet^44,45, these keys can be expanded securely with quantum key distribution^30,46,47. However, it is also possible to distribute the secret keys via secure physical transportation, as implemented in previous demonstrations of relativistic quantum cryptography^{33,34,37,38,39}.

We note that in our proof of unforgeability, our only potential restriction on the technology and capabilities of dishonest Alice is indirectly made through assumption G in photonic setups (see Table 6), in the case where Bob’s photon source does not perfectly conceal phase information. In fact, we believe that assumptions A, B, and G can be significantly weakened. Investigating unforgeability for realistic weaker forms of these assumptions is left as an open problem.

We implemented experimental tests of the quantum part of our scheme (${{{{\mathcal{QT}}}}}_{1}$) using a free space optical setup^48,49 for quantum key distribution (QKD) that was slightly adapted for our scheme, and which can operate at daylight conditions. Importantly, Bob’s transmission device is small, hand-held, and low cost. These type of QKD setups are designed for future daily-life applications, for example with mobile devices (see e.g., ^50,51,52).

Experiments with our relatively low precision devices do not guarantee unforgeability, but show it can be guaranteed with refinements. Crucial experimental parameters that we need to improve to achieve this are the deviations β_PB and β_PS from random basis and state generation, respectively. In our tests we obtained β_PB = 2.4 × 10⁻³ and β_PS = 3.6 × 10⁻³. An implementation in which the uncertainty in basis choices was bounded by θ = 5^∘ and the error rate by E = 0.03 would guarantee unforgeability if β_PB ≈ β_PS ≈ 2.3 × 10⁻⁴ (about a factor of 10 and 16 lower than our values). This highlights that it is crucial to consider the parameters β_PS and β_PB in practical security proofs. For example, if we simply assumed β_PS = β_PB = 0 as our experimental values then our results would imply that we had attained unforgeability, even for θ = 10^∘ (see Fig. 5). Taking β_PS = β_PB = θ = 0, as implicitly assumed in some previous analyses of practical mistrustful quantum cryptography (e.g., ^33,34,36), is unsafe.

User privacy can also be guaranteed by using good enough random number generators. However, further security issues arise from the assumptions that Bob cannot use degrees of freedom not previously agreed for the transmission of the quantum states to affect, or obtain information about, the statistics of Alice’s quantum measurement devices; and, in photonic setups, that Alice’s single-photon detectors have equal efficiencies and equal dark count probabilities (assumptions E and F in Table 6). These issues are not specific to our implementations or to quantum token schemes: they arise quite generally in practical mistrustful quantum cryptographic schemes in which one party measures states sent by the other. The attacks they allow and defences against these (such as requiring single-photon sources and using attenuators to equalize detector efficiencies) are analysed in detail elsewhere⁵³. As noted in ref. ⁵³, further options, such as iterating the scheme and using the XOR of the bits generated, also merit investigation. Importantly, our analyses here take into account multi-photon attacks⁵³ in photonic setups, and the reporting strategies we have considered offer perfect protection against arbitrary multi-photon attacks, given our assumptions (see Fig. 3, and Lemma 5 in Methods).

In conclusion, our theoretical and experimental results give a proof of principle that quantum token schemes are implementable with current technology, and that, conditioned on standard technological assumptions, security can be maintained in the presence of the various experimental imperfections we have considered (see Table 5). As with other practical implementations of mistrustful quantum cryptography (and indeed quantum key distribution), completely unconditional security would require defences against every possible collection of physical systems Bob might transmit to Alice, including programmed nano-robots that could enter and reconfigure her laboratory⁵⁴. Attaining this is beyond current technology, but such far-fetched possibilities also illustrate that security based on suitable technological assumptions (which may depend on the context) may suffice for practical purposes. More work on attacks and defences in practical mistrustful quantum cryptography is undoubtedly needed to reach a consensus on trustworthy technologies. That said, as our schemes are built on simple mistrustful cryptographic primitives, we expect they can be refined to incorporate any agreed practical defences⁵³.

Table 5 Allowed experimental imperfections for ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$.

Methods

Protection against multi-photon attacks in photonic implementations

The following lemma is a straightforward extension of Lemmas 1 and 12 of ref. ⁵³ to the case of N > 1 transmitted photon pulses. Note that Alice (Bob) in our notation refers to Bob (Alice) in the notation of ref. ⁵³. The proof is given in Supplementary Note VI.

Lemma 5

Suppose that Bob sends Alice N photon pulses, labeled by k ∈ [N]. Let the kth pulse have L_k photons. Let ρ be an arbitrary quantum state prepared by Bob in the polarization degrees of freedom of the photons sent to Alice, which can be arbitrarily entangled among all photons in all pulses and can also be arbitrarily entangled with an ancilla held by Bob. Let ${{{{\mathcal{D}}}}}_{0}$ and ${{{{\mathcal{D}}}}}_{1}$ be two arbitrary qubit orthogonal bases. Suppose that either Alice uses the setup of Fig. 3 with reporting strategy 1 to implement the quantum token scheme ${{{{\mathcal{QT}}}}}_{1}$ (see Table 2), or Alice uses the setup of Fig. 3 with reporting strategy 2 to implement the quantum token scheme ${{{{\mathcal{QT}}}}}_{2}$ (see Table 3). Suppose also that assumptions E and F (see Table 6) hold. For k ∈ [N], let m_k = 1 if Alice assigns a successful measurement to the kth pulse and m_k = 0 otherwise; let w_k = 0 (w_k = 1) if Alice assigns a measurement basis to the kth pulse in the basis ${{{{\mathcal{D}}}}}_{0}$ (${{{{\mathcal{D}}}}}_{1}$). If Alice uses the setup of Fig. 3 and reporting strategy 1 to implement the scheme ${{{{\mathcal{QT}}}}}_{1}$, without loss of generality, suppose also that Alice sets w_k = 0 with unit probability, if m_k = 0, for k ∈ [N]. Let m = (m₁, …, m_N), w = (w₁, …, w_N) and L = (L₁, …, L_N).

Table 6 Assumptions for ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$.

If Alice uses the setup of Fig. 3 with reporting strategy 1 to implement the scheme ${{{{\mathcal{QT}}}}}_{1}$, then the probability that Alice reports the string m to Bob and assigns the string of measurement bases w, given ρ and L, is

$${P}_{\,{{\mathrm{rep}}}\,}^{(1)}(m,w| \rho ,L)=\mathop{\prod }\limits_{k=1}^{N}{G}_{{m}_{k},{w}_{k}}^{(1)}({d}_{0},{d}_{1},\eta ,{L}_{k}),$$

(12)

where

$$\begin{array}{l}{G}_{1,b}^{(1)}({d}_{0},{d}_{1},\eta ,a)\,=\,(1-{d}_{0})(1-{d}_{1}){\left(1-\frac{\eta }{2}\right)}^{a} -{(1-{d}_{0})}^{2}{(1-{d}_{1})}^{2}{(1-\eta )}^{a},\\ {G}_{0,0}^{(1)}({d}_{0},{d}_{1},\eta ,a)\,=\,1-2{G}_{1,0}^{(1)}({d}_{0},{d}_{1},\eta ,a),\\ {G}_{0,1}^{(1)}({d}_{0},{d}_{1},\eta ,a)\,=\,0,\end{array}$$

(13)

for b ∈ {0, 1}, m, w ∈ {0, 1}^N and a, L₁, …, L_N ∈ {0, 1, 2, …}. Furthermore, the probability P_MB(w_k) that Alice assigns a measurement in the basis ${{{{\mathcal{D}}}}}_{{w}_{k}}$, conditioned on the value m_k = 1, for the kth pulse, satisfies

$${P}_{{{\mathrm{MB}}}}({w}_{k})=\frac{1}{2},$$

(14)

for w_k ∈ {0, 1} and k ∈ [N].

If Alice uses the setup of Fig. 3 with reporting strategy 2 to implement the scheme ${{{{\mathcal{QT}}}}}_{2}$, then the probability that Alice reports the string m to Bob, given ρ, w, and L, is

$${P}_{\,{{\mathrm{rep}}}\,}^{(2)}(m| w,\rho ,L)=\mathop{\prod }\limits_{k=1}^{N}{G}_{{m}_{k}}^{(2)}({d}_{0},{d}_{1},\eta ,{L}_{k}),$$

(15)

where

$$\begin{array}{rcl}{G}_{0}^{(2)}({d}_{0},{d}_{1},\eta ,a)&=&(1-{d}_{0})(1-{d}_{1}){(1-\eta )}^{a},\\ {G}_{1}^{(2)}({d}_{0},{d}_{1},\eta ,a)&=&1-(1-{d}_{0})(1-{d}_{1}){(1-\eta )}^{a},\end{array}$$

(16)

for m, w ∈ {0, 1}^N and a, L₁, …, L_N ∈ {0, 1, 2, …}.

In any of the two cases, the message m gives Bob no information about the bit entries w_k for which m_k = 1. Equivalently, the set Λ ⊂ [N] of labels transmitted to Bob in step 2 of ${{{{\mathcal{QT}}}}}_{1}$ and ${{{{\mathcal{QT}}}}}_{2}$ gives Bob no information about the string W and the bit z.

Clarification about unforgeability in photonic implementations

A subtle technical issue when implementing our quantum token schemes with photonic setups is that in our schemes we have assumed the quantum systems A_k that Bob transmits to Alice to have finite Hilbert space dimension, for k ∈ [N]. However, some light sources, like weak coherent sources, or other photon sources with Poissonian statistics, can emit pulses with a number of photons J, where J can tend to infinity, although with a probability tending to zero. This issue is easily solved by fixing a maximum number of photons ${J}_{\max }$ and assuming that unforgeability is not guaranteed whenever Bob’s photon source emits a pulse with more than ${J}_{\max }$ photons. By fixing ${J}_{\max }$ to be arbitrarily large, but finite, the probability that among the N emitted pulses there is at least one pulse with more than ${J}_{\max }$ photons can be made arbitrarily small. Thus, with probability arbitrarily close to unity, honest Bob is guaranteed that each of his N emitted pulses does not have more than ${J}_{\max }$ photons, i.e., the internal degrees of freedom—like the polarization degrees of freedom— of each pulse, represented by the quantum system A_k, have a finite Hilbert space dimension.

Experimental setup

Our experimental setup is based on a free space optical quantum key distribution (QKD) system, which can operate at daylight conditions. This setup was developed by one of us (DL) during his PhD⁴⁹, based upon the work of ref. ⁴⁸. The main features of our experimental setup are illustrated in Figs. 3 and 6.

Fig. 6: Photograph of the experimental setup.

Bob’s quantum transmitter (white box in the left) is a small and low-cost hand-held device of ~20 cm × 15 cm × 5 cm. Alice’s quantum receiver is contained within a box of ~20 cm × 12 cm × 5 cm (grey box on the right), with further electronics contained within another box of ~30 cm × 50 cm × 15 cm (bigger black box). At Bob’s site, the QKD transmitter comprises a field programmable gate array (FPGA) which pulses 4 LEDs, each polarized in one of the horizontal (H), vertical (V), diagonal (D), and anti-diagonal (A) states, corresponding to the $\left|0\right\rangle$, $\left|1\right\rangle$, $\left|+\right\rangle$ and $\left|-\right\rangle$ BB84 states, respectively. The light from the LEDs is collimated by a diffraction grating and pinholes. The statistics of Bob’s photon source is assumed Poissonian^49,55. Neutral-density (ND) filters (small black cylinders) are used to attenuate the pulses down to the required mean photon number, which in our experiment was μ = 0.09. Since Bob’s photon source consists of LEDs, and LEDs have low spatiotemporal coherence⁵⁹, no phase randomization is required to satisfy assumption G to a good approximation (see Table 6). At Alice’s site, the received light pulses from Bob are focused from the transmitter pinhole, through a 50:50 beam splitter (BS, small transparent cube) which performs basis selection, and wave plate (WP, thin white cylinder), and polarizing beam splitters (PBS, small black boxes) which perform the measurement of the polarization. The photons are detected with single-photon avalanche diodes (SPAD, small golden cylinders), which are threshold single-photon detectors with efficiency η = 0.21, including the quantum efficiency of the detectors and the transmission efficiency from Bob’s setup to the detectors. An FPGA time tags the detections with 52 bit precision, equivalent to 30.5 ps⁶⁰, and sends them to a PC for processing. Alice’s grey and black boxes are closed during operation to decrease noise due to environment light. But they are shown open here for illustration.

Only minor changes to our quantum setup are needed to implement the quantum stage of ${{{{\mathcal{QT}}}}}_{2}$. For example, the 50:50 beam splitter in Alice’s site can be replaced by a suitably placed mirror directing the received photon pulses to one of the two polarizing beam splitters. This mirror can be set in a movable arm, which positions the mirror in place if z has a specific value (e.g., if z = 1) and out of place, letting the photon pulses reach the other polarizing beam splitter, if z takes the other value (e.g., z = 0). The movable arm putting the mirror in place or out of place does not need to move very fast, as it remains in the same position during the transmission of all N pulses from Bob in the case of two presentation points, or during the transmission of each set of N pulses from the total of NM in the case of 2^M presentation points (see quantum token scheme ${{{{\mathcal{QT}}}}}_{2}^{M}$ in Supplementary Note VIII).

Experimental tests and numerical example

The quantum stage of the token scheme ${{{{\mathcal{QT}}}}}_{1}$ was implemented with the experimental setup described above. Below we describe our experiment and the numerical example of Fig. 5. Unless we consider it necessary or helpful, all values smaller than unity obtained in our experiment and numerical example are given below rounded to two significant figures.

As we explain below, our obtained experimental values for the parameters in Lemmas 2 and 3 and in Theorem 1 are N = 4 × 10⁷, P_det = 0.019, E = 0.058, β_PB = 2.4 × 10⁻³, β_PS = 3.6 × 10⁻³, P_noqub = 3.8 × 10⁻³. We assume an angle θ ≤ 10^∘ in our experiment.

In the numerical example of Fig. 5 we used the previous experimental values, except for θ and E, which were varied as shown in the plots, and for β_PB and β_PS. In the plots of Fig. 5, if ${\beta }_{{{\mathrm{PB}}}}\le {\beta }_{\max }$ and ${\beta }_{{{\mathrm{PS}}}}\le {\beta }_{\max }$ hold, then we obtain from Lemmas 2 and 3 and from Theorem 1 that ϵ_rob, ϵ_cor, ϵ_unf ≤ 10⁻⁹. We do not claim that our numerical example is optimal. In other words, we do not claim that with our experimental parameters every point above the curves of Fig. 5 is insecure, in the sense that the conditions ϵ_rob, ϵ_cor, ϵ_unf ≤ 10⁻⁹ do not hold. Our claim is only that given our experimental parameters, the regions of points below the curves of Fig. 5 satisfy the conditions ϵ_rob, ϵ_cor, ϵ_unf ≤ 10⁻⁹.

For the three curves of Fig. 5, we set γ_det = 0.018. Thus, condition (2) of Lemma 2 is satisfied, and from (3), we have ϵ_rob = e⁻¹⁰⁵² < 10⁻⁹.

For the three curves of Fig. 5, we set ν_unf = 3.9 × 10⁻³. This is the minimum value for which the first term of ϵ_unf in (10) equals $\frac{1{0}^{-9}}{2}$. This is because, as we describe below, we also chose the parameters satisfying that the second term of ϵ_unf in (10) equals $\frac{1{0}^{-9}}{2}$, from which we have ϵ_unf = 10⁻⁹. We recognize that although this particular choice seems natural, it probably does not optimize our results.

Then, for each of the three considered error rates E = 0.01, E = 0.03, and E = 0.058, and for each of the angles θ = 0^∘, 1^∘, …, 11^∘, we set ${\beta }_{{{\mathrm{PB}}}}={\beta }_{{{\mathrm{PS}}}}={\beta }_{\max }$ and varied ${\beta }_{\max }$, ν_cor, and γ_err trying to find the maximum value of ${\beta }_{\max }$ for which both terms of ϵ_cor in (5) and the second term of ϵ_unf in (10) were as close as possible to $\frac{1{0}^{-9}}{2}$, but not bigger than $\frac{1{0}^{-9}}{2}$, while guaranteeing that the constraints (4) and (7) were satisfied. Our results for ${\beta }_{\max }$ are plotted in Fig. 5.

We describe how we obtained the experimental parameters presented above. At a repetition rate of 10 MHz, Bob transmitted photon pulses to Alice during 4 s. Thus, the number of transmitted pulses was N = 4 × 10⁷.

Since the photon statistics of Bob’s source is assumed Poissonian^49,55, the probability that a photon pulse has two or more photons is P_noqub = 1 − (1 + μ)e^−μ. Since in our experiment μ = 0.09, we obtain P_noqub = 3.8 × 10⁻³.

As discussed below, Alice assigned successful measurements using reporting strategy 1. The number of pulses for which Alice assigned successful measurement was n = 742,491. The obtained estimation for the probability P_det, was obtained as ${P}_{{{\mathrm{det}}}}=\frac{n}{N}=0.019$.

The measured detection efficiency, including the quantum efficiency of the detectors and the transmission probability from Bob’s setup to the detectors, was η = 0.21. We note that our obtained value of P_det = 0.01856, which we reported above with the less precise value P_det = 0.019, is a good approximation to the theoretical prediction in which the photon statistics of Bob’s source follow a Poisson distribution with average photon number μ = 0.09, Alice uses reporting strategy 1 with her four detectors having the same efficiency η = 0.21, and the dark count probabilities are assumed to be zero. As follows from (12) and (13) in Lemma 5, this theoretical prediction for P_det is given by

$$\begin{array}{l}{P}_{\,{{\mathrm{det}}}}^{{{\mathrm{theo}}}\,}\,=\,\mathop{\sum }\limits_{k=0}^{\infty }\frac{{e}^{-\mu }{\mu }^{k}}{k!}\left({G}_{1,0}^{(1)}(0,0,\eta ,k)+{G}_{1,1}^{(1)}(0,0,\eta ,k)\right)\\ \qquad\quad=\,2\mathop{\sum }\limits_{k=0}^{\infty }\frac{{e}^{-\mu }{\mu }^{k}}{k!}\left[{\left(1-\frac{\eta }{2}\right)}^{k}-{(1-\eta )}^{k}\right]\\ \qquad\quad=\,2\left({e}^{-\frac{\mu \eta }{2}}-{e}^{-\mu \eta }\right)\\ \qquad\quad=\,0.01863,\end{array}$$

(17)

where in the last line we used our experimental parameters μ = 0.09 and η = 0.21. This gives a ratio $\frac{{P}_{{{\mathrm{det}}}}}{{P}_{{{\mathrm{det}}}}^{{{\mathrm{theo}}}}}=0.996$.

As mentioned in Fig. 3, Alice applies reporting strategy 1, in order to protect against multi-photon attacks⁵³ (see Lemma 5). That is, Alice assigns successful measurement outcomes in the basis ${{{{\mathcal{D}}}}}_{0}$ (${{{{\mathcal{D}}}}}_{1}$) with unit probability for the pulses in which at least one of the detectors D₀ and D₁ (D₊ and D₋) click and D₊ and D₋ (D₀ and D₁) do not click. It is clear that when only the detector D_i clicks, Alice associates the measurement outcome to the BB84 state $\left|i\right\rangle$, for i ∈ {0, 1, +, −}. However, it is not clear how Alice should assign measurement outcomes to the cases in which both D₀ and D₁ (D₊ and D₋) click and D₊ and D₋ (D₀ and D₁) do not click. The results of Lemma 5 are independent of how Alice assigns these outcomes. In order to make clear this generality of the results of Lemma 5, we have not included how these outcomes are assigned by Alice in the definition of reporting strategy 1 in Fig. 3. Nevertheless, how these outcomes are assigned by Alice plays a role in the error rate E, and thus also in the degrees of correctness and unforgeability that can be guaranteed (see Lemma 3 and Theorem 1). In our experiment, Alice assigns a random measurement outcome associated to the state $\left|0\right\rangle$ and $\left|1\right\rangle$ ($\left|+\right\rangle$ and $\left|-\right\rangle$) when both D₀ and D₁ (D₊ and D₋) click and D₊ and D₋ (D₀ and D₁) do not click.

As mentioned above, in our experiment we obtained Alice’s error rate E = 0.058, and deviations from the random distributions for basis and state generation by Bob of β_PB = 2.4 × 10⁻³ and β_PS = 3.6 × 10⁻³, respectively. These values were computed as we describe below.

Statistical information

In our experimental tests, the number of photon pulses transmitted from Bob to Alice was N = 4 × 10⁷. The number of pulses for which Alice assigned successful measurement was n = 742,491. The obtained estimation for the probability P_det, was obtained as ${P}_{{{\mathrm{det}}}}=\frac{n}{N}=0.019$.

The error rate E = 0.058 was computed as follows. From the n pulses that Alice assigned as successful measurements, ${n}_{tu}^{{{\mathrm{same}}}}$ pulses were prepared by Bob with polarization given by the qubit state $\left|{\phi }_{tu}\right\rangle$ and were measured by Alice in the same basis of preparation by Bob (${{{{\mathcal{D}}}}}_{u}={\{\left|{\phi }_{tu}\right\rangle \}}_{t = 0}^{1}$), from which ${n}_{tu}^{\,{{\mathrm{error}}}\,}$ gave Alice the outcome opposite to the state prepared by Bob, i.e., an error, for t, u ∈ {0, 1}. We computed ${E}_{tu}=\frac{{n}_{tu}^{{{\mathrm{error}}}}}{{n}_{tu}^{{{\mathrm{same}}}}}$, for t, u ∈ {0, 1}. The estimation for the error rate E was taken as $E=\max \{{E}_{00},{E}_{10},{E}_{01},{E}_{11}\}$. We obtained ${n}_{00}^{\,{{\mathrm{same}}}\,}=80786$, ${n}_{10}^{\,{{\mathrm{same}}}\,}=121159$, ${n}_{01}^{\,{{\mathrm{same}}}\,}=93618$, ${n}_{11}^{\,{{\mathrm{same}}}\,}=80653$, ${n}_{00}^{\,{{\mathrm{error}}}\,}=4725$, ${n}_{10}^{\,{{\mathrm{error}}}\,}=2250$, ${n}_{01}^{\,{{\mathrm{error}}}\,}=1602$, and ${n}_{11}^{\,{{\mathrm{error}}}\,}=3851$. From these values, we obtained E₀₀ = 0.058, E₁₀ = 0.019, E₀₁ = 0.017, E₁₁ = 0.048, and E = 0.058.

Our experimentally obtained estimations β_PB = 2.4 × 10⁻³ and β_PS = 3.6 × 10⁻³ were obtained from the number n of pulses that Alice reported as successfully measured. We did not use the whole number N of transmitted pulses for these estimations, because the software integrated into our experimental setup is configured to output data for the pulses that produce a detection event in at least one detector. From the n = 742,491 pulses reported above, Bob produced n_tu pulses in the state $\left|{\phi }_{tu}\right\rangle$, for t, u ∈ {0, 1}. We note that n = n₀₀ + n₁₀ + n₀₁ + n₁₁. We computed ${\beta }_{{{\mathrm{PB}}}}=\left|\frac{{n}_{00}+{n}_{10}}{n}-\frac{1}{2}\right|$ and ${\beta }_{{{\mathrm{PS}}}}=\max \left\{\left|\frac{{n}_{00}}{{n}_{00}+{n}_{10}}-\frac{1}{2}\right|,\left|\frac{{n}_{01}}{{n}_{01}+{n}_{11}}-\frac{1}{2}\right|\right\}$. We obtained n₀₀ = 185,166, n₁₀ = 187842, n₀₁ = 184251, n₁₁ = 185232, β_PB = 2.4 × 10⁻³, and β_PS = 3.6 × 10⁻³.