Introduction

Irreversibility is a fundamental feature of our physical world. The degree of irreversibility of thermodynamic transformations is measured by the entropy production, which is always positive according to the second law. At the microscopic level, stochastic thermodynamics1,2 has extended this concept to characterize the evolution of small systems coupled to reservoirs and driven out of equilibrium. Such systems follow stochastic trajectories \({\vec{\Sigma }}\) and the stochastic entropy production \(\Delta _{\mathrm{i}}s[ {{\vec{\Sigma }}}]\) obeys the integral fluctuation theorem (IFT) \(\left\langle {{\mathrm{exp}}\left( { - \Delta _{\mathrm{i}}s\left[ {{\vec{\Sigma }}} \right]} \right)} \right\rangle _{{\vec{\Sigma }}}\) = 1, where \({\left\langle \cdot \right\rangle}_{{\vec{\mathrm \Sigma }}}\) denotes the average over all trajectories \({\vec{\mathrm \Sigma }}\). Jarzynski’s equality (JE)3 is a paradigmatic example of such IFT, that constrains the fluctuations of the entropy produced, whereas driving some initially thermalized system out of equilibrium. Experimental demonstrations of JE especially require the ability to measure the stochastic work \(W\left[ {{\vec{\mathrm \Sigma }}} \right]\) exchanged with the external entity driving the system. In the classical regime, \(W\left[ {{\vec{\mathrm \Sigma }}} \right]\) can be completelym’s trajectory, allowing for successful experimental demonstrations.4,5,6

Defining and measuring the entropy production in the quantum regime is of fundamental interest in the perspective of optimizing the performances of quantum heat engines and the energetic cost of quantum information technologies.7,8,9,10 However, measuring a quantum fluctuation theorem can be problematic in the genuinely quantum situation of a coherently driven quantum system, because of the fundamental and practical issues to define and measure quantum work.11,12,13,14 So far the quantum JE has thus been extended and experimentally verified in closed quantum systems, i.e. systems that are driven, but otherwise isolated. In this case, work corresponds to the change in the system’s internal energy, accessible by a two-points measurement protocol11 or the measurement of its characteristic function.15,16,17 Experimental demonstrations have been realized, e.g. with trapped ions,18,19 ensemble of cold atoms,20 and spins in nuclear magnetic resonance (NMR)21 where the thermodynamic arrow of time was successfully measured.22

On the other hand, realistic strategies must still be developed to measure the fluctuations of entropy production for quantum open systems, i.e. that can be simultaneously driven, and coupled to reservoirs. As work is usually assumed to be provided by a classical entity, most theoretical proposals so far have relied on the measurement of heat fluctuations, i.e. small energy changes of the reservoir. Experimentally, this requires to engineer this reservoir and to develop high efficiency detection schemes, which is very challenging.23,24,25 Experimental demonstrations have remained elusive.

In this article, we propose a new and experimentally feasible strategy to measure the thermodynamic arrow of time for a quantum open system in Jarzynski’s protocol that is based on the direct measurement of work fluctuations. We investigate a so-called hybrid opto-mechanical system,26 that consists in a two-level system (further called a qubit) strongly coupled to a mechanical oscillator (MO) on the one hand, and to a thermal bath on the other hand. Studying single quantum trajectories of the hybrid system, we show that the MO and the qubit remain in a product state all along their joint evolution, allowing to unambiguously define their stochastic energies. We evidence that the mechanical energy fluctuations can be identified with the stochastic work received by the qubit and satisfy JE. Therefore, the MO plays the role of a quantum battery, the ensemble of the qubit and the battery forming an autonomous machine.27,28,29 Originally, the battery behaves as an embedded quantum work meter, encoding information on the stochastic work exchanges. We show that the evolution of the complete machine is characterized by a generalized IFT that quantitatively involves the amount of extracted information. This situation gives rise to so-called absolute irreversibility, in agreement with recent theoretical predictions and experimental results.30,31,32,33 Our proposal is robust against finite measurement precision34,35 and can be probed with state-of-the-art experimental devices.

The paper is divided as follows. First, we introduce hybrid opto-mechanical devices as autonomous machines, and build the framework to model their evolution on average and at the single trajectory level. Focusing on Jarzynski’s protocol, we define stochastic heat, work, and entropy production and study the regime of validity and robustness of JE as a function of the parameters of the problem and experimental imperfections. Finally, we derive and simulate an IFT for the complete machine, evidencing the presence of absolute irreversibility. Our results demonstrate that work fluctuations can be measured directly, by monitoring the energetic fluctuations of the quantum battery. They represent an important step toward the experimental demonstration of quantum fluctuation theorem in a quantum open system.

Results

Hybrid opto-mechanical systems as autonomous machines

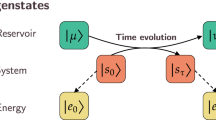
A hybrid opto-mechanical system consists in a qubit of ground (resp. excited) state \(\left| g \right\rangle\) (resp. \(\left| e \right\rangle\)) and transition frequency ω0, parametrically coupled to a mechanical oscillator of frequency Ω ≪ ω0 (Fig. 1a). Recently, physical implementations of such hybrid systems have been realized on various platforms, e.g. superconducting qubits embedded in oscillating membranes,36 nanowires coupled to diamond nitrogen vacancies,37 or to semiconductor quantum dots.38 The complete Hamiltonian of the hybrid system reads Hqm = Hq + Hm + Vqm,26 where \(H_{\mathrm{q}} = \hbar \omega _0\left| e \right\rangle \left\langle e \right| \otimes {\mathbf{1}}_{\mathrm{m}}\) and \(H_{\mathrm{m}} = {\mathbf{1}}_{\mathrm{q}} \otimes \hbar \Omega b^\dagger b\) are the qubit and MO free Hamiltonians, respectively. We have introduced the phonon annihilation operator b, and 1m (resp. 1q) the identity on the MO (resp. qubit) Hilbert space. The coupling Hamiltonian is \(V_{{\mathrm{qm}}} = \hbar g_{\mathrm{m}}\left| e \right\rangle \left\langle e \right| \otimes \left( {b + b^\dagger } \right)\), where gm is the qubit-mechanical coupling strength. Of special interest for the present paper, the so-called ultra-strong coupling regime is defined as gm ≥ Ω, with \(\omega _0\) ≫ gm. It was recently demonstrated experimentally.38

Fig. 1
figure 1

a Situation under study: a qubit exchanging work W with a mechanical resonator and heat Q with a thermal bath at temperature T. The ensemble of the qubit and mechanics constitutes an autonomous machine. This figure includes the image “fire” (https://openclipart.org/detail/23803/fire) by Anonymous/CC0. b Evolution of the complex mechanical amplitude β if the qubit is in the \(\left| e \right\rangle\) (resp. \(\left| g \right\rangle\)) and the MO is initially prepared in the state \(\left| {{\mathrm{i}}\left| {\beta _0} \right|} \right\rangle\). The mechanics can be used as a meter to detect the qubit state if gm/Ω ≫ 1 (ultra-strong coupling regime). The mechanical fluctuations induced by the qubit state are small w.r.t. the free evolution if \(\left| {\beta _0} \right| \gg g_{\mathrm{m}}{\mathrm{/\Omega }}\) (semi-classical regime). These two regimes are compatible (see text). c Stochastic mechanical trajectories \(\vec \beta [\vec \epsilon {\kern 1pt} ]\) in the phase space defined by \((\tilde x,\tilde p)\) (see text). The MO is initially prepared in the coherent state \(\left| {{\mathrm{i}}\left| {\beta _0} \right|} \right\rangle\), and the qubit state is drawn from thermal equilibrium. Inset: Distribution of final states \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle\) within an area of typical width gm/Ω. Parameters: T = 80 K, ħω0 = 1.2kBT, Ω/2π = 100 kHz, γ/Ω = 5, gm/Ω = 100, |β0| = 1000

Full size image

The Hamiltonian of the hybrid system can be fruitfully rewritten \(H_{{\mathrm{qm}}} = \left| e \right\rangle \left\langle e \right| \otimes H_{\mathrm{m}}^e\) + \(\left| g \right\rangle \left\langle g \right| \otimes H_{\mathrm{m}}^g\) with \(H_{\mathrm{m}}^g = \hbar \Omega b^\dagger b\) and \(H_{\mathrm{m}}^e = \hbar \Omega B^\dagger B\) + \(\hbar \left( {\omega _0 - g_{\mathrm{m}}^2{\mathrm{/\Omega }}} \right){\mathbf{1}}_{\mathrm{m}}\), with B = b + (gm/Ω)1m. It appears that the qubit bare energy states \(\epsilon = e,g\) are stable under the dynamics and perfectly determine the evolution of the MO ruled by the Hamiltonian \(H_{\mathrm{m}}^\epsilon\). Interestingly, \(H_{\mathrm{m}}^\epsilon\) preserves the statistics of coherent mechanical states, defined as \(\left| \beta \right\rangle = e^{\beta ^ \ast b - \beta b^\dagger }\left| 0 \right\rangle\), where \(\left| 0 \right\rangle\) is the zero-phonon state and β the complex amplitude of the field. Consequently, if the hybrid system is initially prepared in a product state \(\left| {\epsilon ,\beta _0} \right\rangle\), it remains in a similar product state \(\left| {\epsilon ,\beta _t^\epsilon } \right\rangle\) at any time, with \(\left| {\beta _t^\epsilon } \right\rangle = {\mathrm{exp}}\left( { - iH_{\mathrm{m}}^\epsilon t{\mathrm{/}}\hbar } \right)\left| {\beta _0} \right\rangle\). The two possible mechanical evolutions are pictured in Fig. 1b between time t0 = 0 and t = Ω/2π, in the phase space defined by the mean quadratures of the MO \(\left\langle {\tilde x} \right\rangle = \left\langle {b + b^\dagger } \right\rangle\) and \(\left\langle {\tilde p} \right\rangle = - i\left\langle {b - b^\dagger } \right\rangle\). If the qubit is initially prepared in the state \(\left| e \right\rangle\) (resp. \(\left| g \right\rangle\)), the mechanical evolution is a rotation around the displaced origin (−gm/Ω, 0) (resp. the origin (0, 0)). Such displacement is caused by the force the qubit exerts on the MO, that is similar to the optical radiation pressure in cavity opto-mechanics. Defining \(\delta \beta _t = \beta _t^e - \beta _t^g\), it appears that the distance between the two final mechanical states \(\left| {\delta \beta _t} \right|\) scales like gm/Ω. In the ultra-strong coupling regime, this distance is large such that mechanical states are distinguishable, and can be used as quantum meters to detect the qubit state.

As the hybrid system remains in a pure product state at all times, its mean energy defined as \({\cal E}_{{\mathrm{qm}}}\left( {\epsilon ,\beta _t^\epsilon } \right)\) = \(\left\langle {\epsilon ,\beta _t^\epsilon } \right|H_{{\mathrm{qm}}}\left| {\epsilon ,\beta _t^\epsilon } \right\rangle\) naturally splits into two distinct components, respectively, quantifying the qubit and the mechanical energies:

$${\cal E}_{\mathrm{q}}\left( {\epsilon ,\beta _t^\epsilon } \right) = \hbar \omega \left( {\beta _t^\epsilon } \right)\delta _{\epsilon ,e}$$
(1)
$${\cal E}_{\mathrm{m}}\left( {\beta _t^\epsilon } \right) = \hbar {\mathrm{\Omega }}\left| {\beta _t^\epsilon } \right|^2,$$
(2)

where \(\delta _{\epsilon ,e}\) is the Kronecker delta and ω(β) is the effective transition frequency of the qubit defined as:

$$\omega \left( {\beta _t^\epsilon } \right) = \omega _0 + 2g_{\mathrm{m}}\,{\mathrm{Re}}\left( {\beta _t^\epsilon } \right).$$
(3)

The frequency modulation described by Eq. (3) manifests the back-action of the mechanics on the qubit. Note that the case gm/Ω ≪ |β0| corresponds to \(\left| {\delta \beta _t} \right| \ll \left| {\beta _t^g} \right|\): Then the frequency modulation is independent of the qubit state and follows \(\omega \left( {\beta _t^\epsilon } \right)\sim \omega \left( {\beta _0e^{ - i{\mathrm{\Omega }}t}} \right)\), even in the ultra-strong coupling regime. In what follows, we will be especially interested in the regime where 1 ≪ gm/Ω ≪ |β0|, where the mechanical evolution depends on the qubit state; whereas, the qubit transition frequency is independent of it.

We now take into account that the coupling of the qubit to a bath prepared at thermal equilibrium. The bath of temperature T consists of a spectrally broad collection of electromagnetic modes of frequencies ω′, each mode containing a mean number of photons \(\bar n_{\omega \prime }\) = (exp(ħω′/kBT) − 1)−1. The bath induces transitions between the states \(\left| e \right\rangle\) and \(\left| g \right\rangle\), and is characterized by a typical correlation time τc giving rise to a bare qubit spontaneous emission rate γ.

The hybrid system is initially prepared in the product state ρqm(0) = \(\rho _{\mathrm{q}}(0) \otimes \left| {\beta _0} \right\rangle \left\langle {\beta _0} \right|\). ρq(0) is the qubit state, taken diagonal in the {e, g} basis. \(\left| {\beta _0} \right\rangle \left\langle {\beta _0} \right|\) is the mechanical state, that is chosen pure and coherent. In the rest of the paper, we shall study transformations taking place on typical timescales t ~ Ω−1, such that the mechanical relaxation is neglected. From the properties of the interaction with the bath and the total hybrid system’s Hamiltonian Hqm, it clearly appears that the qubit does not develop any coherence in its bare energy basis. We show in Supplementary that as long as |β0| ≫ gmt, the MO imposes a well-defined modulation of the qubit frequency ω(β0(t)) with β0(t) = β0e−iΩt. This defines the semi-classical regime, where the hybrid system evolution is ruled by the following master equation:

$$\begin{array}{*{20}{l}} {\dot \rho _{{\mathrm{qm}}}(t)} \hfill & = \hfill & { - \frac{{\mathrm{i}}}{\hbar }\left[ {H_{{\mathrm{qm}}},\rho _{{\mathrm{qm}}}(t)} \right]} \hfill \\ {} \hfill & {} \hfill & { + \gamma \bar n_{\omega (\beta _0(t))}D\left[ {\sigma ^\dagger \otimes {\mathbf{1}}_{\mathrm{m}}} \right]\rho _{{\mathrm{qm}}}(t)} \hfill \\ {} \hfill & {} \hfill & { + \gamma \left( {\bar n_{\omega (\beta _0(t))} + 1} \right)D\left[ {\sigma \otimes {\mathbf{1}}_{\mathrm{m}}} \right]\rho _{{\mathrm{qm}}}(t).} \hfill \end{array}$$
(4)

We have defined the super-operator \(D[X]\rho = X\rho X^\dagger - {\textstyle{1 \over 2}}\{ X^\dagger X,\rho \}\) and \(\sigma = \left| g \right\rangle \left\langle e \right|\).

Product states of the form ρqm(t) = ρq(t) ⊗ ρm(t) are natural solutions of Eq. (4), giving rise to two reduced coupled equations, respectively, governing the dynamics of the qubit and the mechanics:

$$\begin{array}{*{20}{l}} {\dot \rho _{\mathrm{q}}(t)} \hfill & = \hfill & { - \frac{{\mathrm{i}}}{\hbar }\left[ {H_{\mathrm{q}}(t),\rho _{\mathrm{q}}(t)} \right] + \gamma \bar n_{\omega (\beta _0(t))}D\left[ {\sigma ^\dagger } \right]\rho _{\mathrm{q}}(t)} \hfill \\ {} \hfill & {} \hfill & { + \gamma \left( {\bar n_{\omega (\beta _0(t))} + 1} \right)D[\sigma ]\rho _{\mathrm{q}}(t),} \hfill \end{array}$$
(5)
$$\dot \rho _{\mathrm{m}}(t) = - \frac{{\mathrm{i}}}{\hbar }[H_{\mathrm{m}}(t),\rho _{\mathrm{m}}(t)].$$
(6)

We have introduced the effective time-dependent Hamiltonians: Hq(t) = Trm[ρm(t)(Hq + Vqm)] = ħω(β0(t)) \(\left| e \right\rangle \left\langle e \right|\) and Hm(t) = Trq[ρq(t)(Hm + Vqm)]. The physical meaning of these semi-classical equations is transparent: The force exerted by the qubit results into the effective Hamiltonian Hm(t) ruling the mechanical evolution. Reciprocally, the mechanics modulates the frequency ω(β0(t)) of the qubit (Eq. (3)), which causes the coupling parameters of the qubit to the bath to be time dependent.

The semi-classical regime of hybrid opto-mechanical systems is especially appealing for quantum thermodynamical purposes, as it allows modeling the time-dependent Hamiltonian ruling the dynamics of a system (the qubit) by coupling this system to a quantum entity, i.e. a quantum battery (the MO). The Hamiltonian of the compound is time-independent, justifying to call it an “autonomous machine”.27,28,29 As demonstrated in a previous work,39 this scenery suggests a new strategy to measure average work exchanges in quantum open systems. Defining the average work rate received by the qubit as \(\left\langle {\dot W} \right\rangle\) = \({\mathrm{Tr}}_{\mathrm{q}}\left[ {\rho _{\mathrm{q}}(t)\dot H_{\mathrm{q}}(t)} \right]\), we have shown that this work rate exactly compensates the mechanical energy variation rate: \(\left\langle {{\cal E}_{\mathrm{m}}} \right\rangle\) = \({\mathrm{Tr}}_{\mathrm{m}}[\dot \rho _{\mathrm{m}}(t)H_{\mathrm{m}}]\) = \(- \left\langle {\dot W} \right\rangle\). Remarkably, this relation demonstrates the possibility of measuring work “in situ”, directly inside the battery. This strategy offers undeniable practical advantages, since it solely requires to measure the mechanical energy at the beginning and at the end of the transformation. The corresponding mechanical energy change is potentially measurable in the ultra-strong coupling regime gm/Ω ≫ 1,39 which is fully compatible with the semi-classical regime gmt ≪ |β0|.

Our goal is now to extend this strategy to work fluctuations. A key point is to demonstrate that the qubit and the mechanical state remain in a pure product state along single realizations of the protocol, allowing to unambiguously define stochastic energies for each entity. This calls for an advanced theoretical treatment based on the quantum trajectories picture.

Quantum trajectories

We shall now describe the evolution of the machine between the time t0 and tN by stochastic quantum trajectories of pure states \({\vec{\mathrm \Sigma }}: = \left\{ {\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle } \right\}_{n = 0}^N\), where \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\) is a vector in the Hilbert space of the machine and tn = t0 + nΔt with Δt the time increment. To introduce our approach, we first consider the semi-classical regime where the master Eq. (4) is valid: The initial state of the machine \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_0} \right)} \right\rangle\) is drawn from the product state \(\rho _{\mathrm{q}}(0) \otimes \left| {\beta _0} \right\rangle \left\langle {\beta _0} \right|\) where ρq(0) is diagonal in the {e, g} basis, and the evolution is studied over a typical duration \(\left( {t_N - t_0} \right) \ll \left| {\beta _0} \right|g_{\mathrm{m}}^{ - 1}\). Equation (4) is unraveled in the quantum jump picture,40,41,42,43,44 giving rise to the following set of Kraus operators {J−1(tn); J+1(tn); J0(tn)}:

$$J_{ - 1}\left( {t_n} \right) = \sqrt {\gamma{\Delta}t \left( {\bar n_{\omega (\beta _0(t_n))} + 1} \right)} \sigma \otimes {\mathbf{1}}_{\mathrm{m}},$$
(7)
$$J_{ + 1}\left( {t_n} \right) = \sqrt {\gamma\Delta{t} \bar n_{\omega (\beta _0(t_n))}} \sigma ^\dagger \otimes {\mathbf{1}}_{\mathrm{m}},$$
(8)
$$J_0\left( {t_n} \right) = {\mathbf{1}}_{{\mathrm{qm}}} - \frac{{{\mathrm{i}}\Delta t}}{\hbar }H_{{\mathrm{eff}}}\left( {t_n} \right).$$
(9)

We have introduced 1qm = 1m ⊗ 1q the identity operator in the Hilbert space of the machine. J−1 and J+1 are the so-called jump operators. Experimentally, they are signaled by the emission or absorption of a photon in the bath, that corresponds to the transition of the qubit in the ground or excited state, respectively. The mechanical state remains unchanged. Reciprocally, the absence of detection event in the bath corresponds the no-jump operator J0, i.e. a continuous, non-Hermitian evolution governed by the effective Hamiltonian Heff(tn) = Hqm + Hnh(tn). Here Hnh(t) = \(- ({\mathrm{i}}\hbar {\mathrm{/}}2)\left( {J_{ + 1}^\dagger (t)J_{ + 1}(t) + J_{ - 1}^\dagger (t)J_{ - 1}(t)} \right)\) is the non-Hermitian part of Heff.

Let us suppose that the machine is initially prepared in a pure state \(\left| {{\mathrm{\Psi }}\left( {t_0} \right)} \right\rangle = \left| {\epsilon _0,\beta _0} \right\rangle\). The quantum trajectory \({\vec{\mathrm \Sigma }}\) is then perfectly defined by the sequence of stochastic jumps/no-jump \(\left\{ {{\cal K}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\}_{n = 1}^N\), where \({\cal K}\) = 0, −1, +1. Namely, \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle\) = \(\left( {\mathop {\prod}\nolimits_{n = 1}^N {\kern 1pt} J_{{\cal K}_{\mathrm{\Sigma }}\left( {t_n} \right)}\left| {\Psi \left( {t_0} \right)} \right\rangle } \right)\)/\(\sqrt {P\left[ {{\vec{\mathrm \Sigma }}|\Psi \left( {t_0} \right)} \right]}\) where we have introduced \(P\left[ {{\vec{\mathrm \Sigma}} |\Psi \left( {t_0} \right)} \right]\) = \(\mathop {\prod}\nolimits_{n = 1}^N {\kern 1pt} P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right)} \right]\) the probability of the trajectory \({\vec{\mathrm \Sigma }}\) conditioned to the initial state \(\left| {{\mathrm{\Psi }}\left( {t_0} \right)} \right\rangle\). \(P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right)} \right]\) = \(\left\langle {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right)} \right|J_{{\cal K}_{\mathrm{\Sigma }}\left( {t_n} \right)}^\dagger J_{{\cal K}_{\mathrm{\Sigma }}\left( {t_n} \right)}\left| {\Psi _\Sigma \left( {t_{n - 1}} \right)} \right\rangle\) denotes the probability of the transition from \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right)} \right\rangle\) to \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\) at time tn. At any time tN, the density matrix of the machine, i.e. the solution of Eq. (4), can be recovered by averaging over the trajectories:

$$\rho _{{\mathrm{qm}}}\left( {t_N} \right) = \mathop {\sum}\limits_{{\vec{\mathrm \Sigma }}} {\kern 1pt} P\left[ {{\vec{\mathrm \Sigma }}} \right]\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle \left\langle {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_N} \right)} \right|.$$
(10)

We have introduced the probability of the trajectory \(P[{\vec{\mathrm \Sigma }}]\) = \(p\left[ {{\mathrm{\Psi }}\left( {t_0} \right)} \right]P\left[ {{\vec{\mathrm \Sigma }} |\Psi\left( {t_0} \right)} \right]\), where p[Ψ(t0)] the probability that the machine is initially prepared in \(\left| {{\mathrm{\Psi }}\left( {t_0} \right)} \right\rangle\).

Interestingly from the expression of the Kraus operators, it appears that starting from the product state \(\left| {\epsilon _0,\beta _0} \right\rangle\), the machine remains in a product state \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\) = \(\left| {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right),\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\) at any time tn, which is the first result of this paper. The demonstration is as follows: At each time step tn, either the machine undergoes a quantum jump J±1, or it evolves under the no-jump operator J0. In the former case, the qubit jumps from \(\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right)\) into \(\epsilon _{\mathrm{\Sigma }}\left( {t_{n + 1}} \right)\) and the mechanical state remains unchanged, such as \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_{n + 1}} \right)} \right\rangle\) = \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\). In the latter case, the evolution of the machine state is governed by the effective Hamiltonian Heff, whose non-Hermitian part can be rewritten Hnh = (−iħ/2)1m ⊗ \(H_{{\mathrm{nh}}}^q\) with \(H_{{\mathrm{nh}}}^q\) diagonal in the bare qubit energy eigenbasis. It naturally derives from the evolution rules that Hnh has no effect on a machine state of the form \(\left| {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right),\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\), such that the no-jump evolution reduces to its unitary component defined by Hqm. As studied above, the qubit energy state is stable under such evolution, such that \(\left| {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle = \left| {\epsilon _{\mathrm{\Sigma }}\left( {t_{n + 1}} \right)} \right\rangle\). Reciprocally, the coherent nature of the mechanical field is preserved by \(H_{\mathrm{m}}^{\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right)}\). Thus the mechanics evolves into \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_{n + 1}} \right)} \right\rangle\) = \({\mathrm{exp}}\left( { - {\mathrm{i}}\Delta tH_{\mathrm{m}}^{\epsilon _\Sigma \left( {t_n} \right)}} \right)\left| {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\), completing the demonstration.

This result invites to recast the machine trajectory as a set of two reduced trajectories \({\vec{\mathrm \Sigma }} = \left\{ {\vec \epsilon ,\vec \beta \left[ {\vec \epsilon } \right]} \right\}\), where \(\vec \epsilon = \left\{ {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\}_{n = 0}^N\) is the stochastic qubit trajectory with \(\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right) = e,g\). In the semi-classical regime considered here, the jump probabilities solely depend on ω(β0(t)), such that the qubit reduced evolution is Markovian. Conversely, \(\vec \beta = \left\{ {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\}_{n = 0}^N\) is the continuous MO trajectory verifying \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\) = \(\mathop {\prod}\nolimits_{k = 0}^{n - 1} {\kern 1pt} {\mathrm{exp}}\left( { - {\mathrm{i}}\Delta tH_{\mathrm{m}}^{\epsilon _{\mathrm{\Sigma }}\left( {t_k} \right)}} \right)\left| {\beta _0} \right\rangle\). At any time tN, the mechanical state depends on the complete qubit trajectory \(\vec \epsilon\).

Examples of numerically generated mechanical trajectories \(\vec \beta \left[ {\vec \epsilon } \right]\) (Methods section) are plotted in Fig. 1c. As it appears in the figure, at the final time the mechanical states \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle\) are restricted within an area of typical dimension gm/Ω. Splitting the mechanical amplitude as βΣ(tN) = β0(tN) + δβΣ(tN), the semi-classical regime is characterized by |δβΣ(tn)| ≪ |β0(tN)| while in the ultra-strong coupling regime \(\left[ {\delta \beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right) \gg 1\). These two regimes are compatible, which is the key of our proposal as we show in the next section.

Interestingly, the modeling of the machine stochastic evolution can be extended over timescales \(t \ge \left| {\beta _0} \right|g_{\mathrm{m}}^{ - 1}\), beyond the semi-classical regime. The key point is that the trajectory picture allows keeping track of the mechanical state at each time step \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\). Therefore at each time tn, a master equation of the form of Eq. (4) can thus be derived and unraveled into a set of trajectory-dependent Kraus operators similar to Eq. (7), taking now ω(βΣ(tn)) as the qubit effective frequency. In this general situation, the machine stochastic evolution still consists in trajectories of pure product states \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\) = \(\left| {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right),\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\), but the mechanical fluctuations |δβΣ(tn)| cannot be neglected anymore with respect to the mean amplitude |β0(tn)|. Consequently, Eq. (10) cannot be written as an average product state of the qubit and the MO, resulting in the emergence of classical correlations between the qubit and the MO average states. Moreover, the jump probabilities at time tn now depend on \(\bar n_{\omega \left( {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right)}\), such that the reduced qubit trajectory \(\vec \epsilon\) is not Markovian anymore. As we show below, this property conditions the validity of our proposal, which is restricted to the Markovian regime.

Stochastic thermodynamics

From now on, we focus on the following protocol: At the initial time t0 the machine is prepared in a product state ρqm(t0) = \(\rho _{\mathrm{q}}^\infty \left( {\beta _0} \right) \otimes \left| {\beta _0} \right\rangle \left\langle {\beta _0} \right|\), where \(\rho _{\mathrm{q}}^\infty \left( {\beta _0} \right)\) is the qubit thermal distribution defined by the effective frequency ω(β0). Note that ρqm(t0) is not an equilibrium state of the whole machine. One performs an energy measurement of the qubit, preparing the state \(\left| {{\mathrm{\Psi }}\left( {t_0} \right)} \right\rangle\) = \(\left| {\epsilon \left( {t_0} \right),\beta _0} \right\rangle\) with probability \(p_{\beta _0}^\infty \left[ \epsilon \right]\) = \({\mathrm{exp}}\left( { - \hbar \omega \left( {\beta _0} \right)\delta _{\epsilon ,e}{\mathrm{/}}k_{\mathrm{B}}T} \right){\mathrm{/}}Z\left( {\beta _0} \right)\). Z(β0) = 1 + exp(−ħω(β0)/kBT) is the partition function. The machine is then coupled to the bath and its evolution is studied between t0 = 0 and tN = π/2Ω. Depending on the choice of thermodynamical system, this physical situation can be studied from two different perspectives, defining two different transformations. If the considered thermodynamical system is the machine, then the studied evolution corresponds to a relaxation toward thermal equilibrium. As the machine Hamiltonian Hqm is time-independent, energy exchanges reduce to heat exchanges between the machine and the bath. On the other hand, if the considered thermodynamical system is the qubit, then the studied transformation consists in driving the qubit out of equilibrium through the time-dependent Hamiltonian Hq(t), the driving work being provided by the mechanics. In the semi-classical regime, the qubit evolution is Markovian, such that this last situation simply corresponds to Jarzynski’s protocol with Hq(t) = ħω(β0(t)) \(\left| e \right\rangle \left\langle e \right|\).

We now define and study the stochastic thermodynamical quantities characterizing the transformation experienced by the system (qubit or machine) for the protocol introduced above. As shown previously, starting from a product state \(\left| {{\mathrm{\Psi }}\left( {t_0} \right)} \right\rangle = \left| {\epsilon _{0},\beta _{0}} \right\rangle\) the machine remains in a product state at any time \(\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle = \left| {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right),\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\). Defining as \({\cal E}_{{\mathrm{qm}}}\left( {{\mathrm{\Psi }}_{{\mathrm{\Sigma }}\left( {t_n} \right)}} \right) = \left\langle {{\mathrm{\Psi }}_{{\mathrm{\Sigma }}\left( {t_n} \right)}} \right|H_{{\mathrm{qm}}}\left| {{\mathrm{\Psi }}_{{\mathrm{\Sigma }}\left( {t_n} \right)}} \right\rangle\) the machine internal energy, it thus naturally splits into a sum of the qubit energy \({\cal E}_{\mathrm{q}}\left( {\epsilon _{\mathrm{\Sigma }}\left( {t_n} \right),\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right)\) (Eq. (1)) and mechanical energy \({\cal E}_{\mathrm{m}}\left( {\beta _{\mathrm{\Sigma }}\left( {t_n} \right)} \right)\) (Eq. (2)). Along the trajectory, the set of internal energies can change in two distinct ways. A quantum jump taking place at time tn stochastically changes the qubit and the machine energies by the same amount \(\delta {\cal E}_{\mathrm{q}}[{\mathrm{\Sigma }},t_n] = \delta {\cal E}_{{\mathrm{qm}}}[{\mathrm{\Sigma }},t_n]_{}^{}\), leaving the MO energy unchanged. Following standard definitions in stochastic thermodynamics,24,45,46 the corresponding energy change is identified with heat q[Σ, tn] provided by the bath. Conversely in the absence of jump, the qubit remains in the same state between tn and tn+1, whereas its energy eigenvalues evolve in time due to the qubit-mechanical coupling. Such energy change is identified with work denoted w[Σ, tn] and verifies \(\delta {\cal E}_{\mathrm{q}}[{\mathrm{\Sigma }},t_n] = w[{\mathrm{\Sigma }},t_n]_{}^{}\). During this time interval, the machine is energetically isolated such that \(\delta {\cal E}_{{\mathrm{qm}}}[\Sigma ,t_n] = 0\). Therefore, the work increment exactly compensates the mechanical energy change \(\delta {\cal E}_{\mathrm{m}}[{\mathrm{\Sigma }},t_n] = - w\left[ {{\mathrm{\Sigma }},t_n} \right]\). Finally, the total work (resp. heat) received by the qubit is defined as \(W\left[ {{\vec{\mathrm \Sigma }}} \right] = \mathop {\sum}\nolimits_{n = 0}^{N - 1} {\kern 1pt} w\left[ {{\mathrm{\Sigma }},t_n} \right]\) (resp. \(Q\left[ {{\vec{\mathrm \Sigma }}} \right] = \mathop {\sum}\nolimits_{n = 0}^{N - 1} {\kern 1pt} q\left[ {{\mathrm{\Sigma }},t_n} \right]\)). By construction, their sum equals the qubit total energy change between t0 and tN, \({\mathrm{\Delta }}{\cal E}_{\mathrm{q}}\left[ {{\vec{\mathrm \Sigma }}} \right] = W\left[ {{\vec{\mathrm \Sigma }}} \right] + Q\left[ {{\vec{\mathrm \Sigma }}} \right]\). From the analysis conducted above, it appears that the heat exchange corresponds to the energy change of the machine, \({\mathrm{\Delta }}{\cal E}_{{\mathrm{qm}}}\left[ {{\vec{\mathrm \Sigma }}} \right] = Q\left[ {{\vec{\mathrm \Sigma }}} \right]\). Reciprocally, the work received by the qubit is entirely provided by the mechanics and verifies:

$$W\left[ {{\vec{\mathrm \Sigma }}} \right] = - {\mathrm{\Delta }}{\cal E}_{\mathrm{m}}\left[ {{\vec{\mathrm \Sigma }}} \right],$$
(11)

which is the second result of this article. Equation (11) extends the results obtained for the average work in a previous work,39 and explicitly demonstrates the one-by-one correspondence between the stochastic work received by the qubit and the mechanical energy change between the start and the end of the trajectory. The MO thus behaves as an ideal embedded quantum work meter at the single trajectory level.

We finally derive the expression of the stochastic entropy production \(\Delta _{\mathrm{i}}s\left[ {{\vec{\mathrm \Sigma }}} \right]\). It is defined by comparing the probability of the forward trajectory in the direct protocol \(P\left[ {{\vec{\mathrm \Sigma }}} \right]\) to the probability of the backward trajectory in the time-reversed protocol \(\tilde P\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over \Sigma } } \right]\):47

$$\Delta _{\mathrm{i}}s\left[ {{\vec{\mathrm \Sigma }}} \right] = {\mathrm{log}}\left( {\frac{{P\left[ {{\vec{\mathrm \Sigma }}} \right]}}{{\tilde P\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over \Sigma } } \right]}}} \right).$$
(12)

The probability of the direct trajectory reads:

$$P\left[ {{\vec{\mathrm \Sigma }}} \right] = p_{\beta _0}^\infty \left[ {\epsilon _{\mathrm{\Sigma }}\left( {t_0} \right)} \right]\mathop {\prod}\limits_{n = 1}^N {\kern 1pt} P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)|{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right)} \right],$$
(13)

The state of the hybrid system averaged over the forward trajectories at time tN is described by Eq. (10). At the end of the protocol, the reduced mechanical average state defined as ρm(tN) = Trq[ρqm(tN)] thus consists in a discrete distribution of the final mechanical states \(\left\{ {\left| {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle } \right\}\). Introducing the probability pm[βf] for the mechanical amplitude to end up in a state of amplitude βf, we shall denote it in the following ρm(tN) = \({\mathrm{\Sigma }}_{\beta _{\mathrm{f}}}p_{\mathrm{m}}\left[ {\beta _{\mathrm{f}}} \right]\left| {\beta _{\mathrm{f}}} \right\rangle \left\langle {\beta _{\mathrm{f}}} \right|\), where \({\mathrm{\Sigma }}_{\beta _{\mathrm{f}}}p_{\mathrm{m}}\left[ {\beta _{\mathrm{f}}} \right] = 1\).

Reciprocally, the time-reversed protocol is defined between tN and t0. It consists in time-reversing the unitary evolution governing the dynamics of the machine, keeping the same stochastic map at each time tn. This leads to the expression of the time-dependent reversed Kraus operators:46,48,49,50

$$\tilde J_0\left( {t_n} \right) = {\mathbf{1}}_{{\mathrm{qm}}} + \frac{{{\mathrm{i}}\Delta t}}{\hbar }H_{{\mathrm{eff}}}^\dagger \left( {t_n} \right),$$
(14)
$$\tilde J_{ - 1}\left( {t_n} \right) = J_{ + 1}\left( {t_n} \right),$$
(15)
$$\tilde J_{ + 1}\left( {t_n} \right) = J_{ - 1}\left( {t_n} \right),$$
(16)

The initial state of the backward trajectory is defined as follows: The mechanical state \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle\) is drawn from the final distribution of states \(\left\{ {\left| {\beta _{\mathrm{f}}} \right\rangle } \right\}\) generated by the direct protocol with probability pm[βf], whereas the qubit state is drawn from the thermal equilibrium defined by βΣ(tN) with probability \(p_{\beta _{\mathrm{\Sigma }}\left( {t_N} \right)}^\infty\). The probability of the backward trajectory reads

$$\begin{array}{*{20}{l}} {\tilde P\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over \Sigma } } \right]} \hfill & = \hfill & {p_{\mathrm{m}}\left[ {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right]p_{\beta _{\mathrm{\Sigma }}\left( {t_N} \right)}^\infty \left[ {\epsilon _\Sigma \left( {t_N} \right)} \right]} \hfill \\ {} \hfill & {} \hfill & { \times \mathop {\prod}\limits_{n = N}^1 {\kern 1pt} \tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right].} \hfill \end{array}$$
(17)

We have introduced the reversed jump probability at time tn\(\tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right]\) = \(\left\langle {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right|\tilde J_{{\cal K}_{\mathrm{\Sigma }}\left( {t_n} \right)}^\dagger \tilde J_{{\cal K}_{\mathrm{\Sigma }}\left( {t_n} \right)}\left| {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right\rangle\). Based on Eqs. (11), (12), (13), and (17), we derive in Supplementary the following expression for the stochastic entropy produced along \({\vec{\mathrm \Sigma }}\):

$$\Delta _{\mathrm{i}}s\left[ {{\vec{\mathrm \Sigma }}} \right] = \sigma \left[ {{\vec{\mathrm \Sigma }}} \right] + I_{{\mathrm{Sh}}}\left[ {{\vec{\mathrm \Sigma }}} \right],$$
(18)

where σ[\({\vec{\mathrm \Sigma }}\)] and ISh[\({\vec{\mathrm \Sigma }}\)] are defined as

$$\sigma \left[ {{\vec{\mathrm \Sigma }}} \right] = - \frac{{{\mathrm{\Delta }}{\cal E}_{\mathrm{m}}\left[ {{\vec{\mathrm \Sigma }}} \right] + {\mathrm{\Delta }}F\left[ {{\vec{\mathrm \Sigma }}} \right]}}{{k_{\mathrm{B}}T}},$$
(19)
$$I_{{\mathrm{Sh}}}\left[ {{\vec{\mathrm \Sigma }}} \right] = - {\mathrm{log}}\left( {p_{\mathrm{m}}\left[ {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right]} \right).$$
(20)

We have introduced the quantity ΔF[\({\vec{\mathrm \Sigma }}\)] = kBT log(Z(β0)/Z(βΣ(tN))) that extends the notion of the qubit free energy change to cases where the reduced qubit trajectory ε is non-Markovian. In the Markovian regime, we simply recover Z(tN) = 1 + exp(−ħω(β0(tN))/kBT) and \({\mathrm{\Delta }}F\left[ {{\vec{\mathrm \Sigma }}} \right] = \Delta F\). As we show below, in this case σ[\({\vec{\mathrm \Sigma }}\)] can be interpreted as the entropy produced along the reduced trajectory of the qubit, that gives rise to a reduced JE. Conversely, ISh[\({\vec{\mathrm \Sigma }}\)] measures the stochastic entropy increase of the MO and is involved in a generalized IFT characterizing the evolution of the whole machine. We now study in detail these two fluctuation theorems.

Reduced Jarzynski’s equality

We first focus on the transformation experienced by the qubit. As mentioned above, in the Markovian regime the applied protocol corresponds to Jarzynski’s protocol: The qubit is driven out of thermal equilibrium, whereas it experiences the frequency modulation ω(β0(t)). As the stochastic work \(W\left[ {{\vec{\mathrm \Sigma }}} \right]\) is provided by the mechanics, one expects the mechanical energy fluctuations to obey a reduced Jarzynski’s equality. We derive in Supplementary the following IFT:

$$\left\langle {{\mathrm{exp}}\left( {\frac{{{\mathrm{\Delta }}{\cal E}_{\mathrm{m}}\left[ {{\vec{\mathrm \Sigma }}} \right]}}{{k_{\mathrm{B}}T}}} \right)} \right\rangle _{{\vec{\mathrm \Sigma }}} = {\mathrm{exp}}\left( { - \frac{{{\mathrm{\Delta }}F}}{{k_{\mathrm{B}}T}}} \right).$$
(21)

Equation (21) corresponds to the usual Jarzynski’s equality, with the remarkable difference that the stochastic work involved in σ[\({\vec{\mathrm \Sigma }}\)] is now replaced by the mechanical energy change \({\mathrm{\Delta }}{\cal E}_{\mathrm{m}}\left[ {{\vec{\mathrm \Sigma }}} \right]\). This is the third and most important result of this paper, which now suggests a new strategy to measure work fluctuations. Instead of reconstructing the stochastic work by monitoring the complete qubit trajectory, one can simply measure the mechanical stochastic energy at the beginning and at the end of the protocol. This can be done, e.g. in time-resolved measurements of the mechanical complex amplitude through to optical deflection techniques.51,52 To do so, the final mechanical states \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle\) should be distinguishable, which requires to reach the ultra-strong coupling regime. As mentioned above, this regime has been experimentally evidenced38 with typical values Ω ~ gm ~ 400 kHz. The strategy we suggest here is drastically different from former proposals aiming at measuring JE in a quantum open system, that involved challenging reservoir engineering techniques24,25 or fine thermometry23 in order to measure heat exchanges.

We have simulated the reduced JE (Fig. 2a). As expected, JE is verified in the Markovian limit where we have checked that the action of the MO is similar to a classical external operator imposing the qubit frequency modulation ω(β0(t)) (Fig. 2b). On the contrary, the Markovian approximation and JE break down in the regime (gm/Ω)/|β0| ≥ 10−2. In what follows, we restrict the study to the range of parameters (gm/Ω)/|β0| < 10−2.

Fig. 2
figure 2

Jarzynski’s equality for the qubit. Parameters: T = 80 K, ħω0 = 1.2kBT, Ω/2π = 100 kHz, γ/Ω = 5. a Deviation from JE as a function of \(\left( {\frac{{g_{\mathrm{m}}}}{{\mathrm{\Omega }}}} \right){\mathrm{/}}\left| {\beta _0} \right|\) (|β0| = 5000). The points were computed by increasing the opto-mechanical coupling strength gm/2π from 1 to 20 MHz, keeping the other parameters constant. b Deviation from JE as a function of |β0| with gm/Ω = 10. Red squares: Case of a classical external drive imposing the qubit frequency modulation ω(β0(t)) (see text). Blue dots: Eq. (21). Green diamonds: \({\mathrm{exp}}\left( { - \left\langle {\sigma \left[ {{\vec{\mathrm \Sigma }}} \right]} \right\rangle _{{\vec{\mathrm \Sigma }}}} \right) - 1\). These green points demonstrate that JE is not trivially reached because the considered transformations are reversible. The error bars represent the standard error of the mean

Full size image

The results presented in Fig. 2 presuppose the experimental ability to measure the mechanical states with an infinite precision. To take into account both quantum uncertainty and experimental limitations, we now assume that the measured complex amplitude βM corresponds to the mechanical amplitude βf in the end of the protocol with a finite precision δβ. For our simulations we have chosen δβ = 2, which corresponds to achievable experimental value.51,52 To quantify this finite precision, we introduce the mutual information between the final distribution of mechanical states pm[βf] introduced above, and the measured distribution pm[βM], defined as:

$$I\left[ {\beta _{\mathrm{f}},\beta ^{\mathrm{M}}} \right] = \mathop {\sum}\limits_{\beta _{\mathrm{f}},\beta ^{\mathrm{M}}} {\kern 1pt} p\left( {\beta _{\mathrm{f}},\beta ^{\mathrm{M}}} \right){\mathrm{log}}\left( {\frac{{p\left( {\beta _{\mathrm{f}},\beta ^{\mathrm{M}}} \right)}}{{p_{\mathrm{m}}\left[ {\beta _{\mathrm{f}}} \right]p_{\mathrm{m}}\left[ {\beta ^{\mathrm{M}}} \right]}}} \right).$$
(22)

p(βf, βM) denotes the joint probability of measuring βM, whereas the mechanical amplitude equals βf. If the measurement precision is infinite, the mutual information I[βf, βM] exactly matches the Shannon entropy characterizing the final distribution of mechanical states SSh[βf] = \(- \mathop {\sum}\nolimits_{\beta _{\mathrm{f}}} {\kern 1pt} p_{\mathrm{m}}[\beta _{\mathrm{f}}]{\mathrm{log}}\left( {p_{\mathrm{m}}[\beta _{\mathrm{f}}]} \right)\). On the opposite, it vanishes in the absence of correlations between the two distributions.

The simulation of the measured JE and the mutual information I[βf, βM] are plotted in Fig. 3 for the measurement precision δβ = 2, as a function of the parameter gm/Ω (Methods section). We have introduced the measured reduced entropy production \(\sigma ^{\mathrm{M}}\left[ {{\vec{\mathrm \Sigma }}} \right] = \left( {W^M\left[ {{\vec{\mathrm \Sigma }}} \right] - {\mathrm{\Delta }}F} \right){\mathrm{/}}k_{\mathrm{B}}T\), where \(W^M\left[ {{\vec{\mathrm \Sigma }}} \right]\) is the measured work distribution \(W^M\left[ {{\vec{\mathrm \Sigma }}} \right]\) = \(- {\mathrm{\Delta }}{\cal E}_{\mathrm{m}}^{\mathrm{M}}\left[ {{\vec{\mathrm \Sigma }}} \right]\) = \(\hbar {\mathrm{\Omega }}\left( {\left| {\beta _0^{\mathrm{M}}} \right|^2 - \left| {\beta _{\mathrm{\Sigma }}^{\mathrm{M}}\left( {t_N} \right)} \right|^2} \right)\). As expected, small values of gm/Ω correspond to a poor ability to distinguish between the different final mechanical states, hence to measure work, which is characterized by a non-optimal mutual information. In this limit, the measured work fluctuations WM[\({\vec{\mathrm \Sigma }}\)] do not verify JE. Increasing the ratio gm/Ω allows to increase the information extracted on the work distribution during the readout. Thus the mutual information converges toward SSh[βf] despite the finite precision readout. JE is recovered for gm\(/{\mathrm{\Omega }}\sim 50\). Such high rates are within experimental reach, by engineering modes of lower mechanical frequency.53

Fig. 3
figure 3

Impact of finite precision readout of the mechanical amplitude. Parameters: δβ = 2, T = 80 K, ħω0 = 1.2kBT, Ω/2π = 1 kHz, γ/Ω = 5. 2gm|β0| was kept constant (2gm|β0|/2π = 600 GHz) whereas increasing gm, such that each point corresponds to the same mean reduced entropy production \(\left\langle {\sigma \left[ {{\vec{\mathrm \Sigma }}} \right]} \right\rangle _{{\vec{\mathrm \Sigma }}}\). Left axis, blue dots: Deviation from measured JE. Right axis, orange squares: Mutual information I[βf, βM]. Orange dashed line: Shannon’s entropy of the final distribution of mechanical states SSh[βf] (see text). The error bars represent the standard error of the mean

Full size image

Generalized integral fluctuation theorem

We finally consider the complete machine as the thermodynamical system under study. Based on Eqs. (12) and (18), we show in Supplementary that the entropy produced along the stochastic evolution of the hybrid system obeys a modified IFT of the form:

$${\mathrm{exp}}\left( { - {\mathrm{\Delta }}_{\mathrm{i}}s\left[ {\vec \Sigma } \right]} \right)_{{\vec{\mathrm \Sigma }}} = 1 - \lambda .$$
(23)

Following,30,31,32,33 we have defined the parameter λ as \(\mathop {\sum}\nolimits_{\mathrm{\Sigma }} {\kern 1pt} \tilde P\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over \Sigma } } \right] = 1 - \lambda\). The case λ ≠ 0 signals the existence of backward trajectories \({\mathrm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle \leftarrow$}} \\ \over \Sigma } }}\) without any forward counterpart, i.e. \(P\left[ {{\vec{\mathrm \Sigma }}} \right] = 0\), a phenomenon that has been dubbed absolute irreversibility (see Supplementary). From Eq. (23) and the convexity of the exponential, it is clear that absolute irreversibility characterizes transformations associated to a strictly positive entropy production. This is the case in the present situation, which describes the relaxation of the machine towards a thermal equilibrium state: Such transformation is never reversible, unless for T = 0.

The IFT (Eq. (23)) and the mean entropy production \(\left\langle {\Delta _{\mathrm{i}}s\left[ {{\vec{\mathrm \Sigma }}} \right]} \right\rangle _{{\vec{\mathrm \Sigma }}}\) are plotted in Fig. 4a, b respectively, as a function of the bath temperature T (Methods section). The limit ħω0 ≫ kBT corresponds to the trivial case of a single reversible trajectory characterized by a null entropy production and λ → 0. In the opposite regime defined by kBT ≫ ħω0, a mean entropy is produced, whereas λ → 1: In this situation, most backward trajectories have no forward counterpart. As we show in Supplementary, such effect arises as a given βf of the final distribution of mechanical states can only be reached by a single-forward trajectory, while it provides a starting point for a large number of backward trajectories.

Fig. 4
figure 4

Deviation from the integral fluctuation theorem a and mean entropy production b for the complete autonomous machine. Parameters: ω0/2π = 2 THz (amounts to ħω0/kBT = 1.2 for T = 80 K used in Fig. 2), Ω/2π = 100 kHz, γ/Ω = 5, gm/Ω = 10 and |β0| = 5000. In both cases, two different expressions were used. The blue dots are computed using the final distribution of mechanical states \(\left\{ {\left| {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right\rangle } \right\}\) and mimic an experiment. The red squares involve the probability of the reversed trajectory, which can only be the result of a theoretical treatment. (See Methods for more details.)

Full size image

As noticed in,30,33,50 absolute irreversibility can also appear in IFTs characterizing the entropy produced by a measurement process. In particular, λ ≠ 0 can signal a perfect information extraction: This typically corresponds to the present situation, which describes the creation of classical correlations between the qubit reduced trajectory \(\vec \epsilon\) and the distributions of final mechanical states \(\vec \beta [\vec \epsilon ]\). Interestingly, the two FTs (21) and (23) are thus deeply related. To be experimentally checked, Eq. (21) requires the MO to behave as a perfect quantum work meter, which is signaled by absolute irreversibility Eq. (23). Therefore absolute irreversibility is constitutive of the protocol, and a witness of its success.

Discussion

We have evidenced a new protocol to measure stochastic entropy production and thermodynamic time arrow in a quantum open system. Based on the direct readout of stochastic work exchanges within an autonomous machine, this protocol is experimentally feasible in state-of-the-art opto-mechanical devices and robust against finite precision measurements. It offers a promising alternative to former proposals relying on the readout of stochastic heat exchanges within engineered reservoirs, which require high efficiency measurements. Originally, our proposal sheds new light on absolute irreversibility, which quantifies information extraction within the quantum work meter and therefore signals the success of the protocol.

In the near future, direct work measurement may become extremely useful to investigate genuinely quantum situations where a battery coherently drives a quantum open system into coherent superpositions. Such situations are especially appealing for quantum thermodynamics as they lead to entropy production and energetic fluctuations of quantum nature,46,54 related to the erasure of quantum coherences.9,10 Recently, small amounts of average work have been directly measured, by monitoring the resonant field coherently driving a superconducting qubit.55 Generalizing our formalism to this experimental situation would relate measurable work fluctuations to quantum entropy production, opening a new chapter in the study of quantum fluctuation theorems.

Methods

The numerical results presented in this article were obtained using the jump and no-jump probabilities to sample the ensemble of possible direct trajectories.44 The average value of a quantity \(A\left[ {{\vec{\mathrm \Sigma }}} \right]\) is then approximated by \(\left\langle {A\left[ {{\vec{\mathrm \Sigma }}} \right]} \right\rangle _{\left[ {{\vec{\mathrm \Sigma }}} \right]} \simeq \frac{1}{{N_{{\mathrm{traj}}}}}\mathop {\sum}\nolimits_{i = 1}^{N_{{\mathrm{traj}}}} {\kern 1pt} A\left[ {{\vec{\mathrm \Sigma }}_i} \right]\), where Ntraj = 5 × 106 is the number of numerically generated trajectories and \({\vec{\mathrm \Sigma }}_i\), denotes the i-th trajectory.

The reduced entropy production \(\sigma \left[ {\vec \Sigma } \right]\) used in Figs. 2 and 4 was calculated with the expression (19), using the numerically generated values of β0 and βΣ(tN) in the trajectory \({\vec{\mathrm \Sigma }}\). One value of βΣ(tN) can be generated by a single direct trajectory Σ: Below we use the equality \(p_{\mathrm{m}}\left[ {\beta _\Sigma \left( {t_N} \right)} \right] = P\left[ {{\vec{\mathrm \Sigma }}} \right]\). Using the expression (17) of the probability of the reversed trajectory, the average entropy production becomes:

$$\begin{array}{*{20}{l}} {\left\langle {{\mathrm{\Delta }}_{\mathrm{i}}s\left[ {\vec \Sigma } \right]} \right\rangle }_{{\vec{\mathrm \Sigma }}} \hfill & = \hfill & {{\mathrm{log}}\left( {\frac{{P\left[ {\vec \Sigma } \right]}}{{\tilde P\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over \Sigma } } \right]}}} \right)_{{\vec{\mathrm \Sigma }}}} \hfill \\ {} \hfill & = \hfill & {\left\langle { - {\mathrm{log}}\left( {p_{\beta _\Sigma \left( {t_N} \right)}^\infty \left[ {\epsilon _{\mathrm{\Sigma }}\left( {t_N} \right)} \right]} \right.} \right.} \hfill \\ {} \hfill & {} \hfill & {\left. {\left. {\quad \quad \quad \times \mathop {\prod}\limits_{n = 1}^N {\kern 1pt} \tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right]} \right)} \right\rangle _{{\vec{\mathrm \Sigma }}}} \hfill \\ {} \hfill & \simeq \hfill & {\frac{{ - 1}}{{N_{{\mathrm{traj}}}}}\mathop {\sum}\limits_{i = 1}^{N_{{\mathrm{traj}}}} {\kern 1pt} {\mathrm{log}}\left( {p_{\beta _{\mathrm{\Sigma }}^i\left( {t_N} \right)}^\infty \left[ {\epsilon ^i\left( {t_N} \right)} \right]} \right.} \hfill \\ {} \hfill & {} \hfill & {\left. {\quad \quad \quad \times \mathop {\prod}\limits_{n = 1}^N {\kern 1pt} \tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}^i\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}^i\left( {t_n} \right)} \right]} \right),} \hfill \end{array}$$

and,

$$\begin{array}{*{20}{l}} {\mathop {\sum}\limits_{{\vec{\mathrm \Sigma }}} {\kern 1pt} \tilde P\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over \Sigma } } \right]} \hfill & = \hfill & {\mathop {\sum}\limits_{{\vec{\mathrm \Sigma }}} {\kern 1pt} p_{\beta _{\mathrm{\Sigma }}\left( {t_N} \right)}^\infty \left[ {\epsilon _{\mathrm{\Sigma }}\left( {t_N} \right)} \right]p_{\mathrm{m}}\left[ {\beta _{\mathrm{\Sigma }}\left( {t_N} \right)} \right]} \hfill \\ {} \hfill & {} \hfill & { \times \mathop {\prod}\limits_{n = 1}^N {\kern 1pt} \tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right]} \hfill \\ {} \hfill & = \hfill & {p_{\beta _{\mathrm{\Sigma }}\left( {t_N} \right)}^\infty \left[ {\epsilon _{\mathrm{\Sigma }}\left( {t_N} \right)} \right]\mathop {\prod}\limits_{n = 1}^N {\kern 1pt} \tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}\left( {t_n} \right)} \right]_{{\vec{\mathrm \Sigma }}}} \hfill \\ {} \hfill & \simeq \hfill & {\frac{1}{{N_{{\mathrm{traj}}}}}\mathop {\sum}\limits_{i = 1}^{N_{{\mathrm{traj}}}} {\kern 1pt} p_{\beta _{\mathrm{\Sigma }}^i\left( {t_N} \right)}^\infty \left[ {\epsilon ^i\left( {t_N} \right)} \right]} \hfill \\ {} \hfill & {} \hfill & { \times \mathop {\prod}\limits_{n = 1}^N {\kern 1pt} \tilde P\left[ {{\mathrm{\Psi }}_{\mathrm{\Sigma }}^i\left( {t_{n - 1}} \right){\mathrm{|\Psi }}_{\mathrm{\Sigma }}^i\left( {t_n} \right)} \right].} \hfill \end{array}$$

To obtain Fig. 3, we considered that the preparation of the initial MO state was not perfect. So instead of starting from exactly \(\left| {\beta _0} \right\rangle\), the MO trajectories start from \(\left| {\beta _{\mathrm{\Sigma }}\left( {t_0} \right)} \right\rangle\) with the βΣ(t0) uniformly distributed in a square of width 2δβ, centered on β0. Similarly, the measuring apparatus has a finite precision, modeled by a grid of cell width 2δβ in the phase plane (Re βf, Im βf). Instead of obtaining the exact value of βΣ(tN), we get \(\beta _\Sigma ^{\mathrm{M}}\left( {t_N} \right)\), the center of the grid cell in which βΣ(tN) is. The value used to compute the thermodynamical quantities are not the exact βΣ(t0) and βΣ(tN) but \(\beta _0^{\mathrm{M}} = \beta _0\) and \(\beta _{\mathrm{\Sigma }}^{\mathrm{M}}\left( {t_N} \right)\).