Introduction

X-ray diffraction (XRD) plays a critical role in materials development, enabling the identification of crystalline phases following their synthesis. With the rise of automated experiments1,2,3, there is a growing need to classify XRD patterns with minimal human intervention. Convolutional neural networks (CNNs) are particularly well suited for this task as they can learn to extract the features that are most useful to identify a given phase4. Nevertheless, there remain several factors that limit the accuracy of these models. Recent work has shown that CNNs exhibit bias toward the largest peaks within each pattern, causing them to overlook the less prominent features5. This bias leads to misclassifications when such features are needed to distinguish similar phases whose largest diffraction peaks overlap. Further complicating matters is the prevalence of measurement noise and diffuse background signal in experimental patterns, which often are not accounted for when training CNNs on simulated data6. Using proper data representation is paramount when training new models, whether to improve their performance or reduce their complexity. This motivates our investigation of the pair distribution function (PDF) as an alternative representation of diffraction data that can be used to supplement the training of ML models for automated phase identification.

The PDF describes the probability of finding a pair of atoms separated by some distance (r) within a material7. Variations in its intensity arise from differences in atomic form factors or scattering lengths, which dictate how each atom scatters incident X-rays or neutrons, as well as the frequency of certain atomic distances within the structure. PDFs are derived from diffraction patterns by converting the data from reciprocal space to real space through a Fourier transform. Whereas conventional diffraction patterns are used to assess long-range order in the average structure of a material, PDFs are often used to inspect short-range order in the local structure while also still accounting for the long-range order that exists8,9,10. This is primarily because PDFs are more sensitive to minor features in the diffraction pattern, such as diffuse scattering, which otherwise might be overlooked when studying the most prominent Bragg peaks. We note that in principle these two representations contain identical information; however, they each highlight different aspects of the material being examined. For this reason, we believe they are particularly well-suited to complement one another in the training of ML algorithms.

Building on recent advances in ML for spectroscopy11,12, Liu et al. pioneered its use in the analysis of PDF data by training a CNN to classify the space groups of crystalline materials, achieving a 70% accuracy on entries from the ICSD13. The model was also found to be robust against changes in experimental parameters related to the choice of distances in real space (\(r\)) and reciprocal space (\(Q\)) included during training14. Generative models have since been developed to solve the structures of metallic nanoparticles from PDF data, providing accurate predictions on systems containing \(\le\) 400 atoms15. To extract structural motifs from bulk materials, Anker et al. used gradient boosted decision trees to iteratively refine structural models in the fitting of measured PDF data16. Related work has shown that DFT calculations can be integrated into the refinement process to ensure the proposed solution is low in energy, thus providing solutions that more accurately represent the experimental sample17. Zhang et al. further showed that when combined with feature extraction methods like principal component analysis and non-negative matrix factorization, machine-learned PDF analysis can also yield accurate predictions of defect concentrations in oxides18. Despite these advancements, there remains no ML technique available to identify specific crystalline phases that match a given PDF in generic chemical spaces, a task that becomes even more challenging when dealing with multi-phase samples.

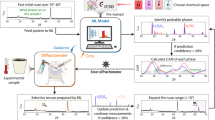
In this work, we introduce an approach to PDF analysis and integrate it with our existing algorithm (XRD-AutoAnalyzer) designed to identify crystalline materials from XRD patterns19. In the original method, a CNN is trained on simulated XRD patterns that are systematically augmented to account for several experimental artifacts that cause changes to peak positions (lattice strain), intensities (crystallographic texture), and widths (small particle size). We now train a second CNN on PDFs obtained through a Fourier transform of these simulated XRD patterns. The trained model can then be used to identify crystalline phases from experimental patterns by first transforming them in a similar fashion. The samples resulting from the Fourier transform are hereafter referred to as virtual PDFs as they require no changes to the experimental procedure20, instead relying on data collected from conventional XRD scans. While the model trained on virtual PDFs is effective when used on its own, we show in this work that improved accuracy can be achieved by aggregating its predictions with those from the original XRD-AutoAnalyzer method. This is accomplished by combining the predictions of each model in a confidence-weighted sum, which leverages the strengths and minimizes the weaknesses of each CNN by assigning greater weight to the model with higher confidence in its prediction accuracy (Fig. 1).

Fig. 1: Combined analysis of XRD patterns and PDFs.
figure 1

Given a pattern to be classified, a Fourier transform (FT) is used to calculate its virtual PDF. Each spectrum is fed to a separately trained CNN that predicts a set of phases (\(i\)), where each has a confidence associated with XRD (\({c}_{{\rm{XRD}}}\)) or PDF (\({c}_{{\rm{PDF}}}\)). These predictions are aggregated using a confidence-weighted sum defined by the equation shown.

Full size image

The models trained on XRD patterns and virtual PDFs are evaluated using four datasets spanning two chemistries, Li-La-Zr-O and Li-Ti-P-O. To examine how the number of phases in a sample affects the performance of each model, we created a dataset that includes 8000 patterns derived from mixtures containing between one and three compounds each. A second dataset is tailored to probe each model’s ability to assess minor features in the diffraction pattern, and as such it contains 440 patterns derived from a single composition (LiTiO2) with varied site occupancy. A third dataset, with 2800 patterns categorized by distinct experimental artifacts, is used to gauge how robust each model is against perturbations of their inputs. A fourth and final dataset is used to validate the models on real data, containing 240 patterns obtained from experimentally prepared samples. Our tests reveal that the models trained on virtual PDFs respond better to low-intensity features in the diffraction pattern, while also being more robust against experimental artifacts, enabling high accuracy on single-phase samples. In contrast, the XRD-trained models perform better on multi-phase samples as they can effectively deconvolute the largest Bragg peaks in each pattern. Notably, combining the predictions of both models in a confidence-weighted sum provides substantially higher accuracy than each standalone model, demonstrating the benefit of using diverse input representations for ML on diffraction data.

Results

Influence of the number of phases present

We generated a total of 8000 simulated XRD patterns and an equivalent number of virtual PDFs from 28 and 45 crystalline phases within the Li-La-Zr-O and Li-Ti-P-O chemistries, respectively. These XRD patterns and their corresponding PDFs include 1400 single-phase, 2400 two-phase, and 4200 three-phase samples. Mixtures comprised of \(\ge\) 2 phases were obtained through linear combinations of the single-phase patterns, from which virtual PDFs were computed via Fourier transform. Two CNNs were trained on each chemical space, as detailed in the Methods, and then applied to the simulated XRD patterns and virtual PDFs. We assessed each model’s performance using the F1-score, a commonly used metric that averages precision and recall:

$${F}_{1}=\frac{{\rm{TP}}}{{\rm{TP}}+\frac{1}{2}\left({\rm{FP}}+{\rm{FN}}\right)}$$
(1)

In the context of this work, TP represents the number of correctly identified phases (true positives), FP is the number of phases incorrectly identified (false positives), and FN is the number missed phases (false negatives). A high F1-score, close to 1, indicates that the model can effectively identify all phases in a sample without incorrectly identifying phases that are not present.

The results from each model trained on XRD patterns or virtual PDFs are shown in Fig. 2, where the bar heights (y-axis) represent F1-scores and the labels (x-axis) denote the phase count in the samples on which they were obtained. Both models performed well on the samples tested, providing F1-scores greater than 0.75 even when given three-phase mixtures. Interestingly, the PDF-trained model slightly outperforms the XRD-trained model on samples containing only a single phase. For reasons outlined in the next two sections, this result suggests that PDFs provide a more effective representation of diffraction patterns in the absence of impurity phases. In contrast, the XRD-trained model performs better than its PDF-trained counterpart when applied to multi-phase samples, and this performance gap widens with increasing phase count. We suspect that the reduced accuracy in identifying multi-phase mixtures using PDFs is due to their inherently broad and overlapping features. Unlike XRD patterns, which often contain distinct peaks that are easier to separate, PDFs possess diffuse characteristics that blend together when multiple phases coexist in one sample.

Fig. 2: Performance on multi-phase mixtures.
figure 2

F1-scores from the predictions of two CNNs that were trained on XRD patterns (blue) or PDFs (red). These models were applied to simulated data from the Li-La-Zr-O and Li-Ti-P-O chemistries. Also included are the F1-scores obtained by aggregating the predictions from both models in a confidence-weighted sum (purple). The data is categorized by the number of phases included in each sample. Yellow stars denote which standalone model performs best, while the shaded portion of each purple bar represents the improvement realized by aggregating the predictions of both models.

Full size image

Even in cases where the overall F1-scores are comparable between the models trained on XRD patterns and virtual PDFs, their failures often occur on different samples. Indeed, 42% of all errors affect samples that are misclassified in one representation but correctly classified in another. We exploit these differences, combined with each model’s ability to evaluate the confidence of its own predictions, to enhance the accuracy of the two models by aggregating their outputs in a confidence-weighted sum. As shown by the purple bars in Fig. 2, our combined approach to phase identification leads to substantially improved accuracy relative to each standalone model. The aggregated predictions yield an average F1-score of 0.88, exceeding the average score of 0.83 obtained by the individually trained models, which corresponds to a near 30% reduction in the total error rate.

The results presented in Fig. 2 correspond to predictions made on samples containing known (previously reported) phases in the Li-La-Zr-O or Li-Ti-P-O chemistries. However, exploratory syntheses can sometimes lead to the formation of novel phases, which do not have any reference structures available in databases like the ICSD. Our models therefore cannot predict the identities of such phases since each CNN needs to be trained on XRD patterns or virtual PDFs generated from known materials. Nevertheless, they can often detect the presence of unknown phases by giving predictions with unusually low confidence. To illustrate this, we performed a series of tests where the models trained on known phases from the Li-La-Zr-O chemistry were applied to 10 compounds randomly selected from other chemistries (Supplementary Table 2). A total of 200 XRD patterns and virtual PDFs were simulated from these compounds, each including a mixture of experimental artifacts (“Methods” section). As shown in Supplementary Fig. 1a, the models give predictions with low confidence (on average, 18%) when applied to these unknown phases. For comparison, the predictions made on data from known phases generally have much higher confidence (on average, 92%) as shown in Supplementary Fig. 1b. One may therefore use low prediction confidence as a possible indicator for the presence of unknown phases.

Assessment of minor diffraction peaks

The tests reported in the previous section reveal that CNNs trained on virtual PDFs perform better than those trained on XRD patterns when dealing with single-phase samples. To clarify why this might be, we inspect the Class Activation Map (CAM) of each model. The CAM illustrates which parts of the input spectrum most significantly contribute to the model’s output4,21. Taking TiO2 as an example, we examine the CAM for each model using its associated input. The XRD pattern and virtual PDF for this sample, as well as their respective CAMs, are shown in Fig. 3. These plots reveal that the CAM for each spectrum directly correlates with its magnitude. In the case of XRD, the model’s output is predominantly influenced by the few largest peaks while the smaller features are overlooked. On the other hand, given the frequent presence of many prominent features in the PDF, a greater portion of the spectrum has a strong influence on the model’s output. This difference highlights a key advantage of using virtual PDFs as input to CNNs; by using a representation that evenly weighs its features, the model can more effectively harness their information. In contrast, it is more difficult for a CNN to leverage minor peaks in XRD patterns. Doing so requires the network to learn high weights in the training process to compensate for these peaks’ low intensities. However, high weights are generally penalized during training due to the use of regularization (e.g., batch normalization and dropout) to avoid overfitting.

Fig. 3: Feature importance in XRD and PDF analysis.
figure 3

Class activation maps (CAMs) are shown for the models trained on XRD patterns as compared to virtual PDFs. a Calculated XRD pattern (solid blue line) for rutile TiO2 and its associated CAM (shaded blue curve). b Virtual PDF (solid red line) for rutile TiO2 and its associated CAM (shaded red curve).

Full size image

To further demonstrate the advantages of using virtual PDFs when examining minor Bragg peaks, we created a dataset of partially disordered LiTiO2 compounds where such minor features must be inspected to distinguish between the different states of order. The dataset contains eleven crystalline phases that share the same composition (LiTiO2) and structural framework (rocksalt), with the only difference being the distribution of their site occupancies. These range from an ordered configuration (space group \({\rm{P}}4/{\rm{mmm}}\)), where Li and Ti strictly occupy the 2a and 2d sites, to a disordered configuration (space group \({\rm{Fm}}\bar{3}{\rm{m}}\)) where Li and Ti are distributed evenly among both sites (Fig. 4a). The site occupancies in each of the eleven structures were determined using a linear interpolation between the fully ordered and disordered configurations. These modified occupancies alter the intensities of several minor Bragg peaks while leaving the largest peaks unchanged (Fig. 4b). Consequently, the dataset provides a useful test case to determine which model can most effectively assess the intensities of minor Bragg peaks to distinguish between materials with similar XRD patterns.

Fig. 4: Predicting site occupancies with XRD and PDF analysis.
figure 4

a Unit cells for LiTiO2 shown with varied degrees of order, controlled by the occupancies of Li/Ti on the 2a and 2d sites. b XRD patterns calculated from these structures, where the minor Bragg peak intensities (purple) correlate with the degree of order. c Density of prediction errors obtained from CNNs trained on XRD patterns and virtual PDFs, defined as the % difference between the predicted and actual occupancies on the 2a site (Eq. 2). Positive prediction errors represent an overestimation of Li/Ti ordering while negative errors represent an underestimation. d Virtual PDFs calculated from the XRD patterns through a Fourier transform.

Full size image

Because the models assessed in the previous section were not trained on any disordered versions of LiTiO2 (Supplementary Fig. 2), we trained two new models on data from the eleven LiTiO2 structures which possess varied Li/Ti ordering. These structures were used to simulate 2200 XRD patterns and an equivalent number of virtual PDFs, each augmented with perturbations corresponding to various experimental artifacts (“Methods” section). The patterns and PDFs were divided using a 60/20/20 split for training, validation, and testing. The performance of each model is evaluated by computing the error of its predictions in terms of % order:

$${\rm{Prediction\; error}}=2\left({{\rm{Li}}}_{{\rm{pred}}}^{2{\rm{a}}}-{{\rm{Li}}}_{{\rm{actual}}}^{2{\rm{a}}}\right)\times 100 \%$$
(2)

Where \({{\rm{Li}}}_{{\rm{pred}}}^{2{\rm{a}}}\) and \({{\rm{Li}}}_{{\rm{actual}}}^{2{\rm{a}}}\) represent the predicted and actual occupancy of Li on the 2a site, respectively. Figure 4c shows the distribution of prediction errors from each CNN when applied to its test set. These distributions reveal that the PDF-trained model performs well on the LiTiO2 dataset, providing an average prediction error of only 9%, which is substantially lower than the 18% error provided by the XRD-trained model.

The improved accuracy provided by using virtual PDFs can be understood by visualizing their changes with respect to different site occupancies. In Fig. 4d, we plot the PDFs calculated from LiTiO2 through a Fourier transform of its XRD patterns with varied site order (Fig. 4b). This plot reveals that the shape and intensity of each feature in the PDF is strongly dependent on the distribution of site occupancies in LiTiO2. The CNN can accurately model this relationship as the corresponding changes affect many high-intensity features that contribute significantly to the model’s classification (see Fig. 3 for CAM analysis). In contrast, the XRD patterns corresponding to varied site occupancies differ only in their low-intensity features (Fig. 4b), which are more difficult to assess when using CNNs. These findings confirm the benefits of using virtual PDFs to better distinguish between materials with similar XRD patterns.

Handling experimental artifacts

Experimentally measured XRD patterns often deviate from their calculated reference patterns owing to the presence of various artifacts including lattice strain, crystallographic texture, small particle size, measurement noise, and diffuse background signal. To determine which model is more robust against each of these experimental artifacts, we generated 2800 XRD patterns and an equivalent number of virtual PDFs from 28 different compounds in the Li-La-Zr-O chemical space. These patterns and PDFs were separated from the data used for model training. Each sample contains only one phase and is categorized by the experimental artifact it contains. The magnitude of each artifact was set beyond the limits used during model training to determine how well the CNNs could handle out-of-distribution data. Further details on the simulation of these artifacts are provided in the Methods. After training two models in the Li-La-Zr-O space, one on simulated XRD patterns and another on virtual PDFs, we applied each to the categorized samples. Table 1 lists the artifacts that were considered and the F1-scores resulting from the predictions of each model on the affected patterns.

Table 1 Comparison of the F1-scores achieved by models trained on simulated XRD patterns and virtual PDFs
Full size table

Only for one experimental artifact does the model trained on XRD patterns outperform its PDF-trained counterpart in a significant way: shifts in peak position that results from lattice strain. An F1-score of 0.917 is achieved when using XRD patterns, in comparison to a score of 0.869 when using virtual PDFs. Lattice strain modifies both XRD patterns and PDFs similarly by shifting features along the x-axis (Supplementary Fig. 3a). However, we suspect that the model trained on PDFs is more impacted by these changes as it equally weighs all features, ranging from low to high r, with equal importance (Fig. 3b). In contrast, the XRD-trained model primarily focuses on the largest Bragg peaks, as demonstrated in the previous section (Fig. 3a). Such peaks are typically found at low \(2{\rm{\theta }}\) values, which are less influenced by lattice strain. As a result, the model trained on XRD patterns is less affected by shifts originating from lattice strain.

In cases where the Bragg peak intensities are altered by crystallographic texture, both models perform comparably, yielding F1-scores of 0.963 and 0.962 when trained on XRD patterns and virtual PDFs, respectively. It appears that texture has a similar effect on each representation, leading to changes in the magnitude of its features while preserving their positions (Supplementary Fig. 3b). Such changes have minimal influence on the performance of each model. Indeed, previous work has shown that CNNs trained on diffraction patterns tend to be influenced much more strongly by the positions of the input features (\(2{\rm{\theta }}\)) rather than their intensities5,19.

For the remaining three artifacts we considered – peak broadening, measurement noise, and diffuse background signal – the model trained on virtual PDFs performs significantly better than the model trained on XRD patterns. As reported in Table 1, the F1-scores that result from using PDFs are on average 0.049 higher than those obtained from XRD patterns when altered by one of these three artifacts, which corresponds to a 46% reduction in the model’s error rate. To understand these improvements, we illustrate in Fig. 5 the impact of each artifact on the XRD pattern and virtual PDF from a sample compound, Li2TiO3. All three artifacts are found to have less influence on the PDF as compared to the XRD pattern.

Fig. 5: Experimental artifacts in XRD and PDF.
figure 5

Visualization of three experimental artifacts on which CNNs perform better when trained on virtual PDFs as opposed to XRD patterns. All the XRD patterns (left) and PDFs (right) shown here are calculated from Li2TiO3. The artifacts include (a) peak broadening, (b) measurement noise, and (c) diffuse background signal. The unperturbed patterns (without artifacts) and PDFs are plotted as blue and red lines, respectively, while the perturbed patterns (with artifacts) and PDFs are plotted as purple lines.

Full size image

Peak broadening (Fig. 5a) causes several peaks to overlap in the XRD pattern, complicating its analysis, whereas it only leads to minor changes in the magnitude of features in the PDF. Its peaks and troughs become more (less) pronounced at low (high) r values in the PDF, but their shapes generally remain unchanged. Measurement noise (Fig. 5b) in XRD has little effect on the virtual PDF throughout the range of values where it is plotted here (1 Å ≤ r ≤ 40 Å). Though, changes to the PDF become more prominent when it is generated using data from higher \(2{\rm{\theta }}\) in the corresponding XRD pattern (Supplementary Fig. 4). These changes are particularly noticeable at very high values of r (> 100 Å), where features have low magnitude and are heavily influenced by noise in the XRD pattern (Supplementary Fig. 5). As such, we restricted all virtual PDFs to r ≤ 40 Å when training the models described in this work (“Methods” section). Features within this range are affected by diffuse background signal in XRD (Fig. 5c), but any such alterations are restricted to low values of r (<5 Å) while the remainder of the spectrum appears unchanged.

Because the PDF representation leads to improved model performance when dealing with three out of the five experimental artifacts considered here, it also provides better results than XRD when used to analyze samples that simultaneously contain all five artifacts. As shown in the final row of Table 1, the PDF-trained model produces an F1-score of 0.813 when applied to these samples with mixed artifacts. In contrast, the XRD-trained model yields a lower F1-score of only 0.781 when applied to the same set of samples. While both scores are lower than those obtained on samples containing just one artifact, they show that each model performs reasonably well even when dealing with realistic samples that are affected by multiple artifacts at once. Further improvements can also be achieved by combining the predictions from each individual model into a confidence-weighted sum; doing so yields a higher F1-score of 0.862.

Validation on experimental samples

As the models presented in this work are trained only on simulated data, whether it be XRD patterns or virtual PDFs, it is important to verify that they maintain a high level of predictive accuracy when applied to data from experimental measurements. To confirm that this is the case, we tested each CNN on a set of 240 patterns obtained from experimentally prepared samples. These samples consisted of various two-phase combinations of eight compounds from the Li-La-Zr-O and Li-Ti-P-O chemistries. For each combination we prepared ten unique samples, each containing progressively larger amounts of the secondary phase. The weight fraction of the secondary phase varied from 2 to 20%. Additional information regarding these measurements can be found in previous work22.

For each chemistry, we trained one CNN on simulated XRD patterns and another on virtual PDFs as described in the Methods. In contrast to previous work22, where the performance of each model was measured only by its ability to successfully detect the impurity phase in each sample, here we evaluate model performance by computing the F1-score – a measure that accounts for both accuracy and precision (Eq. 1). The F1-scores resulting from the predictions of each model on the dataset containing 240 experimental samples are displayed in Fig. 6. These scores are plotted as a function of the secondary phase’s weight fraction in each sample. Both models yield comparably high F1-scores, ranging from 0.73 to 0.88, with their predictions becoming more accurate as the weight fraction of the secondary phase increases. Notably, these F1-scores agree well with those obtained when applying the same models to simulated patterns. As discussed in earlier sections (Fig. 2), the XRD- and PDF-trained models yield F1-scores of 0.90 and 0.91, respectively, when applied to simulated data from two-phase mixtures. The comparable F1-scores generated from both experimental and simulated data highlight the models’ ability to extrapolate beyond their training sets of simulated XRD patterns and PDFs.

Fig. 6: Performance on experimental samples.
figure 6

Calculated F1-scores on experimental patterns obtained from physical two-phase mixtures prepared using materials in the Li-La-Zr-O and Li-Ti-P-O chemical spaces. The F1-score is plotted as a function of weight fraction for the secondary (impurity) phase in each mixture, which ranges from 2 to 20%. Results are separated by the type of input data from which the predictions were made (XRD, PDF, and Aggregate). The shaded portion of each plot represents the improvement given by aggregating the individual results.

Full size image

We also combined the predictions of each model in a confidence-weighted sum and evaluated the resulting F1-scores on the experimental dataset containing 240 samples. As shown by the purple dots in Fig. 6, a substantial improvement in accuracy is achieved by aggregating the predictions from both models. On average, the F1-scores provided by the combined predictions are 0.041 higher than those obtained from the best-performing standalone model trained on either XRD patterns or PDFs, corresponding to a 38% reduction in the error rate. These findings demonstrate that by combining distinct representations of input to the CNNs, improved predictive power on experimental samples can be achieved while requiring no changes to the measurements themselves.

Discussion

Our work shows the importance of representation when using ML to interpret experimental data. By choosing an optimal representation of the data, one can reduce model complexity and improve classification performance. For the training of ML models that can identify materials from their XRD patterns, recent efforts have used a variety of representations that describe these materials in reciprocal space4,5,19,22,23,24. Here we have demonstrated that significantly improved accuracy in phase identification can be achieved by also considering materials in real space, specifically by using PDFs calculated through a Fourier transform of XRD patterns. Such PDFs are called virtual as they require no changes to the experimental procedure, simply being an alternative representation of the data obtained from typical powder diffraction measurements. By training one model on simulated XRD patterns and another on virtual PDFs, we have shown how one can leverage the unique benefits of each input representation for the task of phase identification.

CNNs trained on virtual PDFs outperform those trained on XRD patterns when applied to samples containing a single phase, primarily for two reasons. First, PDFs contain many prominent features that are equally weighed by the CNN, whereas XRD patterns often contain a few prominent peaks that disproportionally bias the CNN. This allows PDF-trained models to more effectively distinguish between similar phases that have substantial peak overlap in XRD. For instance, our models could more precisely determine the degree of Li/Ti order present in LiTiO2 when examining virtual PDFs as opposed to XRD patterns. These patterns could in principle be distinguished by assessing the intensity of several low-intensity Bragg peaks in XRD, which grow larger with increased Li/Ti ordering in LiTiO2. However, detecting such minor variations requires the CNN to learn very high weights associated with the low-intensity peaks. This is discouraged by our use of regularization to avoid overfitting the models during training. In contrast, changes to the low-intensity peaks in XRD lead to variations in the shapes of much larger features in virtual PDFs. As a result, the CNNs can accurately detect these variations without requiring the use of disproportionately large weights.

In addition to the improved detection of low-intensity peaks, transforming XRD patterns into virtual PDFs reduces the impact of measurement noise and diffuse background signal. While the Fourier transform used to generate the PDF does not create or destroy any information associated with the XRD pattern, it isolates much of the effects from high-frequency signal (noise) and low-frequency signal (diffuse background) to high and low values of r, respectively. As a result, the PDF-trained models are more robust against these artifacts so long as an appropriate range of r values is used. In our tests, the models performed best when trained on virtual PDF data ranging from 1−40 Å (Supplementary Fig. 6).

We further note the importance of choosing an optimal range of \(2{\rm{\theta }}\), or more generally, the extent of reciprocal space (\(Q\)) that is used to generate the virtual PDFs. When studying short-range order in disordered solutions or nanomaterials, for example, it is often recommended to collect diffraction data up to at least Q = 10 − 15 Å−1 (beyond what is possible for Cu \({{\rm{K}}}_{{\rm{\alpha }}}\) radiation). In contrast, our method is designed only for the analysis of crystalline materials that possess long-range order, which can typically be identified using much less of \(Q\)-space. For this task, we find that it is beneficial to sample a limited range of \(2{\rm{\theta }}\) (\(10^\circ -90^\circ\)) which corresponds to a smaller portion of \(Q\)-space (0.7 − 5.8 Å−1) when using Cu \({{\rm{K}}}_{{\rm{\alpha }}}\) radiation. Data collected at higher \(2{\rm{\theta }}\) often contains broad peaks with low intensity, causing them to blend in with the background noise that is commonly present in experimental measurements. This leads to modifications of the PDF throughout its entire range of r values (Supplementary Fig. 4), ultimately reducing the accuracy of the corresponding models. We therefore chose to use limited ranges of \(2{\rm{\theta }}\) and r that led to optimal model performance on our test data consisting of crystalline phases (Methods).

Despite their improved performance on single-phase samples, the CNNs trained on virtual PDFs exhibit lower accuracy than XRD-trained models when applied to multi-phase mixtures. This shortcoming can be attributed to the diffuse characteristics of PDFs, which tends to create overlapping features when multiple phases are present in one sample. The models trained on PDFs also underperform those trained on XRD patterns when applied to samples affected by lattice strain, an artifact that shifts the positions where peaks occur within each spectrum. Such shifts appear similar in XRD patterns and PDFs, becoming more pronounced at higher values of \(2{\rm{\theta }}\) and r. Yet, the influence of these shifts on model performance differs between each representation. In XRD patterns, the peaks that are most affected by lattice strain (at high \(2{\rm{\theta }}\)) also tend to be low intensity, and as such, they have little effect on classifications made by the CNN. In contrast, PDFs contain many prominent features at high values of r which have significant influence over the CNN’s predictions. As a result, the models trained on PDFs show reduced classification accuracy when these features are heavily affected by lattice strain.

The unique strengths and weaknesses of models trained on XRD patterns and virtual PDFs provide an opportunity to maximize the benefits of each model while minimizing its drawbacks. We accomplish this by aggregating the predictions from both models in a confidence-weighted sum, which outperforms each standalone model on a variety of test cases including both simulated and experimental data. The success of aggregation largely stems from the ability of each model to assess its own level of prediction confidence on new samples. This is done by using Monte Carlo dropout, a technique that provides an estimate of model uncertainty by running the trained neural network multiple times during inference, each time with different neurons deactivated, creating a distribution of outputs from which confidence can be inferred25. Further enabling the improved accuracy realized by aggregation is the fact that each model tends to succeed or fail on different samples. As a result, the best-suited model can be automatically determined by allocating more weight to the one that exhibits higher prediction confidence.

Our findings build upon previous benchmarks in ML where state-of-the-art performance was achieved by combining distinct input representations. For instance, IBM Watson surpassed previous Jeopardy! champions by using algorithms that processed various representations of the data – from keyword searches to semantic parsing – to determine the most likely answer26. Similarly, DeepMind’s AlphaGo mastered the game of Go by combining neural networks with Monte Carlo tree search algorithms, each of which relied on a unique representation of the board’s layout27. Related strides have been made in materials science and chemistry, with the development of models that can predict a compound’s property by learning from different representations of its structure including atomic descriptors, graph neural networks, and voxel-based images28,29,30,31,32. Our current work shows that X-ray diffraction can also benefit from diverse representations of measurement data, aligning with these recent advancements in AI and ML.

A key benefit of our approach is that it requires no additional experiments beyond traditional XRD measurements, from which virtual PDFs can be calculated through a Fourier transform. The reported improvements in accuracy are therefore realized without any increase in experimental cost, making these methods well-suited for use in high-throughput and automated workflows3. Beyond XRD, data augmentation based on a Fourier transform may be broadly applicable to numerous characterization techniques. For example, ML models trained to interpret images from electron microscopy may benefit from being fed their diffraction patterns, obtained via Fourier transform. Indeed, some work has been reported to this end33,34,35, and our results further showcase the potential of ML to enable automated characterization based on a variety of data formats.

Methods

Simulation of XRD and PDF data

To compute the XRD pattern for a given phase, we first determine the positions (\(2{\rm{\theta }}\)) and heights (I) of its Bragg peaks using Pymatgen36. In this work, all such values are calculated by assuming Cu \({{\rm{K}}}_{{\rm{\alpha }}}\) radiation. The position and height of each peak are used to set the mean and maximum of a Gaussian profile, whose width is determined by the Scherrer equation. The Gaussian profiles associated with all Bragg peaks for a given compound are summed to produce a continuous pattern. Gaussian noise with a standard deviation of 0.25% (relative to the maximum peak height) is also added. We sample 2θ = 10–90° (Q = 0.7 − 5.8 Å−1) for all patterns considered here, which was found to provide maximal accuracy for the identification of crystalline phases, though our methods are generally applicable to any range of \(2{\rm{\theta }}\). To train a CNN for the classification of XRD patterns, we perform data augmentation based on five experimental artifacts. First, the positions of all Bragg peaks are modified to account for lattice strain in the corresponding material, which we randomly sample to include changes in each lattice parameter up to \(\pm 3 \%\). All such changes are constrained to preserve the space group of the material. Second, peak intensities are varied by as much \(\pm 50 \%\) according to crystallographic texture along randomly selected Miller indices. Third, peaks are broadened using the Scherrer equation to mimic the effects of small particle size, including grain sizes between 5 and 30 nm. Fourth, impurity peaks are added at randomly selected positions (\(2{\rm{\theta }}\)) with intensities as large as 50% of the maximum pattern intensity. Based on these artifacts, we generate a total of 200 augmented patterns for each phase that are then used for model training. Further details regarding these augmentations can be found in previous work19. For the simulation of test data used to evaluate our method’s performance, we used broader limits on the magnitude of each artifact. These include up to \(\pm 5 \%\) changes in lattice parameters, \(\pm 70 \%\) changes in peak intensities, and particle sizes ranging from 3 to 40 nm.

For each XRD pattern computed following the methodology outlined in the previous paragraph, a virtual PDF is also generated. Typically, PDFs are obtained from the total scattering function via the following equation37:

$$S\left(Q\right)=\frac{{I}_{{\rm{c}}}(Q)}{N{\left\langle b\right\rangle }^{2}}+\frac{{\left\langle b\right\rangle }^{2}-\left\langle {b}^{2}\right\rangle }{{\left\langle b\right\rangle }^{2}}$$
(3)

Where \({I}_{{\rm{c}}}(Q)\) is the coherent scattering intensity, \(N\) is the number of distinct elemental species in the sample, and \(b\) is the concentration-weighted average of their scattering factors38. However, because the models introduced in this work are designed to handle new samples with unknown compositions, we make a simplification when computing the virtual PDF:

$$S\left(Q\right)={I}_{{\rm{c}}}(Q)$$
(4)

In this case, \({I}_{c}\left(Q\right)\) is obtained by converting each XRD pattern from \(2{\rm{\theta }}\) into \(Q\)-space and applying a rolling ball background subtraction algorithm (from scikit-image)39 with a radius of 0.85 Å−1 to remove the incoherent scattering. A sine Fourier transform is then used to compute the virtual PDF as follows7:

$$G\left(r\right)=\frac{2}{\pi }{\int_{{Q}_{\min }}^{{Q}_{\max }}}Q\left[S\left(Q\right)-1\right]\sin \left({Qr}\right){dQ}$$
(5)

Where \(r\) represents the distance in real space. For all PDFs generated in this work, we sample r from 1 to 40 Å. This range was optimized to produce optimal accuracy when training models for the classification of virtual PDFs (Supplementary Fig. 6).

Convolutional neural networks

Two models were separately trained for the classification of XRD patterns and virtual PDFs in each chemistry that we tested (Supplementary Table 1). Both models share the same input size (4501 values), being equal to the number of datapoints in each XRD pattern or virtual PDF. They also share the same output size, which is set by the number of reference phases included in the training set. Each neuron in the output layer represents a distinct phase that may be output by the CNN at inference. The two models have similar architectures that differ only in their convolution layers. The model trained on XRD patterns contains six convolution layers, whereas the PDF-trained model has only one convolution layer. In both cases, these layers are followed by max pooling. The pooled feature vectors are fed to a fully connected neural network in each model, which contains 3 layers with 50% dropout and batch normalization applied between them during training.

Training is performed on the augmented XRD patterns or virtual PDFs described in the previous section. An early stop is employed at 50 epochs to avoid overfitting on the simulated data. We also use five-fold cross-validation to quantify the model’s variability. All training and validation curves for the models developed in this work are displayed in Supplementary Figs. 7–9. At inference, Monte Carlo dropout is used to generate predictions from these trained models while also providing a measure of their uncertainty25. Each model is applied 100 times to a given sample, each time with 50% of its neurons (in the fully connected layers) randomly excluded. The phase that is predicted most often from these forward passes is given as the final output, and its associated confidence is defined as the fraction (%) of passes where it was predicted.

The models developed in this work are designed to predict only one phase at a time. To handle multi-phase mixtures, we use an algorithm that iterates between the identification of constituent phases and the subtraction of their associated diffraction peaks. Further details on this algorithm can be found in previous work19. Because PDFs contain many diffuse and overlapping features, they are not well-suited for peak subtraction algorithms. Therefore, when classifying multi-phase mixtures using the PDF-trained model, we iteratively convert the data back and forth between \(2{\rm{\theta }}\) and \(Q\)-space. After classifying a virtual PDF using its associated model, the spectrum is converted into an XRD pattern through a Fourier transform, on which peak subtraction is performed. The subtracted XRD pattern is then transformed back into a virtual PDF that represents the sample minus the phase that has already been identified. Classification is again performed on this PDF, and the process is repeated until all phases have been identified.

Given two sets of predicted phases and confidence measures – one set from XRD and another from PDF – we aggregate them using a confidence-weighted sum:

$${c}_{{\rm{agg}}}^{i}=\frac{1}{2}\left({c}_{{\rm{XRD}}}^{i}+{c}_{{\rm{PDF}}}^{i}\right)$$
(6)

Where \({c}_{{\rm{XRD}}}^{i}\) and \({c}_{{\rm{PDF}}}^{i}\) represent the confidence associated with each phase (index \(i\)) predicted by models trained on XRD patterns or virtual PDFs. In cases where a phase is predicted by one model but not the other, its confidence is set to zero for the model where it was not predicted. Following this aggregation, only phases with an average prediction confidence \(\ge 40 \%\) are included in the final prediction. This cutoff was chosen to give optimal performance on the tests reported in this work (Supplementary Fig. 10).