Introduction

Most modern machine-learned interatomic potentials exploit the idea of nearsightedness of interatomic interactions, i.e., they assume that the contribution of an atom to the total energy depends mostly on its local chemical environment, while the influence of atoms that are far away is negligibly small. Following this idea, Behler and Parrinello1 proposed in 2007 the decomposition of the total energy of an extended system into atomic contributions, each computed from a descriptor of the local chemical environment. In that work, the atomic energy was modeled using neural networks (NN), but the same idea can also be combined with kernel regression to construct, for example, Gaussian Approximation Potentials 2. Numerous high-accuracy machine-learned interatomic potentials have been developed based on local descriptors and have been shown to be transferable enough to successfully capture the energetics of systems beyond the conditions they were trained on refs. 2,3,4,5,6,7,8,9,10, including ionic systems such as sodium chloride in solid and liquid phases11.

Despite these successes, it is known that these short-range models are limited by design, and as the non-local interactions such as electrostatics or van der Waals (vdW) effects become more significant in a system, the applicability of a short-range model becomes questionable. For van der Waals effects, one strategy is to include them via ad hoc corrections7, namely, first subtracting this contribution from the reference total energy, then using the remainder as the target of the machine learning training of a short-range potential, and then adding back the long-range contribution to predict the total energy. This approach is suitable if the reference energy is already obtained with an ad hoc description of the vdW effects, as in the Grimme-D212 approach. This range separation scheme has been proposed to account for the long-range part of the electrostatic interactions in a similar way: in refs. 13,14 a two-part neural network interatomic potential was constructed for the water dimer. One neural network was trained to predict the local atomic charge on each atom, and its parameters were optimized to reproduce ab initio charges obtained from the Hirshfeld decomposition scheme15. Using the charges predicted by this model, the electrostatic energy was computed and subtracted from the total energy. A second network, a short-ranged model, was then tasked to learn the remainder. One limitation of this approach is its inability to capture global charge redistribution as atomic charges are only given as functions of the local environment descriptors.

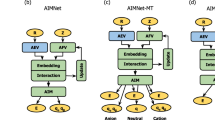
An alternative approach to include long-range electrostatics in NN potentials (NNPs) is the charge equilibration scheme (CENT) proposed by Ghasemi et al.16. In CENT, the total energy is written as the sum of atomic contributions plus a Hartree energy of Gaussian charge distributions centered at ionic positions. A neural network is used to predict atomic electronegativity whose inputs are atomic descriptors. The atomic charges are obtained through a charge equilibration scheme17 where total energy is minimized with respect to atomic charges subject to charge neutrality. This, by construction, results in coupled linear equations for atomic charges, and allows to capture of non-local charge redistribution. It also allows for a seamless way to conserve the total charge (see Results Section for a more detailed description). The CENT scheme has been successfully applied to construct NNPs for ionic systems16,18,19. However, it is not expected to work well for systems with competing covalent and ionic interactions, as the functional form chosen for the total energy lacks any description of covalent bonding.

A combination of the CENT scheme and the standard local atomic energy approach has been proposed independently by Ko et al.20 and Jacobson et al.21. In both 4G-HDNNP (fourth generation high-dimensional neural network potential)20 and QRNN (charge recursive neural network)21, the total energy is obtained in two steps, requiring the construction of two separate NN models: one for the atomic electronegativities and the other for the atomic energies. The predictions of the first model are used for charge equilibration, and optimized against the reference atomic charges. The resulting charges are then used to compute the Coulomb energies, and supplied to the second NN in addition to the local environments, to predict the remainder of the total energy (see Results Section for more details). This approach is shown to accurately predict the energy and forces of systems with competing covalent and ionic interactions. However, it comes at the cost of training and evaluating two separate NNs, and computing forces require the solution of a second linear system.

Several other approaches to include electrostatics in machine learning interatomic potentials have been proposed22,23,24,25,26; we review here the main ones. PhysNet22 is a message-passing high-dimensional neural network that predicts energy and atomic charges to incorporate electrostatics; it requires only total charge as input but it misses a non-local charge redistribution other than the average. CENT223 introduces a short-range term that is independent of the atomic charge and retains the general functional form of CENT for the long-range description while proposing a new trial electrostatic potential energy, which however requires a post-processing of the density functional theory (DFT) self-consistent charge density in addition to the decomposition of the total charge density into nuclear and electronic densities. kQeq24 implements the CENT model with the electronegativity predicted using a kernel model and uses dipole moments as a target rather than atomic charges used in 4G-HDNNP. The long-distance equivariant (LODE)25 framework is a kernel model that implements a long-range kernel symmetrized for long-distance equivariance. Another approach for incorporation of electrostatics in NNP is based on the position of maximally localized Wannier functions26,27. Self-consistent determination of long-range electrostatics in neural network potentials (SCFNN)26, for example, incorporates electrostatics in neural network potentials via two modules, each consisting of two networks: one for short range and the other for long range. While the first module uses the position of the maximally localized Wannier function centers to predict electronic response, the second module predicts nuclear forces, requiring a total of four neural networks.

In this work, we propose an alternative approach that requires the solution of a single linear system and the training and evaluation of only one NN. To do this, we use the total energy for charge equilibration like in the CENT approach, but we retain the higher expressiveness of 4G-HDNNP through learned atomic energy terms. As detailed in Results Section, our method can be seen as a second-order Taylor expansion (in the charge variable) of generic machine-learned energy, depending on local environments and charges. By adopting this approximation we are able to replace a computationally challenging self-consistent optimization that would arise from the first derivative of the short-range energy term with respect to atomic charges, with a single NN predicting all the expansion coefficients. The neural network architecture proposed in this work enables the prediction of the environment-dependent expansion coefficients without a significant increase in the number of parameters of the model. Moreover, the model is highly flexible due to its variational nature and because all expansion coefficients are constructed to be functions of the atomic chemical environments. Thanks to this flexibility, the model can accurately describe electrostatic interactions in ionic, covalent, and mixed ionic-covalent systems. More importantly, this accuracy is reached without requiring reference atomic charges, nor any complicated approach for computing the derivative of energy with respect to atomic positions. Finally, multiple targets can be used for network optimization: while we can train the NN to minimize the error on total energy, forces, and reference atomic charges, the procedure is equally well-defined in the absence of charge targets. Besides allowing training in situations where atomic charges are not available, this additional degree of freedom can lead to the discovery of different charge decompositions, leading to similar or even better force and energy predictions, as we show in the results section.

Results

Existing approaches to including electrostatics in neural network potentials

In this section, we introduce the problem by summarizing the common aspects of the existing approaches. We consider the task of predicting the total energy Etot of a system of N atoms at positions Ri, and relative distances, Rij = ∣Rij∣ = ∣Rj − Ri∣. We assume that a charge qi can be attributed to each atom i, by enforcing the constraint, ∑iqi = Q, where Q is the total charge of the system. In this work, Gi is used to describe a generic descriptor of the environment around atom i, containing information about the neighboring atomic species and their relative positions, and it is an input for the NN.

A common idea of CENT16, 4G-HDNNP20, and the present approach is the division of the energy into a short range and Coulomb terms:

$${E}_{{{{\rm{tot}}}}}={E}_{{{{\rm{SR}}}}}+{E}_{{{{\rm{Coul}}}}}.$$
(1)

The first term has a different expression in each approach but generally depends on the atomic positions {Ri} and charges {qi}. The second term is the Coulomb energy defined in terms of the total charge density ρ(r) as:

$${E}_{{{{\rm{Coul}}}}}=\frac{1}{2}\frac{{e}^{2}}{4\pi {\epsilon }_{0}}\int\frac{\rho ({{{\bf{r}}}})\rho ({{{{\bf{r}}}}}^{{\prime} })}{| {{{\bf{r}}}}-{{{{\bf{r}}}}}^{{\prime} }| }{{{{\rm{d}}}}}^{3}r{{{{\rm{d}}}}}^{3}{r}^{{\prime} }.$$
(2)

Considering ρ(r) to be the sum of atomic contributions normally distributed around each atom with a fixed spread controlled by αi

$${\rho }_{i}({{{\bf{r}}}})=\frac{{q}_{i}}{{\alpha }_{i}^{3}{\pi }^{\frac{3}{2}}}\exp \left(-\frac{| {{{\bf{r}}}}-{{{{\bf{R}}}}}_{i}{| }^{2}}{{\alpha }_{i}^{2}}\right),$$
(3)

the Coulomb energy can be written as \({E}_{{{{\rm{Coul}}}}}=\frac{1}{4\pi {\epsilon }_{0}}{\sum }_{i < j}{V}_{ij}{q}_{i}{q}_{j}\) with

$${V}_{ij}=\frac{{{{\rm{erf}}}}({\gamma }_{ij}{R}_{ij})}{{R}_{ij}},$$
(4)

where \({\gamma }_{ij}={({\alpha }_{i}^{2}+{\alpha }_{j}^{2})}^{-1/2}\).

The other common step in all the approaches is charge equilibration, i.e., the computation of the atomic charges through the minimization of an energy term of the form

$${E}_{{{{\rm{Qeq}}}}}=\mathop{\sum}\limits_{i}\left({\chi }_{i}{q}_{i}+\frac{1}{2}{J}_{i}{q}_{i}^{2}\right)+{E}_{{{{\rm{Coul}}}}},$$
(5)

with some learned parameters, χi, representing electronegativities, and some fixed parameters, Ji, representing atomic hardnesses. Including the constraint of total charge conservation ∑iqi = Q through a Lagrange multiplier, the N + 1 equations system can be solved to obtain the equilibrium atomic charges.

Here, we refer to all contributions other than the Hartree energy defined in Eq. (2) as “short range” as they only depend on local atomic charges. While we use this notation for the sake of simplicity, it has to be noted that, since our charges are obtained from a global charge equilibration process, as discussed later, this term is also dependent, although indirectly, on non-local information.

In the original CENT approach, following the energy decomposition scheme introduced in Eq. (1), the short-range energy is defined as \({E}_{{{{\rm{SR}}}}}={\sum }_{i}\left({E}_{i}^{0}+{\chi }_{i}({G}_{i}){q}_{i}+\frac{1}{2}{J}_{i}{q}_{i}^{2}\right)\), where only the susceptibilities, χi are environment dependent, while \({E}_{i}^{0}\) and Ji are fixed quantities for each species. While this allows the energy to be computed with a single NN evaluation per atom and the solution of a N + 1-dimensional system, it lacks the flexibility to capture non-ionic interactions.

In the 4G-HDNNP scheme20 the problem is split into two stages: a first network predicts electronegativities from the local descriptors, to be used only in Eq. (5) for charge equilibration. These charges are then used in combination with the local atomic descriptors as inputs for a second network that produces atomic energy contributions, summing to the total short-range energy ESR = ∑iEi(Gi, qi). This means that, in contrast with CENT, the charge is equilibrated with respect to a fictitious energy, and the targets of this first network must be some precomputed local charges, e.g., the Hirshfeld atomic charges. The second network has the advantage of improving the expressiveness of the local potential, however, this comes at the cost of two separate NN evaluations per atom. Moreover, computing forces in this scheme require the derivatives of the charges with respect to the positions, which can be obtained by solving another linear system.

Our approach to including electrostatics in neural network potentials

In the most general approach, we can write the short-range energy for each atom as the output of an NN depending on both the local environment and charge ESR = ∑iEi(Gi, qi), and then equilibrate the charges on the resulting total energy. This equilibration however requires the solution of a system of equations containing the derivatives of the NN with respect to the input, a complex optimization problem that could be solved self-consistently but would greatly increase the cost of this approach. To avoid this complication, we propose a simplified functional form in the charge variable, a second-order Taylor expansion around q = 0 local charge state:

$${E}_{{{{\rm{SR}}}}}=\mathop{\sum}\limits_{i}\left[{E}_{i}^{(0)}({G}_{i})+\left({E}_{i}^{(1)}({G}_{i})+{\chi }_{i}^{0}\right){q}_{i}+\frac{1}{2}\left({E}_{i}^{(2)}({G}_{i})+{J}_{i}^{0}\right){q}_{i}^{2}\right],$$
(6)

where all the \({E}_{i}^{(\alpha )}\) are obtained from an NN depending on local environments, while \({\chi }_{i}^{0}\) and \({J}_{i}^{0}\) are fixed offsets for each species meant to simplify the training process. In this sense, our approach is an extension of CENT where all terms are learnable, thus increasing the potential expressiveness of the model. At the same time, the advantage with respect to 4G-HDNNP is that the three environment-dependent terms are independent, which can be exploited by making them three different outputs of the same NN. This way we can obtain the parameters in a single pass, and have a single network to optimize. Once these environment-independent parameters are obtained, the derivatives of the energy with respect to the charges can be computed and the equilibrium charges are solutions of the system of equations:

$$\begin{array}{l}\mathop{\sum}\limits_{j}\left[\left({E}_{i}^{(2)}({G}_{i})+{J}_{i}^{0}\right){\delta }_{ij}+{V}_{ij}\right]{q}_{j}+\\ +{E}_{i}^{(1)}({G}_{i})+{\chi }_{i}^{0}+\lambda =0,\end{array}$$
(7)

where δij is the Kronecker delta and λ is the Lagrange multiplier needed to fix the total charge ∑iqi = Q.

The final energy can thus be obtained after a single network evaluation per atom and a matrix inversion. Due to the flexibility of \({E}_{i}^{(2)}({G}_{i})\), the matrix may be singular, especially at the beginning of the training. Although this is in part regularized by \({J}_{i}^{0}\), we have also implemented an algorithm that ensures that the diagonal term, \({E}_{i}^{(2)}({G}_{i})+{J}_{i}^{0}\), is greater than the negative of the minimum eigenvalue of the matrix in the training dataset, hence ensuring that the matrix remains positive and definite.

The evaluation of forces is also simplified due to the variational characteristics of the model. For the short-range contribution, the derivative of the network with respect to the atomic positions becomes:

$${{{{\bf{F}}}}}_{i}^{{{{\rm{SR}}}}}=-\mathop{\sum}\limits_{j,\mu ,\alpha }\frac{\partial {E}_{j}^{(\alpha )}}{\partial {G}_{j\mu }}{q}_{j}^{\alpha }\frac{\partial {G}_{j\mu }}{\partial {{{{\bf{R}}}}}_{i}},$$
(8)

where j runs over atoms, α over the network outputs, and μ over the elements of the environment vectors. To obtain the total forces, we then need to add the Coulomb component \({{{{\bf{F}}}}}_{i}^{{{{\rm{Coul}}}}}={\sum }_{j}{{{{\bf{F}}}}}_{ij}{q}_{i}{q}_{j}\) with

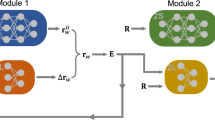
$${{{{\bf{F}}}}}_{ij}=\left(\frac{{{{\rm{erf}}}}({\gamma }_{ik}{R}_{ij})}{{R}_{ij}^{3}}-\frac{2{\gamma }_{ij}}{\sqrt{2}{R}_{ij}^{2}}\exp (-{\gamma }_{ij}^{2}{R}_{ij}^{2})\right){{{{\bf{R}}}}}_{ij}$$
(9)

The complete workflow of this approach is summarized in Fig. 1. We train the NN through the PANNA package8,28, employing the modified atom-centered symmetry functions1,3,8 as implemented there.

Fig. 1: Workflow of our approach for a system of N atoms.
figure 1

For each atom i with Cartesian coordinate Ri, its descriptor, Gi is constructed and serves as the input to the atomic NN. Each atomic network produces three atomic quantities, \({E}_{i}^{(0)}\), \({E}_{i}^{(1)}\) and \({E}_{i}^{(2)}\). These outputs are then used to compute the atomic charges via the charge equilibration scheme of Eq. (7). The short-range energy contribution ESR can then be obtained from Eq. (6), and the Coulomb energy ECoul can be computed from the atomic charges. Their sum represents the prediction for the total energy.

Full size image

The loss function used for training the network is the sum of three contributions, coming from target energy, force, and charge terms. The ground truth reference charges may be obtained from Hirshfeld or other equally valid decomposition schemes. In addition to these terms, we add an optional L2 regularization term to reduce the spread of the model weights and biases. The total loss function is then:

$${{{\mathcal{L}}}}={{{{\mathcal{L}}}}}^{{{{\rm{E}}}}}+{\gamma }_{q}{{{{\mathcal{L}}}}}^{q}+{\gamma }_{{{{\rm{F}}}}}{{{{\mathcal{L}}}}}^{{{{\rm{F}}}}}+{\gamma }_{{{{\rm{R}}}}}{{{{\mathcal{L}}}}}^{{{{\rm{R}}}}},$$
(10)

and each loss term is described as:

$$\left\{\begin{array}{l}{{{{\mathcal{L}}}}}^{{{{\rm{E}}}}}(W)=\mathop{\sum}\limits_{c\in {{{\rm{batch}}}}}{\left({E}_{c}^{{{{\rm{ref}}}}}-{E}_{{{{\rm{tot}}}},c}(W)\right)}^{2}\\ {{{{\mathcal{L}}}}}^{q}(W)=\mathop{\sum}\limits_{c\in {{{\rm{batch}}}}}\frac{1}{{N}_{c}}\mathop{\sum }\limits_{i=1}^{{N}_{c}}{\left({q}_{i}^{{{{\rm{ref}}}}}-{q}_{i}(W)\right)}^{2}\\ {{{{\mathcal{L}}}}}^{{{{\rm{F}}}}}(W)=\mathop{\sum}\limits_{c\in {{{\rm{batch}}}}}\frac{1}{3{N}_{c}}\mathop{\sum }\limits_{i=1}^{{N}_{c}}{\left\vert {{{{\bf{F}}}}}_{i}^{{{{\rm{ref}}}}}-{{{{\bf{F}}}}}_{i}(W)\right\vert }^{2}\\ {{{{\mathcal{L}}}}}^{{{{\rm{R}}}}}(W)=\frac{| W{| }^{2}}{2}.\end{array}\right.$$
(11)

where the γs are prefactors that modify the relative weights of each loss component, c runs over all the examples in a training mini-batch, and i over the Nc atoms in that example. The predictions depend on W, the vector of all the weight parameters of the network.

In particular, we note that the scheme presented here is still well-defined when setting γq = 0, i.e., when completely ignoring the reference information on the charge decomposition. In the following section, we present example cases where doing so does not degrade the predictive performance of the method.

In the following, we test the accuracy of our approach in describing long-range electrostatic energy and forces in different systems. We start with the four emblematic cases proposed in ref. 20: a carbon chain with different terminations, a metallic silver trimer, small sodium chloride clusters, and a gold dimer on a MgO (001) surface. The training dataset including atomic information, energy, forces, and Hirshfeld charges15 is taken from ref. 20. For all systems, we train long-range NNPs with and without considering atomic charge information in the loss function, and in both cases, we impose charge neutrality. We compare these two potentials with our trained short-range model as well as 4G-HDNNP results and short-range model (referred to as 2G) as reported in ref. 20

In addition, we benchmark our approach on solid and liquid sodium chloride configurations, recently generated to study the properties of molten salt at elevated temperatures and pressures11. Furthermore, we present the test of the performance of our proposed approach on Li adsorption on a graphene system. This system has been studied for Li-ion battery applications29,30,31,32,33,34,35,36,37,38,39,40. For these examples, only the total charge is imposed during training.

Benchmarking: carbon chain

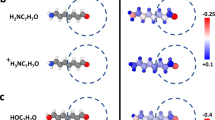
Here, we discuss the benchmark of our approach to the carbon chain. The two benchmark systems are as follows: 1) C10H2, a neutral linear chain of carbons with H-terminated ends (see Fig. 2a). 2) C10H\({}_{3}^{+}\), which is generated by adding an extra H atom to one end of the chain and removing an electron (see Fig. 2b), resulting in a system with a total charge of +1. The additional hydrogen perturbs its local environment and causes a global charge redistribution. Further details about the dataset are presented in the Methods section IV.

Fig. 2: Crystal structures of example systems.
figure 2

a Linear carbon chain clusters C10H2 with total charge 0 and b a protonated carbon chain, C10H\({}_{3}^{+}\) with a total charge of + 1. c Linear chain silver cluster with a net charge of − 1, Ag\({}_{3}^{-}\) d triangular silver cluster with a + 1 total charge, Ag\({}_{3}^{+}\). Charged sodium chloride cluster with + 1 net charge e Na8Cl\({}_{8}^{+}\) f Na9Cl\({}_{8}^{+}\). Periodic structures of MgO (001) surface doped with Au dimers (g) undoped MgO surface and Au dimer adsorbed in the non-wetting configuration (h) doped MgO surface and Au dimer adsorbed in the wetting configuration.

Full size image

Table 1 shows the root mean square error (RMSE) in charge, energy, and force on training and validation sets. When the long-range model is trained on the Hirshfeld target, we obtain an RMSE on the validation set of 1.167 meV per atom and 78.98 meV Å−1 for energy and forces, respectively, which are comparable to the ones obtained with 4G-HDNNP. Remarkably, lower RMSE is obtained for energy and forces when the long-range model is not regressed against Hirshfeld charges (γq = 0). The distribution of atomic charges and the deviation from the Hirshfeld charge decomposition15, in this case, depends on the initial conditions and can be tuned via the parameters χ and J. However, the accuracy of the model is independent of the choice of these parameters and the resulting charge decomposition (see Supplementary Table 2).

Table 1 Training and validation RMSE for carbon chains
Full size table

Next, we examine the charge distributions for the DFT-optimized geometries. In Fig. 3a, b, we depict the charge distribution on the DFT-optimized structures of C10H2 and C10H\({}_{3}^{+}\) systems, respectively, comparing the results obtained when using or neglecting the Hirshfeld charges as a target. For the C10H2 configuration (see Fig. 3a), both models capture the symmetric nature of the charge distribution around the center of the linear chain. A sign difference can be seen in the second C atoms from either edge, to which the two models assign charges with opposite signs. We note that the model regressed against charges should have similar charges to the Hirshfeld ones, which it was trained to reproduce. In the case of C10H\({}_{3}^{+}\) (see Fig. 3b), similar charges are assigned to atoms on the unprotonated edge. Negligibly small negative charges are assigned to the two hydrogens on the protonated edge by the model not trained on reference charges while the model trained on charges assigned larger positive charges. The difference in charge distribution does not influence the accuracy of energy and forces.

Fig. 3: Comparison of charge distribution between long-range model trained and not trained on reference charges on DFT-optimized structures of carbon chains systems.
figure 3

a C10H2 and b C10H\({}_{3}^{+}\). predicted atomic charges on the lowest energy structures in the training dataset of silver clusters systems, c Ag\({}_{3}^{-}\), and d Ag\({}_{3}^{+}\) compared with DFT values obtained with Hirshfeld decomposition.

Full size image

Benchmarking: silver clusters

We now consider an Ag cluster system. The training configurations consist of triangular and linear Ag trimers with +1 and –1 total charges, respectively. Representative structures for the linear and triangular configurations are shown in Fig. 2c, d, respectively.

Due to the size of the systems, a typical cutoff radius, usually chosen between 5–10 Å to describe atomic chemical environments contains all the interactions of the central atom with every other atom in the systems. However, the dependence of the energetically favorable geometry on the total charge of the system makes it an ill-posed problem for machine learning models that are built solely from atom-centered symmetry functions based on atomic coordinates. Indeed, as demonstrated in ref. 20, the 4G-HDNNP model was able to accurately reproduce the energy and forces of these systems, while the 2G model yields a very large root mean square error in both energy and forces. Here, we show that our proposed approach can accurately reproduce the DFT potential energy surface of the systems even when local charge information is not trained on. More interestingly, we attain a lower RMSE in energy, forces, and Hirshfeld charges (when used as a target) than 4G-HDNNP.

Table 2 shows the RMSE on charges, energy, and forces obtained in this work and compared with 2G- and 4G-HDNNP results. The accuracy attained with our short-range model is comparable to those of 2G-HDNNP. As shown in the table, the RMSEs on energy and forces are lower than those obtained with 4G-HDNNP. Similarly, when trained on Hirshfeld charges we obtain a smaller RMSE on charges than the 4G-HDNNP. The RMSE on energy and forces are similar whether trained or not trained on charges. In the case where the Hirshfeld charges are not used as a target (γq = 0), an RMSE of 0.07 e is observed. This deviation of the atomic charge from Hirshfeld is not surprising since there is no uniqueness in the decomposition of the total charge density into atomic contributions, hence the decomposition obtained by our model is as valid as the Hirshfeld DFT atomic charges, provided that physical observables such as energy and forces are accurately predicted.

Table 2 Training and validation RMSE for silver trimers
Full size table

To shed light on the origin of the RMSE in charges when atomic charge information is not used, we examine the charge distribution on the lowest energy structure in the training dataset for each charge state. In Fig. 3c, d, we compare the atomic charges predicted with our long-range models with the Hirshfeld charges results. As can be seen, when regressed against Hirshfeld charges (γq > 0), excellent agreement is observed for both linear and triangular clusters. When the long-range model is not trained on Hirshfeld charges (γq = 0), we obtain a charge distribution that is identical to the Hirshfeld charges for the triangular cluster with a total charge of + 1 but a different charge distribution is found for the linear cluster with total charge of − 1. The NNP-Hirshfeld charge distribution agreement observed for the + 1 charge state is a consequence of the atomic arrangement of the system: all atoms have an equivalent chemical environment, hence there is a unique distribution of charges to atoms, compatible with a total charge of + 1. On the other hand, for the case of the linear system of charge − 1, several distributions are possible, with the only constraint being that the atoms at the edges with similar chemical environments have similar magnitude of charges. Here, we obtain − 0.331 e for the two atoms at the edges and − 0.338 e for the central atom compared to the Hirshfeld charges of − 0.404 e and − 0.192 e, respectively.

Finally, we investigate the accuracy of our NNP models in describing the potential energy surface along a reaction coordinate such that a transformation from the triangular cluster into a linear one can be monitored. In particular, we use the angle between atoms 1, 2, and 3 as the reaction coordinate, denoted as θ132. In Fig. 4a, we depict the relative energy at each charge state as a function of θ132. Both long-range models, γq = 0 and γq > 0, are identical in the relevant region of the reaction coordinates and correctly describe the two energy wells. The equilibrium position for the system with a total charge of + 1 is predicted to be at π/3 while that with a total charge of − 1 is at π. The short-range model fails to capture the expected trends as it cannot distinguish between the two systems around the coexistence region between the Ag\({}_{3}^{+}\) and Ag\({}_{3}^{-}\).

Fig. 4: Comparison of energy and forces between NNPs and DFT.
figure 4

a Potential energy surface along θ132 for Ag\({}_{3}^{+}\) and Ag\({}_{3}^{-}\). For each charge state, energy is referenced to the atomic energies. The short-range model predicts the same energy for Ag\({}_{3}^{+}\) and Ag\({}_{3}^{-}\). Energy and force on Na atom along the arrow shown in Fig. 2f: b the energy as a function of the distance between Na atom 1 and 2. c projected force on Na atom 1 in the direction of the arrow shown, as a function of the distance between Na atom 1 and 2. Our NNP energies are in reference to the average of the minimum energy predicted by the two long-range models. Potential energy surface of Au cluster supported on MgO(001) surface: d energy versus Au-O bond length of our long-range model. e Force on the Au cluster projected along the perpendicular direction as a function of the bond length measured between the closest O atom to the cluster and the closest Au atom to the surface. DFT forces are obtained from ref. 20. The closed squares indicate the position of energy minima.

Full size image

Benchmarking: sodium chloride clusters

In this section, we test our model on sodium chloride clusters and compare its accuracy to that achieved by 4G-HDNNP. The systems considered here consist of Na8Cl\({}_{8}^{+}\) (8 Na atoms and 8 Cl atoms) and Na9Cl\({}_{8}^{+}\) (9 Na atoms and 8 Cl atoms) each having a total charge of + 1. A representation of these configurations is depicted in Fig. 2e, f.

The accuracy of the 4G-HDNNP was evaluated against the DFT potential energy surface as the Na atom is moved along the path indicated by the black arrow in Fig. 2f. The potential energy surface has two distinct minima along the path shown by the arrow for the two configurations. The 4G-HDNNP was demonstrated to accurately reproduce the DFT potential energy surfaces while the short range failed to distinguish these two minima. Here, we show that our approach not only gives lower RMSE in energy and forces than 4G-HDNNP both with and without regressing the model against Hirshfeld charges but also accurately reproduces the DFT potential energy surfaces in a similar manner to the 4G-HDNNP with about two times fewer parameters.

In Table 3, we show the RMSE in charges, energy, and forces for both short-range and long-range models and compare them with 2G- and 4G-HDNNP results. Our long-range and short-range models attain similar RMSE in energy to the results in ref. 20. Instead, we obtain lower RMSE in forces than 4G-HDNNP with our long-range models trained with and without charges.

Table 3 Training and validation RMSE for NaCl clusters
Full size table

To examine the performance of our approach on the potential energy surface of these systems, we compute the energy and force acting on the Na atom, indicated by 1 in Fig. 2f, when moving along the arrow. Figure 4b, c show the energy of the systems and force on the Na atom projected along the direction shown by the arrow in Fig. 2f. The DFT results are obtained from Fig. 7 of ref. 20. For the short-range model, we obtain similar trends to those reported in ref. 20, where the position of the minimum for Na8Cl\({}_{8}^{+}\) and Na9Cl\({}_{8}^{+}\) are the same but separated by constant energy. Our long-range model accurately reproduces the DFT energy minima for both Na9Cl\({}_{8}^{+}\) and Na8Cl\({}_{8}^{+}\) with and without regressing against reference charges. Similarly, the forces on the Na atom computed with our long-range models are indistinguishable from the DFT results. We note that all energies in Fig. 4b, c are referenced to the average minimum energy predicted by our long-range models of the respective systems, while the DFT energy curves are referenced to DFT energy minima.

Benchmarking: gold dimer on MgO(001) surface

Here, we test our model on a periodic system: a gold dimer (Au2) supported on a MgO(001) surface20. The dataset presented in ref. 20 consists of two configurations of Au dimer on the MgO(001) surface: the “wetting” configuration, in which the atoms of the Au dimer lie at a similar distance above two surface Mg atoms, and the “non-wetting” one, in which one Au atom binds to a surface Oxygen and the other Au atom is farther from the surface Oxygen. The relative stability of the wetting and non-wetting configurations is influenced by doping: when the MgO slab is doped with Al atoms, the wetting geometry is more energetically favorable, while the non-wetting geometry is preferred on the surface of the intrinsic MgO(001) surface. Here, we compare the performance of our long-range approach to the 4G-HDNNP model in describing the electronic structure of these systems.

Table 4 shows the RMSE in charges, energy, and forces, compared with those reported in ref. 20. With our long-range model, irrespective of whether it is regressed against reference charges or not, the RMSE in energy is similar to that reported for 4G-HDNNP. Remarkably, our long-range models attain lower RMSE in forces than 4G-HDNNP. The RMSE in charges obtained is larger than that of the 4G-HDNNP even when regressed against reference atomic charges. These results suggest that the Hirshfeld atomic charges as provided in the reference dataset are not necessarily the charge density decomposition that minimizes our long-range energy model.

Table 4 Training and validation RMSE for Au dimer on MgO(001)
Full size table

Next, we compare the charge decomposition predicted with our model to the Hirshfeld charges. In Supplementary Fig. 9, we depict the charge distribution as obtained with our long-range model. In all cases, the charges predicted for O, Mg, and Al follow the trends of the Hirshfeld charges, although the NNP predictions have wider spreads. Similarly, for the Au2 molecules in the non-wetting case, the double peak Hirshfeld charges located in both negative and positive regions are captured. However, for the wetting Au2 geometry, our long-range model predicts positive charges with and without doping while the Hirshfeld charge decomposition assigns positive charges for Au2 without doping and negative charges when the system is doped. Previous DFT studies that use Bader decomposition techniques to assign charges for these systems41,42 found that the Au2 molecule is negatively charged with and without doping, the main effect of the doping being that the charge on Au2 becomes more negative upon doping instead of the sign change observed with the Hirshfeld charge decomposition here. We note that when the long-range model is not regressed against reference charges, we observe negative charges for Au2 irrespective of doping for the wetting geometry (see Supplementary Fig. 10).

From this analysis, we conclude that our long-range model trained on charges minimizes the total energy functional through an atomic charge decomposition different from the reference Hirshfeld charges. We will show in the following that these deviations have no negative consequences on the ability of our model to accurately describe the electronic structure of the systems.

Next, we compute the energy difference between the wetting and non-wetting geometry of the Au2 molecule with and without doping. In the doped system, our long-range models with and without target charges predict an energy difference of −50 meV and −67 meV, respectively, comparable to − 41 meV obtained with the 4G-HDNNP and in qualitative agreement with DFT prediction of − 2.7 meV. For the undoped system, we obtain the energy difference between wetting and non-wetting geometry as 931 meV when our long-range model is trained with target charges and 924 meV when target charges are not used. These values are in excellent agreement with the DFT prediction of 929 meV and similar to the result obtained with 4G-HDNNP of 975 meV. The short-range model predicts the same energy differences for doped and undoped systems, similar to the results obtained with 2G-HDNNP20.

Finally, we report the performance of our approach in describing the potential energy surface of the Au2 molecule on MgO(001) surface. Fig. 4d, e show, respectively, the energy and force on Au2 in the non-wetting geometry as a function of the distance between the closest surface O atom and Au2. The energies obtained in this work are referenced to the average of the minima predicted by the two long-range models (i.e., models obtained with and without training on charges). Our long-range models correctly predict two distinct minima for the non-wetting geometry for doped and undoped configurations and compare well with the DFT predictions, while the short-range model fails to distinguish the adsorption of Au2 on doped and undoped MgO(001) systems except for a constant shift in energy. We then compute the force on Au2 projected along the direction perpendicular to the surface and compare it with DFT results from ref. 20. This force is equivalent to the derivative of the energy depicted in Fig. 4d. Both of our long-range models accurately reproduce the DFT forces for doped and undoped systems. The short-range model gives the same force irrespective of doping.

Benchmarking: molten salt

We now benchmark our method on a dataset that was recently used to construct a neural network potential for molten sodium chloride11 using a short-range model. The dataset comprises a wide variety of chemical structures spanning crystalline and high-temperature and pressure liquid phases of sodium chloride. The dataset does not contain atomic charge information, therefore, only the total charge of the system will be used to train the model. There are ~112,000 configurations including NaCl dimer configurations.

Here, we divide the dataset into 80:20 ratios for training and validation of the performance of our long-range model. As in the previous case, we use a modified Behler-Parrinello descriptor to describe the local atomic environment up to a cutoff of 10 Bohr. Details of the parameters used to describe atomic chemical environments are presented in Supplementary Note 3.

The RMSE on energy and forces obtained by the long-range model are 0.990 meV per atom and 30.22 meV Å−1, respectively. This is a significant improvement over the short-range model that gives 1.349 meV per atom and 40.58 meV Å−1 for the energy and force RMSE, respectively. These results imply the presence of an electrostatic component in the energy and forces that are not well described by the short-range model but are captured by our long-range one, even without regressing against reference atomic charges.

Next, we examine the charge distribution predicted by our long-range model. Figure 5a shows the charge distribution predicted for the configurations in our validation set. The long-range model correctly assigned positive charges around +0.5 e to the Na atoms and negative charges around –0.5 e to the Cl atoms. The distribution rather than a delta-like distribution, expected for perfect crystalline NaCl systems, presents a substantial spread in the predicted charges, due to the presence of amorphous and liquid phases of NaCl in the test dataset, characterized by distorted octahedral chemical environments.

Fig. 5: Charges distribution of liquid and solid states NaCl and potential energy surface Na-Cl dimers.
figure 5

a Atomic charges. the peak around -0.5 e corresponds to the charges for Cl and that around +0.5 e are for Na atoms. The potential energy of NaCl dimer as a function of atom separation. The comparison of DFT energies with b long-range model and c short-range model. d, e, and f are the pressure-volume plots at 1100, 1150, and 1200 K, respectively obtained with our long-range model (LR), short-range model (SR), and the DFT results as reported in ref. 11. The solid and dashed lines correspond to a fit to the Murnaghan equation of state.

Full size image

Next, we discuss the performance of our long-range model in describing the potential energy surfaces of isolated Na-Cl, Na-Na, and Cl-Cl dimers. In Fig. 5b, c, we show the energy of these dimers as a function of interatomic distances obtained with long-range and short-range models, respectively. The DFT potential energy surfaces are well described by both long-range and short-range models at short distances. However, as the interatomic distances approach 5.3 Å, the cutoff radius for the local atomic descriptors, the short-range models fail to distinguish the total energy between the different dimers (see Fig. 5c). On the other hand, our long-range model predicts the expected trends beyond 5.3 Å as shown in Fig. 5b. These results demonstrate the ability of our long-range model to accurately describe the physics of NaCl beyond the cutoff radius.

Furthermore, we investigate the accuracy of the long-range model on the equation of state of liquid phase of NaCl. We perform an NVT (constant number of atoms, volume, and temperature) molecular dynamics (MD) at different volumes using a supercell containing 512 atoms and a timestep of 0.5 fs. The pressure-volume plots at 1100, 1150, and 1200 K are shown in Fig. 5d–f, respectively. The errors estimated as the standard deviation of the MD results are smaller than the open squares for the long-range and filled circles for the short-range model. The DFT results reported in ref. 11 are also shown as black diamonds with their associated errors. The results obtained with short and long-range models are similar, suggesting a significant screening of the electrostatic field generated by the Na and Cl ions in molten salt, which is consistent with the properties of molten salt computed with a short model as reported in ref. 11. More interestingly, our short-range model developed with a maximum cutoff at 5.3 Å yields the radial distribution function of molten salt at 1150 K as accurate as DFT and our long-range electrostatic model (see Supplementary Fig. 11), again strengthening the observation that a local potential may be sufficient to describe the properties of molten salt.

The equilibrium average volume per atom predicted by long-range at 1100, 1150, and 1200 K are 29.99, 30.40, and 30.85 Å3/atom, respectively, while the short-range model gives 30.01, 30.44, and 30.90 Å3/atom, compared to the DFT results of 29.3, 29.7, and 30.1 Å3/atom. Our consistent overestimation can be attributed to the simulation setup, considering the large error in pressure associated with the DFT results. The bulk moduli predicted by the long-range model are 4.89, 4.75, and 4.57 GPa at 1100, 1150, and 1200 K, respectively, while the short-range model predicts 4.85, 4.70 and 4.53 GPa at 1100, 1150, and 1200 K, respectively. The corresponding bulk moduli obtained with DFT are 4.8, 4.2, and 4.3 GPa respectively. Finally, the thermal expansion obtained with long range and short-range models at 1150 K are 2.85 × 10−4 and 2.92 × 10−4 K−1, respectively, which are in agreement with the DFT prediction of 2.7 × 10−4 K−1 11. Although the effects of long-range electrostatics are seen to be minimal, overall, the long-range model performs better than the short-range model.

Benchmarking: lithium adsorption on graphene

In this section, we further demonstrate the importance of long-range electrostatics on a system of general interest: Li on graphene, a prototypical example of Li-C interactions, and a system of general interest for rechargeable battery applications. Li interactions with graphene have been extensively studied, mostly within DFT31,33,34,35,36,37,38,39,40, due to its being a potential standalone alternative anode for lithium-ion batteries (LIBs), and as a model to explain the high Li density observed in disordered, non-graphitic carbon materials29,30. Recently, we have also studied the effect of temperature on Li interaction with graphene using electrostatic energy-corrected cluster expansion techniques32. In that work, we highlighted the importance of incorporating an electrostatic term in the cluster expansion energy in order to accurately describe the binding energy of Li, especially in the dilute limit.

The details about data generation, DFT calculations, and the neural network parameters are in Supplementary Note 3. The RMSEs in energy for the short-range model on the training and validation set are 2.05 and 2.10 meV per atom, respectively. The corresponding RMSEs in forces are 45.40 and 45.75 meV Å−1 for the training and validation dataset. The RMSEs in energy obtained with the long range model are 1.57 and 1.65 meV per atom for the training and validation set. The RMSEs in forces are 43.48 and 44.21 meVÅ−1, respectively.

While the RMSEs alone might seem to indicate that the long-range model is only slightly better than its short-range counterpart, we will now show that the addition of long-range interaction is essential to capture some physically relevant quantities. We will start by investigating the thermodynamics of Li adsorption on graphene, considering the adsorption energy as a function of Li concentration. This quantity is particularly important for the study of Li occupation with grand canonical Monte Carlo. The adsorption energy is defined as:

$${E}_{{{{\rm{ads}}}}}(n)=\frac{E(n{{{\rm{Li}}}}+\,{{\mbox{graphene}}})-E({{\mbox{graphene}}}\,)-nE({{{\rm{Li}}}})}{n},$$
(12)

where E(nLi + graphene) is the total energy of a Li-graphene system with n Li atoms, E(graphene) is the total energy of a bare graphene sheet and E(Li) is the total energy per atom of Li metal in the bcc phase.

We consider the adsorption of single Li atoms and Li dimers on 2 × 2, 3 × 3, 4 × 4, 5 × 5, 6 × 6 and 7 × 7 supercells. Specifically, Li atoms are adsorbed at the “hollow site" (i.e., the center of hexagons on the honeycomb lattice), and a Li dimer corresponds to two Li atoms adsorbed on neighboring hexagon centers. A single Li adsorbate on a 2 × 2 graphene supercell corresponds to 1:8 Li:C ratio, while on a 7 × 7 supercell, the ratio Li:C becomes 1:98. For the Li dimer adsorption, on a 2 × 2 graphene supercell, the ratio of Li to C is 1:4 while on a 7 × 7 supercell, the ratio is 1:49. Additionally, we compute the Li diffusion on the basal plane of graphene, a quantity that measures the kinetic properties of Li. For both Li adsorption energy and Li diffusion, we compare NNP predictions with the underlying PBE-based DFT results.

Figure 6a, b show the adsorption energy of single Li atoms and Li dimers for several supercell sizes, corresponding to different Li concentrations and varying minimum Li-Li distances. The DFT adsorption energy decreases with increased supercell size (i.e., increasing Li-Li distances) for both single Li and Li dimers adsorbates. Remarkably, the DFT trends are excellently captured by our long range model. The short-range model fails to reproduce the DFT adsorption energy, naturally saturating when the Li-Li distance exceeds the cutoff with which the descriptors are built. The inability of the short-range model to describe the binding energy of Li interaction with graphene, especially at low concentrations, makes it unsuitable to accurately describe the thermodynamics of Li-graphene systems and, by extension, Li-C systems. These results again point to the importance of correctly accounting for long-range electrostatics to describe thermodynamics in systems with significant electron transfer.

Fig. 6: Lithium adsorption on graphene.
figure 6

Adsorption energy, Eads of a isolated Li atoms and b Li dimers on graphene supercell. c Li diffusion on the graphene surface along the energy path for Li to migrate between two hexagon centers as indicated in the insets.

Full size image

As a further example, in Fig. 6c, we show the relative energy against reaction coordinates of Li diffusion in a 6 × 6 graphene supercell along the high symmetry points, namely the center of a hexagon (H), the top of a carbon atom (T), and the bridge between two nearest neighbor C atoms (B). In this case, the Li height is fixed at 1.72 Å, the equilibrium height of Li adsorption at the H site. While the short-range model underestimates the energy barrier, due to its inability to capture interactions between periodic images of Li atoms, the long range is almost indistinguishable from the DFT results. To understand the implications of underestimating the activation barriers, we compute the enhancement of the diffusion constant at 300 K, as given by \(\frac{D(T)}{{D}_{0}}=\bar{D}=\exp \left(-\frac{{E}_{a}}{{k}_{B}T}\right)\). The estimated diffusion coefficients from H to B sites, \({\bar{D}}_{H\to B}\) are 766, 650, and 1283 for DFT, long range, and short range, respectively. This implies a slight underestimation of 15% with respect to DFT for the long-range model, while the short-range model overestimates the DFT value by 68%. Similarly, the estimated diffusion coefficients from H to T sites, \({\bar{D}}_{H\to T}\) are 9.4, 7.0, and 13.8 for DFT, long range, and short range, corresponding to a 47% overestimate for the short-range model, much worse than the 25% of the long-range model.

Discussion

In this work, we propose a new scheme to incorporate electrostatic interactions in neural network interatomic potentials. The current scheme decomposes the total energy functional into short-range and Coulomb energies and consistently fixes the Coulomb energy from atomic charges obtained from the minimization of the total energy. The ingredients that enter the linear system which determines the atomic charges are obtained from atomic neural networks. Unlike 4G-HDNNP, only a single network potential for the atomic energy is required and the dependence of atomic forces on the variation of atomic charges with respect to ionic displacement is eliminated.

The approach introduced here is similar to the charge equilibration neural network (CENT) in that the atomic charges are obtained from total energy minimization with respect to the charges themselves. However, it is as general as the 4G-HDNNP, as it is applicable to all chemical systems including systems with competing covalent and ionic bonding, as well as systems with multiple charge states.

We benchmark our model on six examples. In most cases, our long range models perform as accurately as, or sometimes better than, the 4G-HDNNP. We demonstrate that the accurate representation of DFT energy and forces is independent of the details of the local charge distribution. Therefore, even in the case where Hirshfeld atomic charges are not accurately reproduced, the RMSEs in energy and forces are equivalent to or better than the results obtained with 4G-HDNNP, and the potential energy surfaces are in excellent agreement with DFT, even in cases that the short-range model fails to describe.

Our model is easy to incorporate into the existing architecture and, unlike the 4G-HDNNP, does not rely on the availability of any reference atomic charges. Therefore, datasets generated to train models that are derived from local environment descriptors are sufficient to describe electrostatics.

Methods

Computational details

In ref. 20, a neural network architecture with 2 hidden layers of 15 nodes each and a single-node output layer was used for both the short-range atomic energies and electronegativities. In order to compare our model with theirs, we adopt the same NN architecture for the first four examples except that for our long-range model, the output layer has 3 nodes rather than 1. We reiterate that only one NN is evaluated to compute the total energy in our approach while two NNs (one for electronegativity and one for the short-range energy term) need to be evaluated in the case of 4G-HDNNP methods. For the last benchmark example, we used NN architecture with 2 hidden layers each of 64 nodes and either a single-node (for the short-range model) or three-node (for our long-range model) output layer.

For the linear carbon systems, the training dataset20 was generated by performing ab initio molecular dynamics (MD) simulations for each system at 300 K. For each system, ~5000 MD trajectories were generated giving rise to ~ 10,000 configurations. Similarly, for the silver trimers, the training dataset is generated from ab initio MD simulations at 300 K as in the previous example. In the case of the sodium chloride clusters, the training dataset is generated from random displacement of atomic coordinates according to Gaussian distribution with 0 mean and 0.05 Å standard deviation.

In all cases, the atomic environments are described using the modified Behler-Parrinello descriptors as presented in ref. 8,28. The size of the input vectors for the carbon chain, silver cluster, NaCl cluster, and Ag dimer on the MgO surface are respectively, 60, 12, 45, and 256 compared to 60, 12, 45, and 151 used in ref. 20. The NNP for Li on the graphene problem is constructed with environment descriptors of size 112. The specific parameters for each system are highlighted in the Supplementary Note 3.

The relative contributions of each term in the loss function Eq. (10) are tuned with the coefficient γ also specified in each section (except for the constant γR = 10−4). In particular, the case γq = 0 represents models that are not regressed against reference charges.

In all cases, the hidden layers are activated with Gaussian functions while the output layers are linear. While the choice of χ0 and J0 does not influence the accuracy of the predicted energy and forces, the distribution of the atomic charges can depend slightly on these parameters when the model is not regressed against reference atomic charges. Here, we discuss the results obtained with χ0 and J0 as tabulated in Supplementary Table 1. These parameters are computed from ionization potential and electron affinity obtained from the Mendeleev package43.