Transferable equivariant graph neural networks for the Hamiltonians of molecules and solids

Abstract

This work presents an E(3) equivariant graph neural network called HamGNN, which can fit the electronic Hamiltonian matrix of molecules and solids by a complete data-driven method. Unlike invariant models that achieve equivariance approximately through data augmentation, HamGNN employs E(3) equivariant convolutions to construct the Hamiltonian matrix, ensuring strict adherence to all equivariant constraints inherent in the physical system. In contrast to previous models with limited transferability, HamGNN demonstrates exceptional accuracy on various datasets, including QM9 molecular datasets, carbon allotropes, silicon allotropes, SiO₂ isomers, and Bi_xSe_y compounds. The trained HamGNN models exhibit accurate predictions of electronic structures for large crystals beyond the training set, including the Moiré twisted bilayer MoS₂ and silicon supercells with dislocation defects, showcasing remarkable transferability and generalization capabilities. The HamGNN model, trained on small systems, can serve as an efficient alternative to density functional theory (DFT) for accurately computing the electronic structures of large systems.

Introduction

Nowadays machine learning (ML) has a wide range of applications in molecular and materials science, including the direct prediction of various properties of materials^1,2,3, the construction of machine learning interatomic potentials (MLIPs) with quantum mechanical precision^4,5,6,7, the high-throughput generation of molecular and crystal structures^8,9,10, and the construction of more precise exchange-correlation functionals^11,12. However, the determination of materials’ electronic structure still heavily relies on calculations based on density functional theory (DFT). Unfortunately, these methods require a significant amount of time to get the electronic Hamiltonian matrices through self-consistent iterations and exhibit poor scalability with respect to system sizes. Semi-empirical tight-binding (TB) approximations¹³, such as the Slater-Koster method¹⁴, can reduce a lot of computation compared to the DFT methods. However, this approach often directly uses the existing or manually fine-tuned TB parameters and thus cannot accurately reproduce the electronic structure of general systems. Developing truly transferable, fully data-driven TB models that can be applied across various materials, geometries, and boundary conditions can reconcile accuracy with speed but is rather challenging.

Hegde and Brown first used kernel ridge regression (KRR) to learn semi-empirical tight-binding Hamiltonian matrices¹⁵. They successfully fitted the Hamiltonian matrix of the Cu system containing only rotation invariant s orbitals and the diamond system consisting only of s and p orbitals. Similarly, Wang et al. designed a neural network model to obtain semi-empirical TB parameters by fitting the band structures calculated by DFT¹⁶. An important feature of the Hamiltonian matrix is that its components transform equivariantly with the rotation of the coordinate system. However, none of these approaches deals with the rotational equivariance of the Hamiltonian matrix. Moreover, the two methods are limited to fitting the empirical model Hamiltonian matrices rather than the true ab initio tight-binding Hamiltonian matrices generated by the self-consistent iteration of ab initio tight-binding methods such as OpenMX^17,18 and Siesta^19,20.

Because of the spherical harmonic part of the atomic basis functions, the TB Hamiltonian matrix must satisfy two fundamental constraints: rotational equivariance and parity symmetry. Due to the presence of periodic boundary conditions, the tight-binding Hamiltonian matrix for solids also exhibits translational invariance. The fundamental symmetry constraints satisfied by the tight-binding Hamiltonian matrix belong to the E(3) group. The notation E(3) denotes the Euclidean group in three-dimensional (3D) space, i.e., the group of rotations, translations, and inversion in 3D space. If a mapping L(q) is E(3) equivariant, then the following equivariant condition is satisfied for any rotation or inversion operation $\hat{{\rm{g}}}\in O(3)$ and translation operation: $L(\hat{g}\circ {\bf{q}}+{\bf{t}})=\hat{g}\circ L({\bf{q}})$, where t is the translation vector. In other words, the mapping L(q) remains invariant under translation while being equivariant under rotation and inversion. The tight-binding Hamiltonian matrix H({τ_i}) can be viewed as a function of the atomic positions {τ_i} of the system. Here we take the rotational equivariance of the Hamiltonian matrix as an example. When a rotation $\hat{Q}\in SO(3)$ is applied to the system, the equivariance between the rotated and original Hamiltonian matrices can be expressed as $H(\{{{\boldsymbol{\tau }}^{\prime}}_{i}\})=D(\hat{Q})H(\{{{\boldsymbol{\tau }}}_{i}\})D{(\hat{Q})}^{\dagger }$, where $\{{{\boldsymbol{\tau }}^{\prime}}_{i}\}$ is the set of the rotated atomic positions, and D is the Wigner D matrix^21,22. It is crucial for the mapping of atomic coordinates to the Hamiltonian matrix to satisfy equivariance. If equivariance is not achieved in the mapping, the Hamiltonian matrix may undergo an unphysical transformation, resulting in $H(\{{{\boldsymbol{\tau }}^{\prime}}_{i}\})\,\ne\, D(\hat{Q})H(\{{{\boldsymbol{\tau }}}_{i}\})D{(\hat{Q})}^{\dagger }$ when the system undergoes any rotation. Non-equivariant models necessitate a substantial amount of training data to approximately achieve equivariance by learning how to predict the Hamiltonian matrix in all possible directions of the system. Non-equivariant models often struggle with transferability, especially when encountering structures or configurations that differ significantly from the training set. As a consequence, they may lack generalization capabilities when applied to new or complex materials. In contrast, equivariant models possess a more robust ability for complex structures due to their ability to capture and preserve symmetries.

Zhang et al.²³ and Nigam et al.²⁴ proposed a method to predict the ab-initio TB Hamiltonians of small molecules and simple solid systems by constructing an equivariant kernel in Gaussian Process Regression (GPR) to parameterize the Hamiltonian matrices. Due to the fixed kernel and representation used in GPR^25,26,27,28, its training accuracy and multi-element generalization ability are typically inferior to those of deep neural networks like message-passing neural networks (MPNNs)^{29,30,31,32,33,34} when a sufficient number of training samples are available. Hence, the development of graph neural networks (GNNs) with the capability to predict the Hamiltonian matrix of both general periodic and aperiodic systems emerges as the most favorable approach.

However, traditional GNNs are limited to predicting rotation-invariant scalars such as energy, band gap, and the like. To predict equivariant directional properties, GNNs need to encode the directional information of the system suitably. To make the predicted Hamiltonian matrices satisfy the rotational equivariance, Schütt et al. designed the SchNorb neural network architecture by embedding the direction information of the bonds into the message-passing function³⁵. This network constructs the TB Hamiltonian of molecules from the directional edge features of atom pairs. However, SchNorb needs to learn the rotational equivariance of the Hamiltonian matrix through data augmentation, which greatly increases the amounts of training data and redundant parameters of the network. Unke et al. proposed the PhisNet model³⁶, which achieved SE(3) equivariant parameterization of TB Hamiltonian matrix using GNN based on SO(3) representations. Their model demonstrated high accuracy on the Hamiltonian matrices of small molecules such as water and ethanol. However, it should be noted that the PhisNet model cannot be considered a universal representation of Hamiltonian matrices due to its neglect of parity symmetry, which can lead to significant issues in predicting periodic systems.

Recently, Li et al. proposed a GNN model named DeepH to predict the TB Hamiltonian matrix by constructing local coordinate systems in a crystal³⁷. DeepH successfully predicted the TB Hamiltonian matrices of some simple periodic systems such as graphene and carbon nanotubes. Their original intention of introducing the local coordinate system is to solve the rotation equivariance problem of the Hamiltonian, but DeepH still embeds the local directional information of interacting atom pairs in the invariant message passing function, which will undoubtedly increase the number of redundant parameters of the network but may require less data augmentation than a fully invariant model without local coordinate systems. In addition, the hopping distance between two interacting atoms far exceeds the typical lengths of chemical bonds. Taking the smallest hydrogen atom as an example, the cutoff radius of the numerical atomic orbital of the hydrogen atom used by OpenMX is 6 Bohr, so the furthest hopping between any two atomic bases used by OpenMX in periodic systems can exceed at least 12 Bohr (~6.4 Å), a distance that even exceeds the lattice parameters of certain crystals. Therefore, it is difficult to describe such long hopping in a well-defined local coordinate system.

In this work, we developed a general framework to parametrize the Hamiltonian matrix by decomposing each block of the Hamiltonian matrix into a vector coupling of equivariant irreducible spherical tensors³⁸ (ISTs) with appropriate parity symmetry. The parametrized Hamiltonian matrix strictly adheres to rotational equivariance and parity symmetry, and can be further extended to a parameterized Hamiltonian that satisfies SU(2) and time-reversal equivariance to accurately fit the Hamiltonian matrix with spin-orbit coupling (SOC) effects. Based on this universal parametrized Hamiltonian, we designed the E(3) equivariant HamGNN model for predicting the TB Hamiltonian matrices of molecules and solids. HamGNN has demonstrated its universality for the Hamiltonian matrix, showcasing exceptional accuracy across various datasets, including QM9 molecular datasets, carbon allotropes, silicon allotropes, SiO₂ isomers, and Bi_xSe_y compounds. The trained HamGNN model can predict the Hamiltonian matrices, energy bands, and wavefunctions of the structures not present in the training set. The powerful fitting and generalization ability exhibited by HamGNN enables researchers to efficiently compute the electronic structures of large-scale crystal systems that were previously deemed challenging or inaccessible.

Results

E(3) equivariant parametrized Hamiltonian

The core of the electronic structure problem in DFT is to solve the Kohn-Sham equation for electrons. If the Kohn-Sham Hamiltonian is represented by numerical atomic orbitals centered on each atom, such as those defined in packages like OpenMX and Siesta, then the Kohn-Sham equation can be formulated as a generalized eigenvalue problem:

$${H}^{({\bf{k}})}{\psi }_{n{\bf{k}}}={\varepsilon }_{n{\bf{k}}}{S}^{({\bf{k}})}{\psi }_{n{\bf{k}}}$$

(1)

where ${H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({\bf{k}})}=\sum _{{n}_{c}}{e}^{i{\bf{k}}\cdot {{\bf{R}}}_{{n}_{c}}}{H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({{\bf{R}}}_{{n}_{c}})}$ and ${S}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({\bf{k}})}=\sum _{{n}_{c}}{e}^{i{\bf{k}}\cdot {{\bf{R}}}_{{n}_{c}}}{S}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({{\bf{R}}}_{{n}_{c}})}$ are the Kohn-Sham Hamiltonian and overlap matrices at the point k in the reciprocal space. ${H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({\bf{k}})}$ and ${S}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({\bf{k}})}$ are obtained by Fourier transform of the real-space TB Hamiltonian matrix ${H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({{\bf{R}}}_{{n}_{c}})}=\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}({\bf{r}}-{{\boldsymbol{\tau}}}_{i})|\hat{H}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}({\bf{r}}-{{\boldsymbol{\tau}}}_{j}-{{\bf{R}}}_{{n}_{c}})\rangle$ and overlap matrix ${S}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{({{\bf{R}}}_{{n}_{c}})}=\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}({\bf{r}}-{{\boldsymbol{\tau }}}_{i})|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}({\bf{r}}-{{\boldsymbol{\tau }}}_{j}-{{\bf{R}}}_{{n}_{c}})\rangle$, respectively, in the basis of atomic orbitals ${\phi }_{{n}_{i}{l}_{i}{m}_{i}}$ at the site τ_i and ${\phi }_{{n}_{j}{l}_{j}{m}_{j}}$ at the site τ_j + R_nc, where R_nc is the shift vector of the n_c-th periodic image cell. Therefore, once we have obtained the Hamiltonian matrix and overlap matrix in real space, we can further solve the electronic structure in the whole reciprocal space.

Due to the spherical symmetry of the atomic potential, the atomic orbital bases as its eigenfunctions not only satisfy the rotational equivariance under the operation Q ∈ SO (3) but also has a certain parity symmetry under the inversion operation g ∈ {E, I}. Under a rotary-inversion operation gQ ∈ O (3), the TB Hamiltonian matrix element ${H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}$ in real space becomes (we omit the notation R_nc for convenience in the following discussion):

$${H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{{\prime} }=\langle gQ{\phi }_{{n}_{i}{l}_{i}{m}_{i}}|\hat{H}|gQ{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle$$

(2)

The irreducible representation of gQ is σ_p(g)⊗D(Q), where D(Q) is the Wigner D matrix and σ_p(g) is the scalar irreducible representation of the inversion operation, which is defined as follows

$${\sigma }_{p}(g)=\left\{\begin{array}{c}\begin{array}{cc}1, & g=E\end{array}\\ \begin{array}{cc}p, & g=I\end{array}\end{array}\right.$$

(3)

Substitute the irreducible representation of gQ into Eq. (2), we can get

$${H^{\prime} }_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}={\sigma }_{{p}_{i}{p}_{j}}(g)\sum _{{\mu }_{i}{\mu }_{j}}{D}_{{m}_{i}{\mu }_{i}}^{({l}_{i})}(Q){D}_{{m}_{j}{\mu }_{j}}^{({l}_{j})}(Q){H}_{{n}_{i}{l}_{i}{\mu }_{i},{n}_{j}{l}_{j}{\mu }_{j}}$$

(4)

where ${\sigma }_{{p}_{i}{p}_{j}}(g)={\sigma }_{{p}_{i}}(g){\sigma }_{{p}_{j}}(g)$. We further write the right-hand side of Eq. (4) in the form of matrix-vector multiplication:

$${H^{\prime} }_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}={\sigma }_{{p}_{i}{p}_{j}}(g)\sum _{{\mu }_{i}{\mu }_{j}}{[{D}^{{l}_{i}}(Q)\otimes {D}^{{l}_{j}}(Q)]}_{{m}_{i}{m}_{j},{\mu }_{i}{\mu }_{j}}{H}_{{n}_{i}{l}_{i}{\mu }_{i},{n}_{j}{l}_{j}{\mu }_{j}}$$

(5)

It can be seen from the above equation that each sub-block ${H}_{{n}_{i}{l}_{i}{\mu }_{i},{n}_{j}{l}_{j}{\mu }_{j}}$ ($|{\mu }_{i}|\le {l}_{i}$, $|{\mu }_{j}|\le {l}_{j}$) of the TB Hamiltonian matrix based on atomic orbitals can be regarded as a spherical tensor^22,38 ${{\bf{T}}}_{{\boldsymbol{\mu }},{p}_{i}{p}_{j}}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}\equiv {H}_{{n}_{i}{l}_{i}{\mu }_{i},{n}_{j}{l}_{j}{\mu }_{j}}$ with the parity ${p}_{i}{p}_{j}$, which is rotationally equivariant according to the generalized Wigner D matrix ${{\boldsymbol{D}}}_{{\boldsymbol{\mu }}{\boldsymbol{m}}}^{{\boldsymbol{l}}}(Q)={D}_{{\mu }_{i}{m}_{i}}^{{l}_{i}}(Q){D}_{{\mu }_{j}{m}_{j}}^{{l}_{j}}(Q)$, where ${\boldsymbol{l}}\equiv ({l}_{i},{l}_{j})$, ${\boldsymbol{\mu }}\equiv ({\mu }_{i},{\mu }_{j})$, ${\boldsymbol{m}}\equiv ({m}_{i},{m}_{j})$.

According to the angular momentum theory^21,22, ${D}^{{l}_{i}}(Q)\otimes {D}^{{l}_{j}}(Q)$ is a reducible representation and can be further decomposed into the direct sum of several irreducible Wigner D matrices:

$${D}^{{l}_{i}}\otimes {D}^{{l}_{j}}={D}^{|{l}_{i}-{l}_{j}|}\oplus {D}^{|{l}_{i}-{l}_{j}|+1}\oplus \cdots \oplus {D}^{{l}_{i}+{l}_{j}}$$

(6)

Combining the parity of the Hamiltonian matrix block $({n}_{i}{l}_{i},{n}_{j}{l}_{j})$, we can get

$${\sigma }_{{p}_{i}{p}_{j}}(g){D}^{{l}_{i}}(Q)\otimes {D}^{{l}_{j}}(Q)=\mathop{\sum }\limits_{L=|{l}_{i}-{l}_{j}|}^{{l}_{i}+{l}_{j}}\oplus {\sigma }_{{p}_{i}{p}_{j}}(g){D}^{L}(Q)$$

(7)

According to Eq. (7), ${{\boldsymbol{T}}}_{{{\boldsymbol{\mu }}},{p}_{i}{p}_{j}}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$ is reducible and the coupled irreducible spherical tensor ${{T}}_{L,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$ in each order $L=|{l}_{i}-{l}_{j}|,\cdots ,{l}_{i}+{l}_{j}$ can be obtained by the vector coupling of ${{\boldsymbol{T}}}_{{\boldsymbol{\mu }},{p}_{i}{p}_{j}}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$:

$${{T}}_{L,\,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}=\mathop{\sum }\limits_{{\mu }_{i}=-{l}_{i}}^{{l}_{i}}\mathop{\sum }\limits_{{\mu }_{j}=-{l}_{j}}^{{l}_{j}}{C}_{m{\mu }_{i}{\mu }_{j}}^{L{l}_{i}{l}_{j}}{{\boldsymbol{T}}}_{{\boldsymbol{\mu }},{p}_{i}{p}_{j}}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$$

(8)

where ${C}_{m{\mu }_{i}{\mu }_{j}}^{L{l}_{i}{l}_{j}}$ is the vector coupling coefficient, namely the Clebsch-Gordan coefficient. Each IST ${T}_{L,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$ has the parity symmetry of ${p}_{i}{p}_{j}$ and satisfies the rotational equivariance of order L. By inverse linear transformation of Eq. (8), ${{\boldsymbol{T}}}_{{\boldsymbol{\mu }},{p}_{i}{p}_{j}}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$ can be constructed from ISTs ${T}_{L,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$:

$${{\boldsymbol{T}}}_{{\boldsymbol{\mu }},{p}_{i}{p}_{j}}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}=\mathop{\sum }\limits_{L=|{l}_{i}-{l}_{j}|}^{{l}_{i}+{l}_{j}}\mathop{\sum }\limits_{m=-L}^{L}{C}_{{\mu }_{i}{\mu }_{j}m}^{{l}_{i}{l}_{j}L}{T}_{L,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$$

(9)

Therefore, as long as we find all ISTs corresponding to each block of the Hamiltonian matrix, we can construct the entire Hamiltonian matrix in a block-wise manner through Eq. (9). We construct two O(3) equivariant vectors ${\mathbf{\Omega} }_{i}^{on}$ and ${\mathbf{\Omega} }_{ij}^{off}$ by the direct summation of all the ISTs required by the on-site ($i=j$) Hamiltonian and the off-site ($i\,\ne\, j$) Hamiltonian respectively:

$${\mathbf{\Omega}}_{i}^{on}=\sum _{{n}_{i}{l}_{i}}\sum _{{n^{\prime} }_{i}{l^{\prime} }_{i}}\mathop{\sum }\limits_{L=|{l}_{i}-{l^{\prime} }_{i}|}^{{l}_{i}+{l^{\prime} }_{i}}\oplus {[{T}_{L,{p}_{i}{p^{\prime} }_{i},m}^{{n}_{i}{l}_{i},{n^{\prime} }_{i}{l^{\prime} }_{i}}]}_{-L\le m\le L}$$

(10)

$${\mathbf{\Omega}}_{ij}^{off}=\sum _{{n}_{i}{l}_{i}}\sum _{{n}_{j}{l}_{j}}\mathop{\sum }\limits_{L=|{l}_{i}-{l}_{j}|}^{{l}_{i}+{l}_{j}}\oplus {[{T}_{L,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}]}_{-L\le m\le L}$$

(11)

The prediction of the Hamiltonian matrix is transformed into the prediction of ${\mathbf{\Omega} }_{i}^{on}$ and ${\mathbf{\Omega}}_{ij}^{off}$, which can be obtained by mapping from the equivariant features of the nodes and the pair interactions, respectively. The final parameterized Hamiltonian can be expressed as:

$${\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}=\left\{\begin{array}{c}{\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n^{\prime} }_{i}{l^{\prime} }_{i}{m^{\prime} }_{i}}^{on}=\mathop{\sum }\limits_{L=|{l}_{i}-{l^{\prime} }_{i}|}^{{l}_{i}+{l^{\prime} }_{i}}\mathop{\sum }\limits_{m=-L}^{L}{C}_{{m}_{i},{m^{\prime} }_{i},m}^{{l}_{i},{l^{\prime} }_{i},L}{T}_{L,{p}_{i}{p^{\prime} }_{i},m}^{{n}_{i}{l}_{i},{n^{\prime} }_{i}{l^{\prime} }_{i}}\quad i=j\\ {\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{off}=\mathop{\sum }\limits_{L=|{l}_{i}-{l}_{j}|}^{{l}_{i}+{l}_{j}}\mathop{\sum }\limits_{m=-L}^{L}{C}_{{m}_{i},{m}_{j},m}^{{l}_{i},{l}_{j},L}{T}_{L,{p}_{i}{p}_{j},m}^{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}\qquad \,i\,\ne \,j\end{array}\right.$$

(12)

The above formula is O(3) equivariant. Since GNN naturally has translational symmetry, the parameterized Hamiltonian represented by ${\mathbf{\Omega}}_{i}^{on}$ and ${\mathbf{\Omega }}_{ij}^{off}$ obtained from GNN has E(3) equivariance.

When the spin-orbit coupling (SOC) effects are considered, the real-space Hamiltonian matrices are complex-valued and can be divided into four sub-blocks ${\hat{{\boldsymbol{H}}}}_{{s}_{i}{s}_{j}}$(${s}_{i},{s}_{j}=\uparrow or\downarrow$) by the spin degree. In this case, the complete Hamiltonian matrices satisfy the following SU(2) rotational equivariance:

$$\langle gQ({\phi }_{{n}_{i}{l}_{i}{m}_{i}}{s}_{i})|{\hat{{\boldsymbol{H}}}}|gQ({\phi }_{{n}_{j}{l}_{j}{m}_{j}}{s}_{j})\rangle ={\sigma }_{{p}_{i}{p}_{j}}(g)\mathop{\sum }\limits_{{\mu }_{i}=-{l}_{i}}^{{l}_{i}}\mathop{\sum }\limits_{{\mu }_{j}=-{l}_{j}}^{{l}_{j}}\mathop{\sum }\limits_{{s^{\prime} }_{i}=-1/2}^{1/2}\mathop{\sum }\limits_{{s^{\prime} }_{j}=-1/2}^{1/2}\left(\right.{D}_{{m}_{i}{\mu }_{i}}^{({l}_{i})}(Q){D}_{{m}_{j}{\mu }_{j}}^{({l}_{j})}(Q)$$

$${D}_{{s}_{i}{s^{\prime} }_{i}}^{(1/2)\ast }(Q){D}_{{s}_{j}{s^{\prime} }_{j}}^{(1/2)}(Q)\langle {\phi }_{{n}_{i}{l}_{i}{\mu }_{i}}{s^{\prime} }_{i}|\hat{{\boldsymbol{H}}}|{\phi }_{{n}_{j}{l}_{j}{\mu }_{j}}{s^{\prime} }_{j}\rangle \left)\right.$$

(13)

Although each subblock ${\hat{{\boldsymbol{H}}}}_{{s}_{i}{s}_{j}}$ satisfies the O(3) rotational equivariance, they are coupled to each other under the rotational operations. Therefore, the four subblocks predicted independently with the O(3) equivariant parameterized Hamiltonian cannot be used to construct the complete SU(2) equivariant Hamiltonian with the SOC effect. In addition, the real and imaginary parts of the SU(2) equivariant Hamiltonian matrices are also coupled during rotation, so the complete Hamiltonian cannot be constructed by using the independently predicted real and imaginary parts. These methods not only rely on a large number of fitting parameters but also can not make the constructed Hamiltonian matrices strictly meet the SU(2) equivariance. To ensure that the SOC effect learned by the network complies with the physical rules and SU(2) equivariance, we explicitly express the complete Hamiltonian as the sum of the spin-less part and the SOC part:

$${\hat{\bf{H}}}={\hat{H}}\otimes {I}_{2}+{\hat{H}}_{SOC}$$

(14)

where ${\hat{H}}_{SOC}=\frac{1}{2}\xi (r)\hat{{\bf{L}}}\cdot \hat{{\boldsymbol{\sigma }}}=\frac{1}{2}\xi (r)({\hat{L}}_{x}{\hat{\sigma }}_{x}+{\hat{L}}_{y}{\hat{\sigma }}_{y}+{\hat{L}}_{z}{\hat{\sigma }}_{z})$, which satisfies SU(2) rotational equivariance and time-reversal equivariance. ξ(r) is an invariant coefficient describing the strength of the SOC effects³⁹. According to the above equation, we can get the following parameterized Hamiltonian matrices with SOC effect in the atomic orbitals^39,40:

$${\tilde {\mathbf{H}}}_{{n}_{i}{l}_{i}{m}_{i}{s}_{i},{n}_{j}{l}_{j}{m}_{j}{s}_{j}}^{SOC}=\left\{\begin{array}{l}{\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}+\frac{1}{2}{\xi }_{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{z}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle\, {s}_{i}=\uparrow ,{s}_{j}=\uparrow \\ \frac{1}{2}{\xi }_{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}(\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{x}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle -i\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{y}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle )\,{s}_{i}=\uparrow ,{s}_{j}=\downarrow \\ \frac{1}{2}{\xi }_{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}(\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{x}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle +i\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{y}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle )\,{s}_{i}=\downarrow ,{s}_{j}=\uparrow \\ {\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}-\frac{1}{2}{\xi }_{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{z}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle\, {s}_{i}=\downarrow ,{s}_{j}=\downarrow \end{array}\right.$$

(15)

Since the matrix representation of the angular momentum operator $\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}|{\hat{L}}_{\alpha }|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}\rangle =\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}({\bf{r}}_{i})|{\hat{L}}_{\alpha }|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}({\bf{r}}_{j}-{\boldsymbol{\tau }}_{ji})\rangle$ under the atomic orbital basis can be directly calculated analytically, the only learnable parameters in Eq. (15) are ${\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}$ and ${\xi }_{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$. ${\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}$ can be directly expressed by Eq. (12), and ${\xi }_{{n}_{i}{l}_{i},{n}_{j}{l}_{j}}$ is an invariant scalar coefficient that can be mapped from the features of atom pairs ij.

Network Implementation

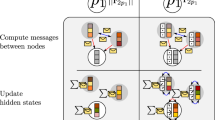
As can be seen from the above discussion, each Hamiltonian matrix block satisfies the rotational equivariance and has a definite parity under the inversion operation, so we designed an E(3) equivariant HamGNN model based on MPNN to fit TB Hamiltonian matrix. This framework directly captures the electronic structure without expensive self-consistent iterations by constructing local equivariant representations of each atomic orbit. The network architecture of HamGNN is shown in Fig. 1a. HamGNN can achieve a direct mapping from atomic species {Z_i} and positions {r_i} to TB Hamiltonian matrix.

Fig. 1: HamGNN architecture and the illustration of its subnetworks.

a The overall architecture of HamGNN. This neural network architecture predicts the Hamiltonian matrix through five steps. The prediction starts from the initial graph embedding of the species, interatomic distances, and interatomic directions of molecules and crystals. The atomic orbital features with angular momentum l in the local environment are included in the l-order components of the E(3) equivariant atom features and are refined through T orbital convolution blocks. In the third step, pair interaction features ${\omega }_{l,p,c,m}^{ij}$ of atomic orbitals are constructed by pair interaction blocks. In the fourth step, the IST representations of on-site and off-site Hamiltonian matrices are constructed by passing the features of atomic orbitals and pair interactions through the on-site layer and off-site layer, respectively. The final step is to construct the on-site and off-site Hamiltonian matrices block-by-block via the parameterized Hamiltonian given by Eq. (12). b Orbital convolution block. The equivariant atomic features that include the features of atomic orbitals of each angular momentum l are refined by the equivariant message passing and update functions. c Pair interaction block. This block is used to construct the pair interaction features between the orbitals of two adjacent atoms by equivariant tensor product. d On-site layer. The equivariant features of atoms are transformed into ISTs of on-site blocks ${\mathbf{\Omega}}_{i}^{on}$ by the on-site layer. e Off-site layer. The pair interaction features between atomic orbitals are transformed into ISTs of the off-site block ${\mathbf{\Omega}}_{ij}^{off}$ by the off-site layer. f Residual block. The residual block is used in the on-site layer and off-site layer to perform a nonlinear equivariant transformation of input features.

Based on the equivariant parameterized Hamiltonian matrix introduced in this work, the prediction of the Hamiltonian matrix is converted to predicting two reducible equivariant tensors: ${\mathbf{\Omega}}_{i}^{on}$ for on-site Hamiltonians and ${\mathbf{\Omega} }_{ij}^{off}$ for off-site Hamiltonians. These tensors satisfy the rotation and inversion equivariance of the O(3) group, therefore we need to construct them in the representation of the O(3) group. HamGNN utilizes equivariant atomic features that are constructed by the direct sum of O(3) representations with different rotation orders l. The O(3) representations of rotation order l can characterize atomic orbitals with angular quantum number l, as they possess the same rotational equivariance. The atomic features are refined through orbital convolution layers (shown in Fig. 2b), which update the atomic features by aggregating equivariant messages constructed from local chemical environments. After refined by T orbital convolution layers, the atomic features are used to construct equivariant pair interaction features via the pair interaction layer (shown in Fig. 2c). ${\mathbf{\Omega}}_{i}^{on}$ and ${\mathbf{\Omega}}_{ij}^{off}$ are obtained by representation transformation of atomic features and pair interaction features, respectively. The Hamiltonian matrix is finally constructed using ${\mathbf{\Omega}}_{i}^{on}$ and ${\mathbf{\Omega}}_{ij}^{off}$ via Eq. (12).

Fig. 2: Application of HamGNN on molecules in the QM9 dataset.

a The comparison between the Hamiltonian matrix elements predicted by HamGNN and those calculated by OpenMX on the QM9 test set. b Comparison of the orbital energies predicted by HamGNN and those calculated by OpenMX for four molecules randomly selected from the QM9 test set.

HamGNN first encodes elements, inter-atomic distances, and relative directions as initial graph embeddings. The atomic numbers ${Z}_{i}$ are encoded as one-hot vectors and are subsequently transformed into initial atomic features through a multilayer perceptron (MLP) layer. The distance between atom i and its neighboring atom j within the cutoff radius r_c is expanded using the Bessel basis function⁴¹:

$$B(|{{\bf{r}}}_{ij}|)=\sqrt{\frac{2}{{r}_{c}}}\frac{\sin (n\pi |{{\bf{r}}}_{ij}|/{r}_{c})}{|{{\bf{r}}}_{ij}|}{f}_{c}(|{{\bf{r}}}_{ij}|)$$

(16)

where f_c is the cosine cutoff function⁴², which guarantees physical continuity for the neighbor atoms close to the cutoff sphere. The list of atomic neighbors is determined by the cutoff radius of each atom’s orbital basis. The interatomic distance is expanded by a set of Bessel functions with $n=\left[\mathrm{1,2},\cdots ,{N}_{b}\right]$, where N_b is the number of Bessel basis functions. In this work, N_b is set to 8. The directional information between atom i and atom j is embedded in a set of real spherical harmonics $\{{Y}_{{m}_{f}}^{{l}_{f}}({\hat{{\bf{r}}}}_{ij})\}$, which will be used to construct the rotation-equivariant filter⁴³ in the equivariant convolution functions.

The atomic feature tensor ${\rm{V}}={V}_{{l}_{0}}\oplus {V}_{{l}_{1}}\oplus \cdots \oplus {V}_{{l}_{\max }}$ in HamGNN is represented as a direct sum of different irreducible representations of the O(3) group up to a maximum rotation order l_max. The features corresponding to each order can characterize the atomic orbitals with distinct angular quantum numbers. If the input structure is rotated, the atomic features will be transformed by the direct sum of the Wigner D matrix, which is represented as a block diagonal matrix ${{D}}={D}_{{{{l}}}_{0}}\oplus {D}_{{{{l}}}_{1}}\oplus \cdots \oplus {D}_{{{{l}}}_{\max }}$. ${V}_{{l}_{i},{p}_{i},{c}_{i},{m}_{i}}^{i,t}$ denotes the tensor element of the equivariant features of atom i in the orbital convolution layer t, where l_i ≤ l_max is the rotation order of the O(3) irreducible representation, ${p}_{i}\in \{1,-1\}$ denotes the parity of the equivariant components of the order l_i, $-{l}_{i}\le {m}_{i}\le {l}_{i}$ is the index of each projection of the equivariant representation, c_i is the channel index (the dimension of the features). We use T orbital convolution layers to construct the equivariant features of the atomic orbits in the local environment. In each orbital convolution layer, the input atomic feature tensor is updated by aggregating the equivariant messages from neighboring atoms. Each equivariant message is generated through the coupling of the feature tensor of neighboring atom j and the convolution filters in an equivariant manner. The rotation equivariant convolution filters are constrained to be a product of learnable radial functions and spherical harmonic functions:

$${F}_{m}^{l}({{\bf{r}}}_{ij})=S(|{{\bf{r}}}_{ij}|){Y}_{{m}_{f}}^{{l}_{{{f}}}}({\hat{{\bf{r}}}}_{ij})$$

(17)

where the radial function $S(|{{\bf{r}}}_{ij}|)=MLP[B(|{{\bf{r}}}_{ij}|)]$ is a mapping that transforms the radial basis $B(|{{\bf{r}}}_{ij}|)$ into the rotation-invariant scalar weights through a multilayer perceptron. The tensor product between the feature tensor of the neighboring atom j and the convolution filter is used to generate the equivariant messages sent to atom i. A tensor product of representations is a mathematical operation for combining two given representations ${x}^{({l}_{1})}\in {l}_{1}$ and ${y}^{({l}_{2})}\in {l}_{2}$ to form another equivariant feature ${x}^{({l}_{1})}\otimes {y}^{({l}_{2})}$. The tensor product ${x}^{({l}_{1})}\otimes {y}^{({l}_{2})}$ is reducible and can be expanded into a direct sum of irreducible representations. The value for the irreducible representation of rotation degree $l\in \{|{l}_{1}-{l}_{2}|,\cdots ,{l}_{1}+{l}_{2}\}$ in the direct sum representation of the tensor product ${x}^{({l}_{1})}\otimes {y}^{({l}_{2})}$ is given by

$${(x\otimes y)}_{m}^{l}=\mathop{\sum }\limits_{{m}_{1}=-{l}_{1}}^{{l}_{1}}\mathop{\sum }\limits_{{m}_{2}=-{l}_{2}}^{{l}_{2}}{C}_{m,{m}_{1},{m}_{2}}^{l,{l}_{1},{l}_{2}}{x}_{{m}_{1}}^{{{{l}}}_{1}}{y}_{{m}_{2}}^{{l}_{2}}$$

(18)

where ${C}_{m,{m}_{1},{m}_{2}}^{l,{l}_{1},{l}_{2}}$ are Clebsch-Gordan coefficients. Finally, the atomic features in each orbital convolution layer are updated by aggregating the equivariant messages of neighboring atoms using the following formulas:

$${m}_{{l}_{i},{p}_{i},c,{m}_{i}}^{ij,t}=\mathop{\sum }\limits_{{m}_{f}=-{l}_{f}}^{{l}_{f}}\mathop{\sum }\limits_{{m}_{j}=-{l}_{j}}^{{l}_{j}}{C}_{{m}_{i},{m}_{f},{m}_{j}}^{{l}_{i},{l}_{f},{l}_{j}}{S}_{{l}_{f},{p}_{f},{l}_{j},{p}_{j}}^{{l}_{i},{p}_{i},c}(|{{\bf{r}}}_{ij}|){Y}_{{m}_{f}}^{{l}_{f}}({\hat{{\bf{r}}}}_{ij}){V}_{{l}_{j},{p}_{j},c,{m}_{j}}^{j,t-1}$$

(19)

$${V}_{{l}_{i},{p}_{i},c,{m}_{i}}^{i,t}={V}_{{l}_{i},{p}_{i},c,{m}_{i}}^{i,t-1}+\sum _{j\in N(i)}{m}_{{l}_{i},{p}_{i},c,{m}_{i}}^{ij,t}$$

(20)

The invariant scalar features of the interatomic distances are used to scale the equivariant output of each rotation order. ${S}_{{l}_{f},{p}_{f},{l}_{j},{p}_{j}}^{{l}_{i},{p}_{i},c}(|{{\bf{r}}}_{ij}|)$ is a learnable scalar weight for each filter-feature tensor product path $({l}_{f},{{{p}}}_{f})\otimes ({l}_{j},{p}_{j},c)\to ({l}_{i},{p}_{i},c)$. To respect the parity equivariance, each filter-feature tensor product path $({l}_{f},{p}_{f})\otimes ({l}_{j},{p}_{j},c)\to ({l}_{i},{p}_{i},c)$ satisfies the parity selection rule: ${p}_{i}={p}_{f}{p}_{j}$. Equation (20) is the update function, which aggregates equivariant messages from neighboring atoms to update the input atomic features. The updated atomic features are passed to a nonlinear gate activation function⁴⁴, which scales the input features equivariantly with the invariant field (l ≠ 0) of the input features as the gate.

The pair interaction features, which are utilized to construct the off-site Hamiltonian, are generated by the pair interaction layer. The pair interaction features are the sum of two parts. The first part is the tensor product between the features of two interacting atoms i and j: $({l}_{i},{p}_{i},c)\otimes ({l}_{j},{p}_{j},c)\to (l,p,c)$, where l and p denote the rotation order and the parity of the pair interaction features, respectively. The second part is the tensor product between the mixed features of atom pairs ij and the convolution filters: $(l{\prime} ,p{\prime} ,c)\otimes ({l}_{f},{p}_{f})\to (l,p,c)$, where l′ and p′ denote the rotation order and the parity of the mixed features of atom pairs ij, respectively. The pair interaction features are finally constructed by the following equation:

$${\omega }_{l,p,c,m}^{ij}=\mathop{\sum }\limits_{{m}_{i}=-{l}_{i}}^{{l}_{i}}\mathop{\sum }\limits_{{m}_{j}=-{l}_{j}}^{{l}_{j}}{C}_{{m}_{i},{m}_{j},m}^{{l}_{i},{l}_{j},l}{S}_{{l}_{i},{p}_{i},{l}_{j},{p}_{j}}^{l,p,c}(|{{\bf{r}}}_{ij}|)\left(\sum _{c{\prime} }{W}_{{l}_{i},{p}_{i},c,c{\prime} }^{i}{V}_{{l}_{i},{p}_{i},c{\prime} ,{m}_{i}}^{i,T}\right)\left(\sum _{c{\prime} }{W}_{{l}_{j},{p}_{j},c,c{\prime} }^{j}{V}_{{l}_{j},{p}_{j},c{\prime} ,{m}_{j}}^{j,T}\right)$$

$$+\mathop{\sum }\limits_{{m}_{f}=-{l}_{f}}^{{l}_{f}}\mathop{\sum }\limits_{m{\prime} =-l{\prime} }^{l{\prime} }{C}_{m{\prime} ,{m}_{f},m}^{l{\prime} ,{l}_{f},l}{S}_{{l}_{f},{p}_{f},l{\prime} ,p{\prime} }^{l,p,c}(|{{\bf{r}}}_{ij}|){Y}_{{m}_{f}}^{{l}_{f}}({\hat{{\bf{r}}}}_{ij}){V}_{l{\prime} ,p{\prime} ,c,m{\prime} }^{ij}$$

(21)

where ${W}_{{l}_{i},{p}_{i},c,c{\prime} }^{i}$ and ${W}_{{l}_{j},{p}_{j},c,c{\prime} }^{j}$ are learnable weight matrices used to linearly couple the equivariant features from different channels, ${V}_{l{\prime} ,p{\prime} ,c,m{\prime} }^{ij}=\sum _{c{\prime} }{W{\prime} }_{l{\prime} ,p{\prime} ,c,c{\prime} }^{i}{V}_{l{\prime} ,p{\prime} ,c{\prime} ,m{\prime} }^{i,T}+\sum _{c{\prime} }{W{\prime} }_{l{\prime} ,p{\prime} ,c,c{\prime\;} }^{j}{V}_{l{\prime} ,p{\prime} ,c{\prime} ,m{\prime} }^{j,T}$ is the mixed feature tensor of the atomic features ${V}_{{l}_{i},{p}_{i},{c}_{i},{m}_{i}}^{i,T}$ and ${V}_{{l}_{j},{p}_{j},{c}_{j},{m}_{j}}^{j,T}$.

The on-site layer and off-site layer are used to convert the node features ${V}_{{l}_{i},{p}_{i},{c}_{i},{m}_{i}}^{i,T}$ and pair interaction features ${\omega }_{l,p,c,m}^{ij}$ into the direct sums ${\mathbf{\Omega}}_{i}^{on}$ and ${\mathbf{\Omega}}_{ij}^{off}$ of the ISTs required to construct on-site and off-site Hamiltonian blocks, respectively. We add shortcut connections in the on-site layer and off-site layer and use a norm activation function that scales the modulus of the irreducible representations of each order nonlinearly to increase the nonlinear fitting ability of the network. In the last step, the network uses the ISTs in ${\mathbf{\Omega} }_{i}^{on}$ and ${\mathbf{\Omega} }_{ij}^{off}$ to construct the on-site and off-site Hamiltonian blocks through Eq. (12). The final predicted Hermitian Hamiltonian is obtained by the following symmetrization:

$${H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}=\left\{\begin{array}{c}{H}_{{n}_{i}{l}_{i}{m}_{i},{n{\prime} }_{i}{l{\prime} }_{i}{m{\prime} }_{i}}^{on}=({\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n{\prime} }_{i}{l{\prime} }_{i}{m{\prime} }_{i}}^{on}+{\tilde{H}}_{{n{\prime} }_{i}{l{\prime} }_{i}{m{\prime} }_{i},{n}_{i}{l}_{i}{m}_{i}}^{on\ast })\,/2i=j\\ {H}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{off}=({\tilde{H}}_{{n}_{i}{l}_{i}{m}_{i},{n}_{j}{l}_{j}{m}_{j}}^{off}+{\tilde{H}}_{{n}_{j}{l}_{j}{m}_{j},{n}_{i}{l}_{i}{m}_{i}}^{off\ast })\,/2i\,\ne\, j\end{array}\right.$$

(22)

Tests and applications

To assess the accuracy and transferability of HamGNN, we trained and tested HamGNN on the Hamiltonian matrices and electronic structures for the periodic and aperiodic systems, including various molecules, periodical solids, a nanoscale dislocation defect, and a Moiré superlattice. Previously reported models such as SchNorb³⁵, PhiSNet³⁶, and DeepH⁴⁵ are trained and tested on the slightly perturbed structures from only one configuration each time. Since HamGNN is based on the universal parameterized Hamiltonian proposed in this work, our model can be trained and tested on structures with the same atomic species but different configurations in the same way as MLIPs.

Molecules

The QM9 dataset^46,47 contains 134k stable small organic molecules made up of CHONF. These small organic molecules are important candidates for drug discovery. The development of general ML models for rapid screening of the electronic structure properties of drug molecules is beneficial for understanding the mechanisms of drugs and shortening the cycle of drug development. We calculated the real-space TB Hamiltonian matrices using OpenMX for 10,000 randomly selected molecules from the QM9 dataset. We divided the whole dataset into the training, validation, and test set with a ratio of 0.8: 0.1: 0.1. As shown in Fig. 2a, the predicted values exhibit a high degree of agreement with the DFT-calculated values of the Hamiltonian matrices for various configurations in the test set. The mean absolute error (MAE) of the Hamiltonian matrix element predicted by the trained HamGNN model on the test set is only 1.49 meV. Please note that all MAEs mentioned in our manuscript refer to the mean absolute errors between predicted values and ground truth (DFT values), unless otherwise stated. Each of the orbital energy calculated by diagonalizing the predicted Hamiltonian matrix coincides almost exactly with each DFT-calculated orbital energy (see Fig. 2b), showing high precision and transferability. The orbital energies calculated by HamGNN and OpenMX for the four molecules shown in Fig. 2b are listed in Supplementary Table 1.

We also trained HamGNN on the Hamiltonians of several specific small molecules generated by ab initio molecular dynamics (MD) and compared the accuracy of HamGNN with two recently reported models, PhiSNet³⁶ and DeepH⁴⁵. The Hamiltonian matrices of these molecules were calculated by OpenMX and divided into the training, validation, and test sets in the same way as PhiSNet in ref. ³⁶. The MAEs of the Hamiltonian matrices predicted by DeepH are from ref. ⁴⁵. As can be seen from Table 1, HamGNN achieves the highest accuracy among the three models. The error of HamGNN as a function of training epochs on both the training and validation sets is highly consistent (see Supplementary Discussion 1). The prediction error of DeepH is higher than that of PhiSNet and HamGNN because the local coordinate system used by DeepH is not strictly equivariant. Although SE(3) equivariant PhiSNet shows high accuracy in predicting the molecules, it is not a universal equivariant model because it does not satisfy the parity symmetry of the Hamiltonian matrix strictly. Our tests have revealed that neglecting parity symmetry can significantly impair its fitting ability for solid materials (see Supplementary Discussion 2).

Table 1 Comparison of the MAEs of the Hamiltonian matrices predicted by HamGNN, DeepH, and PhiSNet for the molecule structures from molecular dynamics trajectories.

Periodic solids

We have collected 426 carbon allotropes from the Samara Carbon Allotrope Database (SACADA)⁴⁸ and 30 silicon allotropes from Materials Project⁴⁹, each containing no more than 60 atoms in its unit cell. We have also collected 221 SiO₂ isomers from the Materials Project, each containing no more than 80 atoms in its unit cell. We have perturbed each of the collected SiO₂ isomers three times, resulting in 663 perturbed SiO₂ structures with a random atomic displacement of 0.1 Å. We performed DFT calculations using OpenMX to obtain the ab initio TB Hamiltonian matrices for these carbon allotropes, silicon allotropes, and perturbed SiO₂ isomers. The Hamiltonian matrices in each dataset were divided into training, validation, and test sets with a ratio of 0.8:0.1:0.1. Three separate HamGNN models were trained on the carbon allotropes, silicon allotropes, and perturbed SiO₂ isomers, respectively.

The MAEs of the Hamiltonian matrix predicted by HamGNN for the structures in the test set of carbon allotropes, silicon allotropes, and SiO₂ isomers are 1.55 meV, 2.01 meV, and 2.29 meV, respectively. There are tiny variations in model accuracy for the HamGNN models trained with different initial random network weights (see Supplementary Discussion 3), indicating the high stability of HamGNN. The MAE of HamGNN on the carbon allotropes is even lower than the error (2.0 meV) of DeepH on the training dataset of only the graphene structures⁴⁵. Most importantly, the HamGNN model trained on the carbon allotropes is transferable and can fit the Hamiltonian matrices of the carbon allotropes with arbitrary sizes and configurations beyond the training set. Achieving transferable predictions for the DeepH model that utilizes local coordinate systems is difficult, as discussed in Supplementary Discussion 4.

We used pentadiamond⁵⁰, Moiré twisted bilayer graphene (TBG), Si (MP-1199894), and SiO₂ (MP-1257168) to test the accuracy and transferability of the HamGNN models trained on the three datasets. The test structures are shown in Fig. 3a-d. Pentadiamond is a three-dimensional carbon foam constructed from carbon pentagons and contains 88 carbon atoms in the unit cell⁵⁰. There are 1084 carbon atoms in the twisted bilayer graphene with a Moiré angle θ ≈ 3.48°. The interlayer spacing of TBG is about 4.0 Å. The carbon atoms within each layer are connected by strong covalent bonds, while the layers are stacked by the weak van der Waals forces. The Si structure labeled MP-1199894 contains 82 atoms in the unit cell and crystallizes in the monoclinic C2/c space group. The SiO₂ structure labeled MP-1257168 is characterized by the complex porous structures built by SiO₄ tetrahedra and has 180 atoms in the unit cell. The MAE of the Hamiltonian matrix elements predicted by HamGNN for the pentadiamond, TBG, Si (MP-1204046), and SiO₂ (MP-667371) is only 1.54 meV, 3.23 meV, 1.39 meV, and 1.67 meV, respectively. The high accuracy can be seen in the scatter plots of the predicted Hamiltonian matrices versus the DFT calculated Hamiltonian matrices shown in Fig. 3e-h. Although our carbon allotropic dataset does not contain any bilayer graphene structures, HamGNN automatically learns van der Waals interactions from this dataset and successfully predicts the Hamiltonian matrix of TBG. The energy bands obtained by diagonalizing the predicted Hamiltonians closely align with those from the DFT calculations, as shown in Fig. 3i-l.

Fig. 3: The prediction of HamGNN on several periodic solids that are not present in the training sets.

a–d Crystal structures of pentadiamond, Moiré twisted bilayer graphene (TBG), Si (MP-1199894), and SiO₂ (MP-1257168). e–h Comparison of the Hamiltonian matrix elements predicted by HamGNN and those calculated by OpenMX for pentadiamond, TBG, Si (MP-1199894), and SiO₂ (MP-1257168). i–l Comparison of the energy bands predicted by HamGNN (solid line) and those (dashed line) calculated by OpenMX for pentadiamond, TBG, Si (MP-1199894), and SiO₂ (MP-1257168).

Dislocation defect

In general, point defects only induce local structural distortions, so the supercell used for point defect simulation does not need a very large size and can be calculated directly using the DFT method^51,52. However, as one-dimensional line defects, edge dislocations induce elastic stress fields in their surroundings^53,54,55, resulting in significantly greater lattice distortions compared to point defects. Simulating an isolated edge dislocation necessitates the utilization of a large supercell to mitigate the strong elastic interactions between the dislocation and its periodic image. The high density of dislocations in small supercells may lead to unrealistic lattice distortion and inaccurate electronic structures. However, the computational complexity of the large supercells required to simulate the edge dislocations is a great challenge for DFT methods. HamGNN enables the direct mapping from structure to the Hamiltonian matrix, providing the possibility to compute electronic structures of dislocation defects in large supercells.

In this work, we take an isolated edge dislocation in a large silicon supercell as an example to demonstrate the high efficiency of the HamGNN model to simulate nanoscale defects in large systems. Crystalline silicon has a diamond-type crystal structure, whose most favorable slip system belongs to the type ½〈110〉{111}. Taking the {111} plane of silicon as the slip plane, we constructed an isolated edge dislocation with Burgers vector 1/2 < 110 > , as shown in Fig. 4a. There are 4284 atoms in this supercell containing an isolated edge dislocation. We utilized the HamGNN model, which was trained on Si allotropes, to predict the Hamiltonian matrix of this supercell. Subsequently, we computed its band structure and charge density of valence band maximum (VBM) using the predicted Hamiltonian matrix.

Fig. 4: The electronic structure prediction on silicon dislocation.

a Atomic structure and charge density of the valence band maximum (VBM) of an isolated dislocation in silicon. The atoms on the dislocation plane are colored red. b The energy bands of the dislocation model along G(0.0, 0.0, 0.0) to Z(0.0, 0.0, 0.5).

The defect energy bands introduced by the dislocation defect appear within the band gap, as shown in Fig. 4b, which significantly narrows the band gap of bulk Si. The predicted valence band maximum (VBM) at the Gamma point is located on an occupied defect energy band. The VBM wave function shown in Fig. 4a is mainly distributed in the dislocation core, indicating that this occupied band is caused by the hanging bonds and structural distortion in the core. The predicted electronic structure in the dislocation core is analogous to that obtained from the DFT simulation for a non-periodical dislocation model containing only 358 atoms⁵⁶. However, the dangling bonds at the boundaries of the non-periodical supercell are saturated by hydrogens⁵⁶, which may introduce unrealistic electronic states from hydrogens. We use HamGNN to directly compute the electronic structures of dislocations in large periodic supercells, thus overcoming the potential issues arising from the use of small or non-periodic supercells. With the ability to establish a shortcut from structure to ab initio Hamiltonian matrix, HamGNN enables direct calculation of electronic structures for large supercells without the costly SCF iterations. HamGNN demonstrated exceptional speed and efficiency, taking only 36 seconds to calculate the Hamiltonian matrix of the silicon supercell containing 4284 atoms on a node equipped with 80 Intel(R) Xeon(R) Gold 6248 CPU cores. To verify the reliability of the trained HamGNN model in predicting the electronic structures for silicon dislocation defects, we constructed a small silicon supercell containing an edge dislocation defect and compared the Hamiltonian matrix, energy bands, and the wave function predicted by HamGNN with those calculated by OpenMX (see Supplementary Discussion 5).

Moiré superlattice of bilayer MoS₂

MoS₂ is a 2D transition metal dichalcogenide (TMD) that has attracted much attention because it is an excellent semiconductor with a wide range of applications in the field of electronics and optoelectronics^57,58,59,60. Different from monolayer or untwisted bilayer MoS₂, the twisted bilayer MoS₂ with Moiré angles has been found to have flat bands and shear solitons^57,61,62,63, which may lead to some interesting physical phenomena, such as superconducting states, quantum Hall insulators, Mott-insulating phases. However, the electronic structure calculation of Moiré twisted bilayer MoS₂ by DFT is relatively expensive due to its large size. To demonstrate the accuracy and efficiency of HamGNN in replacing DFT for calculating the electronic structure of Moiré twisted two-dimensional materials, we conducted a quantitative comparison between the HamGNN prediction and the DFT calculation for twisted bilayer MoS₂ with a Moiré angle of 3.5°. Before predicting the electronic structure of the Moiré twisted bilayer MoS₂ superlattice, we trained a HamGNN model using a dataset consisting of 500 untwisted bilayer MoS₂ structures, each containing 54 atoms. Each MoS₂ bilayer structure in the dataset has a random interlayer sliding distance of up to 2 angstroms along a random direction. The layer spacing of each MoS₂ bilayer structure in the dataset was randomly shifted by a maximum of 0.5 angstroms. We used OpenMX to calculate the Hamiltonian matrices for the untwisted MoS₂ bilayer structures, and divided the dataset into training, validation, and test sets with a ratio of 0.8: 0.1: 0.1. The MAE of the trained HamGNN on the test set is only 0.82 meV.

We used OpenMX and the trained HamGNN model to calculate the Hamiltonian matrix of the twisted bilayer MoS₂ with a Moiré angle of 3.5°, which contains 1626 atoms in a unit cell. HamGNN and OpenMX performed the calculations on a node with 80 Intel(R) Xeon(R) Gold 6248 CPU cores. HamGNN only took about 21 s, while OpenMX required approximately 73,000 s to complete this task. This indicates that HamGNN significantly improves the efficiency of electronic structure calculations. The MAE between the Hamiltonian matrix predicted by HamGNN and that calculated by OpenMX is only 0.89 meV. The energy bands, obtained by diagonalizing the Hamiltonian matrices from HamGNN and OpenMX, are shown in Fig. 5a. The predicted bands show a high level of agreement with those computed by OpenMX. Besides, the appearance of flat bands at the valence band edge and the Dirac cone at the K point agrees well with the energy bands calculated by VASP in ref. ⁶¹. The spatial distribution of the predicted VBM wave function, as illustrated in Fig. 5b, exhibits a high degree of localization around the Moiré patterns, which is consistent with the computational results obtained from VASP calculations under LDA and PBE functionals⁶¹.

Fig. 5: The electronic structure prediction for the twisted bilayer MoS₂ with a Moiré angle of 3.5°.

a Comparison of the energy bands predicted by HamGNN and those calculated by OpenMX for the Moiré twisted bilayer MoS₂. b The spatial distribution of VBM wave function in the Moiré twisted bilayer MoS₂.

Through the quantitative comparisons, we demonstrate that HamGNN models trained on small systems can serve as an efficient alternative to DFT for accurately calculating the electronic structure of large systems. After being trained on the Hamiltonian matrices of small untwisted bilayer structures, the HamGNN model can effectively predict the electronic structure of small-angle twisted materials, which is computationally expensive for DFT calculations. The high accuracy and efficiency of HamGNN demonstrate its immense potential in accelerating the electronic structure calculations for small-angle twisted bilayers of various transition metal dichalcogenides (TMDs). In Supplementary Discussion 6, we have discussed the computational scalability of HamGNN with respect to system sizes and also compared its computational efficiency with OpenMX for bilayer MoS₂ slabs of varying twist angles.

Bi_xSe_y quantum materials

Bi and Se have multiple chemical valences and can form a set of binary compounds Bi_xSe_y with various stoichiometric ratios^64,65. Bi is a heavy element whose d electrons have strong SOC effects. A total of 19 Bi_xSe_y compounds can be found on Materials Project⁴⁹. The compound Bi₈Se₇ (id: MP-680214) shown in Fig. 6a, which contains 45 atoms in the unit cell, was used to test the transferability and accuracy of HamGNN. The remaining 18 Bi_xSe_y compounds, which contain no more than 40 atoms in the unit cell, were used to generate the training set for the network. To increase the size of the training set, we applied a random perturbation up to 0.02 Å to the atoms of each Bi_xSe_y structure to generate 50 perturbed structures and obtained 900 structures in total. These structures were randomly divided into the training, validation, and test sets with a ratio of 0.8: 0.1: 0.1. The MAE of the real part of the SOC Hamiltonian predicted by the trained model for Bi₈Se₇ is 1.29 meV, and the MAE of the imaginary part of the SOC Hamiltonian is only 5.0 × 10⁻⁷ meV. As the SOC effect primarily manifests in the imaginary component of the Hamiltonian matrix, such a low MAE for the imaginary part indicates that our parameterized SOC Hamiltonian has a strong fitting ability across various structures. As shown in Fig. 6b, the predicted energy bands of Bi₈Se₇ are in good agreement with those calculated by OpenMX. Although the training set does not contain any compounds with a stoichiometric ratio of Bi₈Se₇, the HamGNN model still accurately predicted the SOC Hamiltonian matrix and energy bands of this structure, demonstrating its high transferability.

Fig. 6: The electronic structure prediction on the Bi_xSe_y quantum materials.

a The crystal structure of Bi₈Se₇. b Comparison of the energy bands predicted by HamGNN (solid line) with those calculated by DFT (dashed line) for Bi₈Se₇. c Schematic representation of the layered crystal structure of Bi₂Se₃. d Comparison between the energy gaps at G point predicted by HamGNN with those calculated by DFT for the Bi₂Se₃ slab models with various quintuple layers (QLs). e Comparison of the energy bands predicted by HamGNN (solid line) with those calculated by DFT (dashed line) for Bi₂Se₃ slab with 6 QLs. f The predicted spin textures of two unoccupied states near the conduction band minimum (CBM).

Bi₂Se₃ is a widely recognized 3D topological insulator material, which serves as an exceptional platform for exploring quantum phenomena related to the effects of spin-orbit coupling (SOC)^{66,67,68,69,70}. Bulk Bi₂Se₃ is stacked by quintuple layers (QLs) through the van der Waals (vdW) interaction, as is shown in Fig. 6c. Each QL layer is composed of five atomic layers of Se-Bi-Se-Bi-Se combined by strong covalent bonds. As shown in Fig. 6d, the G-point band gaps predicted by HamGNN exhibit a high degree of agreement with those obtained from DFT calculations for Bi₂Se₃ slabs comprising 1 to 7 QLs. As shown in Fig. 6e, the addition of more QL layers results in a gradual decrease of the G-point band gap and a tendency towards linear band dispersion at the G point, ultimately forming a Dirac cone. The spin textures of the lowest unoccupied states, located 0.07 eV and 0.23 eV above the conduction band minimum (CBM), were computed using the Hamiltonian matrix predicted by HamGNN, as illustrated in Fig. 6f. The predicted spin textures are in good agreement with the features of the Dirac cone, which is a topological surface state protected by time-reversal symmetry and characterized by spin-momentum locking.

Discussion

DFT methods are now widely used to calculate various properties of molecules and materials. However, successful implementation of DFT calculations on large systems remains infrequent due to the significant computational resources and running time required. A typical DFT calculation often requires tens to hundreds of self-consistent iterations to obtain the final Hamiltonian and wave function, with the diagonalization of the Hamiltonian matrix performed on a dense k-point grid at each iteration step. This process takes up most of the running time of DFT calculations and can not be circumvented. The emergence of deep learning in recent years has enabled efficient atomic simulations with DFT accuracy, as evidenced by the widespread use of machine learning interatomic potentials (MLIPs) that offer quantum mechanical precision to accelerate long-time molecular dynamics simulations for large systems. As potential energy is just an invariant scalar, the implementation of transferable MLIP models is relatively straightforward. However, due to the rotational equivariance and parity symmetry of the Hamiltonian matrix, developing a transferrable model for directly predicting the Hamiltonian matrix is highly challenging.

In this work, we propose an analytical E(3) equivariant parameterized Hamiltonian matrix that explicitly takes into account rotation equivariance and parity symmetry. Furthermore, we extend it to a parameterized Hamiltonian matrix satisfying SU(2) and time-reversal equivariance to fit the Hamiltonian matrix with SOC effects. Based on this parameterized Hamiltonian matrix, we develop an E(3) equivariant deep neural network called HamGNN to fit the Hamiltonian matrix of various molecules and solids. Previously reported models were trained and tested on the datasets consisting of slightly perturbed molecules or crystals from the same configuration. To demonstrate the accuracy and transferability of our parameterized Hamiltonian matrix, we used the trained HamGNN model to predict the electronic structures of the molecules, periodic solids, the silicon dislocation defect, Moiré twisted bilayer MoS₂, and Bi_xSe_y quantum materials. The results of actual tests demonstrate that our model exhibits a high level of accuracy in comparison to DFT, while also demonstrating a significant degree of transferability similar to that of MLIPs. These performances provide a crucial foundation for the extensive implementation of electronic structure methods in machine learning. Since our model can establish a direct mapping from the structure to the self-consistent Hamiltonian matrix without the time-consuming self-consistent iterations in DFT, it can be used to accelerate the electronic structure calculation of large systems and other costly advanced calculations, such as the electron-phonon coupling matrix via the automatic differentiation ability of the neural network.

Methods

Hamiltonian datasets and DFT calculation details

QM9 structure set and the molecules in Table 1 are available from http://quantum-machine.org/datasets/, SACADA structure set is available from https://www.sacada.info/sacada_3D.php, and the structures of Si allotropes, SiO₂ isomers, and Bi_xSe_y crystals are downloaded from the Materials Project site⁴⁹. To prepare the training set of untwisted bilayer MoS₂, a random perturbation of up to 0.02 Å is applied to each atom, and a slip of up to 2 Å is performed in a random direction within the XY plane. The layer spacing of the bilayer MoS₂ was randomly shifted by a maximum of 0.5 angstroms. We performed DFT calculations on the structures in the above datasets to obtain TB Hamiltonian matrices via OpenMX¹⁷, a software package for nano-scale material simulations based on norm-conserving pseudopotentials and pseudo-atomic localized basis functions. The PBE (Perdew-Burke-Ernzerhof)⁷¹ functional is employed for all OpenMX calculations presented in this study. H6.0-s2p1, C6.0-s2p2d1, N6.0-s2p2d1, O6.0-s2p2d1, F6.0-s2p2d1, Si7.0-s2p2d1, Mo7.0-s3p2d2, Bi8.0-s3p2d2, and Se7.0-s3p2d2 pseudoatomic orbitals (PAOs) were used as the basis for the calculations. The truncation radius of the atomic orbits of H, C, N, O, and F is 6.0 Bohr, the truncation radius of the atomic orbits of Si, Mo, and Se is 7.0 Bohr, the truncation radius of the atomic orbits of Bi is 8.0 Bohr. The cutoff energy and K-point grid used by OpenMX in the calculation of the Hamiltonian matrices for each dataset are listed in Supplementary Table 6. The Si dislocation model was built by Atomsk⁷² and relaxed by GPUMD⁷³ with a force criterion of 0.1 eV ∙ Å⁻¹. The VASP^74,75 results of Moiré superlattice of bilayer MoS₂, which serve to validate the accuracy of our HamGNN predictions, are referenced from Naik et al.‘s work⁶¹. They utilized LDA and PBE functionals to calculate the electronic structure of twisted bilayer MoS₂ with a Moiré angle of 3.5°. For the OpenMX calculation on the Moiré twisted bilayer MoS₂, we used a cutoff energy of 150 Ry and a 4 × 4 × 1 k-point mesh to sample the Brillouin zone.

Hamiltonian construction details

The majority of computational time in DFT calculations is dedicated to self-consistent iterations aimed at obtaining the self-consistent charge density $\rho$, which is used to determine the final Hamiltonian matrix and wave functions. The Kohn-Sham Hamiltonian can be written as $H=T+{V}_{eff}$, where ${V}_{eff}=\sum _{l}{V}_{ec}({\bf{r}}-{{\boldsymbol{\tau }}}_{l})+{V}_{scf}[\rho ]$. ${V}_{ec}({\bf{r}}-{{\boldsymbol{\tau }}}_{l})$ is the Coulomb potential of the core charges of each atom l, ${V}_{scf}[\rho ]=\frac{\delta {E}_{ee}}{\delta \rho }+\frac{\delta {E}_{xc}}{\delta \rho }$ denotes the sum of the potentials that arise from the electron-electron interaction energy ${E}_{ee}[\rho ]$ and the exchange-correlation energy ${E}_{xc}[\rho ]$. The matrix elements of the kinetic energy operator $\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}({\bf{r}}-{{\boldsymbol{\tau }}}_{i})|\hat{T}|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}({\bf{r}}-{{\boldsymbol{\tau }}}_{j}-{{\bf{R}}}_{{n}_{c}})\rangle$ and the Coulomb potential of the atomic cores $\langle {\phi }_{{n}_{i}{l}_{i}{m}_{i}}({\bf{r}}-{{\boldsymbol{\tau }}}_{i})|\sum _{l}{V}_{ec}({\bf{r}}-{{\boldsymbol{\tau }}}_{l})|{\phi }_{{n}_{j}{l}_{j}{m}_{j}}({\bf{r}}-{{\boldsymbol{\tau }}}_{j}-{{\bf{R}}}_{{n}_{c}})\rangle$ are not functionals of the self-consistent charge density and can be calculated analytically without SCF iterations. The complete Hamiltonian can be obtained by the sum of the SCF-independent matrices calculated analytically from the atomic coordinates and the SCF-dependent matrix ${V}_{scf}[\rho ]$ that can be fitted by the equivariant neural networks. The general parameterized Hamiltonian proposed in this work can be applied to all tight-binding Hamiltonian matrices calculated using various exchange-correlation functionals (see Supplementary Discussion 7).

Network and training details

The Pytorch-1.11.0⁷⁶, PyG-2.0.4⁷⁷, Pymatgen⁷⁸, Nequip-0.5.3³³, and e3nn-0.5.0⁷⁹ libraries are used to implement HamGNN. All models used in this work have five orbital convolution layers, a pair interaction layer, an on-site layer, and an off-site layer. The edge distances between each atom and its neighbors are expanded by eight Bessel function bases. The spherical harmonic functions with a maximum degree L_max = 4 are used to embed the directions of the edges. The O(3) representations used for the atom features and pair interaction features have N_fea channels with a maximum degree L_max and parities p = ±1. The number of feature channels N_fea and the maximum degree L_max for each dataset are listed in Supplementary Table 7. A two-layer MLP with 64 neurons is used to map the invariant edge embeddings to the weights of each tensor product path in Eqs. (19) and (21). Shifted softplus³¹ function is used as the activation function in the MLP. The gate activation function scales the input features $(\mathop{\oplus }\limits_{i}{u}_{{p}_{i}}^{(0)})\oplus (\mathop{\oplus }\limits_{j}{v}_{{p{\prime} }_{j}}^{(0)})\oplus (\mathop{\oplus }\limits_{j}{w}_{{p}_{j}}^{({l}_{j} > 0)})$ with its invariant field $(\mathop{\oplus }\limits_{i}{u}_{{p}_{i}}^{(0)})$ and $(\mathop{\oplus }\limits_{j}{v}_{{p{\prime} }_{j}}^{(0)})$ as the gate. The output equivariant features of gate nonlinearity are $[\mathop{\oplus }\limits_{i}{\phi }_{{p}_{i}}^{1}({u}_{{p}_{i}}^{(0)})]\oplus [\mathop{\oplus }\limits_{j}{\phi }_{{p{\prime} }_{j}}^{2}({v}_{{p{\prime} }_{j}}^{(0)}){w}_{{p}_{j}}^{({l}_{j})}]$, where ${\phi }_{{p}_{i}}^{1}$ and ${\phi }_{{p{\prime} }_{j}}^{2}$ are the activation functions that vary with the parity of the scalar input, defined as follows³³:

$${\phi }_{{p}_{i}}^{1}(x)=\left\{\begin{array}{c}ssp(x)=\,{\mathrm{ln}}(0.5\times {e}^{x}+0.5)\,{p}_{i}=1\\ \tanh (x)=\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}{p}_{i}=-1\end{array}\right.$$

(23)

$${\phi }_{{p^{\prime} }_{j}}^{2}(x)=\left\{\begin{array}{c}ssp(x)=\,{\mathrm{ln}}(0.5\times {e}^{x}+0.5)\,{p^{\prime} }_{j}=1\\ |x|{p^{\prime} }_{j}=-1\end{array}\right.$$

(24)

${\phi }_{{p}_{i}}^{1}(x)$ has the same parity as the input scalar x, while ${\phi }_{{p{\prime} }_{j}}^{2}(x)$ always has even parity. This ensures that the parity of the output features of the Gate activation function is equivariant.

To increase transferability and avoid overfitting, we include the error of the calculated energy bands as a regularization term in the loss function:

$$L=\Vert \tilde{H}-H\Vert +\frac{\lambda }{{N}_{orb}\times {N}_{k}}\mathop{\sum }\limits_{k=1}^{{N}_{k}}\mathop{\sum }\limits_{n=1}^{{N}_{orb}}\Vert {\tilde{\varepsilon }}_{nk}-{\varepsilon }_{nk}\Vert$$

(25)

where the variables marked with a tilde refer to the corresponding predictions and λ denotes the loss weight of the band energy error. λ equals 0.001 in our training. When the training of the network has not converged, the error of the predicted Hamiltonian is large, resulting in poor or even divergent prediction values of the energy bands. Adding the band loss value at the beginning of training may cause the total loss value to diverge. Therefore, we train the network in two steps. First, only the mean absolute error of Hamiltonian matrices is used as the loss value to train the network until the network weights converge. The parameters were optimized with AdamW^80,81 optimizer using an initial learning rate of 10⁻³. Then the mean absolute error of each band calculated at N_k random points in the reciprocal space is added to the loss function and starts the training at an initial learning rate of 10⁻⁴. When the accuracy of the model on the validation set is not improved after successive N_patience epochs, the learning rate will be reduced by a factor of 0.5. When the accuracy of the model on the validation set is not improved after successive N_stop epochs or the learning rate is lower than 10⁻⁶, the training will be stopped and the model that has the best accuracy on the validation set will be used on the test set. The values of some key network and training parameters on each dataset are listed in Supplementary Table 7. All models were trained on a single NVIDIA A100 GPU.