Efficient and interpretable graph network representation for angle-dependent properties applied to optical spectroscopy

Abstract

Graph neural networks are attractive for learning properties of atomic structures thanks to their intuitive graph encoding of atoms and bonds. However, conventional encoding does not include angular information, which is critical for describing atomic arrangements in disordered systems. In this work, we extend the recently proposed ALIGNN (Atomistic Line Graph Neural Network) encoding, which incorporates bond angles, to also include dihedral angles (ALIGNN-d). This simple extension leads to a memory-efficient graph representation that captures the complete geometry of atomic structures. ALIGNN-d is applied to predict the infrared optical response of dynamically disordered Cu(II) aqua complexes, leveraging the intrinsic interpretability to elucidate the relative contributions of individual structural components. Bond and dihedral angles are found to be critical contributors to the fine structure of the absorption response, with distortions that represent transitions between more common geometries exhibiting the strongest absorption intensity. Future directions for further development of ALIGNN-d are discussed.

Introduction

In materials science, graph neural networks (GNNs) have gained popularity as a surrogate model for learning properties of materials and molecular systems^1,2,3,4,5,6. This popularity is partly due to the intuitive, physically informed graph encoding that represents atoms with nodes and associated bonds with edges. However, beyond atom and bond features, encoding more sophisticated structural information can be helpful or even required for accurate prediction of certain properties. For example, the bond angle information is necessary for correctly capturing electronic structure and bond hybridization^7,8,9,10. Likewise, for the development of machine learning potentials where accurate energy prediction is needed, three-body (bond angle) and higher-order terms are often required to be included in the descriptor^11,12,13.

One practical scenario in which three- (bond angle) and four-body (dihedral angle) interactions can be critical is spectroscopy prediction. These interactions alter the local electronic structure in ways that are often detectable in X-ray and optical absorption experiments, as well as in local chemical probes, such as nuclear magnetic resonance. The power of these experimental techniques draws in part from their sensitivity to local geometric and electronic environments; however, spectral features are often convoluted and not always straightforward to interpret or predict. This is particularly true for disordered and distorted atomic environments, which are common to interfaces and glassy systems, where slight perturbations in geometry can greatly impact resulting properties^14,15,16,17.

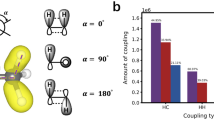
Unfortunately, conventional GNNs for atomic systems do not encode angular information. Recently, several approaches have been proposed to explicitly encode bond angles^18,19,20, or bond directions from which bond angles can be implicitly retrieved^21,22. Many of these were designed for non-periodic molecular structures. Alternatively, the ALIGNN approach²⁰, which explicitly represents bond angles as edges of line graphs, provides a general formulation that is applicable to both non-periodic molecular and periodic crystal graphs^4,23. However, despite its advantages, the ALIGNN encoding may not capture the full structural information of a local geometric environment. This limitation is demonstrated by the example shown in Fig. 1.

Fig. 1: The line graphs, shown as blue and red nodes and edges, encode angular information absent in the original atomic graph (black).

Red edges capture bond angles α, and blue edges capture dihedral angles ${\alpha }^{\prime}$ (defined as the clockwise angle in the Newman projection between two bonds sharing a common bond). Distinguishing these two configurations requires inclusion of the dihedral angle in the graph encoding.

In this work, we expand the ALIGNN encoding to include the dihedral angle information. This enhanced graph representation, named ALIGNN-d, provides not only more complete structural information and but also greater interpretability. To demonstrate these advantages, we train GNN models based on ALIGNN-d alongside competing graph representations to predict infrared optical absorption spectral signatures of Cu(II) aqua complexes. These complexes are optically active and known to have high absorption sensitivity to local geometry. Utilizing configurations derived from first-principles molecular dynamics simulations, we specifically probe the role of local distortion in the GNN encoding and resulting spectroscopic signatures. Based on the results, we identify two primary advantages of the ALIGNN-d representation: (1) ALIGNN-d is a compact description that leads to the same predictive accuracy as the maximally connected graph, in which all pairwise bonds are encoded, but with greater efficiency; and (2) ALIGNN-d enables an intuitive approach to model interpretability, thanks to the explicit graph representation of bond and dihedral angles.

Results

Optical response of Cu(II) aqua complexes

The capabilities of ALIGNN-d were demonstrated by predicting infrared optical absorption spectral signatures of Cu(II) aqua complexes. These systems are broadly representative of transition metal molecular complexes that absorb optically due to d-d transitions, which are leveraged in a variety of materials applications and biological processes²⁴. Configurations were obtained from ab-initio molecular dynamics simulations (AIMD), and optical transitions were calculated using time-dependent density functional theory (TDDFT), as described in the Methods section.

Beyond the practical implications, the high sensitivity of optical properties to the local geometry of the Cu(II) aqua complexes provides an appropriate test for ALIGNN-d. This can be seen in Fig. 2, which presents the optical transitions in the infrared regime computed from TDDFT for complexes with different instantaneous coordination numbers. In these complexes, the coordination number is found to fluctuate between four and six, with fivefold and sixfold coordination as the most and least common, respectively^24,25. The results clearly indicate that the infrared optical absorption is highly sensitive to the water coordination number, with little similarity between the spectral response of the sampled configurations. Moreover, complexes with the same coordination number and visibly similar atomic configurations shown in Fig. 2a, b can generate infrared absorption profiles with noticeably different peak locations and intensities, confirming that absorption in this frequency regime is also sensitive to subtle differences in the local bonding character. The physical origin of this behavior is connected to the fundamental nature of the d-d transitions, which are nominally symmetry forbidden in ideal structures but are activated by thermal distortions. We utilize these distortions and their spectral responses as our basis to test the benefits of ALIGNN-d. Further analysis of the correlation between geometry/shape information and spectral response can be found in Supplementary Information (Supplementary Fig. 1).

Fig. 2: Structures of the Cu(II) aqua complex from AIMD (figure insets) and their corresponding simulated optical transitions.

The central copper ion is surrounded by either (a, b) four, (c) five, or (d) six water molecules, with fivefold coordination being the most common. Slight structural perturbations (a, b) and changes in coordination (c, d) result in noticeably different shifts of the energies and intensities. The discrete spectral peaks were computed from time-dependent density functional theory (TDDFT) simulations.

Graph representations and prediction accuracy

We first introduce our workflow for encoding the molecular features and predicting the spectroscopic signatures. Summarised in Fig. 3, this involves converting the atomic structure of the Cu(II) aqua complexes into a graph representation, followed by predicting the key spectral features from GNNs. The specific outputs of this procedure are unnormalized Gaussian functions that approximate the absorption spectra of the complexes, parameterized by the mean peak position μ_G, spectral width σ_G, and intensity A_G.

Fig. 3: The structure-to-spectrum flow consists of conversion to graph representation, followed by spectroscopy prediction from GNN layers.

The different graph representations discussed in this work are shown schematically. Note that the edge distances in these visualizations do not reflect actual real space distances. The final output is a Gaussian curve parameterized by mean μ_G, standard deviation σ_G, and amplitude A_G, approximating the TDDFT-calculated discrete spectral peaks. This single-peak approximation is detailed in Supplementary Information (Supplementary Fig. 2).

As a key component of the workflow, we compare different graph representations for encoding the molecular structures. First, we consider the minimally connected graph ${{{{\rm{G}}}}}_{\min }$ that encodes only the minimal number of edges representing the nearest-neighbor atomic bonds. This graph contains the least structural information, as the bond angles and dihedral angles are not implicitly included. It can also be considered as the minimal spanning tree of the Cu(II) aqua complexes.

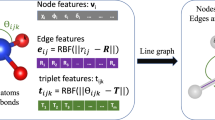
Second, at the opposite extreme, we consider the maximally connected graph ${{{{\rm{G}}}}}_{\max }$, which represents the brute-force approach that encodes all the pairwise bonds, thereby yielding complete geometric information¹⁹. Graph representations that lie between these two extremes are also considered. They are constructed using graphs defined by a specific cutoff radius, in which any pair of atoms within the cutoff distance are considered to be connected. Three values of the cutoff radius of 3, 4, and 5 Å are used, with corresponding graph representations denoted as G_c3, G_c4, and G_c5, respectively. Lastly, following the ALIGNN formulation, we incorporate angle information to ${{{{\rm{G}}}}}_{\min }$ by adding the corresponding line graph L(G), and we extend the ALIGNN formulation to explicitly represent both bond and dihedral angles in the line graph encoding, which is denoted as ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$. Since ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$ is no longer technically a line graph, it is alternatively called the dihedral graph.

ALIGNN and ALIGNN-d, alternatively expressed as ${{{{\rm{G}}}}}_{\min }\cup {{{\rm{L}}}}({{{{\rm{G}}}}}_{\min })$ and ${{{{\rm{G}}}}}_{\min }\cup {{{{\rm{L}}}}}^{\prime}({{{{\rm{G}}}}}_{\min })$, are expected to have improved representation power with respect to ${{{{\rm{G}}}}}_{\min }$. In fact, it is known that atomic numbers, bond lengths, bond angles, and dihedral angles together can fully describe the complete structure of a molecular system. This follows the principle of the Z-matrix²⁶, which has been shown to uniquely convert this set of quantities back to the exact atomic Cartesian coordinates. Whereas ALIGNN encodes atom, bond, and bond angle features, the addition of dihedral angle information (i.e., four-body terms) in ALIGNN-d completes the Z-matrix and is therefore capable of fully describing the atomic structure. As a result, any complex geometric feature, such as distortions, chirality, and disordered configurations, can be exactly represented without explicitly including higher-order terms. In other words, ALIGNN-d implicitly has the same representation power as ${{{{\rm{G}}}}}_{\max }$, despite its considerably smaller basis.

We proceed to compare the validation performance, inference speed, and storage memory requirement based on these graph representations. It is necessary to emphasize that model memory usage during training or at inference time depends on multiple factors, such as hardware implementation, choice of graph convolution, and hyperparameters (e.g., number of channels and convolution layers). Determining such memory usage would require an individual in-depth benchmark analysis; we instead choose to compare the number of edges that fundamentally characterizes the storage memory requirement of the graphs. We also note that inclusion of line/dihedral graphs does not technically introduce additional nodes, since the nodes of line/dihedral graphs are identical to the edges of the original graph.

As expected, the inclusion of auxiliary line/dihedral graphs improves the model performance. Shown in Fig. 4, this leads to significantly improved accuracy, i.e., lower loss, over the minimum baseline ${{{{\rm{G}}}}}_{\min }$. Importantly, the validation loss of ALIGNN and ALIGNN-d lie below the curve formed by the base graphs (Fig. 4a, b), suggesting that they are more expressive relative to normal graphs when constrained to the same compute speed or memory usage. In addition, ALIGNN-d performance is noticeably better than ALIGNN, yielding a similar accuracy as ${{{{\rm{G}}}}}_{\max }$ but with significantly lower inference time (27% less) and number of edges (33% fewer), which translates to more efficient memory usage. These comparisons collectively indicate that ALIGNN-d is capable of fully describing the atomic structure with significantly faster inference speed and less memory requirement compared to ${{{{\rm{G}}}}}_{\max }$. The in-training validation losses of ${{{{\rm{G}}}}}_{\max }$, ALIGNN, and ALIGNN-d are also shown in Fig. 4c, further confirming that ALIGNN-d yields similar performance as ${{{{\rm{G}}}}}_{\max }$, and is significantly better than ALIGNN.

Fig. 4: Comparison of validation loss for the graph representations studied in this work.

The validation loss, which is averaged over 8 repeated training sessions each with random initialization, is plotted with respect to a inference time, b average number of graph edges, and (c) in-training epochs. In a, the inference time is averaged over mini-batches of 64 random samples. In c, the ± 1 standard deviation of the validation loss from the repeated training sessions is shown as the semitransparent regions.

Aside from the minimal ALIGNN graph built on ${{{{\rm{G}}}}}_{\min }$, it is also informative to investigate ALIGNN representations on top of G_c3, G_c4, and G_c5 in comparison with ALIGNN-d. As expected, performance of ALIGNN generally improves when it is built on denser base graphs (Supplementary Figs. 3 and 4). However, the computational cost drastically increases to the extent that the inference compute speed is orders of magnitude higher than the original base graphs, rendering the “dense” versions of ALIGNN impractical. The same conclusion of course applies to ALIGNN-d. Nevertheless, we posit that there is no strong incentive to apply ALIGNN/ALIGNN-d to dense base graphs, as the “minimal” version of ALIGNN yields a significant performance improvement over ${{{{\rm{G}}}}}_{\min }$, and ALIGNN-d built on a minimal graph approaches the accuracy of ${{{{\rm{G}}}}}_{\max }$ while being much faster and more memory-efficient.

Finally, we validate the accuracy of the ALIGNN-d approach in predicting the infrared optical absorption spectra of the Cu(II) aqua complexes. Results presented in Fig. 5 show that our model provides accurate prediction of the mean μ_G and amplitude A_G of the optical spectra, while yielding reasonable results for the standard deviation σ_G. In addition, we include in Supplementary Information a set of randomly sampled predicted peaks versus their target peaks (Supplementary Fig. 3), from which it is clear that ALIGNN-d is capable of accurately predicting a wide variety of optical absorption spectral signatures.

Fig. 5: Parity plots of the ALIGNN-d predictions versus the explicitly computed optical absorption responses of different instantaneous configurations of the Cu(II) aqua complex.

The predicted and target Gaussian functions are parameterized by mean μ_G, amplitude A_G, and standard deviation σ_G. The R² score (coefficient of determination) is provided in each plot.

Discussion

Beyond efficiency and performance, ALIGNN-d can be utilized for model interpretability. Specifically, the final model output can be expressed as the sum of contributions from the individual graph components. In this way, relative contributions from the atoms, bonds, bond angles, and dihedral angles can be independently assessed. This is done by transforming the final embedding vectors (after the interaction layers shown in Fig. 3) of the atoms, bonds, and angles into non-negative scalars, which are then summed to a positive scalar final output.

We trained this interpretable variant of ALIGNN-d to predict the peak intensity A_G of the infrared optical absorption spectral response of Cu(II) aqua complexes. The component-wise decomposition allows the contributions of the atomic, bond, and angular features from the model output to be directly visualized in graph format. This is illustrated in Fig. 6 for a specific aqua complex configuration, where we find that the peak intensity of optical response is primarily attributed to the central copper atom and O-Cu-O bond angles, followed by certain dihedral angles and Cu-O bonds. Other components have negligible contributions to peak intensity (note the logarithmic scale of the colorbar). As the instantaneous configurations of the aqua complex deviate from the ideal symmetry due to thermal perturbations, the individual contributions, even within the same component type, are not always equivalent. For example, some Cu-O bonds have a higher contribution than others when analyzed for a single configuration prior to thermal averaging. This also applies to the bond angles and the dihedral angles, as shown for the instantaneous complex selected in Fig. 6.

Fig. 6: Graph visualization of the relative contributions of atomic, bond, bond angle, and dihedral angle components to spectral peak intensity for one fourfold-coordinated Cu(II) aqua configuration.

The largest contributions are derived from O-Cu-O bond angles and the central copper, followed by Cu-O bonds and certain dihedral angles. Color and line thickness indicate the magnitude of the relative contributions. For the visualizations of the bond and angle components, the atoms are faintly outlined.

This same component decomposition procedure was then applied to all configurations of the aqua complexes. The results, presented in Fig. 7, provide intuitive understanding of the physicochemical origins of the optical absorption response. As expected, the copper atoms feature high contribution relative to the oxygen and hydrogen atoms, consistent with the fact that changes in the copper’s d-shell electronic properties are largely responsible for the optical response. Nearby components that involve Cu atoms, including Cu-O bonds and O-Cu-O angles, also yield relatively higher contributions compared to others, such as water H-O-H angles. Overall, the O-Cu-O bond angles contribute significantly to the model output, consistent with physical intuition that the angular information is critical for informing electronic properties in transition metal complexes. This points to the need for explicitly incorporating angular features in the graph representation.

Fig. 7: Normalized contributions to the peak intensity from individual graph components (atoms, bonds, bond angles, and dihedral angles).

These contributions were obtained from the interpretable variant of ALIGNN-d.

It is shown that contributions from dihedral angles are generally less significant than the O-Cu-O bond angles, which is expected as they represent higher-order interactions. However, they remain relatively significant when compared to features such as the hydrogen atoms, the H-O bonds, and the H-O-H angles. We therefore conclude that contributions from dihedral angles are important for resolving subtle structural differences, including those that result from weak geometric perturbations. In the spectral response, the dihedral contributions can be critical for interpreting and reproducing the fine structure.

Additional information regarding the specific coupling between geometrical distortion and the infrared optical response can be obtained from further examination of the individual distributions in Fig. 7. Specifically, the Cu-O distance, the Cu-O-H angle, and the O-Cu-O angle distributions display some degree of multimodality, suggesting that there are classes of geometries that contribute much more significantly to the optical response. To illustrate this further, we show in Fig. 8a the relationship between peak intensity contribution and bond angle for the specific case of the O-Cu-O bond angle distribution. The Cu(II) aqua complex is known to prefer octahedrally derived geometries, which is also common behavior across a range of other transition metal coordination complexes. Ideally, such geometries should exhibit angles of 90^∘ and 180^∘. From Fig. 8a, we determine that configurations featuring these angles are minimal contributors to peak intensity. However, as the angles are even slightly perturbed (>90^∘ or <180^∘), the peak intensity rapidly climbs several orders of magnitude. This is consistent with the physical understanding of the nominally symmetry-forbidden d-to-d transitions that comprise the infrared optical response of the Cu(II) aqua complex, which require thermal distortion to remove the transition constraints.

Fig. 8: The Cu(II) aqua complexes that temporarily adopt new, uncommon symmetries may be critical contributors to the optical absorption in the infrared region.

This is supported by a the relationship between O-Cu-O bond angles explored by the aqua complex during AIMD and their contributions to the peak intensity; and b the distribution of closest-matching reference geometries based on the minimum CSM value, with AIMD snapshots illustrating the most commonly explored complexes. For this analysis, only fourfold- and fivefold-coordinated complexes are considered.

Interestingly, it can be seen that high contributions to peak intensity occur for bond angles in the 120^∘–140^∘ range. These angles are not merely minor distortions, but rather represent new symmetries that are not octahedrally derived and have a much lower overall probability. To obtain further insight, we examined the symmetries explored during the AIMD simulations using the continuous shape measure (CSM) metric. Briefly, CSM provides a mathematically rigorous way to quantify similarity to reference geometric structures, from which closest matches to ideal symmetries can be assessed. Fig. 8b shows the breakdown of instantaneous closest-matching CSM-derived geometries exhibited during our simulation trajectories, focusing on the fivefold- and fourfold-coordinated complexes that together represent the majority of all configurations. The CSM analysis confirms that the aqua complexes prefer to adopt the square- and pyramid-like configurations, which are octahedrally derived and dominated by 90^∘ and 180^∘ bond angles. The fourfold-coordinated complexes also feature the seesaw configuration, which is likewise octahedrally derived. However, a significant fraction of fivefold-coordinated complexes have the closest match to a trigonal bipyramid, which is geometrically distinct and features bond angles of 120^∘. These configurations are broadly reflective of the new symmetries in the 120^∘–140^∘ region that contribute strongly, with high certainty, to the optical response according to Fig. 8a. We therefore propose that aqua complexes that temporarily adopt new symmetries while actively transitioning from their most common geometries are critical contributors to the optical absorption in the infrared regime. In aqua complexes, such distortions occur occasionally due to thermal/solvent-induced fluctuations. However, one may imagine engineering local environments in frozen or glassy systems to bias these preferences and artificially enhance the frequency of optically responsive configurations.

In summary, our proposed graph representation ALIGNN-d represents a principled approach that efficiently captures the full geometric information of atomic structures. While the original ALIGNN paper²⁰ focuses on predictions of general properties for crystalline materials and small-scale molecules, the center of our work is instead on disordered and distorted systems. We also show the interpretability of the ALIGNN-d approach, which was applied to elucidate contributions of specific structural features of the Cu(II) aqua complexes to their infrared optical absorption spectral signatures.

It is worth mentioning that even though ALIGNN-d is memory-efficient for capturing full structural information, requiring only sparse base graphs, ALIGNN and ALIGNN-d yield less favorable scaling as the base graph becomes dense (Supplementary Fig. 3 and 4). In this regard, ALIGNN-d performance might be less superior for highly complex materials, where a large unit cell is needed to represent the systems and therefore a dense base graph is required. Future study is therefore needed to thoroughly determine the computational cost and scalability of ALIGNN and ALIGNN-d for other classes of material and molecular systems. We also point out that in contrast to paiNN²¹, ALIGNN-d does not incorporate directional information and therefore cannot be used to predict tensorial properties or direction-specific properties. However, ALIGNN-d and paiNN are not necessarily mutually exclusive formulations. An interesting direction for future study is to combine angular encoding (with line graphs) and equivariant directional encoding.

Finally, we point out that our framework is general and applicable to other materials systems and properties. For instance, it could accelerate material design and selection of metal complexation with controlled shift in optical absorption for targeted optical and filtering properties. It could facilitate analysis of other spectroscopic responses in complex, disordered materials, which feature signatures that are often convoluted and difficult to interpret. It could also reveal features in the fine structure of spectra that might otherwise be overlooked. However, we caution that not all physical properties can be manifested as a simple summation of the graph components formulated in this work. In this regard, more elaborate interpretation methods may elucidate contributions of other specific structural or chemical features, opening the door to a broader range of applications.

Methods

Data preparation

Solvated Cu²⁺ ion was modeled using an ion in a cubic supercell with 48 water molecules at the experimental density of liquid water at ambient conditions. We carried out Car-Parrinello molecular dynamics simulations using the Quantum ESPRESSO package²⁷, with interatomic forces derived from density functional theory (DFT) and the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional²⁸. The interaction between valence electrons and ionic cores was represented by ultrasoft pseudopotentials²⁹; we used a plane-wave basis set with energy cutoffs of 30 Ry and 300 Ry for the electronic wavefunction and charge density, respectively. All dynamics were run in the NVT ensemble at an elevated temperature of 380 K to correct for the overstructuring of liquid water at ambient temperatures with the PBE functional³⁰. A time step of 8 a.u. were employed with an effective mass of 500 a.u. with hydrogen substituted with deuterium. The water was first equilibrated for 10 ps before the Cu²⁺ ion was inserted into the system, after which the system was equilibrated for another 10 ps. This was followed by a 40 ps production run to extract the time-averaged properties of the system.

Time dependent density functional theory (TDDFT)³¹ within the Tamm-Dancoff approximation³² was used to obtain the optical excitation energies of the ion complexes. Specifically, 6,846 aqua complexes were extracted roughly uniformly from the AIMD trajectory. Each complex consists of the copper ion and the surrounding water molecules within a radial cutoff of 2.92 Å, which corresponds to the first minimum of the Cu-O partial radial distribution function for the Cu²⁺ oxidation state. All the optical calculations were carried out using the NWChem software package³³. Here, an augmented cc-pVTZ basis was used for the copper ion while an augmented cc-pVDZ basis was used for the water molecules. Four examples of the aqua complexes and their corresponding TDDFT-calculated peaks in roughly the visible-infrared range are shown in Fig. 2. The aqua complexes data was randomly partitioned into a training set of 6,161 samples and a validation set of 685 samples.

To assist with the large number of copper complexes being studied, an AiiDA³⁴ workflow was employed to standardize and provide consistency for all calculations. AiiDA records full provenance between all calculations and ensures a robust framework for generating, storing, and analyzing results.

For GNN spectroscopy prediction, we focus on the TDDFT-calculated spectral peaks roughly in the visible-infrared range. Since the peak positions per complex tend to be close together, we approximated each complex’s discrete peaks into a single unnormalized Gaussian curve. This approximation helps simplify the output format for training a structure-to-spectrum GNN model. For example, the original spectral peaks from TDDFT may be described by a set of tuples (E₁, I₁), (E₂, I₂), . . . , where E is the peak energy, and I is the peak intensity. After the approximation, we can simply describe the spectral signature with an unnormalized Gaussian, parametrized by the mean μ_G, the standard deviation σ_G, and the amplitude A_G. The single-peak approximation is further explained in Supplementary Information.

The continuous shape measure (CSM) provides a mathematically rigorous, normalized measure of the deviation of a molecular fragment geometry from an ideal reference polyhedron. As a similarity metric, CSM is bounded between 0 and 100. Low CSM value indicates high similarity to the reference shape symmetry, and thus to a highly symmetric arrangement of water molecules around the copper ion. The CSM was computed using the SHAPE code³⁵ for the entire standard set of polyhedral reference geometries for four- and five- coordination numbers.

ALIGNN-d representation

With the ALIGNN and ALIGNN-d formulation, two graphs are used to encode one atomic structure: an original atomic graph G and its corresponding line graph L(G) or dihedral graph ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$. The nodes and edges in G represent atoms and bonds, respectively. The nodes and edges in L(G) or ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$, on the other hand, represent bonds and angles, respectively. Note that the edges in G and the nodes in L(G) or ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$ are identical entities and share the same embedding during GNN operation. Different from the original ALIGNN paper, we encoded the atomic, bond, and angular features with only the minimally required information, namely the atom type z, the bond distance d, the bond angle α, and the dihedral angle ${\alpha }^{\prime}$. In other words, in G, each node corresponds to a value of z, and each edge corresponds to a value of d. In L(G), each node also corresponds to a value of d, and each edge corresponds to a value of α. Finally, in ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$, each edge representing a dihedral angle corresponds to a value of ${\alpha }^{\prime}$. Information such as electronegativity, group number, bond type, and so on are not encoded.

We used Atomic Simulation Environment³⁶ and PyTorch Geometric³⁷ to construct the graph representations, and to calculate bond and dihedral angles.

Model architectures

Two different GNN model architectures were defined: one for the base graphs (${{{{\rm{G}}}}}_{\min }$, G_c3, G_c4, G_c5, and ${{{{\rm{G}}}}}_{\max }$); and one for ALIGNN and ALIGNN-d. We kept the two architectures as identical as we could in order to fairly evaluate and compare the model performances as a function of input graph representation. Both architectures consist of three parts: the initial encoding, the interaction operations, and the output layers (Fig. 3).

In the initial encoding, the atom type, the bond distance, and the angular values are converted from scalars to feature vectors for subsequent neural network operations. The atom type z is transformed by an Embedding layer (see PyTorch documentation³⁸). The bond distance d is expanded into the Radial Bessel basis proposed by Klicpera et al.¹⁹. The angles α and ${\alpha }^{\prime}$ are expanded into the Gaussian basis implemented by Schnet³. However, the angular encoding treats bond angles α and dihedral angles ${\alpha }^{\prime}$ differently, and encodes their values at different channels of the expanded feature vector. Further details regarding the angular encoding are described in Supplementary Information.

The interaction operations are also known as graph convolution, aggregation, or message-passing. Following the ALIGNN paper²⁰, we also adopted the edge-gated graph convolution^39,40 for the interaction operations. The node features ${{{{\bf{h}}}}}_{i}^{l+1}$ of node i at the (l + 1)th layer is updated as

$${{{{\bf{h}}}}}_{i}^{l+1}={{{{\bf{h}}}}}_{i}^{l}+{{{\rm{SiLU}}}}\left({{{\rm{LayerNorm}}}}\left({{{{\bf{W}}}}}_{s}^{l}{{{{\bf{h}}}}}_{i}^{l}+\mathop{\sum}\limits_{j\in N(i)}{\hat{{{{\bf{e}}}}}}_{ij}^{l}\odot {{{{\bf{W}}}}}_{d}^{l}{{{{\bf{h}}}}}_{j}^{l}\right)\right),$$

(1)

where SiLU is the Sigmoid Linear Unit activation function⁴¹; LayerNorm is the Layer Normalization operation⁴²; W_s and W_d are weight matrices; the index j denotes the neighbor node of node i; ${\hat{{{{\bf{e}}}}}}_{ij}$ is the edge gate vector for the edge from node i to node j; and ⊙ denotes element-wise multiplication. The edge gate ${\hat{{{{\bf{e}}}}}}_{ij}^{l}$ at the lth layer is defined as

$${\hat{{{{\bf{e}}}}}}_{ij}^{l}=\frac{\sigma ({{{{\bf{e}}}}}_{ij}^{l})}{{\sum }_{{j}^{\prime}\in N(i)}\sigma ({{{{\bf{e}}}}}_{i{j}^{\prime}}^{l})+\epsilon },$$

(2)

where σ is the sigmoid function, ${{{{\bf{e}}}}}_{ij}^{l}$ is the edge feature at the lth layer, and ϵ is a small constant for numerical stability. The edge features ${{{{\bf{e}}}}}_{ij}^{l}$ is updated by

$${{{{\bf{e}}}}}_{ij}^{l+1}={{{{\bf{e}}}}}_{ij}^{l}+{{{\rm{SiLU}}}}\left({{{\rm{LayerNorm}}}}\left({{{{\bf{W}}}}}_{g}^{l}{{{{\bf{z}}}}}_{ij}^{l}\right)\right),$$

(3)

where W_g is a weight matrix, and z_ij is the concatenated vector from the node features h_i, h_j, and the edge features e_ij:

$${{{{\bf{z}}}}}_{ij}={{{{\bf{h}}}}}_{i}\oplus {{{{\bf{h}}}}}_{j}\oplus {{{{\bf{e}}}}}_{ij}.$$

(4)

We applied the same edge-gated convolution scheme (Eq. (1)–(3)) to operate on both the atomic graph G and the line/dihedral graphs L(G), ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$. In the case of G, the edge-gated convolution updates nodes that represent atoms, and edges that represent bonds, while exchanging information between the two, hence the term atom-bond interaction shown in Fig. 3. In the case of L(G) and ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$, the convolution updates nodes that represent bonds, and edges that represent angles, hence the term bond-angle interaction shown in Fig. 3. Note that by iteratively applying the convolution operation on both the original graph and the line/dihedral graph, the angular information stored in L(G) or ${{{\rm{{L}}}^{\prime}\rm{(G)}}}$ can propagate to G. Due to the nature of the edge-gated convolution, all the feature/embedding vectors for atoms, bonds, and angles during the interaction layers have the same length, or the same number of channels D.

Lastly, the final output layers pool (by summation) the node features of G and transform the pooled embedding into an output vector, which is a three-dimentional vector consisted of the parameters of an unnormalized Gaussian curve μ_G, σ_G, and A_G. The two Linear layers have the output lengths of 64 and 3, respectively. For the interpretable variant of the model, the final output layers are replaced by a Linear layer transforming the input vectors into scalars, followed by the softplus activation $\log (1+\exp (\cdot ))$ and global summation. This operation effectively transforms each embedding vector into a non-negative scalar before summing all the scalars into a positive scalar final output. Therefore, these component scalars can be interpreted as the atomic, bond, and angular contributions to the final output.

The model parameters for both architectures in Fig. 3 are the same, and listed in Table 1.

Table 1 Model parameters.

Model training

We used PyTorch Geometric³⁷ to develop the GNN models. Note that although two model architectures were defined, a total of seven GNN models were trained due to the seven different graph representations studied in this work. Nonetheless, these models have the same parameters (Table 1). Similar to the ALIGNN paper²⁰, we trained each model using the Adam optimizer⁴³ and the 1cycle scheduler⁴⁴. Each training was carried out in PyTorch³⁸ and PyTorch Geometric³⁷ on a NVIDIA V100 (Volta) GPU, and repeated eight times with randomly initialized weights for statistical robustness. The mean squared error (MSE) was used as the loss during training. The training parameters are the same for each training session (Table 2). All other parameters, if unspecified in this work, default to values per PyTorch 1.8.1 and PyTorch Geometric 1.7.2.

Table 2 Training parameters.