Modeling and simulation of microstructure in metallic systems based on multi-physics approaches

Abstract

The complex interplay between chemistry, microstructure, and behavior of many engineering materials has been investigated predominantly by experimental methods. Parallel to the increase in computer power, advances in computational modeling methods have resulted in a level of sophistication which is comparable to that of experiments. At the continuum level, one class of such models is based on continuum thermodynamics, phase-field methods, and crystal plasticity, facilitating the account of multiple physical mechanisms (multi-physics) and their interaction during microstructure evolution. This paper reviews the status of simulation approaches and software packages in this field and gives an outlook towards promising research directions.

Introduction

The diversity and complexity of materials and their behavior are rooted in the complex, generally nonlinear interplay between microstructural features such as voids, cracks, phases, grains, dislocations, and local chemical composition with each other and with environmental conditions. Designing improved materials requires an in-depth understanding of several intertwined metastable configurations and intertwined, hierarchical and self-organized networks of defects that influence each other through various interactions across multiple lengths- and timescales¹. The interplay of chemistry and mechanical failure, for example, is important for the longevity of rechargeable batteries^2,3; microscopic cracks which form over time as the electrodes are mechanically deformed during load cycles result in electrical disconnections and loss of capacity. There are numerous other examples where inelastic deformation features and damage are initiated or accelerated due to harsh environmental conditions such as hydrogen embrittlement⁴, stress corrosion cracking⁵, and radiation-inflicted damage⁶. Ni-based superalloys are another example where carefully tuned chemical composition and processing results in a complex microstructure which ultimately gives rise to the high performance of these alloys at elevated temperatures⁷. The number of microstructural and compositional parameters, processes, and configurations to combine to invent a new material is enormous. A complex system (either in terms of composition or microstructure) has a higher potential for exhibiting interesting, unusual, and surprising behavior compared to a simple system. This trend is observed in generations of alloys, where typically the number of alloying elements has increased in the quest to improve material properties and behavior. Most of the current technologically important materials have therefore complex chemical compositions and carefully designed microstructures, however, often with high costs for expensive alloy ingredients and reduced compatibility when subject to recycling. Superalloys⁸, modern Al alloys⁹, and semiconductors¹⁰, are examples of such systems. Improved models that consider both composition and microstructure can be employed to investigate the trade-off between these in the optimization of material properties. This opens up a theory-based design pathway into a competition between the exploitation of conserved parameters (e.g. composition) vs. non-conserved parameters (e.g. microstructure) for optimal materials, process, and performance design. Note that although the spatial distribution of composition, depending on lengthscale, can be regarded as a type of microstructure, in this work, the microstructure is defined as structural variations at small scales. These are often in form of configurational defects in the solid structure and therefore, non-conservative. Multi-scale and multi-physics phenomena are not limited to microscopic and macroscopic lengthscales. The deformation behavior of planetary crusts¹¹ or that of polar ice caps leading to calving^12,13 are specific examples of much larger-scale material behavior where multiple physical processes and lengthscales come together.

In past ages, material design and discovery have relied on trial and error methods. With the advent of the scientific method, however, such discovery has been based increasingly on hypothesis-guided experimentation. Due to the inherent complexity of the task and the vast configuration space, as well as experimental and real-world limitations, however, material design and discovery based on experiments alone is extremely difficult and time-consuming. This is one reason why computational approaches have become an important tool in material science and engineering^14,15,16. Many quantities that are inherently or technologically not measurable in experiments are possible to track and investigate in simulations. In this review, we mostly focus on approaches to model solid materials, in particular metallic systems. In this case, several modeling approaches and simulation packages exist, based on a number of different physical models and mathematical methods that have been proposed to describe these phenomena. Multi-physics approaches in these systems typically involve mechanical deformation, phase transformations, thermal and compositional fluctuations, and solid-state chemical reactions. Crystal plasticity^17,18 for modeling inelastic deformation at mesoscopic lengthscales, phase-field (PF) modeling for spatially-resolved moving boundary problems¹⁹, the Cahn–Hilliard model for component diffusion and spinodal decomposition phenomena^20,21, as well as CALPHAD^22,23 for equilibrium thermodynamic phase diagram calculations are prominent examples of models and computational means for simulation of different phenomena involving microstructure and chemistry. A recent review of multi-scale methods in material science both in terms of historical development and current status can be found in ref. ²⁴. More topic-specific reviews on multi-scale and multi-physics material modeling and simulation are available, for example on additive manufacturing²⁵ or microstructure-property relationships in metals²⁶.

In addition to modeling and simulation, the development of analytical methods based on statistics, machine learning, material information theory (informatics), data science, and artificial intelligence, is providing tools for the investigation and elucidation of very large sets of complex empirical data and simulation results for material systems. Such methods offer unparalleled computational efficiency in navigating and exploring complex material property landscapes^27,28. A particular attractive area of application for such methods is material science, given the extremely large sets of experimental data or simulation results generated for example via microscopy or molecular dynamics. These developments are touched on only briefly at the end of the current review; for a very recent comprehensive treatment of these in the physical sciences, the interested reader is referred to ref. ²⁹.

The ever-increasing computational resources and the development of advanced physical models and numerical algorithms make multi-physics modeling a rapidly growing topic. At the same time, improved experimental techniques make it possible to benchmark the models. The purpose of this review is to concisely present and summarize recent advancements in continuum-based multi-physics and multi-scale modeling and simulation techniques. Figure 1 provides an overview of basic aspects of the modeling of materials with microstructure. In this review, a model is considered multi-physical if it couples at least two different fields representing two different physical phenomena. Although the multi-scale paradigm is most obvious in methods such as direct atomistic-continuum coupling³⁰, FEM²³¹, or FEM-FFT³², scale-bridging is also realized in atomistically-informed continuum models. In such models, the data from small-scale simulations is transferred and employed on a larger scale. The models discussed in the current review are often calibrated by atomistic data and employed for simulation at much larger lengthscales. Despite a large number of proposed models, only a few of them find further use outside of their developer community. Thus, one goal of this review is to explore possibilities for more sustainable and accessible software development that facilitates collaborative use and successive improvement. This is analogous to other fields of open-source software development, such as the widely used community codes for molecular dynamics and density functional theory. The increased computational power, availability of numerous open-source software packages, as well as emergence of data-driven approaches, has led to many research groups employing multi-physics and multi-scale methods for material simulations. Therefore, the current review is beneficial for the community as a summary of important aspects of such methods to note either as a developer or as a user.

Fig. 1: Multi-scale, multi-physics aspects of material modeling and simulation.

a–c Fracture and dislocation activity at the crack tip and triple junction during loading are depicted at the atomic scale (a), the single grain scale (b), and polygrain scale (c). (d) Abstract visualization of microstructure-composition-property space at these scales. (e) Schematic of simulation scale versus the number of parameters involved based on ideas in ref. ²³⁸. The complexity of microstructure-composition-property relationships at different scales poses a tremendous challenge to determining optimal material design and discovering new materials.

The current work begins with a summary of the theoretical framework for the formulation of multi-physics models and a detailed example of the formulation of such a model. This is followed by an overview of software packages based on such models as well as a short discussion of selected technical aspects related to these. Then examples of multi-physics integration in several applications are presented. The review ends with a summary of emerging and ongoing work related to machine learning, data-driven models, and statistics.

Theoretical framework and formulation of models

General considerations and background

The purpose of this section is a brief overview of the theoretical basis for, and approaches to, the formulation of models upon which the modeling and simulation of microstructure evolution and the resulting material behavior in selected engineering materials is based. Examples of the latter include structural (e.g., lightweight metallic alloys), functional (e.g., ferroelectric, ferromagnetic ceramics), energy (i.e., battery materials), high-temperature (e.g., Ni superalloys), and reactive (e.g., oxidation, reduction) materials. Such materials are generally metallic or ceramic in character. The corresponding microstructure consists of phases, grains, grain boundaries, defects (vacancies, voids, dislocations, interfaces, cracks), and so on. Even restricted to these materials, the relevant literature on theory, methods, and models is vast, and one cannot possibly hope to do justice to it in a short review. For a modicum of completeness, consider a few selected relevant approaches and models not treated here. These include for example atomistic computational models for multiphase, multicomponent systems such as (non-kinetic) hybrid Monte Carlo molecular dynamics (e.g., ref. ³³) or (kinetic) diffusive molecular dynamics (e.g., refs. ^34,35,36,37). Likewise neglected in this review is the formulation of continuum balance relations and flux constitutive relations via ensemble and spatial averaging of microstructure dynamics (e.g., refs. ^{38,39,40,41,42,43,44,45,46,47,48,49}). Not considered as well are models for heterogeneous media with random microstructure based on statistics, stochastics, and averaging (e.g., refs. ^50,51), or more generally those based on micromechanics and homogenization theory (e.g., refs. ^52,53,54,55). The latter theory is also employed to formulate relevant models for generalized or extended continua with microstructure micromorphic:⁵⁶; see also for example refs. ^57,58. Another approach to formulate such models is based on a generalization of continuum mechanics to higher-order continua with additional kinematic (i.e., microstructural) degrees of freedom (e.g.,^59,60,61,62). This approach has been applied to materials as diverse as liquid crystals, polymers (e.g., ref. ⁶³), or polar ice (e.g., ref. ⁶⁴).

The recent literature offers several comprehensive reviews of topics related to those addressed in the current work. These include the multi-scale modeling and simulation of interfaces, dislocations, and dislocation field plasticity treated in detail in ref. ⁶⁵. Likewise, as mentioned above,²⁴ discusses recent developments in multi-scale modeling and simulation, in particular, based on high-performance computing and machine learning. The current treatment is restricted to continuum models for microstructure evolution and material behavior formulated in the framework of continuum thermodynamics (e.g., refs. ^66,67,68,69), internal variable theory (e.g., refs. ^70,71), material theory (e.g., refs. ^68,72), and PF methods (e.g., refs. ^19,73). Models formulated in the thermodynamic framework are by definition thermodynamically consistent (e.g., satisfy the dissipation principle identically). This is important in formulating multi-physics models in order to avoid hidden inconsistencies (e.g., negative entropy production). Such inconsistencies could arise for example when relations (e.g., partial differential equations) from different models are coupled together in a fashion independent from the rest of the model formulation, something which could lead to nonphysical results.

In the case of PF methods, the literature offers a number of comprehensive reviews^{74,75,76,77,78,79,80}, including their application to finite-deformation interface mechanics in crystalline solids⁸¹ and to material discovery⁸². Historically, the PF approach is generally considered to have originated in work aimed at extending the thermodynamics of spatially-uniform (bulk) systems to spatial non-uniformity; seminal works to this end include for example van der Waals (1893) (see ref. ⁸³), Cahn and Hilliard (CH)²⁰, Landau⁸⁴, and Allen and Cahn (AC)⁸⁵. In the context of classic density functional theory (CDFT: e.g., ref. ⁸⁶), these early PF models are all weakly non-local. This is in contrast to strongly non-local models formulated via the CDFT of freezing^87,88, atomic density field theory (ADFT: e.g., refs. ^73,89), or PF crystal (PFC: e.g., refs. ^78,90,91). A number of (higher-order) weakly non-local approximations of PFC have also been developed (see for example ref. ⁹²). For more details on ADFT and PFC, the interested reader is referred to⁸⁰. In more recent times, weakly non-local PF-based models have also been formulated via non-CDFT-based approaches (e.g., Clausius–Duhem thermodynamics:^93,94,95).

Generally speaking, PFs and their evolution mediate transitions between thermodynamic states of a system determined by coupled and (energetically, kinetically) competing physical mechanisms. The PFs in ADFT or PFC for example take the form of atomic density fields which are naturally lattice-periodic. In contrast, PFs in microscopic PF models are represented by non-atomic, lattice fields (e.g., lattice disregistry) whose transition regions represent defects such as dislocation cores or interfaces. A prominent example here is PF microelasticity (PFM: e.g., refs. ^96,97,98). Another example of PFs is represented by symmetry-adapted (e.g., strain-based) structural (non-conservative) order parameters (e.g., refs. ^{99,100,101,102}).

In microscopic PF models, there is no scale separation between the gradient energy (internal, material) and system (external) lengthscales. In contrast, these lengthscales are scale-separated in mesoscopic PF models. In this latter case, the gradient energy is physically well-approximated by its sharp-interface (limit) value²⁰. Furthermore, the gradient energy lengthscale loses any physical meaning in the mesoscopic context, in which case it can be employed as a mathematical convergence parameter (e.g., sharp-interface limit^103,104, Γ-convergence¹⁰⁵) and as a numerical regularization parameter (e.g., ref. ¹⁰⁶) for more robust numerical convergence behavior.

Example of multi-physics-based thermodynamic model formulation

In the thermodynamic context, accounting for multiple physical mechanisms (multi-physics) and their (energetic, kinetic) competition or interaction with each other during processes resulting in microstructure evolution is completely natural. Models for materials with continuum microstructure formulated in this context can be classified in particular as being non-isothermal or isothermal. For example, dynamic processes involving in particular melting or solidification and heat transport (e.g., laser-heating- or powder-fusion-based additive manufacturing:^107,108) are clearly non-isothermal. As discussed in more detail below, the (physically) more general non-isothermal case is based on the free entropy (e.g., refs. ^109,110,111). Under certain assumptions (e.g., gradient-free entropy independent of temperature:¹¹²), this more general formulation reduces naturally to one based on the free energy. The majority of multi-physics models for materials with continuum microstructure in the literature are restricted to isothermal conditions, and in the case of elastic behavior, to geometric and physical linearity. In this case, temperature parameterizes energetic and kinetic properties and processes. A prime example here is the pioneering work of Khachaturyan⁷³ on the energetic coupling of elasticity and chemistry to model multicomponent, multiphase crystalline solids.

As a concrete example of the formulation of a multi-physics model, the case of a multicomponent, multiphase, solid mixture with mass exchange (e.g., due to chemical reactions) is considered here. For simplicity, memory and fluctuation effects are neglected, and local thermodynamic equilibrium is assumed (e.g., refs. ^66,68). In addition, attention is restricted to thermochemoelastic solid behavior. Rate-dependent gradient inelasticity (i.e., slip, damage, fracture) can also be formulated in a (non-conservative) PF setting (e.g., refs. ^{113,114,115,116,117,118}); again for simplicity, this is neglected here. Not treated as well, for this reason, is the case of functional materials and processes (e.g., ref. ¹¹⁹), or charged chemical components (e.g., ref. ¹²⁰). Instead, attention is focused on non-isothermal model formulation and its specialization to the isothermal case. Further details on the former are given for example in ref. ¹¹²; more comprehensive treatment of the latter, including non-equilibrium chemo-mechanical interface modeling, can be found for example in ref. ¹²¹.

Consider a non-isothermal mixture of n_c chemical components and n_p solid phases. Neglecting any supplies of momentum, energy, or entropy for simplicity, the balance relations

$${\dot{\varrho }}_{a}=-{{{\rm{div}}}}{{{{\bf{j}}}}}_{a}+{\sigma }_{a}\,,\quad \varrho \ddot{{{{\boldsymbol{\chi }}}}}={{{\rm{div}}}}{{{\bf{P}}}}\,,\quad \dot{\varepsilon }={{{\bf{P}}}}\cdot \nabla \dot{{{{\boldsymbol{\chi }}}}}-{{{\rm{div}}}}{{{\bf{q}}}}\,,\quad \dot{\eta }=\pi -{{{\rm{div}}}}{{{\bf{h}}}}\,,$$

(1)

(e.g., refs. ^66,68) hold for the mass of component a = 1, …, n_c, linear momentum, internal energy, and entropy, respectively. Here, ϱ_a, j_a and σ_a represent the densities of mass, mass flux, and mass supply-rate, respectively, of component a. Mixture fields include the motion χ, as well as the densities of mass $\varrho =\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\varrho }_{a}$, momentum flux P (i.e., first Piola–Kirchhoff stress), internal energy ε, heat flux q, entropy η, entropy flux h, and entropy production-rate π. In the context of (1), the corresponding form

$$\pi -{{{\rm{div}}}}{{{\bf{h}}}}=\dot{\eta }+\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\kappa }_{a}({\dot{\varrho }}_{a}+{{{\rm{div}}}}{{{{\bf{j}}}}}_{a}-{\sigma }_{a})-{\theta }^{-1}(\dot{\varepsilon }+{{{\rm{div}}}}{{{\bf{q}}}}-{{{\bf{P}}}}\cdot \nabla \dot{{{{\boldsymbol{\chi }}}}})\,,$$

(2)

for the generalized Gibbs relation (e.g., refs. ^66,68,122) is central to the formulation of thermodynamically consistent constitutive relations. Here, κ_a is the component entropic chemical potential (having units of entropy per unit mass, i.e. JK⁻¹ Kg⁻¹ in SI), and θ the mixture absolute temperature.

For inhomogeneous thermochemoelastic behavior, the constitutive forms

$$\varepsilon =\varepsilon (\theta ,\nabla {{{\boldsymbol{\chi }}}},{{{{\bf{F}}}}}_{{{{\rm{R}}}}},{{{\mathbf{\varrho }}}},\nabla {{{\mathbf{\varrho }}}},{{{\boldsymbol{\phi }}}},\nabla {{{\boldsymbol{\phi }}}})\,,\quad \eta =\eta (\theta ,\nabla {{{\boldsymbol{\chi }}}},{{{{\bf{F}}}}}_{{{{\rm{R}}}}},{{{\mathbf{\varrho }}}},\nabla {{{\mathbf{\varrho }}}},{{{\boldsymbol{\phi }}}},\nabla {{{\boldsymbol{\phi }}}})\,,$$

(3)

hold for the internal energy and entropy densities, respectively, with ${{{\mathbf{\varrho }}}}:= ({\varrho }_{1},\ldots ,{\varrho }_{{n}_{{{{\rm{c}}}}}})$ and ${{{\boldsymbol{\phi }}}}:= ({\phi }_{1},\ldots ,{\phi }_{{n}_{{{{\rm{p}}}}}})$, where ϕ_α represent the (structural) order parameter associated with phase α = 1, …, n_p. To model for example anisotropic interface energy and faceting (e.g., refs. ^123,124), or lower-symmetry crystalline systems (e.g., ref. ¹²⁵), ε and η would depend on even higher-order gradients of ϱ and ϕ (again for simplicity, such possibilities are neglected here). In particular, (3) determine in turn the thermochemoelastic (dependent) constitutive relations

$${\partial }_{\theta }\varepsilon =\theta \,{\partial }_{\theta }\eta \,,\quad {{{\bf{P}}}}={\partial }_{\nabla {{{\boldsymbol{\chi }}}}}\varepsilon -\theta \,{\partial }_{\nabla {{{\boldsymbol{\chi }}}}}\eta \,,$$

(4)

for the absolute temperature and stress, respectively. The residual local deformation F_R (dimensionless) is due to microstructure evolution resulting in stress relaxation. It represents a geometrically nonlinear generalization of the stress-free strain⁷³ and (elastic) energy reduction. The geometrically exact kinematic constitutive form

$${\dot{{{{\bf{F}}}}}}_{{{{\rm{R}}}}}={{{{\bf{L}}}}}_{{{{\rm{R}}}}}{{{{\bf{F}}}}}_{{{{\rm{R}}}}}\,,\quad {{{{\bf{L}}}}}_{{{{\rm{R}}}}}=\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\dot{\varrho }}_{a}{{{{\bf{N}}}}}_{{{{\boldsymbol{\varrho }}}}a}+\mathop{\sum }\nolimits_{\alpha = 1}^{{n}_{{{{\rm{p}}}}}}{\dot{\phi }}_{\alpha }{{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\alpha }\,,$$

(5)

for the evolution of F_R depends on that of ϱ and ϕ, mediated by the material properties N_ϱ a (having units of volume per unit mass, i.e., m³ kg⁻¹ in SI) and N_ϕ α (dimensionless). Alternative to (5) is the split F_R = F_CF_S with ${\dot{{{{\bf{F}}}}}}_{{{{\rm{C}}}}}=\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\dot{\varrho }}_{a}{{{{\bf{N}}}}}_{{{{\boldsymbol{\varrho }}}}a}\,{{{{\bf{F}}}}}_{{{{\rm{C}}}}}$ and ${\dot{{{{\bf{F}}}}}}_{{{{\rm{S}}}}}=\mathop{\sum }\nolimits_{\alpha = 1}^{{n}_{{{{\rm{p}}}}}}{\dot{\phi }}_{\alpha }{{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\alpha }\,{{{{\bf{F}}}}}_{{{{\rm{S}}}}}$. Given (2)–(5), one obtains the forms

$$\begin{array}{lll}\pi =-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{{{{\bf{j}}}}}_{a}\cdot \nabla {\kappa }_{a}-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\sigma }_{a}\,{\kappa }_{a}-{\theta }^{-2}{{{\bf{q}}}}\cdot \nabla \theta -\mathop{\sum }\nolimits_{\alpha = 1}^{{n}_{{{{\rm{p}}}}}}{\dot{\phi }}_{\alpha }\,[{\delta }_{{\phi }_{\alpha }}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\alpha }]\,,\\ {{{\bf{h}}}}={\theta }^{-1}{{{\bf{q}}}}-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\kappa }_{a}{{{{\bf{j}}}}}_{a}+\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\dot{\varrho }}_{a}\,{\partial }_{\nabla {\varrho }_{a}}\varphi +\mathop{\sum }\nolimits_{\alpha = 1}^{{n}_{{{{\rm{p}}}}}}{\dot{\phi }}_{\alpha }\,{\partial }_{\nabla {\phi }_{\alpha }}\varphi \,,\end{array}$$

(6)

for the entropy production-rate density and entropy flux density (e.g., ref. ¹²⁶), respectively, via the generalized Cahn–Hilliard (CH) form

$${\kappa }_{a}={\delta }_{{\varrho }_{a}}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\mathbf{\varrho }}}}a}\,,\quad {\delta }_{{\varrho }_{a}}\varphi := {\partial }_{{\varrho }_{a}}\varphi -{{{\rm{div}}}}{\partial }_{\nabla {\varrho }_{a}}\varphi \,,$$

(7)

for the entropic chemical potential in the case of inhomogeneous thermochemoelasticity. Here, φ is the negative free entropy density, i.e.,

$$\varphi := {\theta }^{-1}\psi ={\theta }^{-1}\varepsilon -\eta \,,\quad \psi := \varepsilon -\theta \eta \,,$$

(8)

with ψ the free energy density. Note that (6)₂ reduces to its homogeneous form ${{{\bf{h}}}}={\theta }^{-1}{{{\bf{q}}}}-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\kappa }_{a}{{{{\bf{j}}}}}_{a}$ (e.g., ref. ⁶⁶) when the generalized no-flux boundary conditions

$$\begin{array}{l}{\dot{\varrho }}_{a}\,{\partial }_{\nabla {\varrho }_{a}}\varepsilon \cdot {{{\bf{n}}}}=0\,,{\dot{\varrho }}_{a}\,{\partial }_{\nabla {\varrho }_{a}}\eta \cdot {{{\bf{n}}}}=0\,,a=1,\ldots ,{n}_{{{{\rm{c}}}}}\,,\\ {\dot{\phi }}_{\alpha }\,{\partial }_{\nabla {\phi }_{\alpha }}\varepsilon \cdot {{{\bf{n}}}}=0\,,{\dot{\phi }}_{\alpha }\,{\partial }_{\nabla {\phi }_{\alpha }}\eta \cdot {{{\bf{n}}}}=0\,,\alpha =1,\ldots ,{n}_{{{{\rm{p}}}}}\,,\end{array}$$

(9)

are assumed on the boundary of any (referential) mixture region with (outward) unit normal n. These are relevant to purely bulk (i.e., system-size independent: e.g., ref. ²⁰) inhomogeneous behavior. From the residual form (6)₁ of π, one obtains the thermodynamic flux-force relations

$$\begin{array}{lll}{{{{\bf{j}}}}}_{a}=-\mathop{\sum }\limits_{b = 1}^{{n}_{{{{\rm{c}}}}}}\theta \,{{{{\bf{M}}}}}_{ab}\nabla {\kappa }_{b}\,,\\ {\sigma }_{a}=-\mathop{\sum }\limits_{b = 1}^{{n}_{{{{\rm{c}}}}}}\theta \,{k}_{ab}\,{\kappa }_{b}\,,\\ {{{\bf{q}}}}=\,-\,{{{\bf{K}}}}\nabla \theta \,,\\ {\dot{\phi }}_{\alpha }=-\mathop{\sum }\limits_{\beta = 1}^{{n}_{{{{\rm{p}}}}}}\theta \,{m}_{\alpha \beta }\,[{\delta }_{{\phi }_{\beta }}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\beta }]\,,\end{array}$$

(10)

in terms of the thermal conductivity K, component (mass) mobility M_ab, component (mass) exchange coefficient k_ab, and phase mobility m_αβ. For simplicity, the cross-coupling (off-diagonal) contributions to the general forms (e.g., refs. ^66,69) of the flux-force relations are neglected in (10). Substituting (10) into (6)₁ yields a form for the entropy production-rate density π which is (in general quasi-) quadratic in the driving forces and linear in the kinetic properties. As usual, requiring these latter properties to be nonnegative definite is then sufficient to insure π ⩾ 0 in all processes and so nonnegative entropy production.

In summary, the system

$$\begin{array}{l}{\dot{\varrho }}_{a}={{{\rm{div}}}}\mathop{\sum }\limits_{b = 1}^{{n}_{{{{\rm{c}}}}}}\theta \,{{{{\bf{M}}}}}_{ab}\nabla [{\delta }_{{\varrho }_{b}}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\mathbf{\varrho }}}}b}]-\mathop{\sum }\limits_{b = 1}^{{n}_{{{{\rm{c}}}}}}\theta \,{k}_{ab}\,[{\delta }_{{\varrho }_{b}}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\mathbf{\varrho }}}}b}]\,,\\ \varrho \ddot{{{{\boldsymbol{\chi }}}}}={{{\rm{div}}}}{\partial }_{\nabla {{{\boldsymbol{\chi }}}}}\psi \,,\\ {\dot{\phi }}_{\alpha }=-\theta \mathop{\sum }\limits_{\beta = 1}^{{n}_{{{{\rm{p}}}}}}{m}_{\alpha \beta }\,[{\delta }_{{\phi }_{\beta }}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\alpha }]\,,\\ c\dot{\theta }={{{\rm{div}}}}{{{\bf{K}}}}\nabla \theta -\theta \,{\partial }_{\nabla {{{\boldsymbol{\chi }}}}}\eta \cdot \nabla \dot{{{{\boldsymbol{\chi }}}}}\\ \qquad-\mathop{\sum }\limits_{a = 1}^{{n}_{{{{\rm{c}}}}}}[{\delta }_{{\varrho }_{a}}\varepsilon +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varepsilon ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\mathbf{\varrho }}}}a}]\,{\dot{\varrho }}_{a}-\mathop{\sum }\limits_{\alpha = 1}^{{n}_{{{{\rm{p}}}}}}[{\delta }_{{\phi }_{\alpha }}\varepsilon +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varepsilon ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\alpha }]\,{\dot{\phi }}_{\alpha }\,,\end{array}$$

(11)

of evolution-field relations and coupled partial differential equations (PDEs) is obtained for ϱ_a, χ, ϕ_α, θ (recall $\varrho =\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\varrho }_{a}$) from (1)₁₋₃, (4) and (7)–(10). In particular, note that the temperature relation (11)₄ is based on (9). The last three terms on the right-hand side of (11)₄ determine the volumetric heating rate. Once specific model forms for ε, η, N_ϱ a, N_ϱ a, K, M_ab, k_ab, and m_αβ, are given, initial-boundary-value problems based on the system (11) and corresponding boundary conditions can be formulated and numerically solved to simulate microstructure evolution and the corresponding material behavior in multicomponent, multiphase systems undergoing thermochemomechanical loading. As mentioned above, a current and prominent example of the latter is laser-heating- or powder-fusion-based additive manufacturing^107,108.

Consider next a few special cases of the above formulation employed in the literature. For example, assume further that the mixture is closed with respect to mass. In this case, the additional constraints ${{{{\bf{j}}}}}_{{n}_{{{{\rm{c}}}}}}=-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}-1}{{{{\bf{j}}}}}_{a}$ and ${\sigma }_{{n}_{{{{\rm{c}}}}}}=-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}-1}{\sigma }_{a}$ apply, $\varrho =\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\varrho }_{a}$ is constant via (1)₁, and ${\varrho }_{{n}_{{{{\rm{c}}}}}}=\varrho -\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}-1}{\varrho }_{a}$ is no longer independent. In this context, it makes sense to introduce the mass concentration c_a ≔ ϱ_a/ϱ such that ${c}_{{n}_{{{{\rm{c}}}}}}=1-\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}-1}{c}_{a}$ and ${\dot{\varrho }}_{a}=\varrho {\dot{c}}_{a}$. Likewise, the term $\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\kappa }_{a}(\varrho {\dot{c}}_{a}+{{{\rm{div}}}}{{{{\bf{j}}}}}_{a}-{\sigma }_{a})=\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}-1}({\kappa }_{a}-{\kappa }_{{n}_{{{{\rm{c}}}}}})\,[\varrho {\dot{c}}_{a}+{{{\rm{div}}}}{{{{\bf{j}}}}}_{a}-{\sigma }_{a}]$ in the Gibbs relation (2) depends only on ${\kappa }_{a}-{\kappa }_{{n}_{{{{\rm{c}}}}}}$. Further, the dependence of ε and η on ϱ and ∇ ϱ in (3) reduces to one on ${{{\bf{c}}}}:= ({c}_{1},\ldots ,{c}_{{n}_{{{{\rm{c}}}}}-1})$ and ∇ c. The remaining model relations reduce accordingly. Another special case takes the form of the so-called multiphase-field (MPF) approach (e.g., ref. ¹²⁷; broad generalizations of this are considered in ref. ¹²⁸). This is based on the constraint $\mathop{\sum }\nolimits_{\alpha = 1}^{{n}_{{{{\rm{p}}}}}}{\phi }_{\alpha }=1$. This holds for example if (i) each ϕ_α is interpreted as a phase volume density (i.e., the ratio of the phase volume to total mixture volume) and (ii) the mixture is occupied only by the phases. In this case, ϕ_β = 1 − ∑_α≠βϕ_α is dependent for arbitrary β. In addition, ${\delta }_{{\phi }_{\alpha }}\varphi -{\delta }_{{\phi }_{\beta }}\varphi +({\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\varphi ){{{{\bf{F}}}}}_{{{{\rm{R}}}}}^{{{{\rm{T}}}}}\cdot ({{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\alpha }-{{{{\bf{N}}}}}_{{{{\boldsymbol{\phi }}}}\beta })$ becomes the thermodynamic force conjugate to ${\dot{\phi }}_{\alpha }$ in (6)₁ for π, in particular at the α-β interface. Further details on MPF can be found for example in ref. ⁷⁶.

Lastly, consider the isothermal special case. For example, in this case, (2) reduces to $\theta \pi -{{{\rm{div}}}}\theta {{{\bf{h}}}}=\mathop{\sum }\nolimits_{a = 1}^{{n}_{{{{\rm{c}}}}}}{\mu }_{a}(\varrho {\dot{c}}_{a}+{{{\rm{div}}}}{{{{\bf{j}}}}}_{a}-{\sigma }_{a})+{{{\bf{P}}}}\cdot \nabla \dot{{{{\boldsymbol{\chi }}}}}-{{{\rm{div}}}}{{{\bf{q}}}}-\dot{\psi }$ for the generalized Gibbs relation in terms of the dissipation-rate density θπ, energetic chemical potential μ_a = θκ_a, and free energy density ψ from (8)₂. The constitutive form ψ = ψ(θ, ∇ χ, F_R, ϱ, ∇ ϱ, ϕ, ∇ ϕ) for the latter is determined by (3), in which case ${\mu }_{a}={\delta }_{{\varrho }_{a}}\psi +{\partial }_{{{{{\bf{F}}}}}_{{{{\rm{R}}}}}}\psi \cdot {{{{\bf{N}}}}}_{{{{\mathbf{\varrho }}}}a}$ holds via (7). The remaining non-isothermal model relations reduce accordingly. A number of further assumptions and issues are addressed in the context of isothermal conditions in the literature, e.g., the existence of a dissipation potential (e.g., ref. ¹²⁹), rate-variational formulation of initial-boundary-value problems (e.g., refs. ^{115,121,130,131,132}), or the consequences of thermodynamic extremum principles (e.g., ref. ^{133,134,135,136}). A detailed treatment and discussion of these goes beyond the scope of the current review. As mentioned above, the vast majority of PF models for multicomponent, multiphase solid systems in the literature are isothermal. These include for example models for single-component systems containing (i) structural phases (e.g., ref. ¹⁰⁶), (ii) twin phases (e.g., ref. ¹³⁷), (iii) equilibrium phase interfaces (e.g., refs. ^{138,139,140,141,142}), (iv) damage, fracture phases (e.g., refs. ^{118,143,144,145}) or (v) structural phases with dislocations (e.g., ref. ⁹⁹). Equilibrium phase interfaces in two-phase, two-component chemoelastic systems have been treated for example in ref. ¹⁴⁶. A non-mechanical treatment of non-equilibrium phase interfaces in multiphase, multicomponent systems based on the MPF approach discussed above is given for example by ref. ¹⁴⁷. A chemo-mechanical treatment of non-equilibrium phase interfaces in multicomponent, multiphase systems can be found in ref. ¹²¹. Yet another area of application of the above model formulation in the isothermal case is the chemo-mechanical modeling of solute segregation to mechanical defects (e.g., dislocations, stacking faults:^148,149) and its effect on spinodal decomposition, precipitation, and second-phase formation at defects (i.e., defect thermodynamics: e.g., refs. ^150,151; see also for example ref. ¹⁵²). Although the current treatment excludes electromagnetic effects, much of the above treatment still applies to functional materials (e.g., refs. ^{153,154,155,156}) and battery materials (e.g., Li-ion:^{157,158,159,160}). This holds true as well for electrochemical-mechanical systems (e.g., batteries, fuel cells) and processes (e.g., oxidation, reduction) containing charged chemical components or species (e.g., ref. ¹²⁰). Further aspects of such isothermal models, as well as their numerical implementation, and incorporation into software packages, are discussed in the rest of this review.

Numerical methods and software packages

To make the presented theories and models usable, they need to be implemented in computer code and coupled to reliable and robust numerical solvers. To this end, many software packages have been developed for material modeling at different lengthscales or with multiple coupled physical phenomena. In this section, software and tools that are suitable for the multi-scale, multi-physics simulations, in particular for metallic systems, are discussed and three established packages are presented in more detail. These three packages are selected to illustrate the diversity of approaches and numerical methods that are employed in the field of continuum multi-physics modeling.

OpenPhase

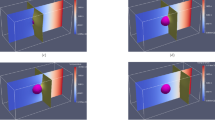
OpenPhase is open-source software, which is developed in general for the simulation of microstructure formation or phase transformation in complex systems¹⁶¹. The software is distributed as a library under the GNU General Public License (GPLv3). It has been used for solving physical phenomena in materials such as solidification, grain growth, creep, recrystallization, foam formation, and solid-solid transformation^{76,162,163,164,165,166,167,168,169}. The software is based on the MPF approach^76,127, where each phase/domain is defined by a PF parameter. The evolution of each phase is captured by solving the respective PF as well as those which are present in its interface. Through the coupling of the MPF approach with different fields, such as chemical, mechanical, and even magnetic fields, the software is used for the simulation of multi-physics problems for different applications. One application of OpenPhase for modeling and simulation of metallic foams as an advanced material is shown in Fig. 2. For this specific example, a model is developed by coupling the MPF approach with fluid dynamics¹⁶². Using MPF provides the possibility to assign the material parameters (such as mass, interface energy) of each bubble separately. Thus, it allows the introduction of an energy barrier (called disjoining pressure) between bubbles arising from the presence of additives which prevents bubble coalescence and stabilizes the foam formation, see Fig. 2¹⁶². However, if the liquid film between two bubbles falls below a threshold and the force pushing two bubbles towards each other exceeds the disjoining pressure, coalescence becomes inevitable. In Fig. 2a–c, for an initial setup including bubble nuclei, the final foam structures are different as a result of using different disjoining pressures (it is highest for Fig. 2a and lowest for Fig. 2c). A 3D simulation of foam and the summary of the model are depicted in Fig. 2d, e, respectively.

Fig. 2: Multi-physics simulation example using OpenPhase.

Microstructure formation in metallic foams (coupling of MPF with fluid dynamics)¹⁶². a–c Formation of foam structures from an identical distribution of bubble nuclei with different disjoining pressures. From a–c the disjoining pressure between bubbles is lowered and thus the number of merged/coalesced bubbles increases. Therefore, in spite of identical bubble nuclei distribution, different structures are formed. d An example of a 3D simulation of foam formation¹⁶². e A schematic representation of the coupling between MPF and fluid dynamics for modeling of microstructure formation in metallic foams¹⁶².

DAMASK

The Düsseldorf Advanced Material Simulation Kit (DAMASK)¹⁷⁰, open-source, multi-physics software including crystal plasticity, is a simulation platform with the capability and flexibility to perform and analyze complex multi-field simulations. It is distributed with pre- and post-processing tools as a standalone software package under the GNU General Public License (GPLv3). Its modular structure allows solving of different field equations in a fully coupled way with a staggered approach, using Fast Fourier Transform (FFT) and Finite Element (FE) based solvers provided by the PETSc numerical library^21,118,171. The pre- and post-processing of DAMASK facilitates coupling with other platforms such as DREAM.3D¹⁷², MTEX¹⁷³, Neper¹⁷⁴, Gmsh¹⁷⁵, and Paraview¹⁷⁶. The integration with other platforms allows for complex workflows. A few multi-physics example simulations using DAMASK are presented and discussed below.

MOOSE

The Multi-physics Object-Oriented Simulation Environment (MOOSE) is an open-source, parallel finite element framework that focuses on coupled multi-physics simulations in a flexible manner¹⁷⁷. The framework includes a variety of plug-in infrastructures, which makes running or post-processing a multi-physics problem convenient. All MOOSE-based applications (apps) and community-developed physics modules are libraries that can be easily linked under the LGPL v2 license. Therefore, this design allows users to focus on their scientific endeavors without having to manually implement the intricacies of modern parallel computing. In MOOSE, the implicit method is used to solve equations from different apps in a fully coupled fashion. Multi-physics and multi-scale (FEM²) simulations can be easily set up by the MultiApp and Transfer system in MOOSE, as illustrated in Fig. 3. Furthermore, parallel solvers like PETSc¹⁷¹ are automatically included in this framework. As a result, users can run the simulations on a workstation or a cluster with multiple cores/CPUs with ease.

Fig. 3: Multi-physics simulation example in MOOSE.

a Chemo-mechanical analysis for the lithium concentration distribution (top row) of a LiNi_xMn_yCo_zO₂ (NMC) particle, and the crack patterns of NMC (bottom row), with the influence of grain boundary interaction²³⁹. b The electro-mechanical analysis of lithium-ion battery cell performance under different discharge conditions¹⁷⁸. c The workflow of multi-apps coupling. Each app is responsible for its own physical model, the data transfer between different apps is implemented by the transfer interface.

The apps in MOOSE can be used to simulate different physical problems. For instance, during the charge and discharge process of lithium-ion batteries (LIBs), the insertion of lithium not only involves the diffusion process of chemical species but also volume changes as well as mechanical deformation. Therefore, as mentioned in^178,179, one can easily define the system’s free energy, as well as its derivative i.e., stress and chemical potential, with the consideration of both the mechanical deformation and diffusion in the ChemoMechanics App. The governing equations can also be defined within this module by using the Kernel from MOOSE.

Other packages

Besides those mentioned above, there is a large number of other open-source packages that could be employed to tackle multi-physics and multi-scale microstructure problems or certain aspects of it. Among them are AMITEX_FFTP for crystal plasticity and PF¹⁸⁰, Prisms-Plasticity¹⁸¹ and Prisms-phase-field¹⁸² for plasticity and PF modeling, respectively, FiPy¹⁸³ a finite volume partial differential equations (PDE) solver with python, FEniCS¹⁸⁴ a computing platform for solving PDEs, and MicroSim¹⁸⁵ to name a few. It should be noted that there is also commercially available software for multi-physics simulations such as COMSOL Multi-physics¹⁸⁶, ANSYS¹⁸⁷, and ABAQUS¹⁸⁸. Although these are often powerful tools for multi-physics simulations, the black-box nature of the closed source codes will make their use limited in new model development and is often targeted to users only. In addition, many research groups have their in-house codes of which several ones are shared within projects or on request. A list of important packages and their features is presented in Table 1.

Table 1 Software packages and important features for multi-physics modeling in metallic systems.

Challenges in multi-physics simulation development

System versus microstructure lengthscales

Materials containing multiple phases and chemical components consist of individual single crystals/grains/phases having distinct material properties (e.g., elastic stiffness) and fields (e.g., deformation gradient, component concentration, temperature) which vary spatially within each grain and across grain boundaries. In the extreme case, the average grain size may be of the same order of magnitude as that of the polycrystal/mixture. In this case, there is no separation of lengthscales, and the question arises as to how single-crystal- /grain- /phase-based properties and fields determine the corresponding properties and fields of the polycrystal/multicomponent, multiphase mixture as a whole.

As it turns out, this issue is related to the treatment of contrasts in phase properties and fields at phase/grain interfaces. Based on mechanical equilibrium and kinematic compatibility at interfaces, the case of equilibrium phase contrasts at elastic phase interfaces has been treated in the purely mechanical case for example by refs. ^{139,140,141,142}. In the more general chemo-mechanical case, equilibrium phase contrasts have been treated in this way by ref. ¹⁴⁶, and non-equilibrium (i.e., evolving) phase contrasts by ref. ¹²¹.

At sufficiently large mixture lengthscales, the assumption of scale separation becomes justified, in which case (e.g., statistical, volume) averaging of phase properties and fields is relevant. In the extreme, this takes the form of homogenization assumptions for phase properties and fields. In the classic (bulk) mechanical case⁵³, for example, these include uniform phase (local) deformation (Voigt–Taylor), or uniform phase stress (Reuss-Sachs), and their generalizations (e.g., laminate theory:⁶⁸). Analogous assumptions in the bulk chemical case are uniform phase chemical concentrations¹⁸⁹ or uniform phase chemical potentials¹⁹⁰. For more details, the interested reader is referred to ref. ¹²¹.

Related to these issues in the PF context is a classic challenge facing PF modeling, i.e., resolving (i) physical mechanisms over multiple lengthscales (i.e., interface and system) and (ii) physical processes over much longer timescales than dictated by interface kinetics. On the physical and mathematical side, methods which have been developed to deal with this include sharp-interface scaling^20,103, thin-interface asymptotic analysis (e.g.,^{19,Appendix A]}), Hamilton–Jacobi- and level-set-based rescaling¹⁹¹, or most recently the so-called sharp PF method¹⁹². On the numerical side, adaptive mesh refinement, or multigrid methods, are employed.

Model parameter identification

Multi-physics simulations take into account several different physical phenomena. It is, therefore, no surprise that they depend on a large number of model parameters. Determining material-specific values for these parameters is often a significant hurdle for the application of such models. Typically models without reliable parametrization are not useful for practical applications. In the extreme case of CALPHAD, the assessment of parameters is the more involved step in comparison to the development of the model itself. Consequently, open databases with contributions from the scientific community have been established¹⁹³. However, the fragmentation of models prohibits a unified notation and exchange of parameters for full-field models. Therefore, common repositories, as opposed to the area of crystal structures^194,195,196 or interatomic potentials¹⁹⁷, have not been established. It remains therefore an open question how expensive parameter fitting¹⁹⁸ can be avoided by sharing data and model implementations between different researchers.

Reproducibility

Coupled multi-physics simulations have predictive capabilities, i.e. they can explain non-trivial phenomena¹⁹⁹. The ability to obtain surprising results comes, however, at a high cost: It is non-trivial to validate whether simulation results reflect reality or whether they are caused by a faulty implementation or nonphysical parameterization. Furthermore, multi-physics models are complex and many papers lack important information like employed numerical methods, tolerances, constitutive parameters, and sometimes even spatial or temporal discretization. Without making the implementation open, the model cannot be used by other researchers. One can of course try to re-implement it, but that is a lot of work and there is no guarantee that one can find solutions for the missing information. Often making the source code and the data available also does not help since one needs to maintain and support software packages with helpful documentation and guides. As a consequence, the FAIR principles for findable, accessible, interoperable, and reusable data management²⁰⁰ are of utmost importance for multi-physics simulations. This holds not only for the used software, which needs to be tested, documented, and versioned but also for the employed datasets. Using public repositories based on Git, e.g. on GitLab and GitHub, is today the de-facto standard for collaborative development of open-source software for scientific applications.

Examples of multi-physics integration

There is a vast trove of literature on multi-physics integration in material science that could be generally categorized into investigation of structural phases^79,106, mechanical phase interfaces^{138,139,142,201}, damage¹¹⁸, fracture¹⁴⁵, polarization phases^153,156, confined systems thermodynamics, defect thermodynamics^{148,150,151,202,203}, chemical liquid and solid phases^189,190, chemo-mechanical solid phases and phase interfaces^121,146, as well as electrochemical-mechanical systems (e.g., batteries, fuel cells) and processes containing charged components or species¹²⁰. A few of these cases are explored in more detail in this section.

Thermo-mechanical coupling is a case that is often not considered in material modeling. However, solving mechanical boundary-value problems only, completely ignoring the effect of other interacting fields is no longer sufficient for the state-of-the-art modeling of the evolution of microstructures in high-strength materials. For example, the effect of plastic dissipation on the evolving microstructure is generally ignored when performing a crystal plasticity simulation. It is, however, known that the dissipation leads to an increase in the temperature of the material, which couples back to the mechanics in the form of thermal lattice expansion, modified elastic constants, and faster dislocation velocity, affecting the overall stress response, as shown in Fig. 4a. Another example of coupling the mechanics and thermal solvers is the microstructural evolution of twinning-induced plasticity (TWIP) steel. In Fig. 4b, the total twin volume fraction shows variation when the effect of plastic dissipation is taken into account. A schematic of the thermo-mechanical coupling in DAMASK is shown in Fig. 4c.

Fig. 4: Multi-physics thermo-mechanical simulation example in DAMASK.

a-left Effect of plastic dissipation on the overall stress-strain response in a uniaxial tension test on bcc-iron starting at room temperature, including the effect of varying temperature on the components of the elastic stiffness tensor and the effect of lattice expansion due to increase in temperature. Simulation using the dislotwin constitutive model^198,240 where only plastic slip was considered, as implemented in DAMASK¹⁷⁰. a-right Deviation in temperature for each material point from the final average temperature of the simulation box. b-left Varying twin volume fraction (f_tw) for TWIP steel assuming both isothermal response and conduction of the dissipated plastic heat causing a change in stacking fault energy and thermal lattice expansion. Simulation using the dislotwin constitutive model²⁴⁰ as implemented in DAMASK¹⁷⁰. b-right Final temperature in the case of conduction. c Schematics of thermo-mechanical coupling in DAMASK.

It is widely acknowledged that the interaction of the solute diffusion and elastoplastic deformation can strongly affect the microstructural evolution and the subsequent performance in many engineering materials^149,204,205. Integration of the PF, Cahn–Hilliard, and crystal plasticity models enables the investigation of the complex role of plastic relaxation in chemo-mechanically coupled processes^{21,23,205,206,207,208,209}, such as the rafting behavior in Ni-based superalloys^{149,210,211,212,213,214}, lithiation of a phase-separating electrode material^205,215, or the hydrogen dissolution and permeation in the metallic components for hydrogen storage and distribution^207,216. The influence of the misfit stress, localized creep strain, and anisotropy of plasticity on the rafting behavior of ${\gamma }^{\prime}$ precipitates in Ni-based and Co-based superalloys has been widely studied at varying lengthscales through coupling PF models with various plasticity theories, such as at the scale of individual dislocations within the PF theory^149,151,217, dislocation-density-based crystal plasticity model^{211,212,213,214}, and the phenomenological mesoscale plasticity model^204,210. In these applications, the multicomponent engineering alloys were generally simplified to binary or ternary simple alloys, due to the limitation of the incorporation of the complex chemical-free energies into the PF model. Recently, a chemical potential-based PF model has been developed based on a semi-analytical inversion of the thermodynamic relations^21,23, which enables the direct incorporation of the CALPHAD-based chemical-free energies into the PF methods and can thus facilitate the application of the coupled CALPHAD/phase-field/crystal plasticity model in many multicomponent engineering alloys.

Figure 5a–c presents some exemplary applications of the multi-physics model developed in DAMASK in the investigation of the chemo-mechanically coupled ternary spinodal decomposition process²¹, grain boundary microchemistry, and precipitation in Al-Zn-Mg-Cu alloys²³, and dislocation-twin interactions in Mg alloys^208,209. Figure 5d shows the general framework of the finite strain and multicomponent chemo-mechanics model developed in DAMASK^21,170. A phenomenological or dislocation-density-based crystal plasticity model was usually employed to predict the heterogeneous distribution of stress, strain, and dislocation activities. The mechanical model was implicitly coupled to an MPF model and a Cahn–Hillard model to describe the concurrent phase transformations, e.g., precipitation, twinning and martensite transformation, and multicomponent solute diffusion during many engineering materials processes.

Fig. 5: Multi-component chemo-mechanics model and examples in DAMASK.

a Influence of the plastic deformation on the ternary spinodal decomposition process, showing the morphology of the decomposition regions, the hydrostatic stress, and the plastic strain²¹. b CALPHAD-informed PF modeling of the grain boundary segregation and precipitation evolution in an Al-Zn-Mg-Cu alloy²³. c Studying the dislocation slip and twinning interaction in the Mg polycrystal with a coupled crystal plasticity--PF model, showing the twinning microstructure and the spatial distribution of basal dislocations^208,209. d Schematic of the finite-strain chemo-mechanical model in DAMASK^21,170.

Hydrogen embrittlement and its effect on the cracking of materials has been modeled by coupling a PF damage model with stress-assisted hydrogen diffusion and mechanics^218,219,220. The hydrogen effect is accounted for by incorporating the atomic concentration of H in the model, which alters the crack resistance of the material. It has been shown that increasing the hydrogen content significantly decreases the mechanical response of a notched plate²¹⁸, which is a direct result of the lowered crack resistance in the presence of hydrogen. Accumulation of the hydrogen occurs in the crack tip due to locally large stresses as shown in ref. ²¹⁸.

Emerging avenues and outlook

Although the simulation methods for multi-physics and multi-scale problems have been continuously improved as summarized above, the complexity of realistic material science problems can still easily overwhelm even the most cutting-edge approaches, both in terms of computation time and model identification. Each important physical phenomenon added to a given problem introduces not only a new set of parameters for that specific model but also the possible dependency of the parameters of the previously included models on the parameters of the new one. Quantifying the intertwined model-parameter dependencies is not an easy task when the system is complex. Model-free and data-driven computational approaches^221,222 along with machine-learning methods²⁸ are emerging as either an alternative or an augmenting tool for material simulations. The recently published works can roughly be organized into three categories: data transfer between scales (such as interatomic potentials based on density functional theory²²³, various forms of homogenization or averaged material-response prediction^224,225), solving or accelerating the solution of PDEs^226,227, and utilizing a physics-informed neural network for better prediction of material processes²²⁸.

In the field of accelerated solution of PDEs, one approach is linearization within the explicit time-stepping setting. The associated linear problems have quadratic complexity if attempted to be solved from scratch, and the memory requirements for matrix-based methods are overwhelming for fine-microstructure studies. Iterative matrix-free solvers (such as MF-FEM) prove to be more efficient if initialization is available, for which a common approach is a prior solution on a coarser grid combined with interpolation (MultiGrid). This strategy, although beneficial in some cases, becomes challenging for high-contrast material phases and fails upon the emergence of critical fractal-like self-organization. For both scenarios, stabilization and acceleration of the approach are achieved by the introduction of intermediate homogenization loops. An example of this approach for the former case is shown in refs. ^229,230. The newly-introduced adaptive smoothening prolongation-based multigrid solver (AMG) designed for ill-conditioned nonlinear problems of structural mechanics – which is a broader problem-space in a part of which fractal-like patterns can emerge—shows robust performance both for benchmark models and real-world calculations (such as fine-microstructure composite-made mechanical tools), a key feature employed in the approach being adaptive factored sparse approximate inverse^231,232,233. A more general study of conditioning the AMG for elliptic PDEs is conducted in ref. ²³⁴. There, the idea of intermediate stabilizing homogenization is addressed as proper identification of stable coarsening degrees of freedom, and a generalization of the Ruge-Stüben algorithm is employed. The aforementioned ill-conditioning of the standard MG approach is especially apparent in elliptic boundary-value problems with stochastic coefficients, where indeed fractal patterns can emerge and stable intermediate coarsening steps are all the more necessary. Construction of MG algorithms for such problems seems to possibly benefit from considering the ideas explored in ref. ²³⁵.

A noteworthy recent work²³⁶ combines the PDE-solution-acceleration effort with the concept of data transfer between scales. There, a finite element procedure is discussed in which instead of the full displacement-based second-order PDE formulation, the problem of plastic deformation in nonlinear materials is treated as a mixed stress-displacement first-order system. Mesh-independence and stable convergence with the increasing resolution are obtained by using a variational-multi-scale stabilization technique, based on the decomposition of the fields into their finite element component and a subscale. The subscale-corrections to the fields are expanded on a basis orthogonal to that of the upper-scale fields (in the Galerkin sense). This work demonstrates an important feature of multiple-scale methods: separation between scales is obtained by preventing resonances between the scales, which ensures the overall stabilization of the scheme. The said separation is achieved by coarse-graining (averaging) over the subscale before adding its correction. Similarly, when acknowledging a physically-distinguished subscale (rather than a numerically-constructed one), as in ref. ²³⁷, where material properties are derived from interatomic potentials, statistical averaging is implemented. For example, ref. ²³⁷ is using the Gauss approximation potential framework. Interestingly enough, in deriving material properties from interatomic potentials, often machine-learning techniques are used (as in ref. ²³⁷), which are based on low-order smooth interpolation, which naturally introduces the coarse-graining stabilizing effect as aforementioned.