Electrically and mechanically driven rotation of polar spirals in a relaxor ferroelectric polymer

Guo, Mengfan; Xu, Erxiang; Huang, Houbing; Guo, Changqing; Chen, Hetian; Chen, Shulin; He, Shan; Zhou, Le; Ma, Jing; Shen, Zhonghui; Xu, Ben; Yi, Di; Gao, Peng; Nan, Ce-Wen; Mathur, Neil. D.; Shen, Yang

doi:10.1038/s41467-023-44395-5

Download PDF

Article
Open access
Published: 08 January 2024

Electrically and mechanically driven rotation of polar spirals in a relaxor ferroelectric polymer

Nature Communications volume 15, Article number: 348 (2024) Cite this article

2549 Accesses
1 Citations
12 Altmetric
Metrics details

Subjects

Abstract

Topology created by quasi-continuous spatial variations of a local polarization direction represents an exotic state of matter, but field-driven manipulation has been hitherto limited to creation and destruction. Here we report that relatively small electric or mechanical fields can drive the non-volatile rotation of polar spirals in discretized microregions of the relaxor ferroelectric polymer poly(vinylidene fluoride-ran-trifluoroethylene). These polar spirals arise from the asymmetric Coulomb interaction between vertically aligned helical polymer chains, and can be rotated in-plane through various angles with robust retention. Given also that our manipulation of topological order can be detected via infrared absorption, our work suggests a new direction for the application of complex materials.

Polar Solomon rings in ferroelectric nanocrystals

Article Open access 04 July 2023

Coupled polarization and nanodomain evolution underpins large electromechanical responses in relaxors

Article 06 October 2022

Subterahertz collective dynamics of polar vortices

Article 14 April 2021

Introduction

Flux-closure structures^1,2, vortices/antivortices^3,4,5,6,7, skyrmions^8,9,10, and merons^11,12 in oxides, metals and polymers represent non-trivial topologies in which a local polar/magnetic order undergoes quasi-continuous spatial variations in a host crystal lattice. These structures are now extensively studied due to emergent functionalities^13,14,15, but the application of electrical/mechanical fields has so far only served to destroy the polar topologies of interest^16,17,18,19.

Here, we modify a ferroelectric polymer, poly(vinylidene-fluoride-ran-trifluoroethylene) [P(VDF-TrFE)], in which toroidal polar topology can be thermally switched^20,21. We increase the TrFE monomer ratio to induce conformational disorder^22,23,24 and noncollinear dipoles^25,26, resulting in relaxor behavior. Enhanced local toroidal order with spiral topology is observed within discretized microregions smaller than 1 μm, reminiscent of the classic polar nanoregion model for relaxor ferroelectrics²⁷. Continuous non-volatile rotation of these in-plane polar spirals can be achieved by applying out-of-plane electric fields or mechanical stresses, cf. ferroelectric domain switching. Asymmetric interactions and weak anisotropy of helical chain conformations facilitate the Néel rotation²⁸ of interchain dipoles that stabilizes the polar spirals. The rotated polar spiral can persist for at least 25 weeks with few changes, outperforming switched domains with depolarization²⁹. The polar spirals can absorb polarized infrared radiation in a way that depends upon the rotation, enabling optical read-out. Our observations should inform the design of flexible materials and relaxor ferroelectrics with complex topologies, and offer guidance for field-controllable manipulations of emergent polar topologies.

Results

Observation of polar spirals

By melt-recrystallizing spin-coated thin films of P(VDF-TrFE) (see dielectric properties in Supplementary Figs. 1 and 2), a 100-nm-thick monolayer of face-on lamellae with vertically aligned polymer chains were produced (Fig. 1a and Supplementary Fig. 3a–c). The interchain dipoles arising from the electronegativity difference are distributed in the film plane²⁰. We therefore used in-plane piezo-response force microscopy (IP-PFM) to characterize the film. Curly stripe domains with width of ~20 nm are predominant (Fig. 1b, c and Supplementary Fig. 3g–i), and they exhibit coiling and coarsening in randomly distributed microregions of typical size ~1 μm, leading to a series of concentric ring-shaped domains (Fig. 1b, c and Supplementary Fig. 3j–l). The curly stripe domains and the concentric ring-shaped domains both indicate a whirl of local polarization. To semiquantitively analyze the inhomogeneous whirls, we mapped the nominal toroidal order (Fig. 1d) by calculating domain-wall curvature under the assumption that the local polarization is parallel to the nearest domain wall. A matrix with low curvatures of ~10⁻⁴ nm⁻¹ (Fig. 1d) contains microregions with high curvatures of ~10⁻²nm⁻¹ corresponding to the concentric ring-shaped domains. This suggests a great increase of local toroidal order within confined microregions, which is analogous to the concept of polar nanoregions in relaxor ferroelectrics.

**Fig. 1: Observation of a microregion containing an in-plane polar spiral.**

Angle-resolved IP-PFM measurements have been performed on an identical microregion (Fig. 1e, f and Supplementary Fig. 4). The IP-PFM phase images vary with respect to each other when the measurement axis is rotated from vertical (Fig. 1e) to horizontal (Fig. 1f), and a blue disk domain appears at the center. The domain walls shift outward for counterclockwise rotations of the measurement axis (Supplementary Fig. 4a–e and Supplementary Movie 1a). A polarization map derived from the angle-resolved results appears in Supplementary Fig. 4f–h. By assuming a finite calculus limit, we calculated the curl (∇ × Ρ, Fig. 1g) and divergence (∇·Ρ, Fig. 1h) of the local polarization P (Supplementary Fig. 4f), both of which present a double spiral that fills nearly all of the microregion. The positive/negative curl (red/blue spiral in Fig. 1g) denotes a counterclockwise/clockwise (CCW/CW) polarization rotation. The positive/negative divergence (red/blue spiral in Fig. 1h) denotes a polar source/sink. We thus infer the topology schematized in Fig. 1i, where a polar source that spirals inwards (red arrows), and a polar sink that spirals outwards (blue arrows), are separated by CW or CCW Néel rotations of polarization (white arrows). Low-angle domain walls are identified at locations where the local polarization is perpendicular to the measurement axis (Supplementary Fig. 4f, g). We choose to use the fact that the polar sink spirals outwards to classify the polar spiral in Fig. 1 as a CCW polar spiral, and the Néel rotation is CCW when moving outwards along all radial directions (Supplementary Fig. 4g, h).

As expected, we have also observed CW polar spirals, which rotate in the opposite sense (Supplementary Fig. 5). For CCW rotations of the measurement axis, domain walls shift inward (Supplementary Fig. 5a–d and Supplementary Movie 1b) as the Néel rotation is CW when moving outwards along all radial directions (Supplementary Fig. 5f, g). Both types of polar spiral can be observed in the same thin film (Supplementary Fig. 6), but the probability of observing both types of polar spiral was found to be asymmetric, as the CW/CCW ratio for 148 polar spirals in two films is 0.85. It should be noted that CW/CCW polar spirals possess a positive/negative electric toroidal moment (Supplementary Fig. 7), indicating that the CW and CCW polar spirals might be mono-chiral and can be converted to each other by a 180° rotation along any in-plane axis. Thus, the uneven distribution might be attributed to the dielectric asymmetry between the air and the substrate.

Rotation of polar spirals

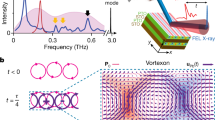
To examine field-response of the polar spirals, we applied electric bias, or mechanical pressure through scanning tips to the microregions. Continuous and non-volatile rotations of the polar spirals were observed after applying either electric or mechanical fields, as illustrated in Fig. 2a. Domain walls of microregions in IP-PFM images have been observed to collectively shift inward, for either negative or positive bias applied through conducting tips (Supplementary Fig. 8 and Supplementary Movie 2). According to the polarization maps, the spiral geometry remains the same after electrically driven changes, except that it is rotated around the center (insets in Fig. 2b and Supplementary Fig. 8). We therefore identify the change as a rotation of the polar spirals, and define CW rotation to have a positive sign. The changes in the rotational angle of the CW and CCW polar spirals versus the applied tip bias are plotted in Fig. 2b. When the bias of ~−6 V is exceeded in magnitude (electric field of <−60 MV m⁻¹), the rotation becomes evident. This rotation persists after withdrawing the bias, and rotation increases with a greater voltage (Fig. 2b). The CW polar spiral is rotated in the CW direction (upper half of Fig. 2b), and symmetrically, the CCW polar spiral is rotated along the CCW direction (lower half of Fig. 2b). The rotational direction is the same when the bias takes a positive sign (Supplementary Fig. 8g–l and Supplementary Fig. 9), suggesting that the electrical rotation should be attributed to the electrostrictive effects which are coupled to the square of electric field. When the magnitude of the tip bias exceeds ~20 V (electric field >200 MV m⁻¹), the polar spiral transform into a monodomain (Supplementary Fig. 10g, h).

Similar rotational changes can also be induced by mechanical stresses applied through scanning tips. Domain walls in IP-PFM images have also been observed to collectively shift inward (Supplementary Fig. 11 and Supplementary Movie 3). When forces exceed ~8 nN (compressive stresses >214 MPa, see Methods), a CW/CCW polar spiral starts to rotate along the CW/CCW direction (Fig. 2c and Supplementary Fig. 11). It transitions into a series of stripe domains when the force exceeds ~46 nN (stress >383 MPa). In our studies, the electrically induced rotation can reach 130°, while the mechanically induced rotation can exceed 780°. The narrower range of rotation induced by electric fields should be attributed to the indirect manipulation through electrostriction, and the early destruction of polar spirals induced by the plastic deformation and the large local electric field near the biased tip³⁰ that exceeds the switching coercive field. Although the sense of rotation is independent on the external field, we can in effect reset a polar spiral back to its initial state after rotating it by 360° (Supplementary Fig. 12). Besides, the sense of polar spirals (CW or CCW) is strongly protected against the electric or mechanical field whilst manipulation.

In addition to the electrical and mechanical stimuli from the tip, we addressed entire films (on substrates) via corona poling or uniaxial pressure (Supplementary Fig. 10a–f), and inward domain-wall shifting is still observed. While the spiral topology is preserved when electric field and mechanic stress are below ~500 MV m⁻¹ and ~390 MPa, respectively, it transforms into either a uniform monodomain or a series of stripe domains in larger fields similar to tip-induced transitions (Supplementary Fig. 10g–n). By comparing the polarization maps before and after applying fields (Supplementary Fig. 13), each local polarization in the polar spiral exhibits rotation along the same direction by almost the same angle. This collective rotation of local polarizations leads to the rotation of polar spirals (Supplementary Movies 4, 5). Thus, the rotation is significantly different from classic ferroelectric domain switching.

Formation of polar spirals

We attribute the emergence of polar spirals and their persistence in external fields to the stereoirregular chain arrangement. Both the main scattering arc at the Q_y axis and the diffraction points (Supplementary Fig. 14a, b) correspond to the (110) and (200) planes, which have very similar spacings in the pseudo-hexagonal lattice, suggesting the face-on lamellae are single crystals with polymer chains (c axis) aligned along the film normal. Nevertheless, splitting of the (110)/(200) peak can be observed after integrating the grazing incidence wide angle X-ray scattering (GI-WAXS) intensity (Fig. 3a). We therefore fitted the experimental data (black line) to two Gaussian peaks (cyan and pink area) centered at Q = 13.49 nm⁻¹ and Q = 13.15 nm⁻¹, with the fitted intensity (red line) agreeing well with the experiment. Similar splitting has also been observed in electron diffraction (Supplementary Fig. 14c), which should be attributed to the coexistence of trans-planar and 3/1-helical phases^22,25,26. Indeed, in the Fourier-transform infrared (FTIR) spectrum (Supplementary Fig. 14d), we observed characteristic bands corresponding to all-trans conformation at 1287 and 888 cm⁻¹, and to the 3/1-helical conformation at 508 cm⁻¹. We calculated the strain-free lattice spacings as a reference according to the X-ray diffraction (XRD) profile of edge-on thick films³¹ (Supplementary Fig. 14e), and we compare them with values from the GI-WAXS results (Supplementary Table 1). There is a little strain in the thin film for both phases as indicated by the nearly identical measured spacings compared to the reference value. It is therefore suggested that compared with the strained non-morphotropic polymer²⁰, the macroscopic strain plays a less important role here in the formation of toroidal order and its influence is negligible in the following discussion.

**Fig. 3: Structural characterizations and calculations for the polar spirals.**

The microscopic phase coexistence is confirmed by PFM and atomic force microscope infrared spectroscopy (AFM-IR) measurements (Fig. 3b, c). Three isolated microregions are shown in Fig. 3b (also see Supplementary Fig. 14f–h). When the same microregion is subjected to AFM-IR measurement using an IR beam polarized along out-of-plane (OOP) direction near the characteristic bands of the trans-planar phase, it exhibits a quenched IR absorption compared with the matrix (Fig. 3c and Supplementary Fig. 14i–k). We therefore suggest the microregions mainly consist of the 3/1-helical phase, whereas the matrix is dominated by the trans-planar phase. The 3/1-helical phase contains (TG)₃ or (${{{\rm{T}}}}{{\bar{{{\rm{G}}}}}}$)₃ conformation (T for trans and G for gauche), with either one generating chains with one sense of helicity periodically in three -CH₂-CF₂- segments (Supplementary Fig. 15a), in line with the Néel rotation along different directions observed in CW and CCW polar spirals.

We established pairs of collinear and noncollinear chains with the (TG)₃ conformation to compare the difference in free energies (Fig. 3d). Two neighboring helical chains along the [010] direction were selected. Their initial alignment is adopted from the reported prediction²², which is in the vicinity of the collinear alignment with the largest energy gain (Supplementary Fig. 15b). The two helical chains, denoted in the inset of Fig. 3d, are then rotated in CW direction by α₁ and α₂, respectively. The gains in free energy per chain compared with the state of (α₁, α₂) = (0°, 0°) have been calculated and are shown in Fig. 3d.

The gray dashed line in Fig. 3d is a collection of points with α₁ = α₂, denoting the collinear states. The region beneath the line represents noncollinear states with α₁ < α₂, whereas the region above represents α₁ > α₂. We found three striking features in Fig. 3d: 1) The most stable polarization state with the largest free energy gain is located in the α₁ < α₂ zone, at (α₁, α₂) = (1.2°, 1.35°) (the white star); 2) The polarization state with the local lowest energy appears at (α₁, α₂) = (7.3°, 7.9°) (the gray star), again lying in the α₁ < α₂ zone; 3) The zone of α₁ > α₂ exhibits a more dramatic rise in free energy (red color at the upper edge) than the α₁ < α₂ zone (green color at the lower edge). These features confirm that helical chains tend to self-organize into noncollinear polarization states, whereas chains with the (TG)₃ conformation tend to result in Néel rotation with α₁ < α₂, and symmetrically, (${{{\rm{T}}}}\bar{{{{{\rm{G}}}}}}$)₃ chains should result in Néel rotation with α₁ > α₂. Tilted intermolecular interactions have been found between neighboring chains (Supplementary Fig. 15c, d), which should facilitate the inhomogeneous rotation. Continuous spatial rotation of polarization also requires low dielectric anisotropy. We therefore performed phase-field simulations with strong and weak anisotropy (Supplementary Fig. 16 and Supplementary Tables 2 and 3). The low depth of the polarization energy surface should enable easier spatial rotation³². Thus, the simulated polarization map in Fig. 3e with weaker anisotropy indicates a polar spiral resembling our experimental observations.

Time-dependent phase-field simulations in electric fields have also been performed. Polar spirals have indeed been predicted to rotate, and would be broken into smaller polar clusters in large fields (Supplementary Figs. 17 and 18). Energy components in 1,000 time steps are collected after the field application (Fig. 3f). Before time steps of 100, the elastic energy (pink) quickly decreases to overcome a small energy barrier and there is a rise in the Landau energy (blue), suggesting an electromechanical conversion. The slight reduction in gradient energy (green) indicates that local toroidal order is suppressed, which may be in favor of dynamic rotational changes. The electric energy (orange) remains nearly unchanged, due to the conserved spiral skeleton in the polar spiral. After time steps of 100, the elastic energy is restored at the expense of decreased electric and gradient energies, suggesting a cross-coupling of electromechanical energy conversion with toroidal order. Thus, electromechanical interconversion triggered by the electric fields involves the evolution of local polarizations, leading to the dynamic rotational change within the polar spirals. A similar energy evolution process has been found in the stress-induced rotation (Supplementary Fig. 19).

Retention of field-manipulated polar spirals

The retention of a rotated polar spiral has been examined and compared with a switched domain (Fig. 4). The rotated polar spiral persisted with nearly no change after 25 weeks (upper insets of Fig. 4), such that the calculated core area changed by ≤2%. The domain in a microregion was switched by addressing it via a biased PFM tip that was rastered over the entire domain, and exhibits fractured switched-back domains right after the switching (blue stripe in the lower left inset of Fig. 4). With prolonged retention time, more fractured domains in blue were switched back (lower insets of Fig. 4). By calculating the unswitched area of the central region, we found the retention ratio of the deterministically switched region dropped to 86% after 25 weeks. The continuous spatial rotation in the polar spirals avoids any sharp discontinuities of polarization, and hence largely suppresses any depolarization fields that could lead to the nucleation and growth of anti-domains.

**Fig. 4: Retention behavior of polar spirals after field-manipulation.**

Optical read out of field-manipulated polar spirals

AFM-IR measurements have been conducted on a microregion to investigate its optical response after field-manipulation, and the domain states (Fig. 5a–c) are consistent with the IR absorption patterns (Fig. 5d–f). Figure 5a shows the original domain states of a microregion. By projecting an IR beam at 1400 cm⁻¹ polarized along IP direction, AFM-IR absorption of the microregion exhibits concentric feature with a periodically varying intensity along the radial direction (Fig. 5d), as predicted by simulation (Supplementary Fig. 20). The IR absorption is also weaker (purple in Fig. 5d) in blue-domain regions and stronger (orange in Fig. 5d) in red-domain regions. After rotating the polar spiral CW by 86°, the collective inward domain-wall shifting (Fig. 5b) leads to the same shifting of the absorption pattern (Fig. 5e). The elliptical weaker absorption region at the center of Fig. 5d disappears, and instead the orange central region in Fig. 5e corresponds to stronger absorption. After further rotating the polar spiral CW by another 88°, the domain state and absorption pattern display simultaneous inward shifting (Fig. 5c, f).

**Fig. 5: Optical response of a polar spiral after field-manipulation.**

In summary, we report the observation of polar spirals within toroidal polar microregions in thin films of relaxor ferroelectric polymers. This represents an unequivocal observation of ordered polar topology in systems that are considered to be “hopeless messes”³³. The polar spirals can be rotated by applying electric fields or mechanical stresses, enabling non-destructive, non-volatile, and continuous rotations, which may have influence on the macroscopic dielectric properties and is promising for multistate memories and neuromorphic systems³⁴. The formation and stabilization of these polar spirals are induced by the asymmetric dielectric interaction and weak dielectric anisotropy within the 3/1-helical phase. The rotated topologies display excellent retention, and infrared absorption pattern permits optical read out, e.g. for use in field-controllable spatial light modulators and structured light beams^35,36. Our observation and manipulation of polar spirals should provide insights and design principles for integrating field-controllable topology into relaxor ferroelectrics.

Methods

Thin film fabrication

The copolymer poly(vinylidene fluoride-ran-trifluoroethylene) [P(VDF-TrFE)] 50/50 mol% was obtained from Arkema Piezotech and used as-received. The copolymer powder was dissolved into methyl ethyl ketone at concentration of 2% w/v. The films were firstly spin-coated onto substrates at 5000 rpm. The substrates include silicon wafer with platinum top layer, quartz wafer with gold top layer, and quartz wafer. After dried in a vacuum oven at 30 °C for 1 h, the films were annealed at 240 °C for 10 min, and the cooling rate was controlled around 1 °C min⁻¹. The film thickness was around 100 nm confirmed by atomic force microscope (AFM).

Scanning probe microscopy measurements

A commercial scanning probe microscope (Asylum, MFP-3D infinity) was applied for AFM and piezo-response force microscope (PFM) measurements. In AFM, in-plane (IP) PFM tests, and PFM lithography tests, Si cantilevers with conducting Pt/Ir coating layer of spring constant around 0.2 N m⁻¹ and tip radius around 25 nm (NanoWorld, Arrow-CONTPt) were used. For PFM imaging, Vector mode was used where tips were modulated at around 240 kHz for IP imaging, with the AC voltage set at 2 V. The images obtained by Vector Mode were double checked by using dual AC resonance tracking (DART) mode and the patterns can be reproduced. For angle-resolved IP-PFM tests, the rotation of sample was controlled by a protractor. To ensure identical position was imaged after rotating the sample, we made cross-scratches as a mark on the sample surface in advance. This method was applied to locate the scanning position in other situations if we had to move the sample in between the scanning probe microscopic studies.

For electric-field-induced manipulations using PFM lithography, the DC voltage on tip was previously edited in the software. The scan speed was set at 1.95 Hz and no AC voltage was applied during the scanning. The DC voltage was divided by film thickness (100 nm) to obtain the electric field value. And an electric field with downward direction is defined with a positive sign.

For stress-induced manipulations, the deflection value of the PFM cantilever, which is a signal from photodetector, was preset to control the stress/force applied onto the sample. The difference in deflection value between a pressed cantilever and a free cantilever reflects how hard the tip and sample surface are pressed to each other. To obtain the force value F, we first calibrated the tips by the thermal noise method, and obtain the inverse optical lever sensitivity (InvOLS) and the spring constant k of the tips³⁷. The force could be obtained by:

$$F={{{{{\rm{InvOLS}}}}}}{{\times }}k{{\times }}\Delta {{{{{\rm{Deflection}}}}}}$$

(1)

We utilized Hertzian contact mechanics of a spherical indenter to simulate the stress field of the film under an AFM tip³⁸. For simplicity, the stress σ₃₃ at the contact center was used to represent the stress distribution under certain loading force, and it can be expressed as:

$${\sigma }_{33}=-\frac{1}{\pi }{\left(\frac{6F{{E}_{{{{{{\rm{e}}}}}}}}^{2}}{{R}^{2}}\right)}^{\frac{1}{3}},$$

(2)

where F is the AFM tip loading force, R is the radius of the AFM tip (~25 nm), and E_e is the effective modulus. The E_e is defined by:

$$\frac{1}{{E}_{e}}=\frac{1-{{\nu }_{{{{{{\rm{s}}}}}}}}^{2}}{{E}_{{{{{{\rm{s}}}}}}}}+\frac{1-{{\nu }_{{{{{{\rm{t}}}}}}}}^{2}}{{E}_{{{{{{\rm{t}}}}}}}} \, \approx \, \frac{1-{{\nu }_{{{{{{\rm{s}}}}}}}}^{2}}{{E}_{{{{{{\rm{s}}}}}}}},$$

(3)

where ν_s is the Poisson ratio of the sample, E_s is the Young’s modulus of the sample, ν_t is the Poisson ratio of the tip, and E_t is the Young’s modulus of the tip. While ν_s and ν_t are similar in value, since E_t is two orders of magnitude larger than E_s, the effective modulus E_e can be approximately calculated from ν_s and E_s. The value of ν_s is 0.305 (ref. ³⁹), and the value of E_s (1.8 GPa) was obtained from a nanoindentation experiment.

For retention measurement of field-manipulation, the retention rate of a rotated polar spiral was calculated by comparing the area encircled by the seventh smallest circular domain wall (upper insets in Fig. 4). The retention rate of a switched microregion was calculated by comparing the non-switching-back area within the lithographed region (lower insets in Fig. 4).

A commercial scanning probe microscope equipped with a quantum cascade laser (Anasys, NanoIR2) was used for AFM-IR measurements. The tips customized and provided by Anasys were contact-mode tips with spring constant between 0.07 to 0.4 N m⁻¹. By operating in the software, the laser can be modulated between 750 cm⁻¹ to 1900 cm⁻¹ and be polarized along OOP or IP directions.

The polar spiral regions we characterized and manipulated are smooth in surface without cracks (surface roughness R_a = 1.568 nm for Supplementary Fig. 3j).

Structural characterization

Optical microscopy measurements were completed by using Olympus BX53M in the reflection mode.

GI-WAXS measurements were conducted at beamline BL16B1 of Shanghai Synchrotron Radiation Facility. X-rays with photon energy of 10 keV were incident on the thin film sample in a rough vacuum environment (10⁻³Torr range) at incident angles of 0.10° and 0.14°, below the critical angle of organic material or the Si substrate, for a 5-second exposure. A pixel array detector (Pilatus 2M, Dectris) was positioned 228 mm from the sample. The spacing d of any scattering unit can be calculated as

$$d=4\pi /Q,$$

(4)

where Q is the reciprocal spacing.

The TEM experiments were carried out at FEI Tecnai F20 at 200 kV by a liquid nitrogen side-entry specimen holder (Gatan 636). The dose rate is estimated to be 0.25 e Å⁻² s⁻¹ during the selected area electron diffraction (SAED) tests. Silicon wafers with silicon oxide layer whose thickness was 300 nm were used as substrate for film deposition. By chemically etching of the substrate in solution with pH value of 14, a layer of free-standing face-on lamellae was obtained. After washed by deionized water, the film was floated onto copper grids. The aperture diameter is 3.8 μm for obtaining SAED pattern.

FT-IR was carried out on a Nicolet iS50 spectrometer (Thermo Fisher) under grazing incidence mode. The spectra were averaged from 128 scans.

X-ray diffraction (XRD) θ-2θ scanning measurements were completed by using PANalytical Empyrean with Cu Kα radiation. The calculation of lattice spacing d follows by the Bragg law, also written as

$$2d\sin \theta={\lambda }_{{{{{{\rm{Cu}}}}}}-{{{{{\rm{K}}}}}}{{{{{\rm{\alpha }}}}}}},$$

(5)

where λ_Cu-Kα is the wavelength of diffraction source.

First-principle computations

First-principle computations were implemented using the Vienna Ab initio Simulation Package. The projector augmented-wave approach was used for the treatment of the core electrons. The generalized gradient approximation using the Perdew-Burke-Ernzerhof functional was employed to approximate the electron exchange correlation interactions. For simplification, PVDF chain was taken for modeling. For the calculations on free energies of (TG)₃ helical chain pairs, the chains are set with the distance of 0.55 nm in vacuum and get individually rotated around the geometric center to yield a series of collinear and noncollinear states. At least 20 Å of vacuum in the x and y directions was used to separate the chain pairs in order to avoid the artificial interaction among the periodic units. The charge density difference is obtained by subtracting the charge density of the two individual PVDF chains from the charge density of helical chain pairs with the most stable angle. A cutoff energy 400 eV was applied for all works. The Brillouin zone was sampled by a Monkhorst–Pack 1 × 1 × 5 k-point grid.

Phase-field simulations

In phase-field simulations, the ferroelectric domain structures in P(VDF-TrFE) films are described by polarization vector P = (P_x, P_y, P_z). The temporal evolution of the polarization field is solved by the time-dependent Ginzburg–Landau (TDGL) equation, which takes into account the coupling and competition among various energies in the system, leading to the minimization of the total energy:

$$\frac{\partial {{P}}_{i}({{{{{\bf{r}}}}}}{,}t)}{\partial t}=-L\frac{{\delta }F}{{\delta }{{P}}_{i}({{{{{\bf{r}}}}}}{,}t)}{,}i=x{,}{y}{,}{z}{,}$$

(6)

Here, r is the spatial coordinate, t is the evolution time, L is the kinetic coefficient that is related to the domain evolution, and F is the total free energy that includes the contributions from the Landau energy, the gradient energy, the elastic energy, and the electric energy:

$$F={\int}\!\!{\int\limits_{V}}\!\!{\int}({f}_{Land}({{P}}_{i})+{f}_{grad}({{P}}_{i,j})+{f}_{elas}({{P}}_{i},{\varepsilon }_{ij})+{f}_{ele}({{P}}_{i},{{E}}_{i}))dV.$$

(7)

The Landau energy density f_Land is given by,

$${f}_{Land}={{\alpha }}_{ij}{P}_{i}{P}_{j}+{{\alpha }}_{ijkl}{P}_{i}{P}_{j}{P}_{k}{P}_{l}+{{\alpha }}_{ijklmn}{P}_{i}{P}_{j}{P}_{k}{P}_{l}{P}_{m}{P}_{n},$$

(8)

where α_ij, α_ijkl, α_ijklmn are the Landau energy coefficients.

The gradient energy density f_grad can be described as follows,

$${f}_{grad}=\frac{1}{2}{G}_{ijkl}{P}_{i{,}j}{P}_{k{,}l},$$

(9)

where G_ijkl are the gradient energy coefficients, and ${P}_{i{,}j}=\partial {P}_{i}/{x}_{j}$.

The elastic energy density f_elas can be written as

$${{f}}_{{elas}}=\frac{1}{2}{{C}}_{{ijkl}}{{e}}_{{ij}}{{e}}_{{kl}}=\frac{1}{2}{{C}}_{{ijkl}}({{\varepsilon }}_{{ij}}-{{\varepsilon }}_{{ij}}^{{0}})({{\varepsilon }}_{{kl}}-{{\varepsilon }}_{{kl}}^{{0}}),$$

(10)

where C_ijkl is the elastic stiffness tensor, e_ij is the elastic strain, ε_ij and ${{\varepsilon }}_{{ij}}^{{0}}$ are the total local strain and eigenstrain, respectively. And ${{\varepsilon }}_{{ij}}^{{0}}={{Q}}_{{ijkl}}{{P}}_{k}{{P}}_{{l}}$, where Q_ijkl are the electrostrictive coefficients. In this study, only the linear elastic region is considered when simulating the low-field response of the polar spirals. Thus, the stresses applied in simulation do not exceed 12.0 MPa, which is lower than the assumed elastic constant by 2–3 orders of magnitude (Supplementary Table 3).

The electric energy density f_ele is expressed as,

$${f}_{ele}=-{E}_{i}\left({P}_{i}{+}\frac{1}{2}{{\varepsilon }}_{{0}}{{\kappa }}_{ij}{E}_{j}\right),$$

(11)

where E_i is the electric field component, ε₀ is the vacuum permittivity, and κ_ij is the dielectric constant.

The thickness and radius of simulated P(VDF-TrFE) nanodisk were 10 nm and 345 nm, respectively. The short circuit condition was applied in the simulation, and the temperature was set to be 25 °C. We used the finite element method to solve the TDGL equations, and the values of the parameters in the simulation are listed in Supplementary Tables 2 and 3.

Polarization analysis based on PFM measurements

To obtain the nominal toroidal order evaluated by the local curvature, the obtained IP-PFM amplitude image was firstly divided into 33 × 33 arrays, and each region was then subjected to a recognition of potential domain walls and measurement of an averaged curvature radius.

To obtain polarization maps, angle-resolved IP-PFM images were first aligned to correct spatial distortion in nanoscale measurement. Positions with specific morphological characteristics were selected as reference points to determine the coordinate. After the correction, improved angle-resolved IP-PFM phase images would be divided into 64 × 64 arrays for deriving polarization maps. We did not use the data from a single pixel to improve statics. Each region in the arrays was assigned with a local orientation in a range 180° according to the direction of measurement axis. By deducing the serial angle-resolved images on a same region but with rotated measurement axes, we refined the orientation of each point within a range of 45°, and defined its orientation to be along the angular bisector.

The curl, divergence and Laplace operator of the polarization vector field P were further calculated to illustrate the feature of polarization distribution in toroidal polar microregions. The curl vector describes the z component of ∇ × Ρ, also written as:

$$\nabla \times {{{{{\bf{P}}}}}}=(\partial {P}_{y}/\partial x-\partial {P}_{x}/\partial y)\hat{{{{{{\bf{z}}}}}}}$$

(12)

where z is the direction of film normal, and x-y plane describes the plane of PFM images.

Likewise, the divergence and the Laplace operator of P in x-y plane can be written as:

$$\nabla \cdot {{{{{\bf{P}}}}}}=\partial {P}_{x}/\partial x+\partial {P}_{y}/\partial y,$$

(13)

$$\Delta {{{{{\bf{P}}}}}}=({\partial }^{2}{P}_{x}/\partial {x}^{2}+{\partial }^{2}{P}_{x}/\partial {y}^{2})\hat{{{{{{\bf{x}}}}}}}+({\partial }^{2}{P}_{y}/\partial {x}^{2}+{\partial }^{2}{P}_{y}/\partial {y}^{2})\hat{{{{{{\bf{y}}}}}}}\, .$$

(14)

The partial derivatives of P mentioned above were calculated by a weighted least-squares fitting method. More specifically, the polarization component of the target point and its six surrounding points were fitted by first-order polynomial, given the Gaussian function f_W(d) as the weighting function:

$${f}_{W}(d)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left\{-\frac{{[(d/{d}_{0})\sigma ]}^{2}}{2{\sigma }^{2}}\right\}=\exp \left(-\frac{{d}^{2}}{2{{d}_{0}}^{2}}\right)$$

(15)

where σ is set to be $1/\sqrt{2\pi }$, d is the distance to the target point, and d₀ is the distance between two neighboring points.

To ensure that partial derivatives at every point are fitted with seven points, the distributions of ∇ × Ρ and ∇·Ρ are given in 58 × 58 arrays, the distributions of the x, y components of ΔΡ are given in 52 × 52 arrays. As a result, the ∇ × Ρ and ∇·Ρ exhibit double-spiral features (Supplementary Figs. 4 and 5), and the x, y components of ΔΡ display concentric ring-shaped features. The geometric center point (x_c, y_c) of the polar spiral was defined by the Laplace operator of P, which is given by:

$${x}_{c}={{\sum }_{x,y=7}^{58}\, x\cdot (\Delta {{{{{\bf{P}}}}}})}^{2}/{{\sum }_{x,y=7}^{58}(\Delta {{{{{\bf{P}}}}}})}^{2}$$

(16)

$${y}_{c}={{\sum }_{x,y=7}^{58}\, y\cdot (\Delta {{{{{\bf{P}}}}}})}^{2}/{{\sum }_{x,y=7}^{58}(\Delta {{{{{\bf{P}}}}}})}^{2}$$

(17)

The normalized electric toroidal moment and the normalized polarization flux of P are expressed as $\hat{{{{{{\bf{r}}}}}}}\times {{{{{\bf{P}}}}}}$ and $\hat{{{{{{\bf{r}}}}}}}\cdot {{{{{\bf{P}}}}}}$, respectively, where $\hat{{{{{{\bf{r}}}}}}}={{{{{\bf{r}}}}}}/|{{{{{\bf{r}}}}}}|$ represents the unit displacement vector from the center point to the local point. Both the normalized electric toroidal moment and the normalized polarization flux reveal double-spiral features (Supplementary Figs. 4 and 5).

To determine the field-induced changes in rotational angle of the polar spiral, we first conducted angle-resolved IP-PFM measurements and fitted the area encircled by the smallest and the second smallest domain wall versus the sample rotational angles. Since the shape of the polar spiral is unchanged during field-manipulation, the yielded fitting can be used as a reference to deduce the field-induced rotational angle. Succinctly, we measured the area encircled by the domain wall corresponding to the previous fit after the field application and compared it with the fit to obtain a characteristic angle. The characteristic angle difference between each state and the initial state would be assigned as the rotational angle of the field-manipulation. Another method we have used to determine the rotational angle is to perform angle-resolved IP-PFM measurements before and after the field-induced manipulation (insets in Fig. 2b, c and Supplementary Figs. 8 and 11). The rotational angle in each local polarization (Supplementary Fig. 13e, k) was calculated by comparing the polarization maps before and after the field-manipulation. The rotational angle of the field-manipulation was defined based on Gaussian fitting (Supplementary Fig. 13f, l). We compared the rotational angles obtained from both methods and found them to agree well with each other.

The above analysis has been implemented with the aid of a self-customized Matlab package.

Data availability

All relevant data in the main text or the supplementary materials are available from the corresponding authors upon reasonable request. Source data are provided with this paper.

Code availability

The codes within this paper are available from the corresponding authors upon reasonable request.

References

Durr, H. A. et al. Chiral magnetic domain structures in ultrathin FePd films. Science 284, 2166–2168 (1999).
Article CAS PubMed Google Scholar
Tang, Y. L. et al. Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO₃ films. Science 348, 547–551 (2015).
Article ADS CAS PubMed Google Scholar
Shinjo, T., Okuno, T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000).
Article ADS CAS PubMed Google Scholar
Wachowiak, A. et al. Direct observation of internal spin structure of magnetic vortex cores. Science 298, 577–580 (2002).
Article ADS CAS Google Scholar
Yadav, A. K. et al. Observation of polar vortices in oxide superlattices. Nature 530, 198–201 (2016).
Article ADS CAS PubMed Google Scholar
Rusu, D. et al. Ferroelectric incommensurate spin crystals. Nature 602, 240–244 (2022).
Article ADS CAS PubMed Google Scholar
Abid, A. Y. et al. Creating polar antivortex in PbTiO₃/SrTiO₃ superlattice. Nat. Commun. 12, 2054 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Muhlbauer, S. et al. Skyrmion Lattice in a Chiral Magnet. Science 323, 915–919 (2009).
Article ADS CAS Google Scholar
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Article ADS CAS PubMed Google Scholar
Das, S. et al. Observation of room-temperature polar skyrmions. Nature 568, 368–372 (2019).
Article ADS CAS PubMed Google Scholar
Yu, X. Z. et al. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 564, 95–98 (2018).
Article ADS CAS PubMed Google Scholar
Wang, Y. J. et al. Polar meron lattice in strained oxide ferroelectrics. Nat. Mater. 19, 881–886 (2020).
Article ADS PubMed Google Scholar
Woo, S. et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Article ADS CAS PubMed Google Scholar
Shafer, P. et al. Emergent chirality in the electric polarization texture of titanate superlattices. Proc. Natl Acad. Sci. USA 115, 915–920 (2018).
Article ADS CAS PubMed PubMed Central Google Scholar
Yadav, A. K. et al. Spatially resolved steady-state negative capacitance. Nature 565, 468–471 (2019).
Article ADS CAS PubMed Google Scholar
Damodaran, A. R. et al. Phase coexistence and electric-field control of toroidal order in oxide superlattices. Nat. Mater. 16, 1003–1009 (2017).
Article ADS CAS PubMed Google Scholar
Chen, P. et al. Atomic imaging of mechanically induced topological transition of ferroelectric vortices. Nat. Commun. 11, 1840 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Zhu, R. et al. Dynamics of Polar Skyrmion Bubbles under Electric Fields. Phys. Rev. Lett. 129, 107601 (2022).
Article ADS CAS PubMed Google Scholar
Han, L. et al. High-density switchable skyrmion-like polar nanodomains integrated on silicon. Nature 603, 63–67 (2022).
Article ADS CAS Google Scholar
Guo, M. et al. Toroidal polar topology in strained ferroelectric polymer. Science 371, 1050 (2021).
Article ADS CAS PubMed Google Scholar
Guo, M. et al. A pyrotoroidic transition in ferroelectric polymer. Matter 5, 3041–3052 (2022).
Article ADS CAS Google Scholar
Liu, Y. et al. Ferroelectric polymers exhibiting behaviour reminiscent of a morphotropic phase boundary. Nature 562, 96–100 (2018).
Article ADS CAS PubMed Google Scholar
Zhang, Z., Litt, M. H. & Zhu, L. Understanding the Paraelectric Double Hysteresis Loop Behavior in Mesomorphic Even-Numbered Nylons at High Temperatures. Macromolecules 50, 5816–5829 (2017).
Article ADS CAS Google Scholar
Zhang, Z., Litt, M. H. & Zhu, L. Achieving Relaxor Ferroelectric-like Behavior in Nylon Random Copolymers and Terpolymers. Macromolecules 50, 9360–9372 (2017).
Article ADS CAS Google Scholar
Lovinger, A. J., Davis, G. T., Furukawa, T. & Broadhurst, M. G. Crystalline forms in a copolymer of vinylidene fluoride and trifluoroethylene (52/48 mol %). Macromolecules 15, 323–328 (1982).
Article ADS CAS Google Scholar
Liu, Y. et al. Chirality-induced relaxor properties in ferroelectric polymers. Nat. Mater. 19, 1169–1174 (2020).
Article ADS CAS PubMed Google Scholar
Bokov, A. A. & Ye, Z. G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 41, 31–52 (2006).
Article ADS CAS Google Scholar
Govinden, V. et al. Spherical ferroelectric solitons. Nat. Mater. 22, 553–561 (2023).
Article ADS CAS PubMed Google Scholar
Lichtensteiger, C., Fernandez-Pena, S., Weymann, C., Zubko, P. & Triscone, J.-M. Tuning of the Depolarization Field and Nanodomain Structure in Ferroelectric Thin Films. Nano Lett. 14, 4205–4211 (2014).
Article ADS CAS PubMed Google Scholar
Soergel, E. Piezoresponse force microscopy (PFM). J. Phys. D Appl. Phys. 44, 464003 (2011).
Article ADS Google Scholar
Guo, M. et al. Flexible Robust and High-Density FeRAM from Array of Organic Ferroelectric Nano-Lamellae by Self-Assembly. Adv. Sci. 6, 1801931 (2019).
Article Google Scholar
Su, R. et al. Nano‐Ferroelectric for High Efficiency Overall Water Splitting under Ultrasonic Vibration. Angew. Chem. Int. Ed. 58, 15076–15081 (2019).
Article CAS Google Scholar
Cohen, R. E. Relaxors go critical. Nature 441, 941–942 (2006).
Article ADS CAS PubMed Google Scholar
Sangwan, V. K. & Hersam, M. C. Neuromorphic nanoelectronic materials. Nat. Nanotechnol. 15, 517–528 (2020).
Article ADS CAS PubMed Google Scholar
Li, S.-Q. et al. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science 364, 1087–1090 (2019).
Article ADS CAS PubMed Google Scholar
Liu, Y. et al. Optical Vector Vortex Generation by Spherulites with Cylindrical Anisotropy. Nano Lett. 22, 2444–2449 (2022).
Article ADS CAS PubMed Google Scholar
Wang, L. et al. Flexoelectronics of centrosymmetric semiconductors. Nat. Nanotechnol. 15, 661–667 (2020).
Article ADS CAS PubMed Google Scholar
Wang, B. et al. Mechanically induced ferroelectric switching in BaTiO₃ thin films. Acta Mater. 193, 151–162 (2020).
Article ADS CAS Google Scholar
Porter, D. A., Hoang, T. V. T. & Berfield, T. A. Effects of in-situ poling and process parameters on fused filament fabrication printed PVDF sheet mechanical and electrical properties. Addit. Manuf. 13, 81–92 (2017).
CAS Google Scholar

Download references

Acknowledgements

We thank Yuhan Liang, Yue Wang, and Fangyuan Zhu for discussions. The authors thank the beamline BL16B1 of Shanghai Synchrotron Radiation Facility for providing the beam time and discussion, and acknowledge Electron Microscopy Laboratory in Peking University for the use of electron microscopes. M.G. acknowledges support from the Shuimu Tsinghua Scholar Program and the Royal Society - Newton International Fellowship. This work was supported by Basic Science Centre Program of NSFC with the Grant No. 52388201 (C.-W.N.), the NSF of China with the Grant No. 52027817 (Y.S.), 52073155 (Y.S.), and 51972028 (H.H.), Tsinghua University Initiative Scientific Research Program with the Grant No. 20211080092 (Y.S.), and China Postdoctoral Science Foundation with the Grant No. 2022T150343 (M.G.).

Author information

These authors contributed equally: Mengfan Guo, Erxiang Xu, Houbing Huang.

Authors and Affiliations

State Key Lab of New Ceramics and Fine Processing, School of Materials Science and Engineering, Tsinghua University, 100084, Beijing, China
Mengfan Guo, Erxiang Xu, Hetian Chen, Shan He, Le Zhou, Jing Ma, Di Yi, Ce-Wen Nan & Yang Shen
Department of Materials Science, University of Cambridge, 27 Charles Babbage Road, CB3 0FS, Cambridge, UK
Mengfan Guo & Neil. D. Mathur
School of Materials Science and Engineering & Advanced Research Institute of Multidisciplinary Science; Beijing Institute of Technology, 100081, Beijing, China
Houbing Huang & Changqing Guo
Changsha Semiconductor Technology and Application Innovation Research Institute, College of Semiconductors (College of Integrated Circuits), Hunan University, 410082, Changsha, China
Shulin Chen
International School of Materials Science and Engineering, Wuhan University of Technology, 430070, Wuhan, China
Zhonghui Shen
Department of Graduate School, China Academy of Engineering Physics, 100193, Beijing, China
Ben Xu
Electron Microscopy Laboratory and International Center for Quantum Materials, School of Physics, Peking University, 100871, Beijing, China
Peng Gao
Center for Flexible Electronics Technology, Tsinghua University, 100084, Beijing, China
Yang Shen

Authors

Mengfan Guo
View author publications
You can also search for this author in PubMed Google Scholar
Erxiang Xu
View author publications
You can also search for this author in PubMed Google Scholar
Houbing Huang
View author publications
You can also search for this author in PubMed Google Scholar
Changqing Guo
View author publications
You can also search for this author in PubMed Google Scholar
Hetian Chen
View author publications
You can also search for this author in PubMed Google Scholar
Shulin Chen
View author publications
You can also search for this author in PubMed Google Scholar
Shan He
View author publications
You can also search for this author in PubMed Google Scholar
Le Zhou
View author publications
You can also search for this author in PubMed Google Scholar
Jing Ma
View author publications
You can also search for this author in PubMed Google Scholar
Zhonghui Shen
View author publications
You can also search for this author in PubMed Google Scholar
Ben Xu
View author publications
You can also search for this author in PubMed Google Scholar
Di Yi
View author publications
You can also search for this author in PubMed Google Scholar
Peng Gao
View author publications
You can also search for this author in PubMed Google Scholar
Ce-Wen Nan
View author publications
You can also search for this author in PubMed Google Scholar
Neil. D. Mathur
View author publications
You can also search for this author in PubMed Google Scholar
Yang Shen
View author publications
You can also search for this author in PubMed Google Scholar

Contributions

M.G. and Y.S. conceived and performed this study. M.G. and E.X. fabricated the films. C.G. and H.H. performed the phase-field simulations. H.C., B.X., and D.Y. performed the first-principle computations. S.C. and P.G. performed the TEM measurements. M.G., E.X., S.H., and J.M. performed the PFM measurements. M.G., E.X., L.Z., and Z.S. performed the field manipulation. M.G. and E.X. performed the AFM-IR measurements and wrote the first draft of the manuscript. Y.S., N.D.M., and C.–W.N. revised the manuscript. All authors discussed the results and edited the manuscript.

Corresponding authors

Correspondence to Mengfan Guo, Neil. D. Mathur or Yang Shen.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Le Lich, Ruijuan Xu and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Peer Review File

Description of Additional Supplementary Files

Supplementary Movie 1

Supplementary Movie 2

Supplementary Movie 3

Supplementary Movie 4

Supplementary Movie 5

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

Guo, M., Xu, E., Huang, H. et al. Electrically and mechanically driven rotation of polar spirals in a relaxor ferroelectric polymer. Nat Commun 15, 348 (2024). https://doi.org/10.1038/s41467-023-44395-5

Download citation

Received: 07 September 2023
Accepted: 12 December 2023
Published: 08 January 2024
DOI: https://doi.org/10.1038/s41467-023-44395-5

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.