Introduction

Lensless imaging is an elegant approach to high-resolution microscopy that is rapidly gaining popularity in applications where the use of imaging optics is problematic. This situation occurs, e.g. in imaging experiments using radiation at extremely short wavelengths, such as in the extreme-ultraviolet (XUV) and X-ray spectral ranges, for which the development of good-quality imaging optics is extremely complex.1,2 Another important application is in the development of miniaturized visible-light microscopes, to avoid the use of imaging optics to optimize the size and cost of the device.3,4

In lensless imaging, an object is illuminated by a coherent light source and the resulting diffraction pattern is recorded. An image of the object must then be reconstructed numerically; this can be performed by field propagation methods if both the intensity and phase of the diffraction pattern are known. As only the intensity is recorded in a typical diffraction measurement, the central issue in lensless imaging is the retrieval of phase information from a recorded diffraction pattern. Solutions to this problem have been found both through numerical and optical means.1,5,6 In coherent diffractive imaging, the missing phase information is numerically reconstructed by iterative algorithms,7 a process that has been shown to have a unique solution as long as the oversampling condition is satisfied.8 This condition can be satisfied by using a finite object support,9,10 a localized illumination profile11 and/or recording multiple partially overlapping diffraction patterns.12,13 Holographic methods, which directly record the phase through interference with a separate reference wave, have also been developed for a lensless imaging context.6,14

There is a growing need for lensless imaging methods that operate with broadband radiation, to make much more efficient use of such state-of-the-art light sources as third generation synchrotrons and table-top high-harmonic generation (HHG) sources for imaging. In particular, HHG-based sources hold promise for compact and cost-effective ultrahigh-resolution microscopy and recent breakthroughs have led to the generation of a significant photon flux in the biologically important water-window spectral range.15,16 However, HHG sources intrinsically produce an ultra-broadband soft-X-ray spectrum, and the need to spectrally filter these sources leads to a reduction in flux of 3–4 orders of magnitude, which severely limits their use for imaging applications. Several pioneering proof-of-concept experiments have already been performed with table-top HHG sources17,18,19,20,21,22 and the ability to use the full flux of such a source for imaging could provide a breakthrough for practical imaging applications.

In general, the use of monochromatic radiation has always been a major requirement for any diffractive imaging experiment, as the angle at which light diffracts from any structure depends on its wavelength. A diffraction pattern generated by a polychromatic source will therefore consist of a superposition of the diffraction patterns of all the individual spectral components.23 Depending on the spectral bandwidth of the source, this effect limits the achievable resolution24 and for more broadband sources, can inhibit image reconstruction entirely. By incorporating knowledge of the source spectrum into the reconstruction algorithm, discrete spectra23 and finite bandwidths25 can be handled. However, such calculations require a stable, accurately calibrated source spectrum and therefore, remains limited to relatively narrow spectral bandwidths (Δλ/λ≈0.028 has been shown25).

We demonstrate that all bandwidth limitations on lensless imaging can be removed by the illumination of the sample with two coherent time-delayed pulses (Figure 1a). If a series of diffraction patterns is recorded as a function of the time delay between the two pulses, methods from Fourier transform spectroscopy26 can be used to obtain spectrally resolved information from the recorded diffraction patterns themselves. No additional measurement of the source spectrum is required, and the spectrum may be ultra-broadband, highly structured and even exhibit significant intensity fluctuations (see the Supplementary Information for detailed simulations). Our two-pulse imaging method is universal and can be applied to any diffractive imaging experiment. In the following sections, we illustrate this with experimental demonstrations for both Fresnel and far-field diffraction, for transmission and reflection geometries and for diffractive imaging using an XUV HHG source.

Figure 1
figure 1

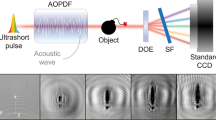
Principle of two-pulse imaging and experimental results in the Fraunhofer regime. (a) A sample is illuminated with two coherent pulses, and a set of diffraction patterns is recorded as a function of time delay T in a lensless imaging geometry. (b) A typical signal recorded on a single pixel during a coherent diffractive imaging experiment using two pulses, as a function of time delay T. (c) Fourier transform of the signal in b, showing the light spectrum diffracted onto that specific pixel. By reconstructing such spectra for all pixels, spectrally resolved diffraction patterns can be extracted throughout the full-source spectrum. (d) White-light microscope image of a laser-machined sample, containing transmitting structures in a gold layer. (e) Measured far-field diffraction pattern (log-scale) using the full-source spectrum. (f) Reconstructed diffraction pattern (log-scale) at 565 nm wavelength, retrieved from a two-pulse scan. (g) Overlay of three retrieved diffraction patterns (log-scale) at wavelengths of 508, 565 and 694 nm. (h) Result of iterative phase retrieval using the broadband diffraction pattern of e. No image can be retrieved due to the excessive spectral bandwidth. (i) Result of iterative phase retrieval using a diffraction pattern retrieved from the two-pulse scan (from f). (j) Overlay of three independent reconstructed images from the diffraction patterns in g, which all show good-quality images of the sample. The field of view is wavelength-dependent, resulting in a different image size for each wavelength.

Full size image

Materials and methods

Two-pulse imaging with an ultra-broadband source

When performing lensless imaging with an ultra-broadband source, the recorded ultra-broadband diffraction patterns can be interpreted as a linear superposition of monochromatic diffraction patterns. Knowledge of the superposition coefficients would therefore enable the spectral decomposition of the diffraction patterns into their individual spectral components. In practice, this approach means that we need a way to measure the distribution of the spectral components that have scattered onto each camera pixel (see Supplementary Information and Supplementary Fig. S1 for details). The key point of our method is that the spectral decomposition of the diffraction patterns can be achieved by recording the scattering signal for each individual camera pixel as a function of the pulse-to-pulse time delay (Figure 1b). For each pixel, this delay time-dependent signal is equal to the Fourier transform of the spectrum of the light scattered onto that individual pixel. Therefore, a Fourier transform converts it back to the frequency domain and reveals the spectral components scattered onto each pixel (Figure 1c). With this information, spectrally resolved diffraction patterns can be reconstructed throughout the entire source spectrum from a single time delay scan (see Supplementary Information for details). The spectral resolution is inversely proportional to the scanned time delay, similar to Fourier transform spectroscopy.26 A powerful feature of this approach, common to many Fourier transform-based methods,26,27,28 is that the full-source spectrum is used throughout the entire measurement, resulting in an efficient use of the available photon flux.

Two-pulse imaging in the Fraunhofer regime

For the first experimental example of two-pulse imaging at visible wavelengths, we use a spatially coherent octave-spanning continuum as the light source. Two time-delayed pulses are generated in a scanning Michelson interferometer and sent into a lensless imaging set-up (Supplementary Fig. S2). Coherent white-light continuum pulses are produced by launching ultrashort laser pulses into a photonic crystal fiber. A time-delayed pulse pair is produced using a Michelson interferometer, with one of the end mirrors mounted on a closed-loop piezo stage. The pulse pair is then used to illuminate a sample, and the diffracted light is recorded using a 14-bit CCD camera with 1936×1456 pixels and 4.54 µm pixel size. We typically acquire 500 individual images with 0.01–1 ms exposure times, while increasing the time delay in 0.67 fs (200 nm) steps.

As a proof-of-concept experiment, we image the test sample shown in Figure 1d, which consists of some small structures that have been laser-etched in a gold layer deposited on a glass substrate. We achieve far-field conditions by positioning the CCD camera 5 cm behind an f=5 cm lens located behind the sample, which ensures both a far-field imaging geometry and a moderate numerical aperture for visible wavelengths.

Results and discussion

The measured diffraction pattern using the full-source spectrum is shown in Figure 1e. A strong radial smearing is present: owing to the wavelength-dependent diffraction angle, each point in the diffraction pattern is convolved with a large spectral bandwidth in the radial dimension. However, from the two-pulse scan and the Fourier transformation, quasimonochromatic diffraction patterns are obtained (Figure 1f) in which the radial structure of the diffraction pattern is clearly resolved. The spectral bandwidth of these retrieved images is determined by the length of the two-pulse scan, and it can readily be made sufficiently small (by a longer delay scan) to treat the images as monochromatic. Figure 1g shows an overlay of three diffraction patterns at different wavelengths, obtained from a single two-pulse scan. The dramatic improvement in image reconstruction is clearly visible from Figure 1h–1j, in which an iterative phase retrieval algorithm is applied to retrieve an image from the diffraction patterns in Figure 1e–1g. For the phase retrieval, a support is defined from the autocorrelation of the diffraction pattern, after which 300 iterations of the error reduction algorithm10 are used with a random initial phase guess. The algorithm is run 20 times and the results are averaged into the final image. Because of the low coherence in the unresolved broadband diffraction pattern of Figure 1e, the requirements for applying Gerchberg–Saxton-type iterative phase retrieval algorithms are not satisfied and the resulting image (Figure 1h) is extremely poor. In stark contrast, the image reconstructed from the two-pulse scan (Figure 1i) is a high-quality image of the test object, with a diffraction-limited resolution of 6 µm (limited by the numerical aperture of 0.046). Three reconstructions at different wavelengths, corresponding to the diffraction patterns shown in Figure 1g, are overlaid in Figure 1j. All the reconstructions provide a clear image of the test object, but their relative sizes are different due to the wavelength-dependent field of view discussed above. After appropriate scaling, all these images can be averaged to improve the final signal-to-noise ratio. In this case, the full-source spectrum is used efficiently for image reconstruction.

Multiwavelength phase retrieval

The spectrally resolved diffraction data also suggest new possibilities for fast and robust phase reconstruction, based on the propagation effects in coherent diffractive imaging in the Fresnel regime. In the far-field (Fraunhofer) regime discussed above, the only effect of propagation is a global scaling of the diffraction pattern. However, in the Fresnel regime, there is an additional propagation and wavelength-dependent spatial phase evolution. This propagation-dependent phase evolution can be exploited for more robust phase retrieval strategies, based on the knowledge of the wavefront curvature29,30,31 or by performing measurements at multiple sample-to-camera distances.32,33

We have developed a novel iterative phase retrieval scheme that explicitly uses the recorded multiwavelength data to reconstruct the phase without the need for support constraints. In the Fresnel regime, wave propagation couples the amplitude and phase of an electric field E(x,y,z) through the Fresnel diffraction integral:

where propagation is along the z-coordinate and λ is the wavelength of the light. Equation (1) states that Fresnel propagation depends on the distance and wavelength in an identical way (aside from a global phase factor), allowing us to exploit our spectrally resolved diffraction data to ‘propagate’ between different spectral components, as schematically depicted in Figure 2a. This scheme does not require sample or camera movement and relies only on measured diffraction patterns at multiple wavelengths as input. It converges reliably and works for extended samples. Keyhole imaging11,34 and ptychography12,13 have also been used successfully to image parts of extended samples, but our multiwavelength approach does have the advantage that spatially confined illumination is not required for stable convergence.

Figure 2
figure 2

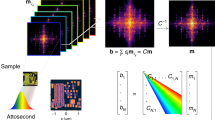
Multiwavelength phase retrieval in the Fresnel regime. (a) Graphic representation of the multiwavelength phase retrieval algorithm. Iterative propagation is performed between Fresnel diffraction patterns recorded at the same distance, but with different wavelengths. (b) Broadband Fresnel diffraction pattern of Convallaria majalis rhizome, recorded using an octave-wide visible light source. (c) Quasimonochromatic Fresnel diffraction pattern of the same Convallaria sample as in b, obtained from a two-pulse imaging scan. Much finer diffraction features are visible. (d) Resulting image after 25 iterations of multiwavelength iterative phase retrieval, using diffraction patterns at five different wavelengths. (e) Close-up of a part of the reconstructed image, clearly showing the individual cells. The intensity scale bar in d also applies to this image.

Full size image

To demonstrate this multiwavelength phase retrieval approach, we record two-pulse scans of Fresnel diffraction patterns of a fixed sample of Convallaria majalis (Lily of the Valley) rhizome, of which a broadband diffraction pattern is shown in Figure 2b. Figure 2c shows a narrow-band (Δλ=5 nm) diffraction pattern of this Convallaria sample at a wavelength of 695 nm, which has been extracted from a two-pulse imaging scan. Sharp diffraction features are clearly visible, whereas they were washed out in the broadband images.

For our multiwavelength Fresnel reconstruction method, phase retrieval is performed in a Gerchberg–Saxton-type iterative scheme, where the intensity data from the first wavelength are propagated to the next wavelength through the evaluation of the Fresnel propagation Equation (1). After propagation, the phase information is retained, while the intensity is replaced with the measured intensity at this new wavelength. A detailed description of the multiwavelength phase retrieval algorithm is provided in Supplementary Information. The choice of wavelengths to be used in the reconstruction is flexible: the main requirement is that they be sufficiently spectrally separated to display significant differences after propagation over a distance z, i.e., the phase term inside the integral in Equation (1) should change by a measurable amount between wavelengths for a detector pixel at position (x,y). This phase shift condition depends on the detection geometry and is readily fulfilled in practice. We typically select 2–5 images separated by 5–20 THz in frequency from the spectrally resolved dataset for iterative phase retrieval. The algorithm converges rapidly, typically requiring only 10–50 iterations to reach its final solution. While the algorithm already works with two images, the use of more wavelengths usually provides superior results. When more wavelengths are used, the algorithm averages over more independent datasets, causing any noisy pixels in a single image to be less influential.

The multiwavelength phase retrieval algorithm results in a high-quality image reconstruction, which is displayed in Figure 2d. Because the sample fills most of the field of view (FOV) and consists of dark structures on a bright illuminated background, the oversampling condition is not satisfied and support-based phase retrieval algorithms would not provide a solution in this situation. In contrast, our multiwavelength algorithm enables image reconstruction at instrument-limited resolution, clearly showing the individual cells as well as some subcellular features (Figure 2e). After the phase has been retrieved, all spectrally resolved images can be propagated to the object plane and averaged to improve the signal-to-noise ratio, resulting in an efficient use of the full-source spectrum. The resolution of this reconstruction is then determined by the imaging geometry and the weighted mean of the spectral bandwidth.

The main prerequisite of our multiwavelength phase retrieval approach is that the phase profile of the object has the same spatial structure for the spectral components used in the reconstruction. However, it should be stressed that the phase does not need to be constant as a function of wavelength: a known wavelength-dependent refractive index can be readily incorporated into the algorithm, as its incorporation requires only an additional refractive index-dependent multiplication factor upon propagation between different wavelength images. Therefore, our multiwavelength phase retrieval approach extends to dispersive samples and can be used for lensless imaging with short wavelengths. Wavelength-dependent differences in absorption result in different signal intensities for the respective images, while still providing a good-quality reconstruction. Only in the case where the phase images are qualitatively different at the different wavelengths, e.g., due to an elemental absorption edge between the wavelengths used, would the algorithm not converge. In this case, support-based iterative phase retrieval schemes can still provide image reconstruction, provided that the object meets the oversampling requirements for such algorithms to converge.7

Lensless imaging in reflection

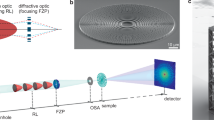
In addition to transmission imaging, lensless imaging in a reflection geometry is important for many applications in nanoscience and technology.2,35 The need for a finite support is particularly challenging to satisfy for reflection geometries,36 which have therefore relied mostly on finite-beam-size methods such as ptychography. In contrast, our multiwavelength approach enables the imaging of large areas of extended samples in a reflection geometry (Figure 3a). Figure 3b shows a spectrally resolved Fresnel diffraction pattern, retrieved from a two-pulse scan in the reflection of a USAF 1951 test target. The reconstructed image obtained through multiwavelength phase retrieval is shown in Figure 3c, demonstrating the ability to image large reflective samples without support requirements.

Figure 3
figure 3

(a) Lensless imaging in a reflection geometry. (b) Quasimonochromatic Fresnel diffraction pattern of a 1951 USAF test target, recorded in a reflection geometry and obtained through a two-pulse Fourier-transform scan. (c) Resulting image after 25 iterations of the multiwavelength iterative phase retrieval, using diffraction patterns at five different wavelengths. The dark (negative) features are due to reflections from the sample's back surface. The dashed red line marks the area in which all wavelengths contribute to the reconstruction. (d) Reconstructed height map from part of the USAF target surface from b showing the chrome structures on the glass substrate. USAF, United States Air Force.

Full size image

In a coherent diffractive imaging experiment, the achievable diffraction-limited resolution is determined by the wavelength of the light and the numerical aperture of the detection geometry (i.e., the size of the camera and the sample-to-camera distance). In the Fresnel geometry, the CCD pixel size also influences the final resolution. This resolution defines the distance between adjacent sampling points and the FOV is then determined by this distance multiplied by the number of pixels in each dimension. Therefore, the FOV is also wavelength-dependent. Consequently, when three diffraction patterns of an object are recorded at different wavelengths, the shorter wavelength pattern will have a slightly smaller FOV than the longer wavelength patterns. In the reconstruction, the FOV will therefore be limited by the shortest wavelength used. This limitation is illustrated in Figure 3c, where the red dashed line indicates the FOV for the shortest wavelength. Outside this line, not all wavelengths contribute to the reconstruction, which results in aberrations.

In general, the iterative phase retrieval algorithm provides accurate phase information. If the diffraction comes from a pure surface reflection, this phase information can be used to reconstruct a height map of the sample. Figure 3d displays a height map of the test target that has been retrieved in this way, clearly showing the 100 nm thick chromium lines deposited on a glass substrate. The phase retrieval algorithm already provides a height resolution of ∼20 nm, which can be increased further by improving the signal-to-noise ratio in the measurement. In this sample, a small reflection from the sample’s back surface was also present, resulting in an additional image that appears negative and shifted. Interference between these two surface images has some influence on the reconstructed phase, which would not be the case for a pure single surface reflection. Note that this measurement is of the optical path length, so that the refractive index of an immersion liquid or phase shifts due to partial reflection should be taken into account when calculating the geometrical height from the retrieved phase.

Ultra-broadband XUV imaging

To demonstrate that our two-pulse imaging approach extends to shorter wavelengths, we perform an imaging experiment with a HHG source. A schematic of the set-up is shown in Figure 4a: the pulse pair is produced in the near infrared with a split-wavefront interferometer in front of the HHG set-up, using quartz wedges to scan the time delay. This particular interferometer implementation is highly stable: it is nearly a common path and there are no mirrors in the set-up that reflect only one of the pulses. These properties eliminate most of the noise caused by vibrations, air flow and acoustics present in conventional Michelson interferometers. We use a 1° wedge to scan the delay, mounted on a closed-loop piezo-stage with 5 nm resolution and a 500 µm scan range. A 100 nm movement of the stage results in a 1.32 nm optical path length difference between the pulses, enabling scans with subnanometer step size.

Figure 4
figure 4

Lensless imaging with ultra-broadband extreme-ultraviolet radiation. (a) Schematic of the set-up for two-pulse imaging with high-harmonic radiation. A variable time delay is introduced by inserting a wedge into the beam (note that this drawing is only for schematic purposes: the actual orientation of the wedges is rotated by 90° with respect to this drawing). (b) Broadband diffraction pattern of a nickel grid on a 300 nm thick Al foil, recorded using harmonics 13, 15 and 17. (c) Spectrum extracted from the two-pulse Fourier transform scan. (d) Retrieved image of the Ni grid at 47 nm wavelength, using the multiwavelength phase retrieval algorithm. The regular features of the grid are clearly visible, as are several damage spots induced by intense laser irradiation in earlier experiments. (e) Enlarged view of part of the image in d, showing the 20 µm wide grid lines. (f) Cross-section of the intensity along the red bar in e (red trace), together with a simulated curve of a square bar convolved with the expected diffraction limited point-spread function (black trace). (g) Phase image of the grid retrieved by the multiwavelength phase retrieval algorithm.

Full size image

A single wedge in the other interferometer arm introduces an angle between the beams. The lens (focal length F) that focuses the pulses into the HHG gas cell is placed at a distance F behind the point where the beams cross. This geometry ensures that the two beams run parallel to each other behind the lens. Both beams focus near the end of the gas cell with a small transverse separation between the focal spots. Thus, ionization due to the first pulse does not influence the HHG process for the second (time-delayed) pulse, allowing linear Fourier transform scans at HHG frequencies.37 The HHG pulses overlap spatially at the imaging target due to their beam divergence. The focal length F is 350 mm and the focal spot diameter is 40 µm full width at half maximum. Harmonics are produced in xenon gas at ∼50 mbar pressure in the gas cell, with an energy of 0.2 mJ in each 40 fs duration pulse. Behind the cell, a differential pumping stage is used to prevent the re-absorption of the produced HHG. Scanning the time delay was performed by moving a wedge into one half of the beam, enabling scans with subnanometer position accuracy.

We use the full HHG flux directly to image a nickel grid, with 20 µm wide bars, attached to a 300 nm thick aluminum foil. The Al foil reflects the fundamental beam while transmitting radiation at a wavelength below 80 nm. In this experiment, the nickel grid is placed 40 cm behind the focus. The diffracted light is detected in a transmission geometry using an XUV-sensitive CCD camera (Andor Technology, Belfast, Northern Ireland) with 1024×1024 pixels, a pixel size of 13 µm and a bit depth of 12 bits. This camera is placed 0.6 m behind the sample. In a typical Fourier transform scan, 512 diffraction images are recorded as a function of the time delay. Between consecutive images, the time interval is increased in steps of 44 attoseconds (corresponding to a physical step size of 13.2 nm). At each time step, five frames are recorded with 0.3 s exposure times and averaged to improve the signal-to-noise ratio.

Figure 4b displays a broadband diffraction pattern of the nickel grid recorded with the transmitted HHG spectrum. Figure 4c shows the HHG spectrum used in these imaging experiments, which is obtained from the two-pulse scan itself. Three harmonics are present, spanning a wavelength range between 47 and 63 nm. Lower harmonics are not transmitted by the Al foil and the xenon gas, while the HHG phase-matching cutoff is near harmonic 17. For the HHG phase retrieval, we use images at harmonics 13, 15 and 17 (center wavelengths 62 nm, 53 nm and 47 nm, respectively) as input for the multiwavelength phase retrieval algorithm. At each harmonic, we filter out a spectral bandwidth of 1.5 nm, which suffices to achieve diffraction-limited resolution in this experiment. Typically, only 10 iterations of the algorithm are required for stable convergence.

Due to the transverse displacement between the two HHG pulses, the recorded data contain two displaced copies of the object's diffraction pattern. This factor can be accounted for by incorporating an additional deconvolution step in the image reconstruction procedure, as the image at each wavelength can be interpreted as the convolution between a single diffraction pattern of the object and a pair of Dirac delta functions. The distance between these Dirac delta functions is calculated from the imaging geometry and the initial separation between the focal spots in the gas cell. The single diffraction patterns can then be retrieved from the spectrally resolved images by deconvolution. The resulting diffraction patterns can then be used in the multiwavelength phase retrieval algorithm. Small angular deviations between the two beams can also be handled, enabling two-pulse imaging even with non-collinear beams from a split-wavefront interferometer.38,39

The resulting reconstructed image of the Ni grid is shown in Figure 4d and 4e. To quantify the image resolution, the image intensity across one of the nickel bars is plotted in Figure 4f. This cross-section is compared to a simulation of the known shape of the bar convolved with a sinc-shaped point-spread function corresponding to the diffraction-limited half-pitch resolution of 6.7 µm. Good agreement is obtained, from which we deduce that the retrieved image resolution is near the diffraction limit for the sample-camera distance used. A small artifact from imperfect deconvolution can be observed in the form of a shadow image (with an intensity of a few percent) on both sides of the main image. Furthermore, some subtle vertical interference fringes are observed in the reconstructed image in Figure 4d, mainly at the right edge of the beam. These fringes are likely caused by imperfections in the incident XUV wavefront. In addition to the regular Ni grid, several dark damage spots are observed, which were caused in earlier experiments with intense laser pulses that partially melted the nickel structures. In addition to the reconstructed intensity image, the retrieved phase profile at 47 nm wavelength is shown in Figure 4g. A relatively constant phase is obtained for the gaps between the nickel bars, while the phase at the position of the bars shows large variations. This observation is explained by the negligible light intensities at the locations of the bars, which are 5 µm thick and do not transmit XUV radiation. Therefore, the phase at these positions is undefined. While the diffraction limit in the current proof-of-concept experiment was relatively low due to geometrical constraints, a much higher resolution can readily be achieved in Fresnel diffractive imaging by illuminating the sample with a curved wavefront,11,29 which is fully compatible with our two-pulse imaging approach.

Conclusions

In summary, we have presented two-pulse imaging as a method that enables lensless microscopy with ultra-broadband light sources. The full spectrum is efficiently used for imaging, making this approach well suited for XUV imaging with compact, low-flux, broadband sources such as table-top HHG systems.

In addition, we have introduced a new approach to robust phase retrieval for lensless imaging in the Fresnel regime, based on the use of diffraction patterns at multiple wavelengths in an iterative phase retrieval scheme. This method provides stable and rapid convergence even for complex samples, without requiring any support constraints or localized illumination. This multiwavelength phase retrieval approach can readily be used with the spectrally resolved data obtained through two-pulse imaging and we have demonstrated its use in both transmission and reflection.

We find that two-pulse imaging enables robust and accurate lensless imaging with broadband and unstable spectra, without a priori knowledge of the spectrum for image reconstruction. This situation is often encountered with HHG sources, where the efficient use of the available photon flux is essential for practical imaging applications. We have performed numerical simulations to study the influence of intensity and timing variations in greater detail (Supplementary Fig. S4 and Supplementary Information) and the simulations indicate that good-quality images can be obtained even in the presence of significant noise. From our measurements, we find a pulse delay stability of 8 nm without active stabilization (Supplementary Fig. S3 and Supplementary Information), which is sufficient for imaging at wavelengths down to 16 nm. With additional stabilization measures,40 an extension to the soft-X-ray domain should be feasible. We therefore foresee that two-pulse imaging will find widespread application in the development of compact table-top HHG-based microscopes, thus providing new possibilities for, e.g., structural biology and nanotechnology by enabling label-free ultrahigh-resolution microscopy in a laboratory-scale environment.